Il punto non ha dimensioni. Una linea è monodimensionale, una superficie è bidimensionale, un volume si estende nelle tre dimensioni. Su questi pilastri della geometria euclidea si è basato tutto lo sviluppo della scienza e della tecnologia, sino ai nostri tempi.

In particolare, il connubio tra geometria e matematica, che parte dalle coordinate cartesiane per arrivare ai sistemi di equazioni differenziali alle derivate parziali, passando attraverso il concetto di funzione ed il calcolo differenziale ed integrale, ha portato alla realizzazione di opere d'ingegneria di altissimo livello, dai grattacieli ai ponti sospesi di lunghezze impressionanti.

Tuttavia, quando strutture di questo tipo, o anche più semplicemente un normale edificio, vengono inserite in un contesto naturale, il nostro occhio è immediatamente in grado di riconoscere la mano dell'uomo, tanto sono diverse dall'ambiente circostante. Ne apprezziamo l'essenza geometrica, ma la geometria della natura circostante è chiaramente diversa.

La geometria dell'uomo......... .......e quella della natura	Spesso ne nasce un conflitto estetico: troppi progetti di costruzioni, agili ed eleganti sulla carta, si sono rilevati stonati al momento della realizzazione.
	Di contro, alberi, nuvole e ruscelli sono strutture, disordinate forse ma certamente non casuali, piacevoli a vedersi ma la cui geometria ci sfugge: non siamo in grado di comprenderla appieno, né tanto meno di descriverla matematicamente in maniera semplice.

Che cosa c'è di sbagliato?

J.D.Barrow (1) scrive: "Nel corso di migliaia di anni, la concezione scientifica del mondo ha concentrato la propria attenzione sulla semplicità e le regolarità della Natura. [Ma] più che nella struttura degli eventi intorno a noi, le regolarità sono state trovate nelle leggi che li governano".

Il fatto che leggi semplici possano dar luogo a strutture complesse, in presenza di meccanismi di retroazione non lineari, è una recente scoperta della teoria del caos (2), ed il parallelo sviluppo della geometria dei frattali permette ora una maggior comprensione della natura.

Ma cos'è esattamente un frattale?

Per inquadrare il problema è opportuno riferirsi ad una ormai classica domanda posta da B.B. Mandelbrot (3), il "padre" dei frattali: quanto è lunga la costa della Gran Bretagna?

Per restare in ambienti più vicini a noi, potremmo calcolare la distanza, lungo la costa, da Genova ad Imperia.

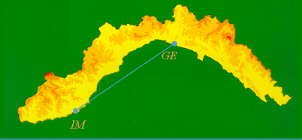In linea d'aria le due città distano circa 60 km, ma la lunghezza della costa è certamente maggiore.

L'orario delle FFSS indica una distanza di 115 km, e su questa distanza paghiamo il biglietto. Ma certamente il treno non segue tutte le anfrattuosità della costa: quando può tira dritto, spesso in galleria.

In realtà, la lunghezza della costa da Genova ad Imperia dipende dall'unità di misura (passo).

Siamo di fronte ad un paradosso: quanto più la misura diventa precisa tanto più il risultato diverge, minando alle fondamenta le basi del calcolo differenziale, non più applicabile nella sua interezza se le strutture sono di questo tipo, se sono cioè frattali.

Tuttavia, se pur irregolari, le curve frattali presentano un'intima regolarità, basata su un concetto profondo, quello dell'invarianza di scala.

Come punto di partenza, potremmo descrivere un frattale come una struttura che rimane simile a se stessa, a qualunque scala la si osservi.

Pensiamo ad esempio ad un ramoscello piantato nel muschio di un presepio, ed a quanto bene simuli un albero: tutta l'informazione strutturale dell'albero nel suo complesso è racchiusa nell'ultimo dei suoi ramoscelli terminali (4).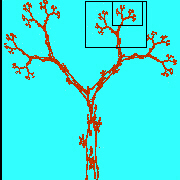

In maniera del tutto analoga, in assenza di un elemento di riferimento (B, cerchio giallo), non sapremmo dire la fotografia di una roccia inquadri un'area di diversi metri quadri o di poche centimetri quadrati. (96K)

Una curiosa applicazione dei concetti di invarianza di scala è uno spot pubblicitario di questo periodo, per una Società che si occupa di crociere: "C'è solo una vacanza che ha dentro un'altra vacanza, che ha dentro un'altra vacanza............."

In ambito urbanistico, l'invarianza di scala è poi una caratteristica di molte città: zoomando dall'alto potremo distinguere approssimativamente una zona commerciale e/o industriale, una zona residenziale, una zona a verde ed una zona libera per ulteriori sviluppi. Ma nella zona residenziale, ad esempio, potremo facilmente individuare una zona a verde, una zona commerciale, una zona abitativa ed una parte con i soliti lavori in corso ..... e così via, sino all'interno di una singola abitazione, con la sua cucina (zona industriale), il suo soggiorno (zona a verde), la camera da letto (zona abitativa) e naturalmente soliti lavori in corso. Da un raggio di diversi chilometri sino a pochi metri, la struttura si ripete, sempre simile a se stessa (5).

Certo, a livello urbanistico non è obbligatorio seguire questo schema, ed è possibile progettare città a scacchiera, a stella o a nido d'ape, con tutti i negozi di qua e tutto il verde di là, ma i risultati potrebbero essere pesanti a livello psicologico per gli abitanti.

Quali esempi di edifici modellati sui principi dell'invarianza di scala, si possono citare le cattedrali gotiche (6), con la stessa struttura che si ripete sino nei minimi particolari (23 K)

oppure la Torre Eiffel, non a caso uno dei pochi edifici moderni che possono assurgere al ruolo di simbolo di un'intera città, con la sua struttura che riecheggia un classico frattale, il triangolo di Sierpinski.

Ma la geometria dei frattali non si estrinseca soltanto a livello qualitativo, sebbene l'aspetto matematico sia diverso da quello classico. Supponiamo di avere due cerchi di raggio diverso. Il primo, con raggio R, avrà un'area A(R) pari a p R², ed il secondo, di raggio nR avrà un'area A(nR) pari a n²pR². Potremo perciò scrivere un'equazione funzionale del tipo

il che è un modo un po' complicato di dire che un cerchio è un oggetto bidimensionale. Per una linea, D=1 e per una sfera o un cubo D=3, come il lettore può agevolmente verificare.

La stessa relazione vale per gli oggetti frattali, ma in questo caso D non è un intero: questo tipo di strutture ha una dimensione frazionaria che le caratterizza.

L'equazione [1] o particolari algoritmi da essa derivati vengono comunemente usati per il calcolo della dimensione frattale (7).

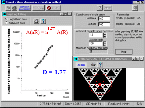Riportando in un grafico bilogaritmico i valori dell'area, ottenuti sperimentalmente, in funzione della risoluzione (raggio) è possibile calcolare il valore di D dalla pendenza della retta interpolante (8). Il triangolo di Sierpinski della figura, ad esempio, ha un valore di D pari a 1,77 e si pone per così dire in una via di mezzo tra una linea monodimensionale ed una superficie bidimensionale.

Similmente, il disegno della cattedrale riportato precedentemente ha un valore di D pari a 1.6, ed in qualche modo la sua struttura riecheggia quella del triangolo di Sierpinski, mentre l'albero stilizzato ha una dimensione frattale pari a circa 1.4.

Si noti che nell'equazione funzionale [1] sopradescritta il parametro D si colloca come esponente, cosicché piccole variazioni possono influire pesantemente sui valori computati delle aree.

Se fotografiamo un insieme di pietre, come il brecciolino in figura (142 K), e sottoponiamo l'immagine al computo delle aree, otteniamo un andamento lognormale, ossia una distribuzione che approssima la distribuzione frattale. Tale approssimazione è dovuta al fatto che il principio di invarianza di scala si dovrebbe estendere per diversi ordini di grandezza (dai decimi di millimetro ai metri), ma l'immagine digitalizzata in figura non copre estremi così ampi.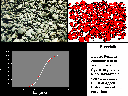

Nel muro di pietre a destra l'andamento lognormale è ancora rispettato (136K),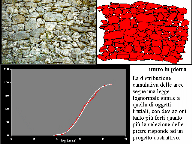

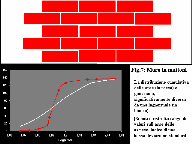ma il muro di mattoni (37K) ha una distribuzione definitivamente diversa (trattandosi in realtà di un andamento gaussiano). Per non parlare di un muro di cemento, che non ha alcuna struttura.

E' per questo motivo che i muri a secco, così comuni nelle fasce liguri, si inseriscono in maniera molto più "naturale" nel paesaggio, mentre la cementificazione provoca danni estetici dalle conseguenze spesso pesanti.

Come secondo esempio di applicazione della geometria dei frattali, pensiamo ad un grafico termoigrometrico.

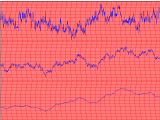Le variazioni di temperatura o di umidità relativa hanno una struttura chiaramente irregolare, e se sottoponiamo i dati ad un'analisi statistica classica (media e deviazione standard) possiamo ottenere risultati fuorvianti: in questa figura le tre curve hanno la stessa media e deviazione standard ma un andamento del tutto diverso.

In questi casi, è prassi comune valutare, oltre agli indici statistici precedentemente indicati, anche altri parametri, quali la media mobile, la distribuzione cumulativa delle fluttuazioni, la trasformata di Fourier. Questi parametri, tuttavia, implicano la presentazione di grafici con un numero di dati dello stesso ordine di grandezza dei dati originali, vanificando così la compressione dell'informazione in pochi indici.

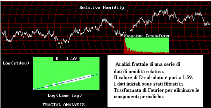L'analisi frattale (9) riportata in figura (16K), evidenzia invece immediatamente la struttura della curva. La conoscenza dei valori di media, deviazione standard e dimensione frattale permette un'immediata ricostruzione mentale o matematica (9) dell'andamento reale dei dati e delle fluttuazioni in essi presenti.

In tale analisi, paradossalmente, è opportuno ripulire i dati dalle regolarità giornaliere e stagionali, filtrando gli stessi in trasformata di Fourier, in quanto proprio tali regolarità, sinora ricercate dagli statistici, deformano l'andamento del grafico bilogaritmico tratto dall'applicazione dell'equazione [1] e possono inficiare la valutazione della dimensione frattale.

La diffusione di strutture simili ai profili termici o igrometrici è riportata nelle rielaborazioni delle figure successive, che usano analoghi profili per simulare

un tratto di costa che si protende nel mare (26K),

e, rovesciando la figura, una montagna contro il cielo (81K)

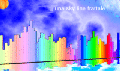e persino la sky-line di Manhattan (99K),

non a caso, insieme alla Torre Eiffel, una struttura moderna conosciuta in tutto il mondo.

L'andamento frattale di queste curve è tipicamente un "rumore 1/f" (10), irregolare ma non casuale, che trova molte applicazioni in campi diversi, dall'andamento del traffico in città (11) alle fluttuazioni della Borsa (12), alle raffiche di errori nel campo delle telecomunicazioni (13).

Sorprendentemente, è stato recentemente valutato che la musica stessa è un "rumore 1/f" (14), e siamo ora in grado di rispondere all'antica domanda di Platone: "Se le arti rappresentano la natura, la musica che cosa rappresenta?".

Semplicemente, la musica rappresenta il modo in cui la natura si evolve e la vita combatte la sua battaglia contro l'apparentemente inesorabile legge dell'entropia.

Certamente, sebbene la teoria dei frattali non proponga attualmente pronte ricette a livello architettonico, sarebbe tuttavia opportuno che la cultura sottostante venisse assorbita, soprattutto da parte di chi è deputato dalla collettività a prendere decisioni che si riflettono inevitabilmente sull'antropizzazione dell'ambiente che ci circonda.

Riferimenti:

1) J.D.Barrow, "L'Universo come opera d'arte", RCS Rizzoli Libri (Milano 1997), p.309. (up)

2) Per un'esposizione semplice e di piacevole lettura della teoria del caos, vedi J.Gleick, "Caos - La nascita di una nuova scienza", RCS Rizzoli Libri (Milano 1989); per un approfondimento fisico e matematico vedi i riferimenti ivi riportati. (up)

4) L'algoritmo di costruzione della figura è tratto da H.Jurgens, H-O.Peitgen & D.Saupe, Il linguaggio dei frattali, Le Scienze 266 (ott.1990), 42-49. (up)

6) L'algoritmo di costruzione della figura è tratto da P.Sommaruga, Modelli frattali di oggetti naturali, Le Scienze 282 (feb.1992), 36-44. (up)

7) Per gli aspetti computazionali e le molte applicazioni pratiche della teoria dei frattali vedi ad esempio B.H.Kaye, "A Random Walk Through Fractal Dimensions", WCH (Weiheim 1989). (up)

8) Per un'applicazione a livello molecolare vedi: D.Farin & D.Avnir, The fractal nature of molecule-surface interactions and reactions, in "The Fractal Approach to Heterogeneos Chemistry", D.Avnir Ed., John Wiley & Sons (Chichester 1989), pp.271-293. (up)

10) Vedi ad esempio, P.Bak e K.Chen, La criticità autorganizzata, Le Scienze 271 (mar.1991), 22-30. (up)

11) Vedi, ad esempio, M.Y. Choi, H.Y. Lee, Traffic flow and 1/f fluctuations, Physical Review E, 52(6), 1995, pp.5979-5984. (up)

12) Vedi, ad esempio, W.B.Arthur, The economy and complexity, in "Lectures in the Sciences of Complexity" Vol.I, (Proceedings of the 1988 Complex Systems Summer School, held June-July, 1988 in Santa Fe, New Mexico), D.L.Stein Ed., Addison-Wesley (Redwood City, CA 1989), pp.713-740. (up)

13) Vedi, ad esempio, B.B.Mandelbrot, "Gli oggetti frattali", Giulio Einaudi (Torino 1987). (up)

14) Vedi rif. 8) pp.40-43 oppure R.F.Voss, Random fractals: self-affinity in noise, music, mountains and clouds, Physica D, 38, 1989, pp.362-371. (up)

Per un costante aggiornamento sulla teoria dei frattali, e delle sue molteplici applicazioni, si consiglia comunque di esplorare Internet con un opportuno motore di ricerca, inserendo le parole chiave "Fractal" o "1/f" seguite da un'identificazione del campo di applicazione d'interesse (es. medicine, psychology, architecture, chemistry, weather, aesthetics ecc.)