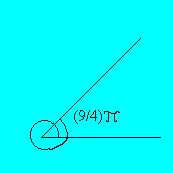Nota: normalmente in matematica si dice che non si può calcolare il valore di una funzione per  o -
o - e una funzione non può assumere come valore
e una funzione non può assumere come valore  o -
o - (
( non viene considerato un numero), ma a scuola talvolta si usa questa terminologia impropria quando non si studiano ancora cose più complesse e qui la userò. Più precisamente si può dire che si può calcolare a cosa tende una funzione per la variabile indipendente (di solito x) che tende a
non viene considerato un numero), ma a scuola talvolta si usa questa terminologia impropria quando non si studiano ancora cose più complesse e qui la userò. Più precisamente si può dire che si può calcolare a cosa tende una funzione per la variabile indipendente (di solito x) che tende a  o -
o - e/o una funzione può tendere a
e/o una funzione può tendere a  o -
o - per valori della variabile indipendente (di solito x) che tendono ad un certo valore (per questo valore abbiamo una "divisione" tra una quantità diversa da 0 e 0; si dice che per questo valore la funzione non è definita). Si tratta del calcolo dei limiti che non tratto in questo sito.
per valori della variabile indipendente (di solito x) che tendono ad un certo valore (per questo valore abbiamo una "divisione" tra una quantità diversa da 0 e 0; si dice che per questo valore la funzione non è definita). Si tratta del calcolo dei limiti che non tratto in questo sito.
 o -
o - e una funzione non può assumere come valore
e una funzione non può assumere come valore  o -
o - (
( non viene considerato un numero), ma a scuola talvolta si usa questa terminologia impropria quando non si studiano ancora cose più complesse e qui la userò. Più precisamente si può dire che si può calcolare a cosa tende una funzione per la variabile indipendente (di solito x) che tende a
non viene considerato un numero), ma a scuola talvolta si usa questa terminologia impropria quando non si studiano ancora cose più complesse e qui la userò. Più precisamente si può dire che si può calcolare a cosa tende una funzione per la variabile indipendente (di solito x) che tende a  o -
o - e/o una funzione può tendere a
e/o una funzione può tendere a  o -
o - per valori della variabile indipendente (di solito x) che tendono ad un certo valore (per questo valore abbiamo una "divisione" tra una quantità diversa da 0 e 0; si dice che per questo valore la funzione non è definita). Si tratta del calcolo dei limiti che non tratto in questo sito.
per valori della variabile indipendente (di solito x) che tendono ad un certo valore (per questo valore abbiamo una "divisione" tra una quantità diversa da 0 e 0; si dice che per questo valore la funzione non è definita). Si tratta del calcolo dei limiti che non tratto in questo sito.
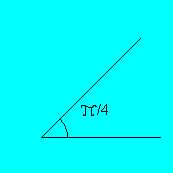
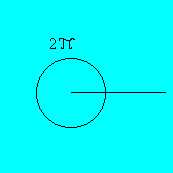
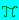 /4 radianti dove
/4 radianti dove