MIKY & GENNY
EQUAZIONI DI SECONDO GRADO AD UNA INCOGNITA ---> INDICE
Richiami sulle equazioni di primo grado
1)-Un'equazione algebrica intera, ad un'incognita x, si dice di grado n, quando ridotta a forma normale, il primo membro è un polinomio di grado n nella variabile x.
2)-Si chiama soluzione o radice di un'equazione algebrica ad un'incognita, ogni numero che, sostituito al posto dell'incognita nell'equazione data, fa assumere al primo membro dell'equazione lo stesso valore del secondo membro.
3)-Risolvere un'equazione significa trovare tutte le soluzioni o radici dell'equazione.
4)-Bisogna tener presente che i principi di equivalenza visti, valgono anche per le equazioni di grado superiore al primo.
5)-Nel campo dei numeri razionali, si è visto come risolvere le equazioni algebriche di primo grado ad un'incognita, cioè le equazioni la cui forma tipica è:
ax=b,
a≠0, e che tali equazioni ammettono sempre una ed una sola soluzione.
Tutto quanto è stato detto per le equazioni di primo grado continua a valere anche se a, b sono numeri reali, quindi:
nel campo dei numeri reali le equazioni algebriche di primo grado ad un'incognita ammettono sempre una ed una sola soluzione.
Nota bene
E' bene ricordare che, quando si afferma che l'equazione ax = b ammette una soluzione nel campo reale, significa che esiste una sezione nel campo razionale, che sostituita al posto della lettera x, trasforma il primo membro in una sezione uguale a quella rappresentata dalla lettera b.
Esempio: l'equazione
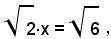
ammette come soluzione la sezione chiamata
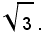
Forma tipica dell'equazione di secondo grado
In base a quanto detto sulla definizione di grado di un'equazione algebrica, si osserva innanzi tutto che ogni equazione intera di secondo grado, nell'incognita x e ridotta a forma normale, è del tipo:
ax2+bx+c=0,
dove a, b, c sono tre numeri reali dati o anche espressioni letterali formate da lettere di cui si suppone noto il valore. I numeri, o le espressioni letterali, a, b, c, si chiamano rispettivamente primo, secondo, terzo coefficiente; quest'ultimo si chiama anche termine noto dell'equazione.
Il primo coefficiente a si deve sempre supporre diverso da zero, altrimenti l'equazione non sarebbe di secondo grado.
Definizione 1) - Un'equazione di secondo grado, ridotta a forma normale, si dice completa, quando tutti e tre i suoi coefficienti sono diversi da zero; si dice incompleta, quando il secondo o il terzo coefficiente, oppure entrambi, sono nulli.
Definizione 2) - Un'equazione di secondo grado, ridotta a forma normale, si dice spuria, quando manca del termine noto, e soltanto di questo; la sua forma tipica è:
ax2+bx=0, con a≠0 e b≠0.
Definizione 3) - Un'equazione di secondo grado, ridotta a forma normale, si dice pura, quando manca del termine contenente l'incognita di primo grado, e soltanto di questo; la sua forma tipica è:
ax2+c=0, con a≠0 e c≠0.
Risoluzione delle equazioni di secondo grado incomplete
Equazione spuria
Si consideri l'equazione spuria: (1)
ax2+bx=0, con a≠0 e b≠0.
Per risolvere tale equazione (1), si mette in evidenza il fattore x ed essa assume la forma: (2)
x(ax+b)=0.
Ricordando che un prodotto è nullo solo quando è nullo uno dei fattori, si vede che le soluzioni dell'equazione (2) sono quei numeri che fanno assumere il valore zero al primo fattore x del prodotto, o al secondo fattore (ax+b), e questi soltanto. Ora, il primo fattore del prodotto (2) si annulla solo per il valore zero, mentre il secondo fattore, ax+b, assume valore zero per quei valori della x che soddisfano l'equazione ax+b=0. Essendo questa equazione di primo grado, si sa che essa ammette una sola soluzione, data da -b/a. Quindi l'equazione (1) ammette due radici, date dai numeri: 0 e -b/a.
Si può quindi dire che:
ogni equazione di secondo grado spuria ammette sempre due, e soltanto due, radici distinte, di cui una è nulla.
Esempi:
1)-risolvere l'equazione spuria: 5x2-9x=0.
Si ha: x(5x-9)=0, da cui x=0, oppure 5x-9 =0. Pertanto le due radici sono: x1=0, oppure x2=9/5.
2)-risolvere l'equazione:
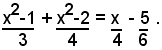
Riducendo l'equazione alla forma tipica, dopo facili calcoli, si trova:
7x2-3x=0,
che è un'equazione spuria di secondo grado. Si ha: x(7x-3) =0, da cui x=0, oppure 7x - 3= 0. Pertanto le due radici sono: x1=0, oppure x2=3/7.
Equazione pura
Si consideri l'equazione pura: (3)
ax2+c=0, con a≠0 e c≠0.
Trasportando il termine noto c nel secondo membro e dividendo poi i due membri dell'equazione ottenuta per il coefficiente a, diverso da zero per ipotesi, si ottiene l'equazione equivalente: (4)
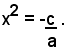
Risolvere l'equazione (4), ossia la (3), significa determinare quei numeri che elevati al quadrato diventano uguali al numero -c/a. Ora si sa che, se il numero -c/a è negativo, non esiste alcun numero reale il cui quadrato sia uguale a -c/a e perciò, in tale ipotesi, l'equazione (3) diventa impossibile, cioè non ammette nessuna radice reale. Se invece il numero -c/a è positivo, si sa che esistono due e soltanto due numeri reali il cui quadrato sia uguale a -c/a, e questi due numeri sono:
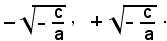
Questi due numeri, e soltanto questi, sono perciò, nell'ipotesi di
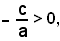
le radici dell'equazione (3).
Si può quindi dire che:
l'equazione di secondo grado pura ax2+c =0, ammette due e soltanto due radici reali, fra loro opposte, se è
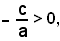
non ammette nessuna radice reale, se è:
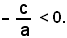
Esempi:
1)-risolvere l'equazione pura:
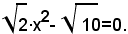
L'equazione è equivalente alla:
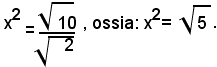
Le due soluzioni di questa equazione sono:
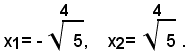
2)-risolvere l'equazione:
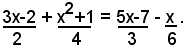
Riducendo l'equazione alla forma tipica, dopo facili calcoli, si trova:
3x2+19=0,
che è un'equazione pura di secondo grado; essa è equivalente all'equazione:
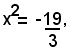
la quale non ammette soluzioni, essendo negativo il secondo membro.
Equazione di secondo grado priva del secondo e del terzo termine
Essa è della forma: ax2=0, ossia, dato che a≠0: x2=0, la quale ammette l'unica soluzione x=0.
Risoluzione dell'equazione di secondo grado completa
Per meglio comprendere le considerazioni che saranno effettuate in seguito, si esamina dapprima qualche esempio di equazioni complete di secondo grado:
1)-risolvere l'equazione: (2x-5)2 =49.
Questa equazione, come si vede facilmente eseguendo le operazioni indicate, è di secondo grado completa. Sono soluzioni dell'equazione quei valori della x che fanno assumere al binomio 2x-5 un valore il cui quadrato sia uguale a 49. Si può quindi dire che soddisfano alla data equazione i valori della x per i quali risulta:

e quelli per i quali risulta:
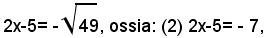
e soltanto questi. Quest'ultime due equazioni sono di primo grado e le loro soluzioni sono rispettivamente: x=6, x=-1. Si può quindi dire che l'equazione data ammette due radici reali distinte, date dai numeri -1 e 6.
2)-risolvere l'equazione: 2x2-11x+5=0.
Si scrive l'equazione sotto la forma: (1) 2x2-11x=-5, e si vede se è possibile trasformarla in un'altra equivalente, il cui primo membro sia il quadrato di un binomio di primo grado in x, in modo da ricondursi al caso precedente. Si raggiunge lo scopo, moltiplicando ambo i membri dell'equazione (2) per 8 e poi aggiungendo ad ambo i membri il quadrato del secondo coefficiente (-11)2=121. Infatti, si ha:
16x2-88x+121=-40+121,
(4x-11)2=81.
Le radici dell'equazione sono i valori della x per cui risulta: 4x-11=+ 9, e quelli per cui risulta: 4x-11=-9. Risolvendo queste due equazioni di primo grado, si trova che le radici dell'equazione data sono: 5 e 1/2.
3)-risolvere l'equazione:
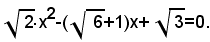
Si procede come nel caso precedente, portando prima il termine noto nel secondo membro, poi moltiplicando ambo i membri dell'equazione per
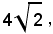
quindi aggiungendo ad ambo i membri:
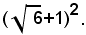
Infatti, si ha:
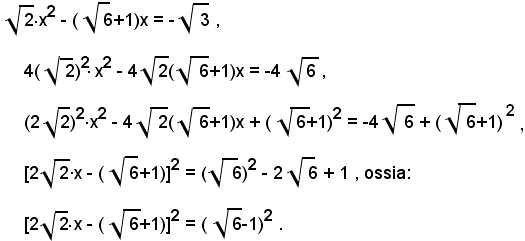
Le radici dell'equazione sono i valori della x per i quali risulta:
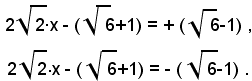
Risolvendo queste due equazioni di primo grado, di trovano le due radici dell'equazione data:
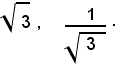
4)-risolvere l'equazione:
Per a=1 e a=-1, il primo coefficiente dell'equazione si annulla perciò l'equazione diventa di primo grado ed il valore della x è espresso da: 2/3a+1.
Supposto a≠1 e a≠-1 e procedendo come nei casi precedenti, cioè portando prima il termine noto nel secondo membro, moltiplicando poi ambo i membri per 4(a2-1) e aggiungendo infine ad ambo i membri (3a+1)2, si ha:
1)-Un'equazione algebrica intera, ad un'incognita x, si dice di grado n, quando ridotta a forma normale, il primo membro è un polinomio di grado n nella variabile x.
2)-Si chiama soluzione o radice di un'equazione algebrica ad un'incognita, ogni numero che, sostituito al posto dell'incognita nell'equazione data, fa assumere al primo membro dell'equazione lo stesso valore del secondo membro.
3)-Risolvere un'equazione significa trovare tutte le soluzioni o radici dell'equazione.
4)-Bisogna tener presente che i principi di equivalenza visti, valgono anche per le equazioni di grado superiore al primo.
5)-Nel campo dei numeri razionali, si è visto come risolvere le equazioni algebriche di primo grado ad un'incognita, cioè le equazioni la cui forma tipica è:
a≠0, e che tali equazioni ammettono sempre una ed una sola soluzione.
Tutto quanto è stato detto per le equazioni di primo grado continua a valere anche se a, b sono numeri reali, quindi:
nel campo dei numeri reali le equazioni algebriche di primo grado ad un'incognita ammettono sempre una ed una sola soluzione.
Nota bene
E' bene ricordare che, quando si afferma che l'equazione ax = b ammette una soluzione nel campo reale, significa che esiste una sezione nel campo razionale, che sostituita al posto della lettera x, trasforma il primo membro in una sezione uguale a quella rappresentata dalla lettera b.
Esempio: l'equazione
ammette come soluzione la sezione chiamata
Forma tipica dell'equazione di secondo grado
In base a quanto detto sulla definizione di grado di un'equazione algebrica, si osserva innanzi tutto che ogni equazione intera di secondo grado, nell'incognita x e ridotta a forma normale, è del tipo:
dove a, b, c sono tre numeri reali dati o anche espressioni letterali formate da lettere di cui si suppone noto il valore. I numeri, o le espressioni letterali, a, b, c, si chiamano rispettivamente primo, secondo, terzo coefficiente; quest'ultimo si chiama anche termine noto dell'equazione.
Il primo coefficiente a si deve sempre supporre diverso da zero, altrimenti l'equazione non sarebbe di secondo grado.
Definizione 1) - Un'equazione di secondo grado, ridotta a forma normale, si dice completa, quando tutti e tre i suoi coefficienti sono diversi da zero; si dice incompleta, quando il secondo o il terzo coefficiente, oppure entrambi, sono nulli.
Definizione 2) - Un'equazione di secondo grado, ridotta a forma normale, si dice spuria, quando manca del termine noto, e soltanto di questo; la sua forma tipica è:
ax2+bx=0, con a≠0 e b≠0.
Definizione 3) - Un'equazione di secondo grado, ridotta a forma normale, si dice pura, quando manca del termine contenente l'incognita di primo grado, e soltanto di questo; la sua forma tipica è:
Risoluzione delle equazioni di secondo grado incomplete
Equazione spuria
Si consideri l'equazione spuria: (1)
Per risolvere tale equazione (1), si mette in evidenza il fattore x ed essa assume la forma: (2)
Ricordando che un prodotto è nullo solo quando è nullo uno dei fattori, si vede che le soluzioni dell'equazione (2) sono quei numeri che fanno assumere il valore zero al primo fattore x del prodotto, o al secondo fattore (ax+b), e questi soltanto. Ora, il primo fattore del prodotto (2) si annulla solo per il valore zero, mentre il secondo fattore, ax+b, assume valore zero per quei valori della x che soddisfano l'equazione ax+b=0. Essendo questa equazione di primo grado, si sa che essa ammette una sola soluzione, data da -b/a. Quindi l'equazione (1) ammette due radici, date dai numeri: 0 e -b/a.
Si può quindi dire che:
ogni equazione di secondo grado spuria ammette sempre due, e soltanto due, radici distinte, di cui una è nulla.
Esempi:
1)-risolvere l'equazione spuria: 5x2-9x=0.
Si ha: x(5x-9)=0, da cui x=0, oppure 5x-9 =0. Pertanto le due radici sono: x1=0, oppure x2=9/5.
2)-risolvere l'equazione:
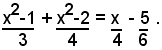
Riducendo l'equazione alla forma tipica, dopo facili calcoli, si trova:
7x2-3x=0,
che è un'equazione spuria di secondo grado. Si ha: x(7x-3) =0, da cui x=0, oppure 7x - 3= 0. Pertanto le due radici sono: x1=0, oppure x2=3/7.
Equazione pura
Si consideri l'equazione pura: (3)
ax2+c=0, con a≠0 e c≠0.
Trasportando il termine noto c nel secondo membro e dividendo poi i due membri dell'equazione ottenuta per il coefficiente a, diverso da zero per ipotesi, si ottiene l'equazione equivalente: (4)
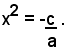
Risolvere l'equazione (4), ossia la (3), significa determinare quei numeri che elevati al quadrato diventano uguali al numero -c/a. Ora si sa che, se il numero -c/a è negativo, non esiste alcun numero reale il cui quadrato sia uguale a -c/a e perciò, in tale ipotesi, l'equazione (3) diventa impossibile, cioè non ammette nessuna radice reale. Se invece il numero -c/a è positivo, si sa che esistono due e soltanto due numeri reali il cui quadrato sia uguale a -c/a, e questi due numeri sono:
Questi due numeri, e soltanto questi, sono perciò, nell'ipotesi di
le radici dell'equazione (3).
Si può quindi dire che:
l'equazione di secondo grado pura ax2+c =0, ammette due e soltanto due radici reali, fra loro opposte, se è
non ammette nessuna radice reale, se è:
Esempi:
1)-risolvere l'equazione pura:
L'equazione è equivalente alla:
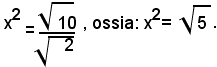
Le due soluzioni di questa equazione sono:
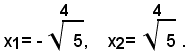
2)-risolvere l'equazione:
Riducendo l'equazione alla forma tipica, dopo facili calcoli, si trova:
3x2+19=0,
che è un'equazione pura di secondo grado; essa è equivalente all'equazione:
la quale non ammette soluzioni, essendo negativo il secondo membro.
Equazione di secondo grado priva del secondo e del terzo termine
Essa è della forma: ax2=0, ossia, dato che a≠0: x2=0, la quale ammette l'unica soluzione x=0.
Risoluzione dell'equazione di secondo grado completa
Per meglio comprendere le considerazioni che saranno effettuate in seguito, si esamina dapprima qualche esempio di equazioni complete di secondo grado:
1)-risolvere l'equazione: (2x-5)2 =49.
Questa equazione, come si vede facilmente eseguendo le operazioni indicate, è di secondo grado completa. Sono soluzioni dell'equazione quei valori della x che fanno assumere al binomio 2x-5 un valore il cui quadrato sia uguale a 49. Si può quindi dire che soddisfano alla data equazione i valori della x per i quali risulta:
e quelli per i quali risulta:
e soltanto questi. Quest'ultime due equazioni sono di primo grado e le loro soluzioni sono rispettivamente: x=6, x=-1. Si può quindi dire che l'equazione data ammette due radici reali distinte, date dai numeri -1 e 6.
2)-risolvere l'equazione: 2x2-11x+5=0.
Si scrive l'equazione sotto la forma: (1) 2x2-11x=-5, e si vede se è possibile trasformarla in un'altra equivalente, il cui primo membro sia il quadrato di un binomio di primo grado in x, in modo da ricondursi al caso precedente. Si raggiunge lo scopo, moltiplicando ambo i membri dell'equazione (2) per 8 e poi aggiungendo ad ambo i membri il quadrato del secondo coefficiente (-11)2=121. Infatti, si ha:
16x2-88x=-40,
16x2-88x+121=-40+121,
(4x-11)2=81.
Le radici dell'equazione sono i valori della x per cui risulta: 4x-11=+ 9, e quelli per cui risulta: 4x-11=-9. Risolvendo queste due equazioni di primo grado, si trova che le radici dell'equazione data sono: 5 e 1/2.
3)-risolvere l'equazione:
Si procede come nel caso precedente, portando prima il termine noto nel secondo membro, poi moltiplicando ambo i membri dell'equazione per
quindi aggiungendo ad ambo i membri:
Infatti, si ha:
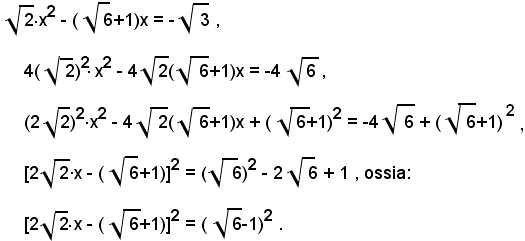
Le radici dell'equazione sono i valori della x per i quali risulta:
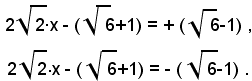
Risolvendo queste due equazioni di primo grado, di trovano le due radici dell'equazione data:
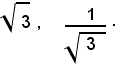
4)-risolvere l'equazione:
(a2-1)x2-(3a+1)x+2=0.
Per a=1 e a=-1, il primo coefficiente dell'equazione si annulla perciò l'equazione diventa di primo grado ed il valore della x è espresso da: 2/3a+1.
Supposto a≠1 e a≠-1 e procedendo come nei casi precedenti, cioè portando prima il termine noto nel secondo membro, moltiplicando poi ambo i membri per 4(a2-1) e aggiungendo infine ad ambo i membri (3a+1)2, si ha:
(a2-1)x2-(3a+1)x=-2,
4(a2-1)2x2--4(a2-1)(3a+1)x=-8(a2-1),
4(a2-1)2x2-4(a2-1)(3a+1)x+(3a+1)2=-8(a2-1)+(3a+1)2,
[2(a2-1)x-(3a+1)]2=(a+3)2,
da cui si ricava::
2(a2-1)x-(3a+1)=+(a+3),
2(a2-1)x-(3a+1)=-(a+3).
Risolvendo queste due equazioni si primo grado, si trova che le due radici dell'equazione sono:
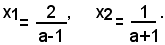
5)-risolvere l'equazione:
In tal caso l'equazione si può scrivere sotto la forma:
(x-3)2=0,
ossia :
x=3.
Quindi l'equazione di secondo grado ammette una sola soluzione.
6)-risolvere l'equazione:
3x2+5x+7=0.
Procedendo come nei casi precedenti, si ha:
3x2+5x=-7,
36x2+60x=-84,
36x2+60x+25=-84+25,
(6x+5)2=-59,
in questo caso si vede che non esiste alcun valore della x che faccia assumere al binomio 6x+5 un valore il cui quadrato sia uguale al numero -59, quindi l'equazione data è impossibile, cioè non ammette nessuna radice reale.
Nota bene
Dagli esempi svolti, si vede che il procedimento di risoluzione di una equazione di secondo grado completa, consiste nel trasformarla in un'altra equivalente il cui primo membro sia il quadrato di un binomio di primo grado in x e il secondo membro un numero noto o un'espressione letterale formata con lettere di cui si suppone noto il valore. Se il secondo membro è positivo, l'equazione equivale a due equazioni di primo grado, se è nullo, equivale a una sola equazione di primo grado, se è negativo, l'equazione è impossibile. Nessuna difficoltà vi sarà quindi a trattare il caso generale, cioè a risolvere l'equazione: (1)
ax2+bx+c=0,
Il binomio b2-4ac, si chiama discriminante dell'equazione di secondo grado ax2+bx+c=0 e si indica con ∆, cioè si pone: ∆=b2-4ac.Si devono distinguere tre casi, a seconda che il numero b2-4ac sia positivo, nullo o negativo.
1° Caso: ∆=b2-4ac>0.
Le soluzioni dell'equazione (2) sono quei numeri, che attribuiti all'incognita x, fanno assumere al binomio 2ax+b un valore il cui quadrato risulta uguale a b2-4ac. Perciò, le soluzioni dell'equazione (2) sono quei valori della x per cui risulta:
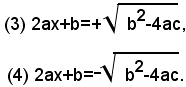
Si vede quindi che l'equazione data è equivalente alle due equazioni di primo grado (3) e (4). Risolvendo queste due equazioni, si trova rispettivamente:
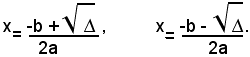
Questi due numeri sono quindi le radici dell'equazione di secondo grado considerata. Solitamente i valori trovati si indicano con l'unica formula: (5)
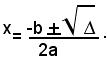
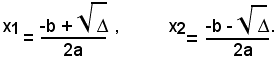
2° Caso: ∆=b2-4ac=0.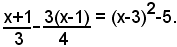
Riducendo l'equazione a forma normale, si ha:
12x2-67x+35=0.
Si calcola il discriminante ∆=b2-4ac=672-1680=4489-1680=2809>0; siccome esso è maggiore di zero, l'equazione ammette due radici reali e distinte, date da:
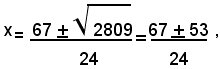
e, indicate con x1, x2, le due radici dell'equazione, si ha:
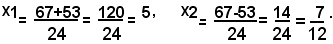
3)-risolvere l'equazione ridotta a forma normale:
3x2-5x+4=0.
Si calcola il discriminante ∆=b2-4ac=52-48=25-48=-23<0; siccome esso è minore di zero, l'equazione non ammette nessuna radice reale.
4)-risolvere l'equazione a coefficienti letterali:
a(a+1)x2+x- a(a-1)=0.
Se a=0, risulta: x=0; se a=-1, risulta: x-2=0, cioè x=2. In tali condizioni, l'equazione si è abbassata di grado è ammette rispettivamente le soluzioni 0 e 2.
Se a≠0 e a≠-1, si calcola il discriminante ∆=1+4a2(a+1)(a-1)=1+4a4-4a2=(1-2a2)2>0; siccome esso è maggiore di zero, l'equazione ammette due radici reali e distinte, date da:
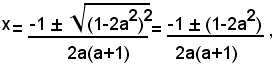
e, indicate con x1, x2, le due radici dell'equazione, si ha:
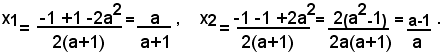
Formula risolutiva ridotta dell'equazione di secondo grado
La formula risolutiva dell'equazione di secondo grado si semplifica quando nell'equazione ridotta a forma normale, il secondo coefficiente è un numero intero pari o un'espressione contenente in evidenza il fattore 2. Infatti, in tal caso, l'equazione può scriversi:
ax2+2βx+c=0,
e la corrispondente formula risolutiva diventa:
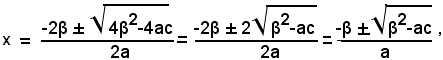
la quale si chiama formula risolutiva ridotta.
In questo caso il discriminante è dato da ∆=4β2-4ac=4(β2-ac).Il binomio:
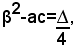
si chiama discriminante ridotto.
Quindi, se il secondo coefficiente è un numero intero pari o un'espressione contenente in evidenza il fattore 2, si può dire che:
le radici sono date da una frazione che ha per numeratore la metà del secondo coefficiente cambiato di segno, aumentata e diminuita della radice quadrata della differenza fra il quadrato della metà del secondo coefficiente e il prodotto del primo e terzo coefficiente; e per denominatore il primo coefficiente.
Esempio: risolvere l'equazione 3x2-8x+4=0.
Dato che il secondo coefficiente dell'equazione è divisibile per 2, si calcola il discriminante ridotto:
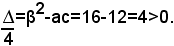
Siccome esso è maggiore di zero, l'equazione ammette due radici reali e distinte, date da:
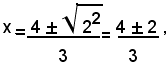
e quindi: x1=2, x2 =2/3.
Equazioni frazionarie
Le equazionI frazionarie si risolvono come quelle intere, numeriche o letterali. In questo caso, per togliere i denominatori, si devono moltiplicare ambo i membri dell'equazione per un multiplo comune dei denominatori. Se questa espressione non si annulla per nessun valore della x, per il secondo principio di equivalenza, le soluzioni della nuova equazione, sono anche soluzioni dell'equazione data. Ma se l'espressione si annulla per certi valori della x, bisogna escluderli.
Esempi
1)-risolvere l'equazione:
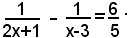
Il denominatore comune è: 5(2x+1)(x-3), quindi si moltiplicano ambo i membri dell'equazione per questa espressione. L'operazione è lecita se x≠-1/2, x≠3, perchè in tal modo il denominatore comune è diverso da zero. Liberando l'equazione dai denominatori ed eseguendo le opportune semplificazioni, si ha:
12x2-25x+2=0.
Si calcola il discriminante ∆=252-96=625-96=529=232>0; siccome esso è maggiore di zero, l'equazione ammette due radici reali e distinte, date da:
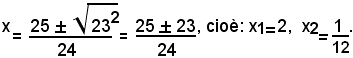
Siccome i valori trovati sono diversi da quelli che annullano i denominatori, cioè diversi da -1/2 e 3, si conclude che 2 e 1/12 sono le radici dell'equazione data.
Relazioni fra i coefficienti e le radici di un'equazione di secondo grado
Considerata l'equazione:
ax2+bx+c=0,
supposto il discriminante positivo o nullo, cioè ∆=b2-4ac≥0 e indicate con x1, x2, le due radici, distinte o coincidenti dell'equazione, risulta:
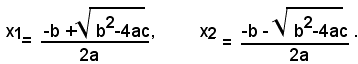
Si vuole calcolare il valore della somma e del prodotto di queste due radici.
Sommando membro a membro, si ha:
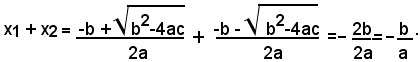
Moltiplicando membro a membro, si ha:
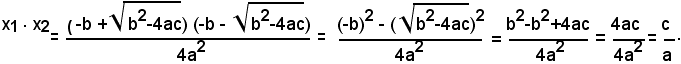
Quindi si ha:
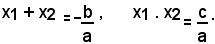
Pertanto, si può enunciare la seguente regola:
in un'equazione di secondo grado ridotta a forma normale, con discriminante non negativo, la somma delle radici è uguale al rapporto fra il secondo coefficiente cambiato di segno e il primo e il prodotto delle radici è uguale al rapporto fra il termine noto e il primo coefficiente.
Nota bene
Si tenga presente che il prodotto della somma di due numeri per la loro differenza è uguale alla differenza dei due numeri, cioè:
(x1 + x2)(x1 - x2) = x21 - x22
e che se nell'equazione ax2+bx+c=0, il primo coefficiente a=1, cioè se l'equazione è del tipo x2+bx+c=0, si ha:
x1 + x2 =- b, x1 . x2 = c.
Pertanto, si può enunciare la seguente regola:
in un'equazione di secondo grado, con discriminante non negativo e primo coefficiente uguale a uno, la somma delle radici è uguale al secondo coefficiente cambiato di segno e il prodotto è uguale al termine noto.
Quindi, senza risolvere l'equazione, si può facilmente calcolare la somma e il prodotto delle radici di un'equazione con discriminante non negativo.
Esempi:
1)-determinare la somma e il prodotto delle radici della seguente equazione senza risolverla:
4x2-21bx+5=0.
Siccome il determinante ∆=212-80=441-80=361>0, si può applicare il teorema precedente, quindi si ha: x1 + x2 = 21/4, x1 . x2 = 5/4.
2)-Conoscendo che una radice dell'equazione
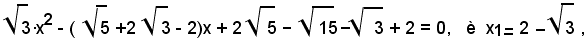
determinare l'altra radice senza risolverla.
Per il teorema precedentemente dimostrato, si ha:
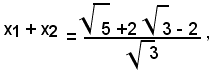
e tenendo conto del valore della radice x1, si ha:
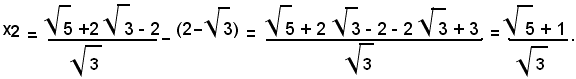
3)-determinare la somma dei quadrati delle radici senza risolvere l'equazione:
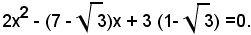
Si osserva dapprima che il discriminante dell'equazione è positivo, come si verifica facilmente. Premesso ciò, ed essendo:
x12 + x22 = (x1 + x2)2 - 2x1x2 ,
e avendosi per il teorema precedente:
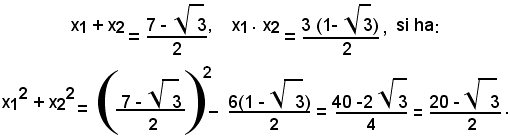
Come applicazioni del teorema dimostrato, si risolvono alcuni problemi:
1)-scrivere un'equazione di secondo grado che abbia come radici i numeri assegnati α e β.
A questo problema soddisfa l'equazione x2 - (α+β)x + αβ=0, di cui il suo primo coefficiente è uguale a uno, il secondo è uguale alla somma cambiata di segno dei due numeri α e β e il termine noto è uguale al prodotto di α e β. Infatti, le radici x1 e x2 di questa equazione sono reali e distinte perchè il discriminante: ∆=(α+β)2-4αβ=α2+β2+2αβ-4αβ=α2+β2-2αβ=(α-β)2>0 e, per il teorema precedentemente dimostrato esse verificano le relazioni: x1 + x2 = α+β, x1 . x2 = αβ, perciò risulta x1 = α e x2 = β o viceversa.
Regola - Per ottenere un'equazione di secondo grado, conoscendo le due radici, è sufficiente scrivere un'equazione di secondo grado avente il primo coefficiente uguale a uno, il secondo uguale alla loro somma cambiata di segno e il termine noto uguale al loro prodotto.
Esempio: scrivere l'equazione di secondo grado, avente per radici i numeri:
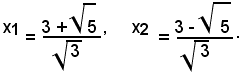
Essendo:
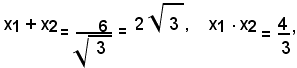
l'equazione richiesta è:
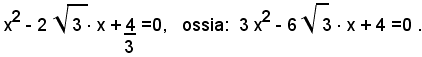
2)-Determinare due numeri conoscendo la loro somma s e il loro prodotto p.
I due numeri cercati, se esistono, sono le radici della seguente equazione:
x2 -sx + p = 0.
Infatti, se il discriminante ∆=s2-4p di questa equazione è positivo o nullo, si sa che la somma delle radici è uguale a s e il prodotto uguale a p, quindi s e p sono i due numeri richiesti.
Precisamente: se il discriminante ∆>0, i due numeri cercati sono reali e distinti, se il discriminante ∆=0, i due numeri cercati sono reali e coincidenti, se ∆<0 non esistono due numeri che abbiano per somma s e per prodotto p.
Esempio: trovare due numeri tali che:
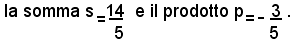
I due numeri cercati sono le radici della seguente equazione:

Regola dei segni di Cartesio
Si consideri l'equazione completa di secondo grado: (1) ax2+bx+c=0 e si supponga che il suo discriminante sia positivo. Si vuole determinare una regola che permetta di stabilire il segno delle radici dell'equazione, dall'esame dei coefficienti della stessa.
Definizione - Si dice che i coefficienti a, b, c, dell'equazione (1), considerati nell'ordine scritto, presentano una permanenza, ogni volta che due di essi consecutivi hanno segni uguali; presentano invece una variazione, ogni volta che due di essi consecutivi hanno segni contrari.
Ad esempio, i coefficienti dell'equazione 2x2-3x-7=0 presentano una variazione e una permanenza, mentre i coefficienti dell'equazione 5x2+11x+3=0, presentano due permanenze.
Teorema di Cartesio - In un'equazione di secondo grado, completa, ridotta alla forma tipica e con discriminante positivo, ad ogni variazione presentata dai suoi coefficienti, corrisponde una radice positiva, e ad ogni permanenza una radice negativa; se l'equazione ha radici di segno contrario, è maggiore, in valore assoluto, quella positiva, se la variazione precede la permanenza, quella negativa, se la permanenza precede la variazione.
Nella dimostrazione si può supporre positivo il primo coefficiente a dell'equazione, perchè se non lo fosse, basterebbe moltiplicare ambo i membri dell'equazione per -1, per ottenere un'equazione equivalente alla data avente lo stesso numero di variazioni e permanenze.
1° Caso: si suppone che i coefficienti dell'equazione presentino due permanenze, cioè sia:
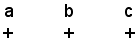
Si dimostra che le due radici dell'equazione sono negative.
Come è già noto, risulta: (1)
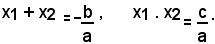
Siccome in questo caso a e c sono positivi, il prodotto delle radici risulta positivo e perciò le due radici devono avere segni uguali, cioè devono essere o entrambe positive o entrambe negative. Ma la somma delle radici, essendo a e b per ipotesi positivi, è negativa e quindi si deduce che le due radici x1 e x2 sono entrambe negative, come volevasi dimostrare.
2° Caso: si suppone che i coefficienti dell'equazione presentino due variazioni, cioè sia:
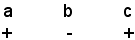
Si dimostra che le due radici dell'equazione sono positive.
In base alle (1) e alle ipotesi fatte, si vede che il prodotto delle radici risulta positivo e positiva è anche la loro somma, perciò le due radici sono entrambe positive, come volevasi dimostrare.
3° Caso: si suppone che i coefficienti dell'equazione presentino una variazione e una permanenza, cioè sia:
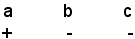
Si dimostra che una radice è positiva e l'altra negativa e inoltre, siccome la variazione precede la permanenza, che la radice positiva è, in valore assoluto, maggiore di quella negativa.
In base alle (1) e alle ipotesi fatte, il prodotto delle radici risulta negativo e perciò le radici x1 e x2 devono avere segni contrari, cioè essere una positiva e l'altra negativa. Siccome la somma delle radici è positiva, delle due radici è maggiore, in valore assoluto quella positiva.
4° Caso: si suppone che i coefficienti dell'equazione presentino una permanenza e una variazione, cioè sia:
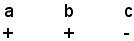
Si dimostra che una radice è negativa e l'altra positiva e inoltre, siccome la permanenza precede la variazione, che la radice negativa è, in valore assoluto, maggiore di quella positiva. La dimostrazione è analoga a quella del 3° caso.
Esempi:
1)-nell'equazione 3x2-7x+2=0, il discriminante ∆=49-24=25>0, cioè positivo, perciò le due radici sono reali e distinte e poichè l'equazione presenta due variazioni, le radici sono entrambe positive.
2)-nell'equazione 5x2+9x+4=0, il discriminante ∆=81-80=1>0, cioè positivo, perciò le due radici sono reali e distinte e poichè l'equazione presenta due permanenze, le radici sono entrambe negative.
3)-nell'equazione 4x2-11x-3=0, il discriminante ∆=121-48=73>0, cioè positivo, perciò le due radici sono reali e distinte e poichè l'equazione presenta una variazione e una permanenza, le radici sono una positiva e l'altra negativa. Inoltre, poichè la variazione precede la permanenza, la radice positiva è, in valore assoluto, la maggiore.
4)-nell'equazione x2+3x-28=0, il discriminante ∆=9+112=121>0, cioè positivo, perciò le due radici sono reali e distinte e poichè l'equazione presenta una permanenza e una variazione, le radici sono di segno contrario. Inoltre, poichè la permanenza precede la variazione, è maggiore , in valore assoluto, la radice negativa.
5)-nell'equazione x2-3x+7=0, il discriminante ∆=9-28=-19<0, cioè negativo, perciò l'equazione non ammette soluzioni nel campo reale, quindi non ha senso parlare di radici positive o negative.
Scomposizione di un trinomio di secondo grado in fattori di primo grado
Si consideri il polinomio di secondo grado nella variabile x: (1) ax2+bx+c, e si supponga il discriminante ∆=b2-4ac>0, cioè positivo, in modo che l'equazione (2) ax2+bx+c=0, ottenuta uguagliando a zero il polinomio, ammetta due radici reali e distinte x1, x2. Le radici x1, x2 sono chiamate anche radici o zeri del trinomio (1).
Si ricordano ora le relazioni:
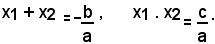
Di seguito, si ottiene:
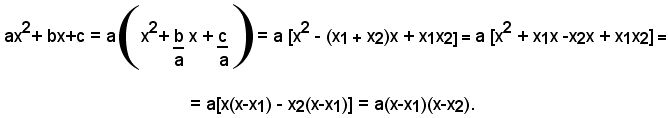
cioè: (3)
ax2+ bx + c = a(x-x1)(x-x2).
Quindi:
un trinomio di secondo grado nella variabile x, con discriminante positivo, si può scomporre in un prodotto di tre fattori, il primo dei quali è uguale al primo coefficiente del trinomio, il secondo è uguale al binomio dato dalla differenza tra la variabile x e la prima radice e il terzo uguale al binomio dato dalla differenza tra la variabile x e la seconda radice.
Cioè:
un trinomio di secondo grado nella variabile x, con discriminante nullo, si può scomporre nel prodotto del primo coefficiente del trinomio, per il quadrato del binomio dato dalla differenza tra la variabile x e la radice dello stesso trinomio.
Esempi:
(1)-scomporre in fattori il polinomio: 3x2-7x+2.
Si scompone il polinomio 2x2-11x+5 che figura al numeratore della frazione; dalla risoluzione dell'equazione 2x2-11x+5=0, si ottengono le radici x1=1/2, x2=5; perciò il numeratore si può scrivere: 2x2-11x+5 = 2(x-1/2)(x-5).
da cui si ricava::
2(a2-1)x-(3a+1)=-(a+3).
Risolvendo queste due equazioni si primo grado, si trova che le due radici dell'equazione sono:
5)-risolvere l'equazione:
x2-6x+9=0.
In tal caso l'equazione si può scrivere sotto la forma:
(x-3)2=0,
ossia :
x=3.
Quindi l'equazione di secondo grado ammette una sola soluzione.
6)-risolvere l'equazione:
3x2+5x+7=0.
Procedendo come nei casi precedenti, si ha:
3x2+5x=-7,
36x2+60x=-84,
36x2+60x+25=-84+25,
(6x+5)2=-59,
in questo caso si vede che non esiste alcun valore della x che faccia assumere al binomio 6x+5 un valore il cui quadrato sia uguale al numero -59, quindi l'equazione data è impossibile, cioè non ammette nessuna radice reale.
Nota bene
Dagli esempi svolti, si vede che il procedimento di risoluzione di una equazione di secondo grado completa, consiste nel trasformarla in un'altra equivalente il cui primo membro sia il quadrato di un binomio di primo grado in x e il secondo membro un numero noto o un'espressione letterale formata con lettere di cui si suppone noto il valore. Se il secondo membro è positivo, l'equazione equivale a due equazioni di primo grado, se è nullo, equivale a una sola equazione di primo grado, se è negativo, l'equazione è impossibile. Nessuna difficoltà vi sarà quindi a trattare il caso generale, cioè a risolvere l'equazione: (1)
nell'ipotesi a≠0. b≠0 e c≠0.
Procedendo come negli esempi svolti, si scrive l'equazione sotto la forma:
ax2+bx=-c,
si moltiplicano poi ambo i membri per 4a, cioè per il quadruplo del primo coefficiente e si ottiene l'equazione equivalente:
4a2x2+4abx=-4ac;
si aggiunge b2 ad ambo i membri, cioè il quadrato del secondo coefficiente della (1), si ha ancora l'equazione equivalente alla data:
che si può scrivere sotto la forma: (2)
(2ax+b)2=b2-4ac.
Procedendo come negli esempi svolti, si scrive l'equazione sotto la forma:
si moltiplicano poi ambo i membri per 4a, cioè per il quadruplo del primo coefficiente e si ottiene l'equazione equivalente:
si aggiunge b2 ad ambo i membri, cioè il quadrato del secondo coefficiente della (1), si ha ancora l'equazione equivalente alla data:
4a2x2+4abx+b2=b2-4ac,
che si può scrivere sotto la forma: (2)
(2ax+b)2=b2-4ac.
Il binomio b2-4ac, si chiama discriminante dell'equazione di secondo grado ax2+bx+c=0 e si indica con ∆, cioè si pone: ∆=b2-4ac.Si devono distinguere tre casi, a seconda che il numero b2-4ac sia positivo, nullo o negativo.
1° Caso: ∆=b2-4ac>0.
Le soluzioni dell'equazione (2) sono quei numeri, che attribuiti all'incognita x, fanno assumere al binomio 2ax+b un valore il cui quadrato risulta uguale a b2-4ac. Perciò, le soluzioni dell'equazione (2) sono quei valori della x per cui risulta:
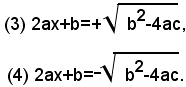
Si vede quindi che l'equazione data è equivalente alle due equazioni di primo grado (3) e (4). Risolvendo queste due equazioni, si trova rispettivamente:
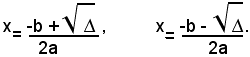
Questi due numeri sono quindi le radici dell'equazione di secondo grado considerata. Solitamente i valori trovati si indicano con l'unica formula: (5)
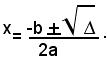
Si può quindi dire che se ∆=b2-4ac>0, l'equazione ammette due radici reali e distinte, date da:
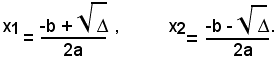
2° Caso: ∆=b2-4ac=0.
In questo caso l'equazione (2ax+b)2=b2-4ac assume la forma: (6)
(2ax+b)2=0.
Ricordando che il quadrato di un numero è uguale a zero soltanto quando è uguale a zero la base, si vede che l'equazione (6), e qundi anche la (1), ammette l'unica soluzione dell'equazione di primo grado: 2ax+b=0, cioè:
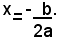
Si può quindi dire che se ∆=b2-4ac=0, l'equazione ammette una sola radice, o radice doppia, data da:
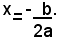
3° Caso: ∆=b2-4ac<0.
In questo caso il secondo membro dell'equazione (2ax+b)2=b2-4ac è negativo e perciò non esiste un numero reale che sostituito alla x faccia assumere al binomio 2ax+b un valore il cui quadrato risulti uguale al numero negativo b2-4ac
Si può quindi dire che se ∆=b2-4ac<0, l'equazione non ammette nessuna radice reale.
Riassumendo, si può dire che:
l'equazione di secondo grado: ax2+bx+c=0, quando:
-il discriminante è positivo, cioè ∆=b2-4ac>0, ammette due radici reali e distinte date da:
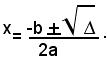
-il discriminante è nullo, cioè ∆=b2-4ac=0, ammette una sola radice reale, o una radice doppia, data da:
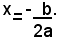
-il discriminante è negativo, cioè ∆=b2-4ac<0, non ammette nessuna radice reale.
Nota bene
E' molto importante la seguente formula: 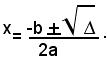
Essa si può anche applicare alle equazioni di secondo grado incomplete.
Infatti, nell'equazione spuria il termine noto c è uguale a zero, pertanto si hanno le radici:
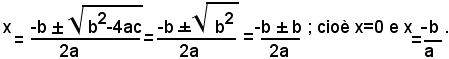
Invece nell'equazione pura il coefficiente b della x è uguale a zero, pertanto si hanno le radici:
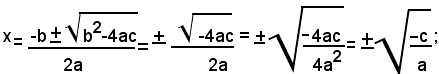
per tale motivo formula (5) si chiama formula risolutiva generale dell'equazione di secondo grado ax2+bx+c=0.
La formula risolutiva può quindi enunciarsi come segue:
le radici di un'equazione di secondo grado, a discriminante non negativo, sono date da una frazione che ha per numeratore il secondo coefficiente cambiato di segno, aumentato e diminuito della radice quadrata della differenza fra il quadrato del secondo coefficiente e il quadruplo del prodotto del primo coefficiente per il terzo; e per denominatore il doppio del primo coefficiente.
Da quanto visto, segue che l'equazione di secondo grado completa: ax2+bx+c=0, ammette soluzioni soltanto quando il suo discriminante risulta positivo o nullo. Pertanto, in pratica, per trovare le eventuali soluzioni di un'equazione di secondo grado ridotta a forma normale, si deve prima calcolare il suo discriminante ∆=b2-4ac, sostituendo ad a, b, c, i valori che queste lettere hanno nell'equazione data. Se esso risulta negativo, l'equazione non ammette soluzioni, mentre se risulta positivo o nullo, le soluzioni si trovano applicando la formula risolutiva (5). Se l'equazione non ha forma normale, cioè è intera e a coefficienti numerici, si deve trasformare a forma normale mediante i due principi noti di equivalenza; poi a questa si applica la formula risolutiva. Se l'equazione è intera e a coefficienti letterali, si deve trasformare a forma normale mediante lo stesso procedimento, ma in questo caso può darsi che per valori particolari delle lettere che compaiono nei coefficienti, l'equazione diventi di primo grado, oppure impossibile o si trasformi in un'identità. Quindi è necessario precisare di volta in volta questi particolari valori delle lettere; in ciò consiste la cosiddetta discussione dell'equazione.
Esempi:
1)-risolvere l'equazione ridotta a forma normale:
2x2-7x+3=0.
Si calcola il discriminante ∆=b2-4ac=49-24=25>0; siccome esso è maggiore di zero, l'equazione ammette due radici reali e distinte, date da:
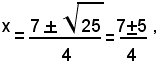
e, indicate con x1, x2, le due radici dell'equazione, si ha:
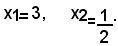
2)-risolvere l'equazione:
(2ax+b)2=0.
Ricordando che il quadrato di un numero è uguale a zero soltanto quando è uguale a zero la base, si vede che l'equazione (6), e qundi anche la (1), ammette l'unica soluzione dell'equazione di primo grado: 2ax+b=0, cioè:
Si può quindi dire che se ∆=b2-4ac=0, l'equazione ammette una sola radice, o radice doppia, data da:
3° Caso: ∆=b2-4ac<0.
In questo caso il secondo membro dell'equazione (2ax+b)2=b2-4ac è negativo e perciò non esiste un numero reale che sostituito alla x faccia assumere al binomio 2ax+b un valore il cui quadrato risulti uguale al numero negativo b2-4ac
Si può quindi dire che se ∆=b2-4ac<0, l'equazione non ammette nessuna radice reale.
Riassumendo, si può dire che:
l'equazione di secondo grado: ax2+bx+c=0, quando:
-il discriminante è positivo, cioè ∆=b2-4ac>0, ammette due radici reali e distinte date da:
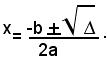
-il discriminante è nullo, cioè ∆=b2-4ac=0, ammette una sola radice reale, o una radice doppia, data da:
-il discriminante è negativo, cioè ∆=b2-4ac<0, non ammette nessuna radice reale.
Nota bene
E' molto importante la seguente formula:
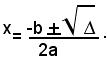
Essa si può anche applicare alle equazioni di secondo grado incomplete.
Infatti, nell'equazione spuria il termine noto c è uguale a zero, pertanto si hanno le radici:
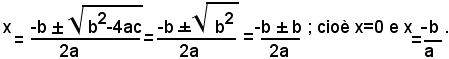
Invece nell'equazione pura il coefficiente b della x è uguale a zero, pertanto si hanno le radici:
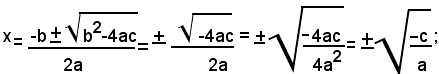
per tale motivo formula (5) si chiama formula risolutiva generale dell'equazione di secondo grado ax2+bx+c=0.
La formula risolutiva può quindi enunciarsi come segue:
le radici di un'equazione di secondo grado, a discriminante non negativo, sono date da una frazione che ha per numeratore il secondo coefficiente cambiato di segno, aumentato e diminuito della radice quadrata della differenza fra il quadrato del secondo coefficiente e il quadruplo del prodotto del primo coefficiente per il terzo; e per denominatore il doppio del primo coefficiente.
Da quanto visto, segue che l'equazione di secondo grado completa: ax2+bx+c=0, ammette soluzioni soltanto quando il suo discriminante risulta positivo o nullo. Pertanto, in pratica, per trovare le eventuali soluzioni di un'equazione di secondo grado ridotta a forma normale, si deve prima calcolare il suo discriminante ∆=b2-4ac, sostituendo ad a, b, c, i valori che queste lettere hanno nell'equazione data. Se esso risulta negativo, l'equazione non ammette soluzioni, mentre se risulta positivo o nullo, le soluzioni si trovano applicando la formula risolutiva (5). Se l'equazione non ha forma normale, cioè è intera e a coefficienti numerici, si deve trasformare a forma normale mediante i due principi noti di equivalenza; poi a questa si applica la formula risolutiva. Se l'equazione è intera e a coefficienti letterali, si deve trasformare a forma normale mediante lo stesso procedimento, ma in questo caso può darsi che per valori particolari delle lettere che compaiono nei coefficienti, l'equazione diventi di primo grado, oppure impossibile o si trasformi in un'identità. Quindi è necessario precisare di volta in volta questi particolari valori delle lettere; in ciò consiste la cosiddetta discussione dell'equazione.
Esempi:
1)-risolvere l'equazione ridotta a forma normale:
Si calcola il discriminante ∆=b2-4ac=49-24=25>0; siccome esso è maggiore di zero, l'equazione ammette due radici reali e distinte, date da:
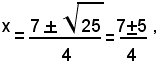
e, indicate con x1, x2, le due radici dell'equazione, si ha:
2)-risolvere l'equazione:
Riducendo l'equazione a forma normale, si ha:
12x2-67x+35=0.
Si calcola il discriminante ∆=b2-4ac=672-1680=4489-1680=2809>0; siccome esso è maggiore di zero, l'equazione ammette due radici reali e distinte, date da:
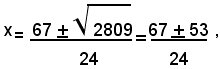
e, indicate con x1, x2, le due radici dell'equazione, si ha:
3)-risolvere l'equazione ridotta a forma normale:
Si calcola il discriminante ∆=b2-4ac=52-48=25-48=-23<0; siccome esso è minore di zero, l'equazione non ammette nessuna radice reale.
4)-risolvere l'equazione a coefficienti letterali:
a(a+1)x2+x- a(a-1)=0.
Se a=0, risulta: x=0; se a=-1, risulta: x-2=0, cioè x=2. In tali condizioni, l'equazione si è abbassata di grado è ammette rispettivamente le soluzioni 0 e 2.
Se a≠0 e a≠-1, si calcola il discriminante ∆=1+4a2(a+1)(a-1)=1+4a4-4a2=(1-2a2)2>0; siccome esso è maggiore di zero, l'equazione ammette due radici reali e distinte, date da:
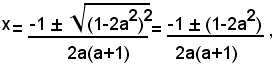
e, indicate con x1, x2, le due radici dell'equazione, si ha:
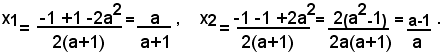
Formula risolutiva ridotta dell'equazione di secondo grado
La formula risolutiva dell'equazione di secondo grado si semplifica quando nell'equazione ridotta a forma normale, il secondo coefficiente è un numero intero pari o un'espressione contenente in evidenza il fattore 2. Infatti, in tal caso, l'equazione può scriversi:
ax2+2βx+c=0,
e la corrispondente formula risolutiva diventa:
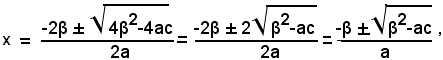
la quale si chiama formula risolutiva ridotta.
In questo caso il discriminante è dato da ∆=4β2-4ac=4(β2-ac).
si chiama discriminante ridotto.
Quindi, se il secondo coefficiente è un numero intero pari o un'espressione contenente in evidenza il fattore 2, si può dire che:
le radici sono date da una frazione che ha per numeratore la metà del secondo coefficiente cambiato di segno, aumentata e diminuita della radice quadrata della differenza fra il quadrato della metà del secondo coefficiente e il prodotto del primo e terzo coefficiente; e per denominatore il primo coefficiente.
Esempio: risolvere l'equazione 3x2-8x+4=0.
Dato che il secondo coefficiente dell'equazione è divisibile per 2, si calcola il discriminante ridotto:
Siccome esso è maggiore di zero, l'equazione ammette due radici reali e distinte, date da:
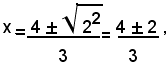
e quindi: x1=2, x2 =2/3.
Equazioni frazionarie
Le equazionI frazionarie si risolvono come quelle intere, numeriche o letterali. In questo caso, per togliere i denominatori, si devono moltiplicare ambo i membri dell'equazione per un multiplo comune dei denominatori. Se questa espressione non si annulla per nessun valore della x, per il secondo principio di equivalenza, le soluzioni della nuova equazione, sono anche soluzioni dell'equazione data. Ma se l'espressione si annulla per certi valori della x, bisogna escluderli.
Esempi
1)-risolvere l'equazione:
Il denominatore comune è: 5(2x+1)(x-3), quindi si moltiplicano ambo i membri dell'equazione per questa espressione. L'operazione è lecita se x≠-1/2, x≠3, perchè in tal modo il denominatore comune è diverso da zero. Liberando l'equazione dai denominatori ed eseguendo le opportune semplificazioni, si ha:
12x2-25x+2=0.
Si calcola il discriminante ∆=252-96=625-96=529=232>0; siccome esso è maggiore di zero, l'equazione ammette due radici reali e distinte, date da:
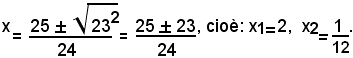
Siccome i valori trovati sono diversi da quelli che annullano i denominatori, cioè diversi da -1/2 e 3, si conclude che 2 e 1/12 sono le radici dell'equazione data.
Relazioni fra i coefficienti e le radici di un'equazione di secondo grado
Considerata l'equazione:
ax2+bx+c=0,
supposto il discriminante positivo o nullo, cioè ∆=b2-4ac≥0 e indicate con x1, x2, le due radici, distinte o coincidenti dell'equazione, risulta:
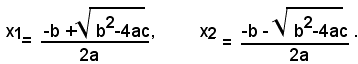
Si vuole calcolare il valore della somma e del prodotto di queste due radici.
Sommando membro a membro, si ha:
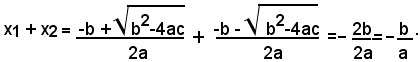
Moltiplicando membro a membro, si ha:
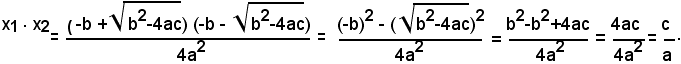
Quindi si ha:
Pertanto, si può enunciare la seguente regola:
in un'equazione di secondo grado ridotta a forma normale, con discriminante non negativo, la somma delle radici è uguale al rapporto fra il secondo coefficiente cambiato di segno e il primo e il prodotto delle radici è uguale al rapporto fra il termine noto e il primo coefficiente.
Nota bene
Si tenga presente che il prodotto della somma di due numeri per la loro differenza è uguale alla differenza dei due numeri, cioè:
e che se nell'equazione ax2+bx+c=0, il primo coefficiente a=1, cioè se l'equazione è del tipo x2+bx+c=0, si ha:
Pertanto, si può enunciare la seguente regola:
in un'equazione di secondo grado, con discriminante non negativo e primo coefficiente uguale a uno, la somma delle radici è uguale al secondo coefficiente cambiato di segno e il prodotto è uguale al termine noto.
Quindi, senza risolvere l'equazione, si può facilmente calcolare la somma e il prodotto delle radici di un'equazione con discriminante non negativo.
Esempi:
1)-determinare la somma e il prodotto delle radici della seguente equazione senza risolverla:
4x2-21bx+5=0.
Siccome il determinante ∆=212-80=441-80=361>0, si può applicare il teorema precedente, quindi si ha: x1 + x2 = 21/4, x1 . x2 = 5/4.
2)-Conoscendo che una radice dell'equazione
determinare l'altra radice senza risolverla.
Per il teorema precedentemente dimostrato, si ha:
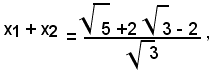
e tenendo conto del valore della radice x1, si ha:
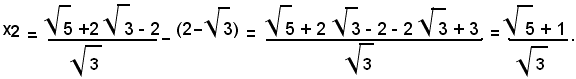
3)-determinare la somma dei quadrati delle radici senza risolvere l'equazione:
2x2 - (7 - 3)x + 3 (1- 3) =0,
Si osserva dapprima che il discriminante dell'equazione è positivo, come si verifica facilmente. Premesso ciò, ed essendo:
x12 + x22 = (x1 + x2)2 - 2x1x2 ,
e avendosi per il teorema precedente:
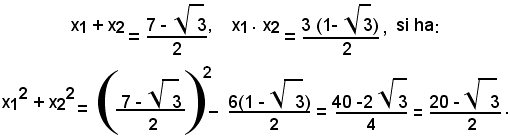
Come applicazioni del teorema dimostrato, si risolvono alcuni problemi:
1)-scrivere un'equazione di secondo grado che abbia come radici i numeri assegnati α e β.
A questo problema soddisfa l'equazione x2 - (α+β)x + αβ=0, di cui il suo primo coefficiente è uguale a uno, il secondo è uguale alla somma cambiata di segno dei due numeri α e β e il termine noto è uguale al prodotto di α e β. Infatti, le radici x1 e x2 di questa equazione sono reali e distinte perchè il discriminante: ∆=(α+β)2-4αβ=α2+β2+2αβ-4αβ=α2+β2-2αβ=(α-β)2>0 e, per il teorema precedentemente dimostrato esse verificano le relazioni: x1 + x2 = α+β, x1 . x2 = αβ, perciò risulta x1 = α e x2 = β o viceversa.
Regola - Per ottenere un'equazione di secondo grado, conoscendo le due radici, è sufficiente scrivere un'equazione di secondo grado avente il primo coefficiente uguale a uno, il secondo uguale alla loro somma cambiata di segno e il termine noto uguale al loro prodotto.
Esempio: scrivere l'equazione di secondo grado, avente per radici i numeri:
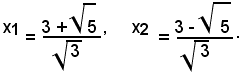
Essendo:
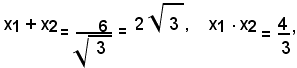
l'equazione richiesta è:
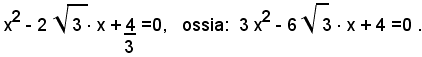
2)-Determinare due numeri conoscendo la loro somma s e il loro prodotto p.
I due numeri cercati, se esistono, sono le radici della seguente equazione:
x2 -sx + p = 0.
Infatti, se il discriminante ∆=s2-4p di questa equazione è positivo o nullo, si sa che la somma delle radici è uguale a s e il prodotto uguale a p, quindi s e p sono i due numeri richiesti.
Precisamente: se il discriminante ∆>0, i due numeri cercati sono reali e distinti, se il discriminante ∆=0, i due numeri cercati sono reali e coincidenti, se ∆<0 non esistono due numeri che abbiano per somma s e per prodotto p.
Esempio: trovare due numeri tali che:
I due numeri cercati sono le radici della seguente equazione:

Regola dei segni di Cartesio
Si consideri l'equazione completa di secondo grado: (1) ax2+bx+c=0 e si supponga che il suo discriminante sia positivo. Si vuole determinare una regola che permetta di stabilire il segno delle radici dell'equazione, dall'esame dei coefficienti della stessa.
Definizione - Si dice che i coefficienti a, b, c, dell'equazione (1), considerati nell'ordine scritto, presentano una permanenza, ogni volta che due di essi consecutivi hanno segni uguali; presentano invece una variazione, ogni volta che due di essi consecutivi hanno segni contrari.
Ad esempio, i coefficienti dell'equazione 2x2-3x-7=0 presentano una variazione e una permanenza, mentre i coefficienti dell'equazione 5x2+11x+3=0, presentano due permanenze.
Teorema di Cartesio - In un'equazione di secondo grado, completa, ridotta alla forma tipica e con discriminante positivo, ad ogni variazione presentata dai suoi coefficienti, corrisponde una radice positiva, e ad ogni permanenza una radice negativa; se l'equazione ha radici di segno contrario, è maggiore, in valore assoluto, quella positiva, se la variazione precede la permanenza, quella negativa, se la permanenza precede la variazione.
Nella dimostrazione si può supporre positivo il primo coefficiente a dell'equazione, perchè se non lo fosse, basterebbe moltiplicare ambo i membri dell'equazione per -1, per ottenere un'equazione equivalente alla data avente lo stesso numero di variazioni e permanenze.
1° Caso: si suppone che i coefficienti dell'equazione presentino due permanenze, cioè sia:
Si dimostra che le due radici dell'equazione sono negative.
Come è già noto, risulta: (1)
Siccome in questo caso a e c sono positivi, il prodotto delle radici risulta positivo e perciò le due radici devono avere segni uguali, cioè devono essere o entrambe positive o entrambe negative. Ma la somma delle radici, essendo a e b per ipotesi positivi, è negativa e quindi si deduce che le due radici x1 e x2 sono entrambe negative, come volevasi dimostrare.
2° Caso: si suppone che i coefficienti dell'equazione presentino due variazioni, cioè sia:
Si dimostra che le due radici dell'equazione sono positive.
In base alle (1) e alle ipotesi fatte, si vede che il prodotto delle radici risulta positivo e positiva è anche la loro somma, perciò le due radici sono entrambe positive, come volevasi dimostrare.
3° Caso: si suppone che i coefficienti dell'equazione presentino una variazione e una permanenza, cioè sia:
Si dimostra che una radice è positiva e l'altra negativa e inoltre, siccome la variazione precede la permanenza, che la radice positiva è, in valore assoluto, maggiore di quella negativa.
In base alle (1) e alle ipotesi fatte, il prodotto delle radici risulta negativo e perciò le radici x1 e x2 devono avere segni contrari, cioè essere una positiva e l'altra negativa. Siccome la somma delle radici è positiva, delle due radici è maggiore, in valore assoluto quella positiva.
4° Caso: si suppone che i coefficienti dell'equazione presentino una permanenza e una variazione, cioè sia:
Si dimostra che una radice è negativa e l'altra positiva e inoltre, siccome la permanenza precede la variazione, che la radice negativa è, in valore assoluto, maggiore di quella positiva. La dimostrazione è analoga a quella del 3° caso.
Esempi:
1)-nell'equazione 3x2-7x+2=0, il discriminante ∆=49-24=25>0, cioè positivo, perciò le due radici sono reali e distinte e poichè l'equazione presenta due variazioni, le radici sono entrambe positive.
2)-nell'equazione 5x2+9x+4=0, il discriminante ∆=81-80=1>0, cioè positivo, perciò le due radici sono reali e distinte e poichè l'equazione presenta due permanenze, le radici sono entrambe negative.
3)-nell'equazione 4x2-11x-3=0, il discriminante ∆=121-48=73>0, cioè positivo, perciò le due radici sono reali e distinte e poichè l'equazione presenta una variazione e una permanenza, le radici sono una positiva e l'altra negativa. Inoltre, poichè la variazione precede la permanenza, la radice positiva è, in valore assoluto, la maggiore.
4)-nell'equazione x2+3x-28=0, il discriminante ∆=9+112=121>0, cioè positivo, perciò le due radici sono reali e distinte e poichè l'equazione presenta una permanenza e una variazione, le radici sono di segno contrario. Inoltre, poichè la permanenza precede la variazione, è maggiore , in valore assoluto, la radice negativa.
5)-nell'equazione x2-3x+7=0, il discriminante ∆=9-28=-19<0, cioè negativo, perciò l'equazione non ammette soluzioni nel campo reale, quindi non ha senso parlare di radici positive o negative.
Scomposizione di un trinomio di secondo grado in fattori di primo grado
Si consideri il polinomio di secondo grado nella variabile x: (1) ax2+bx+c, e si supponga il discriminante ∆=b2-4ac>0, cioè positivo, in modo che l'equazione (2) ax2+bx+c=0, ottenuta uguagliando a zero il polinomio, ammetta due radici reali e distinte x1, x2. Le radici x1, x2 sono chiamate anche radici o zeri del trinomio (1).
Si ricordano ora le relazioni:
Di seguito, si ottiene:
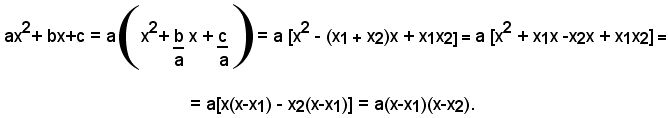
cioè: (3)
ax2+ bx + c = a(x-x1)(x-x2).
Quindi:
un trinomio di secondo grado nella variabile x, con discriminante positivo, si può scomporre in un prodotto di tre fattori, il primo dei quali è uguale al primo coefficiente del trinomio, il secondo è uguale al binomio dato dalla differenza tra la variabile x e la prima radice e il terzo uguale al binomio dato dalla differenza tra la variabile x e la seconda radice.
Se il discriminante ∆=0, si ha x1=x2, e dalla (3) segue:
ax2+ bx+c = a(x-x1)2.
ax2+ bx+c = a(x-x1)2.
Cioè:
un trinomio di secondo grado nella variabile x, con discriminante nullo, si può scomporre nel prodotto del primo coefficiente del trinomio, per il quadrato del binomio dato dalla differenza tra la variabile x e la radice dello stesso trinomio.
Esempi:
(1)-scomporre in fattori il polinomio: 3x2-7x+2.
Dalla risoluzione dell'equazione 3x2-7x+2=0, si ottengono le radici x1=2, x2=1/3, quindi si può scrivere: 3x2-7x+2 = 3(x-2)(x-1/3).
(2)-scomporre in fattori il polinomio: 3x2+30x+75.
(2)-scomporre in fattori il polinomio: 3x2+30x+75.
Dalla risoluzione dell'equazione 3x2+30x+75=0, si ottengono le radici x1=x2=-5, quindi si può scrivere: 3x2+30x+75 = 3(x+5)2.
(3)-scomporre in fattori il polinomio: 5x2-3x+2.
In questo caso il discriminante ∆=9-40=-39<0, cioè è negativo, perciò l'equazione non ammette soluzioni nel campo reale; segue che il polinomio dato non si può scomporre in fattori di primo grado, cioè, come suol dirsi, è irriducibile nel campo dei numeri reali.
Nota bene
La scomposizione in fattori primi di un polinomio di secondo grado, con discriminante positivo o nullo, è utile quando si deve semplificare una frazione algebrica, o ridurre allo stesso denominatore più frazioni algebriche.
Esempio: semplificare la frazione
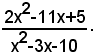
(3)-scomporre in fattori il polinomio: 5x2-3x+2.
In questo caso il discriminante ∆=9-40=-39<0, cioè è negativo, perciò l'equazione non ammette soluzioni nel campo reale; segue che il polinomio dato non si può scomporre in fattori di primo grado, cioè, come suol dirsi, è irriducibile nel campo dei numeri reali.
Nota bene
La scomposizione in fattori primi di un polinomio di secondo grado, con discriminante positivo o nullo, è utile quando si deve semplificare una frazione algebrica, o ridurre allo stesso denominatore più frazioni algebriche.
Esempio: semplificare la frazione
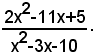
Si scompone il polinomio 2x2-11x+5 che figura al numeratore della frazione; dalla risoluzione dell'equazione 2x2-11x+5=0, si ottengono le radici x1=1/2, x2=5; perciò il numeratore si può scrivere: 2x2-11x+5 = 2(x-1/2)(x-5).
Si scompone il polinomio x2-3x-10 che figura al denominatore della frazione; dalla risoluzione dell'equazione x2-3x-10=0, si ottengono le radici x1=-2, x2=5; perciò il denominatore si può scrivere: x2-3x-10 = (x+2)(x-5). Quindi si ha:
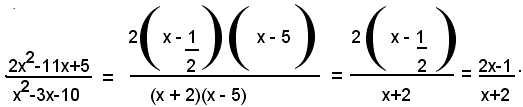
Risoluzione dei problemi sulle equazioni di secondo grado
1)-Determinare il valore della lettera m in modo che una delle radici dell'equazione di secondo grado; (1) 2x2 - (3m + 1)x + 2m - 4 =0, sia uguale a 7.
Siccome 7 è una radice dell'equazione (1), ciò significa che sostituendo tale valore nell'equazione (1), essa risulta soddisfatta; quindi si ha: 98 - 21m -7 + 2m - 4 = 0. Siccome quest'ultima è un'equazione di primo grado nell'incognita m, si trova facilmente m = 87/19.
2)-Determinare il valore della lettera m in modo che l'equazione: (2) x2 - (m + 1)x - (2m + 5)= 0, ammetta una sola radice.
Siccome l'equazione (2) ammette una sola radice, il suo discriminante dev'essere uguale a zero, cioè: ∆ = (m + 1)2 - 4(2m + 5) =0. Siccome quest'ultima è un'equazione di secondo grado nell'incognita m, i valori cercati per m sono le radici m1, m2 di tale equazione. Dalla risoluzione dell'equazione risulta m1 = -3, m2 = -7. Perciò l'equazione (2) avrà una sola soluzione quando alla lettera m si attribuisce il valore -3 oppure -7.
3)-Determinare per quali valori della lettera m l'equazione: (3) (m-2)x2 - 2mx + m - 3= 0, ammette radici reali.
Siccome l'equazione (3) ammette radici reali, il suo discriminante dev'essere positivo o nullo, Applicando la formula ridotta: ∆/4 = m2 - (m-2)(m - 3) ≥0, ossia, dopo le opportune semplificazioni: 5m ≥ 6/5, da cui m ≥ 6/5. Per m=6/5, essendo nullo il discriminante, l'equazione (3) avrà una sola radice, mentre per m>6/5 ammetterà due radici reali e distinte.
Equazioni irrazionali riconducibili a equazioni di primo e secondo grado
Sono irrazionali, ad esempio, le equazioni:
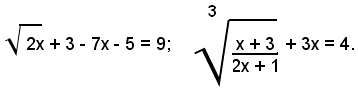
Non sono invece irrazionali, pur contenendo radicali, le equazioni:
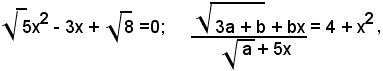
perchè l'incognita x non figura nei radicandi dei radicali contenuti nelle equazioni.
Per vedere come si deve procedere per risolvere le equazioni irrazionali, almeno nei casi più comuni, si considerano prima alcuni esempi:
1)-si consideri l'equazione irrazionale: (1)
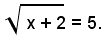
Si vede facilmente che l'equazione ammette una sola radice data da x=23.
Infatti, elevando al quadrato ambo i membri dell'equazione (1), si ha la seguente equazione razionale di primo grado equivalente alla data: x + 2 = 25, da cui x = 23.
2)-si consideri l'equazione irrazionale: (2)
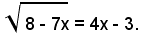
Elevando al quadrato ambo i membri dell'equazione (2), si ha la seguente equazione razionale di secondo grado: (3) 8 - 7x = (4x - 3)2, che ammette, come si vede facilmente, le due radici x1=1, x2=1/16. Si osserva ora che l'equazione (2) è soddisfatta da x1=1, non però da x2=1/16, perciò si può dire che le equazioni (2) e (3) non sono equivalenti.
Teorema - Se si elevano al quadrato ambo i membri di un'equazione, si ottiene un'altra equazione che ha tutte le eventuali soluzioni della data, ma che, in generale, ammette anche altre soluzioni.
Tale teorema sussiste anche quando si elevano ambo i membri di un'equazione algebrica a una qualsiasi potenza di esponente pari. Se invece si elevano ambo i membri di un'equazione algebrica a una potenza di esponente dispari, si ottiene un'equazione equivalente alla data.
Infatti, indicata con (1):
A(x) = B(x)
una qualsiasi equazione algebrica nell'incognita x, si consideri l'equazione algebrica (2)
[ A(x) ]2 = [ B(x) ]2 ,
ottenuta dalla (2) elevando ambo i membri al quadrato. La (2) si può anche scrivere sotto la forma:
[ A(x) ]2 - [ B(x) ]2 =0,
Isolando il radicale, si ha:
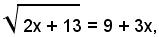
ed elevando al quadrato ambo i membri dell'equazione, si ottiene l'equazione razionale di secondo grado:
2x + 13 = (9 + 3x)2 ,
ossia, dopo facili calcoli:
8x2 + 52x + 68 =0,
le cui radici sono: x1=-2, x2=-34/9.
Di queste due radici solo la prima soddisfa l'equazione data, come è facile verificare.
Tale procedimento vale anche se l'equazione contiene un solo radicale di indice qualunque n; in tal caso, per eliminare il radicale, occorre elevare all'ennesima potenza ambo i membri dell'equazione.
2)-risolvere l'equazione:
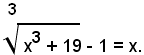
Isolando il radicale, si ha:
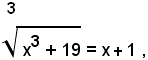
ed elevando al cubo ambo i membri dell'equazione, si ottiene:
x3 + 19 = x3 + 3x2 + 3x +1 ,
da cui, riducendo i termini simili, si ottiene l'equazione:
3x2 + x -1=0 ,
le cui radici sono: x1=2, x2=-3.In
questo caso si può isolare uno dei due radicali
ed elevare ambo i
membri dell'equazione al quadrato, oppure riunire i due radicali in uno
stesso membro trasportando tutti gli altri termini nell'altro
membro ed elevare al quadrato. In entrambi i casi si otterrà
un'equazione contenente un solo radicale quadratico, e percò ci
si ritroverà nel caso precedente.
Esempi:
1)-risolvere l'equazione:
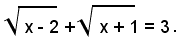
Isolando un radicale, si ha:
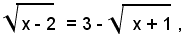
ed elevando al quadrato ambo i membri dell'equazione, si ottiene:
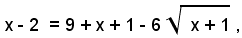
ossia:
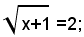
ed elevando nuovamente al quadrato ambo i membri, si ottiene l'equazione di primo grado:
x + 1 =4,
che ammette la soluzione x=3, che è anche soluzione dell'equazione data.
2)-risolvere l'equazione:
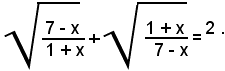
Elevando al quadrato ambo i membri dell'equazione, si ottiene:
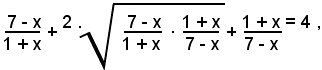
ossia:
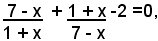
da cui, supposto x≠-1 e x≠7, si ha:
(7 - x)2 + (1 + x)2 -2(1 + x)(7 - x) =0.
Riducendo l'equazione a forma normale, si ha:
x2 - 6x +9 =0,
che ammette l'unica soluzione x=3, che è anche soluzione dell'equazione data, come si verifica facilmente.
3° Caso - L'equazione è intera e contiene tre radicali quadratici, eventualmente insieme a termini razionali, oppure contiene quattro radicali quadratici
In questo caso si lasciano due radicali in un membro e nell'altro si portano tutti gli altri termini, quindi si elevano al quadrato ambo i membri dell'equazione, con ciò si ottiene un'equazione che contiene al massimo due radicali quadratici, e così ci si ritrova nel secondo caso.
Esempi:
1)-risolvere l'equazione:
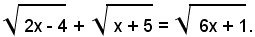
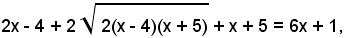
ossia: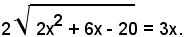
Elevando nuovamente al quadrato ambo i membri e riducendo i termini simili, si ha:
x2 - 24x + 80 =0,
le cui radici sono: x1=20, x2=4, che sono anche radici dell'equazione data, come si verifica facilmente.
2)-risolvere l'equazione:
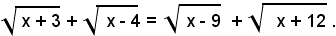
Elevando al quadrato ambo i membri dell'equazione, si ha:
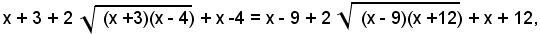
ossia:
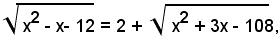
da cui, elevando nuovamente al quadrato ambo i membri, si ha:
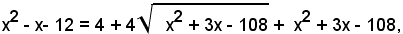
ossia:
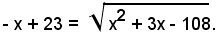
Elevando ancora al quadrato ambo i membri dell'equazione, dopo facili calcoli, si ha l'equazione di primo grado:
49x = 637,
che ammette come soluzione x=13, che è anche soluzione dell'equazione data, come si verifica facilmente.
4° Caso - L'equazione irrazionale non è intera
Esempi:
1)-risolvere l'equazione:
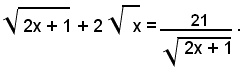
Riducendo a forma intera, si ha:
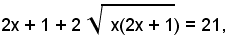
ossia:
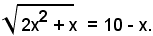
Elevando al quadrato ambo i membri e dopo facili calcoli, si ha:
x2 + 21x - 100 =0.
le cui radici sono: x1=4, x2= - 25. Solo la radice x1=4 soddisfa anche l'equazione data, come si può facilmente verificare.
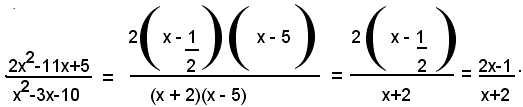
Risoluzione dei problemi sulle equazioni di secondo grado
1)-Determinare il valore della lettera m in modo che una delle radici dell'equazione di secondo grado; (1) 2x2 - (3m + 1)x + 2m - 4 =0, sia uguale a 7.
Siccome 7 è una radice dell'equazione (1), ciò significa che sostituendo tale valore nell'equazione (1), essa risulta soddisfatta; quindi si ha: 98 - 21m -7 + 2m - 4 = 0. Siccome quest'ultima è un'equazione di primo grado nell'incognita m, si trova facilmente m = 87/19.
2)-Determinare il valore della lettera m in modo che l'equazione: (2) x2 - (m + 1)x - (2m + 5)= 0, ammetta una sola radice.
Siccome l'equazione (2) ammette una sola radice, il suo discriminante dev'essere uguale a zero, cioè: ∆ = (m + 1)2 - 4(2m + 5) =0. Siccome quest'ultima è un'equazione di secondo grado nell'incognita m, i valori cercati per m sono le radici m1, m2 di tale equazione. Dalla risoluzione dell'equazione risulta m1 = -3, m2 = -7. Perciò l'equazione (2) avrà una sola soluzione quando alla lettera m si attribuisce il valore -3 oppure -7.
3)-Determinare per quali valori della lettera m l'equazione: (3) (m-2)x2 - 2mx + m - 3= 0, ammette radici reali.
Siccome l'equazione (3) ammette radici reali, il suo discriminante dev'essere positivo o nullo, Applicando la formula ridotta: ∆/4 = m2 - (m-2)(m - 3) ≥0, ossia, dopo le opportune semplificazioni: 5m ≥ 6/5, da cui m ≥ 6/5. Per m=6/5, essendo nullo il discriminante, l'equazione (3) avrà una sola radice, mentre per m>6/5 ammetterà due radici reali e distinte.
Equazioni irrazionali riconducibili a equazioni di primo e secondo grado
Sono irrazionali, ad esempio, le equazioni:
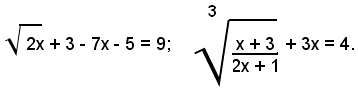
Non sono invece irrazionali, pur contenendo radicali, le equazioni:
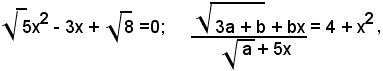
perchè l'incognita x non figura nei radicandi dei radicali contenuti nelle equazioni.
Per vedere come si deve procedere per risolvere le equazioni irrazionali, almeno nei casi più comuni, si considerano prima alcuni esempi:
1)-si consideri l'equazione irrazionale: (1)
Si vede facilmente che l'equazione ammette una sola radice data da x=23.
Infatti, elevando al quadrato ambo i membri dell'equazione (1), si ha la seguente equazione razionale di primo grado equivalente alla data: x + 2 = 25, da cui x = 23.
2)-si consideri l'equazione irrazionale: (2)
Elevando al quadrato ambo i membri dell'equazione (2), si ha la seguente equazione razionale di secondo grado: (3) 8 - 7x = (4x - 3)2, che ammette, come si vede facilmente, le due radici x1=1, x2=1/16. Si osserva ora che l'equazione (2) è soddisfatta da x1=1, non però da x2=1/16, perciò si può dire che le equazioni (2) e (3) non sono equivalenti.
Teorema - Se si elevano al quadrato ambo i membri di un'equazione, si ottiene un'altra equazione che ha tutte le eventuali soluzioni della data, ma che, in generale, ammette anche altre soluzioni.
Tale teorema sussiste anche quando si elevano ambo i membri di un'equazione algebrica a una qualsiasi potenza di esponente pari. Se invece si elevano ambo i membri di un'equazione algebrica a una potenza di esponente dispari, si ottiene un'equazione equivalente alla data.
Infatti, indicata con (1):
una qualsiasi equazione algebrica nell'incognita x, si consideri l'equazione algebrica (2)
[ A(x) ]2 = [ B(x) ]2 ,
ottenuta dalla (2) elevando ambo i membri al quadrato. La (2) si può anche scrivere sotto la forma:
[ A(x) ]2 - [ B(x) ]2 =0,
ossia:
[ A(x) - B(x) ] . [ A(x) + B(x) ] =0.
Questa equazione ha come soluzioni quelle delle due equazioni:
[ A(x) - B(x) ] . [ A(x) + B(x) ] =0.
Questa equazione ha come soluzioni quelle delle due equazioni:
[ A(x) - B(x) ] =0, [ A(x) + B(x) ] =0.
ossia della (1) A(x) = B(x) e della (3) A(x) = - B(x), e ciò prova il teorema enunciato.
Nota bene
Solo quando l'equazione (3) è impossibile, cioè non ammette soluzioni, allora le due equazioni (1) e (2) sono equivalenti.
Dal teorema dimostrato, segue che quando si è costretti al elevare al quadrato ambo i membri di un'equazione per risolverla, è necessario verificare infine se le soluzioni trovate sono soluzioni o no dell'equazione data.
Tipologia delle equazioni irrazionali
1° Caso - L'equazione è intera e contiene un solo radicale quadratico
In questo caso il radicale deve comparire da solo in uno dei due membri dell'equazione e poi si elevano ambo i membri al quadrato.
Esempi:
1)-risolvere l'equazione:
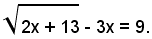
ossia della (1) A(x) = B(x) e della (3) A(x) = - B(x), e ciò prova il teorema enunciato.
Nota bene
Solo quando l'equazione (3) è impossibile, cioè non ammette soluzioni, allora le due equazioni (1) e (2) sono equivalenti.
Dal teorema dimostrato, segue che quando si è costretti al elevare al quadrato ambo i membri di un'equazione per risolverla, è necessario verificare infine se le soluzioni trovate sono soluzioni o no dell'equazione data.
Tipologia delle equazioni irrazionali
1° Caso - L'equazione è intera e contiene un solo radicale quadratico
In questo caso il radicale deve comparire da solo in uno dei due membri dell'equazione e poi si elevano ambo i membri al quadrato.
Esempi:
1)-risolvere l'equazione:
Isolando il radicale, si ha:
ed elevando al quadrato ambo i membri dell'equazione, si ottiene l'equazione razionale di secondo grado:
ossia, dopo facili calcoli:
8x2 + 52x + 68 =0,
le cui radici sono: x1=-2, x2=-34/9.
Di queste due radici solo la prima soddisfa l'equazione data, come è facile verificare.
Tale procedimento vale anche se l'equazione contiene un solo radicale di indice qualunque n; in tal caso, per eliminare il radicale, occorre elevare all'ennesima potenza ambo i membri dell'equazione.
2)-risolvere l'equazione:
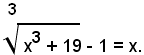
Isolando il radicale, si ha:
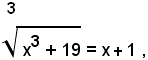
ed elevando al cubo ambo i membri dell'equazione, si ottiene:
x3 + 19 = x3 + 3x2 + 3x +1 ,
da cui, riducendo i termini simili, si ottiene l'equazione:
3x2 + x -1=0 ,
le cui radici sono: x1=2, x2=-3.
Queste due radici soddisfano l'equazione data, come è facile verificare.
2° Caso - L'equazione è intera e contiene due radicali quadratici con altri termini razionali
2° Caso - L'equazione è intera e contiene due radicali quadratici con altri termini razionali
Esempi:
1)-risolvere l'equazione:
Isolando un radicale, si ha:
ed elevando al quadrato ambo i membri dell'equazione, si ottiene:
ossia:
ed elevando nuovamente al quadrato ambo i membri, si ottiene l'equazione di primo grado:
x + 1 =4,
che ammette la soluzione x=3, che è anche soluzione dell'equazione data.
2)-risolvere l'equazione:
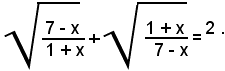
Elevando al quadrato ambo i membri dell'equazione, si ottiene:
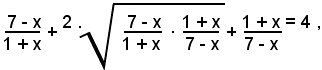
ossia:
da cui, supposto x≠-1 e x≠7, si ha:
(7 - x)2 + (1 + x)2 -2(1 + x)(7 - x) =0.
Riducendo l'equazione a forma normale, si ha:
che ammette l'unica soluzione x=3, che è anche soluzione dell'equazione data, come si verifica facilmente.
3° Caso - L'equazione è intera e contiene tre radicali quadratici, eventualmente insieme a termini razionali, oppure contiene quattro radicali quadratici
In questo caso si lasciano due radicali in un membro e nell'altro si portano tutti gli altri termini, quindi si elevano al quadrato ambo i membri dell'equazione, con ciò si ottiene un'equazione che contiene al massimo due radicali quadratici, e così ci si ritrova nel secondo caso.
Esempi:
1)-risolvere l'equazione:
Elevando al quadrato ambo i membri dell'equazione, si ha:
ossia:
Elevando nuovamente al quadrato ambo i membri e riducendo i termini simili, si ha:
x2 - 24x + 80 =0,
le cui radici sono: x1=20, x2=4, che sono anche radici dell'equazione data, come si verifica facilmente.
2)-risolvere l'equazione:
Elevando al quadrato ambo i membri dell'equazione, si ha:
ossia:
da cui, elevando nuovamente al quadrato ambo i membri, si ha:
ossia:
Elevando ancora al quadrato ambo i membri dell'equazione, dopo facili calcoli, si ha l'equazione di primo grado:
49x = 637,
che ammette come soluzione x=13, che è anche soluzione dell'equazione data, come si verifica facilmente.
4° Caso - L'equazione irrazionale non è intera
Esempi:
1)-risolvere l'equazione:
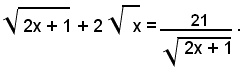
Riducendo a forma intera, si ha:
ossia:
Elevando al quadrato ambo i membri e dopo facili calcoli, si ha:
x2 + 21x - 100 =0.
le cui radici sono: x1=4, x2= - 25. Solo la radice x1=4 soddisfa anche l'equazione data, come si può facilmente verificare.