MIKY & GENNY
LOGARITMI ---> INDICE
Si è visto che, se a e b sono due numeri reali, tali che a>0, b>0, a≠1, l'equazione:
(1) ax=b,
ammette una ed una sola soluzione.
Questa soluzione, cioè il numero reale che soddisfa la (1), si indica con il simbolo logab e si legge logaritmo di b in base a.
Definizione - Si chiama logaritmo di un numero reale positivo b, rispetto alla base a, positiva e diversa dall'unità, quel numero reale α a cui bisogna elevare la base a, affinchè il valore della potenza sia uguale a b, cioè affinchè risulti:
Siccome il logaritmo di b in base α, si indica con
per definizione di logaritmo, si ha:
Per il teorema di esistenza e di unicità, dimostrato per le equazioni esponenziali nelle ipotesi che a>0, b>0, a≠1, esiste sempre ed è unico il logaritmo del numero b rispetto alla base a. In base alla definizione data, determinare il logaritmo del numero b rispetto alla base positiva a, con a≠1, vuol dire trovare l'esponente a cui si deve elevare la base a per ottenere il numero b.
Esempi
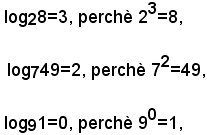
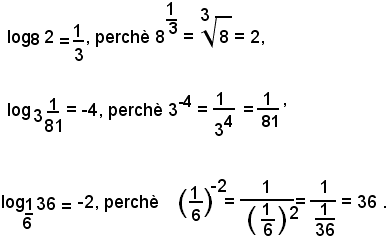
Siccome:

Dal teorema di esistenza e di unicità, dimostrato per le equazioni esponenziali e dalla definizione di logaritmo di un numero b rispetto ad una base a, segue:
-se a>1, i numeri maggiori di 1 hanno logaritmi positivi,
-se a>1, i numeri positivi minori di 1 hanno logaritmi negativi,
-se a è positiva e minore di 1, i numeri maggiori di 1 hanno logaritmi negativi,
-se a è positiva e minore di 1, i numeri positivi minori di 1 hanno logaritmi positivi,
Non si può parlare di:
-logaritmo di un numero rispetto alla base 1, perchè l'equazione 1x=b, con b≠1, non ammette soluzioni,
-logaritmo rispetto ad una base negativa o nulla, perchè la potenza ax è definita per solo per a>0 e poi quando a=0, l'equazione 0x=b, con b≠0, non ammette soluzioni,
-esistenza di un logaritmo di un numero negativo, perchè l'equazione ax=b, con b<0, non ammette soluzioni, in quanto e sempre ax>0.
Il logaritmo del numero 1, rispetto ad una qualsiasi base reale e positiva a, con a≠1, è uguale a 0, perchè risulta a0=1.
Non si può parlare di:
-logaritmo di un numero rispetto alla base 1, perchè l'equazione 1x=b, con b≠1, non ammette soluzioni,
-logaritmo rispetto ad una base negativa o nulla, perchè la potenza ax è definita per solo per a>0 e poi quando a=0, l'equazione 0x=b, con b≠0, non ammette soluzioni,
-esistenza di un logaritmo di un numero negativo, perchè l'equazione ax=b, con b<0, non ammette soluzioni, in quanto e sempre ax>0.
Il logaritmo del numero 1, rispetto ad una qualsiasi base reale e positiva a, con a≠1, è uguale a 0, perchè risulta a0=1.
ll logaritmo della base a è uguale ad 1, perchè risulta a1=a.
Tenendo presente che, quando la base di una potenza è maggiore di 1, la potenza aumenta all'aumentare dell'esponente, mentre quando la base è minore di 1, la potenza diminuisce, si può concludere che:
-se la base a è maggiore di 1, all'aumentare del numero b, aumenta anche il suo logaritmo; se invece la base a è positiva e minore di 1, all'aumentare del numero b, il logaritmo diminuisce, cioè, da
se a>1, segue
se 0<a<1, segue
logab<logac.
L'insieme di tutti i logaritmi dei numeri positivi, aventi una data base a, si chiama sistema di logaritmi a base a. Esistono infiniti sistemi di logaritmi perchè le possibili basi sono infinite.
Proprietà dei logaritmi
Si trattano ora alcune proprietà importanti dei logaritmi, le cui dimostrazioni si effettuano tenendo presente la definizione di logaritmo e le proprietà delle potenze. Questi teoremi valgono per qualsiasi base dei logaritmi, che dev'essere positiva e diversa da 1.
Teorema 1 - Il logaritmo del prodotto di due o più numeri positivi è uguale alla somma dei logaritmi dei singoli fattori del prodotto.
Indicando con a la base dei logaritmi e con b, c, due numeri reali positivi, cioè ci si limita per semplicità al caso di due soli fattori, si deve dimostrare che:
Infatti, ponendo
(3) x=logab, y=logac,
per definizione di logaritmo, si ha:
per definizione di logaritmo, si ha:
ax=b, ay=c,
ossia
axay=bc
e, per la nota proprietà delle potenze, risulta
ax+y=bc.
Da quest'ultima uguaglianza si vede che, elevando la base a all'esponente x+y, si ottiene il numero bc e quindi, per definizione di logaritmo, il numero x+y è il logaritmo in base a del numero bc, cioè:
loga(bc)=x+y
e per le (3) risulta
loga(bc)=logab+logac,
come volevasi dimostrare.
Nota bene
Nell'applicazione di questo teorema e di quelli futuri, è necessario che i numeri, dei quali si considerano i logaritmi, siano positivi.
Ad esempio, considerato il prodotto (x-5)(x-7), applicando il teorema 1, si ha:
a) loga(x-5)(x-7)=loga(x-5)+loga(x-7).
A tal punto, bisogna supporre di attribuire alla x solo quei valori che rendono positivi contemporaneamente i due polinomi x-5 e x-7, cioè attribuire alla x solo valori maggiori di 7.
Infatti, per x=3, dalla a) si ricava:
loga8=loga(-2)+loga(-4).
Tale uguaglianza è assurda, perchè non esistono i logaritmi dei numeri -2 e -4, esiste solo il logaritmo di 8.
e per le (3) risulta
loga(bc)=logab+logac,
come volevasi dimostrare.
Nota bene
Nell'applicazione di questo teorema e di quelli futuri, è necessario che i numeri, dei quali si considerano i logaritmi, siano positivi.
Ad esempio, considerato il prodotto (x-5)(x-7), applicando il teorema 1, si ha:
a) loga(x-5)(x-7)=loga(x-5)+loga(x-7).
A tal punto, bisogna supporre di attribuire alla x solo quei valori che rendono positivi contemporaneamente i due polinomi x-5 e x-7, cioè attribuire alla x solo valori maggiori di 7.
Infatti, per x=3, dalla a) si ricava:
loga8=loga(-2)+loga(-4).
Tale uguaglianza è assurda, perchè non esistono i logaritmi dei numeri -2 e -4, esiste solo il logaritmo di 8.
Esempio:
log2(8 x 32 x 64)=log28 + log232 + log264 = 3 + 5 + 6= 14.
Teorema 2 - Il logaritmo del quoziente di due numeri positivi è uguale alla differenza fra il logaritmo del dividendo ed il logaritmo del divisore.
Indicando con a la base dei logaritmi e con b, c, due numeri reali positivi, si deve dimostrare che:
Infatti, ponendo
per definizione di logaritmo, si ha:
Dividendo membro a membro le due uguaglianze, si ha:
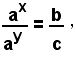
e per la nota proprietà delle potenze risulta
Da quest'ultima uguaglianza si vede che, elevando la base a all'esponente x-y, si ottiene il numero b/c e quindi, per definizione di logaritmo, il numero x-y è il logaritmo in base a del numero b/c, cioè:
e per le (5) risulta:
come volevasi dimostrare.
Teorema 3 - Il logaritmo di una potenza di un numero positivo ad esponente reale qualunque è uguale al prodotto dell'esponente della potenza per il logaritmo della base della potenza, cioè:
(6) logabc = c·logab.
Infatti, ponendo
(7) x=logab,
per definizione di logaritmo, si ha:
ax=b.
Elevando ambo i membri di questa uguaglianza allo stesso esponente c, si ottiene:
(ax)c=bc,
e per la nota proprietà delle potenze risulta
axc=bc.
Da quest'ultima uguaglianza si vede che, elevando la base a all'esponente xc, si ottiene il numero bc e quindi, per definizione di logaritmo, il numero xc è il logaritmo in base a del numero bc, cioè:
logabc=xc,
cioè per la (7):
logabc=c·logab,
come volevasi dimostrare.
Esempio:
log7495=5log749=5x2=10.
Teorema 4 - Il logaritmo di un radicale è uguale al quoziente del logaritmo del radicando per l'indice del radicale, cioè:
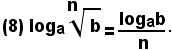
Questo teorema è un caso particolare del precedente; infatti:
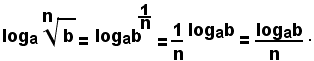
Esempio:
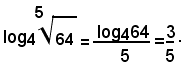
Nota bene
Dalle (2), (4), (6), (8), per la proprietà simmetrica dell'uguaglianza, si deducono i teoremi inversi di quelli dimostrati, tenendo conto che i numeri, dei quali si considerano i logaritmi, siano positivi.
1°) - La somma dei logaritmi di due o più numeri positivi è uguale al logaritmo del prodotto dei numeri, cioè:
logab+logac=loga(bc).
2°) - La differenza dei logaritmi di due numeri positivi è uguale al logaritmo del quoziente dei due numeri, cioè:
3°) - Il prodotto di un numero c per il logaritmo del numero positivo b è uguale al logaritmo della ciesima potenza di b, cioè:
4°) - Il quoziente fra il logaritmo del numero positivo b ed il numero intero positivo n è uguale al logaritmo della radice ennesima di b, cioè:
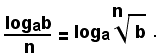
Esempio - Esprimere il logaritmo della seguente espressione aritmetica:
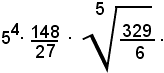
Per il teorema del logaritmo di un prodotto, si ha:
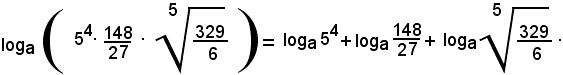
Pe i teoremi del logaritmo di una potenza, di un quoziente e di un radicale, l'uguaglianza si può scrivere:
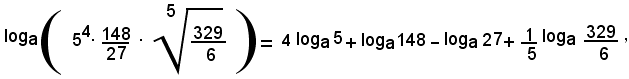
ossia
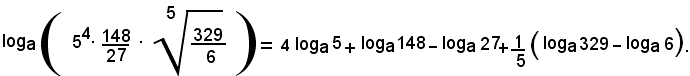
Passaggio da un sistema di logaritmi ad un altro
Siccome esistono infiniti sistemi di logaritmi, conoscendo il logaritmo di un numero positivo rispetto alla base a, si vuole trovare il logaritmo dello stesso numero rispetto ad un'altra base b.
Infatti, ponendo
(9) x=logaN, y=logbN,
Siccome esistono infiniti sistemi di logaritmi, conoscendo il logaritmo di un numero positivo rispetto alla base a, si vuole trovare il logaritmo dello stesso numero rispetto ad un'altra base b.
Infatti, ponendo
per definizione di logaritmo, si ha:
Considerando i logaritmi rispetto alla base a di ambo i membri, si ottiene:
logaby=logaN,
quindi per il 3°) teorema, si ha
ylogab=logaN,
da cui si ricava
e, assegnando alla y il valore espresso dalla seconda delle (9), si ha
Regola - ll logaritmo di un numero positivo N rispetto alla base b, è uguale al logaritmo dello stesso numero N rispetto alla base a per il reciproco del logaritmo di b rispetto alla base a.
Nota bene
Il numero
per il quale si deve moltiplicare il logaritmo logaN, per ottenere il logbN, non dipende dal numero N, ma soltanto dalle due basi a e b. Si può quindi dire che:
-i logaritmi dei numeri positivi rispetto alla base b, si ottengono tutti moltiplicando i logaritmi dei numeri positivi rispetto alla base a, per il numero fisso
Questo numero si chiama modulo di trasformazione per il passaggio dal sistema di base a al sistema di base b.
Quindi, si ha che: il logaritmo in base b di un numero è uguale al prodotto del logaritmo in base a, per il modulo di trasformazione.
Tra gl'infiniti sistemi di logaritmi, comunemente si considerano:
-il sistema dei logaritmi decimali a base 10, che si chiama anche sistema dei logaritmi volgari o di Briggs.
-il sistema dei logaritmi decimali a base e, numero irrazionale il cui valore approssimato per difetto a meno di 1/105 è uguale a 2,71828, che si chiama sistema dei logaritmi naturali, iperbolici o neperiani.
Tale sistema viene usato nella matematica superiore.
Logaritmi decimali
I logaritmi decimali si usano nei calcoli pratici e si indicano con logN, anzichè log10N, oppure con LogN. Siccome la base dei logaritmi decimali ovviamente è maggiore di 1, si può dire che:
-i logaritmi decimali dei numeri maggiori di 1 sono positivi,
-i logaritmi decimali dei numeri minori di 1 sono negativi,
-il logaritmo decimale di 1 è uguale a zero,
-il logaritmo decimale di 10 è uguale a uno.
Essendo quindi log10=1, per il teorema sul logaritmo di una potenza, si ha:
cioè: il logaritmo decimale di una potenza del 10, è uguale all'esponente di quella potenza.
Esempi
Si può dimostrare il seguente teorema, ma ci si limita solo all'enunciato:
-i logaritmi decimali dei numeri razionali positivi che non sono potenze di 10, sono numeri irrazionali.
Da questo teorema segue che: se si vuole esprimere il logaritmo decimale di un numero razionale positivo non potenza di 10 mediante un numero decimale, ci si deve accontentare di conoscere solo un suo valore approssimato, cioè la parte intera ed un certo numero di cifre decimali. In pratica, di un numero positivo non potenza di 10, si calcola sempre il logaritmo decimale con una prefissata approssimazione.
Caratteristica e mantissa del logaritmo
Definizione - La parte intera del logaritmo di un numero positivo si chiama caratteristica, mentre la parte decimale mantissa.
-si chiama parte intera di un numero, il più grande degl'interi che non superano il numero.
-si chiama parte decimale di un numero, la differenza tra il numero e la sua parte intera.
Da queste definizioni segue che, quando un numero non è intero, la sua parte intera è il più piccolo dei due numeri interi consecutivi tra cui il numero è compreso; quindi la parte decimale di un numero non intero è un numero positivo minore di 1. Pertanto, ogni numero risulta uguale alla sua parte intera più la sua parte decimale.
Esempi
1)-Trovare la parte intera e la parte decimale del numero 3,729.
Essendo:
3<3,729<4,
per le definizioni date, la parte intera del numero 3,729 è 3 e la sua parte decimale è 3,729-3=0,729. Si osservi che risulta 3,729=3+0,729, cioè il numero risulta uguale alla sua parte intera più la sua parte decimale.
2)-Trovare la parte intera e la parte decimale del numero 0,78.
Essendo:
0<0,78<1,
la parte intera è uguale a 0 e perciò la parte decimale è uguale a 0,78-0=0,78.
3)-Trovare la parte intera e la parte decimale del numero -5,459.
Essendo:
la parte intera è uguale a -6 e perciò la parte decimale è uguale a -5,459-(-6)=-5,459+6=0,541.
In tale esempio si poteva erroneamente dire che la parte intera del numero -5,459 era -5, anzichè -6, come è stato visto.
Da questi esempi si nota che la parte intera di un numero decimale può essere positiva, nulla o negativa, mentre la parte decimale è positiva e minore di 1, quindi:
-la caratteristica del logaritmo di un numero decimale può essere positiva, nulla o negativa, mentre la mantissa è positiva e minore di 1.
Caratteristica del logaritmo decimale di un numero
Si vuole vedere come si determina la caratteristica del logaritmo decimale di un numero positivo. A tale scopo si fanno prima le seguenti osservazioni:
-un numero maggiore o uguale a 1 è sempre compreso fra due successive potenze di 10 con esponente non negativo, ad esempio:
100<8,75<101; 102<782,42<103; 103≤1000<104; 103<4728,1<104; 104<54328,83<105;
100≤1<101.
In generale, come si vede dagli esempi suddetti, un numero N, avente la parte intera composta da n cifre, è compreso fra 10n-1 e 10n, cioè risulta:
10n-1≤N<10n.
-un numero positivo minore di 1 è sempre compreso fra due successive potenze con esponente non positivo del numero 10, ad esempio:
10-1<0,54<100; 10-2<0,0754<10-1; 10-3<0,0048<10-2; 10-3<0,00327<10-2; 10-4≤0,0001<10-3.
In generale, come si vede anche da questi ultimi esempi, un numero positivo M minore di 1, avente in totale n zeri che precedono la prima cifra significativa, contando fra questi anche quello che precede la virgola, è compreso fra 10-n e 10-(n-1), cioè risulta:
10-n≤M<10-(n-1).
Teorema 1 - La caratteristica del logaritmo decimale di un numero maggiore o uguale ad 1, è uguale al numero delle cifre della parte intera del numero dato, diminuito di 1.
Infatti, se N è un numero avente la parte intera composta da n cifre, si può scrivere, come si è visto,
10n-1≤N<10n.
Siccome la base dei logaritmi decimali è maggiore di 1, vale la disuguaglianza seguente, già stabilita in precedenza:
log10n-1≤logN<log10n
e, per il teorema del logaritmo di una potenza, si ha
(n-1)log10≤logN<nlog10,
tenendo conto che log10=1, in definitiva si ha
Queste disuguaglianze esprimono che la parte intera di logN è n-1, come volevasi dimostrare.
Teorema 2 - La caratteristica del logaritmo decimale di un numero positivo minore di 1, è uguale a tante unità negative quanti sono gli zeri che precedono la prima cifra significativa del numero dato, compreso quello che precede la virgola.
Infatti, se M è un numero postiivo minore di 1 avente complessivamente n zeri che precedono la sua prima cifra significativa, compreso lo zero che precede la virgola, si può scrivere, come si è visto,
da cui segue
log10-n≤logM<log10-(n-1),
cioè
-nlog10≤logM<-(n-1)log10,
tenendo conto che log10=1, in definitiva si ha
Queste disuguaglianze esprimono che la parte intera di logM è -1, come volevasi dimostrare.
Esempi - La caratteristica del logaritmo di:

Mantissa del logaritmo decimale di un numero
Teorema - La mantissa dei logaritmi decimali di due numeri positivi, che differiscono solo per il posto occupato dalla virgola, sono uguali.
Infatti, se a e b sono due numeri che differiscono solo per il posto occupato dalla virgola, supposto, ad esempio, b>a, si può certamente scrivere:
dove n è un numero intero positivo. Passando ai logaritmi, si ha:
ossia
logb=loga+log10n,
cioè
Questa uguaglianza mostra che loga e logb differiscono per un numero intero n; pertanto le loro mantisse sono uguali.
Tale teorema ha un'importanza pratica notevole; infatti, la mantissa del logaritmo decimale di un numero non dipende dal posto occupato dalla virgola nello stesso numero, se è decimale, ed anche dagli eventuali zeri posti alla destra del numero, se questo è intero.
Esempi
-I logaritmi dei seguenti numeri:
28,83; 2,883; 288,3; 0,02883; 2883; 288300
hanno la stessa mantissa; quindi:
-nella ricerca della mantissa del logaritmo decimale di un numero, si può trascurare la virgola e non tenere conto degli eventuali zeri finali.
Calcolo di un logaritmo di un numero positivo - Forma mista - Tavole dei logaritmi
Sia b un numero positivo, indicati con c la caratteristica e con m la mantissa, per calcolare il logaritmo decimale di un numero positivo b, si procede come segue:
-si determina la caratteristica c,
-si determina la mantissa m,
-se la caratteristica è positiva, logb=c+m è positivo.
Esempi
1)-se la caratteristica di un numero b è c=5 e la mantissa m=0,34215, risulta logb=5+0,34215=5,34215.
2)-se la caratteristica è negativa, logb=c+m è negativo.
c=-3, m=0,48312, risulta: logb=-3+0,48312=-2,51688.
In tale caso, invece di eseguire la somma algebrica della caratteristica e della mantissa, è utile lasciarle distinte e scrivere ogni logaritmo negativo sotto la cosiddetta forma mista e precisamente:
si scrive la caratteristica e, invece di anteporle il segno meno, lo si scrive sopra e poi, separata da una virgola, si scrive la mantissa. Quindi nell'esempio considerato, invece di scrivere: logb=-2,51688, si può scrivere:
Ora resta da risolvere il problema del calcolo della mantissa del logaritmo di un numero decimale con l'approssimazione desiderata.
Nell'algebra elementare, non è possibile trattare dei metodi, con cui si procede nel calcolo della mantissa dei logaritmi decimali, con l'approssimazione desiderata, si può dire soltanto che esistono delle tavole, chiamate tavole dei logaritmi, nelle quali sono raccolte, con una data approssimazione, con 5 o più decimali, le mantisse dei logaritmi decimali dei numeri interi compresi entro certi limiti. In queste tavole sono riportate, in modo dettagliato, tutte le istruzioni necessarie per la loro consultazione.
Nota bene
In seguito saranno riportate parzialmente le tavole dei logaritmi.
Si vede come i logaritmi decimali permettono di eseguire, in modo semplice, operazioni aritmetiche molto complicate, o addirittura di esecuzione praticamente impossibile; infatti, i teoremi dimostrati,1°), 2°), 3°), 4°):
1°) - La somma dei logaritmi di due o più numeri positivi è uguale al logaritmo del prodotto dei numeri;
2°) - La differenza dei logaritmi di due numeri positivi è uguale al logaritmo del quoziente dei due numeri;
3°) - Il prodotto di un numero c per il logaritmo del numero positivo b è uguale al logaritmo della ciesima potenza di b;
4°) - Il quoziente fra il logaritmo del numero positivo b ed il numero intero positivo n è uguale al logaritmo della radice ennesima di b;
permettono di sostituire le operazioni di moltiplicazione, divisione, potenza, ed estrazione di radice, in modo ordinato, con le operazioni più semplici di addizione, sottrazione, moltiplicazione e divisione.
Prima di trattare le applicazioni dei logaritmi, si definisce il cologaritmo di un numero.
Definizione - Si chiama cologaritmo di un numero positivo, l'opposto del logaritmo del numero stesso e si indica con colog, cioè si pone:
cologb=-logb.
Da questa definizione segue che:
-se il logaritmo di un numero positivo è positivo, il suo cologaritmo è negativo,
-se il logaritmo è negativo, il cologaritmo è positivo.
E' conveniente usare la forma mista usata per i logaritmi negativi anche per i cologaritmi negativi. Si mostra ora, con degli esempi, un modo rapido per trovare il cologaritmo di un numero, noto il logaritmo dello stesso numero.
Esempi
1)-Se risulta:
(10) logb=2,31427,
si ha
cologb=-2,31427=-(2+0,31427),
ossia
cologb=-2-0,31427.
Togliendo e aggiungendo 1, si ottiene:
cologb=(-2-1)+1-0,31427=-3+0,68573
e quindi
Confrontando le uguaglianze (10) e (11), si nota che il cologb si può ottenere dal logb come segue:
-la caratteristica del cologb si ottiene da quella del logb aumentandola di +1 e cambiando il segno alla somma,
-ogni cifra della mantissa del cologb si ottiene sottraendo da 9 la corrispondente cifra di posto uguale di quella di logb, ad eccezione dell'ultima, che si ottiene sottraendo da 10 l'ultima cifra della mantissa di logb.
2)-Se risulta
si ha:
cologb=-(-2+0,54851)=+2-0,54851
e, togliendo e aggiungendo 1, si ottiene
cologb=(+2-1)+(1-0,54851)=1+0,45149,
cioè
Confrontando le uguaglianze (12) e (13), anche in tale esempio, il cologb si può ottenere dal logb con la stessa regola applicata nel primo esempio.
Si può quindi enunciare la seguente regola pratica per il passaggio dal logaritmo di un numero al suo cologaritmo:
-la caratteristica del cologb si ottiene da quella del logb aumentandola di +1 e cambiando il segno alla somma,
-la mantissa del cologb si ottiene da quella del logaritmo sottraendo ogni sua cifra da 9, tranne l'ultima cifra significativa, che si sottrae da 10.
Esempi

Operazioni con i logaritmi
Nelle varie operazioni che si effettuano con i logaritmi si deve tenere presente che la mantissa è sempre positiva o nulla e che la caratteristica è un numero intero relativo.
Addizione
Tale operazione sui logaritmi si può effettuare anche quando la caratteristica è negativa, osservando che le mantisse si sommano normalmente, perchè sono tutte positive o nulle, e che l'eventuale riporto positivo si somma algebricamente con le caratteristiche.
Esempi
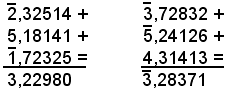
Sottrazione
Per la sottrazione di due logaritmi basta aggiungere al minuendo il cologaritmo del sottraendo.
Esempi

Moltiplicazione
Per la moltiplicazione di un logaritmo per un numero intero occorre osservare che:
-se la caratteristica è positiva o nulla, tale operazione si identifica nella solita moltiplicazione di un numero numero decimale per un numero intero.
-se la caratteristica è negativa, basta separare la caratteristica dalla mantissa e poi applicare la proprietà distributiva della moltiplicazione.
-se il numero intero è composto da una sola cifra, il calcolo si effettua come nelle solite moltiplicazioni di un numero decimale per un numero intero, tenendo conto che, al termine della moltiplicazione delle cifre decimali, l'eventuale riporto è positivo e quindi va sommato algebricamente al prodotto ottenuto moltiplicando la caratteristica per il numero intero.
Esempi

Nelle varie operazioni che si effettuano con i logaritmi si deve tenere presente che la mantissa è sempre positiva o nulla e che la caratteristica è un numero intero relativo.
Addizione
Tale operazione sui logaritmi si può effettuare anche quando la caratteristica è negativa, osservando che le mantisse si sommano normalmente, perchè sono tutte positive o nulle, e che l'eventuale riporto positivo si somma algebricamente con le caratteristiche.
Esempi
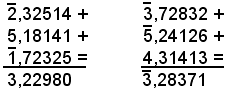
Sottrazione
Per la sottrazione di due logaritmi basta aggiungere al minuendo il cologaritmo del sottraendo.
Esempi

Moltiplicazione
Per la moltiplicazione di un logaritmo per un numero intero occorre osservare che:
-se la caratteristica è positiva o nulla, tale operazione si identifica nella solita moltiplicazione di un numero numero decimale per un numero intero.
-se la caratteristica è negativa, basta separare la caratteristica dalla mantissa e poi applicare la proprietà distributiva della moltiplicazione.
-se il numero intero è composto da una sola cifra, il calcolo si effettua come nelle solite moltiplicazioni di un numero decimale per un numero intero, tenendo conto che, al termine della moltiplicazione delle cifre decimali, l'eventuale riporto è positivo e quindi va sommato algebricamente al prodotto ottenuto moltiplicando la caratteristica per il numero intero.
Esempi

Divisione
Per la divisione di un logaritmo per un numero intero, si procede nel solito modo, se la caratteristica del logaritmo è positiva o nulla. Quando invece la caratteristica è negativa, occorre distinguere il caso in cui essa è multipla del divisore, oppure no. Nel primo caso il quoziente si ottiene dividendo separatamente per il numero intero la caratteristica e la mantissa.
Esempio
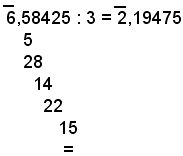
Quando invece la caratteristica non è multipla del divisore, si separa la caratteristica dalla mantissa e poi si aggiungono alla caratteristica tante unità negative quante bastano per renderla multipla del divisore ed altrettante unità positive si aggiungono alla mantissa; in tal modo il valore complessivo non viene modificato. Si applica infine la proprietà distributiva.
Esempi
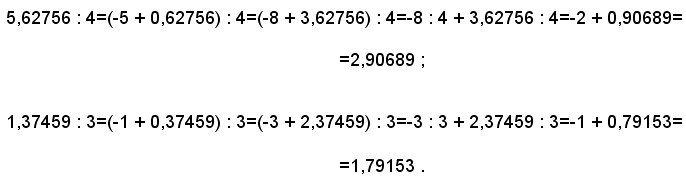
Si osservi infine che se si devono moltiplicare o dividere fra loro due logaritmi in forma mista, conviene eseguire le operazioni con le solite regole, abbandonando la forma mista.
Esempio:
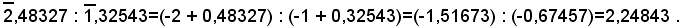
Servendosi dei logaritmi, si vuole ora calcolare il valore di alcune espressioni aritmetiche.
Esempi
1)-Calcolare un valore approssimato del prodotto
X = 412,6 x 0,00358 x 9,278 x 0,063 .
Applicando il teorema relativo alla somma dei logaritmi di due o più numeri positivi, che è uguale al logaritmo del prodotto dei numeri, si ha:
logX = log(412,6 x 0,00358 x 9,278 x 0,063 = log412,6 + log0,00358 + log 9,278 + log0,063.
Applicando le tavole e sommando, si ottiene:
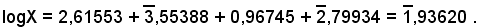
Risalendo dal logaritmo al numero corrispondente, si trova approssimativamente:
X=0,86338 .
2)-Calcolare un valore approssimato del quoziente
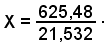
Applicando il teorema relativo alla differenza dei logaritmi di due numeri positivi, che è uguale al logaritmo del quoziente dei due numeri, si ha:
logX = log 625,48 - log21,532 = log 625,48 + colog21,532.
Usando le tavole, facendo un'interpolazione (che sarà trattata in seguito) e addizionando, si ha:
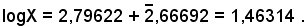
da cui si trova approssimativamente
X = 29,05 .
3)-Calcolare un valore approssimato della potenza
X = 35,483.
Applicando il teorema relativo al prodotto di un numero c per il logaritmo del numero positivo b, che è uguale al logaritmo della ciesima potenza di b, si ha:
logX =3log35,48 .
Usando le tavole, si ha:
logX =3 x 1,54998 = 4,64994 ,
da cui si trova approssimativamente
X = 44662 .
4)-Calcolare un valore approssimato del radicale
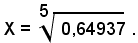
Applicando il teorema relativo al al quoziente fra il logaritmo del numero positivo b ed il numero intero positivo n è uguale al logaritmo della radice ennesima di b, si ha:
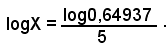
Usando le tavole, si ha:
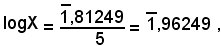
da cui si trova approssimativamente
X = 0,91726 .
Applicazioni dei logaritmi nella risoluzione delle equazioni esponenziali
E' noto che si chiama equazione esponenziale ogni equazione in cui l'incognita figura come esponente di una o più potenze. L'equazione esponenziale più semplice è:
ax = b ,
dove a e b sono numeri positivi e quando a è diverso da 1, ammette una ed una sola soluzione. Per risolvere questa equazione, si prendono i logaritmi decimali di ambo i membri e si ottiene:
xloga = logb ,
da cui si ha la soluzione
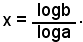
Esempi
1)-L'equazione
15x =728,6
ammette come soluzione
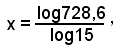
cioè, approssimativamente
x = 2,43 .
2)-L'equazione
0,7x =0,4
ammette come soluzione
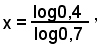
cioè, approssimativamente
x = 2,566 .
E' già noto comunque che in alcuni casi si trova la soluzione dell'equazione esponenziale del tipo considerato, senza ricorrere ai logaritmi.
Esempi

5)-L'equazione 62-x 3x+1= 864, che per note proprietà sulle potenze si può scrivere sotto la forma
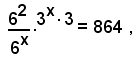
ossia
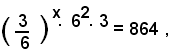
cioè
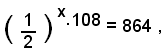
od anche
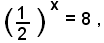
da cui
x = -3 ,
che è l'unica soluzione dell'equazione data.
Si possono risolvere, senza l'impiego dei logaritmi, anche le equazioni esponenziali il cui primo e secondo membro sono, o si possono mettere in tale forma, potenze con la stessa base.
Esempi
1)-Risolvere l'equazione esponenziale
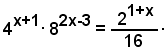
L'equazione si può scrivere sotto la forma
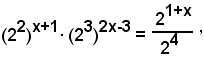
per le note proprietà delle potenze, si ha;
(22)x+1 (23)2x-3 = 21+x-4 ,
ossia
22x+2+6x-9 = 2x-3 ,
cioè
28x-7 = 2x-3 ,
Dall'uguaglianza delle potenze e delle loro basi si deduce l'uguaglianza degli esponenti, pertanto si ha:
8x - 7 = x - 3 ,
ossia
7x = 4 ,
da cui
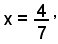
che è l'unica soluzione dell'equazione data.
2)-Risolvere l'equazione esponenziale
(3x+1)x-2 93x+2 = 81x+2 .
L'equazione si può scrivere sotto la forma
3(x+1)(x-2) 32(3x+2) = 34(x+2) ,
ossia
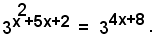
Dall'uguaglianza delle potenze e delle loro bas, si deduce l'uguaglianza degli esponenti, pertanto si ha l'equazione:
x2 + 5x +2 = 4x + 8 ,
ossia
x2 + x - 6 = 0 ,
le cui radici sono x1 = 2, x2 = -3.
Quindi l'equazione esponenziale ammette due soluzioni date dai numeri 2 e -3.
Per risolvere equazioni esponenziali di tipo più generale di quelle considerate in precedenza, non è possibile fornire una regola, pertanto ci si limita ad indicare con alcuni esempi il modo di risolvere alcuni tipi particolari.
1° Caso - EquazionI esponenziali il cui primo e secondo membro sono, o si possono mettere, sotto forma di potenze con base diversa.
Esempi
1)-Risolvere l'equazione esponenziale
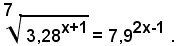
Prendendo i logaritmi di ambo i membri, si ottiene:
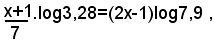
da cui
x(14log7,9-log3,28)= log3,28 + 7log7,9
e quindi
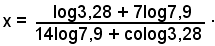
Con l'uso delle tavole, si trova approssimativamente
x = 0,56 .
2)-Risolvere l'equazione esponenziale
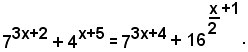
Per le note proprietà delle potenze, si può scrivere;
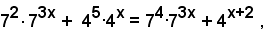
ossia
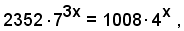
cioè
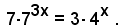
Prendendo i logaritmi di ambo i membri, si ottiene:
log7 + 3xlog7 = log3 + xlog4 ,
ossia
x(3log7 - log4) = log3 - log7 ,
da cui
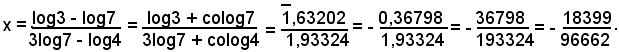
2° Caso - Equazioni esponenziali riconducibili ad una delle forme:
amx + b = 0,
am2x + bmx + c = 0 .
Posto (1) mx = y, le equazioni suddette diventano equazioni algebriche, rispettivamente di primo e di secondo grado. Se queste due equazioni ammettono radici positive, e si sostituiscono nella (1), si ottengono equazioni che permettono di calcolare i valori della x.
Esempi
1)-Risolvere l'equazione esponenziale
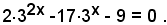
Posto:
(*) 3x =
y,
si ottiene la seguente equazione algebrica di secondo grado
2y2 - 17y - 9 = 0 .
le cui radici sono y1 = 9, y2 =-1/2.
Tenendo conto della posizione (*), si hanno le seguenti due equazioni:
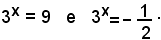
La prima ha per soluzione x=2, mentre la seconda non ammette soluzioni, quindi l'equazione data ammette l'unica soluzione x=2.
2)-Risolvere l'equazione esponenziale
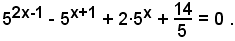
Per le note proprietà sulle potenze, si può scrivere
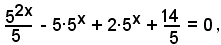
ossia
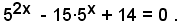
Posto:
(**) 5x = y,
si ottiene la seguente equazione algebrica di secondo grado
y2 - 15y - 14 = 0 .
le cui radici sono y1 = 14, y2 =-1
Equazioni logaritmiche
log(x2 -6) = log(5x + 8) .
Bisogna prima osservare che i logaritmi contenuti nell'equazione suddetta hanno significato soltanto per valori della x tali da rendere positivi entrambi i polinomi (x2 - 6) e (5x + 8).Premesso ciò, passando dai logarimi ai numeri, si ottiene l'equazione
x2 -6 = 5x + 8 ,
ossia
x2 - 5x - 14 = 0 ,
le cui radici sono x1 = -2, x2 = 7. E' accettabile soltanto la seconda soluzione, perchè per x=-2 i logaritmi dell'equazione perdono di significato.
2)-Risolvere l'equazione
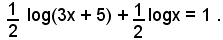
Bisogna prima osservare che i logaritmi contenuti nell'equazione suddetta hanno significato soltanto per valori della x tali da rendere positivi entrambi i polinomi (3x + 5) e x.
Premesso ciò, servendosi degl'inversi dei teoremi sui logaritmi, l'equazione si può scrivere
sotto la forma
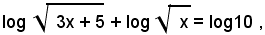
ossia
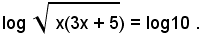
Passando dai logaritmi ai numeri, si ottiene:
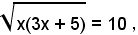
ossia
x(3x + 5) = 100 ,
cioè
3x2 + 5x -100 =0 ,
le cui radici sono x1 = 5, x2 = -20/3. E' accettabile soltanto la radice positiva.
3)-Risolvere il sistema
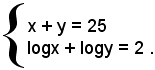
Si ha:
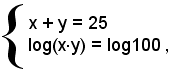
ossia
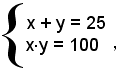
le cui soluzioni sono
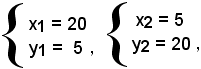
entrambe accettabili.
LE TAVOLE LOGARITMICHE
Di solito, le tavole dei logaritmi sono a 5 cifre decimali e riportano soltante le mantisse dei logaritmi dei numeri da 1 a 9999, poichè la caratteristica si ricava dal computo delle cifre della parte intera o degli zeri che precedono la prima cifra non nulla mediante l'applicazione dei due teoremi della caratteristica. Quindi, le tavole forniscono l'approssimazione al centomillesimo, che nei calcoli ordinari è sufficiente. Di seguito si riporta, a titolo di esempio, la tavola dei logaritmi dei numeri da 4500 a 4800.
Esse permettono di risolvere i due problemi seguenti:1)-ricerca del logaritmo dato il numero;
2)-ricerca del numero dato il logaritmo (ricerca dell'antilogaritmo).
Ciascuno dei due problemi presenta due casi:
a)-il numero è contenuto nelle tavole (è composto al massimo di 4 cifre tra intere e decimali), oppure non è contenuto nelle tavole (è composto da più di 4 cifre tra intere e decimali);
b)-la mantissa del logaritmo è contenuta nelle tavole oppure no.
1° Problema - 1° Caso: il numero dato è contenuto nelle tavole
La caratteristica è data dai teoremi della cararatteristica e di solito non si trova sulle tavole.
La mantissa del logaritmo si legge direttamente sulle tavole nella colonna m. log, vedi tavola suddetta.
Esempi
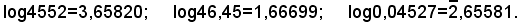
1° Problema - 2° Caso: il numero dato non è contenuto nelle tavole perchè ha più di 4 cifre
REGOLO CALCOLATORE
Il regolo calcolatore è uno strumento con il quale si possono eseguire in modo rapido determinate operazioni con numeri interi e decimali, ad esempio moltiplicazioni, divisioni, quadrati, radici quadrate, ecc., con risultati che in pratica danno sufficienti approssimazioni. I primi tipi sono stati costruiti in legno, quelli più recenti in "alastron", materiale sintetico indeformabile e indilatabile nonchè difficile a rompersi.
Esso è formato da un regolo, striscia orizzontale, detto fisso, che è incavato secondo la sua lunghezza in modo da formare una scalanatura anch'essa rettangolare nella quale scorre un'altro regolo più piccolo, detto scorrevole, i cui bordi combaciano perfettamente con quelli del regolo fisso.
REGOLO FISSO
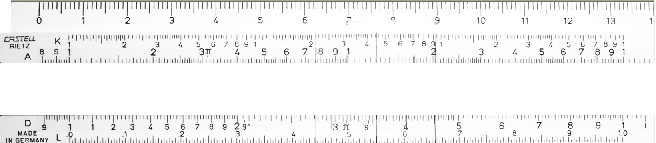
REGOLO SCORREVOLE

Una parte accessoria del regolo calcolatore è il corsoio, il quale abbraccia in larghezza il regolo ed è guidato da altre due scanalature sui margini del fisso. Si tratta di un telaietto quadrato o rettangolare di materiale trasparente, celluloide, che porta incisa una linea perpendicolare alla lunghezza del regolo, che ha lo scopo di rendere più agevole e precisa la lettura del numero sulle scale del regolo.
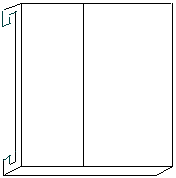
REGOLO CALCOLATORE

Se si considerano i due bordi del fisso prospicenti la scanalatura centrale e i due bordi dello scorrevole con quelli combacianti, si hanno quattro bordi sui quali si segnano le scale a due a due identiche e perfettamente uguali, che prendono il nome di scale superiori e scale inferiori a seconda che, per chi guarda il regolo in modo da leggervi, quelle sono le superiori e le inferiori.
FORMAZIONE DELLE SCALE INFERIORI
Fissata ad arbitrio la lunghezza a del regolo, di solito cm 25, sui bordi inferiori del fisso e dello scorrevole si riportano i segmenti le cui misure sono:
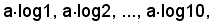
segnando però negli estremi i numeri 1, 2, 3, ..., 10,
cioè gli antilogaritmi delle misure suddette. Risulta che le nove parti in cui resta suddivisa la lunghezza del regolo non sono uguali, ma dalla prima all'ultima sono di grandezze decrescenti, così come decrescono le differenze tra due logaritmi consecutivi dei numeri da 1 10, i quali sono: 0,000000; 0,30103; 0,47712; 0,60206; 0,69897; 0,77815; 0,84510; 0,90309; 0,95424; 1. Nell'origine della scala si segna 1 (e non 0, essendo il log1=0) e nell'estremo si segna 10 (essendo log10=1). L'intervallo fra i due estremi si chiama segmento base del regolo. Si hanno così le scale inferiori; esse sono logaritmiche, ma le suddivisioni sono distinte dai numeri corrispondenti.
FORMAZIONE DELLE SCALE SUPERIORI
Sui bordi superiori del fisso e dello scorrevole si segnano, sulla stessa lunghezza, non una ma due scale identiche alle precedenti, perfettamente uguali fra loro, in modo che ciascuna sia di metà lunghezza di quella inferiore.

Risulta che, rispetto a quelli delle scale inferiori, i numeri a, 2, 3, ..., 10, corrispondono ai valori:
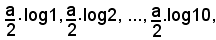
SUDDIVISIONE DELLE SCALE
Il tratto 1-2 delle scale inferiori, che è il più lungo, si divide ordinariamente in 100 parti logaritmiche; il tratto 2-3, 3-4, 4-5 in 20 parti, i rimanenti, che sono via via più corti, soltanto in 10 parti. Nelle scale superiori, ciascuna di metà lunghezza di quelle inferiori, le suddivisioni si fanno nello stesso modo, ma specialmente nei regoli di forma ridotta (di lunghezza cm 15), il loro numero si pùo ridurre alla metà di quello delle scale inferiori.
LETTURA DEI NUMERI SULLE SCALE
Sul regolo, con le suddivisioni così apportate (la figura sottostante è quella di un regolo completo), si possono leggere numeri di due cifre, la prima data dal numero che corrisponde ad una linea di divisione principale e in scrittura più grande e la seconda ad una linea di divisione secondaria.
Si possono leggere anche numeri di tre cifre, se si conviene di considerare quale terza cifra, quella che corrisponde ad una divisione intermedia tra due divisioni segnate sulla scala, divisione apportata a giudizio dell'occhio umano e della propria sensibilità. Agevola il compito di queste suddivisioni la linea incisa sul corsoio che può meglio far osservare quale sia la divisione più conveniente.
Si deduce intanto che il regolo non è adatto per il calcolo di operazioni con numeri composti da più di 3 cifre, fra intere e decimali, se si escudono gli zeri che eventualmente precedono la prima cifra diversa da zero o seguono l'ultima.
Il calcolo di operazioni con più di 3 cifre potrebbe condurre ad errori non indifferenti, specialmente se il regolo presenta qualche difetto nella graduazione o nella costruzione, come capita alle volte per quelli in commercio.
E' facile riconoscere inoltre che alla stessa suddivisione che nella scala del regolo indica, ad esempio, il numero 1,2 si può leggere indifferentemente 12, oppure 120, ecc., oppure 0,12, oppure 0,012, ecc. così come sulla riga centrimetrata si può leggere 12 cm, oppure 120 mm, oppure 1,2 dm, oppure 0,12 m, ecc. Basta a tale scopo immaginare che l'unità di misura sia di 10, 100, 1000, ... volte più piccola o più grande.
Identiche considerazioni si fanno per le scale superiori, con l'avvertenza che in esse si leggono bene solo i numeri di due cifre; per quelli di 3 cifre, dovendo ricorrere alla suddivisione visiva, data la piccolezza dei tratti, la lettura è poco esatta.
I numeri da 10 a 100, si leggono generalmente sulla scala a destra.
Nella figura suddetta sono riportati per la lettura i numeri 236; 23,6, 2,36; 0,236; 0,0236; ... nella scala inferiore del fisso; i numeri 27, 39, 87, ... nella scala superiore a destra del fisso.
PRINCIPIO SU CUI E' COSTRUITO IL REGOLO
Gli orli di due doppi decimetri devono combaciare e devono avere lo zero, l'uno, il due, ... l'uno di fronte all'altro. Se si fa scorrere uno dei dei doppi decimetri sull'altro, ad esempio, in modo che lo zero dello scorrevole venga a coincidere con il 4 del fisso, si trova ora combaciati 1 e 5; 2 e 6; 3 e 7; ecc. Si può verificare che un numero dello scorrevole aggiunto al 4 del fisso dà per somma il numero del fisso con il quale combacia; che la differenza fra i due numeri combacianti dà il numero 4; ed infine che la differenza fra i due numeri del fisso dà quello dello scorrevole.
Ad esempio, se si sceglie la coppia combaciante 5 e 9, si ha: 4+5=9; 9-5=4 e infine 9-4=5.
La semplice lettura dei numeri sui doppi decimetri dà immediatamente la somma dei numeri 4 e 5 e le differenze dei numeri 9 e 4 oppure 9 e 5. Ma la somma non supera 20, come le differenze non possono avere per minuendo un numero maggiore di 20.
Però, se si leggesse 40 mm, 50 mm, 90 mm, la somma sarebbe ancora 90 e al massimo si potrebbe avere per somma 200 con i 2 doppi decimetri. Sostituendo i decimillesimi, centimillesimi, ecc., la somma potrebbe raggiungere qualunque numero e così il minuendo delle differenze. E' logico che si potrà leggere m 0,65, m 0,09 ecc. e la somma e la differenza sarebbero estese ai numeri razionali.
Si procede ora allo stesso modo con il regolo
Ad esempio, facendo combaciare l'1 dello scorrevole (l'estremo sinistro), con il 2 del fisso di una qualunque delle scale, si troverà il 2 dello scorrevole di fronte al 4, il 3 di fronte al 6, il 4 di fronte all'8, ...del fisso. In questa posizione, il regolo mostra i seguenti risultati:
1)-il prodotto del numero sul fisso, combaciante con l'1 dello scorrevole, per quello dello scorrevole combaciante con l'altro del fisso, che ne è il prodotto,
2)-il quoziente dei numeri sull fisso, che è quello dello scorrevole.
Infatti, si ha: 2x3=6, 2x4=8, ecc.; viceversa, 8:4=2, 6:3=2, ecc.; infine, 8:2=4, 6:2=3, ecc.
In effetti, alla somma dei numeri sui doppi centimetri, corrisponde il prodotto sul regolo.
Infatti, ad esempio, 2 sul regolo è log2 e 3 è log3; ma log2+log3=log(2x3)=log6, che sulla scala del regolo è segnato 6, quindi 2x3=6.
Alla differenza log6-log3=log(6:3)=log2, che sulla scala del regolo è segnato 2, corrisponde il quoziente 6:2=3.
Quindi, segue che:
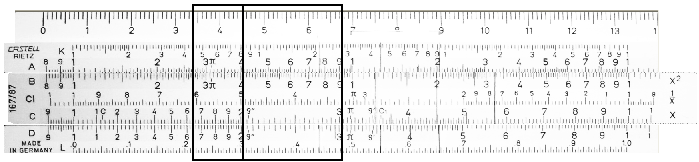
-dati due numeri r e s, per avere il prodotto con il regolo, basta addizionare i due segmenti corrispondenti ad r e s uno sul fisso e l'altro sullo scorrevole dopo aver reso il segmento dello scorrevole adiacente a quello del fisso. La somma delle misure dei segmenti, essendo somma di logaritmi, per il noto teorema dul logaritmo del prodotto, corrisponde al prodotto dei numeri, che si legge sul fisso in corrispondenza dell'estremo del segmento s dello scorrevole.
Avendo addizionato un segmento del fisso ad uno dello scorrevole, per avere un segmento del fisso loro somma, viceversa, togliendo a questo segmento quello del fisso, si avrà quello dello scorrevole, e togliendo quello dello scorrevole si avrà quello del fisso, a queste operazioni sui segmenti, corrispondono le seguenti sui logaritmi:
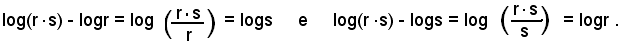
Il quoziente dei due numeri si ottiene con una semplice lettura sul regolo.
Esempi
1)-Calcolare, con la scala inferiore, il prodotto 2,5 x 3,4 = 8,50.
Deve combaciare l'1 dello scorrevole con il 2,5 del fisso; si legge poi sul fisso il numero che combacia con 3,4 dello scorrevole. La linea del corsoio unisce il 3, 4 dello scorrevole con 85 del fisso. Siccome il numero delle cifre intere del prodotto è dato dalla somma delle cifre delle parti intere meno una, e in tale caso dà 1+1-1=1, il prodotto è 8,5.
2)-Calcolare, con la scala inferiore, il prodotto 4,7 x 16 = 75,2.
Deve combaciare l'1 dello scorrevole con il 4,7 del fisso; si porta poi la linea del corsoio su 1,6 dello scorrevole e si legge il numero 752 sotto la linea del corsoio sul fisso. Il numero delle cifre della parte intera del prodotto è 1+2-1=2, ed il prodotto è 75,2.
3)-Calcolare, con la scala inferiore, il prodotto 8,5 x 2,3.
Con l'estremo sinistro dello scorrevole, coincidente con l'8,5 del fisso, l'operazione non sarebbe possibile perchè 2,3 dello scorrevole si troverebbe fuori dalla lunghezza del fisso. In questo caso si usa (*) l'estremo destro dello scorrevole e si procede allo stesso modo:
8,5 x 2,3 =19,55 .
L'estremo destro dello scorrevole si fa coincidere con 8,5 del fisso; si porta la linea del corsoio su 2,3 dello scorrevole. In corrispondenza si legge sul fisso il prodotto. Il numero delle cifre della parte intera, nel caso che si usa l'estremo destro è uguale alla somma delle cifre delle parti intere dei fattori.(*)-se
il regolo avesse non una scala inferiore, ma due identiche e
adiacenti come le due della superiore, usando l'estremo sinistro il
prodotto si leggerebbe sulla scala di destra. Usare l'estremo destro,
dunque, significa spostare il regolo di tutta la sua lunghezza per
portarlo sulla scala stessa nella posizione che esso avrebbe se si
dovesse leggere sulla seconda scala. Si osservi che lo scorrevole
capita fuori del fisso quando il prodotto della prima cifra dell'uno e
dell'altro dei fattori supera 10.
Nota bene
Se il prodotto della prima cifra, diversa da zero, del moltiplicando e del moltiplicatore, non tenendo conto delle virgole, supera 10, lo scorrevole esce fuori del fisso; in tale caso si usa l'estremo destro dello scorrevole e le scale superiori. Con le scale superiori e con lo stesso procedimento delle inferiori, si avrebbe:
8,5 x 2,3 =19,5(5) .
L'estremo sinistro dello scorrevole si porta a combaciare con 8,5 del fisso della scala superiore a sinistra, si sposta il corsoio in modo da sovrapporre la linea su 2,3 dello scorrevole e si legge il prodotto 19,5 sul fisso coincidente con la linea del corsoio sulla seconda scala superiore. Qui si deve osservare che, adoperando le scale superiori, non può aversi nel prodotto la quarta cifra, perchè è difficile decidere ad occhio quale sia la divisione da scegliersi. Si può però notare che il prodotto delle due ultime cifre dei numeri dati 5x3, ha appunto come ultima cifra il 5.
4)-Calcolare il prodotto 3,14 x 2,65.
Sui regoli è di solito segnata la divisione corrispondente a π (costante ciclometrica del valore 3,14159), che risulta segnato in grassetto nella figura seguente.
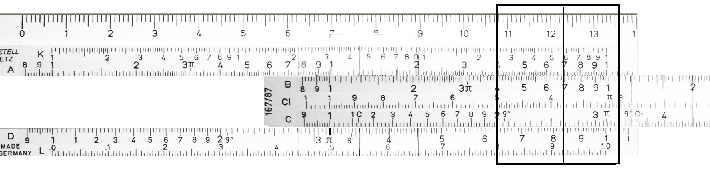
Si porta a combaciare l'estremo dello scorrevole con π, si porta la linea del corsoio su 2,65 dello scorrevole ed in corrispondenza si legge il prodotto sul fisso.
Quoziente
Esempi
1)-Calcolare il quoziente 82 : 34 = 2,4.
Si porta 34 dello scorrevole a combaciare con 82 del fisso, il quoziente si trova sul fisso combaciante con l'estremo sinistro.
Il numero delle cifre intere del quoziente è dato dalla differenza delle cifre delle parti intere del dividendo e del divisore aumentata di 1, se si è usato l'estremo sinistro, dalla sola differenza, se si è usato l'estremo destro.
2)-Calcolare il quoziente 2 : 46,5 = 0,043.
Si porta 46,5 dello scorrevole a combaciare con 2 del fisso, Siccome l'estremo destro esce fuori, il quoziente si legge in corrispondenza dell'estremo destro (come si è osservato in precedenza e nelle note). Lo stesso per le scale superiori.
Le cifre del quoziente sono date da 1-2=-1. Alle differenze negative corrispondono tanti zeri dopo la virgola quante sono le unità negative.
Quadrati
Basterebbe effettuare il prodotto della base per se stessa.
L'osservazione del regolo chiuso convince subito che i numeri delle scale superiori sono i quadrati dei corrispondenti delle scale inferiori. Sono infatti in corrispondenza 1 e 1, 2 e 4, 3 e 9, 4 e 16; ed anche, ad esempio, 2,3 in corrispondenza di 5,29, 7 con 49, ecc.
Del resto, le gradazioni delle scale inferiori sono doppie di quelle superiori; ma 2loga=loga2, quindi per il noto teorema sul logaritmo di una potenza, deve aversi sulle scale superiori il quadrato dei corrispondenti numeri di quelle inferiori.
Le cifre decimali della parte intera sono date ancora dalle regole sul prodotto e, più semplicemente, sono il doppio meno una delle cifre della parte intera del numero, se il quadrato si legge sulla prima scala superiore, e il doppio, se si legge sulla seconda scala superiore.
Radice quadrata
Inversamente all'operazione di quadrato, si ha che la radice quadrata è il numero della scala inferiore corrispondente al numero che invece si deve leggere su una scala superiore (regolo chiuso).
Esempi
1)-Calcolare la radice quadrata seguente:
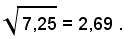
Si legge il numero nella prima scala superiore quando il numero delle cifre del radicando è dispari, come in questo caso (le cifre decimali si considerano sempre a coppie e se è necessario si aggiunge uno zero a destra dell'ultima cifra). Se il numero delle cifre è dispari, il primo gruppo non supera 9 e la prima cifra della radice, dovendo non superare 3, si troverà nella prima metà del regolo. Si sa dall'aritmetica quante cifre ha la parte intera della radice.
2)-Calcolare la radice quadrata seguente:
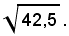
Tale radice vale anche come 42,50; numero pari di cifre.
Si legge nella seconda scala superiore: in corrispondenza, nella inferiore, si trova 6,4, che è la radice richiesta.
Quarta potenza
E' il quadrato del quadrato.
Cubo di un numero
E' il prodotto del numero per il suo quadrato.
E' preferibile eseguirlo nel modo seguente, perchè comporta il minor numero di spostamenti del regolo.
Se il numero di cui si cerca il cubo è minore di 4,64, si fissa l'estremo sinistro dello scorrevole sul numero del fisso ci cui si cerca il cubo.
Lo stesso numero, letto sullo scorrevole nella scala superiore, combacia con il numero della scala superiore del fisso che è il cubo.
Per la divisione di un logaritmo per un numero intero, si procede nel solito modo, se la caratteristica del logaritmo è positiva o nulla. Quando invece la caratteristica è negativa, occorre distinguere il caso in cui essa è multipla del divisore, oppure no. Nel primo caso il quoziente si ottiene dividendo separatamente per il numero intero la caratteristica e la mantissa.
Esempio
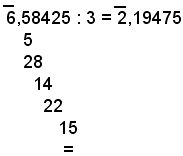
Quando invece la caratteristica non è multipla del divisore, si separa la caratteristica dalla mantissa e poi si aggiungono alla caratteristica tante unità negative quante bastano per renderla multipla del divisore ed altrettante unità positive si aggiungono alla mantissa; in tal modo il valore complessivo non viene modificato. Si applica infine la proprietà distributiva.
Esempi
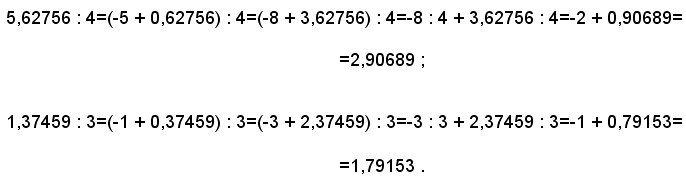
Si osservi infine che se si devono moltiplicare o dividere fra loro due logaritmi in forma mista, conviene eseguire le operazioni con le solite regole, abbandonando la forma mista.
Esempio:
Servendosi dei logaritmi, si vuole ora calcolare il valore di alcune espressioni aritmetiche.
Esempi
1)-Calcolare un valore approssimato del prodotto
X = 412,6 x 0,00358 x 9,278 x 0,063 .
Applicando il teorema relativo alla somma dei logaritmi di due o più numeri positivi, che è uguale al logaritmo del prodotto dei numeri, si ha:
logX = log(412,6 x 0,00358 x 9,278 x 0,063 = log412,6 + log0,00358 + log 9,278 + log0,063.
Applicando le tavole e sommando, si ottiene:
Risalendo dal logaritmo al numero corrispondente, si trova approssimativamente:
X=0,86338 .
2)-Calcolare un valore approssimato del quoziente
Applicando il teorema relativo alla differenza dei logaritmi di due numeri positivi, che è uguale al logaritmo del quoziente dei due numeri, si ha:
logX = log 625,48 - log21,532 = log 625,48 + colog21,532.
Usando le tavole, facendo un'interpolazione (che sarà trattata in seguito) e addizionando, si ha:
da cui si trova approssimativamente
X = 29,05 .
3)-Calcolare un valore approssimato della potenza
X = 35,483.
Applicando il teorema relativo al prodotto di un numero c per il logaritmo del numero positivo b, che è uguale al logaritmo della ciesima potenza di b, si ha:
logX =3log35,48 .
Usando le tavole, si ha:
logX =3 x 1,54998 = 4,64994 ,
da cui si trova approssimativamente
X = 44662 .
4)-Calcolare un valore approssimato del radicale
Applicando il teorema relativo al al quoziente fra il logaritmo del numero positivo b ed il numero intero positivo n è uguale al logaritmo della radice ennesima di b, si ha:
Usando le tavole, si ha:
da cui si trova approssimativamente
X = 0,91726 .
Applicazioni dei logaritmi nella risoluzione delle equazioni esponenziali
E' noto che si chiama equazione esponenziale ogni equazione in cui l'incognita figura come esponente di una o più potenze. L'equazione esponenziale più semplice è:
dove a e b sono numeri positivi e quando a è diverso da 1, ammette una ed una sola soluzione. Per risolvere questa equazione, si prendono i logaritmi decimali di ambo i membri e si ottiene:
da cui si ha la soluzione
Esempi
1)-L'equazione
15x =728,6
ammette come soluzione
cioè, approssimativamente
x = 2,43 .
2)-L'equazione
ammette come soluzione
cioè, approssimativamente
x = 2,566 .
E' già noto comunque che in alcuni casi si trova la soluzione dell'equazione esponenziale del tipo considerato, senza ricorrere ai logaritmi.
Esempi

5)-L'equazione 62-x 3x+1= 864, che per note proprietà sulle potenze si può scrivere sotto la forma
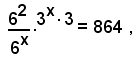
ossia
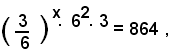
cioè
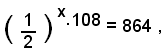
od anche
da cui
x = -3 ,
che è l'unica soluzione dell'equazione data.
Si possono risolvere, senza l'impiego dei logaritmi, anche le equazioni esponenziali il cui primo e secondo membro sono, o si possono mettere in tale forma, potenze con la stessa base.
Esempi
1)-Risolvere l'equazione esponenziale
L'equazione si può scrivere sotto la forma
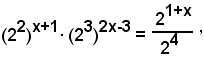
per le note proprietà delle potenze, si ha;
ossia
22x+2+6x-9 = 2x-3 ,
cioè
28x-7 = 2x-3 ,
Dall'uguaglianza delle potenze e delle loro basi si deduce l'uguaglianza degli esponenti, pertanto si ha:
ossia
7x = 4 ,
da cui
che è l'unica soluzione dell'equazione data.
2)-Risolvere l'equazione esponenziale
(3x+1)x-2 93x+2 = 81x+2 .
L'equazione si può scrivere sotto la forma
3(x+1)(x-2) 32(3x+2) = 34(x+2) ,
ossia
Dall'uguaglianza delle potenze e delle loro bas, si deduce l'uguaglianza degli esponenti, pertanto si ha l'equazione:
ossia
x2 + x - 6 = 0 ,
le cui radici sono x1 = 2, x2 = -3.
Quindi l'equazione esponenziale ammette due soluzioni date dai numeri 2 e -3.
Per risolvere equazioni esponenziali di tipo più generale di quelle considerate in precedenza, non è possibile fornire una regola, pertanto ci si limita ad indicare con alcuni esempi il modo di risolvere alcuni tipi particolari.
1° Caso - EquazionI esponenziali il cui primo e secondo membro sono, o si possono mettere, sotto forma di potenze con base diversa.
Esempi
1)-Risolvere l'equazione esponenziale
Prendendo i logaritmi di ambo i membri, si ottiene:
da cui
x(14log7,9-log3,28)= log3,28 + 7log7,9
e quindi
Con l'uso delle tavole, si trova approssimativamente
x = 0,56 .
2)-Risolvere l'equazione esponenziale
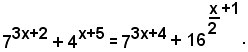
Per le note proprietà delle potenze, si può scrivere;
ossia
cioè
Prendendo i logaritmi di ambo i membri, si ottiene:
log7 + 3xlog7 = log3 + xlog4 ,
ossia
x(3log7 - log4) = log3 - log7 ,
da cui
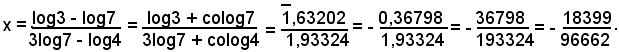
2° Caso - Equazioni esponenziali riconducibili ad una delle forme:
amx + b = 0,
am2x + bmx + c = 0 .
Posto (1) mx = y, le equazioni suddette diventano equazioni algebriche, rispettivamente di primo e di secondo grado. Se queste due equazioni ammettono radici positive, e si sostituiscono nella (1), si ottengono equazioni che permettono di calcolare i valori della x.
Esempi
1)-Risolvere l'equazione esponenziale
Posto:
si ottiene la seguente equazione algebrica di secondo grado
le cui radici sono y1 = 9, y2 =-1/2.
Tenendo conto della posizione (*), si hanno le seguenti due equazioni:
La prima ha per soluzione x=2, mentre la seconda non ammette soluzioni, quindi l'equazione data ammette l'unica soluzione x=2.
2)-Risolvere l'equazione esponenziale
Per le note proprietà sulle potenze, si può scrivere
ossia
Posto:
(**) 5x = y,
si ottiene la seguente equazione algebrica di secondo grado
y2 - 15y - 14 = 0 .
le cui radici sono y1 = 14, y2 =-1
Tenendo conto della posizione (**), si hanno le seguenti due equazioni:
5x = 1, 5x = 14 .
La prima ha per soluzione x=0; dalla seconda si ricava:
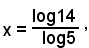
quindi, x = 1,639 approssimativamente.
5x = 1, 5x = 14 .
La prima ha per soluzione x=0; dalla seconda si ricava:
quindi, x = 1,639 approssimativamente.
Equazioni logaritmiche
Un'equazione si dice logaritmica quando in essa compare il logaritmo dell'incognita, o qualche espressione contenente l'incognita.
Per risolvere un'equazione logaritmica, servendosi degl'inversi dei teoremi sui logaritmi, si dovrà scrivere un'equazione della forma:
logA(x) = logB(x),
dove A(x) e B(x) sono espressioni algebriche contenenti l'incognita. I valori dell'incognita, dovendo rendere uguali i logaritmi, delle due espressioni A(x) e B(x), devono soddisfare l'equazione
(1) A(x) = B(x) .
E' bene ricordare che non vale la proprietà inversa, cioè una soluzione della (1) non può soddisfare l'equazione data. Ciò si verificherà per quelle soluzioni della (1) che fanno perdere di significato ad almeno un logaritmo dell'equazione data. Perciò, dopo aver risolto la (1), bisogna verificare se le soluzioni trovate soddisfano o no l'equazione data.
Esempi
1)-Risolvere l'equazione logaritmica
Per risolvere un'equazione logaritmica, servendosi degl'inversi dei teoremi sui logaritmi, si dovrà scrivere un'equazione della forma:
logA(x) = logB(x),
dove A(x) e B(x) sono espressioni algebriche contenenti l'incognita. I valori dell'incognita, dovendo rendere uguali i logaritmi, delle due espressioni A(x) e B(x), devono soddisfare l'equazione
(1) A(x) = B(x) .
E' bene ricordare che non vale la proprietà inversa, cioè una soluzione della (1) non può soddisfare l'equazione data. Ciò si verificherà per quelle soluzioni della (1) che fanno perdere di significato ad almeno un logaritmo dell'equazione data. Perciò, dopo aver risolto la (1), bisogna verificare se le soluzioni trovate soddisfano o no l'equazione data.
Esempi
1)-Risolvere l'equazione logaritmica
log(x2 -6) = log(5x + 8) .
Bisogna prima osservare che i logaritmi contenuti nell'equazione suddetta hanno significato soltanto per valori della x tali da rendere positivi entrambi i polinomi (x2 - 6) e (5x + 8).
ossia
le cui radici sono x1 = -2, x2 = 7. E' accettabile soltanto la seconda soluzione, perchè per x=-2 i logaritmi dell'equazione perdono di significato.
2)-Risolvere l'equazione
Bisogna prima osservare che i logaritmi contenuti nell'equazione suddetta hanno significato soltanto per valori della x tali da rendere positivi entrambi i polinomi (3x + 5) e x.
Premesso ciò, servendosi degl'inversi dei teoremi sui logaritmi, l'equazione si può scrivere
sotto la forma
ossia
Passando dai logaritmi ai numeri, si ottiene:
ossia
x(3x + 5) = 100 ,
cioè
3x2 + 5x -100 =0 ,
le cui radici sono x1 = 5, x2 = -20/3. E' accettabile soltanto la radice positiva.
3)-Risolvere il sistema
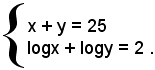
Si ha:
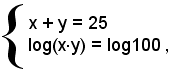
ossia
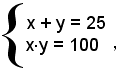
le cui soluzioni sono
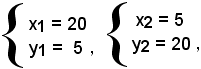
entrambe accettabili.
LE TAVOLE LOGARITMICHE
Di solito, le tavole dei logaritmi sono a 5 cifre decimali e riportano soltante le mantisse dei logaritmi dei numeri da 1 a 9999, poichè la caratteristica si ricava dal computo delle cifre della parte intera o degli zeri che precedono la prima cifra non nulla mediante l'applicazione dei due teoremi della caratteristica. Quindi, le tavole forniscono l'approssimazione al centomillesimo, che nei calcoli ordinari è sufficiente. Di seguito si riporta, a titolo di esempio, la tavola dei logaritmi dei numeri da 4500 a 4800.
| N. | m. log | D | N. | m. log | D | N. | m. log | D | N. | m. log | D | N. | m. log | D |
| 4500 | 65321 | - | 4560 | 65895 | - | 4620 | 66464 | - | 4680 | 67025 | - | 4740 | 67578 | - |
| 4501 | 65331 | 10 | 4561 | 65906 | 10 | 4621 | 66474 | 10 | 4681 | 67034 | 9 | 4741 | 67587 | 9 |
| 4502 | 65341 | 10 | 4562 | 65916 | 10 | 4622 | 66483 | 9 | 4682 | 67043 | 9 | 4742 | 67596 | 9 |
| 4503 | 65350 | 9 | 4563 | 65925 | 9 | 4623 | 66492 | 9 | 4683 | 67052 | 9 | 4743 | 67605 | 9 |
| 4504 | 65360 | 10 | 4564 | 65935 | 10 | 4624 | 66502 | 10 | 4684 | 67062 | 10 | 4744 | 67614 | 9 |
| 4505 | 65369 | 9 | 4565 | 65944 | 9 | 4625 | 66511 | 9 | 4685 | 67071 | 9 | 4745 | 67624 | 10 |
| 4506 | 65379 | 10 | 4566 | 65954 | 10 | 4626 | 66521 | 10 | 4686 | 67080 | 9 | 4746 | 67633 | 9 |
| 4507 | 65389 | 10 | 4567 | 65963 | 9 | 4627 | 66530 | 9 | 4687 | 67089 | 9 | 4747 | 67642 | 9 |
| 4508 | 65393 | 9 | 4568 | 65973 | 10 | 4628 | 66539 | 9 | 4688 | 67099 | 10 | 4748 | 67651 | 9 |
| 4509 | 65408 | 10 | 4569 | 65932 | 9 | 4629 | 66549 | 10 | 4689 | 67108 | 9 | 4749 | 67660 | 9 |
| - | 10 | - | 10 | - | 9 | - | 9 | - | 9 | |||||
| P. P. RAPPRESENTA LE PARTI PROPORZIONALI | ||||||||||||||
 | ||||||||||||||
| N. | m. log | D | N. | m. log | D | N. | m. log | D | N. | m. log | D | N. | m. log | D |
| 4510 | 65418 | - | 4570 | 65992 | - | 4630 | 66558 | - | 4690 | 67117 | - | 4750 | 67669 | - |
| 4511 | 65427 | 9 | 4571 | 66001 | 9 | 4631 | 66567 | 9 | 4691 | 67127 | 10 | 4751 | 67679 | 10 |
| 4512 | 65437 | 10 | 4572 | 66011 | 10 | 4632 | 66577 | 10 | 4692 | 67136 | 9 | 4752 | 67688 | 9 |
| 4513 | 65447 | 10 | 4573 | 66020 | 9 | 4633 | 66585 | 9 | 4693 | 67145 | 9 | 4753 | 67697 | 9 |
| 4514 | 65456 | 9 | 4574 | 66030 | 10 | 4634 | 66596 | 10 | 4694 | 67154 | 9 | 4754 | 67706 | 9 |
| 4515 | 65466 | 10 | 4575 | 66039 | 9 | 4635 | 66605 | 9 | 4695 | 67164 | 10 | 4755 | 67715 | 9 |
| 4516 | 65475 | 9 | 4576 | 66049 | 10 | 4636 | 66614 | 9 | 4696 | 67173 | 9 | 4756 | 67724 | 9 |
| 4517 | 65485 | 10 | 4577 | 66058 | 9 | 4637 | 66624 | 10 | 4697 | 67182 | 9 | 4757 | 67733 | 9 |
| 4518 | 65495 | 10 | 4578 | 66068 | 10 | 4638 | 66633 | 9 | 4698 | 67191 | 9 | 4758 | 67742 | 9 |
| 4519 | 65504 | 9 | 4579 | 66077 | 9 | 4639 | 66642 | 9 | 4699 | 67201 | 10 | 4759 | 67752 | 10 |
| - | 10 | - | 10 | - | 10 | - | 9 | - | 9 | |||||
| N. | m. log | D | N. | m. log | D | N. | m. log | D | N. | m. log | D | N. | m. log | D |
| 4520 | 65514 | - | 4580 | 66087 | - | 4640 | 66652 | - | 4700 | 67210 | - | 4760 | 67761 | - |
| 4521 | 65523 | 9 | 4581 | 66096 | 9 | 4641 | 66661 | 9 | 4701 | 67219 | 9 | 4761 | 67770 | 9 |
| 4522 | 65533 | 10 | 4582 | 66105 | 10 | 4642 | 66671 | 10 | 4702 | 67228 | 9 | 4762 | 67779 | 9 |
| 4523 | 65543 | 10 | 4583 | 66115 | 9 | 4643 | 66680 | 9 | 4703 | 67237 | 9 | 4763 | 67788 | 9 |
| 4524 | 65552 | 9 | 4584 | 66124 | 9 | 4644 | 66689 | 9 | 4704 | 67247 | 10 | 4764 | 67797 | 9 |
| 4525 | 65562 | 10 | 4585 | 66134 | 10 | 4645 | 66699 | 10 | 4705 | 67256 | 9 | 4765 | 67806 | 9 |
| 4526 | 65571 | 9 | 4586 | 66143 | 9 | 4646 | 66708 | 9 | 4706 | 67265 | 9 | 4766 | 67815 | 9 |
| 4527 | 65581 | 10 | 4587 | 66153 | 10 | 4647 | 66717 | 9 | 4707 | 67274 | 9 | 4767 | 67825 | 10 |
| 4528 | 65591 | 10 | 4588 | 66162 | 9 | 4648 | 66727 | 10 | 4708 | 67284 | 10 | 4768 | 67834 | 9 |
| 4529 | 65600 | 9 | 4589 | 66172 | 10 | 4649 | 66736 | 9 | 4709 | 67293 | 9 | 4769 | 67843 | 9 |
| - | 10 | - | 9 | - | 9 | - | 9 | - | 9 | |||||
| N. | m. log | D | N. | m. log | D | N. | m. log | D | N. | m. log | D | N. | m. log | D |
| 4530 | 65610 | - | 4590 | 66181 | - | 4650 | 66745 | - | 4710 | 67302 | - | 4770 | 67852 | - |
| 4531 | 65619 | 9 | 4591 | 66191 | 10 | 4651 | 66755 | 10 | 4711 | 67311 | 9 | 4771 | 67861 | 9 |
| 4532 | 65629 | 10 | 4592 | 66200 | 9 | 4652 | 66764 | 9 | 4712 | 67321 | 10 | 4772 | 67870 | 9 |
| 4533 | 65639 | 10 | 4593 | 66210 | 10 | 4653 | 66773 | 9 | 4713 | 67330 | 9 | 4773 | 67879 | 9 |
| 4534 | 65648 | 9 | 4594 | 66219 | 9 | 4654 | 66783 | 10 | 4714 | 67339 | 9 | 4774 | 67888 | 9 |
| 4535 | 65658 | 10 | 4595 | 66229 | 10 | 4655 | 66792 | 9 | 4715 | 67348 | 9 | 4775 | 67897 | 9 |
| 4536 | 65667 | 9 | 4596 | 65238 | 9 | 4656 | 66801 | 9 | 4716 | 67357 | 9 | 4776 | 67906 | 9 |
| 4537 | 65677 | 10 | 4597 | 66247 | 9 | 4657 | 66811 | 10 | 4717 | 67367 | 10 | 4777 | 67916 | 10 |
| 4538 | 65686 | 9 | 4598 | 66257 | 10 | 4658 | 66820 | 9 | 4718 | 67376 | 9 | 4778 | 67925 | 9 |
| 4539 | 65696 | 10 | 4599 | 66266 | 9 | 4659 | 66829 | 9 | 4719 | 67385 | 9 | 4779 | 67934 | 9 |
| - | 10 | - | 10 | - | 10 | - | 9 | - | 9 | |||||
| N. | m. log | D | N. | m. log | D | N. | m. log | D | N. | m. log | D | N. | m. log | D |
| 4540 | 65706 | - | 4600 | 66276 | - | 4660 | 66839 | - | 4720 | 67394 | - | 4780 | 67943 | - |
| 4541 | 65715 | 9 | 4601 | 66285 | 9 | 4661 | 66848 | 9 | 4721 | 67403 | 9 | 4781 | 67952 | 9 |
| 4542 | 65725 | 10 | 4602 | 66295 | 10 | 4662 | 66857 | 9 | 4722 | 67413 | 10 | 4782 | 67961 | 9 |
| 4543 | 65734 | 9 | 4603 | 66304 | 9 | 4663 | 66867 | 10 | 4723 | 67422 | 9 | 4783 | 67970 | 9 |
| 4544 | 65744 | 10 | 4604 | 66314 | 10 | 4664 | 66876 | 9 | 4724 | 67431 | 9 | 4784 | 67979 | 9 |
| 4545 | 65753 | 9 | 4605 | 66323 | 9 | 4665 | 66885 | 9 | 4725 | 67440 | 9 | 4785 | 67988 | 9 |
| 4546 | 65763 | 10 | 4606 | 66332 | 9 | 4666 | 66894 | 9 | 4726 | 67449 | 9 | 4786 | 67997 | 9 |
| 4547 | 65772 | 9 | 4607 | 66342 | 10 | 4667 | 66904 | 10 | 4727 | 67459 | 10 | 4787 | 68006 | 9 |
| 4548 | 65782 | 10 | 4608 | 66351 | 9 | 4668 | 66913 | 9 | 4728 | 67468 | 9 | 4788 | 68015 | 9 |
| 4549 | 65792 | 10 | 4609 | 66361 | 10 | 4669 | 66922 | 9 | 4729 | 67477 | 9 | 4789 | 68024 | 9 |
| - | 9 | - | 9 | - | 10 | - | 9 | - | 10 | |||||
| N. | m. log | D | N. | m. log | D | N. | m. log | D | N. | m. log | D | N. | m. log | D |
| 4550 | 65801 | - | 4610 | 66370 | - | 4670 | 66932 | - | 4730 | 67486 | - | 4790 | 68034 | - |
| 4551 | 65811 | 10 | 4611 | 66380 | 10 | 4671 | 66941 | 9 | 4731 | 67495 | 9 | 4791 | 68043 | 9 |
| 4552 | 65820 | 9 | 4612 | 66389 | 9 | 4672 | 66950 | 9 | 4732 | 67504 | 9 | 4793 | 68052 | 9 |
| 4553 | 65830 | 10 | 4613 | 66398 | 9 | 4673 | 66960 | 10 | 4733 | 67514 | 10 | 4794 | 68061 | 9 |
| 4554 | 65839 | 9 | 4614 | 66408 | 10 | 4674 | 66969 | 9 | 4734 | 67523 | 9 | 4795 | 68070 | 9 |
| 4555 | 65849 | 10 | 4615 | 66417 | 9 | 4675 | 66978 | 9 | 4735 | 67532 | 9 | 4796 | 68079 | 9 |
| 4556 | 65858 | 9 | 4616 | 66427 | 10 | 4676 | 66987 | 9 | 4736 | 67541 | 9 | 4797 | 68088 | 9 |
| 4557 | 65868 | 10 | 4517 | 66436 | 9 | 4677 | 66997 | 10 | 4737 | 67550 | 9 | 4798 | 68097 | 9 |
| 4558 | 65877 | 9 | 4618 | 66445 | 9 | 4678 | 67006 | 9 | 4738 | 67560 | 10 | 4799 | 68106 | 9 |
| 4559 | 65887 | 10 | 4619 | 66455 | 10 | 4679 | 67015 | 9 | 4739 | 67569 | 9 | 4800 | 68115 | 9 |
| - | 9 | - | 9 | - | 10 | - | 9 | - | 9 | |||||
| N. | m. log | D | N. | m. log | D | N. | m. log | D | N. | m. log | D | N. | m. log | D |
| 4559 | 65896 | - | 4620 | 66494 | - | 4680 | 67025 | - | 4620 | 67578 | - | 4620 | 68124 | - |
Esse permettono di risolvere i due problemi seguenti:
2)-ricerca del numero dato il logaritmo (ricerca dell'antilogaritmo).
Ciascuno dei due problemi presenta due casi:
a)-il numero è contenuto nelle tavole (è composto al massimo di 4 cifre tra intere e decimali), oppure non è contenuto nelle tavole (è composto da più di 4 cifre tra intere e decimali);
b)-la mantissa del logaritmo è contenuta nelle tavole oppure no.
1° Problema - 1° Caso: il numero dato è contenuto nelle tavole
La caratteristica è data dai teoremi della cararatteristica e di solito non si trova sulle tavole.
La mantissa del logaritmo si legge direttamente sulle tavole nella colonna m. log, vedi tavola suddetta.
Esempi
1° Problema - 2° Caso: il numero dato non è contenuto nelle tavole perchè ha più di 4 cifre
La caratteristica è data dai teoremi della caratteristica.
Per
trovare la mantissa del numero dato, intero o decimale, lo si rende
decimale con una virgola o si sposta la virgola in modo che la parte
intera abbia sempre 4 cifre. Ciò equivale a dividere o
moltiplicare il numero per 10, 100, ... Il numero dato, così
trasformato, ha quindi la mantissa invariata e, risultando compreso
fra due numeri interi consecutivi, anche la mantissa del suo logaritmo
risulterà compresa fra quelle dei logaritmi dei due numeri
interi. Ammettendo che gli aumenti della mantissa siano proporzionali
agli aumenti dei numeri, si ricava mediante una proporzione, di quanto
si deve aumentare la mantissa del logaritmo del numero intero minore
per ottenere quella del numero dato. Questo principio di
proporzionalità si ammette senza dimostrazione; si dà
solamente il concetto di interpolazione, che è il procedimento che si usa nel calcolo.
Interpolazione lineare - Quando di una funzione y=f(x) si conoscono più valori corrispondenti a determinati valori della variabile x, per altri valori della x tra questi compresi, si ritiene che la variazione dei valori della funzione y siano (approssimativamente) proporzionali a quelli corrispondenti della variabile x.
Differenza tabulare
Si chiama differenza tabulare la differenza tra la mantissa maggiore e quella minore e si indica con d.
La differenza fra due numeri corrispondenti è l'unità. La differenza fra Il numero dato, reso decimale, e il numero intero minore è uguale alla parte decimale del numero dato e si indica con a; inoltre si indica con x l'aumento della mantissa corrispondente al dato aumento del numero.
Per la proporzionalità suddetta, si ha:
-se il numero aumenta di 1, la mantissa aumenta di d;
-se il numero aumenta di a, la mantissa aumenta di x.
Sussiste quindi la seguente proporzione:
1 : a = d : x ,
da cui
x = ad.
Il prodotto della differenza tabulare d per la parte decimale a del numero indica senz'altro di quanto si deve aumentare la mantissa minore per avere quella del logaritmo del numero dato.
Se il prodotto ad è decimale si scarta la parte decimale, se è minore di 5 decimi si aumenta di 1 la parte intera scartando la parte decimale, se questa non è minore di 5 decimi.
Esempi
1)-Calcolare il logaritmo del numero 479876.
La caratteristica è 5, perchè il numero è di 6 cifre.
Separando con la virgola le prime 4 cifre del numero, si ha il numero decimale:
4798,76 .
Sono vere le disuguaglianze:
4798<4798,76<4799 .
Dalle tavole si rileva che la mantissa di 4798 è 68106 e quella di 4799 è 68115; e sono vere anche le seguenti disuguaglianze:
mantissa 68106<mantissa 4798,76<mantissa 4799.
La differenza fra i numeri è 4799-4798=1, la differenza tabulare, cioè la differenza fra la mantissa per eccesso e quella per difetto, che si indica con D. T., è D. T.=68115-68106=9, quindi:
-se il numero aumenta di 1, la mantissa aumenta di 9,
-se il numero aumenta di 0,76, la mantissa aumenta di x,
per cui si ha la proporzione:
1 : 0,76 = 9 : x,
quindi
x=6,84.
Siccome, il prodotto ha per parte decimale 84/100 (>5/10), si considera come prodotto 7 (parte intera 6 aumentata di 1) che aggiunto alla mantissa minore 68106, dà 68113, quindi:
log479876 = 5,68113.
In pratica, l'operazione si può eseguire nel modo in cui è disposto il seguente schema:
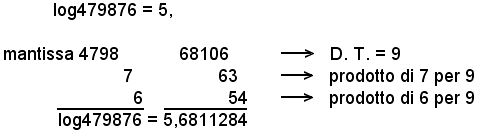
Siccome la sesta cifra non è minore di 5, la quinta cifra decimale si arrotonda per eccesso e si ha: 5,68113.
Nota bene
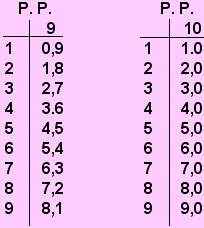
I prodotti della D. T. per le singole cifre del numero, dopo la quarta, sono già calcolati e si leggono sulle tavole nella colonna indicata P. P. (Parti Proporzionali).
2)-Calcolare il logaritmo del numero 0,046863.
La caratteristica è:
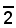
e, separando con la virgola le prime 4 cifre non nulle del numero, si ha: 4686,3. Si hanno le disuguaglianze:
4686<4686,3<4687
e procedendo come nell'esempio precedente, si trova:
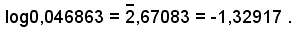
2° Problema - 1° Caso: ricerca del numero, dato il logaritmo (ricerca dell'antilogaritmo).
E' il procedimento inverso del 1° problema, 1° caso. La mantissa si legge nelle tavole. il numero si legge nella colonna N in corrispondenza della mantissa, che si trova nella colonna logaritmi. La parte intera di questo numero sarà di tante cifre quante sono le unità della caratteristica, aumentate di 1 unità, se la caratteristica è positiva, e sarà 0 se la caratteristica è negativa; in questo caso seguono la virgola tanti altri zeri quante sono le unità negative meno una della caratteristica, dopo le quali verrà scritto il numero dato nella colonna N. Se la caratteristica supera 3, dovendo il numero avere più di 4 cifre, sarà quello che si ottiene scrivendo di seguito al numero della colonna N tanti zeri a destra quanti ne occorrono.
Esempi
1)-Calcolare il numero il cui logaritmo è: 2,66229.
Alla mantissa 66229, colonna m. log delle tavole, corrisponde il numero 4595, colonna N delle tavole. Siccome la caratteristica del logaritmo è 2, il numero richiesto deve avere la parte intera composta da tre cifre, perciò sarà 459,5, cioè:
antilog2,66229 = 459,5 .
2)-Calcolare il numero il cui logaritmo è: 5,66764.
antilog5,66764 = 465200 .
3)-Calcolare il numero il cui logaritmo è:
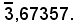
Alla mantissa 67357, colonna m. log delle tavole, corrisponde il numero 4716, colonna N delle tavole. Siccome la caratteristica del logaritmo è
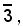
il numero richiesto è 0,004716, cioè:
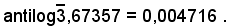
2° Problema - 2° Caso: ricerca dell'antilogaritmo quando la mantissa non è contenuta nella tavole.
67916<67920<67925 .
Il numero corrispondente alla mantissa 67916 è 4777, quello corrispondente alla mantissa 67925 è 4778 e quello corrispondente alla mantissa data sarà compreso tra 4777 e 4778; perciò si hanno le altre disuguaglianze:
4777<4777,...<4778 .
La differenza tabulare è 9, la differenza (D. M.) tra la mantissa data 67920 e la minore 67916 è 4. Per l'ammessa proporzionalità, nel caso in esame, se il numero aumenta di 1 la mantissa aumenta di 9, di quanto aumenterà il numero 4777 se la mantissa aumenta di 4? Si può scrivere la seguente proporzione:
1 : x = 9 : 4 .
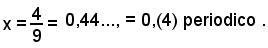
Il numero 4777 dovrà aumentare di 0,(4) e sarà 4777,(4)
Siccome il numero richiesto deve avere la parte intera di 2 cifre, dato che la caratteristica è 1, perciò risulta:
antilog1,67920 = 47,77(4) .
2)-Calcolare l'antilogaritmo di: -1,14046.
e, con procedimento analogo a quello degli altri esempi e mediante l'uso della tavole, si ha:
85950<85954<85956 ,
ed anche
7236<7236, ...<7237 .
D. T. = 6 , D. M. = 4 ,
1 : x = 6 : 4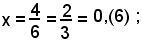
da cui
7236<7236(6)<7237 .
Essendo
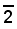
la caratteristica sarà:

Interpolazione lineare - Quando di una funzione y=f(x) si conoscono più valori corrispondenti a determinati valori della variabile x, per altri valori della x tra questi compresi, si ritiene che la variazione dei valori della funzione y siano (approssimativamente) proporzionali a quelli corrispondenti della variabile x.
Differenza tabulare
Si chiama differenza tabulare la differenza tra la mantissa maggiore e quella minore e si indica con d.
La differenza fra due numeri corrispondenti è l'unità. La differenza fra Il numero dato, reso decimale, e il numero intero minore è uguale alla parte decimale del numero dato e si indica con a; inoltre si indica con x l'aumento della mantissa corrispondente al dato aumento del numero.
Per la proporzionalità suddetta, si ha:
-se il numero aumenta di 1, la mantissa aumenta di d;
-se il numero aumenta di a, la mantissa aumenta di x.
Sussiste quindi la seguente proporzione:
1 : a = d : x ,
da cui
x = ad.
Il prodotto della differenza tabulare d per la parte decimale a del numero indica senz'altro di quanto si deve aumentare la mantissa minore per avere quella del logaritmo del numero dato.
Se il prodotto ad è decimale si scarta la parte decimale, se è minore di 5 decimi si aumenta di 1 la parte intera scartando la parte decimale, se questa non è minore di 5 decimi.
Esempi
1)-Calcolare il logaritmo del numero 479876.
La caratteristica è 5, perchè il numero è di 6 cifre.
Separando con la virgola le prime 4 cifre del numero, si ha il numero decimale:
4798,76 .
Sono vere le disuguaglianze:
4798<4798,76<4799 .
Dalle tavole si rileva che la mantissa di 4798 è 68106 e quella di 4799 è 68115; e sono vere anche le seguenti disuguaglianze:
mantissa 68106<mantissa 4798,76<mantissa 4799.
La differenza fra i numeri è 4799-4798=1, la differenza tabulare, cioè la differenza fra la mantissa per eccesso e quella per difetto, che si indica con D. T., è D. T.=68115-68106=9, quindi:
-se il numero aumenta di 1, la mantissa aumenta di 9,
-se il numero aumenta di 0,76, la mantissa aumenta di x,
per cui si ha la proporzione:
1 : 0,76 = 9 : x,
quindi
x=6,84.
Siccome, il prodotto ha per parte decimale 84/100 (>5/10), si considera come prodotto 7 (parte intera 6 aumentata di 1) che aggiunto alla mantissa minore 68106, dà 68113, quindi:
log479876 = 5,68113.
In pratica, l'operazione si può eseguire nel modo in cui è disposto il seguente schema:

Siccome la sesta cifra non è minore di 5, la quinta cifra decimale si arrotonda per eccesso e si ha: 5,68113.
Nota bene
I prodotti della D. T. per le singole cifre del numero, dopo la quarta, sono già calcolati e si leggono sulle tavole nella colonna indicata P. P. (Parti Proporzionali).
2)-Calcolare il logaritmo del numero 0,046863.
La caratteristica è:
e, separando con la virgola le prime 4 cifre non nulle del numero, si ha: 4686,3. Si hanno le disuguaglianze:
e procedendo come nell'esempio precedente, si trova:
2° Problema - 1° Caso: ricerca del numero, dato il logaritmo (ricerca dell'antilogaritmo).
E' il procedimento inverso del 1° problema, 1° caso. La mantissa si legge nelle tavole. il numero si legge nella colonna N in corrispondenza della mantissa, che si trova nella colonna logaritmi. La parte intera di questo numero sarà di tante cifre quante sono le unità della caratteristica, aumentate di 1 unità, se la caratteristica è positiva, e sarà 0 se la caratteristica è negativa; in questo caso seguono la virgola tanti altri zeri quante sono le unità negative meno una della caratteristica, dopo le quali verrà scritto il numero dato nella colonna N. Se la caratteristica supera 3, dovendo il numero avere più di 4 cifre, sarà quello che si ottiene scrivendo di seguito al numero della colonna N tanti zeri a destra quanti ne occorrono.
Esempi
1)-Calcolare il numero il cui logaritmo è: 2,66229.
Alla mantissa 66229, colonna m. log delle tavole, corrisponde il numero 4595, colonna N delle tavole. Siccome la caratteristica del logaritmo è 2, il numero richiesto deve avere la parte intera composta da tre cifre, perciò sarà 459,5, cioè:
antilog2,66229 = 459,5 .
2)-Calcolare il numero il cui logaritmo è: 5,66764.
Alla mantissa 66764, colonna m. log
delle tavole, corrisponde il numero 4652, colonna N delle tavole.
Siccome la caratteristica del logaritmo è 5, il numero richiesto deve
avere la parte intera composta da sei cifre, perciò sarà 465200, cioè:
antilog5,66764 = 465200 .
3)-Calcolare il numero il cui logaritmo è:
Alla mantissa 67357, colonna m. log delle tavole, corrisponde il numero 4716, colonna N delle tavole. Siccome la caratteristica del logaritmo è
il numero richiesto è 0,004716, cioè:
2° Problema - 2° Caso: ricerca dell'antilogaritmo quando la mantissa non è contenuta nella tavole.
E' il procedimento inverso del 1° problema, 2° caso.
Esempi
1)-Calcolare il numero il cui logaritmo è: 1,67920.
Esempi
1)-Calcolare il numero il cui logaritmo è: 1,67920.
Sulle tavole sono contenute le mantisse 67916 e 67925 e sono vere le seguenti disuguaglianze:
67916<67920<67925 .
Il numero corrispondente alla mantissa 67916 è 4777, quello corrispondente alla mantissa 67925 è 4778 e quello corrispondente alla mantissa data sarà compreso tra 4777 e 4778; perciò si hanno le altre disuguaglianze:
La differenza tabulare è 9, la differenza (D. M.) tra la mantissa data 67920 e la minore 67916 è 4. Per l'ammessa proporzionalità, nel caso in esame, se il numero aumenta di 1 la mantissa aumenta di 9, di quanto aumenterà il numero 4777 se la mantissa aumenta di 4? Si può scrivere la seguente proporzione:
1 : x = 9 : 4 .
Il numero 4777 dovrà aumentare di 0,(4) e sarà 4777,(4)
Siccome il numero richiesto deve avere la parte intera di 2 cifre, dato che la caratteristica è 1, perciò risulta:
antilog1,67920 = 47,77(4) .
2)-Calcolare l'antilogaritmo di: -1,14046.
Risulta:
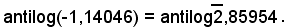
e, con procedimento analogo a quello degli altri esempi e mediante l'uso della tavole, si ha:
ed anche
7236<7236, ...<7237 .
D. T. = 6 , D. M. = 4 ,
1 : x = 6 : 4
da cui
7236<7236(6)<7237 .
Essendo
la caratteristica sarà:
REGOLO CALCOLATORE
Il regolo calcolatore è uno strumento con il quale si possono eseguire in modo rapido determinate operazioni con numeri interi e decimali, ad esempio moltiplicazioni, divisioni, quadrati, radici quadrate, ecc., con risultati che in pratica danno sufficienti approssimazioni. I primi tipi sono stati costruiti in legno, quelli più recenti in "alastron", materiale sintetico indeformabile e indilatabile nonchè difficile a rompersi.
Esso è formato da un regolo, striscia orizzontale, detto fisso, che è incavato secondo la sua lunghezza in modo da formare una scalanatura anch'essa rettangolare nella quale scorre un'altro regolo più piccolo, detto scorrevole, i cui bordi combaciano perfettamente con quelli del regolo fisso.

REGOLO SCORREVOLE

CORSOIO
Una parte accessoria del regolo calcolatore è il corsoio, il quale abbraccia in larghezza il regolo ed è guidato da altre due scanalature sui margini del fisso. Si tratta di un telaietto quadrato o rettangolare di materiale trasparente, celluloide, che porta incisa una linea perpendicolare alla lunghezza del regolo, che ha lo scopo di rendere più agevole e precisa la lettura del numero sulle scale del regolo.


Se si considerano i due bordi del fisso prospicenti la scanalatura centrale e i due bordi dello scorrevole con quelli combacianti, si hanno quattro bordi sui quali si segnano le scale a due a due identiche e perfettamente uguali, che prendono il nome di scale superiori e scale inferiori a seconda che, per chi guarda il regolo in modo da leggervi, quelle sono le superiori e le inferiori.
Fissata ad arbitrio la lunghezza a del regolo, di solito cm 25, sui bordi inferiori del fisso e dello scorrevole si riportano i segmenti le cui misure sono:
segnando però negli estremi i numeri 1, 2, 3, ..., 10,

cioè gli antilogaritmi delle misure suddette. Risulta che le nove parti in cui resta suddivisa la lunghezza del regolo non sono uguali, ma dalla prima all'ultima sono di grandezze decrescenti, così come decrescono le differenze tra due logaritmi consecutivi dei numeri da 1 10, i quali sono: 0,000000; 0,30103; 0,47712; 0,60206; 0,69897; 0,77815; 0,84510; 0,90309; 0,95424; 1. Nell'origine della scala si segna 1 (e non 0, essendo il log1=0) e nell'estremo si segna 10 (essendo log10=1). L'intervallo fra i due estremi si chiama segmento base del regolo. Si hanno così le scale inferiori; esse sono logaritmiche, ma le suddivisioni sono distinte dai numeri corrispondenti.
FORMAZIONE DELLE SCALE SUPERIORI
Sui bordi superiori del fisso e dello scorrevole si segnano, sulla stessa lunghezza, non una ma due scale identiche alle precedenti, perfettamente uguali fra loro, in modo che ciascuna sia di metà lunghezza di quella inferiore.

Risulta che, rispetto a quelli delle scale inferiori, i numeri a, 2, 3, ..., 10, corrispondono ai valori:
SUDDIVISIONE DELLE SCALE
Il tratto 1-2 delle scale inferiori, che è il più lungo, si divide ordinariamente in 100 parti logaritmiche; il tratto 2-3, 3-4, 4-5 in 20 parti, i rimanenti, che sono via via più corti, soltanto in 10 parti. Nelle scale superiori, ciascuna di metà lunghezza di quelle inferiori, le suddivisioni si fanno nello stesso modo, ma specialmente nei regoli di forma ridotta (di lunghezza cm 15), il loro numero si pùo ridurre alla metà di quello delle scale inferiori.
LETTURA DEI NUMERI SULLE SCALE
Sul regolo, con le suddivisioni così apportate (la figura sottostante è quella di un regolo completo), si possono leggere numeri di due cifre, la prima data dal numero che corrisponde ad una linea di divisione principale e in scrittura più grande e la seconda ad una linea di divisione secondaria.

Si possono leggere anche numeri di tre cifre, se si conviene di considerare quale terza cifra, quella che corrisponde ad una divisione intermedia tra due divisioni segnate sulla scala, divisione apportata a giudizio dell'occhio umano e della propria sensibilità. Agevola il compito di queste suddivisioni la linea incisa sul corsoio che può meglio far osservare quale sia la divisione più conveniente.
Si deduce intanto che il regolo non è adatto per il calcolo di operazioni con numeri composti da più di 3 cifre, fra intere e decimali, se si escudono gli zeri che eventualmente precedono la prima cifra diversa da zero o seguono l'ultima.
Il calcolo di operazioni con più di 3 cifre potrebbe condurre ad errori non indifferenti, specialmente se il regolo presenta qualche difetto nella graduazione o nella costruzione, come capita alle volte per quelli in commercio.
E' facile riconoscere inoltre che alla stessa suddivisione che nella scala del regolo indica, ad esempio, il numero 1,2 si può leggere indifferentemente 12, oppure 120, ecc., oppure 0,12, oppure 0,012, ecc. così come sulla riga centrimetrata si può leggere 12 cm, oppure 120 mm, oppure 1,2 dm, oppure 0,12 m, ecc. Basta a tale scopo immaginare che l'unità di misura sia di 10, 100, 1000, ... volte più piccola o più grande.
Identiche considerazioni si fanno per le scale superiori, con l'avvertenza che in esse si leggono bene solo i numeri di due cifre; per quelli di 3 cifre, dovendo ricorrere alla suddivisione visiva, data la piccolezza dei tratti, la lettura è poco esatta.
I numeri da 10 a 100, si leggono generalmente sulla scala a destra.
Nella figura suddetta sono riportati per la lettura i numeri 236; 23,6, 2,36; 0,236; 0,0236; ... nella scala inferiore del fisso; i numeri 27, 39, 87, ... nella scala superiore a destra del fisso.
PRINCIPIO SU CUI E' COSTRUITO IL REGOLO
Gli orli di due doppi decimetri devono combaciare e devono avere lo zero, l'uno, il due, ... l'uno di fronte all'altro. Se si fa scorrere uno dei dei doppi decimetri sull'altro, ad esempio, in modo che lo zero dello scorrevole venga a coincidere con il 4 del fisso, si trova ora combaciati 1 e 5; 2 e 6; 3 e 7; ecc. Si può verificare che un numero dello scorrevole aggiunto al 4 del fisso dà per somma il numero del fisso con il quale combacia; che la differenza fra i due numeri combacianti dà il numero 4; ed infine che la differenza fra i due numeri del fisso dà quello dello scorrevole.
Ad esempio, se si sceglie la coppia combaciante 5 e 9, si ha: 4+5=9; 9-5=4 e infine 9-4=5.
La semplice lettura dei numeri sui doppi decimetri dà immediatamente la somma dei numeri 4 e 5 e le differenze dei numeri 9 e 4 oppure 9 e 5. Ma la somma non supera 20, come le differenze non possono avere per minuendo un numero maggiore di 20.
Però, se si leggesse 40 mm, 50 mm, 90 mm, la somma sarebbe ancora 90 e al massimo si potrebbe avere per somma 200 con i 2 doppi decimetri. Sostituendo i decimillesimi, centimillesimi, ecc., la somma potrebbe raggiungere qualunque numero e così il minuendo delle differenze. E' logico che si potrà leggere m 0,65, m 0,09 ecc. e la somma e la differenza sarebbero estese ai numeri razionali.
Si procede ora allo stesso modo con il regolo
Ad esempio, facendo combaciare l'1 dello scorrevole (l'estremo sinistro), con il 2 del fisso di una qualunque delle scale, si troverà il 2 dello scorrevole di fronte al 4, il 3 di fronte al 6, il 4 di fronte all'8, ...del fisso. In questa posizione, il regolo mostra i seguenti risultati:
1)-il prodotto del numero sul fisso, combaciante con l'1 dello scorrevole, per quello dello scorrevole combaciante con l'altro del fisso, che ne è il prodotto,
2)-il quoziente dei numeri sull fisso, che è quello dello scorrevole.
Infatti, si ha: 2x3=6, 2x4=8, ecc.; viceversa, 8:4=2, 6:3=2, ecc.; infine, 8:2=4, 6:2=3, ecc.
In effetti, alla somma dei numeri sui doppi centimetri, corrisponde il prodotto sul regolo.
Infatti, ad esempio, 2 sul regolo è log2 e 3 è log3; ma log2+log3=log(2x3)=log6, che sulla scala del regolo è segnato 6, quindi 2x3=6.
Alla differenza log6-log3=log(6:3)=log2, che sulla scala del regolo è segnato 2, corrisponde il quoziente 6:2=3.
Quindi, segue che:
-dati due numeri r e s, per avere il prodotto con il regolo, basta addizionare i due segmenti corrispondenti ad r e s uno sul fisso e l'altro sullo scorrevole dopo aver reso il segmento dello scorrevole adiacente a quello del fisso. La somma delle misure dei segmenti, essendo somma di logaritmi, per il noto teorema dul logaritmo del prodotto, corrisponde al prodotto dei numeri, che si legge sul fisso in corrispondenza dell'estremo del segmento s dello scorrevole.
Avendo addizionato un segmento del fisso ad uno dello scorrevole, per avere un segmento del fisso loro somma, viceversa, togliendo a questo segmento quello del fisso, si avrà quello dello scorrevole, e togliendo quello dello scorrevole si avrà quello del fisso, a queste operazioni sui segmenti, corrispondono le seguenti sui logaritmi:
Il quoziente dei due numeri si ottiene con una semplice lettura sul regolo.
Esempi
1)-Calcolare, con la scala inferiore, il prodotto 2,5 x 3,4 = 8,50.
Deve combaciare l'1 dello scorrevole con il 2,5 del fisso; si legge poi sul fisso il numero che combacia con 3,4 dello scorrevole. La linea del corsoio unisce il 3, 4 dello scorrevole con 85 del fisso. Siccome il numero delle cifre intere del prodotto è dato dalla somma delle cifre delle parti intere meno una, e in tale caso dà 1+1-1=1, il prodotto è 8,5.
2)-Calcolare, con la scala inferiore, il prodotto 4,7 x 16 = 75,2.
Deve combaciare l'1 dello scorrevole con il 4,7 del fisso; si porta poi la linea del corsoio su 1,6 dello scorrevole e si legge il numero 752 sotto la linea del corsoio sul fisso. Il numero delle cifre della parte intera del prodotto è 1+2-1=2, ed il prodotto è 75,2.
3)-Calcolare, con la scala inferiore, il prodotto 8,5 x 2,3.
Con l'estremo sinistro dello scorrevole, coincidente con l'8,5 del fisso, l'operazione non sarebbe possibile perchè 2,3 dello scorrevole si troverebbe fuori dalla lunghezza del fisso. In questo caso si usa (*) l'estremo destro dello scorrevole e si procede allo stesso modo:
L'estremo destro dello scorrevole si fa coincidere con 8,5 del fisso; si porta la linea del corsoio su 2,3 dello scorrevole. In corrispondenza si legge sul fisso il prodotto. Il numero delle cifre della parte intera, nel caso che si usa l'estremo destro è uguale alla somma delle cifre delle parti intere dei fattori.
Nota bene
Se il prodotto della prima cifra, diversa da zero, del moltiplicando e del moltiplicatore, non tenendo conto delle virgole, supera 10, lo scorrevole esce fuori del fisso; in tale caso si usa l'estremo destro dello scorrevole e le scale superiori. Con le scale superiori e con lo stesso procedimento delle inferiori, si avrebbe:
L'estremo sinistro dello scorrevole si porta a combaciare con 8,5 del fisso della scala superiore a sinistra, si sposta il corsoio in modo da sovrapporre la linea su 2,3 dello scorrevole e si legge il prodotto 19,5 sul fisso coincidente con la linea del corsoio sulla seconda scala superiore. Qui si deve osservare che, adoperando le scale superiori, non può aversi nel prodotto la quarta cifra, perchè è difficile decidere ad occhio quale sia la divisione da scegliersi. Si può però notare che il prodotto delle due ultime cifre dei numeri dati 5x3, ha appunto come ultima cifra il 5.
4)-Calcolare il prodotto 3,14 x 2,65.
Sui regoli è di solito segnata la divisione corrispondente a π (costante ciclometrica del valore 3,14159), che risulta segnato in grassetto nella figura seguente.

Si porta a combaciare l'estremo dello scorrevole con π, si porta la linea del corsoio su 2,65 dello scorrevole ed in corrispondenza si legge il prodotto sul fisso.
Quoziente
Esempi
1)-Calcolare il quoziente 82 : 34 = 2,4.
Si porta 34 dello scorrevole a combaciare con 82 del fisso, il quoziente si trova sul fisso combaciante con l'estremo sinistro.
Il numero delle cifre intere del quoziente è dato dalla differenza delle cifre delle parti intere del dividendo e del divisore aumentata di 1, se si è usato l'estremo sinistro, dalla sola differenza, se si è usato l'estremo destro.
2)-Calcolare il quoziente 2 : 46,5 = 0,043.
Si porta 46,5 dello scorrevole a combaciare con 2 del fisso, Siccome l'estremo destro esce fuori, il quoziente si legge in corrispondenza dell'estremo destro (come si è osservato in precedenza e nelle note). Lo stesso per le scale superiori.
Le cifre del quoziente sono date da 1-2=-1. Alle differenze negative corrispondono tanti zeri dopo la virgola quante sono le unità negative.
Quadrati
Basterebbe effettuare il prodotto della base per se stessa.
L'osservazione del regolo chiuso convince subito che i numeri delle scale superiori sono i quadrati dei corrispondenti delle scale inferiori. Sono infatti in corrispondenza 1 e 1, 2 e 4, 3 e 9, 4 e 16; ed anche, ad esempio, 2,3 in corrispondenza di 5,29, 7 con 49, ecc.
Del resto, le gradazioni delle scale inferiori sono doppie di quelle superiori; ma 2loga=loga2, quindi per il noto teorema sul logaritmo di una potenza, deve aversi sulle scale superiori il quadrato dei corrispondenti numeri di quelle inferiori.
Le cifre decimali della parte intera sono date ancora dalle regole sul prodotto e, più semplicemente, sono il doppio meno una delle cifre della parte intera del numero, se il quadrato si legge sulla prima scala superiore, e il doppio, se si legge sulla seconda scala superiore.
Radice quadrata
Inversamente all'operazione di quadrato, si ha che la radice quadrata è il numero della scala inferiore corrispondente al numero che invece si deve leggere su una scala superiore (regolo chiuso).
Esempi
1)-Calcolare la radice quadrata seguente:
Si legge il numero nella prima scala superiore quando il numero delle cifre del radicando è dispari, come in questo caso (le cifre decimali si considerano sempre a coppie e se è necessario si aggiunge uno zero a destra dell'ultima cifra). Se il numero delle cifre è dispari, il primo gruppo non supera 9 e la prima cifra della radice, dovendo non superare 3, si troverà nella prima metà del regolo. Si sa dall'aritmetica quante cifre ha la parte intera della radice.
2)-Calcolare la radice quadrata seguente:
Tale radice vale anche come 42,50; numero pari di cifre.
Si legge nella seconda scala superiore: in corrispondenza, nella inferiore, si trova 6,4, che è la radice richiesta.
Quarta potenza
E' il quadrato del quadrato.
Cubo di un numero
E' il prodotto del numero per il suo quadrato.
E' preferibile eseguirlo nel modo seguente, perchè comporta il minor numero di spostamenti del regolo.
Se il numero di cui si cerca il cubo è minore di 4,64, si fissa l'estremo sinistro dello scorrevole sul numero del fisso ci cui si cerca il cubo.
Lo stesso numero, letto sullo scorrevole nella scala superiore, combacia con il numero della scala superiore del fisso che è il cubo.
Se
il numero di cui si cerca il cubo è maggiore di 4,64, lo
scorrevole esce fuori e perciò si fissa l'estremo destro. Quando
il cubo si può leggere su tutte e due le scale superiori,
è meglio leggerlo su quella a sinistra.
Il numero delle cifre intere del cubo, se si usa l'estremo destro, è il triplo di quello del numero dato. Se si usa il sinistro, e si legge il cubo nella prima scala superiore a sinistra, è il triplo meno 2 se si legge nella seconda scala superiore a destra è il triplo meno 1.
Esistono vari tipi di regoli calcolatori, i quali portano diverse specie di scale:
-quelle per i seni e le tangenti,
-quelle per il calcolo delle percentuali,
-quelle commerciali, senza le scale superiori, ma porta invece i divisori degl'interessi,
-quelle per la riduzione delle sterline e per i suoi sottomultipli e viceversa,
-quelle per elettrotecnici,
-altre.
Il numero delle cifre intere del cubo, se si usa l'estremo destro, è il triplo di quello del numero dato. Se si usa il sinistro, e si legge il cubo nella prima scala superiore a sinistra, è il triplo meno 2 se si legge nella seconda scala superiore a destra è il triplo meno 1.
Esistono vari tipi di regoli calcolatori, i quali portano diverse specie di scale:
-quelle per i seni e le tangenti,
-quelle per il calcolo delle percentuali,
-quelle commerciali, senza le scale superiori, ma porta invece i divisori degl'interessi,
-quelle per la riduzione delle sterline e per i suoi sottomultipli e viceversa,
-quelle per elettrotecnici,
-altre.