MIKY & GENNY
I NUMERI REALI ---> INDICE
Concetto generale di numero
I primi numeri conosciuti furono i numeri interi assoluti: 0, 1, 2, 3, ..., che ebbero origine dalla necessità di contare per stabilire quanti sono gli oggetti di un gruppo, o per stabilire quante volte avviene un fatto, ecc. Per tali numeri sono stati stabiliti i concetti di uguaglianza e definite le quattro operazioni fondamentali, addizione, sottrazione, moltiplicazione, divisione, dimostrando che esse godono della cosiddette proprietà formali: commutativa e associativa dell'addizione e della moltiplicazione, distributiva della moltiplicazione rispetto all'addizione, ecc. In passato, si osservò che la conoscenza dei soli numeri interi assoluti non era sufficiente per risolvere problemi, anche facili, che si presentavano nelle applicazioni pratiche, e ciò in virtù del fatto che, oltre alle unità intere, si dovevano considerare anche le loro parti. Se, ad esempio, si dovevano dividere in parti uguali fra 7 ragazzi 5 tavolette di cioccolata, si notava subito che, per rispondere a tale problema, ci si deveva servire non di un solo numero intero, ma di due: del numero 7, che indica in quante parti si deve dividere ogni tavoletta di cioccolata e del numero 5 che indica quante di queste parti ha ricevuto ogni ragazzo. Perciò la risposta al problema è data dalla coppia ordinata di numeri interi (5, 7), nel senso che dev'essere stabilito quale dei due numeri si deve considerare primo nella coppia e quale come secondo. Quindi, per risolvere problemi in cui oltre ad unità intere vi sono anche parti dell'unità intera, si è costretti a considerare una nuova entità, costituita da una coppia di numeri interi, il secondo dei quali sia diverso da zero. Queste coppie ordinate di numeri interi, pur rappresentando concettualmente entità molto diverse dai numeri interi assoluti, sono state chiamate anche esse numeri e, per distinguerle dai numeri interi assoluti, alla parola numero si è aggiunto l'attributo frazionario assoluto. La ragione del perchè le coppie ordinate di numeri interi, con il secondo diverso da zero, sono state chiamate numeri, va ricercata nel fatto che anche per questi numeri è stato possibile definire le quattro operazioni fondamentali, in modo che per esse valessero le note proprietà formali per le stesse operazioni fatte con i numeri interi assoluti.
I numeri interi assoluti e i numeri frazionari assoluti si chiamano numeri razionali assoluti.
Si è visto che, per individuare determinate grandezze, ci si deve servire di un numero razionale assoluto e di un segno distintivo. Anche a tali nuove entità, costituite da un numero razionale assoluto e da un segno distintivo, si è dato il nome di numeri, e ciò sempre per il fatto che anche per essi sono state definite le quattro operazioni fondamentali, in modo tale da conservare le proprietà formali.
Questi numeri, per distinguerli dai precedenti, sono stati chiamati numeri razionali relativi. Se si osservano le tre specie di numeri conosciuti, si vede che esse differiscono fra loro, non solo nel concetto, ma anche nel modo di fare i calcoli, ad esempio, un'addizione di numeri frazionari è un calcolo assai più complicato di quello di un'addizione di numeri interi, un'addizione di numeri relativi diventa, quando i numeri sono di segno opposto, una sottrazione fra i valori assoluti, ecc.
Nonostante ciò, la ragione del comune nome di numero, attribuito a queste entità fra loro diverse, si deve ricercare nel fatto che per esse si sono potute definire le quattro operazioni fondamentali, in modo che godessero delle cosiddette proprietà formali. Tali proprietà formali sono quindi comuni tanto alle operazioni con i numeri interi, quanto a quelle con i numeri frazionari, tanto con i numeri assoluti, come con i numeri relativi. In tali proprietà formali, che sono alla base del calcolo letterale, sta dunque l'essenza del concetto di numero. In altri termini, si può dare la definizione generale di numero.
Definizione - Sia dato un insieme di entità di natura qualsiasi, esse si chiamano numeri, quando si possono definire le quattro operazioni fondamentali in modo che valgano le consuete proprietà formali.
Quindi, introdurre un nuovo tipo di numeri, significa considerare un nuovo insieme di entità che soddisfino le condizioni della definizione suddetta.
Considerazioni a carattere generale sulla necessità di introdurre nuovi numeri
Si vuol far vedere come ancora esigenze di carattere pratico portano a dover considerare un certo insieme di entità diverse da quelle che definiscono i numeri razionali assoluti o relativi. In seguito si vedrà come anche per questi nuovi enti si potranno definire le quattro operazioni fondamentali in modo che esse godano delle consuete proprietà formali; dopo di ciò, a queste nuove entità si potrà attribuire il nome di numeri, in base alla definizione di numero. A tale scopo, anche se sommariamente, sarà trattato il problema della misura dei segmenti e quello dell'estrazione di radice quadrata da un numero razionale assoluto, che non sia un quadrato perfetto. Si ora ricordano alcune definizioni date in geometria elementare:
1)-dopo aver stabilito l'uguaglianza e la disuguaglianza fra segmenti, è stata stabilita la somma di due o più segmenti e si è visto che questa operazione gode delle consuete proprietà formali. Se m è un numero maggiore di uno e se con u si indica un segmento, con la scrittura mu si è convenuto di indicare quel segmento che risulta dalla somma di m segmenti uguali ad u; cioè, per definizione, si è posto: mu=u+u+u+ ...+u (m volte).
2)-se n è un numero intero maggiore di uno, con la scrittura:
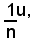
si indica un sottomultiplo di u secondo il numero n, cioè quel segmento che è uguale all'ennesima parte di u. Con la scrittura:
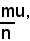
si indica quel segmento che è uguale alla somma di m segmenti tutti uguali all'ennesima parte di u. In altri termini, dire che il segmento
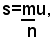
significa che l'ennesima parte di u è contenuta in s esattamente m volte. In tal caso si suol dire anche che il segmento s è uguale al prodotto del segmento u per il numero razionale m/n.
3)-due segmenti s e u si dicono commensurabili quando esiste un numero razionale assoluto
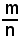
per il quale risulta:
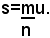
Si osserva che può essere n=1,
4)-due segmenti s e u si dicono incommensurabili quando qualunque sia il numero razionale assoluto, risulta sempre:
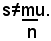
E' facile provare l'esistenza di segmenti fra loro incommensurabili, ad esempio, si dimostra il seguente teorema:
la diagonale e il lato di un quadrato sono segmenti fra loro incommensurabili.
Sia ABCD il quadrato. Ragionando per assurdo, si supponga che la diagonale BD e il lato AB del quadrato siano fra loro commensurabili. Se BD e AB sono fra loro commensurabili, esiste un numero razionale m/n per il quale risulta: (1)
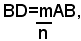
dove i numeri m e n si possono supporre, evidentemente primi fra loro.
Posto: (2)
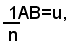
cioè indicato con u il segmento uguale all'ennesima parte di AB, dalla (1) e (2), si ricava: BD=mu, AB=nu, cioè il segmento u è contenuto esattamente m volte in BD e n volte in AB.
Premesso ciò, si costruiscono i quadrati sopra la diagonale BD e sopra i lati, fra loro uguali, AB, BD. Si divide poi ciascun lato del quadrato costruito su BD, in m parti uguali, e ciascuno dei lati dei quadrati costruiti su AB e AD in n parti uguali, e si congiungono poi i punti di divisione dei lati opposti. Nella figura seguente si è supposto m=4 e n=3.
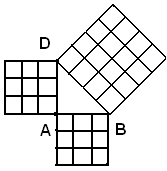
In tal modo il quadrato costruito su BD risulta scomposto in m2 quadratini e ciascuno dei quadrati costruiti su AB e AD in n2 quadratini; tutti questi quadratini sono fra loro uguali, perchè ognuno di lato u. Per il teorema di Pitagora, applicato al triangolo rettangolo isoscele ABD, si ha: m2=2n2, ossia: (3)
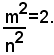
Si vede facilmente che la (3) non può essere verificata per n=1, perchè non esiste un numero intero il cui quadrato sia uguale a 2. Ma la (3) non può essere verificata nemmeno per n>1; infatti, ricordando che se due numeri m e n sono primi fra loro, la frazione m2/n2 èirriducibile e perciò non può essere uguale al numero
intero 2. La (3) è quindi assurda. Siccome l'assurdo è
derivato dall'aver supposto che la diagonale BD e il lato AB del quadrato fossero fra loro commensurabili, si può concludere che non lo sono.
Da tale ragionamento segue che non esiste nessun numero razionale positivo il cui quadrato risulti uguale al numero 2. E' evidente poi che non esiste nemmeno un numero razionale negativo il cui quadrato sia uguale a 2, perchè se un numero negativo elevato al quadrato valesse 2, anche il suo opposto, cioè un numero positivo, dovrebbe dare lo stesso risultato, il che è assurdo.
Problema della misura dei segmenti
Si definisce ora la misura di un segmento s, rispetto ad un altro segmento u, preso come unità di misura; si distinguono due casi:
1° Caso - Segmenti fra loro commensurabili.
Se il segmento u è contenuto esattamente in s, ad esempio sia s=6u, il numero 6 si chiama misura di s rispetto a u. Se non si verifica un tal caso, dato che per ipotesi s e u sono fra loro commensurabili, esisterà un sottomultiplo di u, ad esempio la sua quinta parte, che è contenuto esattamente in s, ad esempio 21 volte, in modo che:
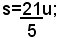
il numero
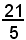
si chiama misura di s rispetto a u.
In generale, se l'ennesima parte di u è contenuta in s esattamente m volte di modo che risulti:
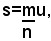
il numero
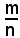
si chiama misura di s rispetto a u.
Quindi si può dare la seguente definizione: se s e u sono due segmenti fra loro commensurabili, si chiama misura di s rispetto a u, preso come unità di misura, il numero
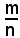
per il quale risulta:
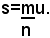
Dalla definizione data segue non soltanto la misura si s rispetto a u è un numero ben determinato, fratto o in particolare intero, ma, viceversa, dato il segmento u e preso ad arbitrio un qualsiasi numero razionale assoluto p/q, diverso da zero, esiste sempre un determinato segmento avente, rispetto a u, per misura il numero p/q; questo segmento commensurabile con u è (p/q)u. Si può quindi dire che:
i numeri razionali assoluti risolvono completamente il problema della misura per i segmenti commensurabili con l'unità di misura e solo per essi.
In altri termini, si può dire che mediante le coppie ordinate di numeri interi, con il secondo diverso da zero, si può definire la misura dei segmenti commensurabili con l'unità di misura.
2° Caso - Segmenti fra loro incommensurabili.
Supponendo i segmenti s e u incommensurabili fra loro, si vuol vedere come si risolve praticamente il problema della misura di s rispetto a u. Si consideri che u sia il metro e si misuri il segmento s fino al centimetro, si troverà, ad esempio che 5,16 è minore di s e 5,17 maggiore di s. Se il centimetro è trascurabile, si prende come misura di s tanto 5,16 come misura approssimata per difetto, quanto 5,17 come misura approssimata per eccesso. Analogamente si procede se è richiesta un'approssimazione maggiore. Siccome in ogni problema vi sono sempre quantità trascurabili, si vede che per ogni approssimazione prefissata, il problema della misura di s viene risolto come nel caso della commensurabilità. Ma questa risoluzione del problema della misura, per i segmenti incommensurabili con l'unità di missura, non dà per risultato un numero razionale ben determinato, come nel caso della commensurabilità, ma vari numeri, secondo l'ordine di approssimazione che si vuole. Si può dire, per comprendere tutti i casi possibili di approssimazione, che il problema della misura dei segmenti incommensurabili con l'unità di misura viene risolto assegnando due classi di numeri razionali, mettendo nella prima tutte le misure approssimate per difetto e nella seconda tutte le misure approssimate per eccesso. Precisamente, se
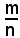
è un numero razionale diverso da zero, non potrà mai risultare:
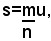
perchè altrimenti i segmenti s e u sarebbero fra loro commensurabili, e ciò è contro l'ipotesi.
Perciò risulterà:

Siccome il segmento
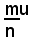
è commensurabile con u e la sua misura rispetto a u è
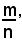
allora, se risulterà
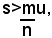
si dirà che il numero m/n è una misura approssimata per difetto di s rispetto a u.
Se invece risulterà
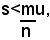
si dirà che il numero m/n è una misura approssimata per eccesso di s rispetto a u.
In altri termini: si dirà che il numero razionale assoluto m/n è una misura approssimata per difetto o per eccesso di s rispetto a u, a seconda che risulti

Cioè: le misure per difetto e per eccesso di s rispetto a u sono le misure dei segmenti commensurabili con u, rispettivamente minori e maggiori di s.
Premesso ciò, si indica con A la classe contenente tutti i numeri razionali assoluti che esprimono per difetto le misure di s rispetto a u, e con B la classe contenente tutti i numeri razionali assoluti che esprimono, per eccesso le misure di s rispetto a u; se si osservano le due classi così costruite, si vede facilmente che esse godono di quattro proprietà.
1)-Ogni numero contenuto in A è minore di ogni numero contenuto in B.
2)-Se un numero appartiene alla prima classe A, ogni numero razionale diverso da zero e minore di esso, appartiene anche alla prima classe; se un numero appartiene alla seconda classe B, ogni numero razionale maggiore di esso appartiene anche alla seconda classe.
3)-La prima classe non ha massimo, la seconda classe non ha minimo.
Infatti, presa una qualsiasi misura per difetto del segmento s, esiste un'altra misura più approssimata ancora per difetto; dunque A non ha un massimo; analogamente si prova che A non ha un minimo.
4)-Ogni numero razionale assoluto, diverso da zero, trova posto o nella classe A oppure nella classe B.
Infatti, essendo i segmenti s e u incommensurabili, ogni numero razionale assoluto, diverso da zero, è la misura per difetto o per eccesso di s rispetto a u.
Due classi di numeri razionali assoluti che soddisfano le quattro condizioni suddette, si suol dire che formano una sezione o taglio del campo dei numeri razionali assoluti.
Ricapitolando, si può dire:
-quando il segmento s è commensurabile con u, e si confronta s con u e con i suoi sottomultipli, si perviene a costruire due classi di numeri razionali assoluti soddisfacenti le quattro condizioni dette, e tali che i numeri contenuti nella prima classe esprimono le misure di s rispetto a u, mentre i numeri della seconda classe esprimono le misure per eccesso di s rispetto a u.
Si potrebbe inoltre dimostrare che: esiste soltanto il segmento s che ha, rispetto a u, come misure per difetto i numeri contenuti in A e come misure per eccesso i numeri contenuti in B, Cioè la conoscenza delle classi A e B determina il segmento s per mezzo di u, così pure un numero razionale assoluto m/n determina completamente il segmento che, rispetto a u, ha per misura il numero m/n. Pertanto, mentre nel primo caso il legame fra s e u può esprimersi mediante un numero razionale assoluto, cioè mediante la coppia ordinata di numeri interi, nel caso dell'incommensurabilità il legame tra s e u si può esprimere soltanto a mezzo delle classi A e B delle misure per difetto e per eccesso.
Da quanto detto, si vede chiaramente che quando i due segmenti s e u sono incommensurabili fra loro, si possono dare tutte le misure approssimate per difetto e per eccesso, cioè le due classi A e B. Ora si può osservare che ci si trova di fronte a una questione analoga a quella in cui in alcuni problemi intervenivano, oltre alle unità intere, anche parti dell'unità intera. Si è visto che la soluzione di quei problemi si poteva esprimere solamente per mezzo di una coppia ordinata di numeri interi, Si è superata la difficoltà attribuendo il nome di numero anche a queste coppie ordinate di numeri interi, (ciò fu possibile, perchè anche con queste coppie di numeri interi si sono potute definire le quattro operazioni fondamentali in modo che godessero delle proprietà formali), e dicendo che le soluzioni di quei problemi erano date dai numeri definiti da quelle coppie.
Se si vuole ora risolvere il problema della misura dei segmenti incommensurabili con l'unità di misura, viene spontanea l'idea di chiamare numero la coppia di classi (A, B) di cui si è parlato in precedenza e dire che la misura di s rispetto a u è il numero definito dalla coppia (A, B).
In altri termini, per risolvere in generale il problema della misura dei segmenti, si è costretti a introdurre una nuova entità, costituita da una coppia di classi di numeri razionali soddisfacenti alle quattro condizioni enunciate in precedenza e attribuire a questa nuova entità il nome di numero; per distinguerlo dai numeri già noti, verrà chiamato numero irrazionale.
Definizione - Se s e u sono due segmenti incommensurabili, si chiama misura di s rispetto a u, il numero irrazionale definito dalla coppia di classi di numeri razionali:
(A, B) ove A contiene tutte le misure approssimate per difetto di s rispetto a u e la classe B contiene tutte le misure approssimate per eccesso.
Quindi, si può dire che, fissata l'unità di misura, ogni segmento ha una sua misura, che sarà un numero razionale, se il segmento è commensurabile con l'unitò di misura, sarà invece un numero irrazionale nel caso dell'incommensurabilità.
Problema di estrazione di radice quadrata
Come è noto, si chiama radice quadrata aritmetica di un numero razionale assoluto, quel numero razionale assoluto, se esiste, che elevato al quadrato, riproduce il numero dato.
Esempi:
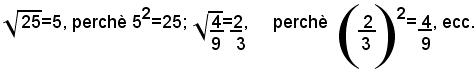
E' facile convincersi che non sempre esiste la radice quadrata di numero razionale assoluto, cioè non sempre, dato un un numero razionale assoluto a, esiste un numero razionale che, elevato al quadrato dia per risultato il numero a.
In altri termini, non sempre l'equazione x2=a, ammette soluzioni fra i numeri razionali. Ad esempio, si è già visto che non esiste nè un numero intero, nè un numero frazionario che elevato al quadrato dia per risultato il numero 2. Perciò l'equazione x2=2, non ammette soluzioni fra i numeri razionali. Però anche in questo caso, si può procedere in modo del tutto analogo a quanto si è fatto nel problema precedente per la misura fra segmenti incommensurabili.
Si dice che il numero razionale assoluto
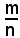
è una soluzione approssimata per difetto o per eccesso dell'equazione x2=2, a seconda che risulta:

si mettono poi in una classe H tutti i numeri razionali assoluti diversi da zero, il cui quadrato è minore di 2, e in una classe K tutti i numeri razionali assoluti il cui quadrato è maggiore di 2.
Si potrebbe vedere che anche questo le classi H e K soddisfano le quattro condizioni viste in precedenza, cioè anch'esse formano una sezione del campo dei numeri razionali assoluti, e quindi, mantenendo la nomenclatura introdotta nel problema precedente, si può dire che le due classi H, K definiscono un numero irrazionale; pertanto:
una soluzione dell'equazione x2=2, è data dal numero irrazionale definito dalla sezione (H, K), dove la prima classe H contiene tutti i numeri razionali assoluti diversi da zero, il cui quadrato è minore di 2, cioè tutte le soluzioni approssimate per difetto dell'equazione x2=2, e la seconda classe H contiene tutti i numeri irrazionali assoluti, il cui quadrato è maggiore di 2, cioè tutte le soluzioni approssimate per eccesso dell'equazione x2=2.
Si vede dunque che anche questo problema si può risolvere solamente se conviene chiamare numero questa nuova entità costruita, cioè se si chiamano numeri le sezioni fatte nel campo dei numeri razionali assoluti. Dai due problemi considerati, e da moltissimi altri che si potrebbero trattare, si vede in pratica si presentano dei problemi che non ammettono soluzioni con la sola conoscenza dei numeri razionali. Soltanto introducendo nella matematica una nuova entità, la sezione, si può dare la risposta a tali problemi. Occorre ora giustificare il nome di numero dato alle sezioni, facendo vedere che anche per le sezioni valgono le quattro operazioni fondamentali e le solite proprietà formali.
La definizione generale di numero fa sì che non ci si deve meravigliare che il nome di numero possa essere dato a una coppia formata da due classi di numeri razionali che formano una sezione. Non si deve mai dimenticare che numeri vuol dire entità qualsiasi, cioè, qualunque sia la loro natura, purchè con essi si possano definire le quattro operazioni fondamentali, in modo che godano delle consuete proprietà formali. E' vero che la natura di quello che verrà chiamato numero irrazionale è diversa da quella di numero razionale, in quanto il numero irrazionale è una coppia di classi costituite ciascuna da infiniti numeri razionali mentre il numero razionale è una coppia di numeri interi, ma questo non ha nessuna importanza; l'essenziale è soltanto che anche le operazioni con questi nuovi numeri godano delle stesse proprietà delle operazioni fatte con i numeri razionali.
Le sezioni del campo razionale
Osservato che le sezioni considerate nei due problemi trattati, sono state costruite, per maggiore semplicità di ragionamento, solamente con i numeri razionali assoluti, ci si pone ora, per maggiore generalità sin dall'inizio, nel campo dei numeri razionali relarivi.
Definizione - Si dice che le due classi A e B di numeri razionali relativi formano una sezione del campo dei numeri razionali relativi, quando soddisfano le seguenti quattro condizioni:
1)-ogni numero della classe A è minore di ogni numero della classe B;
2)-se un numero appartiene alla prima classe A, ogni numero razionale minore di esso appartiene pure alla prima classe; se un numero appartiene alla seconda classe B, ogni numero razionale maggiore di esso appartiene pure alla seconda classe;
3)-la prima classe A non ha massimo, la seconda classe B non ha minimo (una classe A di numeri razionali distinti ammette un massimo, quando esiste in A un numero che è maggiore di tutti gli altri numeri contenuti in A; ammette un minimo quando esiste in A un numero che è minore di tutti gli altri numeri contenuti in A).
E' facile vedere che esistono delle classi di numeri razionali che non ammettono, ad esempio il massimo.
Infatti, se nella classe A si mettono tutti i numeri razionli minori del numero 5, questa classe evidentemente non ammette il massimo. In modo analogo si prova che vi sono classi di numeri razionali che non ammettono il minimo.
4)-Ogni numero razionale relativo, eccetto l'1, dev'essere contenuto o nella classe A oppure nella classe B.
Questa condizione è più generale della condizione 4) enunciata in precedenza. Infatti, questa impone che non vi sia nessun numero razionale relativo escluso dalle due classi A e B, mentre la 4) precedente ammette che vi possa essere un numero razionale relativo escluso sia da A che da B.
La classe A si chiama classe inferiore della sezione, la classe B, classe superiore della sezione. La sezione formata con le classi A e B si indica con (A, B).
Dalla condizione 4) segue che da una sezione può essere o escluso un solo numero razionale oppure nessuno.
Quando dalla sezione (A, B) è escluso un numero razionale, esso dovrà risultare maggiore di tutti i numeri contenuti nella classe inferiore A e minore di tutti i numeri contenuti nella classe superiore B. Infatti, se c'è un numero che non appartiene nè alla classe A nè alla classe B, esso non può essere minore di un numero di A, perchè altrimenti, per la condizione 2) dovrebbe appartenere ad A. Analogamente si vede che il numero c non può essere maggiore di un numero B, perchè altrimenti, per la condizione 2) dovrebbe appartenere a B, contro l'ipotesi fatta.
Si vede subito che esistono sia sezioni che escludono un numero razionale, sia sezioni che non escludono nessun numero razionale; dopo di ciò sarà giustificata la seguente definizione:
-le sezioni del campo dei numeri razionali si dicono di prima specie quando escludono un numero razionale, di seconda specie quando non escludono nessun numero razionale.
Esempi di sezioni di 1^ e 2^ specie
1^ specie
Sia r un numero razionale qualsiasi, fratto o intero, e si pongano nella classe inferiore A tutti i numeri razionali minori del numero r e nella classe inferiore b tutti i numeri razionali maggiori del numero r. Le due classi A e B così costruite soddisfano, evidentemente, le condizioni 1), 2), 3) e 4). La sezione (A, B), così costruita, escludendo il numero r, è una sezione di prima specie.
Si può dimostrare che:
le sezioni che escludono un numero razionale sono tutte e sole quelle costruite come sopra, ossia, preso ad arbitrio un numero razionale r, esse sono costruite mettendo nella prima classe tutti i numeri razionali minori di r, e nella seconda classe quelli maggiori di r.
2^ specie
Si mettono nella classe inferiore A tutti i numeri razionali negativi, lo zero e tutti i numeri razionali positivi il cui quadrato è minore di 2 e nella classe superiore B tutti i numeri razionali positivi il cui quadrato è maggiore di 2. Come già visto, si osservi che qualsiasi numero razionale, nessuno escluso, ha il suo quadrato o minore o maggiore di 2. Quindi ogni numero razionale o appartiene alla classe A, oppure alla classe B. Segue che, se si dimostra che le due classi A e B, così costruite, formano una sezione, questa sarà di seconda specie. Le due classi A e B, soddisfano evidentemente le condizioni 1), 2). 4); si prova ora che soddisfano anche la condizione 3). Si incomincia col far vedere che la classe A non ammette massimo. A tale scopo, si ragiona per assurdo, supponendo che il numero positivo m sia il massimo della classe A. Evidentemente sarà m>1, perchè nella classe A vi sono numeri maggiori di 1. Inoltre, in quanto m appartiene ad A, dev'essere m2<2. Si verificherà un assurdo se si prova che esiste un numero maggiore di m, appartenente anch'esso alla classe A. A tal scopo, posto (1)
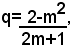
si osserva che il numero q è positivo e minore di 1, infatti il numeratore 2-m2 è positivo e minore di 1 perchè m2<2, m>1, mentre il denominatore 2m+1>3; perciò si può scrivere: (2) 2m+q<m+1, da cui segue, moltiplicando ambo i membri della (2) per il numero positivo q: (3) q(2mìq)<q(2m+1). Sostituendo nel secondo membro della (3), al posto di q il suo valore dato dalla (1), si ottiene:
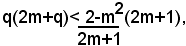
ossia: 2mq+q2<2-m2.
Aggiungendo il numero m2 ad ambo i membri di quest'ultima disuguaglianza, si ha: 2mq+q2+m2<2-m2-m2, cioè: (m+q)2<2.
Ciò dimostra che il numero m+q appartiene alla classe A, perchè il suo quadrato è minore di 2, e quindi, dato che m+q>m, è assurdo supporre che m sia il massimo della classe A. Analogamente si dimostra che la classe B non ha minimo.
Le due classi A e B, sopra costruite, formano una sezione e, per quanto detto, essa è di seconda specie.
In modo del tutto analogo si prova che sono sezioni di seconda specie anche quelle costruite nel modo seguente:
sia r un numero razionale positivo qualsiasi, fratto o in particolare intero, che non sia quadrato perfetto, e si mettano nella classe inferiore H tutti i numeri negativi, lo zero, e i numeri razionali positivi il cui quadrato è minore di r; nella classe K tutti i numeri razionali positivi il cui quadrato è maggiore di r. Queste particolari sezioni si seconda specie si chiamano, per una ragione che si vedrà in seguito, radice quadrata aritmetica di r, e per indicare ciò si suole scrivere:
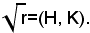
Nota bene
Siccome i numeri che appartengono a ciascuna delle due classi A e B di una sezione sono infiniti, non sarà mai possibile scrivere tutti i numeri contenuti in A e B.
Perciò, si dirà che una sezione è data quando è assegnata una legge, o una proprietà, che permetta di decidere quali numeri stanno in A e quali in B. In altri termini, si può dire che una sezione è nota quando è data una legge mediante la quale, preso ad arbitrio un qualsiasi numero razionale r, si riesca a stabilire se un numero sta nella classe inferiore della sezione oppure in quella superiore, o l'eventuale numero escluso da entrambe le classi.
Definizione di numero reale
Si chiama numero reale una qualsiasi sezione nel campo dei numeri interi relativi.
In base a tale definizione la parola "numero reale" è sinonimo di "sezione nel campo dei numeri razionali". Assegnare quindi un numero reale, equivale ad assegnare una sezione nel campo dei numeri razionali. Il nome di numero dato ad una sezione è giustificato dal fatto che con esse si potranno definire le quattro operazioni fondamentali e che per esse valgano tutte le proprietà formali, in accordo con la definizione di numero data. Per brevità, spesso è utile indicare con una lettera, ad esempio α, il numero reale individuato da una data sezione (A, B) del campo razionale, scrivendo α=(A, B).
La totalità dei numeri reali coincide quindi con la totalità delle sezioni del campo reazionale.
ConvenzioneQuando
la sezione (A, B) è di prima specie, cioè quando esclude
un numero razionale r, si conviene che essa rappresenti il numero
razionale stesso, e si scriverà r=(A, B). Ad esempio, se A
è la classe dei numeri razionali minori di 5 e B è la
classe dei numeri razionali maggiori di 5, si conviene che la sezione
(A, B) rappresenti il numero razionale 5, e si scrive: 5=(A,
B). Le sezioni di seconda specie, cioè quelle che non
escludono nessun numero razionale, si chiamano numeri irrazionali,
quindi si pone la seguente definizione:
si chiama numero irrazionale una sezione del campo razionale che non esclude nessun numero razionale.
Dalla convenzione fatta, segue che:
a)-i numeri razionali sono contenuti nel campo dei numeri reali;
b)-i numeri reali sono quindi costituiti dai numeri razionali e dai numeri irrazionali.
Confronto di numeri reali
Siano dati due numeri reali, cioè due sezioni del campo dei numeri razionali:
α=(A, B), β=(C, D); si danno le seguenti definizioni:
1)-si dice che i numeri reali α e β sono uguali, e si scrive α=β, quando le due classi A e C coincidono, e quindi anche B e D;
2)-si dice che il numero reale α è maggiore di β, e si scrive α>β, quando esiste qualche numero della classe A che appartiene alla classe D.
E' inteso che A contiene tutti i numeri di C.
3)-si dice che il numero reale α è minore di β, e si scrive α<β, quando esiste qualche numero della classe B che appartiene a C. E' inteso che C contiene tutti i numeri di A.
Dalle tre definizioni segue che: dati due numeri reali α e β, si presenta necessariamente uno, ed uno solo dei seguenti tre casi: α=β; α>β; α<β.
4)-un numero reale α=(A, B), si dice positivo, se è maggiore di zero, negativo se è minore di zero.
Si deve ricordare che lo zero è individuato dalla sezione di prima specie (N, P), ove la classe inferiore N è formata da tutti i numeri razionali negativi e la classe superiore P da tutti i numeri razionali positivi, in base alle definizioni 2) e 3), si può dire che:
un numero reale α=(A, B) è positivo, quando in A vi sono numeri razionali positivi, è invece negativo quando in B vi sono numeri razionali negativi.
Esempio: considerati i due numeri irrazionali:

Per provare ciò, in base alla definizione 2), basta far vedere che nella classe A esiste almeno un numero contenuto nella classe D. Infatti, il numero 2 sta in A, perchè risulta 22<5, e sta anche in D, perchè risulta 22>2.
Valore approssimato di un numero irrazionale
Definizione
Sia dato il numero irrazionale α=(A, B).

Esempi: determinare il valore approssimato per difetto e per eccesso del numero (1)

Essendo:
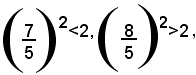
si vede che il numero 7/5 sta nella classe A, mentre il numero 8/5 sta nella classe B. Perciò 7/5 è un valore approssimato per difetto, a meno di 1/5 del numero (1), mentre 8/5 è un valore approssimato per eccesso, a meno di 1/5 del numero (1).
Analogamente, essendo:
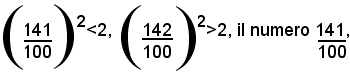
ossia 1,41, è un valore approssimato per difetto, a meno di 1/102, del numero (1), mentre 1,42 è un valore approssimato per eccesso, a meno di 1/102 del numero (1).
Operazioni con i numeri reali
Somma di due o più numeri reali
Siano dati due numeri reali, cioè due sezioni del campo dei numeri razionali:
α=(A, B). β=(C, D). Si considerino la classe A+C ottenuta sommando ciascun numero di A con ciascun numero di C e la classe B+D, ottenuta sommando ciascun numero di B con ciascun numero di D. Si può dimostrare il seguente teorema che ci si limita soltanto ad enunciare:
le due classi A+C e B+D, così definite, costituiscono una sezione del campo dei numeri razionali; la sezione (A+C, B+D) definisce quindi un numero reale che, per definizione, si chiama somma dei due numeri reali α e β; si pone quindi la seguente definizione:
si chiama somma dei due numeri reali α=(A, B). β=(C, D), il numero reale definito dalla sezione la cui classe inferiore si ottiene sommando ciascun numero di A con ciascun numero di C e quella superiore sommando ciascun numero di B con ciascun numero di D.
Indicando con α e β la somma dei due numeri, per definizione, si ha: α+β=(A+C, B+D).
Si chiama somma dei numeri reali α, β e γ il numero, che si indica con α+β+γ, ottenuto sommando α con β e aggiungendo γ alla somma ottenuta.
In modo analodo si definisce la somma di più numeri reali dati in un certo ordine.
Si potrebbe inoltre dimostrare che: l'addizione gode della proprietà commutativa e associativa.
Numeri opposti
Sia α=(A, B) un numero reale, cioè una sezione nel campo dei numeri razionali; indicato con -B e -A le classi dei numeri che si ottengono rispettivamente da B e da A, considerando gli opposti dei numeri razionali che lo compongono, osservando che, essendo ogni numero della classe A minore di ogni numero della classe B, segue che ogni numero della classe -B è minore di ogni numero della classe -A. E' evidente che le classi -B e -A formano una sezione.
Il numero definito dalla sezione (-B, -A) si chiama opposto del numero α, e si indica con il simbolo -α. Si pùo quindi dare la seguente definizione:
si chiama opposto del numero reale α=(A, B), e si indica con -α, il numero definito dalla sezione (-B, -A), ove con -B, e -A si indicano le classi dei numeri che si ottengono rispettivamente da B e A, prendendo gli opposti dei numeri razionali che lo compongono.
Si dimostra che: la somma di due numeri opposti è uguale a zero.
Infatti: α+(-α)=[A+(-B), B+(-A)]=(A-B, B-A). Ora la classe A-B contiene solo i numeri negativi, dato che i numeri della classe B sono maggiori di quelli della classe A, mentre i numeri della classe B-A sono tutti positivi. Perciò il numero individuato dalla sezione (A-B, B-A) è lo zero, come volevasi dimostrare.
Si osservi inoltre che se il numero α=(A, B) è positivo, cioè se nella classe A sono contenuti i numeri positivi, allora il numero opposto -α=(-B, -A) sarà negativo, perchè nella classe -A sono contenuti dei numeri negativi. Viceversa, se α è negativo, ai prova che il suo opposto -α è positivo. Si può dare quindi la seguente definizione:
si chiama valore assoluto del numero reale α, e si indica con |α|, il numero stesso se α è positivo, il suo opposto se α è negativo; se α=0, il suo valore assoluto, per definizione, è uguale a zero.
Sottrazione di due numeri realiSiano dati due numeri reali, cioè due sezioni del campo dei numeri razionali: α=(A, B), β=(C, D).
Definizione - Si chiama differenza fra due numeri reali α e β, nell'ordine considerato, e si indica con α-β, la somma del numero reale α con l'opposto del numero reale β. Cioè, per definizione, si ha: α-β=α+(-β)=(A, B)+(-D, C)=(A-D, B-C), ove la classe A-D si ottiene togliendo da ogni numero di A successivamente ogni numero di D, e la classe B-C togliendo da ogni numero di B successivamente ogni numero di C.
Prodotto di numeri reali
Siano dati due numeri reali positivi: α=(A, B), β=(C, D). Si indica ora con F la classe costituita da numeri razionali negativi, dallo zero e dai numeri positivi che risultano dal prodotto di ciascun numero positivo della classe A con ciascun numero positivo della classe C; e con G la classe costituita dai prodotti di ciascun numero di B con ciascun numero di D.
Si dimostra, e ci si limita solo ad enunciarlo, il seguente teorema:
le due classi F e G costituiscono una sezione del campo dei numeri razionali.
La sezione: (F, G), definisce quindi un numero reale che, per definizione, si chiama prodotto dei due numeri reali positivi α e β.
Definizione - Si chiama prodotto dei due numeri reali positivi α=(A, B) e β=(C, D), il numero reale definito dalla sezione la cui classe inferiore F è formata dai numeri razionali negarivi, dallo zero, e dai prodotti di ciascun numero positivo di A per ciascun numero positivo di C; e la cui classe superiore G è quella formata dai prodotti di ciascun numero di B per ciascun numero di D.
Se poi i due numeri reali α e β sono entrambi negativi, oppure uno positivo e l'altro negativo, si pone la seguente definizione:
si chiama prodotto dei due numeri reali α e β, non nulli, e non entrambi positivi, il prodotto dei loro valori assoluti, se i due numeri sono entrambi negativi; l'opposto del prodotto dei valori assoluti, se i due numeri sono l'uno positivo e l'altro negativo. Si pone uguale a zero, per definizione, il prodotto di un numero reale per zero.
Se poi: α, β, γ, sono tre numeri reali, si chiama loro prodotto, per definizione, il numero che si indica con αβγ, ottenuto moltiplicando prima α con β e poi il prodotto ottenuto con γ. In modo analogo si definisce il prodotto di più numeri reali dati in un certo ordine.
Si potrebbe inoltre dimostrare che:
la moltiplicazione fra numeri reali gode della propprietà commutativa, associativa e della proprietà distributiva rispetto all'addizione.
Teorema - Dato un qualsiasi numero razionale positivo r, che non sia un quadrato perfetto, esiste sempre un numero irrazionale positivo il cui quadrato risulta uguale a r.
Per dimostrare ciò, si indica con (A, B) la sezione così formata:
-nella classe A si mettono tutti i numeri razionali negativi, lo zero e i numeri razionali positivi il cui quadrato è minore di r;
-nella classe B si mettono tutti i numeri razionali positivi il cui quadrato risulta maggiore di r. Come è noto, la sezione così costruita è di seconda specie e perciò essa definisce un numero irrazionale che è positivo, dato che la classe A contiene dei numeri razionali positivi.
Si vuole provare che risulta: (A, B)(A, B)=r, ossia: [(A, B)]2=r, e con ciò sarà dimostrato il teorema.
Infatti, detta (F, G) la sezione prodotto, cioè posto: (F, G)=(A, B)(A, B), si osservi che la classe F è costituita dai numeri negativi, dallo zero, e dai prodotti, a due a due, dei numeri positivi contenuti in A. Perciò, se si indicano con α1 e α2 due numeri positivi qualsiasi, distinti o no, di A, il numero α1α2 è contenuto in F. Essendo: α12<r, α22<r, perchè α1 e α2 stanno nella classe A, moltiplicando membro a membro le due disuguaglianze suddette, si ha: α12α22<r2, ossia: (α1α2)2<r2, e quindi α1α2<r, dato che α1 e α2 sono numeri positivi. Si vede quindi che tutti i numeri contenuti in F sono minori di r.
Nello stesso modo si prova che tutti i numeri contenuti in G sono maggiori di r.
La sezione (F, G), escludendo il numero r, è una sezione di prima specie e rappresenta quindi proprio il numero stesso r, cioè: (F, G)=R, ossia [(A, B)]2=r, come volevasi dimostrare.
Siccome in seguito sarà dimostrato che esiste un numero irrazionale positivo il cui quadrato vale r, è naturale chiamare il numero razionale (A, B) radice quadrata aritmetica del numero razionale positivo r, e scrivere:
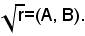
Nota bene
Per non incorrere in errori grossolani è bene riflettere sul teorema precedente, per chiarire ulteriormente quanto detto. Ci si pone la domanda: cosa rappresenta il simbolo:
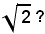
Esso rappresenta un numero irrazionale, cioè una sezione (A, B) di seconda specie del campo razionale. Precisamente: quella sezione in cui la classe A è formata dai numeri razionali negativi, dallo zero e dai numeri razionali positivi, il cui quadrato è minore di 2; e la cui classe superiore B è formata dai numeri razionali positivi, il cui quadrato è maggiore di 2. E questa sezione si chiama
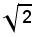
perchè, elevata al quadrato, dà per risultato la sezione che rappresenta il numero 2, e ciò in accordo con la definizione di radice quadrata aritmetica di un numero razionale. Non si deve dire, come spesso si sente ripetere, che la radice quadrata aritmetica di 2 è 1,4; oppure 1,5 o 1,41, perchè il quadrato di questi numeri, come di qualsiasi altro numero razionale, non è uguale a 2! L'entità il cui quadrato risulta uguale a 2 non può essere un numero razionale, cioè una coppia di numeri interi, perchè nessun numero razionale, come si è visto, elevato al quadrato diventa uguale al numero 2. Solamente l'ente costituito dalla sezione (A, B), sopra costruita, ha per quadrato il numero 2. Avendo quindi le idee chiare sul concetto di numero irrazionale, si potranno comprendere affermazioni, che si faranno in seguito, del tipo:
1)-la misura del doppio dell'altezza di un triangolo equilatero, rispetto al suo lato, preso come unità di misura, è uguale a: (1)
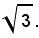
Ciò vuol dire che la misura del doppio dell'altezza del triangolo equilatero, rispetto al suo lato, preso come unità di misura, è espressa dalla sezione chiamata:
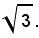
In altri termini, ciò vuol dire che la classe A formata dalle misure approssimate per difetto del doppio dell'altezza del triangolo equilatero, rispetto al suo lato, nella quale classe si siano aggiunti anche i numeri negativi e lo zero, e la classe B, formata dalle misure approssimate per eccesso, formano la sezione (A, B), in tal caso chiamata:
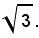
Il quadrato di tale sezione è uguale a 3.
2)-Quattro segmenti, a, b, c, d, dati in un certo ordine, si dicono in proporzione, quando il rapporto dei primi due è uguale al rapporto degli altri due. Ciò vuol dire che la sezione rappresentante la misura del segmento a rispetto a b, è uguale alla sezione che rappresenta la misura del segmento c rispetto a d.
3)-La misura del segmento che rappresenta la lunghezza di una circonferenza, rispetto al diametro, preso come unità di misura, è un numero irrazionale chiamato π.Ciò
vuol dire che, il segmento esprimente la lunghezza della circonferenza,
ha una misura rispetto al diametro della circonferenza, che
è espressa da una sezione di seconda specie, che viene indicata
con la lettera π. E si eviterà di di dire che π è uguale a 3,14, come spesso si sente dire, perchè sapendo che π
indica un numero irrazionale, cioè una sezione di seconda
specie, non può essere uguale al numero razionale 3,14. Questo
numero rappresenta la misura approssimata per difetto, cioè 3,14
è un numero appartenente alla classe inferiore della suddetta
sezione di seconda specie.
Reciproco di un numero reale non nullo
Sia α=(A, B) un numero reale positivo, si vuole definire il reciproco di tale numero.
Innanzitutto si deve osservare che, essendo per ipotesi α>0, i numeri razionali contenuti in B sono tutti positivi. Si mettono ora in una classe C i numeri razionali negativi, lo zero e quei numeri razionali posiivi che si ottengono calcolando i reciproci dei numeri di B e poi in una classe D i reciproci dei numeri positivi di A, che certamente ci sono, in quanto per ipotesi si è supposto α positivo.
Si dimostra, e ci si limita solo ad enunciarlo, il seguente teorema:
le classi C e D, così costruite, formano una sezione del campo dei numeri razionali.
Il numero definito dalla sezione (C, D) si chiama reciproco del numero positivo α e si indica con il simbolo:
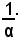
Definizione - Si chiama reciproco del numero reale positivo α=(A, B), il numero reale definito dalla sezione (C, D) la cui classe inferiore C è costituita dai numeri razionali negativi, dallo zero e dai reciproci dei numeri razionali di B e la cui classe superiore è costituita dai reciproci dei numeri positivi di A.
Si osservi che il reciproco del numero positivo α è anch'esso un numero reale positivo. Se invece α è un numero negativo, allora il suo reciproco viene definito come l'opposto del reciproco del numero positivo -α, cioè si pone:
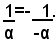
Il reciproco dello zero non si definisce.
Teorema - Il prodotto di due numeri reciproci è uguale ad uno.Si dimostra facilmente.
Quoziente di due numeri reali
Siano α=(A, B), β=(C, D), due numeri reali, il secondo dei quali diverso da zero.
Definizione - Si chiama quoziente dei due numeri reali α e β, e si indica con
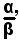
il prodotto del numero α per il reciproco del numero β, cioè si pone:
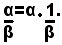
Il quoziente di due numeri reali non si definisce se il divisore è uguale a zero.
Potenze ad esponente intero di un numero reale
Sia α=(A, B) un numero reale e n un numero intero.
Se n è un numero intero maggiore di 1, si chiama potenza ennesima del numero reale α, il prodotto di n fattori uguali ad α. Cioè: αn=αα ...α (n volte).
Per definizione, si pone: α1=α, se n=1; α0=1, se n=0 e a≠0; infine,
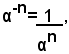
se n è un numero intero positivo e a≠0.
Il simbolo 00 non ha significato.
Dalle definizioni segue che i teoremi dimostrati sulle potenze a esponente intero dei numeri razionali, valgono anche per le potenze dei numeri reali. Pertanto si ha:
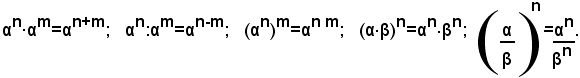
Si vuol vedere ora se le sezioni fatte con i numeri reali possono essere ancora di due specie.
A tale scopo si dimostra il seguente teorema, che ci si limita solo all'enunciato:
ogni sezione (A, B) fatta nel campo dei numeri reali è di prima specie, cioè esclude un numero reale che è maggiore di tutti i numeri reali contenuti in A e minore di tutti i numeri contenuti in B.
Da questo teorema segue che nel campo dei numeri reali si possono costruire solo sezioni di prima specie. Questa proprietà del campo dei numeri reali si esprime dicendo che il campo dei numeri reali è continuo. In contrapposizione, il campo dei numeri razionali si dice discontinuo.
Se (A, B) è una sezione nel campo dei numeri reali e α è il numero da essa escluso, si usa scrivere α=(A, B), e il numero α si suole chiamare l'elemento di separazione delle due classi A e B.
I primi numeri conosciuti furono i numeri interi assoluti: 0, 1, 2, 3, ..., che ebbero origine dalla necessità di contare per stabilire quanti sono gli oggetti di un gruppo, o per stabilire quante volte avviene un fatto, ecc. Per tali numeri sono stati stabiliti i concetti di uguaglianza e definite le quattro operazioni fondamentali, addizione, sottrazione, moltiplicazione, divisione, dimostrando che esse godono della cosiddette proprietà formali: commutativa e associativa dell'addizione e della moltiplicazione, distributiva della moltiplicazione rispetto all'addizione, ecc. In passato, si osservò che la conoscenza dei soli numeri interi assoluti non era sufficiente per risolvere problemi, anche facili, che si presentavano nelle applicazioni pratiche, e ciò in virtù del fatto che, oltre alle unità intere, si dovevano considerare anche le loro parti. Se, ad esempio, si dovevano dividere in parti uguali fra 7 ragazzi 5 tavolette di cioccolata, si notava subito che, per rispondere a tale problema, ci si deveva servire non di un solo numero intero, ma di due: del numero 7, che indica in quante parti si deve dividere ogni tavoletta di cioccolata e del numero 5 che indica quante di queste parti ha ricevuto ogni ragazzo. Perciò la risposta al problema è data dalla coppia ordinata di numeri interi (5, 7), nel senso che dev'essere stabilito quale dei due numeri si deve considerare primo nella coppia e quale come secondo. Quindi, per risolvere problemi in cui oltre ad unità intere vi sono anche parti dell'unità intera, si è costretti a considerare una nuova entità, costituita da una coppia di numeri interi, il secondo dei quali sia diverso da zero. Queste coppie ordinate di numeri interi, pur rappresentando concettualmente entità molto diverse dai numeri interi assoluti, sono state chiamate anche esse numeri e, per distinguerle dai numeri interi assoluti, alla parola numero si è aggiunto l'attributo frazionario assoluto. La ragione del perchè le coppie ordinate di numeri interi, con il secondo diverso da zero, sono state chiamate numeri, va ricercata nel fatto che anche per questi numeri è stato possibile definire le quattro operazioni fondamentali, in modo che per esse valessero le note proprietà formali per le stesse operazioni fatte con i numeri interi assoluti.
I numeri interi assoluti e i numeri frazionari assoluti si chiamano numeri razionali assoluti.
Si è visto che, per individuare determinate grandezze, ci si deve servire di un numero razionale assoluto e di un segno distintivo. Anche a tali nuove entità, costituite da un numero razionale assoluto e da un segno distintivo, si è dato il nome di numeri, e ciò sempre per il fatto che anche per essi sono state definite le quattro operazioni fondamentali, in modo tale da conservare le proprietà formali.
Questi numeri, per distinguerli dai precedenti, sono stati chiamati numeri razionali relativi. Se si osservano le tre specie di numeri conosciuti, si vede che esse differiscono fra loro, non solo nel concetto, ma anche nel modo di fare i calcoli, ad esempio, un'addizione di numeri frazionari è un calcolo assai più complicato di quello di un'addizione di numeri interi, un'addizione di numeri relativi diventa, quando i numeri sono di segno opposto, una sottrazione fra i valori assoluti, ecc.
Nonostante ciò, la ragione del comune nome di numero, attribuito a queste entità fra loro diverse, si deve ricercare nel fatto che per esse si sono potute definire le quattro operazioni fondamentali, in modo che godessero delle cosiddette proprietà formali. Tali proprietà formali sono quindi comuni tanto alle operazioni con i numeri interi, quanto a quelle con i numeri frazionari, tanto con i numeri assoluti, come con i numeri relativi. In tali proprietà formali, che sono alla base del calcolo letterale, sta dunque l'essenza del concetto di numero. In altri termini, si può dare la definizione generale di numero.
Definizione - Sia dato un insieme di entità di natura qualsiasi, esse si chiamano numeri, quando si possono definire le quattro operazioni fondamentali in modo che valgano le consuete proprietà formali.
Quindi, introdurre un nuovo tipo di numeri, significa considerare un nuovo insieme di entità che soddisfino le condizioni della definizione suddetta.
Considerazioni a carattere generale sulla necessità di introdurre nuovi numeri
Si vuol far vedere come ancora esigenze di carattere pratico portano a dover considerare un certo insieme di entità diverse da quelle che definiscono i numeri razionali assoluti o relativi. In seguito si vedrà come anche per questi nuovi enti si potranno definire le quattro operazioni fondamentali in modo che esse godano delle consuete proprietà formali; dopo di ciò, a queste nuove entità si potrà attribuire il nome di numeri, in base alla definizione di numero. A tale scopo, anche se sommariamente, sarà trattato il problema della misura dei segmenti e quello dell'estrazione di radice quadrata da un numero razionale assoluto, che non sia un quadrato perfetto. Si ora ricordano alcune definizioni date in geometria elementare:
1)-dopo aver stabilito l'uguaglianza e la disuguaglianza fra segmenti, è stata stabilita la somma di due o più segmenti e si è visto che questa operazione gode delle consuete proprietà formali. Se m è un numero maggiore di uno e se con u si indica un segmento, con la scrittura mu si è convenuto di indicare quel segmento che risulta dalla somma di m segmenti uguali ad u; cioè, per definizione, si è posto: mu=u+u+u+ ...+u (m volte).
2)-se n è un numero intero maggiore di uno, con la scrittura:
si indica un sottomultiplo di u secondo il numero n, cioè quel segmento che è uguale all'ennesima parte di u. Con la scrittura:
si indica quel segmento che è uguale alla somma di m segmenti tutti uguali all'ennesima parte di u. In altri termini, dire che il segmento
significa che l'ennesima parte di u è contenuta in s esattamente m volte. In tal caso si suol dire anche che il segmento s è uguale al prodotto del segmento u per il numero razionale m/n.
3)-due segmenti s e u si dicono commensurabili quando esiste un numero razionale assoluto
per il quale risulta:
Si osserva che può essere n=1,
4)-due segmenti s e u si dicono incommensurabili quando qualunque sia il numero razionale assoluto, risulta sempre:
E' facile provare l'esistenza di segmenti fra loro incommensurabili, ad esempio, si dimostra il seguente teorema:
la diagonale e il lato di un quadrato sono segmenti fra loro incommensurabili.
Sia ABCD il quadrato. Ragionando per assurdo, si supponga che la diagonale BD e il lato AB del quadrato siano fra loro commensurabili. Se BD e AB sono fra loro commensurabili, esiste un numero razionale m/n per il quale risulta: (1)
dove i numeri m e n si possono supporre, evidentemente primi fra loro.
Posto: (2)
cioè indicato con u il segmento uguale all'ennesima parte di AB, dalla (1) e (2), si ricava: BD=mu, AB=nu, cioè il segmento u è contenuto esattamente m volte in BD e n volte in AB.
Premesso ciò, si costruiscono i quadrati sopra la diagonale BD e sopra i lati, fra loro uguali, AB, BD. Si divide poi ciascun lato del quadrato costruito su BD, in m parti uguali, e ciascuno dei lati dei quadrati costruiti su AB e AD in n parti uguali, e si congiungono poi i punti di divisione dei lati opposti. Nella figura seguente si è supposto m=4 e n=3.

In tal modo il quadrato costruito su BD risulta scomposto in m2 quadratini e ciascuno dei quadrati costruiti su AB e AD in n2 quadratini; tutti questi quadratini sono fra loro uguali, perchè ognuno di lato u. Per il teorema di Pitagora, applicato al triangolo rettangolo isoscele ABD, si ha: m2=2n2, ossia: (3)
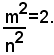
Si vede facilmente che la (3) non può essere verificata per n=1, perchè non esiste un numero intero il cui quadrato sia uguale a 2. Ma la (3) non può essere verificata nemmeno per n>1; infatti, ricordando che se due numeri m e n sono primi fra loro, la frazione m2/n2 è
Da tale ragionamento segue che non esiste nessun numero razionale positivo il cui quadrato risulti uguale al numero 2. E' evidente poi che non esiste nemmeno un numero razionale negativo il cui quadrato sia uguale a 2, perchè se un numero negativo elevato al quadrato valesse 2, anche il suo opposto, cioè un numero positivo, dovrebbe dare lo stesso risultato, il che è assurdo.
Problema della misura dei segmenti
Si definisce ora la misura di un segmento s, rispetto ad un altro segmento u, preso come unità di misura; si distinguono due casi:
1° Caso - Segmenti fra loro commensurabili.
Se il segmento u è contenuto esattamente in s, ad esempio sia s=6u, il numero 6 si chiama misura di s rispetto a u. Se non si verifica un tal caso, dato che per ipotesi s e u sono fra loro commensurabili, esisterà un sottomultiplo di u, ad esempio la sua quinta parte, che è contenuto esattamente in s, ad esempio 21 volte, in modo che:
il numero
si chiama misura di s rispetto a u.
In generale, se l'ennesima parte di u è contenuta in s esattamente m volte di modo che risulti:
il numero
si chiama misura di s rispetto a u.
Quindi si può dare la seguente definizione: se s e u sono due segmenti fra loro commensurabili, si chiama misura di s rispetto a u, preso come unità di misura, il numero
per il quale risulta:
Dalla definizione data segue non soltanto la misura si s rispetto a u è un numero ben determinato, fratto o in particolare intero, ma, viceversa, dato il segmento u e preso ad arbitrio un qualsiasi numero razionale assoluto p/q, diverso da zero, esiste sempre un determinato segmento avente, rispetto a u, per misura il numero p/q; questo segmento commensurabile con u è (p/q)u. Si può quindi dire che:
i numeri razionali assoluti risolvono completamente il problema della misura per i segmenti commensurabili con l'unità di misura e solo per essi.
In altri termini, si può dire che mediante le coppie ordinate di numeri interi, con il secondo diverso da zero, si può definire la misura dei segmenti commensurabili con l'unità di misura.
2° Caso - Segmenti fra loro incommensurabili.
Supponendo i segmenti s e u incommensurabili fra loro, si vuol vedere come si risolve praticamente il problema della misura di s rispetto a u. Si consideri che u sia il metro e si misuri il segmento s fino al centimetro, si troverà, ad esempio che 5,16 è minore di s e 5,17 maggiore di s. Se il centimetro è trascurabile, si prende come misura di s tanto 5,16 come misura approssimata per difetto, quanto 5,17 come misura approssimata per eccesso. Analogamente si procede se è richiesta un'approssimazione maggiore. Siccome in ogni problema vi sono sempre quantità trascurabili, si vede che per ogni approssimazione prefissata, il problema della misura di s viene risolto come nel caso della commensurabilità. Ma questa risoluzione del problema della misura, per i segmenti incommensurabili con l'unità di missura, non dà per risultato un numero razionale ben determinato, come nel caso della commensurabilità, ma vari numeri, secondo l'ordine di approssimazione che si vuole. Si può dire, per comprendere tutti i casi possibili di approssimazione, che il problema della misura dei segmenti incommensurabili con l'unità di misura viene risolto assegnando due classi di numeri razionali, mettendo nella prima tutte le misure approssimate per difetto e nella seconda tutte le misure approssimate per eccesso. Precisamente, se
è un numero razionale diverso da zero, non potrà mai risultare:
perchè altrimenti i segmenti s e u sarebbero fra loro commensurabili, e ciò è contro l'ipotesi.
Perciò risulterà:
è commensurabile con u e la sua misura rispetto a u è
allora, se risulterà
si dirà che il numero m/n è una misura approssimata per difetto di s rispetto a u.
Se invece risulterà
si dirà che il numero m/n è una misura approssimata per eccesso di s rispetto a u.
In altri termini: si dirà che il numero razionale assoluto m/n è una misura approssimata per difetto o per eccesso di s rispetto a u, a seconda che risulti
Cioè: le misure per difetto e per eccesso di s rispetto a u sono le misure dei segmenti commensurabili con u, rispettivamente minori e maggiori di s.
Premesso ciò, si indica con A la classe contenente tutti i numeri razionali assoluti che esprimono per difetto le misure di s rispetto a u, e con B la classe contenente tutti i numeri razionali assoluti che esprimono, per eccesso le misure di s rispetto a u; se si osservano le due classi così costruite, si vede facilmente che esse godono di quattro proprietà.
1)-Ogni numero contenuto in A è minore di ogni numero contenuto in B.
2)-Se un numero appartiene alla prima classe A, ogni numero razionale diverso da zero e minore di esso, appartiene anche alla prima classe; se un numero appartiene alla seconda classe B, ogni numero razionale maggiore di esso appartiene anche alla seconda classe.
3)-La prima classe non ha massimo, la seconda classe non ha minimo.
Infatti, presa una qualsiasi misura per difetto del segmento s, esiste un'altra misura più approssimata ancora per difetto; dunque A non ha un massimo; analogamente si prova che A non ha un minimo.
4)-Ogni numero razionale assoluto, diverso da zero, trova posto o nella classe A oppure nella classe B.
Infatti, essendo i segmenti s e u incommensurabili, ogni numero razionale assoluto, diverso da zero, è la misura per difetto o per eccesso di s rispetto a u.
Due classi di numeri razionali assoluti che soddisfano le quattro condizioni suddette, si suol dire che formano una sezione o taglio del campo dei numeri razionali assoluti.
Ricapitolando, si può dire:
-quando il segmento s è commensurabile con u, e si confronta s con u e con i suoi sottomultipli, si perviene a costruire due classi di numeri razionali assoluti soddisfacenti le quattro condizioni dette, e tali che i numeri contenuti nella prima classe esprimono le misure di s rispetto a u, mentre i numeri della seconda classe esprimono le misure per eccesso di s rispetto a u.
Si potrebbe inoltre dimostrare che: esiste soltanto il segmento s che ha, rispetto a u, come misure per difetto i numeri contenuti in A e come misure per eccesso i numeri contenuti in B, Cioè la conoscenza delle classi A e B determina il segmento s per mezzo di u, così pure un numero razionale assoluto m/n determina completamente il segmento che, rispetto a u, ha per misura il numero m/n. Pertanto, mentre nel primo caso il legame fra s e u può esprimersi mediante un numero razionale assoluto, cioè mediante la coppia ordinata di numeri interi, nel caso dell'incommensurabilità il legame tra s e u si può esprimere soltanto a mezzo delle classi A e B delle misure per difetto e per eccesso.
Da quanto detto, si vede chiaramente che quando i due segmenti s e u sono incommensurabili fra loro, si possono dare tutte le misure approssimate per difetto e per eccesso, cioè le due classi A e B. Ora si può osservare che ci si trova di fronte a una questione analoga a quella in cui in alcuni problemi intervenivano, oltre alle unità intere, anche parti dell'unità intera. Si è visto che la soluzione di quei problemi si poteva esprimere solamente per mezzo di una coppia ordinata di numeri interi, Si è superata la difficoltà attribuendo il nome di numero anche a queste coppie ordinate di numeri interi, (ciò fu possibile, perchè anche con queste coppie di numeri interi si sono potute definire le quattro operazioni fondamentali in modo che godessero delle proprietà formali), e dicendo che le soluzioni di quei problemi erano date dai numeri definiti da quelle coppie.
Se si vuole ora risolvere il problema della misura dei segmenti incommensurabili con l'unità di misura, viene spontanea l'idea di chiamare numero la coppia di classi (A, B) di cui si è parlato in precedenza e dire che la misura di s rispetto a u è il numero definito dalla coppia (A, B).
In altri termini, per risolvere in generale il problema della misura dei segmenti, si è costretti a introdurre una nuova entità, costituita da una coppia di classi di numeri razionali soddisfacenti alle quattro condizioni enunciate in precedenza e attribuire a questa nuova entità il nome di numero; per distinguerlo dai numeri già noti, verrà chiamato numero irrazionale.
Definizione - Se s e u sono due segmenti incommensurabili, si chiama misura di s rispetto a u, il numero irrazionale definito dalla coppia di classi di numeri razionali:
(A, B) ove A contiene tutte le misure approssimate per difetto di s rispetto a u e la classe B contiene tutte le misure approssimate per eccesso.
Quindi, si può dire che, fissata l'unità di misura, ogni segmento ha una sua misura, che sarà un numero razionale, se il segmento è commensurabile con l'unitò di misura, sarà invece un numero irrazionale nel caso dell'incommensurabilità.
Problema di estrazione di radice quadrata
Come è noto, si chiama radice quadrata aritmetica di un numero razionale assoluto, quel numero razionale assoluto, se esiste, che elevato al quadrato, riproduce il numero dato.
Esempi:
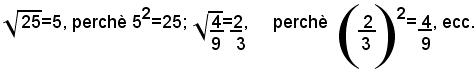
E' facile convincersi che non sempre esiste la radice quadrata di numero razionale assoluto, cioè non sempre, dato un un numero razionale assoluto a, esiste un numero razionale che, elevato al quadrato dia per risultato il numero a.
In altri termini, non sempre l'equazione x2=a, ammette soluzioni fra i numeri razionali. Ad esempio, si è già visto che non esiste nè un numero intero, nè un numero frazionario che elevato al quadrato dia per risultato il numero 2. Perciò l'equazione x2=2, non ammette soluzioni fra i numeri razionali. Però anche in questo caso, si può procedere in modo del tutto analogo a quanto si è fatto nel problema precedente per la misura fra segmenti incommensurabili.
Si dice che il numero razionale assoluto
è una soluzione approssimata per difetto o per eccesso dell'equazione x2=2, a seconda che risulta:

si mettono poi in una classe H tutti i numeri razionali assoluti diversi da zero, il cui quadrato è minore di 2, e in una classe K tutti i numeri razionali assoluti il cui quadrato è maggiore di 2.
Si potrebbe vedere che anche questo le classi H e K soddisfano le quattro condizioni viste in precedenza, cioè anch'esse formano una sezione del campo dei numeri razionali assoluti, e quindi, mantenendo la nomenclatura introdotta nel problema precedente, si può dire che le due classi H, K definiscono un numero irrazionale; pertanto:
una soluzione dell'equazione x2=2, è data dal numero irrazionale definito dalla sezione (H, K), dove la prima classe H contiene tutti i numeri razionali assoluti diversi da zero, il cui quadrato è minore di 2, cioè tutte le soluzioni approssimate per difetto dell'equazione x2=2, e la seconda classe H contiene tutti i numeri irrazionali assoluti, il cui quadrato è maggiore di 2, cioè tutte le soluzioni approssimate per eccesso dell'equazione x2=2.
Si vede dunque che anche questo problema si può risolvere solamente se conviene chiamare numero questa nuova entità costruita, cioè se si chiamano numeri le sezioni fatte nel campo dei numeri razionali assoluti. Dai due problemi considerati, e da moltissimi altri che si potrebbero trattare, si vede in pratica si presentano dei problemi che non ammettono soluzioni con la sola conoscenza dei numeri razionali. Soltanto introducendo nella matematica una nuova entità, la sezione, si può dare la risposta a tali problemi. Occorre ora giustificare il nome di numero dato alle sezioni, facendo vedere che anche per le sezioni valgono le quattro operazioni fondamentali e le solite proprietà formali.
La definizione generale di numero fa sì che non ci si deve meravigliare che il nome di numero possa essere dato a una coppia formata da due classi di numeri razionali che formano una sezione. Non si deve mai dimenticare che numeri vuol dire entità qualsiasi, cioè, qualunque sia la loro natura, purchè con essi si possano definire le quattro operazioni fondamentali, in modo che godano delle consuete proprietà formali. E' vero che la natura di quello che verrà chiamato numero irrazionale è diversa da quella di numero razionale, in quanto il numero irrazionale è una coppia di classi costituite ciascuna da infiniti numeri razionali mentre il numero razionale è una coppia di numeri interi, ma questo non ha nessuna importanza; l'essenziale è soltanto che anche le operazioni con questi nuovi numeri godano delle stesse proprietà delle operazioni fatte con i numeri razionali.
Le sezioni del campo razionale
Osservato che le sezioni considerate nei due problemi trattati, sono state costruite, per maggiore semplicità di ragionamento, solamente con i numeri razionali assoluti, ci si pone ora, per maggiore generalità sin dall'inizio, nel campo dei numeri razionali relarivi.
Definizione - Si dice che le due classi A e B di numeri razionali relativi formano una sezione del campo dei numeri razionali relativi, quando soddisfano le seguenti quattro condizioni:
1)-ogni numero della classe A è minore di ogni numero della classe B;
2)-se un numero appartiene alla prima classe A, ogni numero razionale minore di esso appartiene pure alla prima classe; se un numero appartiene alla seconda classe B, ogni numero razionale maggiore di esso appartiene pure alla seconda classe;
3)-la prima classe A non ha massimo, la seconda classe B non ha minimo (una classe A di numeri razionali distinti ammette un massimo, quando esiste in A un numero che è maggiore di tutti gli altri numeri contenuti in A; ammette un minimo quando esiste in A un numero che è minore di tutti gli altri numeri contenuti in A).
E' facile vedere che esistono delle classi di numeri razionali che non ammettono, ad esempio il massimo.
Infatti, se nella classe A si mettono tutti i numeri razionli minori del numero 5, questa classe evidentemente non ammette il massimo. In modo analogo si prova che vi sono classi di numeri razionali che non ammettono il minimo.
4)-Ogni numero razionale relativo, eccetto l'1, dev'essere contenuto o nella classe A oppure nella classe B.
Questa condizione è più generale della condizione 4) enunciata in precedenza. Infatti, questa impone che non vi sia nessun numero razionale relativo escluso dalle due classi A e B, mentre la 4) precedente ammette che vi possa essere un numero razionale relativo escluso sia da A che da B.
La classe A si chiama classe inferiore della sezione, la classe B, classe superiore della sezione. La sezione formata con le classi A e B si indica con (A, B).
Dalla condizione 4) segue che da una sezione può essere o escluso un solo numero razionale oppure nessuno.
Quando dalla sezione (A, B) è escluso un numero razionale, esso dovrà risultare maggiore di tutti i numeri contenuti nella classe inferiore A e minore di tutti i numeri contenuti nella classe superiore B. Infatti, se c'è un numero che non appartiene nè alla classe A nè alla classe B, esso non può essere minore di un numero di A, perchè altrimenti, per la condizione 2) dovrebbe appartenere ad A. Analogamente si vede che il numero c non può essere maggiore di un numero B, perchè altrimenti, per la condizione 2) dovrebbe appartenere a B, contro l'ipotesi fatta.
Si vede subito che esistono sia sezioni che escludono un numero razionale, sia sezioni che non escludono nessun numero razionale; dopo di ciò sarà giustificata la seguente definizione:
-le sezioni del campo dei numeri razionali si dicono di prima specie quando escludono un numero razionale, di seconda specie quando non escludono nessun numero razionale.
Esempi di sezioni di 1^ e 2^ specie
1^ specie
Sia r un numero razionale qualsiasi, fratto o intero, e si pongano nella classe inferiore A tutti i numeri razionali minori del numero r e nella classe inferiore b tutti i numeri razionali maggiori del numero r. Le due classi A e B così costruite soddisfano, evidentemente, le condizioni 1), 2), 3) e 4). La sezione (A, B), così costruita, escludendo il numero r, è una sezione di prima specie.
Si può dimostrare che:
le sezioni che escludono un numero razionale sono tutte e sole quelle costruite come sopra, ossia, preso ad arbitrio un numero razionale r, esse sono costruite mettendo nella prima classe tutti i numeri razionali minori di r, e nella seconda classe quelli maggiori di r.
2^ specie
Si mettono nella classe inferiore A tutti i numeri razionali negativi, lo zero e tutti i numeri razionali positivi il cui quadrato è minore di 2 e nella classe superiore B tutti i numeri razionali positivi il cui quadrato è maggiore di 2. Come già visto, si osservi che qualsiasi numero razionale, nessuno escluso, ha il suo quadrato o minore o maggiore di 2. Quindi ogni numero razionale o appartiene alla classe A, oppure alla classe B. Segue che, se si dimostra che le due classi A e B, così costruite, formano una sezione, questa sarà di seconda specie. Le due classi A e B, soddisfano evidentemente le condizioni 1), 2). 4); si prova ora che soddisfano anche la condizione 3). Si incomincia col far vedere che la classe A non ammette massimo. A tale scopo, si ragiona per assurdo, supponendo che il numero positivo m sia il massimo della classe A. Evidentemente sarà m>1, perchè nella classe A vi sono numeri maggiori di 1. Inoltre, in quanto m appartiene ad A, dev'essere m2<2. Si verificherà un assurdo se si prova che esiste un numero maggiore di m, appartenente anch'esso alla classe A. A tal scopo, posto (1)
si osserva che il numero q è positivo e minore di 1, infatti il numeratore 2-m2 è positivo e minore di 1 perchè m2<2, m>1, mentre il denominatore 2m+1>3; perciò si può scrivere: (2) 2m+q<m+1, da cui segue, moltiplicando ambo i membri della (2) per il numero positivo q: (3) q(2mìq)<q(2m+1). Sostituendo nel secondo membro della (3), al posto di q il suo valore dato dalla (1), si ottiene:
ossia: 2mq+q2<2-m2.
Aggiungendo il numero m2 ad ambo i membri di quest'ultima disuguaglianza, si ha: 2mq+q2+m2<2-m2-m2, cioè: (m+q)2<2.
Ciò dimostra che il numero m+q appartiene alla classe A, perchè il suo quadrato è minore di 2, e quindi, dato che m+q>m, è assurdo supporre che m sia il massimo della classe A. Analogamente si dimostra che la classe B non ha minimo.
Le due classi A e B, sopra costruite, formano una sezione e, per quanto detto, essa è di seconda specie.
In modo del tutto analogo si prova che sono sezioni di seconda specie anche quelle costruite nel modo seguente:
sia r un numero razionale positivo qualsiasi, fratto o in particolare intero, che non sia quadrato perfetto, e si mettano nella classe inferiore H tutti i numeri negativi, lo zero, e i numeri razionali positivi il cui quadrato è minore di r; nella classe K tutti i numeri razionali positivi il cui quadrato è maggiore di r. Queste particolari sezioni si seconda specie si chiamano, per una ragione che si vedrà in seguito, radice quadrata aritmetica di r, e per indicare ciò si suole scrivere:
Nota bene
Siccome i numeri che appartengono a ciascuna delle due classi A e B di una sezione sono infiniti, non sarà mai possibile scrivere tutti i numeri contenuti in A e B.
Perciò, si dirà che una sezione è data quando è assegnata una legge, o una proprietà, che permetta di decidere quali numeri stanno in A e quali in B. In altri termini, si può dire che una sezione è nota quando è data una legge mediante la quale, preso ad arbitrio un qualsiasi numero razionale r, si riesca a stabilire se un numero sta nella classe inferiore della sezione oppure in quella superiore, o l'eventuale numero escluso da entrambe le classi.
Definizione di numero reale
Si chiama numero reale una qualsiasi sezione nel campo dei numeri interi relativi.
In base a tale definizione la parola "numero reale" è sinonimo di "sezione nel campo dei numeri razionali". Assegnare quindi un numero reale, equivale ad assegnare una sezione nel campo dei numeri razionali. Il nome di numero dato ad una sezione è giustificato dal fatto che con esse si potranno definire le quattro operazioni fondamentali e che per esse valgano tutte le proprietà formali, in accordo con la definizione di numero data. Per brevità, spesso è utile indicare con una lettera, ad esempio α, il numero reale individuato da una data sezione (A, B) del campo razionale, scrivendo α=(A, B).
La totalità dei numeri reali coincide quindi con la totalità delle sezioni del campo reazionale.
Convenzione
si chiama numero irrazionale una sezione del campo razionale che non esclude nessun numero razionale.
Dalla convenzione fatta, segue che:
a)-i numeri razionali sono contenuti nel campo dei numeri reali;
b)-i numeri reali sono quindi costituiti dai numeri razionali e dai numeri irrazionali.
Confronto di numeri reali
Siano dati due numeri reali, cioè due sezioni del campo dei numeri razionali:
α=(A, B), β=(C, D); si danno le seguenti definizioni:
1)-si dice che i numeri reali α e β sono uguali, e si scrive α=β, quando le due classi A e C coincidono, e quindi anche B e D;
2)-si dice che il numero reale α è maggiore di β, e si scrive α>β, quando esiste qualche numero della classe A che appartiene alla classe D.
E' inteso che A contiene tutti i numeri di C.
3)-si dice che il numero reale α è minore di β, e si scrive α<β, quando esiste qualche numero della classe B che appartiene a C. E' inteso che C contiene tutti i numeri di A.
Dalle tre definizioni segue che: dati due numeri reali α e β, si presenta necessariamente uno, ed uno solo dei seguenti tre casi: α=β; α>β; α<β.
4)-un numero reale α=(A, B), si dice positivo, se è maggiore di zero, negativo se è minore di zero.
Si deve ricordare che lo zero è individuato dalla sezione di prima specie (N, P), ove la classe inferiore N è formata da tutti i numeri razionali negativi e la classe superiore P da tutti i numeri razionali positivi, in base alle definizioni 2) e 3), si può dire che:
un numero reale α=(A, B) è positivo, quando in A vi sono numeri razionali positivi, è invece negativo quando in B vi sono numeri razionali negativi.
Esempio: considerati i due numeri irrazionali:
Per provare ciò, in base alla definizione 2), basta far vedere che nella classe A esiste almeno un numero contenuto nella classe D. Infatti, il numero 2 sta in A, perchè risulta 22<5, e sta anche in D, perchè risulta 22>2.
Valore approssimato di un numero irrazionale
Definizione
Sia dato il numero irrazionale α=(A, B).


Essendo:
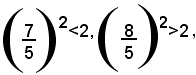
si vede che il numero 7/5 sta nella classe A, mentre il numero 8/5 sta nella classe B. Perciò 7/5 è un valore approssimato per difetto, a meno di 1/5 del numero (1), mentre 8/5 è un valore approssimato per eccesso, a meno di 1/5 del numero (1).
Analogamente, essendo:
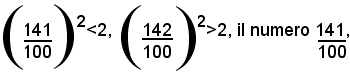
ossia 1,41, è un valore approssimato per difetto, a meno di 1/102, del numero (1), mentre 1,42 è un valore approssimato per eccesso, a meno di 1/102 del numero (1).
Operazioni con i numeri reali
Somma di due o più numeri reali
Siano dati due numeri reali, cioè due sezioni del campo dei numeri razionali:
α=(A, B). β=(C, D). Si considerino la classe A+C ottenuta sommando ciascun numero di A con ciascun numero di C e la classe B+D, ottenuta sommando ciascun numero di B con ciascun numero di D. Si può dimostrare il seguente teorema che ci si limita soltanto ad enunciare:
le due classi A+C e B+D, così definite, costituiscono una sezione del campo dei numeri razionali; la sezione (A+C, B+D) definisce quindi un numero reale che, per definizione, si chiama somma dei due numeri reali α e β; si pone quindi la seguente definizione:
si chiama somma dei due numeri reali α=(A, B). β=(C, D), il numero reale definito dalla sezione la cui classe inferiore si ottiene sommando ciascun numero di A con ciascun numero di C e quella superiore sommando ciascun numero di B con ciascun numero di D.
Indicando con α e β la somma dei due numeri, per definizione, si ha: α+β=(A+C, B+D).
Si chiama somma dei numeri reali α, β e γ il numero, che si indica con α+β+γ, ottenuto sommando α con β e aggiungendo γ alla somma ottenuta.
In modo analodo si definisce la somma di più numeri reali dati in un certo ordine.
Si potrebbe inoltre dimostrare che: l'addizione gode della proprietà commutativa e associativa.
Numeri opposti
Sia α=(A, B) un numero reale, cioè una sezione nel campo dei numeri razionali; indicato con -B e -A le classi dei numeri che si ottengono rispettivamente da B e da A, considerando gli opposti dei numeri razionali che lo compongono, osservando che, essendo ogni numero della classe A minore di ogni numero della classe B, segue che ogni numero della classe -B è minore di ogni numero della classe -A. E' evidente che le classi -B e -A formano una sezione.
Il numero definito dalla sezione (-B, -A) si chiama opposto del numero α, e si indica con il simbolo -α. Si pùo quindi dare la seguente definizione:
si chiama opposto del numero reale α=(A, B), e si indica con -α, il numero definito dalla sezione (-B, -A), ove con -B, e -A si indicano le classi dei numeri che si ottengono rispettivamente da B e A, prendendo gli opposti dei numeri razionali che lo compongono.
Si dimostra che: la somma di due numeri opposti è uguale a zero.
Infatti: α+(-α)=[A+(-B), B+(-A)]=(A-B, B-A). Ora la classe A-B contiene solo i numeri negativi, dato che i numeri della classe B sono maggiori di quelli della classe A, mentre i numeri della classe B-A sono tutti positivi. Perciò il numero individuato dalla sezione (A-B, B-A) è lo zero, come volevasi dimostrare.
Si osservi inoltre che se il numero α=(A, B) è positivo, cioè se nella classe A sono contenuti i numeri positivi, allora il numero opposto -α=(-B, -A) sarà negativo, perchè nella classe -A sono contenuti dei numeri negativi. Viceversa, se α è negativo, ai prova che il suo opposto -α è positivo. Si può dare quindi la seguente definizione:
si chiama valore assoluto del numero reale α, e si indica con |α|, il numero stesso se α è positivo, il suo opposto se α è negativo; se α=0, il suo valore assoluto, per definizione, è uguale a zero.
Sottrazione di due numeri reali
Definizione - Si chiama differenza fra due numeri reali α e β, nell'ordine considerato, e si indica con α-β, la somma del numero reale α con l'opposto del numero reale β. Cioè, per definizione, si ha: α-β=α+(-β)=(A, B)+(-D, C)=(A-D, B-C), ove la classe A-D si ottiene togliendo da ogni numero di A successivamente ogni numero di D, e la classe B-C togliendo da ogni numero di B successivamente ogni numero di C.
Prodotto di numeri reali
Siano dati due numeri reali positivi: α=(A, B), β=(C, D). Si indica ora con F la classe costituita da numeri razionali negativi, dallo zero e dai numeri positivi che risultano dal prodotto di ciascun numero positivo della classe A con ciascun numero positivo della classe C; e con G la classe costituita dai prodotti di ciascun numero di B con ciascun numero di D.
Si dimostra, e ci si limita solo ad enunciarlo, il seguente teorema:
le due classi F e G costituiscono una sezione del campo dei numeri razionali.
La sezione: (F, G), definisce quindi un numero reale che, per definizione, si chiama prodotto dei due numeri reali positivi α e β.
Definizione - Si chiama prodotto dei due numeri reali positivi α=(A, B) e β=(C, D), il numero reale definito dalla sezione la cui classe inferiore F è formata dai numeri razionali negarivi, dallo zero, e dai prodotti di ciascun numero positivo di A per ciascun numero positivo di C; e la cui classe superiore G è quella formata dai prodotti di ciascun numero di B per ciascun numero di D.
Se poi i due numeri reali α e β sono entrambi negativi, oppure uno positivo e l'altro negativo, si pone la seguente definizione:
si chiama prodotto dei due numeri reali α e β, non nulli, e non entrambi positivi, il prodotto dei loro valori assoluti, se i due numeri sono entrambi negativi; l'opposto del prodotto dei valori assoluti, se i due numeri sono l'uno positivo e l'altro negativo. Si pone uguale a zero, per definizione, il prodotto di un numero reale per zero.
Se poi: α, β, γ, sono tre numeri reali, si chiama loro prodotto, per definizione, il numero che si indica con αβγ, ottenuto moltiplicando prima α con β e poi il prodotto ottenuto con γ. In modo analogo si definisce il prodotto di più numeri reali dati in un certo ordine.
Si potrebbe inoltre dimostrare che:
la moltiplicazione fra numeri reali gode della propprietà commutativa, associativa e della proprietà distributiva rispetto all'addizione.
Teorema - Dato un qualsiasi numero razionale positivo r, che non sia un quadrato perfetto, esiste sempre un numero irrazionale positivo il cui quadrato risulta uguale a r.
Per dimostrare ciò, si indica con (A, B) la sezione così formata:
-nella classe A si mettono tutti i numeri razionali negativi, lo zero e i numeri razionali positivi il cui quadrato è minore di r;
-nella classe B si mettono tutti i numeri razionali positivi il cui quadrato risulta maggiore di r. Come è noto, la sezione così costruita è di seconda specie e perciò essa definisce un numero irrazionale che è positivo, dato che la classe A contiene dei numeri razionali positivi.
Si vuole provare che risulta: (A, B)(A, B)=r, ossia: [(A, B)]2=r, e con ciò sarà dimostrato il teorema.
Infatti, detta (F, G) la sezione prodotto, cioè posto: (F, G)=(A, B)(A, B), si osservi che la classe F è costituita dai numeri negativi, dallo zero, e dai prodotti, a due a due, dei numeri positivi contenuti in A. Perciò, se si indicano con α1 e α2 due numeri positivi qualsiasi, distinti o no, di A, il numero α1α2 è contenuto in F. Essendo: α12<r, α22<r, perchè α1 e α2 stanno nella classe A, moltiplicando membro a membro le due disuguaglianze suddette, si ha: α12α22<r2, ossia: (α1α2)2<r2, e quindi α1α2<r, dato che α1 e α2 sono numeri positivi. Si vede quindi che tutti i numeri contenuti in F sono minori di r.
Nello stesso modo si prova che tutti i numeri contenuti in G sono maggiori di r.
La sezione (F, G), escludendo il numero r, è una sezione di prima specie e rappresenta quindi proprio il numero stesso r, cioè: (F, G)=R, ossia [(A, B)]2=r, come volevasi dimostrare.
Siccome in seguito sarà dimostrato che esiste un numero irrazionale positivo il cui quadrato vale r, è naturale chiamare il numero razionale (A, B) radice quadrata aritmetica del numero razionale positivo r, e scrivere:
Nota bene
Per non incorrere in errori grossolani è bene riflettere sul teorema precedente, per chiarire ulteriormente quanto detto. Ci si pone la domanda: cosa rappresenta il simbolo:
Esso rappresenta un numero irrazionale, cioè una sezione (A, B) di seconda specie del campo razionale. Precisamente: quella sezione in cui la classe A è formata dai numeri razionali negativi, dallo zero e dai numeri razionali positivi, il cui quadrato è minore di 2; e la cui classe superiore B è formata dai numeri razionali positivi, il cui quadrato è maggiore di 2. E questa sezione si chiama
perchè, elevata al quadrato, dà per risultato la sezione che rappresenta il numero 2, e ciò in accordo con la definizione di radice quadrata aritmetica di un numero razionale. Non si deve dire, come spesso si sente ripetere, che la radice quadrata aritmetica di 2 è 1,4; oppure 1,5 o 1,41, perchè il quadrato di questi numeri, come di qualsiasi altro numero razionale, non è uguale a 2! L'entità il cui quadrato risulta uguale a 2 non può essere un numero razionale, cioè una coppia di numeri interi, perchè nessun numero razionale, come si è visto, elevato al quadrato diventa uguale al numero 2. Solamente l'ente costituito dalla sezione (A, B), sopra costruita, ha per quadrato il numero 2. Avendo quindi le idee chiare sul concetto di numero irrazionale, si potranno comprendere affermazioni, che si faranno in seguito, del tipo:
1)-la misura del doppio dell'altezza di un triangolo equilatero, rispetto al suo lato, preso come unità di misura, è uguale a: (1)
Ciò vuol dire che la misura del doppio dell'altezza del triangolo equilatero, rispetto al suo lato, preso come unità di misura, è espressa dalla sezione chiamata:
In altri termini, ciò vuol dire che la classe A formata dalle misure approssimate per difetto del doppio dell'altezza del triangolo equilatero, rispetto al suo lato, nella quale classe si siano aggiunti anche i numeri negativi e lo zero, e la classe B, formata dalle misure approssimate per eccesso, formano la sezione (A, B), in tal caso chiamata:
Il quadrato di tale sezione è uguale a 3.
2)-Quattro segmenti, a, b, c, d, dati in un certo ordine, si dicono in proporzione, quando il rapporto dei primi due è uguale al rapporto degli altri due. Ciò vuol dire che la sezione rappresentante la misura del segmento a rispetto a b, è uguale alla sezione che rappresenta la misura del segmento c rispetto a d.
3)-La misura del segmento che rappresenta la lunghezza di una circonferenza, rispetto al diametro, preso come unità di misura, è un numero irrazionale chiamato π.
Reciproco di un numero reale non nullo
Sia α=(A, B) un numero reale positivo, si vuole definire il reciproco di tale numero.
Innanzitutto si deve osservare che, essendo per ipotesi α>0, i numeri razionali contenuti in B sono tutti positivi. Si mettono ora in una classe C i numeri razionali negativi, lo zero e quei numeri razionali posiivi che si ottengono calcolando i reciproci dei numeri di B e poi in una classe D i reciproci dei numeri positivi di A, che certamente ci sono, in quanto per ipotesi si è supposto α positivo.
Si dimostra, e ci si limita solo ad enunciarlo, il seguente teorema:
le classi C e D, così costruite, formano una sezione del campo dei numeri razionali.
Il numero definito dalla sezione (C, D) si chiama reciproco del numero positivo α e si indica con il simbolo:
Definizione - Si chiama reciproco del numero reale positivo α=(A, B), il numero reale definito dalla sezione (C, D) la cui classe inferiore C è costituita dai numeri razionali negativi, dallo zero e dai reciproci dei numeri razionali di B e la cui classe superiore è costituita dai reciproci dei numeri positivi di A.
Si osservi che il reciproco del numero positivo α è anch'esso un numero reale positivo. Se invece α è un numero negativo, allora il suo reciproco viene definito come l'opposto del reciproco del numero positivo -α, cioè si pone:
Il reciproco dello zero non si definisce.
Teorema - Il prodotto di due numeri reciproci è uguale ad uno.
Quoziente di due numeri reali
Siano α=(A, B), β=(C, D), due numeri reali, il secondo dei quali diverso da zero.
Definizione - Si chiama quoziente dei due numeri reali α e β, e si indica con
il prodotto del numero α per il reciproco del numero β, cioè si pone:
Il quoziente di due numeri reali non si definisce se il divisore è uguale a zero.
Potenze ad esponente intero di un numero reale
Sia α=(A, B) un numero reale e n un numero intero.
Se n è un numero intero maggiore di 1, si chiama potenza ennesima del numero reale α, il prodotto di n fattori uguali ad α. Cioè: αn=αα ...α (n volte).
Per definizione, si pone: α1=α, se n=1; α0=1, se n=0 e a≠0; infine,
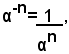
se n è un numero intero positivo e a≠0.
Il simbolo 00 non ha significato.
Dalle definizioni segue che i teoremi dimostrati sulle potenze a esponente intero dei numeri razionali, valgono anche per le potenze dei numeri reali. Pertanto si ha:
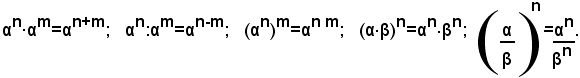
Si potrebbero dimostrare anche i seguenti teoremi, che ci si limita solo ad enunciare: se α e β sono due numeri reali positivi e n un numero intero positivo, allora:
1)-da α=β, segue αn=βn, e viceversa da αn=βn segue α=β;
2)-da α>β oppure α<β, segue αn>βn oppure αn<βn, e inversamente.
Radice ennesima aritmetica di un numero reale positivo
Si e visto che, dato un numero razionale positivo r, esiste sempre un numero reale positivo il cui quadrato risulta uguale a r.
Teorema - Dato un qualsiasi numero reale positivo α=(A, B) e un numero intero positivo n, esiste un unico numero reale positivo, la cui potenza ennesima è uguale ad α, cioè tale da soddisfare l'equazione (1) xn=α.
Si mettono in una classe H tutti i numeri razionali negativi, lo zero e i numeri razionali positivi la cui ennesima potenza sia minore di α e in una classe K tutti i nueri razionali positivi la cui ennesima potenza sia maggiore di α. Anche in questo caso si può provare, ma ci si limita solo all'enunciato, che le due classi H e K formano una sezione nel campo dei numeri razionali e quindi individuano un numero reale positivo β=(H, K). Con un ragionamento analogo a quello fatto in precedenza, si prova che: [(H, K)]n=(A, B), cioè: βn=β, e con ciò resta provato che il numero positivo β, così costruito, verifica l'equazione (1). Per provare l'unicità del numero β, si ragiona per assurdo, cioè si suppone che esista un secondo numero reale positivo γ, con γ≠β, che verifichi l'equazione (1). Dovendo quindi risultare: βn=α, γn=α, segue che: βn=γn; e per il teorema enunciato in precedenza, si ha β=γ, il che è assurdo, avendo per ipotesi supposto β≠γ.
Il numero positivo β, di cui si è provata l'unicità, si chiama radice ennesima aritmetica del numero α e si indica con il simbolo:
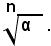
Tale simbolo rappresenta una sezione del campo razionale, e precisamente quella sezione che elevata all'ennesima potenza riproduce la sezione che definisce il numero reale positivo α. Ad esempio, il simbolo
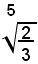
rappresenta una sezione costruita con la legge enunciata nella dimostrazione precedente, precisamente, il simbolo
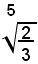
rappresenta una sezione (H, K) la cui classe inferiore H contiene tutti i numeri razionali negativi, lo zero e i numeri razionali positivi la cui quinta potenza è minore di 2/3 e quella superiore K contiene tutti i numeri razionali positivi la cui quinta potenza è maggiore di 2/3. La ragione del nome è dovuta, come già visto, al fatto che elevando alla quinta potenza questa sezione (H, K), si ottiene la sezione che rappresenta il numero razionale 2/3.
Così pure bisogna ricordare che la scrittura:
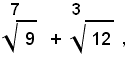
rappresenta la sezione che si ottiene sommando la sezione chiamata
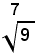
con la sezione chiamata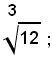
e che la scrittura:
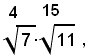
rappresenta la sezione che risulta dal prodotto delle due sezioni chiamate rispettivamente con i nomi:
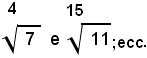
In altri termini, si deve ricordare che, operare secondo le regole trovate con i numeri reali, significa operare con le sezioni, così come operare con i numeri razionali, significa operare con le coppie ordinate di numeri interi, il cui secondo sia diverso da zero. Osservato che il calcolo letterale sviluppato nel campo dei numeri razionali, ha la sua validità nelle sole proprietà formali delle quattro operazioni fondamentali fatte con questi numeri, si può senz'altro dire che questo calcolo letterale si estende anche al calcolo dei numeri reali.
Continuità del campo dei numeri reali
Si è visto in precedenza che le sezioni costruite nel campo dei numeri razionali sono di due specie: quelle che escludono un numero razionale e quelle che non escludono nessun numero razionale. Le prime due sono identificate con numeri razionali, le seconde hanno permesso di introdurre un nuovo tipo di numero, il numero irrazionale.
Si può quindi dire che le sezioni di seconda specie hanno permesso di ampliare il campo dei numeri razionali introducendo i numeri irrazionali.
E' evidente che di possono ora costruire anche sezioni nel campo dei numeri reali, precisamente:
si dice che le due classi A e B, di numeri reali formano una sezione, quando esse soddisfano alle quattro condizioni, già viste:
1)-ogni numero della classe A è minore di ogni numero della classe B;
2)-se un numero appartiene alla prima classe A, ogni numero razionale minore di esso appartiene pure alla prima classe; se un numero appartiene alla seconda classe B, ogni numero razionale maggiore di esso appartiene pure alla seconda classe;
3)-la prima classe A non ha massimo, la seconda classe B non ha minimo,
4)-Ogni numero razionale assoluto, diverso da zero, trova posto o nella classe A oppure nella classe B.
1)-da α=β, segue αn=βn, e viceversa da αn=βn segue α=β;
2)-da α>β oppure α<β, segue αn>βn oppure αn<βn, e inversamente.
Radice ennesima aritmetica di un numero reale positivo
Si e visto che, dato un numero razionale positivo r, esiste sempre un numero reale positivo il cui quadrato risulta uguale a r.
Teorema - Dato un qualsiasi numero reale positivo α=(A, B) e un numero intero positivo n, esiste un unico numero reale positivo, la cui potenza ennesima è uguale ad α, cioè tale da soddisfare l'equazione (1) xn=α.
Si mettono in una classe H tutti i numeri razionali negativi, lo zero e i numeri razionali positivi la cui ennesima potenza sia minore di α e in una classe K tutti i nueri razionali positivi la cui ennesima potenza sia maggiore di α. Anche in questo caso si può provare, ma ci si limita solo all'enunciato, che le due classi H e K formano una sezione nel campo dei numeri razionali e quindi individuano un numero reale positivo β=(H, K). Con un ragionamento analogo a quello fatto in precedenza, si prova che: [(H, K)]n=(A, B), cioè: βn=β, e con ciò resta provato che il numero positivo β, così costruito, verifica l'equazione (1). Per provare l'unicità del numero β, si ragiona per assurdo, cioè si suppone che esista un secondo numero reale positivo γ, con γ≠β, che verifichi l'equazione (1). Dovendo quindi risultare: βn=α, γn=α, segue che: βn=γn; e per il teorema enunciato in precedenza, si ha β=γ, il che è assurdo, avendo per ipotesi supposto β≠γ.
Il numero positivo β, di cui si è provata l'unicità, si chiama radice ennesima aritmetica del numero α e si indica con il simbolo:
Tale simbolo rappresenta una sezione del campo razionale, e precisamente quella sezione che elevata all'ennesima potenza riproduce la sezione che definisce il numero reale positivo α. Ad esempio, il simbolo
rappresenta una sezione costruita con la legge enunciata nella dimostrazione precedente, precisamente, il simbolo
rappresenta una sezione (H, K) la cui classe inferiore H contiene tutti i numeri razionali negativi, lo zero e i numeri razionali positivi la cui quinta potenza è minore di 2/3 e quella superiore K contiene tutti i numeri razionali positivi la cui quinta potenza è maggiore di 2/3. La ragione del nome è dovuta, come già visto, al fatto che elevando alla quinta potenza questa sezione (H, K), si ottiene la sezione che rappresenta il numero razionale 2/3.
Così pure bisogna ricordare che la scrittura:
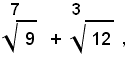
rappresenta la sezione che si ottiene sommando la sezione chiamata
con la sezione chiamata
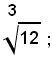
e che la scrittura:
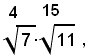
rappresenta la sezione che risulta dal prodotto delle due sezioni chiamate rispettivamente con i nomi:
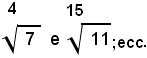
In altri termini, si deve ricordare che, operare secondo le regole trovate con i numeri reali, significa operare con le sezioni, così come operare con i numeri razionali, significa operare con le coppie ordinate di numeri interi, il cui secondo sia diverso da zero. Osservato che il calcolo letterale sviluppato nel campo dei numeri razionali, ha la sua validità nelle sole proprietà formali delle quattro operazioni fondamentali fatte con questi numeri, si può senz'altro dire che questo calcolo letterale si estende anche al calcolo dei numeri reali.
Continuità del campo dei numeri reali
Si è visto in precedenza che le sezioni costruite nel campo dei numeri razionali sono di due specie: quelle che escludono un numero razionale e quelle che non escludono nessun numero razionale. Le prime due sono identificate con numeri razionali, le seconde hanno permesso di introdurre un nuovo tipo di numero, il numero irrazionale.
Si può quindi dire che le sezioni di seconda specie hanno permesso di ampliare il campo dei numeri razionali introducendo i numeri irrazionali.
E' evidente che di possono ora costruire anche sezioni nel campo dei numeri reali, precisamente:
si dice che le due classi A e B, di numeri reali formano una sezione, quando esse soddisfano alle quattro condizioni, già viste:
1)-ogni numero della classe A è minore di ogni numero della classe B;
2)-se un numero appartiene alla prima classe A, ogni numero razionale minore di esso appartiene pure alla prima classe; se un numero appartiene alla seconda classe B, ogni numero razionale maggiore di esso appartiene pure alla seconda classe;
3)-la prima classe A non ha massimo, la seconda classe B non ha minimo,
4)-Ogni numero razionale assoluto, diverso da zero, trova posto o nella classe A oppure nella classe B.
A tale scopo si dimostra il seguente teorema, che ci si limita solo all'enunciato:
ogni sezione (A, B) fatta nel campo dei numeri reali è di prima specie, cioè esclude un numero reale che è maggiore di tutti i numeri reali contenuti in A e minore di tutti i numeri contenuti in B.
Da questo teorema segue che nel campo dei numeri reali si possono costruire solo sezioni di prima specie. Questa proprietà del campo dei numeri reali si esprime dicendo che il campo dei numeri reali è continuo. In contrapposizione, il campo dei numeri razionali si dice discontinuo.
Se (A, B) è una sezione nel campo dei numeri reali e α è il numero da essa escluso, si usa scrivere α=(A, B), e il numero α si suole chiamare l'elemento di separazione delle due classi A e B.