MIKY & GENNY
POTENZE DEI NUMERI RELATIVI ---> INDICE
Come nel caso dei numeri assoluti, si dice potenza di un dato numero relativo ogni prodotto di fattori uguali a quel numero. Anche in tale caso il numero considerato si chiama base, mentre si dice esponente il numero, intero e positivo, dei fattori uguali alla base, che compaiono nella potenza.
Potenza di un numero relativo secondo l'esponente 1 e secondo l'esponente zero
Esempi: (+5)2=(+5)(+5)=)+25; (-2)3=(-2)(-2)(-2)=-8; (-2/3)4=(-2/3)(-2/3)(-2/3)(-2/3)=16/81.
La potenza di esponente 1 di un numero relativo è assunta uguale al numero stesso, e la potenza di esponente zero è assunta uguale a 1, quale che sia la base, purchè diversa da zero.
E' bene ricordare che l'esponente della potenza viene scritto sottintendendo sempre il segno +; quando l'esponente è uguale a 1, esso non viene scritto.
Esempi: (+5)1=+5; (-7)1=-7; 01=0; (3/2)0=+1; (-5/4)0=+1.
Non si definisce la potenza del numero zero con esponente zero: il simbolo 00 è privo di significato.
Ricordando infine la regola dei segni della moltiplicazione, si verifica facilmente che:
-ogni potenza di base positiva è positiva;
-ogni potenza di base negativa è positiva o negativa a seconda che l'esponente sia pari o dispari.
Infatti, nel primo caso si ha un prodotto di un numero pari di fattori negativi, nel secondo, di un numero dispari di fattori negativi.
Potenza ennesima di un numero relativo
Servendoci ora della notazione letterale, si vogliono ora dimostrare, in generale, le proprietà delle potenze dei numeri relativi, secondo un esponente intero e positivo. Allo scopo, si indica con a un qualsiasi numero relativo, positivo o negativo o anche zero, con n un numero intero positivo maggiore di 1; ciò premesso si dà la seguente definizione:
-dato un numero relativo a ed un numero intero positivo n maggiore di uno, si chiama potenza ennesima di a, il prodotto di n fattori uguali ad a.
La potenza ennesima di a si indica con la scrittura an. Il numero a si chiama base della potenza, l'intero n si chiama esponente. In virtù della definizione data, si ha perciò: a=a·a·a·a·...·a. (n volte).
Potenza di un numero relativo secondo l'esponente 1 e secondo l'esponente zero
Siccome un prodotto deve avere due fattori, si vede allora che la definizione di potenza data non vale più se l'esponente n è uguale ad 1. Volendo perciò definire la potenza di un numero a con esponente 1 oppure 0, bisogna dare una nuova definizione. Si è convenuto quanto segue:
-si chiama potenza di un numero relativo a secondo l'esponente 1, il numero a stesso, cioè per definizione si pone: a1=a.
-si chiama potenza di un numero relativo a, diverso da zero, secondo l'esponente 0, il numero +1, cioè, per definizione si pone: a0=+1.
Non si definisce invece la potenza in base 0, ed esponente 0, cioè, il simbolo 00, in quanto è privo di significato. In seguito, la base e l'esponente delle potenze saranno sempre considerate non simultaneamente nulle.
Potenza di un numero relativo secondo l'esponente 1 e secondo l'esponente zero
Esempi: (+5)2=(+5)(+5)=)+25; (-2)3=(-2)(-2)(-2)=-8; (-2/3)4=(-2/3)(-2/3)(-2/3)(-2/3)=16/81.
La potenza di esponente 1 di un numero relativo è assunta uguale al numero stesso, e la potenza di esponente zero è assunta uguale a 1, quale che sia la base, purchè diversa da zero.
E' bene ricordare che l'esponente della potenza viene scritto sottintendendo sempre il segno +; quando l'esponente è uguale a 1, esso non viene scritto.
Esempi: (+5)1=+5; (-7)1=-7; 01=0; (3/2)0=+1; (-5/4)0=+1.
Non si definisce la potenza del numero zero con esponente zero: il simbolo 00 è privo di significato.
Ricordando infine la regola dei segni della moltiplicazione, si verifica facilmente che:
-ogni potenza di base positiva è positiva;
-ogni potenza di base negativa è positiva o negativa a seconda che l'esponente sia pari o dispari.
Infatti, nel primo caso si ha un prodotto di un numero pari di fattori negativi, nel secondo, di un numero dispari di fattori negativi.
Potenza ennesima di un numero relativo
Servendoci ora della notazione letterale, si vogliono ora dimostrare, in generale, le proprietà delle potenze dei numeri relativi, secondo un esponente intero e positivo. Allo scopo, si indica con a un qualsiasi numero relativo, positivo o negativo o anche zero, con n un numero intero positivo maggiore di 1; ciò premesso si dà la seguente definizione:
-dato un numero relativo a ed un numero intero positivo n maggiore di uno, si chiama potenza ennesima di a, il prodotto di n fattori uguali ad a.
La potenza ennesima di a si indica con la scrittura an. Il numero a si chiama base della potenza, l'intero n si chiama esponente. In virtù della definizione data, si ha perciò: a=a·a·a·a·...·a. (n volte).
Potenza di un numero relativo secondo l'esponente 1 e secondo l'esponente zero
Siccome un prodotto deve avere due fattori, si vede allora che la definizione di potenza data non vale più se l'esponente n è uguale ad 1. Volendo perciò definire la potenza di un numero a con esponente 1 oppure 0, bisogna dare una nuova definizione. Si è convenuto quanto segue:
-si chiama potenza di un numero relativo a secondo l'esponente 1, il numero a stesso, cioè per definizione si pone: a1=a.
-si chiama potenza di un numero relativo a, diverso da zero, secondo l'esponente 0, il numero +1, cioè, per definizione si pone: a0=+1.
Non si definisce invece la potenza in base 0, ed esponente 0, cioè, il simbolo 00, in quanto è privo di significato. In seguito, la base e l'esponente delle potenze saranno sempre considerate non simultaneamente nulle.
Proprietà delle potenze
Prodotto di due potenze aventi la stessa base
Dalla definizione di potenza seguono importanti proprietà, le quali danno luogo ad importanti regole di calcolo. Per comprendere ciò che si vuole dimostrare, si comincia a ragionare su un esempio numerico: si calcola il seguente prodotto: (-2)3(2)5. Da come si nota, si tratta di calcolare il prodotto di due potenze aventi la stessa base; per definizione di potenza, si ha:(-2)3=(-2)(-2)(-2); (2)5=(-2)(-2)(-2)(-2)(-2) e quindi (-2)3(2)5=(-2)(-2)(-2)(-2)(-2)(-2)(-2)(-2). Siccome il secondo membro di tale uguaglianza è formato dal prodotto di otto fattori uguali al numero (-2), esso rappresenta il valore di (-2)8. Quindi: (-2)3(2)5=(-2)8.
Da questa uguaglianza risulta che, quando si deve calcolare il prodotto di due potenze aventi la stessa base, invece di calcolare separatamente le singole potenze e poi calcolare fra loro i due risultati ottenuti, si può calcolare una sola potenza che ha per base la stessa base delle due potenze date e per esponente la somma dei loro esponenti. Questa proprietà, in generale, vale per due potenze qualsiasi aventi la stessa base; si dimostra il seguente:
Teorema 1) - Il prodotto di due potenze aventi la stessa base, è uguale ad una potenza che ha per base la stessa base e per esponente la somma degli esponenti, cioè se m e n sono due numeri interi positivi ed a un numero relativo qualsiasi, si ha : an·am=an+m.
Dimostrazione
Infatti, per definizione di potenza, si ha: an=a·a·a·...·a (n volte), am=a·a·a·...·a (m volte) e quindi: an·am=(a·a·a·...·a).(a·a·a·...·a) (n+m volte). Per la proprietà dissociativa della moltiplicazione, si può scrivere: an·am=a·a·a·...·a (n+m volte) (1). A tal punto bisogna osservare che il secondo membro di quest'ultima uguaglianza è un prodotto di m+n fattori tutti uguali ad a. Perciò, per definizione di potenza, questo prodotto rappresenta il valore della potenza an·am. Quindi la (1) si può scrivere: an·am=an+m, come volevasi dimostrare.
Esempi:
1) (+3)2(+3)3=(+3)5=243;
2) (-1/2)2(-1/2)4=(-1/2)6=+1/64;
3) (+2/3)3(+2/3)=(+2/3)4=16/81;
4) (-2)4(+2)3=(+2)4(+2)3=(+2)7=128.
Prodotto di più potenze aventi la stessa base
Il teorema precedente è anche valido per un prodotto di più potenze aventi la stessa base, cioè risulta: an·am·ap=an+m+p.
Esempi:
1) (-2)2(-2)4(-2)3=(-2)9=-512;
2) (-3)2(+3)3(-3)4=(+3)2(+3)3(+3)4=(+3)9=19683;
3) (+2/3)(+2/3)2(+2/3)3(+2/3)2=(+2/3)8=256/6561.
Quoziente di più potenze aventi la stessa base
Teorema 2)- Il quoziente di più potenze aventi la stessa base, tali che l'esponente del dividendo non sia minore di quello del divisore, è una potenza che ha per base la stessa base e per esponente la differenza degli esponenti, cioè se n ed m sono due numeri interi positivi ed n è minore di m, ed a è un numero relativo diverso da zero, si ha: an:am=an-m (2).
Se n=m, il teorema è evidente, perchè si è posto, per definizione a0=+1.
Supponendo ora n>m, per dimostrare la (2), per definizione di quoziente, si deve dimostrare che il prodotto di an-m per am è uguale ad an, cioè: an-mam=an.
Infatti, per il teorema dimostrato in precedenza, si ha: an-mam=an-m+n (3). Essendo n-m+n=m, la (3) si può scrivere sotto la forma seguente: an-mam=an, come volevasi dimostrare. Esempi:
1) (-2)7:(-2)4=(-2)3=-8;
2) (+3/5)3:(+3/5)=(+3/5)2=9/25;
3) (-5)12:(+5)9=(+5)12:(+5)9=(+5)3=125.
Nota bene
Supponendo che le due potenze abbiano lo stesso esponente, cioè n=m, il teorema enunciato esprime che an:an=a0 (4). Siccome risulta an:an=+1, in quanto il quoziente di due numeri uguali è sempre uguale a +1, la (4) è vera solo perchè in precedenza si è convenuto che per definizione a0=+1. Perciò il motivo per il quale si è posto a0=+1, e non ad un altro numero, si deve ricercare nel fatto che, con tale definizione, quest'ultimo teorema è valido anche quando gli esponenti delle due potenze sono uguali. Alcune volte si dice: "Si dimostra che a0=+1"; e la dimostrazione che si tenta di dare è "siccome an:an=+1, ed inoltre an:an=a0, segue che a0=+1". Ma in che modo si può affermare che an:an=a0 senza aver prima definito a0, cioè senza aver prima definito a0? Prima si dovrà dire quale numero s'intende indicare con la scrittura a0 e poi si dovrà vedere se risulta, oppure no, an:an=a0. Ad esempio, se si ponesse a0=+25, non risulterebbe an:an=a0.
Si deve quindi ricordare che si è posto a0=+1 per definizione, e tale definizione si giustifica con il fatto che, mediante questa posizione, l'ultimo teorema è valido anche per n=m.
Teorema 3) - La potenza di una potenza di data base è uguale ad una potenza avente la stessa base e per esponente il prodotto degli esponenti, cioè (an)m=anm. Per m=1 il teorema è evidente. Per dimostrare il teorema per m>1, è bene ricordare che elevare all'emmesima potenza il numero an, vuol dire moltiplicare an per se stesso m volte, cioè: (an)m=ananan....an (m volte) (*). Si osservi ora che nel secondo membro di tale uguaglianza si deve effettuare il prodotto di m potenze aventi la stessa base. Allora, per il primo teorema visto, tale prodotto è uguale ad una potenza avente per base a e per esponente la somma degli esponenti. Essendo (m volte) n+n+n....+n=nm, il secondo membro di (*) è uguale ad anm, come volevasi dimostrare.
Esempi:
1) [(-3)2]4=(-3)8=+6561;
2) [(-1/2)3]2=(-1/2)6=+1/64.
Teorema 4) - La potenza di un prodotto è uguale al prodotto delle potenze dei singoli fattori, cioè se si indicano con a, b, c, tre numeri relativi qualsiasi e con n un numero intero positivo, si ha: (a·b·c)n=an·bn·cn (**).
Infatti, per definizione di potenza, si ha: (a·b·c)n=(a·b·c).(a·b·c).(a·b·c)....(a·b·c) (n volte). Applicando prima la proprietà dissociativa e poi la proprietà commutativa al prodotto che sta al secondo membro, si ha: (a·b·c)n=a·a·a·...·a·b·b·b·...·b·c·c·c·...·c. dove i prodotti a·a·a·...·a, b·b·b·...·b, c·c·c·...·c si devono rispettivamente considerare n volte. Per definizione di potenza, quest'ultima uguaglianza si può scrivere: (a·b·c)n=an·bn·cn, come volevasi dimostrare.
Esempi:
1) [(-1/2)(-3/5)]3=(-1/2)3(-3/5)3=(-1/8)(-27/125)=+27/1000;
2) [(-1/2)3(+2/3)2]3=(-1/2)9(+2/3)6=(-1/512)(+64/729)=-1/5832.
Dall'uguaglianza (**), per la proprietà simmetrica dell'uguaglianza, si ha: an·bn·cn=(a·b·c)n, e quindi: il prodotto di più potenze con esponenti uguali è uguale ad una potenza avente per base il prodotto delle basi e per esponente, l'esponente comune.
Esempi:
1) (+1/3)3(-3/2)3(-4)3=[(+1/3)(-3/2)(-4)]3=(+2)3=+8;
2) (+3)4(-2/3)4(+5/4)4= [(+3)(-2/3)(+5/4)]4=(-5/2)4=(+625/16).
Teorema 5)- La potenza di un quoziente è uguale al quoziente delle potenze del dividendo e del divisore, cioè: (a:b)n=an:bn, ossia (a/b)n=an/bn.
Per dimostrare tale teorema, si indicano con q il quoziente fra a e b, cioè si pone a:b=q (***). Per definizione di quoziente, si ha: a=bq. Elevando alla potenza ennesima i due numeri uguali a e bq, si ottiene: an=(bq)n. Per il teorema 4), si ha: (bq)n=bnqn e quindi si può scrivere an=bnqn. Ma se il prodotto di un numero bn per un numero qn dà per risultato an, ciò significa, per definizione di quoziente, che il quoziente fra an e bn è uguale a qn, cioè si ha: an:bn=qn, ossia, per (***) risulta: an:bn=(a:b)n, come volevasi dimostrare.
Esempio:
[(-1/2):(-5/4)]3=(-1/2)3:(-5/4)3=(-1/8):(-125/64)=(-1/8)(-64/125)=+8/125.
Nei calcoli conviene spesso applicare l'inverso del teorema 5), precisamente si considera an:bn=(a:b)n, e quindi si ha che:
-il quoziente di due potenze di esponente uguale, è una potenza dello stesso esponente avente per base il quoziente delle basi.
Esempi:
1) (-3/5)3:(+3/2)3=[(-3/5):(+3/2)]3=(-2/5)3=-8/125;
2) (+1/7)5:(-1/21)5=[(+1/7):(-1/21)]5=[(+1/7)(-/21)]5=(-3)5=-243.
Nota bene
Dai teoremi dimostrati segue che il prodotto di più potenze aventi la stessa base, si può calcolare mediante un'unica potenza che ha la stessa base e per esponente la somma degli esponenti delle singole potenze. Così pure, il quoziente di due potenze aventi la stessa base, si può calcolare mediante un'unica potenza che ha la stessa base e per esponente la differenza degli esponenti. Attenzione: tale proprietà non vale per la somma algebrica di potenze aventi la stessa base, cioè la somma algebrica di più potenze aventi la stessa base, non si può calcolare con una potenza. In questi casi, bisogna calcolare le potenze dei singoli termini dell'addizione e poi sommare i risultati ottenuti.
Esempio: (-2)3+(-2)4-(-2)5=-8+16+32=+40.
Il teorema 4) afferma che per calcolare la potenza di un prodotto si può effettuare il prodotto delle potenze dei singoli fattori, mentre il teorema 5) afferma che per calcolare la potenza di un quoziente si deve effettuare il quoziente delle potenze del dividendo e del divisore. Attenzione: la potenza della somma dei due numeri non è uguale alla somma delle potenze dei singoli addendi della somma, cioè (a+b)n non è uguale ad an+bn. Per calcolare (a+b)n, almeno fino a questo momento si deve calcolare la somma a+b, e poi, del risultato ottenuto, si deve calcolare la potenza ennesima.
Esempi:
1) (-3+7)2=(+4)5=1024;
2) (-5+9/2)6=(-1/2)6=1/64;
3) (-3/2+6/5)3=(-3/10)3=-27/1000.
Potenze con esponente negativo
E' noto che, per il teorema 2), dimostrato per le potenze con esponente positivo, si ha: (+) an:am=an-m, e che esso è valido per n>m, o per n=m. Si vuol vedere ora quale convenzione bisogna fare affinchè la formula (+) sia valida quando n<m. Per chiarire il concetto, si suppone n=3, m=5. Se in (+) si sostituiscono i valori di n e di m, si ha: a3:a5=a-2 (++), uguaglianza al momento assurda, perchè il secondo membro a-2, è un simbolo ancora privo di significato. Però, se nel primo membro della (++), cioè in a3:a5, si dividono dividendo e divisore per a3, si ottiene: a3:a5=1:a-2=1/a2. Segue che, per rendere valida l'uguaglianza (++), si è costretti a porre, per definizione: a-2=1/a2. Da questo esempio, risulta giustificata la seguente definizione:
chiamasi potenza di un numero relativo, diverso da zero e con esponente negativo, il reciproco della potenza della stessa base, elevato all'esponente opposto al dato.
Quindi, se a è un numero relativo diverso da zero, ed n un numero intero positivo, si ha, per definizione: a-n=1/an.
Esempi:
1) (+3)-2=1/(+3)2=+1/9;
2) (-5)-2=1/(-5)2=+1/125.
Con l'introduzione delle potenze ad esponente negativo, è valida la seguente uguaglianza: an:am=an-m, anche quando n<m. Il fatto importante è che i teoremi 1), 2), 3), 4), 5), dimostrati validi con esponenti positivi, continuano a sussistere anche quando gli esponenti sono negativi. In altri termini, si può dimostrare facilmente che per le potenze ad esponente negativo valgono tutti i teoremi dimostrati per le potenze ad esponente positivo. Tali dimostrazioni si omettono.
Esempio: (-2)-3(-2)-5=(-2)-8=1/(-2)8=+1/256.
Espressione letterale o algebrica
Definizione - Chiamasi espressione letterale o algebrica l'indicazione di un complesso di operazioni da eseguirsi su numeri rappresentati tutti, o in parte, da lettere.
Esempio di espressioni letterali:
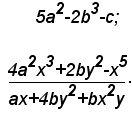
Espressione algebrica intera e frazionaria
Ad esempio, fra le operazioni sopra indicate, la prima espressione algebrica è intera, la seconda frazionaria.
Definizione - Un'espressione algebrica si dice intera rispetto ad una lettera in essa contenuta, quando tale lettera non compare mai come divisore.
Definizione - Chiamasi valore di una espressione letterale per dati valori attribuiti alle lettere in essa contenute, il numero relativo che si ottiene sostituendo nell'espressione letterale considerata, ad ogni lettera il valore fissato e poi eseguendo le operazioni indicate nell'espressione numerica così ottenuta.
Esempio: calcolare il valore numerico della seguente espressione algebrica: 5a2-3ab+ 2b2, per a=-2/3 e b=-3/2.
Si ha: 5a2-3ab+2b2=5(-2/3)2-3(-2/3)(-3/2)+2(-3/2)2=5(+4/9)-3(+1)+2(9/4)=+20/9-3+9/2=67/18.