MIKY & GENNY
PROBLEMI DI GRADO SUPERIORE AL PRIMO ---> INDICE
La risoluzione di molti problemi che si presentano, si può ricondurre a quella di un'equazione o di un sistema di grado superiore al primo, come già esaminato in precedenza. Le considerazioni fatte per la risoluzione dei problemi di primo grado, valgono anche per quelli di secondo grado.
Definizione - Si chiamano problemi di secondo, terzo, quarto,... grado, quei problemi la cui risoluzione algebrica si può ricondurre a un'equazione o a un sistema rispettivamente di secondo, terzo, quarto,... grado.
Definizione - Si chiamano problemi di secondo, terzo, quarto,... grado, quei problemi la cui risoluzione algebrica si può ricondurre a un'equazione o a un sistema rispettivamente di secondo, terzo, quarto,... grado.
Se un problema di secondo grado, o di grado superiore, si traduce in un'equazione, o in un sistema a coefficienti numerici, le soluzioni dell'equazione, o del sistema, sono anche numeriche e allora è facile decidere quali di esse sono accettabili per il problema. Se invece il problema si traduce in un'equazione, o in un sistema a coefficienti letterali, decidere se le soluzioni trovate sono o no accettabili per il problema, porta, almeno in generale, a considerazioni al di fuori di un corso di algebra elementare. Quindi si esaminano soltanto alcuni casi elementari.
Problemi:
1)-determinare un numero intero tale che la differenza fra il suo quadrato e i 2/3 dello stesso numero sia uguale a 52.
Indicato con x il numero cercato, il problema si traduce nella seguente equazione:
ossia:
che ammette le radici
La prima radice è un numero intero che soddisfa il problema, mentre la seconda, non essendo un numero intero, non può essere una sua soluzione. Quindi, il problema proposto ammette l'unica soluzione x1=8.
2)-In un rettangolo, la misura dell'altezza supera di m 7 quella della base; determinare le misure dei lati del rettangolo, sapendo che la diagonale è m 13.
Considerato il rettangolo ABCD e indicata con x la misura della base AB, la misura dell'altezza BC è uguale a x+7.
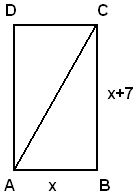
Applicando il teorema di Pitagora al triangolo ABC, il problema si traduce nella seguente equazione:
x2-(x+7)2=132,
che ridotta a forma normale, x2-108x+4=0, diventa (1)
x2+7x-60=0.
osserva ora che, avendo indicato con x la misura della base del rettangolo, x dev'essere un numero positivo minore della misura della diagonale del rettangolo, che è m 13. Perciò le radici dell'equazione (1) soddisfano il problema, se esse sono positive e minori di 13. Risolvendo l'equazione, si trova:
Scartando la radice negativa, si ha che il problema ammette una sola soluzione, cioè: la base del rettangolo è uguale a m 5 e, di conseguenza, l'altezza è uguale a m 12.
3)-Se ad un numero di due cifre si aggiunge 18, si ha un numero che da esso si ottiene invertendo le cifre. Sapendo inoltre che il numero è uguale al triplo del prodotto delle due cifre, trovare il numero.
Indicata con x la cifra delle unità, e con u quella delle decine, il numero cercato viene indicato con: 10y+x. Per le condizioni date, il problema si traduce nel seguente sistema:
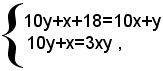
ossia
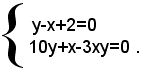
Le soluzioni di questo sistema sono anche le soluzioni del problema proposto, se x e y risultano interi, positivi e non superiori a 9. Risolvendo il sistema con il metodo di sostituzione, si trova:
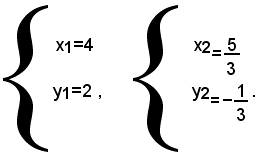
Siccome soltanto la prima soluzione verifica anche il problema, il numero cercato è 24.
4)-Calcolare le misure dei cateti di un triangolo rettangolo sapendo che la superficie è m 542 e l'ipotenusa m 15.
Considerato il triangolo ABC e indicate con x e y le misure dei cateti, espresse in metri, siccome la superficie del triangolo è m 542, si può scrivere l'equazione:
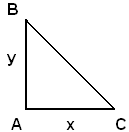
Applicando il teorema di Pitagora al triangolo ABC, si ha:
Quindi il problema si traduce nel seguente sistema: (1)
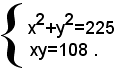
Le soluzioni di questo sistema soddisfano anche il problema proposto, se esse risultano positive e minori di 15, dato che in un triangolo rettangolo i cateti sono minori dell'ipotenusa. Il sistema (1) è un sistema simmetrico di quarto grado, che risolto, dà le seguenti radici:
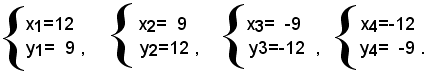
Le ultime due soluzioni si devono scartare, perchè negative; le prime due invece soddisfano il problema, perchè sono formate da numeri positivi minori di 15. Esse però danno luogo allo stesso triangolo rettangolo, quindi si può dire che il problema ammette una sola soluzione: i cateti del triangolo misurano m 12 e m 9.
5)-In un semicerchio avente il raggio di m 13, si considera una corda tale che la somma della stessa e della sua distanza dal centro risulti m 22; determinare la misura della corda.
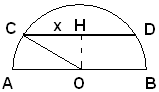
Indicata con 2x la misura della corda CD, applicando il teorema di Pitagora al triangolo rettangolo OHC, si ha:
quindi il problema si traduce nella seguente equazione
ossia (1)
Elevando ambo i membri al quadrato, si ha l'equazione (2):
169-x2=(22-2x)2,
la quale, come è noto, ammette tutte le soluzioni sella (1), ma può averne delle altre. Perciò, le soluzioni della (2) soddisfano il problema se risultano positive e minori della misura del raggio, cioè di 13, e se sono radici anche dell'equazione (2). Risolvendo la (2), si trova:
Si vede facilmente che il secondo valore non verifica l'equazione (1), quindi il problema ammette l'unica soluzione x=5; di conseguenza la misura della corda è m 12.
6)-Trovare le misure delle basi di un trapezio isoscele circoscritto a un cerchio il cui raggio è cm 6, sapendo che il suo perimetro è cm 52.
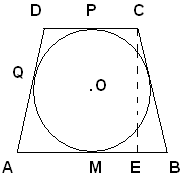
Indicate con x e y le misure delle semibasi del trapezio e ricordando che i segmenti delle tangenti condotte da un punto a una circonferenza sono fra loro uguali, si ha:
e quindi
Premesso ciò, sapendo che il perimetro del trapezio è cm 52, si può scrivere la seguente equazione:
4x+4y=52.
Dal triangolo rettangolo EBC, osservando che:
per il teorema di Pitagora, si ha
122+(x-y)2=(x+y)2 ,
quindi il problema si traduce nel seguente sistema
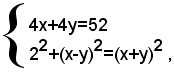
che semplificato diventa
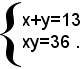
Le soluzioni di questo sistema sono positive, e quindi accettabili, come risulta dalla risoluzione del sistema nel modo noto:
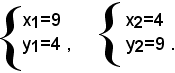
Quindi le basi del trapezio misurano rispettivamente cm 18 e cm 8.
7)-Il perimetro di un triangolo rettangolo è m 40 e la sua superficie m2 60; determinare le misure dei lati.
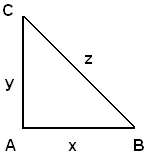
Indicate con x e y le misure dei cateti e con z l'ipotenusa del triangolo rettangolo, applicando il teorema di Pitagora, facilmente si vede che il problema si traduce nel seguente sistema di quarto grado:
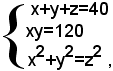
che si può scrivere sotto la forma
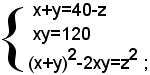
ossia, sostituendo nella terza equazione a x+y il valore 40-z, risultante nella prima equazione, e a xy, il valore 120 risultante nella seconda equazione, si ha (1)
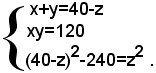
Dalla terza equazione, dopo facili semplificazioni, si trova z=17. Sostituendo tale valore nell'equazione del sistema (1), si ottiene il sistema:
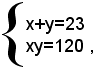
le cui soluzioni sono
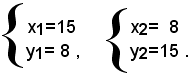
Quindi, le misure dei due cateti del triangolo sono m 15 e m 8, mentre la misura dell'ipotenusa è m 17.
8)-Determinare le misure dei lati di un rettangolo, sapendo che il Il perimetro è uguale a 2p e l'area a2.
Indicate con x e y le misure dei lati del rettangolo, per le condizioni del problema, si ha: (1)
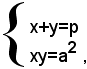
la cui equazione risolvente è (2)
z2-4pz+a2=0.
Discussione: il problema proposto ha soluzione se il sistema (1), ovvero l'equazione (2) ammette radici reali e positive. E' noto che un'equazione ammette radici reali soltanto quando il suo discriminante risulta positivo o nullo, cioè quando risulta:
p2-4a2≥0,
ossia
p2≥4a2,
da cui si ricava, tenendo presente che che le lettere p e a rappresentano numeri positivi (3)
Una volta soddisfatta la condizione (3), le radici della (2), oltre ad essere reali, sono anche positive, perchè l'equazione presenta due variazioni. Concludendo, si può dire che, quando risulta p>2a, cioè quando alla lettera p si attrubuisce un valore positivo più grande del doppio di quello attribuito alla lettera a, il sistema (1) ammette due soluzioni reali positive:
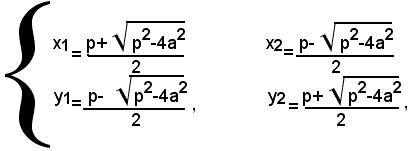
e perciò le misure dei lati di un rettangolo sono:

Quando risulta p<2a, il discriminante dell'equazione (2) è nullo, quindi l'equazione ammette l'unica soluzione:
in tal caso, il rettangolo è il quadrato di lato a.
Se
risulta p=2a, il problema non ammette soluzioni, perchè
l'equazione (2), che traduce algebricamente il problema, non ha radici
reali.
9)-Determinare le misure dei cateti di un triangolo rettangolo, sapendo che la loro somma è uguale ad a e l'ipotenusa uguale a b.
Indicate con x e y le misure dei cateti del triangolo rettangolo, per ipotesi risulta x+y=a, e applicando il teorema di Pitagora, risulta anche x2+y2=b2, pertanto il problema si traduce nel seguente sistema simmetrico:
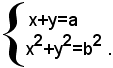
9)-Determinare le misure dei cateti di un triangolo rettangolo, sapendo che la loro somma è uguale ad a e l'ipotenusa uguale a b.
Indicate con x e y le misure dei cateti del triangolo rettangolo, per ipotesi risulta x+y=a, e applicando il teorema di Pitagora, risulta anche x2+y2=b2, pertanto il problema si traduce nel seguente sistema simmetrico:
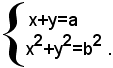
Essendo:
x2+y2=(x+y)2-2xy,
si ricava
e quindi si ha il seguente sistema trasformato, equivalente a quello proposto
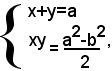
la cui equazione risolvente è
ossia
z2-az+(a2-b2)=0.
Discussione: affinchè il problema sia possibile, è necessario che le soluzioni del problema (1), ossia le radici dell'equazione (2), risultino reali e positive. Per la realtà delle radici della (2), il discriminante deve risultare positivo o nullo, ossia, applicando la formula ridotta, deve risultare:
a2-2(a2-b2)≥0,
ossia
oppure
a2≤2b2,
quindi, tenendo conto che le lettere a e b rappresentano numeri positivi poichè misure di segmenti, si ricava
Inoltre, dopo aver verificato questa condizione, affinchè le radici dell'equazione (2) siano positive, essa deve presentare, per la regola di Cartesio, due variazioni; pertanto, dev'essere:
a2>b2,
ossia
ossia
a>b.
Concludendo, le radici dell'equazione (2) risultano reali ed entrambe positive, quando alle lettere a e b si attribuiscono valori che soddisfano le seguenti condizioni
e in tal caso le misure dei cateti del triangolo sono date dalle radici della (2).
Nota bene
Da questi ultimi esempi si vede che, quando i dati del problema sono letterali, la discussione che si deve fare per stabilire se il sistema ammette o no soluzioni non è semplice, e di solito richiede delle conoscenze di livello superiore rispetto agli argomenti trattati.