MIKY & GENNY
PROBLEMI DI PRIMO GRADO AD UNA INCOGNITA ---> INDICE
La risoluzione di alcuni problemi si può tradurre in un'equazione di primo grado ad un'incognita.
Esempi:
1)-se ad una certa somma si aggiungono € 50, si troverebbe lo stesso risultato, se dal doppio di tale somma si prelevassero € 30. A quanto ammonta tale somma?
Si indica con x il numero degli euro che rappresentano la somma. Se a questo numero si aggiungono € 50, si ottiene € (x+50). Se invece dal doppio della somma, 2x, si tolgono € 30, si ottiene (2x-30). Il problema esprime quindi che: x+50=2x-30. Risolvendo tale equazione, si trova: x=80, che rappresenta il valore della somma incognita del problema.
2)-dividere € 2345 fra due persone in modo che la prima abbia i 3/4 della somma spettante alla seconda.
Si indica con x il numero degli euro spettanti alla seconda persona. Alla prima persona spettano:
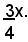
Nota bene
La soluzione dell'equazione considerata, può interpretarsi come segue: l'età del padre tre anni addietro era tripla di quella del figlio. Infatti, tre anni fa il padre aveva 39 anni ed il figlio 13, e si vede appunto che 39 è il triplo di 13.
4)-un contadino possiede dei polli e dei conigli. Gli animali hanno in totale 30 teste e 95 zampe. Quanti polli e quanti conigli ha quel contadino?
Si indica ora con x il numero dei polli, quindi il numero dei conigli sarà 30-x. Il numero delle zampe dei polli sarà 2x e quelle dei conigli 4(30-x). Avendo gli animali in totale 95 zampe, si ha l'equazione: 2x+4(30-x)=95. Risolvendo l'equazione, si trova x=25/2, ed anche in questo caso la soluzione trovata non va bene, perchè il numero dei polli dev'essere un numero intero. Il problema proposto è perciò impossibile.
5)-in un trapezio isoscele il lato obliquo è i 2/3 della base minore e la base maggiore è uguale alla metà della somma del lato obliquo con il quintuplo della base minore. Sapendo che il perimetro del trapezio è cm 372, trovare le misure dei lati del trapezio.
Si indica ora con x la misura, espressa in cm, della base minore del trapezio. La misura di ciascuno dei lati obliqui è allora
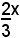
e la misura della base maggiore è
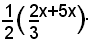
Siccome il perimetro del trapezio vale cm 372, si avrà la seguente equazione:
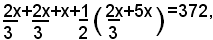
ossia:
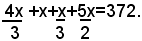
Risolvendo questa equazione, si trova x=72. Perciò la base minore è lunga cm 72; il lato obliquo è cm 72X2/3=cm 48 e la base maggiore
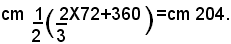
6)-due treni partono dalla stessa stazione e vanno nella stessa direzione. Il secondo parte 3 ore dopo la partenza del primo. Il primo treno percorre a km all'ora ed il secondo b km all'ora. Può il secondo treno raggiungere il primo? E dopo quante ore dalla partenza?
Supponendo che il secondo treno raggiunga il primo dopo x ore dalla sua partenza, nel frattempo il secondo treno avrà percorso km bx, mentre il primo avrà fatto lo stesso percorso in 3+x ore, e percorrendo a km all'ora, avrà percorso km (3+x)a. Ma i due treni all'istante dell'incontro avranno percorso uno stesso numero di km, dunque deve risultare: bx=(3+x)a, ossia bx=3a+ax, cioè (1) (b-a)x=3a, da cui, se b-a≠0, ciè se è b≠a, si deduce:
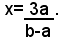
Esempi:
1)-se ad una certa somma si aggiungono € 50, si troverebbe lo stesso risultato, se dal doppio di tale somma si prelevassero € 30. A quanto ammonta tale somma?
Si indica con x il numero degli euro che rappresentano la somma. Se a questo numero si aggiungono € 50, si ottiene € (x+50). Se invece dal doppio della somma, 2x, si tolgono € 30, si ottiene (2x-30). Il problema esprime quindi che: x+50=2x-30. Risolvendo tale equazione, si trova: x=80, che rappresenta il valore della somma incognita del problema.
2)-dividere € 2345 fra due persone in modo che la prima abbia i 3/4 della somma spettante alla seconda.
Si indica con x il numero degli euro spettanti alla seconda persona. Alla prima persona spettano:
Il problema esprime che:
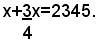
Quindi, si deduce: 4x+3x=9380, ossia x=1340.
Alla seconda persona spettano quindi € 1340, e perciò alla prima € (2345-21340)= € 1005.
3)-un padre ha 42 anni e uno dei suoi figli 16. Fra quanti anni l'età del padre sarà tripla di quella del figlio?
Si indica ora con x il numero degli anni che devono trascorrere affinchè l'età del padre diventi tripla di quella del figlio. Il numero cercato x deve essere quindi intero e positivo. Premesso ciò, si ossevi che fra x anni l'età del padre sarà 42+x e quella del figlio 16+x, e se l'età del padre dovrà essere tripla di quella del figlio, sarà 42+x=3(16+x). Segue che: 42+x=48+3x, ossia x=-3. Essendo la soluzione negativa, essa non sarà soluzione del problema proposto, il quale è pertanto impossibile, cioè l'età del padre non potrà mai diventare tripla di quella del figlio.
Da questo esempio si vede che un problema può essere impossibile anche quando l'equazione che lo traduce abbia soluzione. Ciò avviene quando la soluzione dell'equazione non si trova nell'insieme dei numeri assegnati dal problema.
Alla seconda persona spettano quindi € 1340, e perciò alla prima € (2345-21340)= € 1005.
3)-un padre ha 42 anni e uno dei suoi figli 16. Fra quanti anni l'età del padre sarà tripla di quella del figlio?
Si indica ora con x il numero degli anni che devono trascorrere affinchè l'età del padre diventi tripla di quella del figlio. Il numero cercato x deve essere quindi intero e positivo. Premesso ciò, si ossevi che fra x anni l'età del padre sarà 42+x e quella del figlio 16+x, e se l'età del padre dovrà essere tripla di quella del figlio, sarà 42+x=3(16+x). Segue che: 42+x=48+3x, ossia x=-3. Essendo la soluzione negativa, essa non sarà soluzione del problema proposto, il quale è pertanto impossibile, cioè l'età del padre non potrà mai diventare tripla di quella del figlio.
Da questo esempio si vede che un problema può essere impossibile anche quando l'equazione che lo traduce abbia soluzione. Ciò avviene quando la soluzione dell'equazione non si trova nell'insieme dei numeri assegnati dal problema.
Nota bene
La soluzione dell'equazione considerata, può interpretarsi come segue: l'età del padre tre anni addietro era tripla di quella del figlio. Infatti, tre anni fa il padre aveva 39 anni ed il figlio 13, e si vede appunto che 39 è il triplo di 13.
4)-un contadino possiede dei polli e dei conigli. Gli animali hanno in totale 30 teste e 95 zampe. Quanti polli e quanti conigli ha quel contadino?
Si indica ora con x il numero dei polli, quindi il numero dei conigli sarà 30-x. Il numero delle zampe dei polli sarà 2x e quelle dei conigli 4(30-x). Avendo gli animali in totale 95 zampe, si ha l'equazione: 2x+4(30-x)=95. Risolvendo l'equazione, si trova x=25/2, ed anche in questo caso la soluzione trovata non va bene, perchè il numero dei polli dev'essere un numero intero. Il problema proposto è perciò impossibile.
5)-in un trapezio isoscele il lato obliquo è i 2/3 della base minore e la base maggiore è uguale alla metà della somma del lato obliquo con il quintuplo della base minore. Sapendo che il perimetro del trapezio è cm 372, trovare le misure dei lati del trapezio.
Si indica ora con x la misura, espressa in cm, della base minore del trapezio. La misura di ciascuno dei lati obliqui è allora
e la misura della base maggiore è
ossia:
Risolvendo questa equazione, si trova x=72. Perciò la base minore è lunga cm 72; il lato obliquo è cm 72X2/3=cm 48 e la base maggiore
6)-due treni partono dalla stessa stazione e vanno nella stessa direzione. Il secondo parte 3 ore dopo la partenza del primo. Il primo treno percorre a km all'ora ed il secondo b km all'ora. Può il secondo treno raggiungere il primo? E dopo quante ore dalla partenza?
Supponendo che il secondo treno raggiunga il primo dopo x ore dalla sua partenza, nel frattempo il secondo treno avrà percorso km bx, mentre il primo avrà fatto lo stesso percorso in 3+x ore, e percorrendo a km all'ora, avrà percorso km (3+x)a. Ma i due treni all'istante dell'incontro avranno percorso uno stesso numero di km, dunque deve risultare: bx=(3+x)a, ossia bx=3a+ax, cioè (1) (b-a)x=3a, da cui, se b-a≠0, ciè se è b≠a, si deduce:
Discussione
Affinchè la soluzione trovata dell'equazione sia anche soluzione del problema proposto, è evidentemente necessario che il valore trovato per la x risulti positivo, e quindi dec'essere b>a, cioè la velocità del secondo treno dev'essere maggiore di quella del primo, come del resto è evidente. Per b<a, il problema è impossibile, perchè il valore trovato per la x risulta negativo. Per b=a, l'equazione (1) non ammette soluzioni, e quindi anche in questo caso il problema è impossibile. Concludendo, il secondo treno può raggiungere il primo soltanto se b>a, e lo raggiungerebbe dopo ore
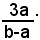
Affinchè la soluzione trovata dell'equazione sia anche soluzione del problema proposto, è evidentemente necessario che il valore trovato per la x risulti positivo, e quindi dec'essere b>a, cioè la velocità del secondo treno dev'essere maggiore di quella del primo, come del resto è evidente. Per b<a, il problema è impossibile, perchè il valore trovato per la x risulta negativo. Per b=a, l'equazione (1) non ammette soluzioni, e quindi anche in questo caso il problema è impossibile. Concludendo, il secondo treno può raggiungere il primo soltanto se b>a, e lo raggiungerebbe dopo ore
Questo
esempio mostra che in problemi i cui dati sono rappresentati da
lettere, si rende spesso necessaria una discussione per decidere sotto
quali condizioni il problema sia possibile.
7)-una persona ha a anni, un'altra ne ha b. Fra quanti anni l'età della prima sarà m volte quella della seconda?
Questo problema generalizza il problema 3). Indicando con x il numero degli anni, perchè cioè avvenga, si trova: a+x=m(b+x), ossia (1) (m-1)x=a-mb.
Se m≠1, si ricava: (2)
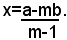
7)-una persona ha a anni, un'altra ne ha b. Fra quanti anni l'età della prima sarà m volte quella della seconda?
Questo problema generalizza il problema 3). Indicando con x il numero degli anni, perchè cioè avvenga, si trova: a+x=m(b+x), ossia (1) (m-1)x=a-mb.
Se m≠1, si ricava: (2)
Discussione
In tale discussione è inteso che m sia un numero intero positivo. Allora per m>1, la soluzione trovata (2) è positiva se è a>mb; negativa per a<mb. Ciò vuol dire che quanto richiesto si verificherà se a>mb, cioè se l'età della prima persona attualmente supera m volte l'età della seconda; nel caso contrario è accaduto in passato. Se a=mb, si trova x=0, cioè il fatto richiesto accade appunto nell'anno presente. Se è m=1 e a≠b, l'equazione (1) diventa: 0=a-b, la quale non ammette soluzioni e quindi il problema è impossibile. Ciò è evidente perchè in questo caso il problema richiederebbe quando è che due persone, attualmente di età diversa, avranno la stessa età. Se poi m=1, a=b, la (1) diventa: 0=0, ed è perciò soddisfatta da qualsiasi numero. Il problema è quindi sempre possibile e ciò è evidente, per chè in questo caso si chiederebbe quando è che l'età di due persone, che attualmente hanno la stessa età, avranno la stessa età!
Nota bene
Dagli esempi svolti, si è visto che, quando si vuol risolvere un problema col sussidio dell'algebra, bisogna prima fissare la grandezza che si assume come incognita, indicandola con la lettera x; dopo si deve scrivere il legame che, secondo l'enunciato del problema, intercorre fra la quantità incognita x ed i dati dello stesso, questi ultimi assegnati numericamente o rappresentati da lettere. Il legame fra l'incognita e i dati del problema si esprimerà, in generale, con un'equazione che, nei problemi considerati, sarà di primo grado. Si risolverà poi quest'equazione. Se i dati sono assegnati numericamente, anche i coefficienti dell'equazione saranno espressi in tal modo e quindi anche la sua soluzione. In generale, la soluzione trovata rappresenterà la soluzione del problema proposto. Però in certi casi, come si è visto nei problemi 3) e 4), la soluzione dell'equazione può non essere valida per il problema, e ciò potrà accadere quando il numero x deve soddisfare a certe limitazioni, come ad esempio, essere positivo, o intero, ecc., condizioni queste che non si possono tradurre in equazione. In questi casi, il problema sarà impossibile. Se poi i dati sono rappresentati da lettere, allora anche i coefficienti dell'equazione sono espressi da lettere, e così pure la soluzione. In questi casi, come si è visto nei problemi 6) e 7), bisognerà vedere, sia per quali valori delle lettere l'equazione ammette soluzione, sia per quali valori delle lettere la soluzione trovata può andare bene anche per il problema. In ciò consiste la cosiddetta discussione del problema.
In tale discussione è inteso che m sia un numero intero positivo. Allora per m>1, la soluzione trovata (2) è positiva se è a>mb; negativa per a<mb. Ciò vuol dire che quanto richiesto si verificherà se a>mb, cioè se l'età della prima persona attualmente supera m volte l'età della seconda; nel caso contrario è accaduto in passato. Se a=mb, si trova x=0, cioè il fatto richiesto accade appunto nell'anno presente. Se è m=1 e a≠b, l'equazione (1) diventa: 0=a-b, la quale non ammette soluzioni e quindi il problema è impossibile. Ciò è evidente perchè in questo caso il problema richiederebbe quando è che due persone, attualmente di età diversa, avranno la stessa età. Se poi m=1, a=b, la (1) diventa: 0=0, ed è perciò soddisfatta da qualsiasi numero. Il problema è quindi sempre possibile e ciò è evidente, per chè in questo caso si chiederebbe quando è che l'età di due persone, che attualmente hanno la stessa età, avranno la stessa età!
Nota bene
Dagli esempi svolti, si è visto che, quando si vuol risolvere un problema col sussidio dell'algebra, bisogna prima fissare la grandezza che si assume come incognita, indicandola con la lettera x; dopo si deve scrivere il legame che, secondo l'enunciato del problema, intercorre fra la quantità incognita x ed i dati dello stesso, questi ultimi assegnati numericamente o rappresentati da lettere. Il legame fra l'incognita e i dati del problema si esprimerà, in generale, con un'equazione che, nei problemi considerati, sarà di primo grado. Si risolverà poi quest'equazione. Se i dati sono assegnati numericamente, anche i coefficienti dell'equazione saranno espressi in tal modo e quindi anche la sua soluzione. In generale, la soluzione trovata rappresenterà la soluzione del problema proposto. Però in certi casi, come si è visto nei problemi 3) e 4), la soluzione dell'equazione può non essere valida per il problema, e ciò potrà accadere quando il numero x deve soddisfare a certe limitazioni, come ad esempio, essere positivo, o intero, ecc., condizioni queste che non si possono tradurre in equazione. In questi casi, il problema sarà impossibile. Se poi i dati sono rappresentati da lettere, allora anche i coefficienti dell'equazione sono espressi da lettere, e così pure la soluzione. In questi casi, come si è visto nei problemi 6) e 7), bisognerà vedere, sia per quali valori delle lettere l'equazione ammette soluzione, sia per quali valori delle lettere la soluzione trovata può andare bene anche per il problema. In ciò consiste la cosiddetta discussione del problema.