MIKY & GENNY
RADICALI ---> INDICE
Definizione
- Dato un numero reale positivo a e un numero intero positivo n, si
chiama radice ennesima aritmetica del numero a quel numero reale
positivo b la cui potenza ennesima è uguale ad a.
La radice ennesima di a si indica con il simbolo (1)
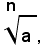
e si chiama radicale; il numero a si chiama radicando e il numero intero n si chiama indice del radicale.
Indicato con b il numero positivo rappresentato dal simbolo (1), cioè posto:
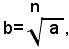
per definizione di radicale si ha: bn=a, ossia sostituendo a b il suo valore:
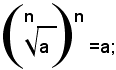
cioè: la potenza ennesima della radice ennesima aritmetica di un numero reale positivo è uguale al numero stesso.
Si osserva ora che, per qualsiasi intero positivo n, in quanto 0n=0, risulta:
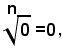
Quando l'indice della radice è uguale a 2, si omette e si scrive semplicemente:
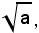
invece di:
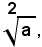
e si legge radice quadrata di a; inoltre, la radice di indice 3 si legge radice cubica. Se l'indice della radice è uguale a 1, per definizione di potenza con esponente 1, risulta:
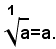
Da qui si vede che, quando l'indice della radice è uguale a 1, il segno di radice è superfluo e quindi in seguito non sarà usato.
Infine, al simbolo:
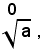
non si attribuisce nessun significato.L'espressione mediante la quale si passa dal numero a alla sua radice si chiama estrazione di radice.
In un radicale, il radicando può essere una potenza di un numero reale, ad esempio, nel radicale:
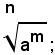
il numero m, esponente di tale potenza, si chiama esponente del radicando.
S'intende quindi che, nel radicale:
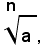
l'esponente del radicando è uguale a 1.
Infine, se a è un numero reale positivo, anche la radice ennesima aritmetica di a è anche un numero reale positivo, mentre se a=0 è anche :
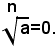
Proprietà invariantiva dei radicali aritmetici
Si dimostra il seguente teorema:
il valore di un radicale aritmetico non si altera se il suo indice e l'esponente del suo radicando vengono moltiplicati per uno stesso numero intero positivo.
Se n e p sono due numeri interi positivi e a un numero reale positivo, o nullo, si tratta di dimostrare che: (1)
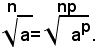
Siccome: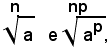
rappresentano due numeri reali positivi, o nulli, per provare la (1), basta provare che, elevando alla potenza np-esima ambo i membri della (1), si ottengono risultati uguali. Infatti, ricordando che per elevare un numero alla potenza np-esima si deve prima elevare il numero all'ennesima potenza e poi elevare il risultato ottenuto alla p-esima potenza, dal primo membro si ottiene: (2)
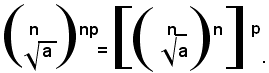
Essendo per definizione di radice ennesima aritmetica:
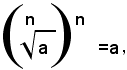
si ha: (3)
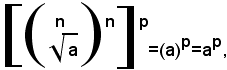
e quindi dalla (2) e (3), per la proprietà transitiva dell'uguaglianza, segue:
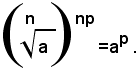
Dal secondo membro della (1), per definizione di radice aritmetica, si ha:
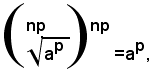
e quindi si ha lo stesso risultato ottenuto elevando a potenza np-esima il primo membro della (1), e ciò dimostra il teorema.
Si osservi ora che, quando il radicando è una potenza di esponente intero m, con m>1, la (1) diventa: (4)
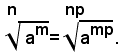
Esempi: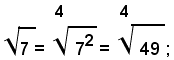
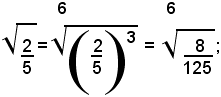
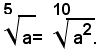
Dalla (4), per la proprietà simmetrica dell'uguaglianza, si ha:
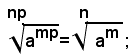
cioè: dividendo l'indice di un radicale e l'esponente del suo radicando per un loro divisore comune, si ottiene un radicale uguale a quello assegnato.Questo teorema si potrà applicare quando l'indice del radicale e l'esponente del radicando non sono primi fra loro.
Definizione - Un radicale si dice irriducibile quando il suo indice e l'esponente del suo radicando sono primi fra loro.
Ogni radicale non irriducibile si potrà trasformare, per il teorema suddetto, in un altro uguale o irriducibile, dividendo il suo indice e l'esponente del suo radicando per il loro M. C. D. Tale operazione si chiama semplificazione di un radicale e la proprietà espressa dal teorema enunciato, e dal suo inverso, si chiama proprietà invariantiva dei radicali aritmetici.
Esempi:
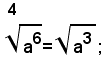
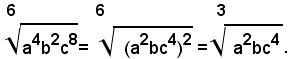
Non sono invece semplificabili i seguenti radicali:
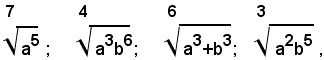
o perchè, come nel 1° e nel 2° esempio, pur essendo il radicando una potenza, l'esponente di questa e l'indice del radicale sono numeri primi fra loro, oppure perchè non è possibile considerare il radicando come una potenza, come accade nel 3° e nel 4° esempio.
Nota bene
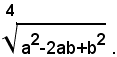
iI radicale si può scrivere sotto la forma:
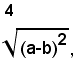
il radicando è positivo se a≠b, la base a-b è positiva se a>b, negativa se a<b. Perciò, avendo definito la radice ennesima aritmetica soltanto dei numeri positivi, per semplificare il radicale assegnato, si devono distinguere due casi:
1)-se a>b, segue a-b>0, pertanto si ha:
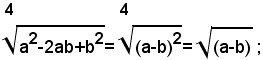
2)-se a<b, segue a-b<0, cioè b-a>0, pertanto si ha:
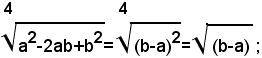
in tale caso, essendo a<b, se si scrivesse (1)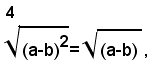
tale uguaglianza sarebbe assurda in quanto il primo membro della (1) rappresenta un numero reale positivo e il secondo non rappresenta nessun numero reale il cui quadrato risulti uguale al numero negativo a-b.
Se non si vogliono distinguere i due casi, si deve scrivere:
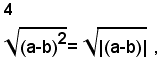
dove |(a-b)| indica il valore assoluto dei numero a-b.
Si ricorda che si chiama valore assoluto di un numero, il numero stesso, se questo è positivo, l'opposto, se esso è negativo, quindi: se a-b>0, si ha |a-b|=a-b; se a-b<0, |a-b|=-(a-b)=b-a.
2)-semplificare il radicale:
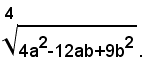
Si ha:
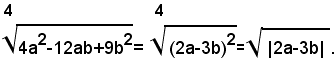
3)-semplificare il radicale:
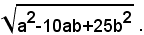
Si ha:
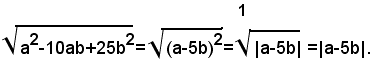
Se fosse a-5b<0, e si scrivesse
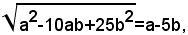
si scriverebbe un'uguaglianza assurda perchè il primo membro rappresenta un numero positivo, mentre il secondo è negativo.
Riduzione di più radicali allo stesso indice
Il teorema dimostrato in precedenza, esprimente che "il valore di un radicale aritmetico non si altera, se il suo indice e l'esponente del suo radicando vengono moltiplicati per uno stesso numero intero positivo", permette di ridurre più radicali aritmetici allo stesso indice senza alterarne il valore. Ad esempio, se si hanno i due radicali:
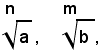
per il teorema suddetto, essi si riducono allo stesso indice, moltiplicando l'indice del primo radicale e l'esponente del suo radicando per l'indice del secondo radicale e l'indice del secondo radicale e l'esponente del suo radicando per l'indice del primo radicale. Si ottengono così due radicali rispettivamente uguali a quelli assegnati:
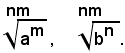
In pratica conviene prendere come indice comune ai due radicali assegnati, il m. c. m. degl'indici.
Esempio: ridurre allo stesso indice i radicali:
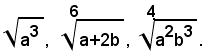
Il m. c. m. degl'indici dei radicali è 12; dividendo il m. c. m. per gl'indici dei singoli radicali, si ha 12:2=6, 12:6=2, 12:4=3; quindi i radicali, uguali rispettivamente a quelli assegnati, sono:
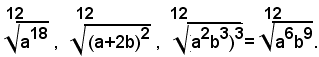
Da questo esempio si vede che la riduzione dei radicali allo stesso indice è un'operazione formalmente uguale alla riduzione delle frazioni allo stesso denominatore; l'indice corrisponde al denominatore e l'esponente del radicando al numeratore della frazione. Si può pertanto enunciare la seguente regola:
per ridurre più radicali irriducibili al minimo indice comune, si trova il m. c. m. degl'indici e lo si assume come indice comune a tutti i radicali. Il radicando di ciascun radicale trasformato, si ottiene elevando il corrispondente radicando a un esponente uguale al quoziente che si ottiene dividendo il m. c. m. trovato per l'indice del radicale assegnato. Se i radicali non sono irriducibili, prima di tutto si semplifica, poi si opera sui radicali ottenuti come detto sopra.
Esempi:
1)-ridurre allo stesso indice i radicali: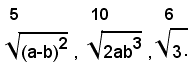
Poichè i radicali sono irriducibili e il m. c. m. degl'indici è 30, i radicali uguali a quelli assegnati ridotti allo stesso indice sono:
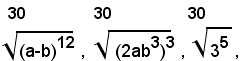
La radice ennesima di a si indica con il simbolo (1)
e si chiama radicale; il numero a si chiama radicando e il numero intero n si chiama indice del radicale.
Indicato con b il numero positivo rappresentato dal simbolo (1), cioè posto:
per definizione di radicale si ha: bn=a, ossia sostituendo a b il suo valore:
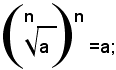
cioè: la potenza ennesima della radice ennesima aritmetica di un numero reale positivo è uguale al numero stesso.
Si osserva ora che, per qualsiasi intero positivo n, in quanto 0n=0, risulta:
Quando l'indice della radice è uguale a 2, si omette e si scrive semplicemente:
invece di:
e si legge radice quadrata di a; inoltre, la radice di indice 3 si legge radice cubica. Se l'indice della radice è uguale a 1, per definizione di potenza con esponente 1, risulta:
Da qui si vede che, quando l'indice della radice è uguale a 1, il segno di radice è superfluo e quindi in seguito non sarà usato.
Infine, al simbolo:
non si attribuisce nessun significato.
In un radicale, il radicando può essere una potenza di un numero reale, ad esempio, nel radicale:
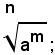
il numero m, esponente di tale potenza, si chiama esponente del radicando.
S'intende quindi che, nel radicale:
l'esponente del radicando è uguale a 1.
Infine, se a è un numero reale positivo, anche la radice ennesima aritmetica di a è anche un numero reale positivo, mentre se a=0 è anche :
Proprietà invariantiva dei radicali aritmetici
Si dimostra il seguente teorema:
il valore di un radicale aritmetico non si altera se il suo indice e l'esponente del suo radicando vengono moltiplicati per uno stesso numero intero positivo.
Se n e p sono due numeri interi positivi e a un numero reale positivo, o nullo, si tratta di dimostrare che: (1)
Siccome:
rappresentano due numeri reali positivi, o nulli, per provare la (1), basta provare che, elevando alla potenza np-esima ambo i membri della (1), si ottengono risultati uguali. Infatti, ricordando che per elevare un numero alla potenza np-esima si deve prima elevare il numero all'ennesima potenza e poi elevare il risultato ottenuto alla p-esima potenza, dal primo membro si ottiene: (2)
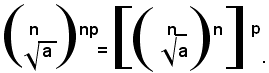
Essendo per definizione di radice ennesima aritmetica:
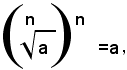
si ha: (3)
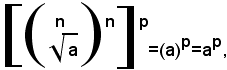
e quindi dalla (2) e (3), per la proprietà transitiva dell'uguaglianza, segue:
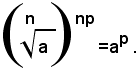
Dal secondo membro della (1), per definizione di radice aritmetica, si ha:
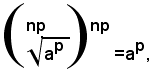
e quindi si ha lo stesso risultato ottenuto elevando a potenza np-esima il primo membro della (1), e ciò dimostra il teorema.
Si osservi ora che, quando il radicando è una potenza di esponente intero m, con m>1, la (1) diventa: (4)
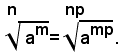
Esempi:
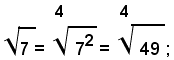
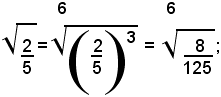
Dalla (4), per la proprietà simmetrica dell'uguaglianza, si ha:
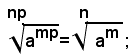
cioè: dividendo l'indice di un radicale e l'esponente del suo radicando per un loro divisore comune, si ottiene un radicale uguale a quello assegnato.
Definizione - Un radicale si dice irriducibile quando il suo indice e l'esponente del suo radicando sono primi fra loro.
Ogni radicale non irriducibile si potrà trasformare, per il teorema suddetto, in un altro uguale o irriducibile, dividendo il suo indice e l'esponente del suo radicando per il loro M. C. D. Tale operazione si chiama semplificazione di un radicale e la proprietà espressa dal teorema enunciato, e dal suo inverso, si chiama proprietà invariantiva dei radicali aritmetici.
Esempi:
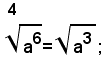
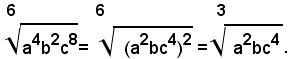
Non sono invece semplificabili i seguenti radicali:
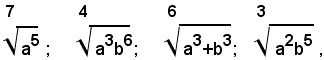
o perchè, come nel 1° e nel 2° esempio, pur essendo il radicando una potenza, l'esponente di questa e l'indice del radicale sono numeri primi fra loro, oppure perchè non è possibile considerare il radicando come una potenza, come accade nel 3° e nel 4° esempio.
Nota bene
Nel dire inverso
del teorema dimostrato, si è implicitamente ammesso che la base
della potenza, che costituisce il radicando, fosse positiva e, nelle
applicazioni fatte, tale condizione era sempre soddisfatta, dato che le
lettere a, b, c, ecc. rappresentano numeri reali positivi. Si vuol
vedere ora come si deve procedere quando non è determinato il
segno della base della potenza che costituisce il radicando.
Esempi:
1)-semplificare il radicale:
Esempi:
1)-semplificare il radicale:
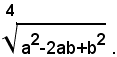
iI radicale si può scrivere sotto la forma:
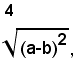
il radicando è positivo se a≠b, la base a-b è positiva se a>b, negativa se a<b. Perciò, avendo definito la radice ennesima aritmetica soltanto dei numeri positivi, per semplificare il radicale assegnato, si devono distinguere due casi:
1)-se a>b, segue a-b>0, pertanto si ha:
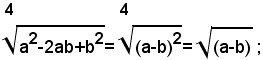
2)-se a<b, segue a-b<0, cioè b-a>0, pertanto si ha:
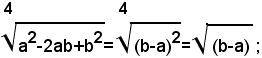
in tale caso, essendo a<b, se si scrivesse (1)
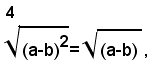
tale uguaglianza sarebbe assurda in quanto il primo membro della (1) rappresenta un numero reale positivo e il secondo non rappresenta nessun numero reale il cui quadrato risulti uguale al numero negativo a-b.
Se non si vogliono distinguere i due casi, si deve scrivere:
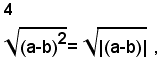
dove |(a-b)| indica il valore assoluto dei numero a-b.
Si ricorda che si chiama valore assoluto di un numero, il numero stesso, se questo è positivo, l'opposto, se esso è negativo, quindi: se a-b>0, si ha |a-b|=a-b; se a-b<0, |a-b|=-(a-b)=b-a.
2)-semplificare il radicale:
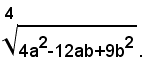
Si ha:
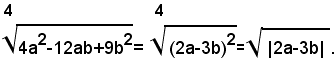
3)-semplificare il radicale:
Si ha:
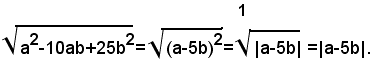
Se fosse a-5b<0, e si scrivesse
si scriverebbe un'uguaglianza assurda perchè il primo membro rappresenta un numero positivo, mentre il secondo è negativo.
Riduzione di più radicali allo stesso indice
Il teorema dimostrato in precedenza, esprimente che "il valore di un radicale aritmetico non si altera, se il suo indice e l'esponente del suo radicando vengono moltiplicati per uno stesso numero intero positivo", permette di ridurre più radicali aritmetici allo stesso indice senza alterarne il valore. Ad esempio, se si hanno i due radicali:
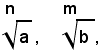
per il teorema suddetto, essi si riducono allo stesso indice, moltiplicando l'indice del primo radicale e l'esponente del suo radicando per l'indice del secondo radicale e l'indice del secondo radicale e l'esponente del suo radicando per l'indice del primo radicale. Si ottengono così due radicali rispettivamente uguali a quelli assegnati:
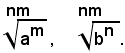
In pratica conviene prendere come indice comune ai due radicali assegnati, il m. c. m. degl'indici.
Esempio: ridurre allo stesso indice i radicali:
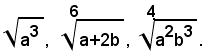
Il m. c. m. degl'indici dei radicali è 12; dividendo il m. c. m. per gl'indici dei singoli radicali, si ha 12:2=6, 12:6=2, 12:4=3; quindi i radicali, uguali rispettivamente a quelli assegnati, sono:
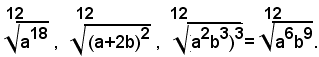
Da questo esempio si vede che la riduzione dei radicali allo stesso indice è un'operazione formalmente uguale alla riduzione delle frazioni allo stesso denominatore; l'indice corrisponde al denominatore e l'esponente del radicando al numeratore della frazione. Si può pertanto enunciare la seguente regola:
per ridurre più radicali irriducibili al minimo indice comune, si trova il m. c. m. degl'indici e lo si assume come indice comune a tutti i radicali. Il radicando di ciascun radicale trasformato, si ottiene elevando il corrispondente radicando a un esponente uguale al quoziente che si ottiene dividendo il m. c. m. trovato per l'indice del radicale assegnato. Se i radicali non sono irriducibili, prima di tutto si semplifica, poi si opera sui radicali ottenuti come detto sopra.
Esempi:
1)-ridurre allo stesso indice i radicali:
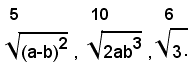
Poichè i radicali sono irriducibili e il m. c. m. degl'indici è 30, i radicali uguali a quelli assegnati ridotti allo stesso indice sono:
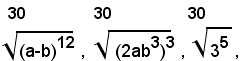
ossia:
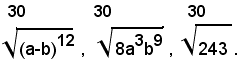
2)-ridurre allo stesso indice i radicali:
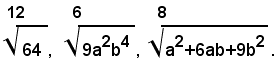
I radicali si possono scrivere sotto la forma:
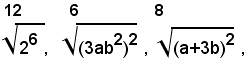
e quindi, in forma irriducibile:
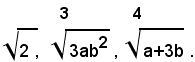
Il m. c. m. degl'indici è 12, quindi i radicali uguali a quelli assegnati sono:
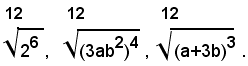
Ossia:
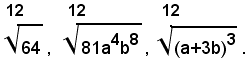
3)-ridurre allo stesso indice i radicali:
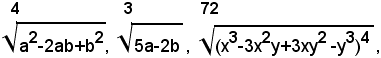
i radicali si possono scrivere sotto la forma:
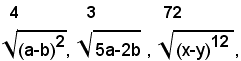
e quindi, in forma irriducibile:
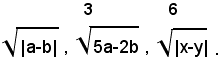
Il m. c. m. degl'indici è 6, quindi i radicali uguali a quelli assegnati sono:
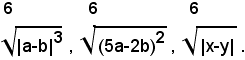
Operazioni con i radicali
Nel calcolo dei radicali, si usano frequentemente alcune regole di trasformazione e semplificazione, che derivano da quattro teoremi fondamentali.
Teorema 1) - Il prodotto di due o più radicali aventi lo stesso indice è uguale ad un radicale avente lo stesso indice di quelli assegnati e per radicando il prodotto dei singoli radicandi.
Si deve quindi dimostrare che, se a, b, c, sono tre numeri reali positivi e n un numero intero positivo, risulta: (1)
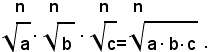
Per dimostrare che vale la (1), tenendo conto dell'inverso di un teorema precedente, è sufficiente dimostrare che elevando ambo i membri all'ennesima potenza, si ottengono risultati uguali.
Infatti, elevando all'ennesima potenza il primo membro della (1) e ricordando che la potenza di un prodotto è uguale al prodotto delle potenze dei singoli fattori, si ha: (2)
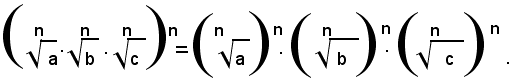
In base poi alla definizione di radice ennesima aritmetica di un numero positivo, si ha: (3)
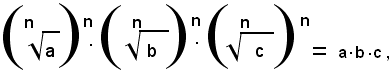
e quindi, dalla (2) e (3), per la proprietà transitiva dell'uguaglianza, segue:
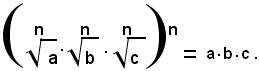
Elevando all'ennesima potenza il secondo membro della 1), per definizione di radice ennesima aritmetica, si ha:
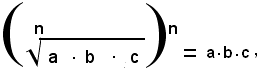
cioè, si ha lo stesso risultato ottenuto elevando alla potenza ennesima il primo membro della 1), quindi il teorema è dimostrato.
Nota bene
Quando si vuole effettuare il prodotto di radicali aventi indici disuguali, si riducono prima allo stesso indice e poi si applica il teorema 1).
Esempi:
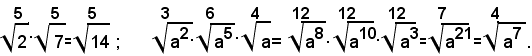
Dalla 1), per la proprietà simmetrica dell'uguaglianza, si ha:
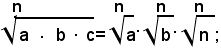
cioè: la radice ennesima aritmetica di un prodotto di fattori positivi è uguale al prodotto delle radici ennesime dei singoli fattori.
Esempi:
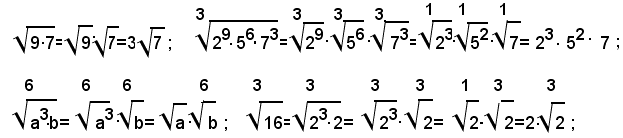
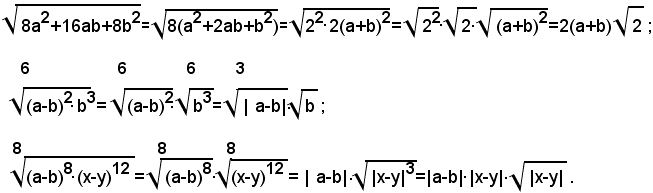
Teorema 2) - Il quoziente di due radicali aventi lo stesso indice, dei quali il secondo abbia il radicando diverso da zero, è uguale ad un radicale avente lo stesso indice di quelli assegnati e per radicando il quoziente dei singoli radicandi, cioè: 1)
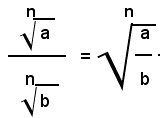
Infatti, elevando all'ennesima potenza il primo membro della (1) e ricordando che la potenza di un quoziente è uguale al quoziente delle potenze del dividendo e del divisore, si ha: (2)
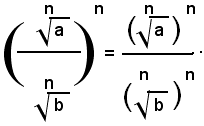
Inoltre, per definizione di radice ennesima aritmetica, si ha: (3)
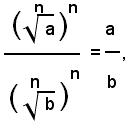
e quindi, dalla (2) e (3), per la proprietà transitiva dell'uguaglianza, segue:
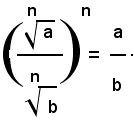
Elevando all'ennesima potenza il secondo membro della 1), per definizione di radice ennesima aritmetica, si ha:
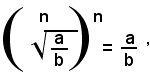
cioè si ha lo stesso risultato ottenuto elevando all'ennesima potenza il primo membro della 1), quindi il teorema è dimostrato.
Nota bene
Quando si vuole effettuare il quoziente di radicali aventi indici disuguali, si riducono prima allo stesso indice e poi si applica il teorema 2).
Esempi:
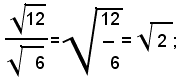
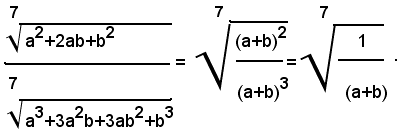
Dalla 1), per la proprietà simmetrica dell'uguaglianza, si ha:
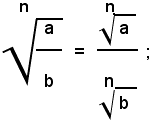
cioè: la radice ennesima aritmetica di un quoziente a termini positivi è uguale al quoziente delle radici ennesime aritmetiche del dividendo e del divisore.
Esempio:
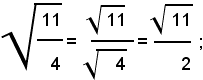
Trasporto di un fattore sotto il segno di radice
Si considera ora un caso particolare di moltiplicazione, quello in cui uno dei due fattori del prodotto è un radicale e l'altro no. Si abbia, ad esempio:
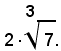
Siccome si può scrivere:
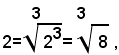
applicando il teorema 1), si ha:
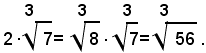
In generale, se a e b, sono due numeri reali positivi, si può dire:
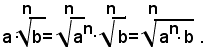
Si può quindi enunciare la seguente regola:
quando si moltiplica un radicale per un numero positivo, tale fattore si può trasportare sotto il segno di radice, come fattore del radicando, purchè lo si elevi a una potenza uguale all'indice del radicale.
Tale operazione si chiama: trasporto di un fattore sotto il segno di radice.
Analoghe considerazioni si possono fare nel caso di una divisione in cui dei due termini uno solo ha la forma di un radicale. Evidentemente, dati due numeri a, b, reali positivi, si ha:
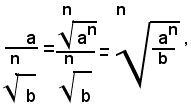
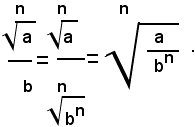
Esempio:
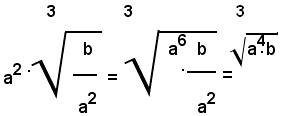
Nota bene
La regola enunciata in precedenza trattava del trasporto di un numero reale positivo sotto il segno di radice; si vuol vedere ora, con alcuni esempi, come si deve procedere nel caso in cui il fattore che si vuole trasportare sotto il segno di radice sia positivo, o senza alcun segno.Ad esempio, si considera il prodotto:
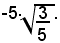
Evidentemente, questo prodotto è negativo, essendo negativo il fattore -5 e positivo
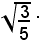
Pertanto, eseguendo il prodotto, si ha:
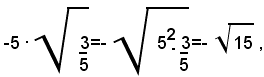
e quindi in tale uguaglianza sussiste anche il segno; dunque:
quando il fattore con cui si moltiplica il radicale è negativo, si deve portare sotto il segno di radice il suo valore assoluto, lasciando sotto il segno di radice il segno meno.
Esempi:
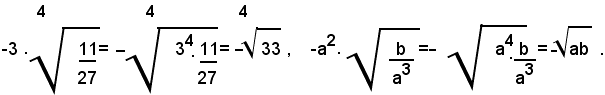
Si vede ora come si deve procedere nel caso in cui non è noto il segno del fattore che moltiplica il radicale.
1)-Portare sotto il segno di radice il fattore esterno nel prodotto seguente:
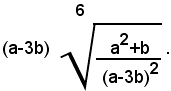
Il prodotto dato rappresenta un numero negativo, se a<3b, positivo se a>3b; si devono distinguere quindi i due casi:
1° - per a<3b, cioè per a-3b<0, si ha:
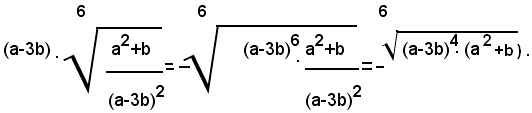
2° - per a<3b, cioè per a-3b>0, si ha:
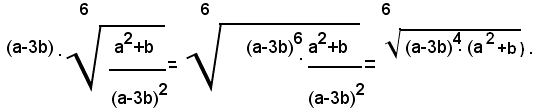
2)-Semplificare l'espressione: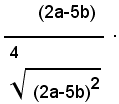
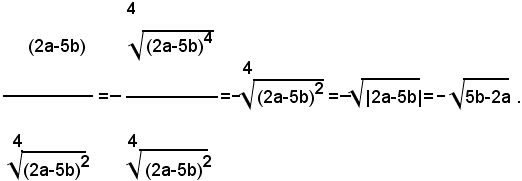
2° - per 2a>5b, cioè per 2a-5b>0, si ha: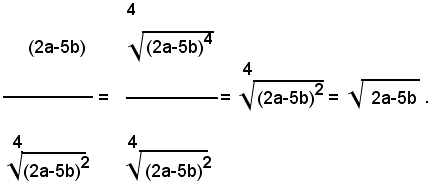
3)-Portare sotto il segno di radice il fattore esterno nel prodotto seguente:
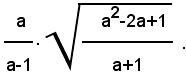
1° - per 0<a<1, si ha:
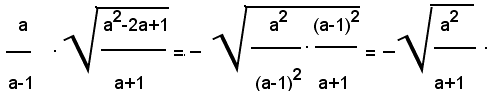
2° - per a>1, si ha:
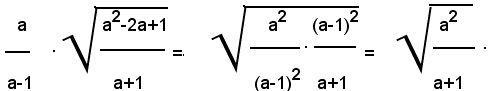
4)-Portare sotto il segno di radice il fattore esterno nel prodotto seguente:
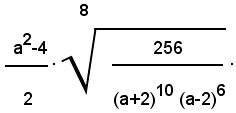
1° - per 0≤a<2, si ha:
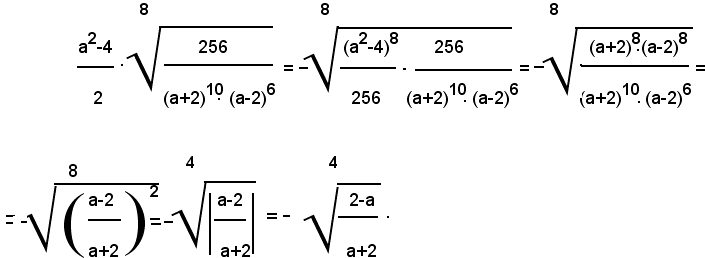
2° - per a>2, si ha:
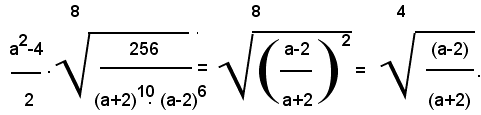
5)-Portare sotto il segno di radice il fattore esterno nel prodotto seguente:
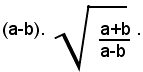
Siccome il radicando deve essere positivo, è a-b>0; pertanto si ha:
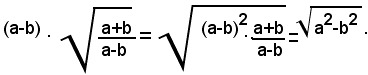
Trasporto di un fattore fuori dal segno di radice
Dal teorema "Il valore di un radicale aritmetico non si altera, se il suo indice e l'esponente del suo radicando vengono moltiplicati per uno stesso numero intero positivo", segue facilmente che la radice ennesima aritmetica di una potenza a base positiva, con esponente multiplo dell'indice n, è uguale ad una potenza avente la stessa base, il cui esponente è uguale al quoziente fra l'esponente della potenza assegnata e l'indice del radicale.
Esempi:
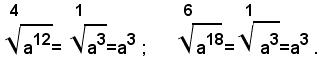
Da tale osservazione e dall'inverso del teorema 1), si può facilmente vedere che se il radicando di un radicale, avente indice n, contiene come fattore una potenza a base positiva con esponente multiplo di n, questa potenza può essere portata come fattore, fuori dal segno di radice, con esponente uguale all'ennesima parte di quello prima posseduto.
Esempi: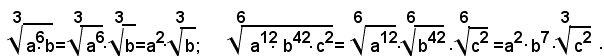
Regola - Una potenza a base positiva, che compare come fattore sotto il segno di radice ennesima con esponente multiplo di n, può essere portata fuori dal segno di radice con esponente uguale all'ennesima parte di quello posseduto.
Quando si compie una tale operazione, si dice che si effettua il trasporto di un fattore fuori dal segno di radice.
Esempio:
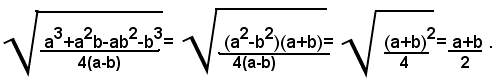
Nota bene
La regola precedente mostra come si può portar fuori dal segno di radice una potenza a base positiva; si vuole vedere ora, con alcuni esempi, come si deve procedere quando non si conosce il segno della base della potenza.
Esempi:
1)-portare fuori dal segno di radice i fattori possibili, nel seguente radicale:
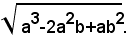
Si ha:
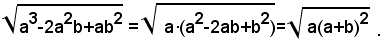
Se si vuole portare fuori dal segno di radice la potenza (a+b)2, affinchè l'uguaglianza sussista anche nel segno, si dovrà scrivere |a-b|, dato che la base della potenza pùo essere sia positiva che negativa; quindi si ha:
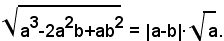
Se si vuole specificare tale uguaglianza, si deve scrivere:
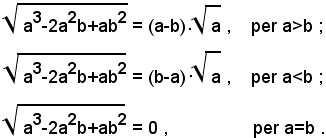
2)-portare fuori dal segno di radice i fattori possibili, nel seguente radicale:
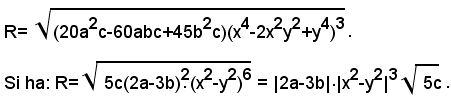
2)-portare fuori dal segno di radice i fattori possibili, nella seguente espressione:
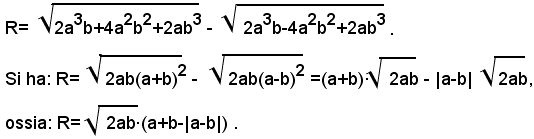
Si distinguono tre casi:
1° - a>b, essendo quindi a-b>0, si ha |a-b|=a-b; pertanto risulta:
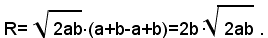
2° - a=b, essendo quindi a-b=0, si ha:
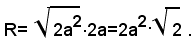
3° - a<b, essendo quindi a-b<0, si ha |a-b|=-(a-b); pertanto risulta:
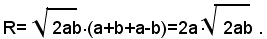
Nota bene
In generale, se m è un numero reale qualsiasi, e si vuole semplificare il radicale:
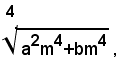
si deve scrivere: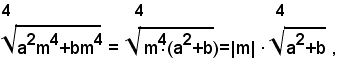
e poi distinguere i tre casi ponendo:
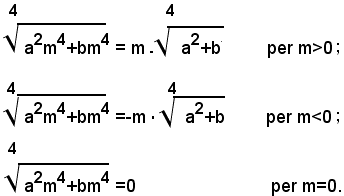
Teorema 3) - La potenza p-esima di un radicale è uguale a un radicale avente lo stesso indice di quello assegnato e per radicando la potenza p-esima dello stesso, cioè: (1)
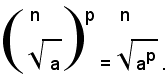
Per p=0 e p=1 il teorema è evidente; supponendo p>1, per definizione di potenza, si ha: (2)
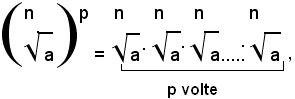
e, per il teorema 1), si ha: (3)
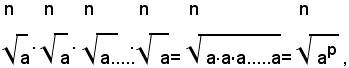
dalla (2) e (3), per la proprietà transitiva dell'uguaglianza, si ha:
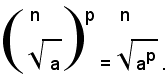
Il teorema è così dimostrato.
Esempi:
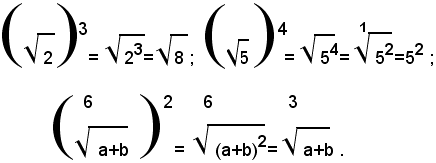
Dalla (1), per la proprietà simmetrica dell'uguaglianza, si ha:
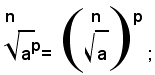
cioè: per estrarre la radice da una potenza a base positiva, è sufficiente estrarre la radice della potenza ed elevare il risultato ottenuto all'esponente della potenza data.
Esempi:
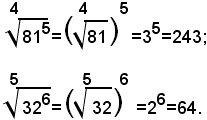
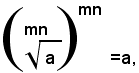
Teorema 4) - La radice m-esima della radice n-esima aritmetica di un numero reale positivo a, è uguale alla radice aritmetica di indice mn del numero a, cioè: (1)
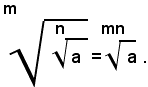
Per dimostrare l'uguaglianza (1), si eleva il primo membro all'esponente mn, ricordando che per elevare un numero alla potenza mn basta elevarlo prima alla potenza m-esima e poi il risultato ottenuto alla potenza n-esima; quindi, si ha: (2)
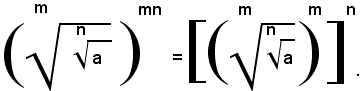
Siccome per definizione di radice n-esima risulta:
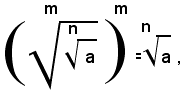
si ha: (3)
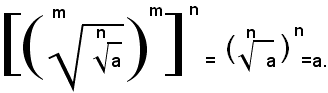
Quindi, dalla (2) e (3), per la proprietà simmetrica dell'uguaglianza, segue:
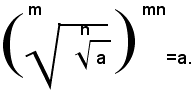
Elevando alla stessa potenza di esponente mn il secondo membro della (1), per definizione di radice, si ha:
Il teorema è così dimostrato.la (1) si può scrivere sotto la forma: (2)
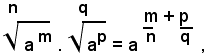
e quindi per (1) e (2), per la proprietà distributiva dell'uguaglianza, segue:
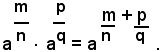
Teorema (1) - Se a è un numero reale maggiore di 1, ogni sua potenza con esponente razionale positivo è maggiore di 1, se invece a è un numero positivo minore di 1, ogni sua potenza con esponente razionale positivo è minore di 1.
Si dimostra la prima parte del teorema nell'ipotesi a>1. Se l'esponente è un numero intero positivo m, evidentemente risulta am>1, perchè am è un prodotto di m fattori tutti maggiori di 1. Se poi m/n è un numero razionale positivo, siccome per definizione:
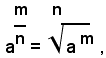
ed essendo am>1, e dato che la radice ennesima aritmetica di un numero maggiore di 1 è anch'essa maggiore di 1, si ha:
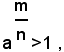
come volevasi dimostrare.
Teorema (2) - Se a è un numero reale maggiore di 1, ogni sua potenza con esponente razionale negativo è minore di 1, se invece a è un numero reale positivo minore di 1, ogni sua potenza con esponente razionale negativo è maggore di 1.
Infatti, supposto a>1 e detto m/n un numero razionale positivo, per definizione si ha:
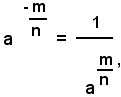
ed essendo, per la prima parte del teorema (1):
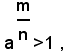
sarà:
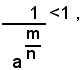
perciò:
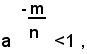
come volevasi dimostrare.
Teorema (3) - Se a è un numero reale maggiore di 1, e r, s due numeri razionali relativi, si ha:
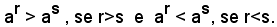
Infatti, si ha:
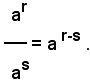
Ora se r>s, l'esponente r-s è positivo e pertanto, per la prima parte del teorema (1) è ar-s >1, e quindi:
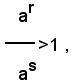
da cui: ar>as.
Se invece r<s, l'esponente r-s è negaivo e pertanto, per la prima parte del teorema (2) è ar-s <1, e quindi:
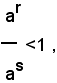
da cui: ar<as.
Teorema (4) - Se a è un numero reale positivo minore di 1, e r, s due numeri razionali relativi, si ha:
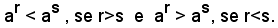
La dimostrazione è analoga a quella del teorema precedente.
Le proprietà espresse dagli ultimi due teoremi possono enunciarsi nel modo seguente:
il valore della potenza di un numero reale maggiore di 1 cresce al crescere dell'esponente, mentre il valore della potenza di un numero reale positivo minore di uno diminuisce al crescere dell'esponente.
Radicali algebrici
Finora si è trattato il problema dell'estrazione della radice ennesima di soli numeri reali positivi, cioè dato un numero reale positivo a, si è cercata l'esistenza di un numero reale positivo b, tale che fosse bn=a e si è visto che di tali numeri ne esiste uno ed uno solo. Si vuole ora considerare l'analogo problema nel campo dei numeri reali relativi, cioè, dato un numero reale relativo a e un numero intero positivo n, si vogliono ricercare tutti quei numeri reali relativi, se esistono, che soddisfano l'equazione: (1)
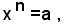
ossia che, elevati all'ennesima potenza, diventano uguali al numero a.I numeri reali relativi che soddisfano questa equazione, se esistono, si chiamano radici ennesime algebriche del numero a.
Per vedere se l'equazione (1) ammette o no soluzioni, si distinguono 4 casi:
1° Caso: a>0, n pari.
In questo caso è stato dimostrato che esiste un numero reale positivo che soddisfa l'equazione (1), cioè che elevato all'ennesima potenza, risulta uguale ad a; questo numero è stato indicato con:
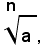
e chiamato radice ennesima di a.
In tal caso, anche l'opposto di tale numero, cioè:
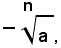
soddisfa l'equazione (1).
Infatti, essendo n pari, si ha:
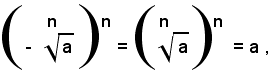
e quindi anche il numero negativo:
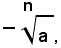
è una radice ennesima di a. Inoltre è chiari che, oltre a:
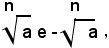
l'equazione (1) non ammette altre soluzioni, perchè ogni altro numero reale diverso da questi due, ha una potenza ennesima diversa dal numero a.
2° Caso: a>0, n dispari. In questo caso solo il numero:
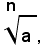
soddisfa l'equazione (1), infatti, essendo n dispari, si ha:
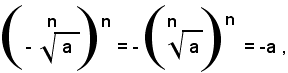
e quindi il numero negativo:
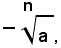
non soddisfa la (1), cioè non è una radice di a.
3° Caso: a<0, n pari.
In questo caso l'equazione (2) non ammette soluzioni, cioè non esiste nessun numero reale relativo che elevato a n, risulti uguale ad a. Basta ricordare che la potenza di esponente pari di un numero reale qualsiasi, diverso da zero, è un numero positivo.
4° Caso: a<0, n dispari. In questo caso il numero:
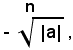
soddisfa l'equazione (1). Infatti, per n dispari risulta:

D'altra parte nessun altro numero diverso da:
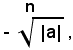
può soddisfare l'equazione.
Riassumendo, si ha:
per n pari, ogni numero reale positivo ammette due radici ennesime algebriche fra loro opposte; mentre ogni numero reale negativo non ne ammette alcuna.per
n dispari, ogni numero reale positivo ammette una radice ennesima
algebrica e una sola, la quale è positiva o negativa a seconda che tale sia il numero considerato. Perciò, estendendo il segno di radice, cioè indicando con:
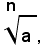
tutti i numeri reali relativi la cui potenza ennesima sia uguale ad a, si può dire che:
il simbolo:
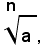
per n dispari, rappresenta un unico numero reale relativo che ha lo stesso segno di a; mentre quando n è pari, esso rappresenta due numeri reali opposti se a è positivo, e non rappresenta alcun numero reale se a è negativo. In tal senso si può scrivere:
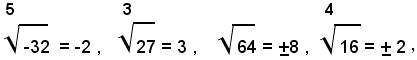
mentre i simboli:
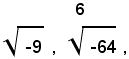
non rappresentano alcun numero.
Nota bene
In seguito, quando si considereranno radicali di indice pari, sarà preso solo il valore positivo.
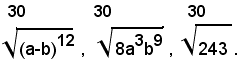
2)-ridurre allo stesso indice i radicali:
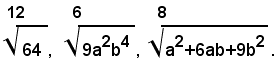
I radicali si possono scrivere sotto la forma:
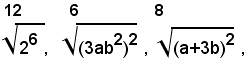
e quindi, in forma irriducibile:
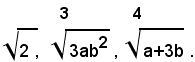
Il m. c. m. degl'indici è 12, quindi i radicali uguali a quelli assegnati sono:
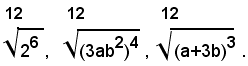
Ossia:
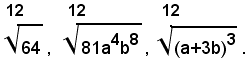
3)-ridurre allo stesso indice i radicali:
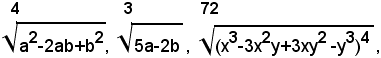
i radicali si possono scrivere sotto la forma:
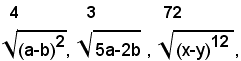
e quindi, in forma irriducibile:
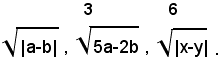
Il m. c. m. degl'indici è 6, quindi i radicali uguali a quelli assegnati sono:
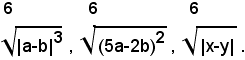
Operazioni con i radicali
Nel calcolo dei radicali, si usano frequentemente alcune regole di trasformazione e semplificazione, che derivano da quattro teoremi fondamentali.
Teorema 1) - Il prodotto di due o più radicali aventi lo stesso indice è uguale ad un radicale avente lo stesso indice di quelli assegnati e per radicando il prodotto dei singoli radicandi.
Si deve quindi dimostrare che, se a, b, c, sono tre numeri reali positivi e n un numero intero positivo, risulta: (1)
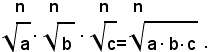
Per dimostrare che vale la (1), tenendo conto dell'inverso di un teorema precedente, è sufficiente dimostrare che elevando ambo i membri all'ennesima potenza, si ottengono risultati uguali.
Infatti, elevando all'ennesima potenza il primo membro della (1) e ricordando che la potenza di un prodotto è uguale al prodotto delle potenze dei singoli fattori, si ha: (2)
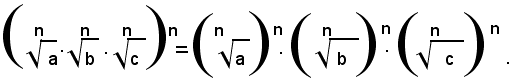
In base poi alla definizione di radice ennesima aritmetica di un numero positivo, si ha: (3)
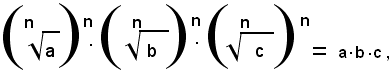
e quindi, dalla (2) e (3), per la proprietà transitiva dell'uguaglianza, segue:
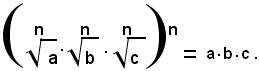
Elevando all'ennesima potenza il secondo membro della 1), per definizione di radice ennesima aritmetica, si ha:
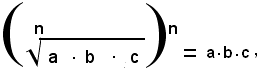
cioè, si ha lo stesso risultato ottenuto elevando alla potenza ennesima il primo membro della 1), quindi il teorema è dimostrato.
Nota bene
Quando si vuole effettuare il prodotto di radicali aventi indici disuguali, si riducono prima allo stesso indice e poi si applica il teorema 1).
Esempi:
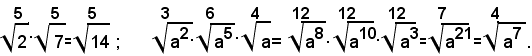
Dalla 1), per la proprietà simmetrica dell'uguaglianza, si ha:
cioè: la radice ennesima aritmetica di un prodotto di fattori positivi è uguale al prodotto delle radici ennesime dei singoli fattori.
Esempi:
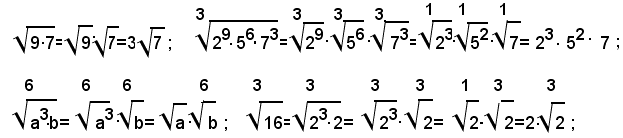
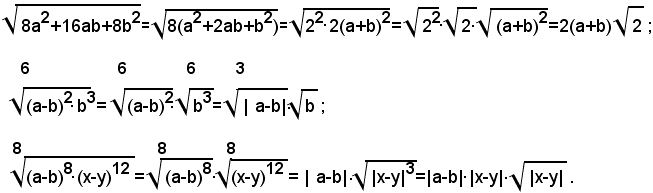
Teorema 2) - Il quoziente di due radicali aventi lo stesso indice, dei quali il secondo abbia il radicando diverso da zero, è uguale ad un radicale avente lo stesso indice di quelli assegnati e per radicando il quoziente dei singoli radicandi, cioè: 1)
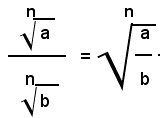
Infatti, elevando all'ennesima potenza il primo membro della (1) e ricordando che la potenza di un quoziente è uguale al quoziente delle potenze del dividendo e del divisore, si ha: (2)
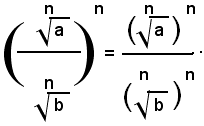
Inoltre, per definizione di radice ennesima aritmetica, si ha: (3)
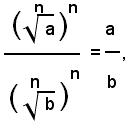
e quindi, dalla (2) e (3), per la proprietà transitiva dell'uguaglianza, segue:
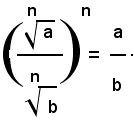
Elevando all'ennesima potenza il secondo membro della 1), per definizione di radice ennesima aritmetica, si ha:
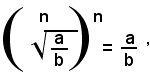
cioè si ha lo stesso risultato ottenuto elevando all'ennesima potenza il primo membro della 1), quindi il teorema è dimostrato.
Nota bene
Quando si vuole effettuare il quoziente di radicali aventi indici disuguali, si riducono prima allo stesso indice e poi si applica il teorema 2).
Esempi:
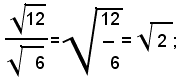
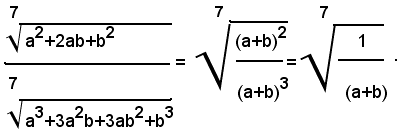
Dalla 1), per la proprietà simmetrica dell'uguaglianza, si ha:
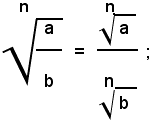
cioè: la radice ennesima aritmetica di un quoziente a termini positivi è uguale al quoziente delle radici ennesime aritmetiche del dividendo e del divisore.
Esempio:
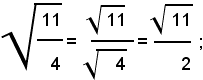
Trasporto di un fattore sotto il segno di radice
Si considera ora un caso particolare di moltiplicazione, quello in cui uno dei due fattori del prodotto è un radicale e l'altro no. Si abbia, ad esempio:
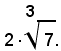
Siccome si può scrivere:
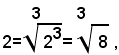
applicando il teorema 1), si ha:
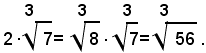
In generale, se a e b, sono due numeri reali positivi, si può dire:
Si può quindi enunciare la seguente regola:
quando si moltiplica un radicale per un numero positivo, tale fattore si può trasportare sotto il segno di radice, come fattore del radicando, purchè lo si elevi a una potenza uguale all'indice del radicale.
Tale operazione si chiama: trasporto di un fattore sotto il segno di radice.
Analoghe considerazioni si possono fare nel caso di una divisione in cui dei due termini uno solo ha la forma di un radicale. Evidentemente, dati due numeri a, b, reali positivi, si ha:
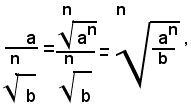
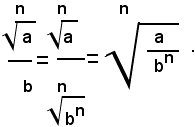
Esempio:
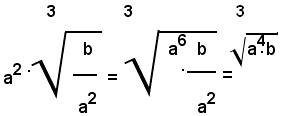
Nota bene
La regola enunciata in precedenza trattava del trasporto di un numero reale positivo sotto il segno di radice; si vuol vedere ora, con alcuni esempi, come si deve procedere nel caso in cui il fattore che si vuole trasportare sotto il segno di radice sia positivo, o senza alcun segno.
Evidentemente, questo prodotto è negativo, essendo negativo il fattore -5 e positivo
Pertanto, eseguendo il prodotto, si ha:
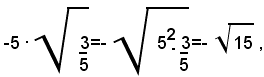
e quindi in tale uguaglianza sussiste anche il segno; dunque:
quando il fattore con cui si moltiplica il radicale è negativo, si deve portare sotto il segno di radice il suo valore assoluto, lasciando sotto il segno di radice il segno meno.
Esempi:
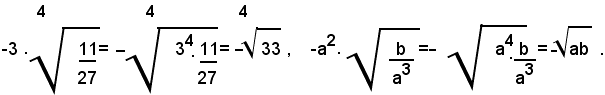
Si vede ora come si deve procedere nel caso in cui non è noto il segno del fattore che moltiplica il radicale.
1)-Portare sotto il segno di radice il fattore esterno nel prodotto seguente:
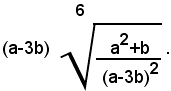
Il prodotto dato rappresenta un numero negativo, se a<3b, positivo se a>3b; si devono distinguere quindi i due casi:
1° - per a<3b, cioè per a-3b<0, si ha:
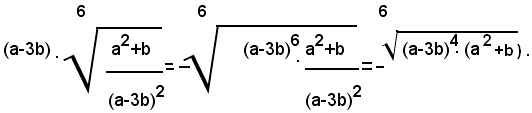
2° - per a<3b, cioè per a-3b>0, si ha:
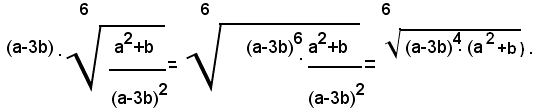
2)-Semplificare l'espressione:
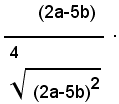
1° - per 2a<5b, cioè per 2a-5b<0, si ha:
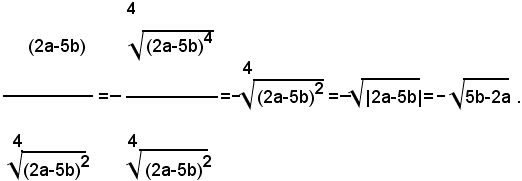
2° - per 2a>5b, cioè per 2a-5b>0, si ha:
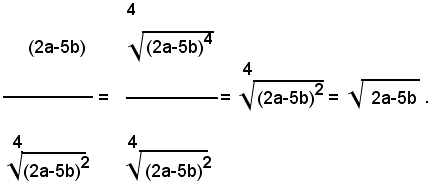
3)-Portare sotto il segno di radice il fattore esterno nel prodotto seguente:
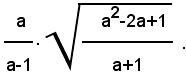
1° - per 0<a<1, si ha:
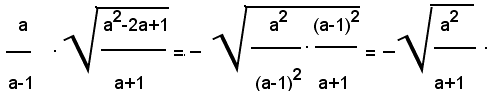
2° - per a>1, si ha:
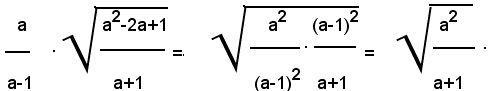
4)-Portare sotto il segno di radice il fattore esterno nel prodotto seguente:

1° - per 0≤a<2, si ha:

2° - per a>2, si ha:
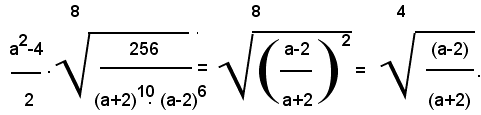
5)-Portare sotto il segno di radice il fattore esterno nel prodotto seguente:
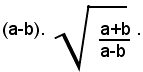
Siccome il radicando deve essere positivo, è a-b>0; pertanto si ha:
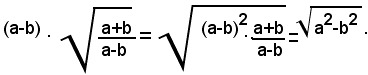
Trasporto di un fattore fuori dal segno di radice
Dal teorema "Il valore di un radicale aritmetico non si altera, se il suo indice e l'esponente del suo radicando vengono moltiplicati per uno stesso numero intero positivo", segue facilmente che la radice ennesima aritmetica di una potenza a base positiva, con esponente multiplo dell'indice n, è uguale ad una potenza avente la stessa base, il cui esponente è uguale al quoziente fra l'esponente della potenza assegnata e l'indice del radicale.
Esempi:
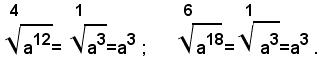
Da tale osservazione e dall'inverso del teorema 1), si può facilmente vedere che se il radicando di un radicale, avente indice n, contiene come fattore una potenza a base positiva con esponente multiplo di n, questa potenza può essere portata come fattore, fuori dal segno di radice, con esponente uguale all'ennesima parte di quello prima posseduto.
Esempi:
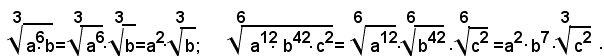
Regola - Una potenza a base positiva, che compare come fattore sotto il segno di radice ennesima con esponente multiplo di n, può essere portata fuori dal segno di radice con esponente uguale all'ennesima parte di quello posseduto.
Quando si compie una tale operazione, si dice che si effettua il trasporto di un fattore fuori dal segno di radice.
Esempio:
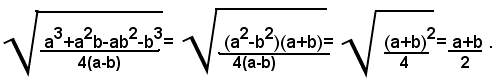
Nota bene
La regola precedente mostra come si può portar fuori dal segno di radice una potenza a base positiva; si vuole vedere ora, con alcuni esempi, come si deve procedere quando non si conosce il segno della base della potenza.
Esempi:
1)-portare fuori dal segno di radice i fattori possibili, nel seguente radicale:
Si ha:
Se si vuole portare fuori dal segno di radice la potenza (a+b)2, affinchè l'uguaglianza sussista anche nel segno, si dovrà scrivere |a-b|, dato che la base della potenza pùo essere sia positiva che negativa; quindi si ha:
Se si vuole specificare tale uguaglianza, si deve scrivere:
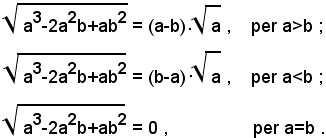
2)-portare fuori dal segno di radice i fattori possibili, nel seguente radicale:
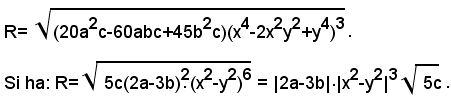
2)-portare fuori dal segno di radice i fattori possibili, nella seguente espressione:
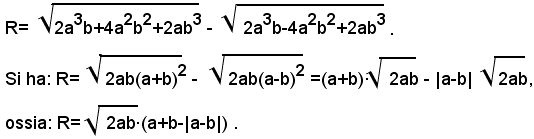
Si distinguono tre casi:
1° - a>b, essendo quindi a-b>0, si ha |a-b|=a-b; pertanto risulta:
2° - a=b, essendo quindi a-b=0, si ha:
3° - a<b, essendo quindi a-b<0, si ha |a-b|=-(a-b); pertanto risulta:
Nota bene
In generale, se m è un numero reale qualsiasi, e si vuole semplificare il radicale:
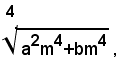
si deve scrivere:
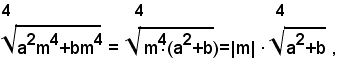
e poi distinguere i tre casi ponendo:
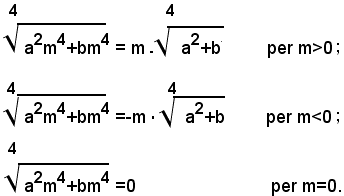
Teorema 3) - La potenza p-esima di un radicale è uguale a un radicale avente lo stesso indice di quello assegnato e per radicando la potenza p-esima dello stesso, cioè: (1)
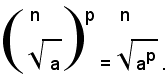
Per p=0 e p=1 il teorema è evidente; supponendo p>1, per definizione di potenza, si ha: (2)
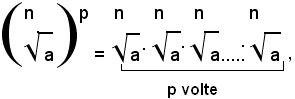
e, per il teorema 1), si ha: (3)
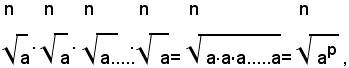
dalla (2) e (3), per la proprietà transitiva dell'uguaglianza, si ha:
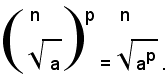
Il teorema è così dimostrato.
Esempi:
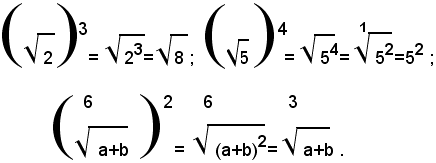
Dalla (1), per la proprietà simmetrica dell'uguaglianza, si ha:
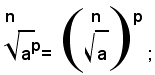
cioè: per estrarre la radice da una potenza a base positiva, è sufficiente estrarre la radice della potenza ed elevare il risultato ottenuto all'esponente della potenza data.
Esempi:
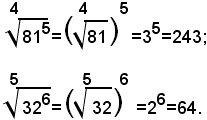
Teorema 4) - La radice m-esima della radice n-esima aritmetica di un numero reale positivo a, è uguale alla radice aritmetica di indice mn del numero a, cioè: (1)
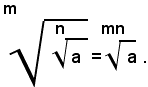
Per dimostrare l'uguaglianza (1), si eleva il primo membro all'esponente mn, ricordando che per elevare un numero alla potenza mn basta elevarlo prima alla potenza m-esima e poi il risultato ottenuto alla potenza n-esima; quindi, si ha: (2)
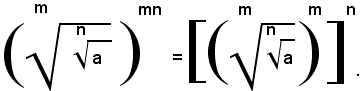
Siccome per definizione di radice n-esima risulta:
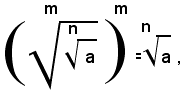
si ha: (3)
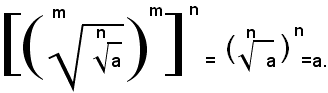
Quindi, dalla (2) e (3), per la proprietà simmetrica dell'uguaglianza, segue:
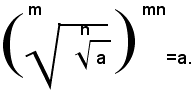
Elevando alla stessa potenza di esponente mn il secondo membro della (1), per definizione di radice, si ha:

Il teorema è così dimostrato.
Il
teorema si estende facilmente nel caso in cui si debbano eseguire su
uno stesso numero, tre o più estrazioni di radice:
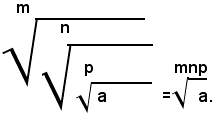
Esempio:
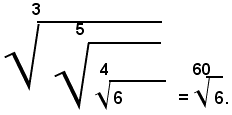
Dala (1), per la proprietà simmetrica dell'uguaglianza, si ha:
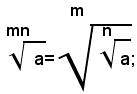
cioè: estrarre da un numero reale positivo la radice aritmetica di indice mn, equivale ad estrarre la radice m-esima dalla radice n-esima del numero considerato.
Si vede quindi che quando l'indice di un radicale è un numero non primo, invece di una radice si possono estrarre due o più radici successive:
Esempio:
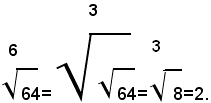
Nota bene
1)-Evidentemente, due estrazioni successive di radici da eseguire sullo stesso numero reale positivo, sono due operazioni commutabili, cioè:
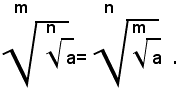
Esempio:
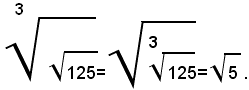
2)-I teoremi 1) e 2) permettono di esprimere il prodotto e il quoziente di radicali a mezzo di un solo radicale, però non esistono teoremi analoghi per l'addizione e la sottrazione di radicali, o di numeri e di radicali. In altri termini: la somma algebrica di due o più radicali non si può esprimere con un solo radicale.
Ad esempio, per indicare la somma di due radicali, si dovrà semplicemente scrivere:
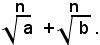
E' bene ricordare che:

Si potrebbe dimostrare che per a>0, b>0, risulta sempre:
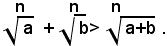
Dunque, della somma e differenza di due radicali, non è possibile, salvo in casi particolari, avere un'espressione più semplice di quella che si ha scrivendo:
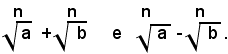
Definizione - Due o più radicali irriducibili si dicono simili, quando hanno lo stesso indice, lo stesso radicando e differiscono eventualmente solo per il fattore che si moltiplica, il quale si chiama coefficiente del radicale.
Esempio di radicali simili:
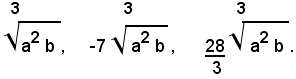
In questo caso le addizioni e sottrazioni di radicali simili si possono eseguire con le stesse regole con cui si esegue la riduzione dei monomi simili in un polinomio, cioè:
la somma algebrica di due o più radicali simili è un radicale, simile a quelli assegnati, avente per coefficiente la somma algebrica dei coefficienti.
Esempio:
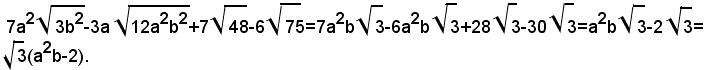
Nota bene
Non sono sostituibili, con due o più radicali, quei radicali in cui il radicando è una somma algebrica.

cioè: quando in un radicale il radicando è una somma, non si può portare fuori dalla radice un addendo.
Quando si vuol semplificare un radicale, il cui radicando sia una potenza, si deve prima cercare di trasformare il radicando in un prodotto e poi portare fuori dalla radice quei fattori, se ve ne sono, che sono potenze con esponente multiplo dell'indice della radice,
Esempio: semplificare la seguente espressione:
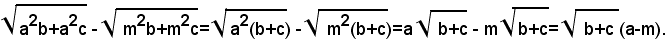
Razionalizzazione del denominatore di una frazione
Quando nel denominatore di una frazione compaiono dei radicali, conviene sempre trasformare la frazione in un'altra equivalente nella quale il denominatore non contenga più radicali, moltiplicando numeratore e denominatore per uno stesso numero, distinguendo 7 casi.
1° Caso: si consideri una frazione il cui denominatore sia un radicale quadratico irriducibile:
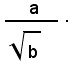
Per liberare il denominatore dal radicale quadratico, basta moltiplicare numeratore e denominatore della frazione per
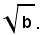
Infatti, si ha:
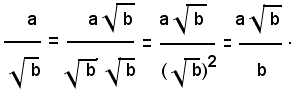
Esempio: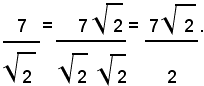
2° Caso: si consideri una frazione il cui denominatore sia una un radicale irriducibile di indice n:
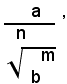
con m<n.
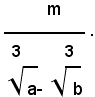
Infatti, ricordando che: a3-b3=(a-b)(a+-ab+b2), basta moltiplicare numeratore e denominatore della frazione data per:
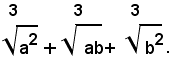
Esempio:
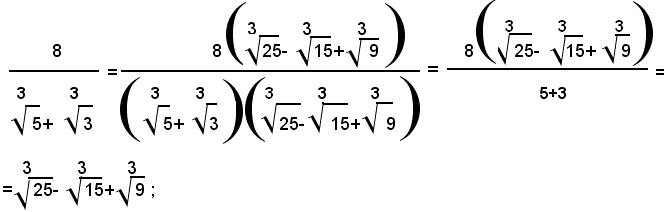
Radicali doppi
Definizione - si chiama radicale quadratico doppio ogni espressione della forma:
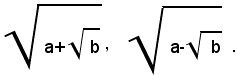
Teorema - Se i numeri a, b, , a2-b sono positivi, valgono le seguenti identità:
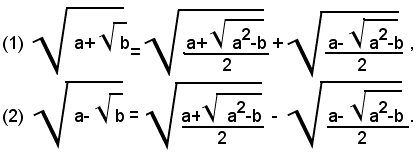
Si osserva prima che, per le ipotesi fatte sui numeri a, b, a2-b, tutti i radicandi dei radicali che compaiono nella formula (1), sono positivi, e tale è anche il secondo membro. Ciò premesso, si elevano al quadrato ambo i membri della (1) e si ottiene:
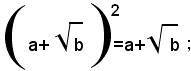
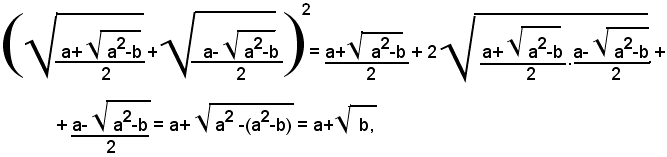
avendo ottenuto risultati uguali, resta dimostrato che vale la (1): analogamente si dimostra la (2).
Nota bene
Quando il numero a2-b è un quadrato perfetto, la (1) e (2) permettono di trasformare un radicale doppio nella somma o differenza di due radicali quadratici semplici.
Esempio:
1)-trasformare il seguente radicale doppio nella somma di due radicali semplici:
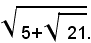
In tal caso: a=5, b=21, a2-b=4 e, applicando la formula (1), si ha:
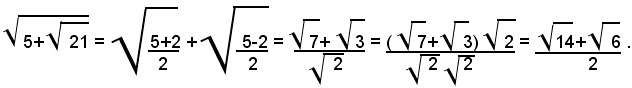
Potenze con esponente frattoLa potenza
di un numero reale a qualsiasi è stata finora definita, nel caso
dell'esponente intero e positivo con a≠0, anche nel caso
dell'esponente nullo e intero negativo. Ora si vuole far vedere come le
proprietà stabilite per i radicali conducano a estendere il
concetto di potenza di un numero reale nel caso dell'esponente
frazionario. A tale scopo, si deve imporre una restrizione e
precisamente i numeri che si impiegherenno come base si dovranno sempre supporre positivi.
Per ottenere tale estensione, è bene osservare che per un teorema precedente, si può, ad esempio, scrivere:

Analogamente si può scrivere:
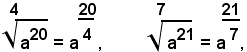
e ciò perchè 20/4=5, 21/7=3, e le potenze con esponente intero sono state già definite.Questa
riduzione del radicale a una potenza non è più possibile
quando l'esponente del radicando non è divisibile esattamente
per l'indice della radice, come ad esempio, nel caso di:
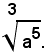
Se si vuole anche in tal caso esprimere il radicale mediante una potenza, in modo analogo ai casi precedenti, si dovrà porre, per definizione:
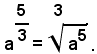
Definizione - Si chiama potenza con esponente frazionario positivo m/n di un numero reale non negativo a, quel radicale che ha come indice il denominatore n della frazione esponente e come radicando il numero a elevato alla potenza di esponente uguale al numeratore m della frazione, cioè:
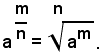
Si definiscono ora le potenze con esponente frazionario negativo di un numero reale positivo a, ponendo, se m/n è maggiore di zero:
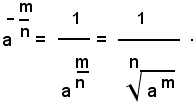
Non si definiscono le potenze di base zero con esponente razionale negativo.
In base alle definizioni date, ogni potenza a base positiva e esponente frazionario equivale a un radicale e viceversa.
Esempi:
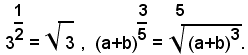
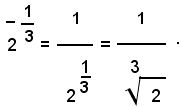
Nota bene
Dalla definizione data di potenza con esponente fratto, si vede non solo perchè la base debba essere sempre positiva, o nulla se l'esponente è positivo, ma anche che ogni potenza a esponente razionale relativo risulta sempre positiva, e ciò perchè è positiva la radice ennesima aritmetica di un numero positivo.
L'importanza della definizione data di potenza con esponente frazionario è dovuta al fatto che, anche per queste potenze valgono tutti i teoremi dimostrati per le potenze con esponente intero, positivo o negativo. Precisamete, limitandosi al caso di esponenti frazionari positivi, valgono le relazioni:
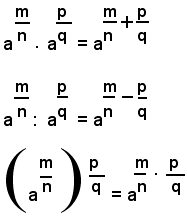
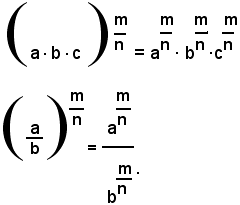
Delle uguaglianze suddette si dimostra soltanto la prima, perchè in modo analogo si dimostrano le altre quattro. A tal fine, si osserva prima che, per definizione di potenza con esponente frazionario, positivo, si ha:
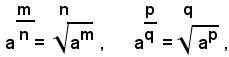
e quindi risulta:
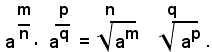
Riducendo allo stesso indice i radicali del secondo membro quest'ultima uguaglianza e riducendo poi allo stesso indice, si ha: (1)
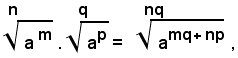
Siccome per l'inversa di definizione di potenza con esponente frazionario risulta:
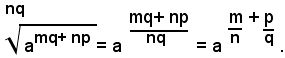
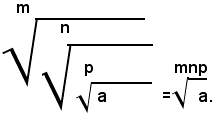
Esempio:
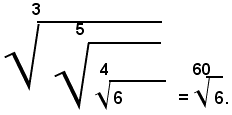
Dala (1), per la proprietà simmetrica dell'uguaglianza, si ha:
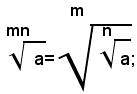
cioè: estrarre da un numero reale positivo la radice aritmetica di indice mn, equivale ad estrarre la radice m-esima dalla radice n-esima del numero considerato.
Si vede quindi che quando l'indice di un radicale è un numero non primo, invece di una radice si possono estrarre due o più radici successive:
Esempio:
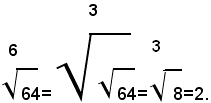
Nota bene
1)-Evidentemente, due estrazioni successive di radici da eseguire sullo stesso numero reale positivo, sono due operazioni commutabili, cioè:
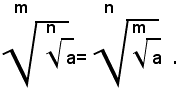
Esempio:
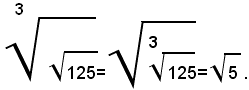
2)-I teoremi 1) e 2) permettono di esprimere il prodotto e il quoziente di radicali a mezzo di un solo radicale, però non esistono teoremi analoghi per l'addizione e la sottrazione di radicali, o di numeri e di radicali. In altri termini: la somma algebrica di due o più radicali non si può esprimere con un solo radicale.
Ad esempio, per indicare la somma di due radicali, si dovrà semplicemente scrivere:
E' bene ricordare che:

Si potrebbe dimostrare che per a>0, b>0, risulta sempre:
Dunque, della somma e differenza di due radicali, non è possibile, salvo in casi particolari, avere un'espressione più semplice di quella che si ha scrivendo:
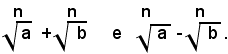
Definizione - Due o più radicali irriducibili si dicono simili, quando hanno lo stesso indice, lo stesso radicando e differiscono eventualmente solo per il fattore che si moltiplica, il quale si chiama coefficiente del radicale.
Esempio di radicali simili:
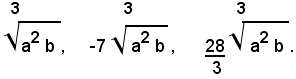
In questo caso le addizioni e sottrazioni di radicali simili si possono eseguire con le stesse regole con cui si esegue la riduzione dei monomi simili in un polinomio, cioè:
la somma algebrica di due o più radicali simili è un radicale, simile a quelli assegnati, avente per coefficiente la somma algebrica dei coefficienti.
Esempio:
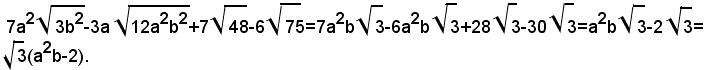
Nota bene
Non sono sostituibili, con due o più radicali, quei radicali in cui il radicando è una somma algebrica.

cioè: quando in un radicale il radicando è una somma, non si può portare fuori dalla radice un addendo.
Quando si vuol semplificare un radicale, il cui radicando sia una potenza, si deve prima cercare di trasformare il radicando in un prodotto e poi portare fuori dalla radice quei fattori, se ve ne sono, che sono potenze con esponente multiplo dell'indice della radice,
Esempio: semplificare la seguente espressione:
Razionalizzazione del denominatore di una frazione
Quando nel denominatore di una frazione compaiono dei radicali, conviene sempre trasformare la frazione in un'altra equivalente nella quale il denominatore non contenga più radicali, moltiplicando numeratore e denominatore per uno stesso numero, distinguendo 7 casi.
1° Caso: si consideri una frazione il cui denominatore sia un radicale quadratico irriducibile:
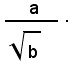
Per liberare il denominatore dal radicale quadratico, basta moltiplicare numeratore e denominatore della frazione per
Infatti, si ha:
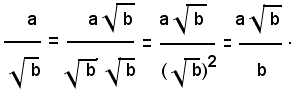
Esempio:
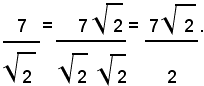
2° Caso: si consideri una frazione il cui denominatore sia una un radicale irriducibile di indice n:
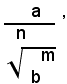
con m<n.
Per liberare il denominatore dal radicale irriducibile, basta moltiplicare numeratore e denominatore della frazione per
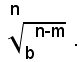
Infatti, si ha:
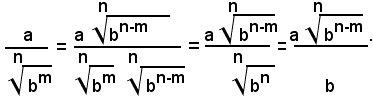
Esempio:
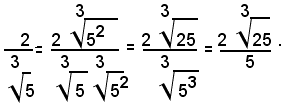
Nota bene
Se m>n, si semplifica prima il radicale e poi si applica il procedimento suddetto.
3° Caso: si consideri una frazione il cui denominatore sia la somma di due radicali quadratici:
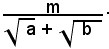
Per liberare il denominatore dalla somma dei due radicali quadratici, basta moltiplicare numeratore e denominatore della frazione per
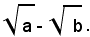
Infatti, si ha:
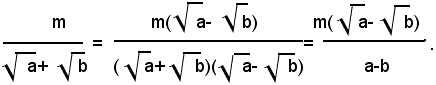
Nota bene
Si è applicato il prodotto notevole (a+b)(a-b)=a2-b2, al prodotto della somma dei due radicali per la relativa differenza.
Esempio:
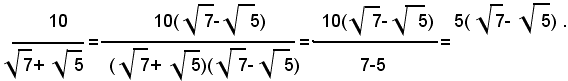
4° Caso: si consideri una frazione il cui denominatore sia la differenza di due radicali quadratici:
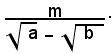
Per liberare il denominatore dalla differenza dei due radicali quadratici, basta moltiplicare numeratore e denominatore della frazione per
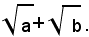
Esempio:
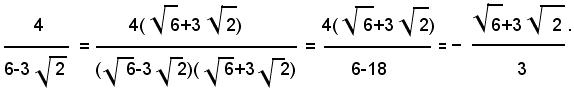
5° Caso: si considerino le seguenti frazioni:
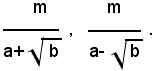
Per liberare i denominatori di queste due frazioni, si moltiplica numeratore e denominatore, rispettivamente della prima e della seconda per:
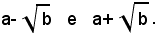
Esempio:
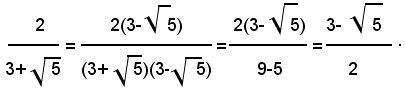
6° Caso: si consideri la frazione il cui denominatore sia la somma di tre radicali quadratici:
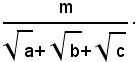
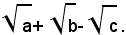
Si ha:
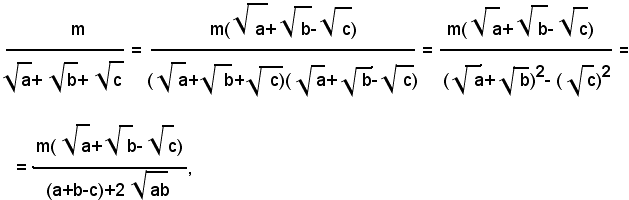
quindi ci si trova nel caso precedente.
In modo analogo si opera quando la frazione ha il denominatore somma di quattro radicali quadratici:
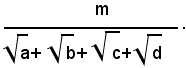
Per liberare il denominatore dalla somma dei quattro radicali quadratici, basta moltiplicare numeratore e denominatore della frazione per:
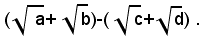
Esempio:
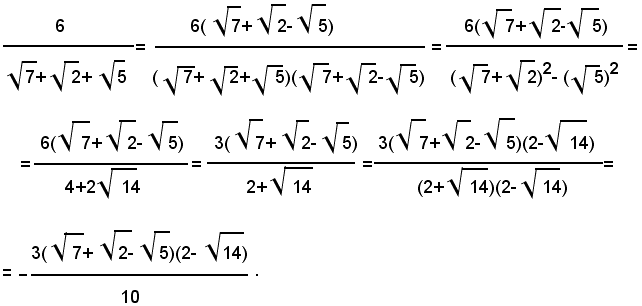
7° Caso: si consideri la frazione il cui denominatore sia la somma di due radicali cubici:
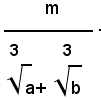
Ricordando che: a3+b3=(a+b)(a2-ab+b2), in tal caso si ha:
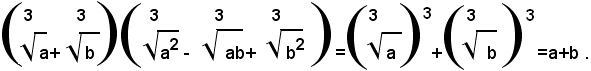
e quindi si razionalizza il denominatore, moltiplicando numeratore e denominatore della frazione data per:
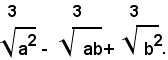
In modo analogo si procede quando si ha la frazione:
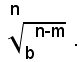
Infatti, si ha:
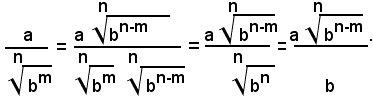
Esempio:
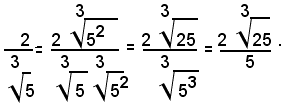
Nota bene
Se m>n, si semplifica prima il radicale e poi si applica il procedimento suddetto.
3° Caso: si consideri una frazione il cui denominatore sia la somma di due radicali quadratici:
Per liberare il denominatore dalla somma dei due radicali quadratici, basta moltiplicare numeratore e denominatore della frazione per
Infatti, si ha:
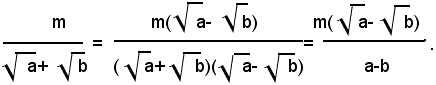
Nota bene
Si è applicato il prodotto notevole (a+b)(a-b)=a2-b2, al prodotto della somma dei due radicali per la relativa differenza.
Esempio:
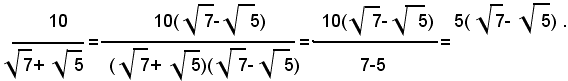
4° Caso: si consideri una frazione il cui denominatore sia la differenza di due radicali quadratici:
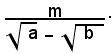
Per liberare il denominatore dalla differenza dei due radicali quadratici, basta moltiplicare numeratore e denominatore della frazione per
Esempio:
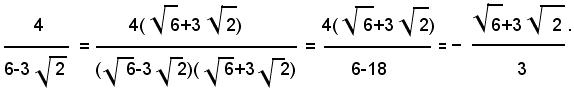
5° Caso: si considerino le seguenti frazioni:
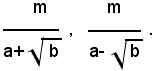
Per liberare i denominatori di queste due frazioni, si moltiplica numeratore e denominatore, rispettivamente della prima e della seconda per:
Esempio:
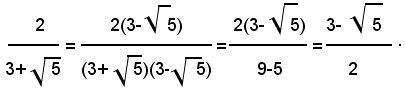
6° Caso: si consideri la frazione il cui denominatore sia la somma di tre radicali quadratici:
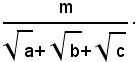
Si ha:
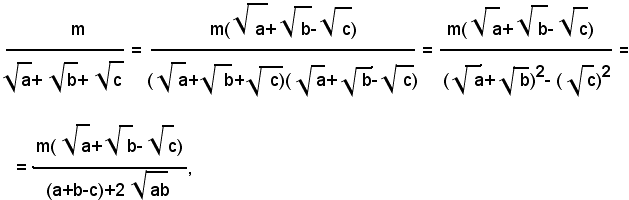
quindi ci si trova nel caso precedente.
In modo analogo si opera quando la frazione ha il denominatore somma di quattro radicali quadratici:
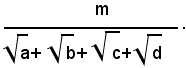
Per liberare il denominatore dalla somma dei quattro radicali quadratici, basta moltiplicare numeratore e denominatore della frazione per:
Esempio:
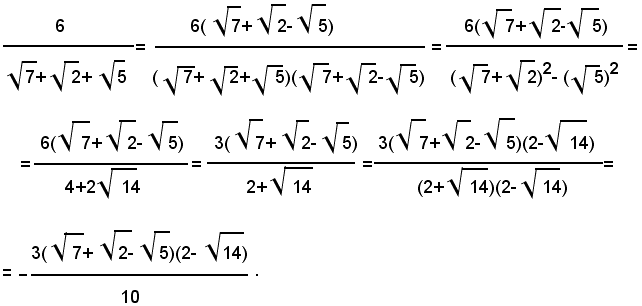
7° Caso: si consideri la frazione il cui denominatore sia la somma di due radicali cubici:
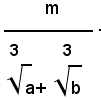
Ricordando che: a3+b3=(a+b)(a2-ab+b2), in tal caso si ha:
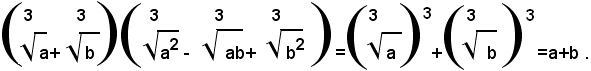
e quindi si razionalizza il denominatore, moltiplicando numeratore e denominatore della frazione data per:
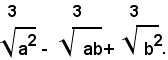
In modo analogo si procede quando si ha la frazione:
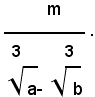
Infatti, ricordando che: a3-b3=(a-b)(a+-ab+b2), basta moltiplicare numeratore e denominatore della frazione data per:
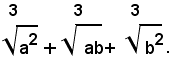
Esempio:
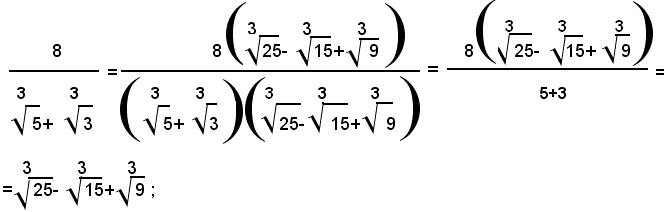
Radicali doppi
Definizione - si chiama radicale quadratico doppio ogni espressione della forma:
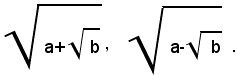
Teorema - Se i numeri a, b, , a2-b sono positivi, valgono le seguenti identità:
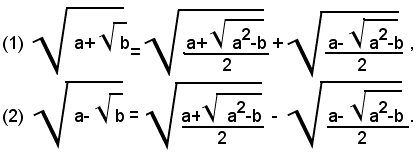
Si osserva prima che, per le ipotesi fatte sui numeri a, b, a2-b, tutti i radicandi dei radicali che compaiono nella formula (1), sono positivi, e tale è anche il secondo membro. Ciò premesso, si elevano al quadrato ambo i membri della (1) e si ottiene:
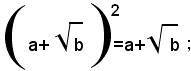
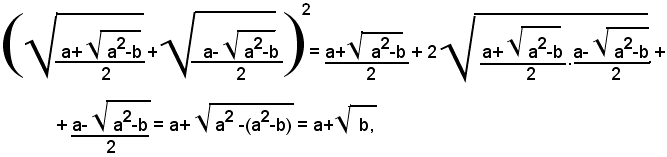
avendo ottenuto risultati uguali, resta dimostrato che vale la (1): analogamente si dimostra la (2).
Nota bene
Quando il numero a2-b è un quadrato perfetto, la (1) e (2) permettono di trasformare un radicale doppio nella somma o differenza di due radicali quadratici semplici.
Esempio:
1)-trasformare il seguente radicale doppio nella somma di due radicali semplici:
In tal caso: a=5, b=21, a2-b=4 e, applicando la formula (1), si ha:
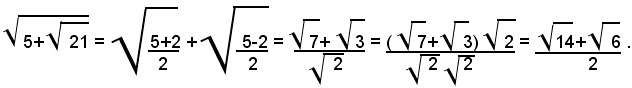
Potenze con esponente fratto
Per ottenere tale estensione, è bene osservare che per un teorema precedente, si può, ad esempio, scrivere:

Analogamente si può scrivere:
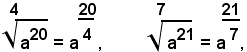
e ciò perchè 20/4=5, 21/7=3, e le potenze con esponente intero sono state già definite.
Se si vuole anche in tal caso esprimere il radicale mediante una potenza, in modo analogo ai casi precedenti, si dovrà porre, per definizione:
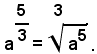
Definizione - Si chiama potenza con esponente frazionario positivo m/n di un numero reale non negativo a, quel radicale che ha come indice il denominatore n della frazione esponente e come radicando il numero a elevato alla potenza di esponente uguale al numeratore m della frazione, cioè:
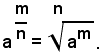
Si definiscono ora le potenze con esponente frazionario negativo di un numero reale positivo a, ponendo, se m/n è maggiore di zero:
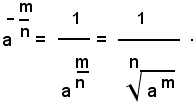
Non si definiscono le potenze di base zero con esponente razionale negativo.
In base alle definizioni date, ogni potenza a base positiva e esponente frazionario equivale a un radicale e viceversa.
Esempi:
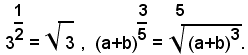
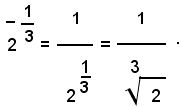
Nota bene
Dalla definizione data di potenza con esponente fratto, si vede non solo perchè la base debba essere sempre positiva, o nulla se l'esponente è positivo, ma anche che ogni potenza a esponente razionale relativo risulta sempre positiva, e ciò perchè è positiva la radice ennesima aritmetica di un numero positivo.
L'importanza della definizione data di potenza con esponente frazionario è dovuta al fatto che, anche per queste potenze valgono tutti i teoremi dimostrati per le potenze con esponente intero, positivo o negativo. Precisamete, limitandosi al caso di esponenti frazionari positivi, valgono le relazioni:
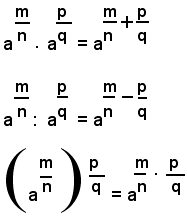
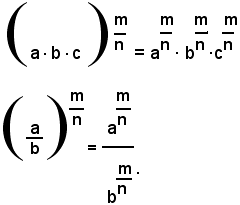
Delle uguaglianze suddette si dimostra soltanto la prima, perchè in modo analogo si dimostrano le altre quattro. A tal fine, si osserva prima che, per definizione di potenza con esponente frazionario, positivo, si ha:
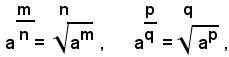
e quindi risulta:
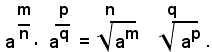
Riducendo allo stesso indice i radicali del secondo membro quest'ultima uguaglianza e riducendo poi allo stesso indice, si ha: (1)
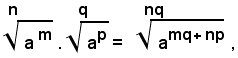
Siccome per l'inversa di definizione di potenza con esponente frazionario risulta:
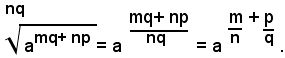
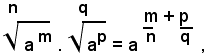
e quindi per (1) e (2), per la proprietà distributiva dell'uguaglianza, segue:
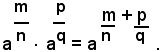
Teorema (1) - Se a è un numero reale maggiore di 1, ogni sua potenza con esponente razionale positivo è maggiore di 1, se invece a è un numero positivo minore di 1, ogni sua potenza con esponente razionale positivo è minore di 1.
Si dimostra la prima parte del teorema nell'ipotesi a>1. Se l'esponente è un numero intero positivo m, evidentemente risulta am>1, perchè am è un prodotto di m fattori tutti maggiori di 1. Se poi m/n è un numero razionale positivo, siccome per definizione:
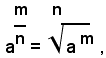
ed essendo am>1, e dato che la radice ennesima aritmetica di un numero maggiore di 1 è anch'essa maggiore di 1, si ha:
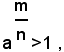
come volevasi dimostrare.
Teorema (2) - Se a è un numero reale maggiore di 1, ogni sua potenza con esponente razionale negativo è minore di 1, se invece a è un numero reale positivo minore di 1, ogni sua potenza con esponente razionale negativo è maggore di 1.
Infatti, supposto a>1 e detto m/n un numero razionale positivo, per definizione si ha:
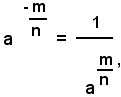
ed essendo, per la prima parte del teorema (1):
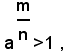
sarà:
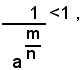
perciò:
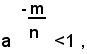
come volevasi dimostrare.
Teorema (3) - Se a è un numero reale maggiore di 1, e r, s due numeri razionali relativi, si ha:
Infatti, si ha:
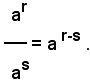
Ora se r>s, l'esponente r-s è positivo e pertanto, per la prima parte del teorema (1) è ar-s >1, e quindi:
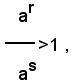
da cui: ar>as.
Se invece r<s, l'esponente r-s è negaivo e pertanto, per la prima parte del teorema (2) è ar-s <1, e quindi:
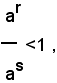
da cui: ar<as.
Teorema (4) - Se a è un numero reale positivo minore di 1, e r, s due numeri razionali relativi, si ha:
La dimostrazione è analoga a quella del teorema precedente.
Le proprietà espresse dagli ultimi due teoremi possono enunciarsi nel modo seguente:
il valore della potenza di un numero reale maggiore di 1 cresce al crescere dell'esponente, mentre il valore della potenza di un numero reale positivo minore di uno diminuisce al crescere dell'esponente.
Radicali algebrici
Finora si è trattato il problema dell'estrazione della radice ennesima di soli numeri reali positivi, cioè dato un numero reale positivo a, si è cercata l'esistenza di un numero reale positivo b, tale che fosse bn=a e si è visto che di tali numeri ne esiste uno ed uno solo. Si vuole ora considerare l'analogo problema nel campo dei numeri reali relativi, cioè, dato un numero reale relativo a e un numero intero positivo n, si vogliono ricercare tutti quei numeri reali relativi, se esistono, che soddisfano l'equazione: (1)
ossia che, elevati all'ennesima potenza, diventano uguali al numero a.
Per vedere se l'equazione (1) ammette o no soluzioni, si distinguono 4 casi:
1° Caso: a>0, n pari.
In questo caso è stato dimostrato che esiste un numero reale positivo che soddisfa l'equazione (1), cioè che elevato all'ennesima potenza, risulta uguale ad a; questo numero è stato indicato con:
e chiamato radice ennesima di a.
In tal caso, anche l'opposto di tale numero, cioè:
soddisfa l'equazione (1).
Infatti, essendo n pari, si ha:
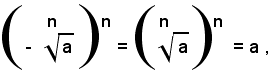
e quindi anche il numero negativo:
è una radice ennesima di a. Inoltre è chiari che, oltre a:
l'equazione (1) non ammette altre soluzioni, perchè ogni altro numero reale diverso da questi due, ha una potenza ennesima diversa dal numero a.
2° Caso: a>0, n dispari. In questo caso solo il numero:
soddisfa l'equazione (1), infatti, essendo n dispari, si ha:
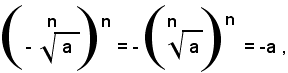
e quindi il numero negativo:
non soddisfa la (1), cioè non è una radice di a.
3° Caso: a<0, n pari.
In questo caso l'equazione (2) non ammette soluzioni, cioè non esiste nessun numero reale relativo che elevato a n, risulti uguale ad a. Basta ricordare che la potenza di esponente pari di un numero reale qualsiasi, diverso da zero, è un numero positivo.
4° Caso: a<0, n dispari. In questo caso il numero:
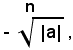
soddisfa l'equazione (1). Infatti, per n dispari risulta:

D'altra parte nessun altro numero diverso da:
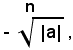
può soddisfare l'equazione.
Riassumendo, si ha:
per n pari, ogni numero reale positivo ammette due radici ennesime algebriche fra loro opposte; mentre ogni numero reale negativo non ne ammette alcuna.
tutti i numeri reali relativi la cui potenza ennesima sia uguale ad a, si può dire che:
il simbolo:
per n dispari, rappresenta un unico numero reale relativo che ha lo stesso segno di a; mentre quando n è pari, esso rappresenta due numeri reali opposti se a è positivo, e non rappresenta alcun numero reale se a è negativo. In tal senso si può scrivere:
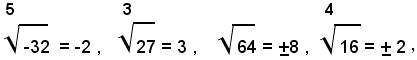
mentre i simboli:
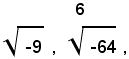
non rappresentano alcun numero.
Nota bene
In seguito, quando si considereranno radicali di indice pari, sarà preso solo il valore positivo.