MIKY & GENNY
SISTEMI DI EQUAZIONI DI GRADO SUPERIORE AL PRIMO ---> INDICE
Sistemi di secondo grado
Quando si trattarono in generale le proprietà dei sistemi di equazioni, si dette la seguente definizione:
-si dice grado di un sistema algebrico in due o più equazioni, con altrettante incognite e ridotto a forma normale, il prodotto dei gradi delle equazioni che lo compongono.
Esempi di grado dei sistemi: il primo sistema è di quarto grado, perchè il prodotto dei gradi delle due equazioni è 2x2=4, il secondo di dodicesimo grado, perchè 3x4=12, il terzo di secondo grado perchè 1x2=2.
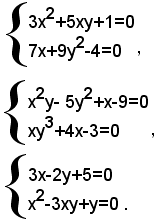
Si trattarono inoltre alcuni metodi per risolvere, nel campo dei numeri razionali, i sistemi di primo grado con due o più equazioni con altrettante incognite, e visto che i sistemi di questo tipo sono impossibili, cioè non ammettono nessuna soluzione, o ammettono una sola soluzione, oppure sono indeterminati, cioè ammettono infinite soluzioni. Tutto quanto è stato detto allora continua, evidentemente a valere anche nel campo più ampio dei numeri reali e quindi si può dire che:
-nel campo dei numeri reali i sistemi di primo grado, aventi tante equazioni quante sono le incognite, o sono impossibili, o indeterminati oppure ammettono una sola soluzione.
Si riprende lo studio dei sistemi, esponendo il modo con cui si risolvono i sistemi algebrici di secondo grado di due o più equazioni con altrettante incognite, incominciando dal più semplice dei sistemi, quello di due equazioni a due incognite. In base alla definizione suddetta, un sistema algebrico di secondo grado, è costituito da un'equazione di secondo grado e da una o più altre equazioni di primo grado, perchè solo in questo caso il prodotto dei gradi delle singole equazioni risulta uguale a due. Perciò, un sistema di secondo grado con due equazioni e con due incognite, ridotto a forma normale, e del tipo: (1)

dove α, β, γ, a, b, c, d, e, f, sono numeri noti o espressioni letterali formate con lettere di cui si suppone noto il valore. I sistemi di questo tipo si possono risolvere tutti applicando il metodo di sostituzione. Infatti, se si risolve l'equazione di primo grado rispetto ad un'incognita, ad esempio la y, si ha: (2)
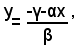
e, sostituendo a y, nell'altra equazione l'espressione:
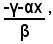
si ha: (3)
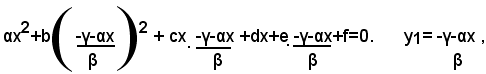
e questa equazione è al massimo di secondo grado, perchè dopo averla ridotta a forma normale, essa può anche ridursi ad un'equazione di primo grado, oppure di grado zero, quando si elidono tutti i termini contenenti l'incognita x, mentre il termine noto è diverso da zero, oppure ad un'identità. Se x1 è una sua soluzione, ammesso che esista, sostituendo nella (2 ) alla x il valore x1, si ottiene per la y il valore:
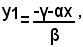
che assieme ad x1 costituisce una soluzione del sistema dato. Perciò, il sistema (1) avrà tante soluzioni quante sono le radici dell'equazione (3). Ricordando che la (3) può non avere nessuna radice, oppure averne due, o essere un'identità, cioè essere soddisfatta per qualsiasi valore attribuito alla x, si conclude che:
-un sistema algebrico di secondo grado di due o più equazioni con altrettante incognite, o è impossibile, o indeterminato, oppure ammette al massimo due soluzioni.
Esempi:
1)-risolvere il sistema:
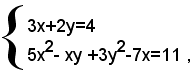
rIsolvendo la prima equazione rispetto a y, si ha: (1)
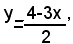
e sostituendo tale valore della y nella seconda equazione, si ha:
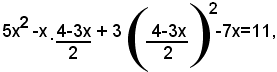
che è un'equazione di secondo grado nell'incognita x. Riducendola a forma normale, si ha:
53x2-108x+4=0,
che ammette due radici reali e distinte x1=2, x2=2/53. Sostituendo nell'equazione (1), al posto della x il valore 2, si ha y1=-1; ponendovi invece il valore 2/53, si ha y2=103/53.Il sistema ammette dunque due soluzioni date da:
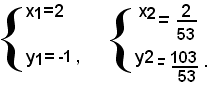
2)-risolvere il sistema:
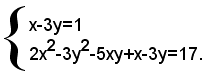
Risolvendo la prima equazione rispetto, a x, si ha: (1)
x=1+3y,
e sostituendo tale valore della x nella seconda equazione, si ottiene:
2(1+3y)2-3y2-5y(1+3y)+(1+3y)-3y=17.
Riducendola a forma normale, risulta:
7y=14,
che è un'equazione di primo grado nell'incognita y, la cui soluzione è y=2.Sostituendo nell'equazione (1), al posto della y il valore 2, si ha x=-7. Quindi il sistema dato ammette solo la soluzione x=-7, y=2.
3)-risolvere il sistema:
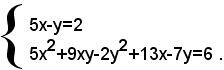
Risolvendo la prima equazione rispetto, a y, si ha: (1)
y=5x-2,
e sostituendo tale valore della y nella seconda equazione, si ha:
5x2+9x(5x-2)-2(5x-2)2+13x-7(5x-2)=6,
ossia, dopo facili calcoli, si perviene all'identità:
6=6.
Il sistema si riduce alla sola equazione (1), che come è noto, ammette infinite soluzioni. In tal caso il sistema è indeterminato.
4)-risolvere il sistema:
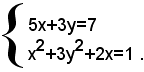
Risolvendo la prima equazione rispetto a y, si ha: (1)
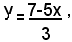
e sostituendo tale valore della y nella seconda equazione, si ottiene:
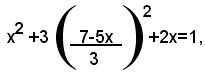
e riducendola a forma normale, risulta:
5)-risolvere il sistema a coefficienti letterali:

Per liberare la prima equazione dal denominatore, si deve supporre a≠-b, pertanto si ha:
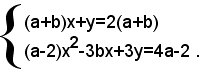
Dalla prima equazione si ricava: (1)
y=2(a+b)-(a+b)x,
e sostituendo tale espressione, al posto della y, nella seconda equazione, si ha:
(a-2)x2-3bx+6(a+b)-3(a+b)x=4a-2,
ossia:
(a-2)x2-(3a+6b)x+2a+6b+2=0.
Se a=2, b≠-1, questa equazione risulta di primo grado, ed ammette come unica soluzione:
x1= 2a+6b+2 = 6a+6b =1;
3a+6b 6a+6b
a questo valore della x, per la (1), corrisponde per y il valore:
y1=2(2+b)-(2+b)=2+b.
Se a=2, b=-1, l'equazione si trasforma in un'identità e perciò il sistema si riduce alla sola equazione (1); in tal caso, il sistema dato è indeterminato.Se a≠2, l'equazione è di secondo grado e si trova dopo facili calcoli che essa ammette le radici
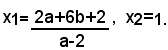
A questi valori della x, per la (1), corrispondono per la y rispettivamente i valori:
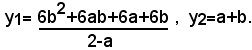
Riassumendo:
se a=-b, il sistema non ammette soluzioni;
se a≠-b, a=2, b≠-1, il sistema ammette una sola soluzione;
se a=2, b=-1, il sistema è indeterminato;
se a≠-b, a≠2, il sistema ammette due soluzioni.
6)-risolvere il sistema fratto:
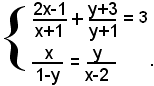
Per liberare la prima equazione dai denominatori, si devono liberare ambo i membri per (x+1)(y+1), e perciò bisogna supporre x≠-1, y≠-1. Per liberare la seconda equazione dai denominatori, si devono liberare ambo i membri per (x+1)(y+1), e perciò bisogna supporre x≠2, y≠1, pertanto, si ottiene il sistema:
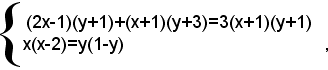
ossia, dopo facili semplificazioni:
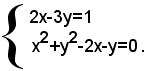
Applicando a questo sistema il metodo di sostituzione, si trova che esso ammette le soluzioni:
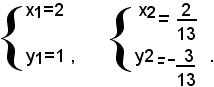
La prima soluzione non soddisfa il sistema dato, perchè per x=2, y=1, si annullano i denominatori della seconda equazione, dunque il sistema dato ammette soltanto la soluzione:
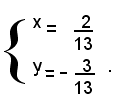
6)-risolvere il sistema: (1)
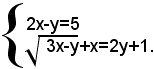
Isolando il radicale ed elevando al quadrato ambo i membri della seconda equazione, dopo facili semplificazioni, si ottiene il sistema di secondo grado seguente: (2)
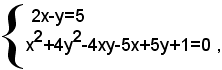
che non si può considerare equivalente al sistema dato, perchè, come è noto, oltre alle soluzioni del sistema dato, esso può averne anche altre. Perciò dopo aver trovato le soluzioni del sistema (2), bisognerà verificare quali di queste sono anche soluzioni del sistema (1). Risolvendo il sistema (2) con il metodo di sostituzione, si trova che esso ammette le seguenti soluzioni:
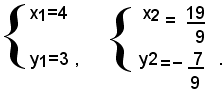
Si verifica facilmente che la seconda non soddisfa il sistema (1), quindi si conclude che il sistema dato ha un'unica soluzione: x=4, y=3.
Il metodo di sostituzione si può anche applicare alla risoluzione dei sistemi di secondo grado composti da più di due equazioni con altrettante incognite. Questi sistemi sono formati da un certo numero di sistemi di primo grado e da una sola equazione di secondo grado.
Esempio: risolvere il sistema
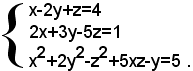
Dalla prima equazione si ricava: (1)
x=4+2y-z
e si sostituisce al posto della x nella seconda e terza equazione, ottenendo così il sistema:
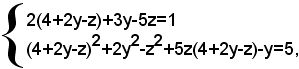
di due equazioni nelle incognite y e z. Riducendo a forma normale, si ha: (2)
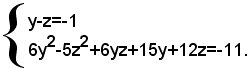
Risolvendo ora la prima equazione di quest'ultimo sistema rispetto alla y, si ha: (3)
y=z-1.
Sostituendo tale valore di y nella seconda equazione del sistema (2), si ottiene la seguente equazione di secondo grado nell'incognita z:
6(z-1)2-5z2+6(z-1)+15(z-1)+12z=-11,
la cui forma normale è:
7z2+9z+2=0
le cui radici sono: (4)
z1=-2/7, z2=-1 ,
Sostituendo di seguito tali valori al posto della z nella (3), si ha: (5)
y1=-9/7, y2=-2.
Sostituendo infine i valori (4) e (5) nella (1), si ha:
x1=12/7, x2=1.
Quindi, il sistema dato ammette le seguenti due soluzioni:
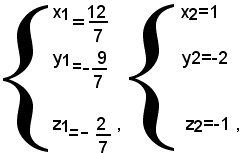
Sistemi particolari di secondo grado
Esistono dei sistemi di secondo grado che per la loro forma particolare si possono risolvere con metodi più veloci del metodo di sostituzione. Prima di esaminarli, si dà la seguente definizione:
un sistema di due equazioni a due incognite x e y si dice simmetrico, quando le equazioni del sistema non si modificano se si scambiano fra loro le due incognite, cioè sostituendo la x con la y e la y con la x.
Esempi:
1)-è simmetrico il sistema:
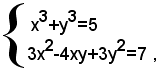
perchè, sostituendo la x con la y, si ottiene il sistema seguente, uguale a quello dato.
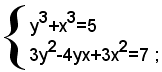
2)-non è simmetrico il sistema:
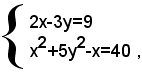
perchè, sostituendo la x con la y, si ottiene il sistema seguente, non uguale a quello dato.
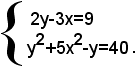
E' evidente che se x=a, y=b è una soluzione del sistema simmetrico, anche x=b e y=a è una soluzione del sistema.
Premesso ciò, si considera il più semplice dei sistemi simmetrici, cioè: (1)
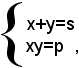
dove s p indicano due numeri noti.
Risolvere il sistema (1) equivale a trovare due numeri x e y tali che la loro somma sia uguale ad s ed il loro prodotto uguale a p. I numeri cercati, quando esistono, come si è visto in precedenza, sono le radici dell'equazione di secondo grado nell'incognita z: (2)
z2-sz+p=0.
Perciò, se z1 e z2 indicano le eventuali incognite dell'equazione (2), le soluzioni del sistema sono:
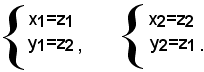
Pertanto la (2) si chiama equazione risolvente del sistema (1).
Esempio: risolvere il sistema
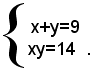
L'equazione risolvente è:
z2-9z+14=0,
le cui radici sono:
L'equazione risolvente è:
Quindi le soluzioni del sistema sono:
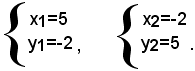
Vi sono sistemi di secondo grado non simmetrici che si possono risolvere senza applicare il metodo di sostituzione, sono i seguenti:
1)-si consideri il sistema:
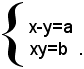
dove a e b sono numeri noti.
Scrivendo le due equazioni sotto la forma:
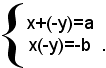
si ottiene un sistema simmetrico nelle due incognite x e -y, la cui equazione risolvente è:
z2-az-b=0,
Se z1=5 e z2 sono le eventuali radici di questa equazione, esse rappresentano i valori di x e -y; quindi le soluzioni del sistema dato sono:
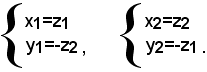
Esempio: risolvere il sistema
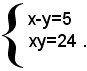
Scrivendo le due equazioni sotto la forma:
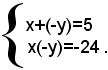
L'equazione risolvente è:
z2-5z-24=0.
Le soluzioni del sistema dato sono:
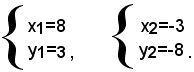
2)-si consideri il sistema:
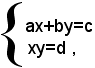
dove a, b, c, d, sono numeri noti.
Scrivendo le due equazioni sotto la forma:
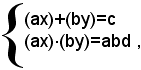
si ottiene un sistema simmetrico rispetto alle incognite ax e by, del tipo già visto; dalla sua risoluzione si ottengono i valori di ax e by, e quindi di x e y.
Esempio: risolvere il sistema
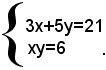
moltiplicando ambo i membri della seconda equazione per 15, si ha:
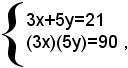
e questo sistema risulta simmetrico rispetto alle incognite 3x e 5y.
L'equazione risolvente è:
z2-21z+90=0,
le cui radici sono:
z1=15 e z2=6.
Perciò, si ha:
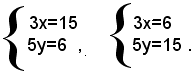
Cioè:
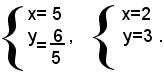
3)-si consideri il sistema:
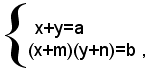
dove a, b, m, n, sono numeri noti.
Aggiungendo ad ambo i membri della prima equazione il numero m+n, si ottiene il sistema equivalente:
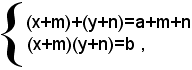
che è simmetrico rispetto alle incognite x+m e y+n, del tipo già visto; dalla sua risoluzione si ottengono i valori di x+m e y+n, e quindi di x e y.
Esempio: risolvere il sistema
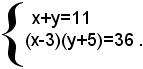
Aggiungendo ad ambo i membri della prima equazione il numero -3+5=2, si ottiene il sistema equivalente:
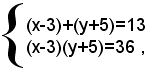
che è simmetrico rispetto alle incognite x-3 e y+5.L'equazione risolvente è:
z2-13z+36=0,
le cui radici sono: z1=9 e z2=4. Perciò, si ha:
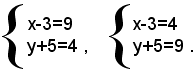
Cioè:
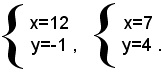
Esempio: risolvere il sistema
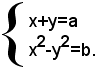
Esso si può scrivere sotto la forma:
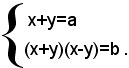
Ponendo nella seconda equazione, al posto di x+y il valore a della prima equazione, si ha:
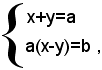
ossia:
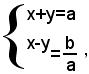
che è un sistema di primo grado.
Analogamente si risolve il sistema:
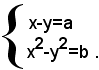
Esempio: risolvere il sistema
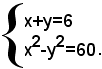
Esso si può scrivere sotto la forma:
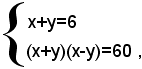
quindi
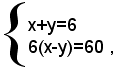
cioè
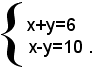
Prima addizionando e poi sottraendo membro a membro le due equazioni, si ha:

che è l'unica soluzione del sistema dato.
Esempio: risolvere il sistema
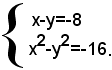
Esso si può scrivere sotto la forma:
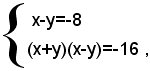
e quindi
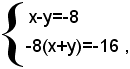
cioè
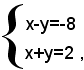
da cui, prima addizionando e poi sottraendo membro a membro le due equazioni, si ha:
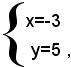
che è l'unica soluzione del sistema dato.
Sistemi particolari di grado superiore al secondo
Si esaminano ora alcuni particolari tipi di sistemi di due equazioni di grado superiore al secondo la cui risoluzione dipende da un'equazione di secondo grado, o da un'equazione di grado superiore, del tipo trattato in precedenza. Si comincia dal seguente sistema simmetrico di terzo grado: (1)
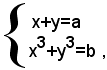
dove a e b sono due numeri noti.
Dall'identità:
(x+y)3=x3+3x2y+3xy2+y3,
si ricava:
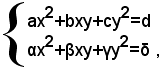
a, b, c, d, α, β, γ, δ, sono numeri assegnati.
Si vede ora come si risolvono i sistemi di questo tipo; si distinguono due casi:
1° caso: si suppone d=0, cioè si abbia il sistema: (2)
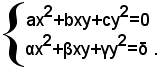
Se a=0, la prima equazione si può scrivere sotto la forma y(bx+cy)=0 e perciò il sistema (2) sarà equivalente all'insieme dei seguenti due sistemi di secondo grado:
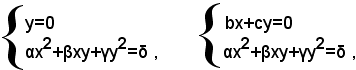
la cui risoluzione è nota.
Se invece è a≠0, δ=0, cioè se si ha il sistema: (3)
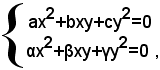
sottraendo membro a membro dalla prima equazione, dopo averla moltiplicata per α, la seconda, dopo averla moltiplicata per a, si ottiene il sistema equivalente al sistema: (3)
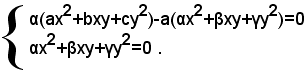
Riducendo la prima equazione a forma normale, si vede che essa non contiene più il termine x2, e perciò il sistema (3) è del tipo discusso in precedentemente.
Si supponga allora a≠0, δ≠0, e si osservi che in questo caso il sistema (2) non può essere soddisfatto da x=0, y=0, perchè è δ≠0; e neanche da x≠0, y=0, perchè a≠0. Essendo allora y≠0, dividendo ambo i membri della prima equazione per y2, si ottiene il sistema equivalente: (4)
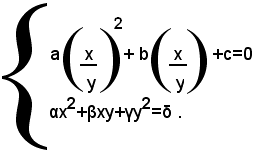
La prima equazione di questo sistema è di secondo grado nell'incognita x/y. Se essa ammette soluzioni, dette queste z1, z2, il sistema (4) si scinde nei seguenti due sistemi di secondo grado:
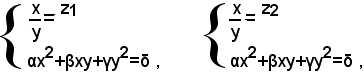
la cui risoluzione con il metodo di sostituzione è nota.
Esempi:
1)-risolvere il seguente sistema omogeneo:
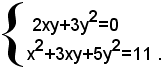
Il sistema si può scrivere sotto la forma:
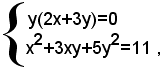
e perciò è equivalente all'insieme dei due sistemi di secondo grado seguenti:
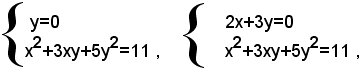
che, risolti con il metodo di sostituzione, permettono di calcolare le soluzioni del sistema dato; si trova
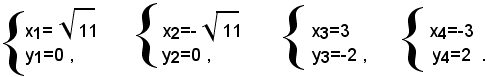
2)-risolvere il sistema:
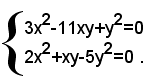
sottraendo dalla prima equazione, moltiplicata per 2, la seconda, moltiplicata per 3, si ottiene il sistema equivalente:
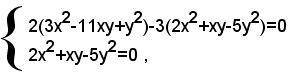
ossia, dopo facili semplificazioni:
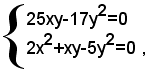
cioè:
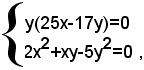
che è equivalente all'insieme dei due sistemi di secondo grado seguenti:
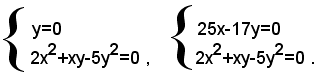
Entrambi i sistemi ammettono soltanto la soluzione x=0, y=0, che è l'unica soluzione del sistema dato.
3)-risolvere il sistema:
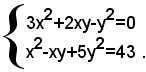
Dividendo ambo i membri della prima equazione per y2, si ottiene l'equazione:
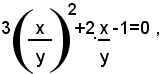
che è di secondo grado nell'incognita x/y. Risolvendola, si trova che ammette le radici:
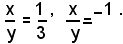
Il sistema (1) si scinde quindi nei due sistemi di secondo grado seguenti:

che, risolti con il metodo di sostituzione, si trovano per il sistema dato le seguenti soluzioni.
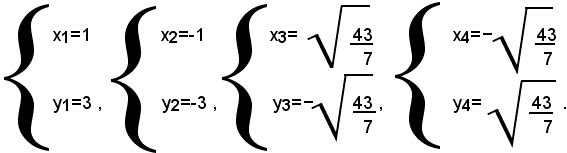
2° Caso: siano d≠0, δ≠0.
Questo caso si può facilmente ricondurre al precedente. Infatti, sottraendo membro a membro, dalla prima equazione del sistema: (1)
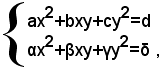
dopo averla moltiplicata per δ, la seconda, dopo averla moltiplicata per d, si ottiene il sistema:
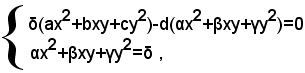
che è del tipo considerato nel caso precedente.
Esempio: risolvere il sistema
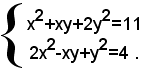
Sottraendo membro a membro, dalla prima equazione, moltiplicata per 4, la seconda, moltiplicata per 11, si ottiene il sistema equivalente:
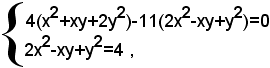
ossia:
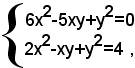
che
è del tipo considerato nel caso precedente e che si sa risolvere
Si trova che esso ammette le seguenti soluzioni:
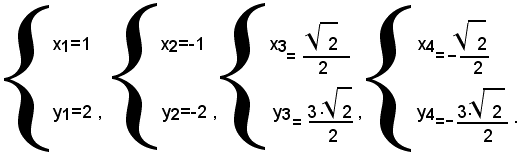
Sistemi risolvibili mediante artifici
In vari casi, nella risoluzione di un sistema di equazioni, è utile ricorrere ad opportuni artifici, che permettono di trasformare un sistema in un altro, o in più altri sistemi, che nel loro complesso sono equivalenti a quello assegnato, e che non si sanno risolvere.
Esempi:
1)-risolvere il seguente sistema di quarto grado:

Sottraendo membro a membro, dalla prima equazione, la seconda, dopo averla moltiplicata per 2, si ottiene il sistema equivalente:
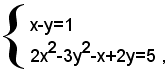
che è di secondo grado e quindi si può risolvere con il metodo di sostituzione. Dopo averlo risolto, si trova che ammette le soluzioni:

2)-risolvere il seguente sistema:
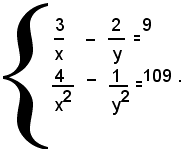
Eliminando i denominatori, si ha il sistema:
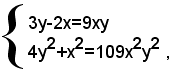
che è di ottavo grado; se invece si pone
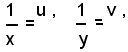
il sistema si trasforma nel sistema di secondo grado seguente
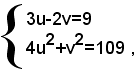
che, risolto con il metodo di sostituzione, dà
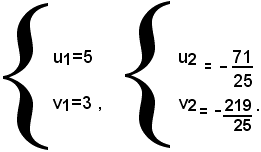
Poichè x e y sono i reciproci di u e v, le soluzioni del sistema proposto sono:

3)-risolvere il seguente sistema simmetrico di quarto grado :
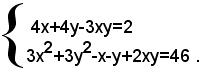
Si scrive il sistema sotto la forma:
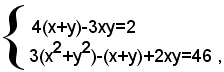
ossia
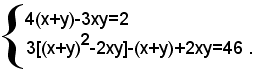
Posto:
x+y=u, xy=v,
il sistema si trasforma nel seguente di secondo grado
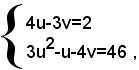
che risolto dà le due soluzioni
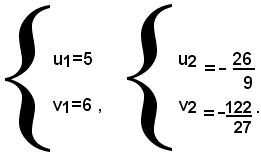
In base al significato attribuito alle lettere u e v, si può dire che il sistema dato è equivalente al complesso dei due sistemi:
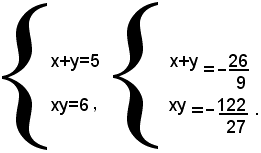
Risolvendo questi due sistemi, si trovano le soluzioni del sistema proposto.
4)-risolvere il sistema:
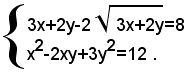
Posto:

la prima equazione del sistema si trasforma nella seguente:
u2-2u-8=0 ,
le cui radici sono: u1=4, .
Per il significato attribuito alla lettera u, essa deve rappresentare un numero positivo e perciò la radice u2=-2, si deve scartare. Pertanto si deve risolvere soltanto il seguente sistema di secondo grado:

le cui soluzioni sono

Nota bene
Dagli esempi si è visto che un sistema di tante equazioni quante sono le incognite e qualunque sia il suo grado può essere impossibile o indeterminato, oppure ammette un numero di soluzioni che non può mai superare il suo grado. Questo risultato è generale, cioè si dimostra il seguente teorema, di cui si dà soltanto l'enunciato:
nel campo dei numeri reali, un sistema algebrico di grado n, di tante equazioni quante sono le incognite, è impossibile, indeterminato, oppure ammette un numero di soluzioni che non può mai superare il grado n del sistema.
Quando si trattarono in generale le proprietà dei sistemi di equazioni, si dette la seguente definizione:
-si dice grado di un sistema algebrico in due o più equazioni, con altrettante incognite e ridotto a forma normale, il prodotto dei gradi delle equazioni che lo compongono.
Esempi di grado dei sistemi: il primo sistema è di quarto grado, perchè il prodotto dei gradi delle due equazioni è 2x2=4, il secondo di dodicesimo grado, perchè 3x4=12, il terzo di secondo grado perchè 1x2=2.
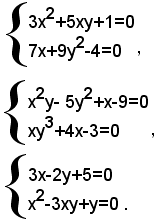
Si trattarono inoltre alcuni metodi per risolvere, nel campo dei numeri razionali, i sistemi di primo grado con due o più equazioni con altrettante incognite, e visto che i sistemi di questo tipo sono impossibili, cioè non ammettono nessuna soluzione, o ammettono una sola soluzione, oppure sono indeterminati, cioè ammettono infinite soluzioni. Tutto quanto è stato detto allora continua, evidentemente a valere anche nel campo più ampio dei numeri reali e quindi si può dire che:
-nel campo dei numeri reali i sistemi di primo grado, aventi tante equazioni quante sono le incognite, o sono impossibili, o indeterminati oppure ammettono una sola soluzione.
Si riprende lo studio dei sistemi, esponendo il modo con cui si risolvono i sistemi algebrici di secondo grado di due o più equazioni con altrettante incognite, incominciando dal più semplice dei sistemi, quello di due equazioni a due incognite. In base alla definizione suddetta, un sistema algebrico di secondo grado, è costituito da un'equazione di secondo grado e da una o più altre equazioni di primo grado, perchè solo in questo caso il prodotto dei gradi delle singole equazioni risulta uguale a due. Perciò, un sistema di secondo grado con due equazioni e con due incognite, ridotto a forma normale, e del tipo: (1)

dove α, β, γ, a, b, c, d, e, f, sono numeri noti o espressioni letterali formate con lettere di cui si suppone noto il valore. I sistemi di questo tipo si possono risolvere tutti applicando il metodo di sostituzione. Infatti, se si risolve l'equazione di primo grado rispetto ad un'incognita, ad esempio la y, si ha: (2)
e, sostituendo a y, nell'altra equazione l'espressione:
si ha: (3)
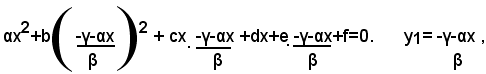
e questa equazione è al massimo di secondo grado, perchè dopo averla ridotta a forma normale, essa può anche ridursi ad un'equazione di primo grado, oppure di grado zero, quando si elidono tutti i termini contenenti l'incognita x, mentre il termine noto è diverso da zero, oppure ad un'identità. Se x1 è una sua soluzione, ammesso che esista, sostituendo nella (2 ) alla x il valore x1, si ottiene per la y il valore:
che assieme ad x1 costituisce una soluzione del sistema dato. Perciò, il sistema (1) avrà tante soluzioni quante sono le radici dell'equazione (3). Ricordando che la (3) può non avere nessuna radice, oppure averne due, o essere un'identità, cioè essere soddisfatta per qualsiasi valore attribuito alla x, si conclude che:
-un sistema algebrico di secondo grado di due o più equazioni con altrettante incognite, o è impossibile, o indeterminato, oppure ammette al massimo due soluzioni.
Esempi:
1)-risolvere il sistema:
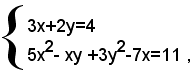
rIsolvendo la prima equazione rispetto a y, si ha: (1)
e sostituendo tale valore della y nella seconda equazione, si ha:
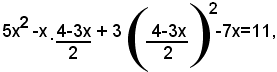
che è un'equazione di secondo grado nell'incognita x. Riducendola a forma normale, si ha:
53x2-108x+4=0,
che ammette due radici reali e distinte x1=2, x2=2/53. Sostituendo nell'equazione (1), al posto della x il valore 2, si ha y1=-1; ponendovi invece il valore 2/53, si ha y2=103/53.
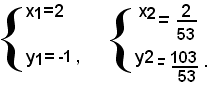
2)-risolvere il sistema:
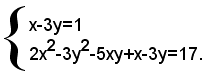
Risolvendo la prima equazione rispetto, a x, si ha: (1)
x=1+3y,
e sostituendo tale valore della x nella seconda equazione, si ottiene:
2(1+3y)2-3y2-5y(1+3y)+(1+3y)-3y=17.
Riducendola a forma normale, risulta:
7y=14,
che è un'equazione di primo grado nell'incognita y, la cui soluzione è y=2.
3)-risolvere il sistema:
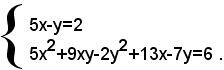
Risolvendo la prima equazione rispetto, a y, si ha: (1)
y=5x-2,
e sostituendo tale valore della y nella seconda equazione, si ha:
5x2+9x(5x-2)-2(5x-2)2+13x-7(5x-2)=6,
ossia, dopo facili calcoli, si perviene all'identità:
6=6.
Il sistema si riduce alla sola equazione (1), che come è noto, ammette infinite soluzioni. In tal caso il sistema è indeterminato.
4)-risolvere il sistema:
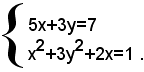
Risolvendo la prima equazione rispetto a y, si ha: (1)
e sostituendo tale valore della y nella seconda equazione, si ottiene:
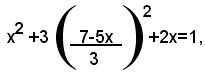
e riducendola a forma normale, risulta:
14x2-32x+23=0.
Si calcola ora il discriminante ridotto ∆/4
=256-322=-66<0, quindi l'equazione non ammette nessuna radice e si
conclude che anche il sistema dato non ammette nessuna soluzione,
perciò è impossibile.
5)-risolvere il sistema a coefficienti letterali:

Per liberare la prima equazione dal denominatore, si deve supporre a≠-b, pertanto si ha:
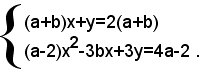
Dalla prima equazione si ricava: (1)
y=2(a+b)-(a+b)x,
e sostituendo tale espressione, al posto della y, nella seconda equazione, si ha:
ossia:
(a-2)x2-(3a+6b)x+2a+6b+2=0.
Se a=2, b≠-1, questa equazione risulta di primo grado, ed ammette come unica soluzione:
x1= 2a+6b+2 = 6a+6b =1;
a questo valore della x, per la (1), corrisponde per y il valore:
y1=2(2+b)-(2+b)=2+b.
Se a=2, b=-1, l'equazione si trasforma in un'identità e perciò il sistema si riduce alla sola equazione (1); in tal caso, il sistema dato è indeterminato.
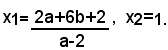
A questi valori della x, per la (1), corrispondono per la y rispettivamente i valori:
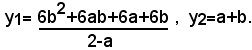
Riassumendo:
se a=-b, il sistema non ammette soluzioni;
se a≠-b, a=2, b≠-1, il sistema ammette una sola soluzione;
se a=2, b=-1, il sistema è indeterminato;
se a≠-b, a≠2, il sistema ammette due soluzioni.
6)-risolvere il sistema fratto:
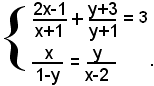
Per liberare la prima equazione dai denominatori, si devono liberare ambo i membri per (x+1)(y+1), e perciò bisogna supporre x≠-1, y≠-1. Per liberare la seconda equazione dai denominatori, si devono liberare ambo i membri per (x+1)(y+1), e perciò bisogna supporre x≠2, y≠1, pertanto, si ottiene il sistema:
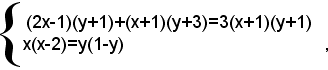
ossia, dopo facili semplificazioni:
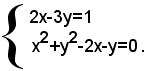
Applicando a questo sistema il metodo di sostituzione, si trova che esso ammette le soluzioni:
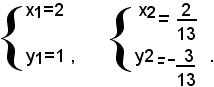
La prima soluzione non soddisfa il sistema dato, perchè per x=2, y=1, si annullano i denominatori della seconda equazione, dunque il sistema dato ammette soltanto la soluzione:
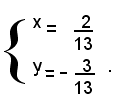
6)-risolvere il sistema: (1)
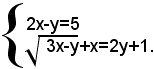
Isolando il radicale ed elevando al quadrato ambo i membri della seconda equazione, dopo facili semplificazioni, si ottiene il sistema di secondo grado seguente: (2)
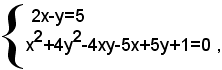
che non si può considerare equivalente al sistema dato, perchè, come è noto, oltre alle soluzioni del sistema dato, esso può averne anche altre. Perciò dopo aver trovato le soluzioni del sistema (2), bisognerà verificare quali di queste sono anche soluzioni del sistema (1). Risolvendo il sistema (2) con il metodo di sostituzione, si trova che esso ammette le seguenti soluzioni:
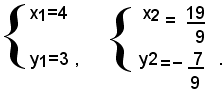
Si verifica facilmente che la seconda non soddisfa il sistema (1), quindi si conclude che il sistema dato ha un'unica soluzione: x=4, y=3.
Il metodo di sostituzione si può anche applicare alla risoluzione dei sistemi di secondo grado composti da più di due equazioni con altrettante incognite. Questi sistemi sono formati da un certo numero di sistemi di primo grado e da una sola equazione di secondo grado.
Esempio: risolvere il sistema
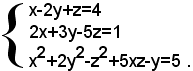
Dalla prima equazione si ricava: (1)
x=4+2y-z
e si sostituisce al posto della x nella seconda e terza equazione, ottenendo così il sistema:
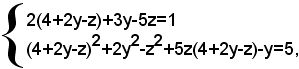
di due equazioni nelle incognite y e z. Riducendo a forma normale, si ha: (2)
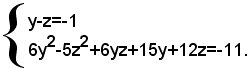
y=z-1.
Sostituendo tale valore di y nella seconda equazione del sistema (2), si ottiene la seguente equazione di secondo grado nell'incognita z:
6(z-1)2-5z2+6(z-1)+15(z-1)+12z=-11,
la cui forma normale è:
7z2+9z+2=0
le cui radici sono: (4)
z1=-2/7, z2=-1 ,
Sostituendo di seguito tali valori al posto della z nella (3), si ha: (5)
y1=-9/7, y2=-2.
Sostituendo infine i valori (4) e (5) nella (1), si ha:
x1=12/7, x2=1.
Quindi, il sistema dato ammette le seguenti due soluzioni:
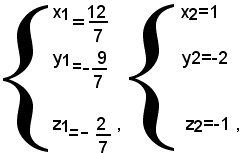
Sistemi particolari di secondo grado
Esistono dei sistemi di secondo grado che per la loro forma particolare si possono risolvere con metodi più veloci del metodo di sostituzione. Prima di esaminarli, si dà la seguente definizione:
un sistema di due equazioni a due incognite x e y si dice simmetrico, quando le equazioni del sistema non si modificano se si scambiano fra loro le due incognite, cioè sostituendo la x con la y e la y con la x.
Esempi:
1)-è simmetrico il sistema:
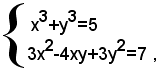
perchè, sostituendo la x con la y, si ottiene il sistema seguente, uguale a quello dato.
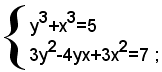
2)-non è simmetrico il sistema:
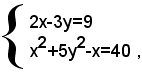
perchè, sostituendo la x con la y, si ottiene il sistema seguente, non uguale a quello dato.
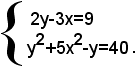
E' evidente che se x=a, y=b è una soluzione del sistema simmetrico, anche x=b e y=a è una soluzione del sistema.
Premesso ciò, si considera il più semplice dei sistemi simmetrici, cioè: (1)
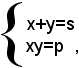
dove s p indicano due numeri noti.
Risolvere il sistema (1) equivale a trovare due numeri x e y tali che la loro somma sia uguale ad s ed il loro prodotto uguale a p. I numeri cercati, quando esistono, come si è visto in precedenza, sono le radici dell'equazione di secondo grado nell'incognita z: (2)
z2-sz+p=0.
Perciò, se z1 e z2 indicano le eventuali incognite dell'equazione (2), le soluzioni del sistema sono:
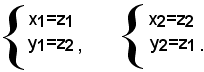
Pertanto la (2) si chiama equazione risolvente del sistema (1).
Esempio: risolvere il sistema
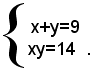
L'equazione risolvente è:
z2-9z+14=0,
le cui radici sono:
z1=7 e z2=2.
Quindi le soluzioni del sistema sono:

Un altro sistema simmetrico di secondo grado, la cui risoluzione si può ricondurre a quella di un sistema del tipo precedente è il seguente: (1)
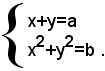
Infatti, tenendo presente l'identità:
x2+y2=(x+y)2-2xy,
il sistema (1) si trasforma nel sistema equivalente:
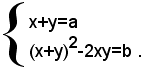
Sostituendo nella seconda equazione il valore di a dato dalla prima equazione, si ha:
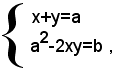
ossia:
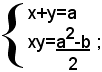
così ci si ritrova nel caso precedente.
Esempio: risolvere il sistema
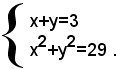
Procedendo come sopra, si ha:
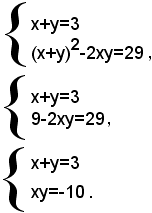
Quindi le soluzioni del sistema sono:

Un altro sistema simmetrico di secondo grado, la cui risoluzione si può ricondurre a quella di un sistema del tipo precedente è il seguente: (1)
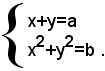
Infatti, tenendo presente l'identità:
x2+y2=(x+y)2-2xy,
il sistema (1) si trasforma nel sistema equivalente:
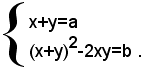
Sostituendo nella seconda equazione il valore di a dato dalla prima equazione, si ha:
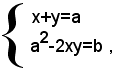
ossia:
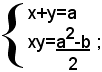
così ci si ritrova nel caso precedente.
Esempio: risolvere il sistema
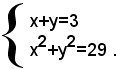
Procedendo come sopra, si ha:
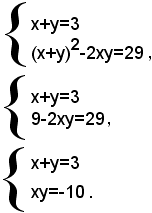
L'equazione risolvente è:
z2-3z-10=0,
le cui radici sono:
le cui radici sono:
z1=5 e z2=-2.
Quindi le soluzioni del sistema sono:
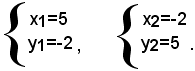
Vi sono sistemi di secondo grado non simmetrici che si possono risolvere senza applicare il metodo di sostituzione, sono i seguenti:
1)-si consideri il sistema:
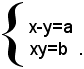
dove a e b sono numeri noti.
Scrivendo le due equazioni sotto la forma:
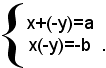
si ottiene un sistema simmetrico nelle due incognite x e -y, la cui equazione risolvente è:
Se z1=5 e z2 sono le eventuali radici di questa equazione, esse rappresentano i valori di x e -y; quindi le soluzioni del sistema dato sono:
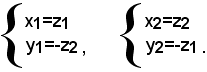
Esempio: risolvere il sistema
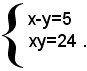
Scrivendo le due equazioni sotto la forma:
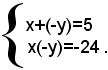
L'equazione risolvente è:
Le soluzioni del sistema dato sono:
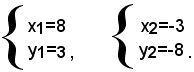
2)-si consideri il sistema:
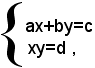
dove a, b, c, d, sono numeri noti.
Scrivendo le due equazioni sotto la forma:
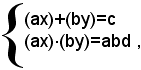
si ottiene un sistema simmetrico rispetto alle incognite ax e by, del tipo già visto; dalla sua risoluzione si ottengono i valori di ax e by, e quindi di x e y.
Esempio: risolvere il sistema
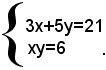
moltiplicando ambo i membri della seconda equazione per 15, si ha:
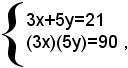
e questo sistema risulta simmetrico rispetto alle incognite 3x e 5y.
L'equazione risolvente è:
z2-21z+90=0,
le cui radici sono:
z1=15 e z2=6.
Perciò, si ha:
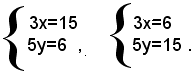
Cioè:
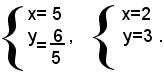
3)-si consideri il sistema:
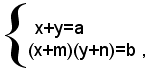
dove a, b, m, n, sono numeri noti.
Aggiungendo ad ambo i membri della prima equazione il numero m+n, si ottiene il sistema equivalente:
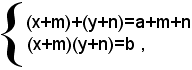
che è simmetrico rispetto alle incognite x+m e y+n, del tipo già visto; dalla sua risoluzione si ottengono i valori di x+m e y+n, e quindi di x e y.
Esempio: risolvere il sistema
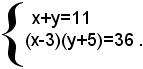
Aggiungendo ad ambo i membri della prima equazione il numero -3+5=2, si ottiene il sistema equivalente:
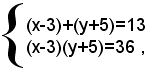
che è simmetrico rispetto alle incognite x-3 e y+5.
le cui radici sono: z1=9 e z2=4. Perciò, si ha:
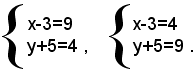
Cioè:
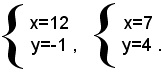
Esempio: risolvere il sistema
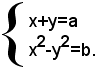
Esso si può scrivere sotto la forma:
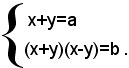
Ponendo nella seconda equazione, al posto di x+y il valore a della prima equazione, si ha:
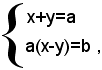
ossia:
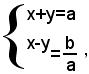
che è un sistema di primo grado.
Analogamente si risolve il sistema:
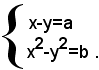
Esempio: risolvere il sistema
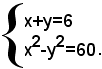
Esso si può scrivere sotto la forma:
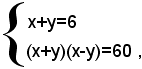
quindi
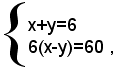
cioè
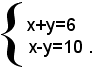
Prima addizionando e poi sottraendo membro a membro le due equazioni, si ha:

che è l'unica soluzione del sistema dato.
Esempio: risolvere il sistema
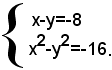
Esso si può scrivere sotto la forma:
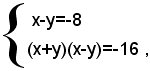
e quindi
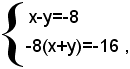
cioè
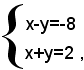
da cui, prima addizionando e poi sottraendo membro a membro le due equazioni, si ha:
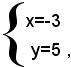
che è l'unica soluzione del sistema dato.
Sistemi particolari di grado superiore al secondo
Si esaminano ora alcuni particolari tipi di sistemi di due equazioni di grado superiore al secondo la cui risoluzione dipende da un'equazione di secondo grado, o da un'equazione di grado superiore, del tipo trattato in precedenza. Si comincia dal seguente sistema simmetrico di terzo grado: (1)
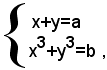
dove a e b sono due numeri noti.
Dall'identità:
che può scriversi sotto la forma:
(x+y)3=x3+y3+3xy(x+y),
si ricava:
x3+y3=(x+y)3-3xy(x+y)
.
Il sistema (1) si può quindi scrivere sotto la forma equivalente:
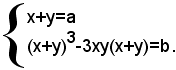
Sostituendo, nella seconda equazione, al posto di x+y il valore a dato dalla prima equazione, si ha:
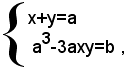
e quindi il sistema (1) è equivalente al sistema: (2)
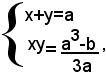
la cui risoluzione dipende, come è noto, da un'equazione di secondo grado.
Nota bene
Siccome il sistema (1) è equivalente al sistema (2), si può dire che il sistema (1) è impossibile, oppure ammette al massimo due soluzioni.
Esempio: risolvere il sistema
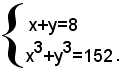
Ricordando che:
x3+y3=(x+y)3-3xy(x+y),
il sistema si può scrivere sotto la forma:
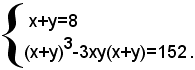
Sostituendo, nella seconda equazione, al posto di x+y il valore 8, dato dalla prima equazione, e risolvendo poi rispetto ad xy, si ha:
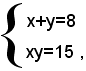
la cui equazione risolvente è:
che ammette come radici i numeri
Le soluzioni del sistema proposto sono quindi:
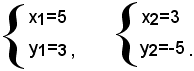
Si consideri ora il seguente sistema simmetrico di quarto grado: (1)
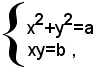
dove a e b sono due numeri noti. Il sistema si può scrivere sotto la forma:
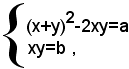
Sostituendo, nella prima equazione, al posto di xy il valore b, dato dalla seconda equazione, si ottiene il seguente sistema equivalente a quello dato: (2)
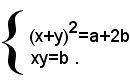
Ora, se a+2b<0, il sistema (2) evidentemente non ammette nessuna soluzione, cioè è impossibile, e quindi è tale anche il sistema proposto (1). Escluso questo caso, il sistema (2) risulta soddisfatto da tutte le eventuali soluzioni di entrambi i sistemi seguenti:
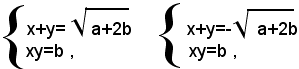
la cui risoluzione è nota. Il sistema (3) può quindi ammettere quattro soluzioni, o due o nessuna.
Esempi:
1)-risolvere il sistema
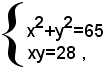
che si può scrivere sotto la forma:
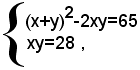
e, sostituendo, nella prima equazione, al posto di xy il valore 28 dato dalla seconda equazione, si ottiene:
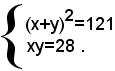
Esso risulta soddisfatto da tutte e sole le soluzioni di entrambi i sistemi seguenti:
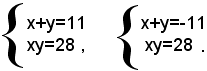
Risolvendo i due sistemi, si trova che il sistema proposto ammette le seguenti quattro soluzioni:
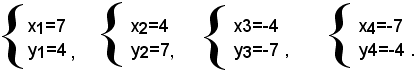
2)-risolvere il sistema
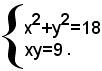
Successivamente, si ottiene:
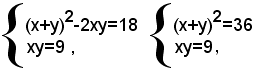
quindi il sistema dato equivale ai seguenti due sistemi:
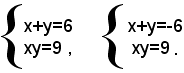
Il primo sistema ammette l'unica soluzione x=3, y=3, il secondo, l'unica soluzione x=-3, y=-3.
Pertanto, il sistema dato ammette soltanto due soluzioni:
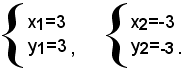
3)-risolvere il sistema
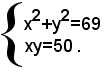
Successivamente, si ottiene:
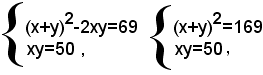
e quindi:
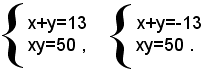
Entrambi i sistemi non ammettono soluzioni e quindi il sistema dato è impossibile.
Se un sistema di due equazioni con due incognite è formato da un'equazione di primo grado e da un'equazione di secondo, di terzo o di quarto grado, lo si può risolvere con il metodo di sostituzione, se si perviene a un'equazione in una incognita del tipo trattato in precedenza.
Esempi:
1)-risolvere il seguente sistema di quarto grado: (1)
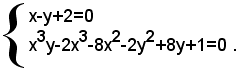
Dalla prima equazione si ha: (2)
y=x+2,
e, sostituendo x+2 al posto della y nella seconda equazione, si ottiene:
x3(x+2)-2x3-8x2-2(x+2)2+8(x+2)+1=0 ;
ossia, dopo facili calcoli:
x4-10x2+9=0 ,
che è un'equazione biquadratica nell'incognita x. Risolvendola, con il procedimento noto, si vede che essa ammette quattro radici date da: x1=3, x2=-3, x3=1, x4=-1. A tali valori dell'incognita x, per la (2), corrispondono i seguenti valori dell'incognita y: y1=5, y2=-1, y3=3, y4=1. Si può quindi dire che il sistema ammette le seguenti quattro soluzioni:
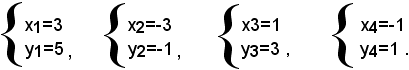
Nota bene
Se nel risolvere il sistema 1), si ricava il valore della x, anzichè quello della y, e lo si sostituisce nella seconda equazione, si ottiene la seguente equazione completa di quarto grado in y:
y4-8y314y2+8y-15=0 ,
2)-risolvere il seguente sistema di quarto grado:
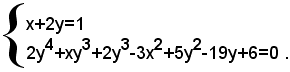
Risolvendo la prima equazione rispetto ad x, si ha: (1)
3y3-7y2-7y-3=0 ,
che è un'equazione reciproca di terzo grado. Risolvendo quest'equazione con il metodo già trattato, si trova che essa ammette le radici: y1=-1, y2=3, y3=1/3. A queste radici, per la (1), corrispondono per l'incognita x i valori: x1=3, x2=-5, x3=1/3. Il sistema dato ammette quindi le seguenti tre soluzioni:
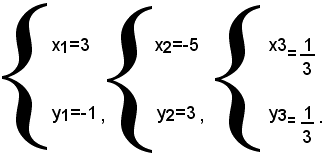
3)-risolvere il seguente sistema di quarto grado:

Dalla prima equazione si ricava:
y=x-1 ,
e, sostituendo x-1 al posto della y nella seconda equazione, si ottiene:
x4-2x3(x-1)+x2(x-1)2-x3+x2(x-1)+2x-2(x-1)=2 ;
e, dopo facili semplificazioni, si ha:
Il metodo di sostituzione può talvolta essere utile anche per risolvere sistemi nei quali non figuri nessuna equazione di primo grado, ma almeno una delle due dev'essere di primo grado rispetto a un'incognita.
Ad esempio, con il metodo di sostituzione, si può risolvere il seguente sistema di quarto grado:
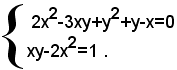
In questo sistema la seconda equazione è di primo grado rispetto all'incognita y. Risolvendola rispetto a tale incognita, si ha: (1)
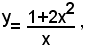
e, sostituendo tale valore nella prima equazione, si ha l'equazione:
x3+x2+x+1=0 ,
che è reciproca di terzo grado. Risolvendola, si trova l'unica soluzione x=-1. Sostituendo questo valore nella (1), si trova che il sistema proposto ammette l'unica soluzione:
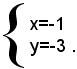
SistemI omogenei
Definizione - Un sistema di due equazioni in due incognite si dice omogeneo quando, ridotto a forma normale e trasportati i termini noti nei secondi membri, i primi membri delle due equazioni sono polinomi omogenei di secondo grado rispetto alle incognite.
Si ricorda che un polinomio nelle variabili x e y si dice omogeneo di secondo grado, quando tutti i suoi termini sono di secondo grado. Esso perciò ha la forma:
ax2+bxy+cy2=0 ,
ove a, b, c sono i coefficienti che si devono considerare come numeri noti.
Premesso ciò, un sistema omogeneo è dunque del tipo: (1)
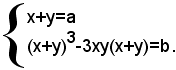
Sostituendo, nella seconda equazione, al posto di x+y il valore a dato dalla prima equazione, si ha:
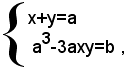
e quindi il sistema (1) è equivalente al sistema: (2)
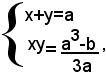
la cui risoluzione dipende, come è noto, da un'equazione di secondo grado.
Nota bene
Siccome il sistema (1) è equivalente al sistema (2), si può dire che il sistema (1) è impossibile, oppure ammette al massimo due soluzioni.
Esempio: risolvere il sistema
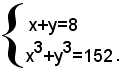
Ricordando che:
x3+y3=(x+y)3-3xy(x+y),
il sistema si può scrivere sotto la forma:
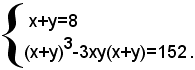
Sostituendo, nella seconda equazione, al posto di x+y il valore 8, dato dalla prima equazione, e risolvendo poi rispetto ad xy, si ha:
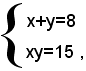
la cui equazione risolvente è:
z2-8z+15=0,
che ammette come radici i numeri
z1=5 e z2=3.
Le soluzioni del sistema proposto sono quindi:
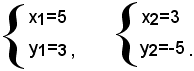
Si consideri ora il seguente sistema simmetrico di quarto grado: (1)
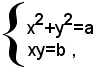
dove a e b sono due numeri noti. Il sistema si può scrivere sotto la forma:
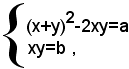
Sostituendo, nella prima equazione, al posto di xy il valore b, dato dalla seconda equazione, si ottiene il seguente sistema equivalente a quello dato: (2)
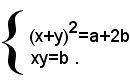
Ora, se a+2b<0, il sistema (2) evidentemente non ammette nessuna soluzione, cioè è impossibile, e quindi è tale anche il sistema proposto (1). Escluso questo caso, il sistema (2) risulta soddisfatto da tutte le eventuali soluzioni di entrambi i sistemi seguenti:
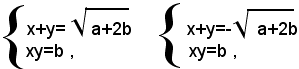
la cui risoluzione è nota. Il sistema (3) può quindi ammettere quattro soluzioni, o due o nessuna.
Esempi:
1)-risolvere il sistema
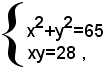
che si può scrivere sotto la forma:
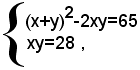
e, sostituendo, nella prima equazione, al posto di xy il valore 28 dato dalla seconda equazione, si ottiene:
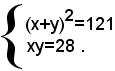
Esso risulta soddisfatto da tutte e sole le soluzioni di entrambi i sistemi seguenti:
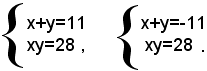
Risolvendo i due sistemi, si trova che il sistema proposto ammette le seguenti quattro soluzioni:
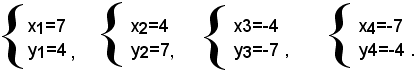
2)-risolvere il sistema
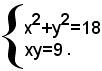
Successivamente, si ottiene:
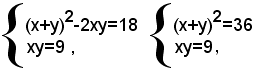
quindi il sistema dato equivale ai seguenti due sistemi:
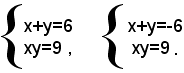
Il primo sistema ammette l'unica soluzione x=3, y=3, il secondo, l'unica soluzione x=-3, y=-3.
Pertanto, il sistema dato ammette soltanto due soluzioni:
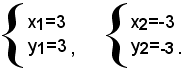
3)-risolvere il sistema
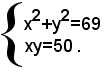
Successivamente, si ottiene:
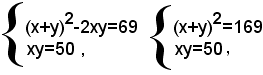
e quindi:
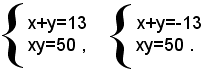
Entrambi i sistemi non ammettono soluzioni e quindi il sistema dato è impossibile.
Se un sistema di due equazioni con due incognite è formato da un'equazione di primo grado e da un'equazione di secondo, di terzo o di quarto grado, lo si può risolvere con il metodo di sostituzione, se si perviene a un'equazione in una incognita del tipo trattato in precedenza.
Esempi:
1)-risolvere il seguente sistema di quarto grado: (1)
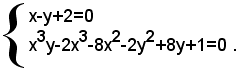
Dalla prima equazione si ha: (2)
e, sostituendo x+2 al posto della y nella seconda equazione, si ottiene:
ossia, dopo facili calcoli:
x4-10x2+9=0 ,
che è un'equazione biquadratica nell'incognita x. Risolvendola, con il procedimento noto, si vede che essa ammette quattro radici date da: x1=3, x2=-3, x3=1, x4=-1. A tali valori dell'incognita x, per la (2), corrispondono i seguenti valori dell'incognita y: y1=5, y2=-1, y3=3, y4=1. Si può quindi dire che il sistema ammette le seguenti quattro soluzioni:
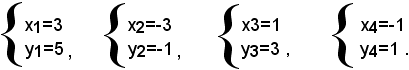
Nota bene
Se nel risolvere il sistema 1), si ricava il valore della x, anzichè quello della y, e lo si sostituisce nella seconda equazione, si ottiene la seguente equazione completa di quarto grado in y:
y4-8y314y2+8y-15=0 ,
la cui risoluzione non è nota.
Si vede quindi che non è indifferente ricavare dall'equazione di primo grado, l'una o l'altra incognita. Perciò, se risolvendo l'equazione di primo grado rispetto ad un'incognita, si perviene ad un'equazione che non si sa risolvere, prima di rinunciare, conviene provare anche a risolverla rispetto all'altra incognita.
Si vede quindi che non è indifferente ricavare dall'equazione di primo grado, l'una o l'altra incognita. Perciò, se risolvendo l'equazione di primo grado rispetto ad un'incognita, si perviene ad un'equazione che non si sa risolvere, prima di rinunciare, conviene provare anche a risolverla rispetto all'altra incognita.
2)-risolvere il seguente sistema di quarto grado:
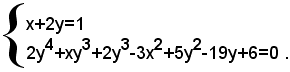
Risolvendo la prima equazione rispetto ad x, si ha: (1)
x=1-2y ,
e, sostituendo 1-2y al posto della x nella seconda equazione, dopo facili calcoli, si ottiene:
e, sostituendo 1-2y al posto della x nella seconda equazione, dopo facili calcoli, si ottiene:
3y3-7y2-7y-3=0 ,
che è un'equazione reciproca di terzo grado. Risolvendo quest'equazione con il metodo già trattato, si trova che essa ammette le radici: y1=-1, y2=3, y3=1/3. A queste radici, per la (1), corrispondono per l'incognita x i valori: x1=3, x2=-5, x3=1/3. Il sistema dato ammette quindi le seguenti tre soluzioni:
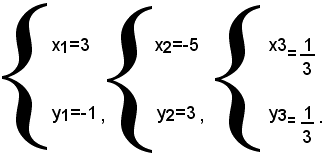
3)-risolvere il seguente sistema di quarto grado:

Dalla prima equazione si ricava:
y=x-1 ,
e, sostituendo x-1 al posto della y nella seconda equazione, si ottiene:
e, dopo facili semplificazioni, si ha:
2=2,
cioè un'identità. Il sistema proposto ammette quindi infinite soluzioni, e precisamente tutte quelle dell'equazione:
cioè un'identità. Il sistema proposto ammette quindi infinite soluzioni, e precisamente tutte quelle dell'equazione:
x-y-1=0 .
Il metodo di sostituzione può talvolta essere utile anche per risolvere sistemi nei quali non figuri nessuna equazione di primo grado, ma almeno una delle due dev'essere di primo grado rispetto a un'incognita.
Ad esempio, con il metodo di sostituzione, si può risolvere il seguente sistema di quarto grado:
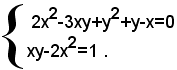
In questo sistema la seconda equazione è di primo grado rispetto all'incognita y. Risolvendola rispetto a tale incognita, si ha: (1)
e, sostituendo tale valore nella prima equazione, si ha l'equazione:
che è reciproca di terzo grado. Risolvendola, si trova l'unica soluzione x=-1. Sostituendo questo valore nella (1), si trova che il sistema proposto ammette l'unica soluzione:
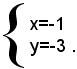
SistemI omogenei
Definizione - Un sistema di due equazioni in due incognite si dice omogeneo quando, ridotto a forma normale e trasportati i termini noti nei secondi membri, i primi membri delle due equazioni sono polinomi omogenei di secondo grado rispetto alle incognite.
Si ricorda che un polinomio nelle variabili x e y si dice omogeneo di secondo grado, quando tutti i suoi termini sono di secondo grado. Esso perciò ha la forma:
ax2+bxy+cy2=0 ,
ove a, b, c sono i coefficienti che si devono considerare come numeri noti.
Premesso ciò, un sistema omogeneo è dunque del tipo: (1)
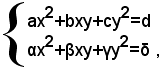
a, b, c, d, α, β, γ, δ, sono numeri assegnati.
Si vede ora come si risolvono i sistemi di questo tipo; si distinguono due casi:
1° caso: si suppone d=0, cioè si abbia il sistema: (2)
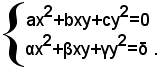
Se a=0, la prima equazione si può scrivere sotto la forma y(bx+cy)=0 e perciò il sistema (2) sarà equivalente all'insieme dei seguenti due sistemi di secondo grado:
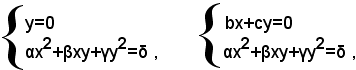
la cui risoluzione è nota.
Se invece è a≠0, δ=0, cioè se si ha il sistema: (3)
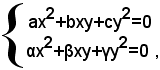
sottraendo membro a membro dalla prima equazione, dopo averla moltiplicata per α, la seconda, dopo averla moltiplicata per a, si ottiene il sistema equivalente al sistema: (3)
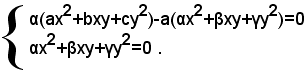
Riducendo la prima equazione a forma normale, si vede che essa non contiene più il termine x2, e perciò il sistema (3) è del tipo discusso in precedentemente.
Si supponga allora a≠0, δ≠0, e si osservi che in questo caso il sistema (2) non può essere soddisfatto da x=0, y=0, perchè è δ≠0; e neanche da x≠0, y=0, perchè a≠0. Essendo allora y≠0, dividendo ambo i membri della prima equazione per y2, si ottiene il sistema equivalente: (4)
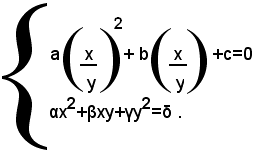
La prima equazione di questo sistema è di secondo grado nell'incognita x/y. Se essa ammette soluzioni, dette queste z1, z2, il sistema (4) si scinde nei seguenti due sistemi di secondo grado:
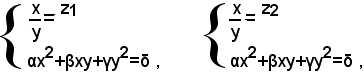
la cui risoluzione con il metodo di sostituzione è nota.
Esempi:
1)-risolvere il seguente sistema omogeneo:
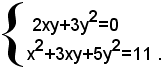
Il sistema si può scrivere sotto la forma:
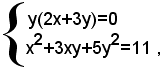
e perciò è equivalente all'insieme dei due sistemi di secondo grado seguenti:
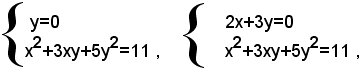
che, risolti con il metodo di sostituzione, permettono di calcolare le soluzioni del sistema dato; si trova
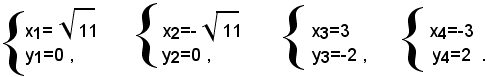
2)-risolvere il sistema:
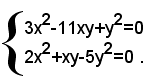
sottraendo dalla prima equazione, moltiplicata per 2, la seconda, moltiplicata per 3, si ottiene il sistema equivalente:
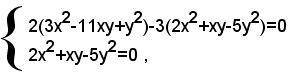
ossia, dopo facili semplificazioni:
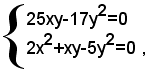
cioè:
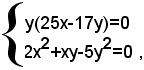
che è equivalente all'insieme dei due sistemi di secondo grado seguenti:
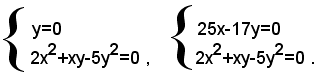
Entrambi i sistemi ammettono soltanto la soluzione x=0, y=0, che è l'unica soluzione del sistema dato.
3)-risolvere il sistema:
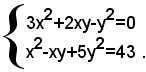
Dividendo ambo i membri della prima equazione per y2, si ottiene l'equazione:
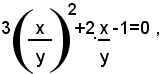
che è di secondo grado nell'incognita x/y. Risolvendola, si trova che ammette le radici:
Il sistema (1) si scinde quindi nei due sistemi di secondo grado seguenti:

che, risolti con il metodo di sostituzione, si trovano per il sistema dato le seguenti soluzioni.

2° Caso: siano d≠0, δ≠0.
Questo caso si può facilmente ricondurre al precedente. Infatti, sottraendo membro a membro, dalla prima equazione del sistema: (1)
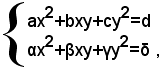
dopo averla moltiplicata per δ, la seconda, dopo averla moltiplicata per d, si ottiene il sistema:
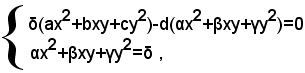
che è del tipo considerato nel caso precedente.
Esempio: risolvere il sistema
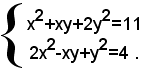
Sottraendo membro a membro, dalla prima equazione, moltiplicata per 4, la seconda, moltiplicata per 11, si ottiene il sistema equivalente:
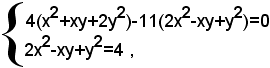
ossia:
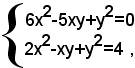
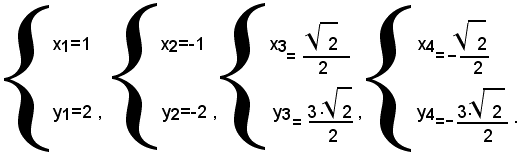
In vari casi, nella risoluzione di un sistema di equazioni, è utile ricorrere ad opportuni artifici, che permettono di trasformare un sistema in un altro, o in più altri sistemi, che nel loro complesso sono equivalenti a quello assegnato, e che non si sanno risolvere.
Esempi:
1)-risolvere il seguente sistema di quarto grado:

Sottraendo membro a membro, dalla prima equazione, la seconda, dopo averla moltiplicata per 2, si ottiene il sistema equivalente:
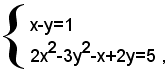
che è di secondo grado e quindi si può risolvere con il metodo di sostituzione. Dopo averlo risolto, si trova che ammette le soluzioni:

2)-risolvere il seguente sistema:
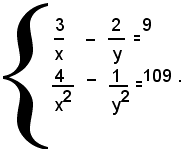
Eliminando i denominatori, si ha il sistema:
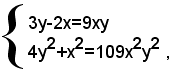
che è di ottavo grado; se invece si pone
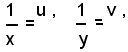
il sistema si trasforma nel sistema di secondo grado seguente
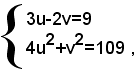
che, risolto con il metodo di sostituzione, dà

Poichè x e y sono i reciproci di u e v, le soluzioni del sistema proposto sono:

3)-risolvere il seguente sistema simmetrico di quarto grado :
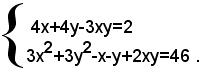
Si scrive il sistema sotto la forma:
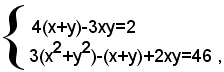
ossia
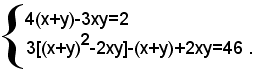
Posto:
x+y=u, xy=v,
il sistema si trasforma nel seguente di secondo grado
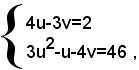
che risolto dà le due soluzioni

In base al significato attribuito alle lettere u e v, si può dire che il sistema dato è equivalente al complesso dei due sistemi:
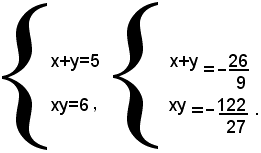
Risolvendo questi due sistemi, si trovano le soluzioni del sistema proposto.
4)-risolvere il sistema:
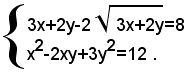
Posto:
la prima equazione del sistema si trasforma nella seguente:
u2-2u-8=0 ,
le cui radici sono: u1=4, .
Per il significato attribuito alla lettera u, essa deve rappresentare un numero positivo e perciò la radice u2=-2, si deve scartare. Pertanto si deve risolvere soltanto il seguente sistema di secondo grado:

le cui soluzioni sono

Nota bene
Dagli esempi si è visto che un sistema di tante equazioni quante sono le incognite e qualunque sia il suo grado può essere impossibile o indeterminato, oppure ammette un numero di soluzioni che non può mai superare il suo grado. Questo risultato è generale, cioè si dimostra il seguente teorema, di cui si dà soltanto l'enunciato:
nel campo dei numeri reali, un sistema algebrico di grado n, di tante equazioni quante sono le incognite, è impossibile, indeterminato, oppure ammette un numero di soluzioni che non può mai superare il grado n del sistema.