MIKY & GENNY
CALCOLO COMBINATORIO SEMPLICE ---> INDICE
Generalità
1)-Si supponga di avere un certo numero n, intero positivo, di elementi, oggetti, tutti distinti, indicati con:
1)-Si supponga di avere un certo numero n, intero positivo, di elementi, oggetti, tutti distinti, indicati con:
a1, a2, a3, ..., an-2, an-1, an
e si considerino k, altro numero intero positivo, posti, con n ≥ k. Ci si propone di sistemare gli elementi sui posti in modo che ogni elemento occupi un solo posto e nessun posto resti vuoto.
Se n > k, nel fare dette sistemazioni, si può tener conto sia degli elementi, ossia di quali di essi o della natura di essi, sistemati, che dell'ordine con cui essi vengono sistemati, o solo della prima condizione.
Nel 1° caso si hanno le cosiddette disposizioni semplici; nel 2° caso le combinazioni semplici.
Se n = k, poichè tutti gli elementi vengono sistemati, le stesse sistemazioni potranno differire solo per l'ordine degli elementi e si hanno le permutazioni semplici.
Definizione 1 - Le disposizioni semplici sono le sistemazioni che si possono fare con n elementi su k posti, essendo n > k, e nell'ipotesi di considerare due sistemazioni diverse tra loro o perchè differiscono per la natura di qualche elemento sistemato o per l'ordine con cui si susseguono gli stessi elementi già sistemati.
Si indicano con Dn, k, che si legge in uno dei seguenti modi:
a)-disposizioni di n elementi su k posti;
b)-disposizioni di n elementi a k a k;
c)-disposizioni di n elementi di classe k.
Definizione 2 - Le permutazioni semplici sono le sistemazioni che si possono fare con n elementi su altrettanti posti, quindi n = k, per cui due di esse potranno differire solo per l'ordine con cui gli elementi sistemati si susseguono sui posti.
Si indicano con Pn, (= Pk), e si legge: permutazioni di n o k elementi.
Definizione 3 - Le combinazioni semplici sono le sistemazioni che si possono fare con n elementi su k posti, con n > k, nell'ipotesi di considerare diverse tra loro due sistemazioni che differiscono solo per la natura degli elementi sistemati.
Si indicano con Cn, k, e si legge in uno dei seguenti modi:
a)-combinazioni di n elementi su k posti;
b)-combinazioni di n elementi a k a k;
c)-combinazioni di n elementi di classe k.
Si vuole ora calcolare il numero delle Dn, k, Pn, Cn, k.
Calcolo delle Dn, k
Si segue il metodo induttivo, cioè si perverrà alla formula generale dall'esame delle formule relative ai casi più semplici.
Considerati sempre gli n elementi:
a1, a2, a3, ..., an-2, an-1, an,
si supponga k = 1.
Poichè ogni elemento deve occupare un solo posto, ovviamente si ha:
Dn, 1 = n (numero degli elementi).
Si supponga ora k = 2; le disposizioni diventano:

Dal riquadro si vede che ogni elemento occupa il 1° posto, mentre tutti gli altri occupano il 2° posto e, pertanto, non vi sono altre possibili sistemazioni. Lo stesso riquadro è costituito da n colonne di sistemazioni, una per ogni elemento che occupa il 1° posto, e ciascuna colonna è, a sua volta, costituita da n - 1 righe, per contarle conviene seguire l'indice degli elementi occupanti il 2° posto, pertanto, si ha:
Dn, 2 = n·(n - 1).
Si supponga ancora k = 3; le disposizioni diventano:



Il 1° gruppo è caratterizzato dall'avere sempre il 1° elemento sul 1° posto; uno alla volta gli altri (n - 1) sul 2° posto e i rimanenti (n - 2) ogni volta rotanti sul 3° posto.
Il 2° gruppo è caratterizzato dall'avere sempre il 2 elemento sul 1° posto; uno alla volta gli altri (n - 1) sul 2° posto e i rimanenti (n - 2) ogni volta rotanti sul 3° posto.
L'nmo gruppo, infine, è caratterizzato dall'avere sempre l'nmo elemento sul 1° posto; uno alla volta gli altri (n - 1) sul 2° posto e i rimanenti (n - 2) ogni volta rotanti sul 3° posto.
Pertanto, i gruppi sono n, cioè tanti quanti sono gli elementi, perchè ognuno di essi deve occupare il 1° posto; ogni gruppo è costituito da n - 1 colonne, per contarle conviene seguire gl'indici degli elementi che si susseguono sul 2° posto, i quali sono 2, 3, ... n e quindi in tutto n - 1; infine, ogni colonna è costituita da n - 2 righe, per contarle conviene seguire gl'indici degli elementi che si susseguono sul 3° posto, che ovviamente sono n - 2, in quanto ogni volta due elementi sono già stati sistemati sui primi due posti.
Allora è:
Dn, 3 = n(n - 1)(n - 2).
Dalla formazione dei riquadri analoghi e relativi a k = 4, k = 5, ...., si avrebbe:
Dn, 4 = n(n - 1)(n - 2)(n - 3),
Dn, 5 = n(n - 1)(n - 2)(n - 3)(n - 4),
e così via.
Prima di scrivere la formula generale delle Dn, k, si osserva quanto segue:
a)-ogni formula trovata è espressa da un prodotto di fattori, il cui numero è uguale a quello dei posti;
b)-i fattori sono numeri interi consecutivi a partire dal numero n degli elementi;
c)-l'ultimo fatrtore si ottiene aumentando di una unità la differenza fra il numero degli elementi, sempre n, e quello dei posti, in ciascun caso.
Quindi, in generale è:
Dn, k = n(n - 1)(n - 2)(n - 3) ... (n - k + 1),
ovvero:
-il numero delle disposizioni semplici è dato dal prodotto di tanti fattori consecutivi descescenti, a partire dal numero degli elementi, quante sono le unità del numero dei posti.
Esempi
e si considerino k, altro numero intero positivo, posti, con n ≥ k. Ci si propone di sistemare gli elementi sui posti in modo che ogni elemento occupi un solo posto e nessun posto resti vuoto.
Se n > k, nel fare dette sistemazioni, si può tener conto sia degli elementi, ossia di quali di essi o della natura di essi, sistemati, che dell'ordine con cui essi vengono sistemati, o solo della prima condizione.
Nel 1° caso si hanno le cosiddette disposizioni semplici; nel 2° caso le combinazioni semplici.
Se n = k, poichè tutti gli elementi vengono sistemati, le stesse sistemazioni potranno differire solo per l'ordine degli elementi e si hanno le permutazioni semplici.
Definizione 1 - Le disposizioni semplici sono le sistemazioni che si possono fare con n elementi su k posti, essendo n > k, e nell'ipotesi di considerare due sistemazioni diverse tra loro o perchè differiscono per la natura di qualche elemento sistemato o per l'ordine con cui si susseguono gli stessi elementi già sistemati.
Si indicano con Dn, k, che si legge in uno dei seguenti modi:
a)-disposizioni di n elementi su k posti;
b)-disposizioni di n elementi a k a k;
c)-disposizioni di n elementi di classe k.
Definizione 2 - Le permutazioni semplici sono le sistemazioni che si possono fare con n elementi su altrettanti posti, quindi n = k, per cui due di esse potranno differire solo per l'ordine con cui gli elementi sistemati si susseguono sui posti.
Si indicano con Pn, (= Pk), e si legge: permutazioni di n o k elementi.
Definizione 3 - Le combinazioni semplici sono le sistemazioni che si possono fare con n elementi su k posti, con n > k, nell'ipotesi di considerare diverse tra loro due sistemazioni che differiscono solo per la natura degli elementi sistemati.
Si indicano con Cn, k, e si legge in uno dei seguenti modi:
a)-combinazioni di n elementi su k posti;
b)-combinazioni di n elementi a k a k;
c)-combinazioni di n elementi di classe k.
Si vuole ora calcolare il numero delle Dn, k, Pn, Cn, k.
Calcolo delle Dn, k
Si segue il metodo induttivo, cioè si perverrà alla formula generale dall'esame delle formule relative ai casi più semplici.
Considerati sempre gli n elementi:
a1, a2, a3, ..., an-2, an-1, an,
si supponga k = 1.
Poichè ogni elemento deve occupare un solo posto, ovviamente si ha:
Dn, 1 = n (numero degli elementi).
Si supponga ora k = 2; le disposizioni diventano:

Dal riquadro si vede che ogni elemento occupa il 1° posto, mentre tutti gli altri occupano il 2° posto e, pertanto, non vi sono altre possibili sistemazioni. Lo stesso riquadro è costituito da n colonne di sistemazioni, una per ogni elemento che occupa il 1° posto, e ciascuna colonna è, a sua volta, costituita da n - 1 righe, per contarle conviene seguire l'indice degli elementi occupanti il 2° posto, pertanto, si ha:
Dn, 2 = n·(n - 1).
Si supponga ancora k = 3; le disposizioni diventano:



Il 1° gruppo è caratterizzato dall'avere sempre il 1° elemento sul 1° posto; uno alla volta gli altri (n - 1) sul 2° posto e i rimanenti (n - 2) ogni volta rotanti sul 3° posto.
Il 2° gruppo è caratterizzato dall'avere sempre il 2 elemento sul 1° posto; uno alla volta gli altri (n - 1) sul 2° posto e i rimanenti (n - 2) ogni volta rotanti sul 3° posto.
L'nmo gruppo, infine, è caratterizzato dall'avere sempre l'nmo elemento sul 1° posto; uno alla volta gli altri (n - 1) sul 2° posto e i rimanenti (n - 2) ogni volta rotanti sul 3° posto.
Pertanto, i gruppi sono n, cioè tanti quanti sono gli elementi, perchè ognuno di essi deve occupare il 1° posto; ogni gruppo è costituito da n - 1 colonne, per contarle conviene seguire gl'indici degli elementi che si susseguono sul 2° posto, i quali sono 2, 3, ... n e quindi in tutto n - 1; infine, ogni colonna è costituita da n - 2 righe, per contarle conviene seguire gl'indici degli elementi che si susseguono sul 3° posto, che ovviamente sono n - 2, in quanto ogni volta due elementi sono già stati sistemati sui primi due posti.
Allora è:
Dn, 3 = n(n - 1)(n - 2).
Dalla formazione dei riquadri analoghi e relativi a k = 4, k = 5, ...., si avrebbe:
e così via.
Prima di scrivere la formula generale delle Dn, k, si osserva quanto segue:
a)-ogni formula trovata è espressa da un prodotto di fattori, il cui numero è uguale a quello dei posti;
b)-i fattori sono numeri interi consecutivi a partire dal numero n degli elementi;
c)-l'ultimo fatrtore si ottiene aumentando di una unità la differenza fra il numero degli elementi, sempre n, e quello dei posti, in ciascun caso.
Quindi, in generale è:
ovvero:
-il numero delle disposizioni semplici è dato dal prodotto di tanti fattori consecutivi descescenti, a partire dal numero degli elementi, quante sono le unità del numero dei posti.
Esempi
D7, 3 = 7·6·5,
D8, 5 = 8·7·6·5·4,
Dn, 6 = n(n - 1)(n - 2)(n - 3)(n - 4)(n - 5),
D5, 9 non ha senso perchè (n = 5) < (k = 9),
contro l'ipotesi, perchè n > k.
Calcolo delle Pn
Le permutazioni si presentano come caso particolare delle disposizioni ed il numero di esse si ottiene da quello delle Dn, k per n = k:
Pn = Dn, n = n(n - 1)(n - 2) ... (n - n + 1) = n(n - 1)(n - 2) ...1.
Quindi:
- il numero delle permutazioni semplici è dato dal prodotto di tutti gl'interi consecutivi decrescenti, a partire da quello degli elementi, uguale a quello dei posti, fino ad uno.
Tale prodotto solitamente viene indicato con uno dei seguenti simboli:

dei quali in seguito si preferirà il 1°, e si leggerà
n! = n fattoriale.
Quindi:
Pn = n! = n(n - 1)(n - 2) ... 1.
Esempio:
P6 = 6! = 6·5·4·3·2·1.
Nota bene
a)-indipendentemente dalle permutazioni e dal calcolo combinatorio vale la seguente definizione o posizione:
-fattoriale di un numero è il prodotto di tutti gl'interi consecutivi decrescenti, a partire da quel numero fino all'unità;
b)-applicando la proprietà associativa della moltiplicazione, si ha
6! = 6·(5·4·3·2·1) = 6·5!,
6! = 6·5·(4·3·2·1) = 6·5·4!,
cioè:
-quando si sviluppa il fattoriale di un numero, ci si può fermare al fattoriale di un qualsiasi numero fino all'unità (proprietà dello sviluppo del fattoriale di un numero).
c)-Applicazioni:
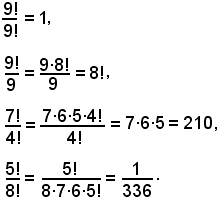
Calcolo delle Cn, k
Poichè la combinazione semplice è una sistemazione di n elementi su k posti, con n > k, che tiene conto solo della natura degli elementi e non dell'ordine degli stessi, è ovvio che se su una Dn, k si effettuano tutte le permutazioni degli n = k elementi, cambiamento di ordine, si ha sempre la stessa combinazione, quindi è:
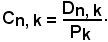
Sostituendo in quest'ultima uguaglianza le formule di Dn, k e Pk, si ha:
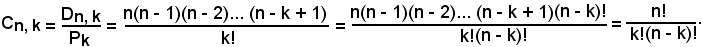
Nota bene
Nei vari passaggi si è moltiplicato numeratore e denominatore per (n - k)! e si è applicata la proprietà dello sviluppo del fattoriale di un numero.
Pertanto risulta:
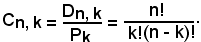
Tale numero si suole indicare con il simbolo
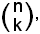
si legge "n su k" e si chiama coefficiente binomiale; n si chiama 1° indice e k 2° indice.
Dunque:
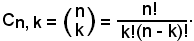
Dalla posizione fatta, segue la regola di sviluppo di un coefficiente binomiale:
-un coefficiente binomiale è uguale al fattoriale del 1° indice, fratto il prodotto del fattoriale del 2° indice per il fattoriale della differenza fra il 1° ed il 2° indice.
Esempi
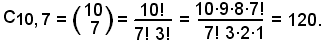
C5, 11 non ha significato perchè (n = 5) < (k = 11).
Nota bene
Con molta efficacia, ma senza alcuna presa di calcolo:

con il rapporto si elimina quanto interessa l'ordine.
Applicazioni: gioco del lotto
Un'applicazione delle combinazioni semplici si ha nel gioco del lotto su ciascuna ruota, sulla quale gli elementi, tutti distinti, sono i numeri interi da 1a 90 ed i posti 2, 3, 4, 5, a seconda che si tratti di ambi, terni, quaterne, cinquine.
Ossia, gli ambi su una ruota sono le C90, 2, i terni le C90, 3, le quaterne le le C90, 4, le cinquine le C90, 5, per cui, sempre su ogni ruota:
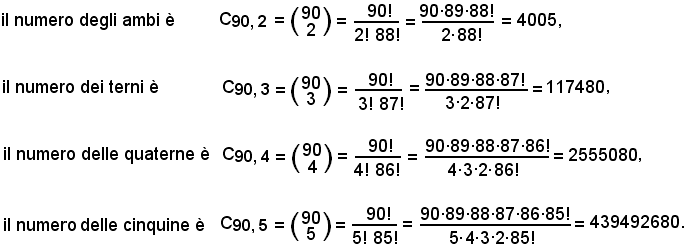
Il gioco del Totocalcio non rientra in questo calcolo combinatorio semplice in quanto gli elementi 1, X, 2, potendosi ripetere, non sono tutti distinti.
Proprietà dei coefficienti binomiali
Si ricordi che in precedenza si è posto:
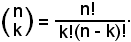
1)-Ogni coefficiente binomiale è uguale ad un altro che ha lo stesso 1° indice e per 2° indice la differenza fra il 1° e il 2° indice:
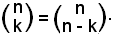
Infatti:
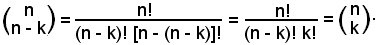
2)-Ogni coefficiente binomiale avente per 2° indice 1 è uguale al 1° indice:
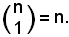
Infatti:
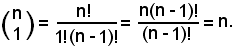
D'altra parte, è evidente che:
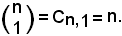
3)-Ogni coefficiente binomiale con i due indici uguali è uguale ad 1:
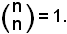
Infatti:
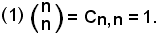
in quanto, se n = k, non potendo variare la natura degli elementi sistemati, non è possibile avere un'altra combinazione oltre quella effettuata.
Si noti che sviluppando il coefficiente binomiale, si avrebbe:
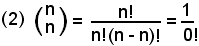
e 0! non ha significato, in base alla definizione di fattoriale di un numero.
Dall'uguaglianza dei primi membri della 1) e della 2) segue quella dei secondi membri, cioè:
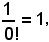
per la validità della quale occorre che si consideri 0! = 1.
4)-Ogni coefficiente binomiale avente per 2° indice lo zero è uguale ad 1:
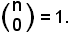
Infatti:
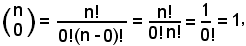
avendo considerato 0! = 1.
Si osservi che, applicando la proprietà 1), si avrebbe avuto ugualmente:
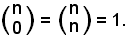
5)-Proprietà di Stiffel - Ogni coefficiente binomiale è uguale alla somma di due coefficienti binomiali:
-il primo avente il 1° indice diminuito di un'unità rispetto a quello dato e il 2° indice uguale a quello dato;
-il secondo avente il 1° ed il 2° indice rispettivamente diminuiti di un'unità rispetto a quelli dati:
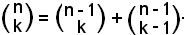
Infatti:
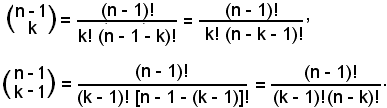
Sommando membro a membro, si ha:
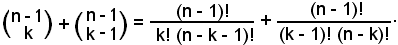
Poichè
k! = k(k - 1)! e (n - k)! = (n - k)(n - k - 1)!,
il m. c. m. dei denominatori è k!(n - k)!, pertanto:
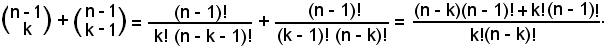
Raccogliendo il fattore comune (n - 1)!, si ha:
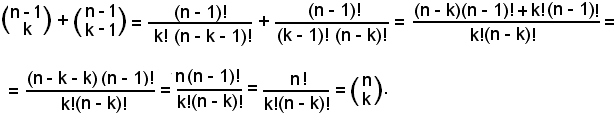
Sviluppo delle potenze dei binomi
1)-Nell'algebra elementare si è visto che:
(a + b)0= 1,
(a + b)1= a + b,
(a + b)2= a2 + 2ab + b2,
(a + b)3= a3 + 3a2b + 3ab2 + b3,
(a + b)4= a4+ 4a3b + 6a2b2 + 4ab3 + b4,
(a + b)5= a5 + 5a4b + 10a3b2 + 10a2b3 + 5ab4 + b5,
. . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . .
ossia, lo sviluppo della potenza di un binomio è un polinomio omogeneo:
a)-avente un numero di termini uguale all'unità dell'esponente aumentate di una,
b)-ordinato secondo le potenze decrescenti del 1° termine e crescenti del secondo,
c)- i cui coefficienti si possono trovare con il triangolo numerico di Tartaglia o con la regola di Newton che seguono.
Triangolo di Tartaglia
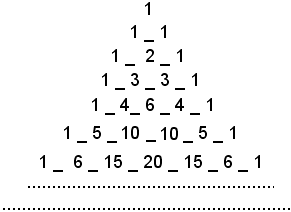
Da esso risulta che:
a)-tutti i primi e gli ultimi coefficienti sono uguali ad 1,
b)-i secondi esponenti indicano l'esponente della potenza sviluppata,
c)-i coefficienti equidistanti dagli estremi sono uguali,
d)-ogni coefficiente è la somma dei due immediatamente superiori da sinistra a destra.
Tale triangolo presenta l'inconveniente che per avere i coefficienti dei termini relativi allo sviluppo di una certa potenza, bisogna conoscere quella dei termini relativi agli sviluppi delle potenze precedenti.
Per eliminare questo inconveniente, Newton fornì la seguente regola:
-il coefficiente di un termine è dato dal prodotto del coefficiente del termine precedente per l'esponente della 1^ lettera di detto termine, diviso il numero dei termini a cui si è pervenuti.
2)-Il triangolo di Tartaglia si può scrivere, usando i coefficienti binomiali, come segue:

che gode delle stesse caratteristiche di quello numerico, come si può controllare applicando le proprietà viste dei coefficienti binomiali.
I coefficienti dei termini relativi allo sviluppo di una certa potenza sono coefficienti binomiali aventi per 1° indice sempre l'esponente della potenza che si vuole sviluppare e per 2° indice i numeri interi consecutivi crescenti a partire da zero fino ad arrivare al 1° indice.
In tal modo i coefficienti diventano indipendenti da quelli precedenti e si potrà scrivere subito lo sviluppo di una qualsiasi potenza di un binomio.
Esempio - Sviluppare (a + b)7.
Si ha:
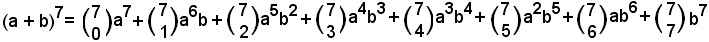
e in generale
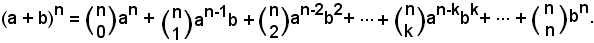
Questo è il cosiddetto binomio di Newton, che si può scrivere nella seguente forma abbreviata:
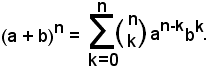
Nota bene
1°)-Dall'ulteriore esame del binomio, risulta che i coefficienti binomiali forniscono anche una regola per ricavare le potenze della parte letterale di ciascun termine.
L'esponente della parte letterale del 1° termine del binomio è dato dalla differenza fra il 1° ed il 2° indice del suo coefficiente binomiale; l'esponente della parte letterale del 2° termine è uguale al 2° indice del suo coefficienrte binomiale.
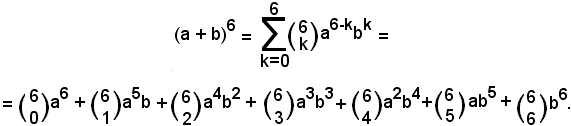
2°)-Se in mezzo al binomio il segno è " - ", i termini sono con segni alternati.
3°)-E' possibile scrivere addirittura un solo termine di una data potenza, in quanto il suo coefficiente binomiale ha per 1° indice l'esponente della data potenza e per 2° indice il numero cardinale, corrispondente a quello ordinale che esprime il posto occupato dal termine, diminuito di una unità, mentre la parte letterale è determinata come detto in 1°).
Esempio
L'undicesimo termine di (a + b)29 è:
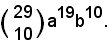
Applicazioni
1)-Se nel binomio di Newton
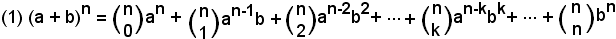
si pone a = b = 1, si ha:
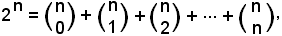
cioè:
-la somma di tutti i coefficienti binomiali relativi all'esponente n è uguale a 2n.
2)-Se nella (1) si pone a = 1 e b = -1, si ha:
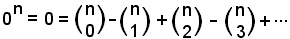
da cui
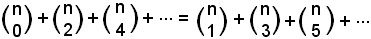
cioè
-la somma dei coefficienti binomiali di posto dispari è uguale a quella dei coefficienti binomiali di posto pari e ciascuna delle due somme è uguale a 2n-1, poichè la somma delle due somme è, per la a), uguale a 2n.
3)-Somma delle potenze simili dei numeri naturali.
Si vuole calcolare:
(2) 1k + 2k + 3k+ ... + (n - 1)k + nk.
Nel caso in cui è k = 1, la (2) diventa:
S1 = 1 + 2 + 3 + ... + (n - 1) + n,
che è la somma dei primi n termini della progressione aritmetica di ragione 1, e quindi:
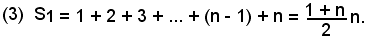
Nel caso in cui è k = 2, la (2) diventa:
(4) S2 = 12 + 22 + 32 + ... + (n - 1)2 + n2.
Per calcolare la somma, si consideri l'identità che si ottiene dallo sviluppo del cubo del binomio:
(1 + x)3 - x3 = 1 + 3x + 3x2,
dalla quale, considerando successivamente x = 1, 2, 3, ... (n - 1), n, si ha:
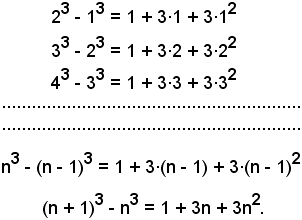
Sommando membro a membro, semplificando e raccogliendo opportunamente, si ha:
e per la (3) e la (4) risulta
(n + 1)3 - 1 = n + 3S1 + 3S2,
per cui
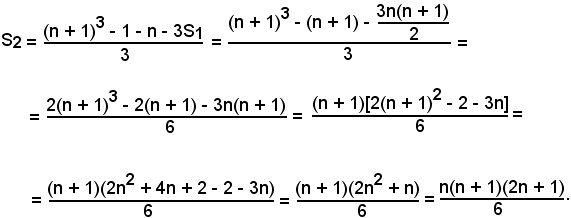
Dunque:
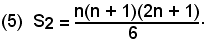
Analogamente si procede per ricavare S3, S4, ... formule che, però, non interessano in seguito.
D8, 5 = 8·7·6·5·4,
Dn, 6 = n(n - 1)(n - 2)(n - 3)(n - 4)(n - 5),
D5, 9 non ha senso perchè (n = 5) < (k = 9),
contro l'ipotesi, perchè n > k.
Calcolo delle Pn
Le permutazioni si presentano come caso particolare delle disposizioni ed il numero di esse si ottiene da quello delle Dn, k per n = k:
Pn = Dn, n = n(n - 1)(n - 2) ... (n - n + 1) = n(n - 1)(n - 2) ...1.
Quindi:
- il numero delle permutazioni semplici è dato dal prodotto di tutti gl'interi consecutivi decrescenti, a partire da quello degli elementi, uguale a quello dei posti, fino ad uno.
Tale prodotto solitamente viene indicato con uno dei seguenti simboli:
dei quali in seguito si preferirà il 1°, e si leggerà
n! = n fattoriale.
Quindi:
Pn = n! = n(n - 1)(n - 2) ... 1.
Esempio:
P6 = 6! = 6·5·4·3·2·1.
Nota bene
a)-indipendentemente dalle permutazioni e dal calcolo combinatorio vale la seguente definizione o posizione:
-fattoriale di un numero è il prodotto di tutti gl'interi consecutivi decrescenti, a partire da quel numero fino all'unità;
b)-applicando la proprietà associativa della moltiplicazione, si ha
6! = 6·(5·4·3·2·1) = 6·5!,
6! = 6·5·(4·3·2·1) = 6·5·4!,
cioè:
-quando si sviluppa il fattoriale di un numero, ci si può fermare al fattoriale di un qualsiasi numero fino all'unità (proprietà dello sviluppo del fattoriale di un numero).
c)-Applicazioni:
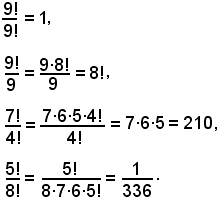
Calcolo delle Cn, k
Poichè la combinazione semplice è una sistemazione di n elementi su k posti, con n > k, che tiene conto solo della natura degli elementi e non dell'ordine degli stessi, è ovvio che se su una Dn, k si effettuano tutte le permutazioni degli n = k elementi, cambiamento di ordine, si ha sempre la stessa combinazione, quindi è:
Sostituendo in quest'ultima uguaglianza le formule di Dn, k e Pk, si ha:
Nota bene
Nei vari passaggi si è moltiplicato numeratore e denominatore per (n - k)! e si è applicata la proprietà dello sviluppo del fattoriale di un numero.
Pertanto risulta:
Tale numero si suole indicare con il simbolo
si legge "n su k" e si chiama coefficiente binomiale; n si chiama 1° indice e k 2° indice.
Dunque:
Dalla posizione fatta, segue la regola di sviluppo di un coefficiente binomiale:
-un coefficiente binomiale è uguale al fattoriale del 1° indice, fratto il prodotto del fattoriale del 2° indice per il fattoriale della differenza fra il 1° ed il 2° indice.
Esempi
C5, 11 non ha significato perchè (n = 5) < (k = 11).
Nota bene
Con molta efficacia, ma senza alcuna presa di calcolo:
con il rapporto si elimina quanto interessa l'ordine.
Applicazioni: gioco del lotto
Un'applicazione delle combinazioni semplici si ha nel gioco del lotto su ciascuna ruota, sulla quale gli elementi, tutti distinti, sono i numeri interi da 1a 90 ed i posti 2, 3, 4, 5, a seconda che si tratti di ambi, terni, quaterne, cinquine.
Ossia, gli ambi su una ruota sono le C90, 2, i terni le C90, 3, le quaterne le le C90, 4, le cinquine le C90, 5, per cui, sempre su ogni ruota:
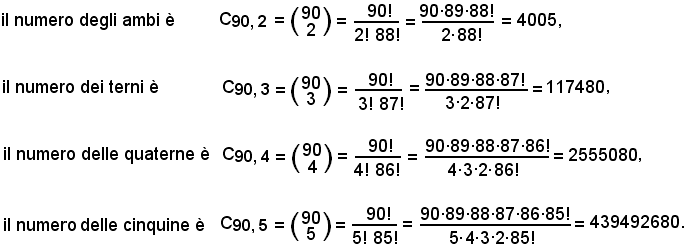
Il gioco del Totocalcio non rientra in questo calcolo combinatorio semplice in quanto gli elementi 1, X, 2, potendosi ripetere, non sono tutti distinti.
Proprietà dei coefficienti binomiali
Si ricordi che in precedenza si è posto:
1)-Ogni coefficiente binomiale è uguale ad un altro che ha lo stesso 1° indice e per 2° indice la differenza fra il 1° e il 2° indice:
Infatti:
2)-Ogni coefficiente binomiale avente per 2° indice 1 è uguale al 1° indice:
Infatti:
D'altra parte, è evidente che:
3)-Ogni coefficiente binomiale con i due indici uguali è uguale ad 1:
Infatti:
in quanto, se n = k, non potendo variare la natura degli elementi sistemati, non è possibile avere un'altra combinazione oltre quella effettuata.
Si noti che sviluppando il coefficiente binomiale, si avrebbe:
e 0! non ha significato, in base alla definizione di fattoriale di un numero.
Dall'uguaglianza dei primi membri della 1) e della 2) segue quella dei secondi membri, cioè:
per la validità della quale occorre che si consideri 0! = 1.
4)-Ogni coefficiente binomiale avente per 2° indice lo zero è uguale ad 1:
Infatti:
avendo considerato 0! = 1.
Si osservi che, applicando la proprietà 1), si avrebbe avuto ugualmente:
5)-Proprietà di Stiffel - Ogni coefficiente binomiale è uguale alla somma di due coefficienti binomiali:
-il primo avente il 1° indice diminuito di un'unità rispetto a quello dato e il 2° indice uguale a quello dato;
-il secondo avente il 1° ed il 2° indice rispettivamente diminuiti di un'unità rispetto a quelli dati:
Infatti:
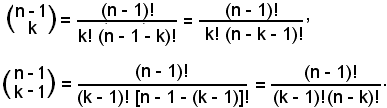
Sommando membro a membro, si ha:
Poichè
k! = k(k - 1)! e (n - k)! = (n - k)(n - k - 1)!,
il m. c. m. dei denominatori è k!(n - k)!, pertanto:
Raccogliendo il fattore comune (n - 1)!, si ha:
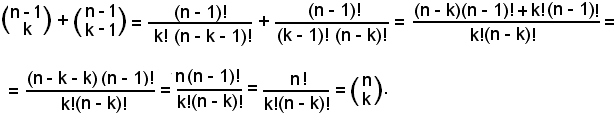
Sviluppo delle potenze dei binomi
1)-Nell'algebra elementare si è visto che:
(a + b)0= 1,
(a + b)1= a + b,
(a + b)2= a2 + 2ab + b2,
(a + b)3= a3 + 3a2b + 3ab2 + b3,
(a + b)4= a4+ 4a3b + 6a2b2 + 4ab3 + b4,
(a + b)5= a5 + 5a4b + 10a3b2 + 10a2b3 + 5ab4 + b5,
. . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . .
ossia, lo sviluppo della potenza di un binomio è un polinomio omogeneo:
a)-avente un numero di termini uguale all'unità dell'esponente aumentate di una,
b)-ordinato secondo le potenze decrescenti del 1° termine e crescenti del secondo,
c)- i cui coefficienti si possono trovare con il triangolo numerico di Tartaglia o con la regola di Newton che seguono.
Triangolo di Tartaglia

Da esso risulta che:
a)-tutti i primi e gli ultimi coefficienti sono uguali ad 1,
b)-i secondi esponenti indicano l'esponente della potenza sviluppata,
c)-i coefficienti equidistanti dagli estremi sono uguali,
d)-ogni coefficiente è la somma dei due immediatamente superiori da sinistra a destra.
Tale triangolo presenta l'inconveniente che per avere i coefficienti dei termini relativi allo sviluppo di una certa potenza, bisogna conoscere quella dei termini relativi agli sviluppi delle potenze precedenti.
Per eliminare questo inconveniente, Newton fornì la seguente regola:
-il coefficiente di un termine è dato dal prodotto del coefficiente del termine precedente per l'esponente della 1^ lettera di detto termine, diviso il numero dei termini a cui si è pervenuti.
2)-Il triangolo di Tartaglia si può scrivere, usando i coefficienti binomiali, come segue:

che gode delle stesse caratteristiche di quello numerico, come si può controllare applicando le proprietà viste dei coefficienti binomiali.
I coefficienti dei termini relativi allo sviluppo di una certa potenza sono coefficienti binomiali aventi per 1° indice sempre l'esponente della potenza che si vuole sviluppare e per 2° indice i numeri interi consecutivi crescenti a partire da zero fino ad arrivare al 1° indice.
In tal modo i coefficienti diventano indipendenti da quelli precedenti e si potrà scrivere subito lo sviluppo di una qualsiasi potenza di un binomio.
Esempio - Sviluppare (a + b)7.
Si ha:
e in generale
Questo è il cosiddetto binomio di Newton, che si può scrivere nella seguente forma abbreviata:
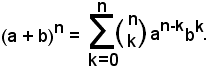
Nota bene
1°)-Dall'ulteriore esame del binomio, risulta che i coefficienti binomiali forniscono anche una regola per ricavare le potenze della parte letterale di ciascun termine.
L'esponente della parte letterale del 1° termine del binomio è dato dalla differenza fra il 1° ed il 2° indice del suo coefficiente binomiale; l'esponente della parte letterale del 2° termine è uguale al 2° indice del suo coefficienrte binomiale.
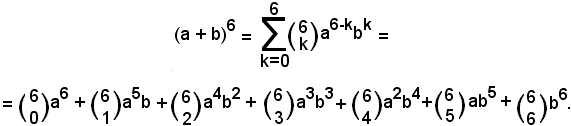
2°)-Se in mezzo al binomio il segno è " - ", i termini sono con segni alternati.
3°)-E' possibile scrivere addirittura un solo termine di una data potenza, in quanto il suo coefficiente binomiale ha per 1° indice l'esponente della data potenza e per 2° indice il numero cardinale, corrispondente a quello ordinale che esprime il posto occupato dal termine, diminuito di una unità, mentre la parte letterale è determinata come detto in 1°).
Esempio
L'undicesimo termine di (a + b)29 è:
Applicazioni
1)-Se nel binomio di Newton
si pone a = b = 1, si ha:
cioè:
-la somma di tutti i coefficienti binomiali relativi all'esponente n è uguale a 2n.
2)-Se nella (1) si pone a = 1 e b = -1, si ha:
da cui
cioè
-la somma dei coefficienti binomiali di posto dispari è uguale a quella dei coefficienti binomiali di posto pari e ciascuna delle due somme è uguale a 2n-1, poichè la somma delle due somme è, per la a), uguale a 2n.
3)-Somma delle potenze simili dei numeri naturali.
Si vuole calcolare:
(2) 1k + 2k + 3k+ ... + (n - 1)k + nk.
Nel caso in cui è k = 1, la (2) diventa:
S1 = 1 + 2 + 3 + ... + (n - 1) + n,
che è la somma dei primi n termini della progressione aritmetica di ragione 1, e quindi:
Nel caso in cui è k = 2, la (2) diventa:
(4) S2 = 12 + 22 + 32 + ... + (n - 1)2 + n2.
Per calcolare la somma, si consideri l'identità che si ottiene dallo sviluppo del cubo del binomio:
(1 + x)3 - x3 = 1 + 3x + 3x2,
dalla quale, considerando successivamente x = 1, 2, 3, ... (n - 1), n, si ha:
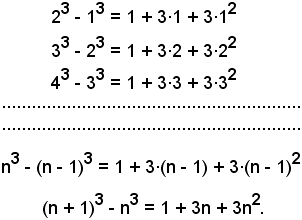
Sommando membro a membro, semplificando e raccogliendo opportunamente, si ha:
(n + 1)3 - 13 = 1 + 1 + ... + 1 + 1 + 3[1 + 2 + 3 + ... + (n - 1) + n] + 3[12 + 22 + 32 + ... + (n - 1)2 + n2],
e per la (3) e la (4) risulta
(n + 1)3 - 1 = n + 3S1 + 3S2,
per cui
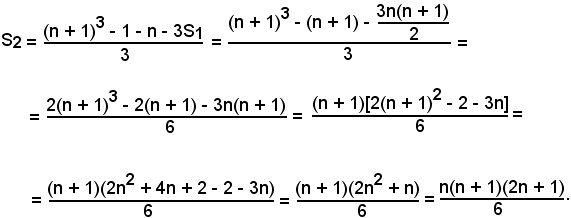
Dunque:
Analogamente si procede per ricavare S3, S4, ... formule che, però, non interessano in seguito.