MIKY & GENNY
DERIVATE E APPLICAZIONI ---> INDICE
Concetto di derivata
1)-Rapporto incrementale di una funzione
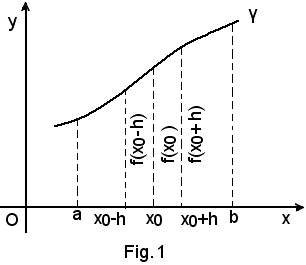
Sia y = f(x) una funzione definita in un intervallo (a, b) aperto o chiuso, limitato o illimitato e sia γ la curva da essa rappresentata.
Considerato un punto x0 di (a, b), sia y0 = f(x0) il valore che la funzione assume in esso.
Incrementando positivamente x0 di una quantità h = Δx0, si ottiene alla sua destra il punto x0 + h oppure x0 + Δx0.
Incrementando negativamente x0 di una quantità -h = -Δx0, si ottiene alla sua sinistra il punto x0 - h oppure x0 - Δx0.
Siano f(x0 + h) e f(x0 - h) i valori della funzione in questi due nuovi punti.
Le differenze
(1) Δy = f(x0 + h) - f(x0),
(1') Δy = f(x0 - h) - f(x0)
si chiamano, rispettivamente, incremento destro e sinistro della funzione.
I rapporti
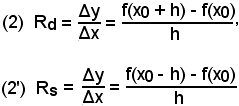
si chiamano, rispettivamente, rapporto incrementale destro e rapporto incrementale sinistro della funzione.
Per come è stato considerato, ognuno dei rapporti incrementali Rd e Rs diventa, a sua volta, una funzione dell'incremento h dato a x0. Il limite di Rd per l'incremento , quando esiste determinato e finito, si chiama derivata a destra della funzione e si scrive:
, quando esiste determinato e finito, si chiama derivata a destra della funzione e si scrive:
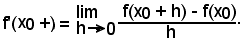
Analogamente, il limite di Rs per , quando esiste determinato e finito, si chiama derivata a sinistra della funzione e si scrive:
, quando esiste determinato e finito, si chiama derivata a sinistra della funzione e si scrive:
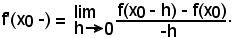
Quando accade che
f'(x0 +) = f'(x0 -),
cioè
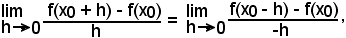
il valore determinato, finito e comune dei due limiti, si chiama derivata della funzione nel punto x0.
Quindi:
-la derivata prima della funzione in un punto è il limite, per l'incremento della variabile tendente a zero, comune e finito, quando esiste, dei due rapporti incrementali.
2)-Osservazioni
1^) Dire che esiste f'(x0) significa, per quanto detto, che è f'(x0 +) = f'(x0 -). Si badi però che l'esistenza della f'(x0 +) e della f'(x0 -) non implica l'esistenza della f'(x0), perchè potrebbe essere f'(x0 +) ≠ f'(x0 -).
2^) Se il punto x0 coincide con un estremo dell'intervallo (a, b) di esistenza della funzione, si può considerare solo il Rd, se x0 = a oppure il Rs, se x0 = b, e quindi per la funzione si ha, rispettivamente, solo la derivata a destra o quella a sinistra del punto. Si parla ugualmente solo di derivata a destra o a sinistra di un punto, quando è f'(x0 +) ≠ f'x0 -).
3^) Una funzione che ammette la derivata in un punto dell'intervallo di esistenza, si dice derivabile in tale punto.
Se poi la funzione ha derivata in tutti i punti dell'intervallo, che può essere anche tutto l'asse x, la funzione si dice derivabile nell'intervallo.
4^) La derivata prima di una funzione in un punto x0 si indica con uno dei seguenti simboli:
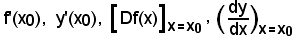
e, quindi, la derivata prima di una funzione in un punto generico dell'intervallo si indica con uno dei seguenti simboli
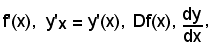
quest'ultimo da leggere, per ora, "derivata di y rispetto alla variabile x" e non diversamente.
5^) Per le funzioni che solitamente si considerano è sempre
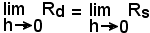
e quindi, per avere la derivata della funzione, si calcola uno solo dei limiti, e solitamente, per comodità e abitudine, quello di Rd.
Pertanto si scrive:
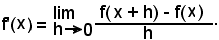
6^) Si osservi che se si calcolasse il
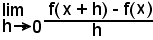
ponendo 0 al posto di h, si avrebbe la forma indeterminata
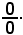
Ciò dice che il numeratore e il denominatore, ossia l'incremento Δy della funzione è quello della Δx = h della variabile indipendente sono due infinitesimi.
Poichè per definizione la derivata è il valore finito del limite, l'esistenza della derivata esprime che i due infinitesimi suddetti sono dello stesso ordine.
7^) Se fosse
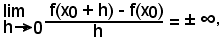
in base a quanto detto, non esisterebbe la f'(x0); tuttavia si suol dire che esiste la derivata impropria della funzione nel punto x0.
3)-Derivabilità e continuità
Teorema - Se una funzione y = f(x) è derivabile in un punto x0, è anche continua in x0.
Infatti, essendo y = f(x) derivabile in x0, è noto che
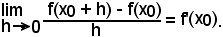
Allora, potendo scrivere
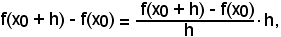
considerando il limite per di ambo i membri, si ha:
di ambo i membri, si ha:
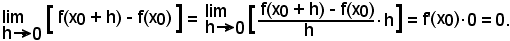
Quindi, dire che
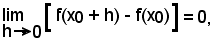
significa
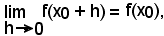
cioè è dimostrata la continuità della funzione nel punto x0.
Non vale il teorema inverso, ossia non è sempre vero che se una funzione è continua in un punto è in esso anche derivabile, pertanto si dice che:
-la continuità di una funzione in un punto è condizione solo necessaria, ma non anche sufficiente, per la derivabilità della stessa nel punto considerato.
Da ciò segue che la condizione di derivabilità di una funzione è più restrittiva della continuità.
Derivata delle funzioni elementari
Per avere la derivata di una funzione occorre formare sempre il rapporto incrementale della funzione relativo al punto che si vuole e che può anche essere quello generico e calcolare il suo limite finito per .
.
1^) Derivata della variabile indipendente:
y = x.
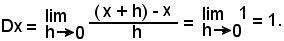
Quindi:
Dx = 1.
2^) Derivata della potenza ad esponente intero positivo della variabile indipendente:
y = xn.
Ricordando che
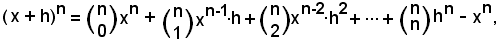
da cui
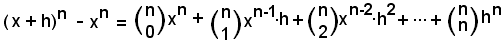
e che
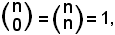
si considera
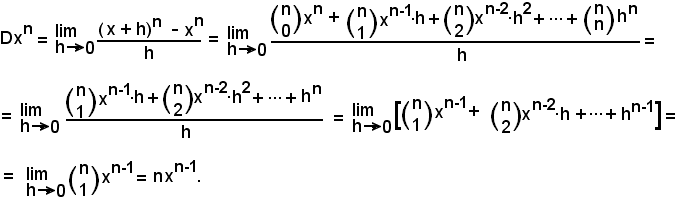
Quindi:
Dxn = nxn-1.
Nota bene
La terzultima espressione delle uguaglianze suddette si è ottenuta dalla precedente dividendo numeratore e denominatore per h, mentre la penultima si è ottenuta dalla precedente tenendo conto che tutti i termini dal secondo in poi tendono a zero per h tendente a zero.
Si osservi ora che per n = 1 la derivata suddetta diventa Dx = 1, vista in precedenza.
3^) Derivata di una costante:
y = k.
Tenendo presente che y = k rappresenta la parallela all'asse x alla distanza k da esso, si ha:
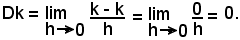
Quindi:
4^) Derivata della radice quadrata della variabile indipendente:
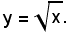
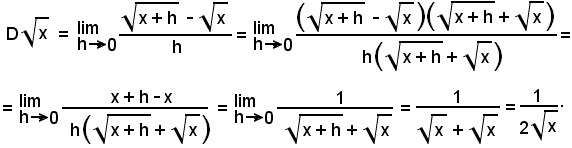
Quindi:
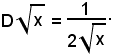
Nota bene
La terza espressione delle uguaglianze suddette si è ottenuta dalla precedente moltiplicando il numeratore e il denominatore per
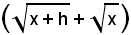
e poi si è sviluppato e semplificato.
5^) Derivata del logaritmo neperiano della variabile indipendente:
y = logx.
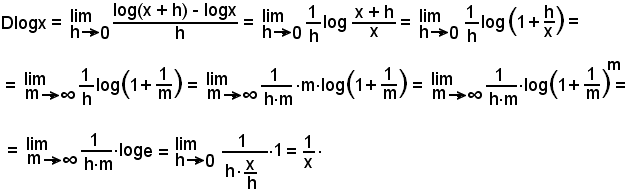
Quindi:
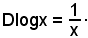
Nota bene
Per la dimostrazione suddetta, sono stati effettuati in sequenza i seguenti passaggi, partendo da Dlogx:
a)-si è applicata la definizione di derivata;
b)-si è applicato il teorema del logaritmo di un quoziente;
c)-si è considerata la forma equivalente;
d)-si è posto
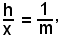
ossia
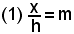
e osservato che per
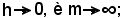
e)-si è moltiplicato e diviso per m;
f)-si è applicato il teorema del logaritmo di una potenza;
g)-si è tenuto conto che
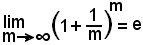
e che loge = 1, inoltre si è sostituito ad m il valore espresso dalla (1);
h)-si è ottenuto il risultato.
6^) Derivata della funzione:
y = senx.
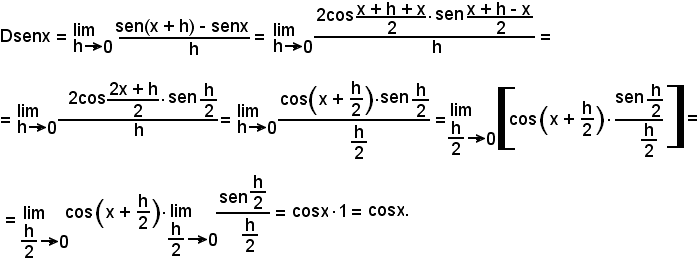
Quindi:
Dsenx = cosx.
Nota bene
Per la dimostrazione suddetta, sono stati effettuati in sequenza i seguenti passaggi, partendo da Dsenx:
a)-si è applicata la definizione di derivata;
b)-si è applicata la formula di prostaferesi
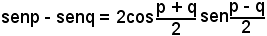
al numeratore;
c)-si è semplificato;
d)-si è considerata la forma equivalente;
e)-si è osservato che

f)-si è applicato il teorema del limite di un prodotto;
g)-si è tenuto conto che il limite del rapporto tra il seno di un arco e l'arco stesso, misurato in radianti, quando questo tende a zero, è uguale ad uno, cioè:
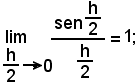
h)-si è ottenuto il risultato.
7^) Derivata della funzione:
y = cosx.
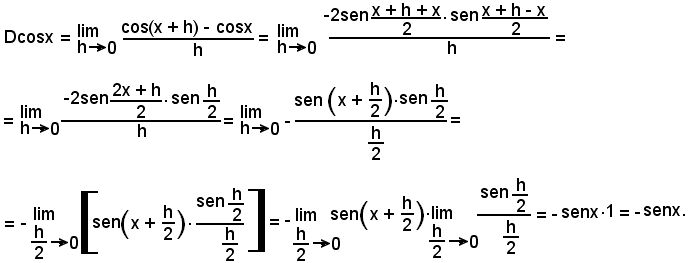
Quindi:
Dcosx = -senx.
Nota bene
Per la dimostrazione suddetta, sono stati effettuati in sequenza i seguenti passaggi, partendo da Dcosx:
a)-si è applicata la definizione di derivata;
b)-si è applicata la formula di prostaferesi

al numeratore e si è seguito lo stesso ragionamento della 6).
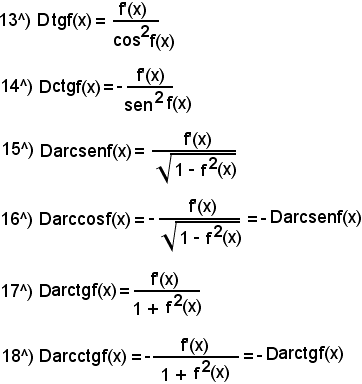
8^) Derivata della funzione:
y = tgx.
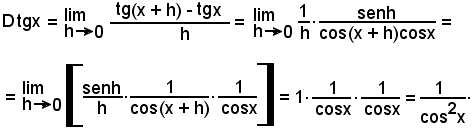
Quindi:
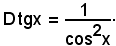
Nota bene
Per la dimostrazione suddetta, sono stati effettuati in sequenza i seguenti passaggi, partendo da Dtgx:
a)-si è applicata la definizione di derivata;
b)-si è applicata la formula di prostaferesi
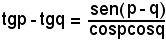
al numeratore; il resto è ovvio.
9^) Derivata della funzione:
y = ctgx.
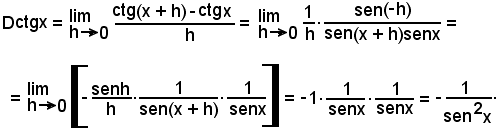
Quindi:
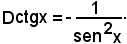
Nota bene
Per la dimostrazione suddetta, sono stati effettuati in sequenza i seguenti passaggi, partendo da Dctgx:
a)-si è applicata la definizione di derivata;
b)-si è applicata la formula di prostaferesi
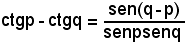
al numeratore;
c)-si è tenuto conto che sen(-h) = -senh;
il resto è ovvio.
10^) Derivata della funzione:
y = ex.
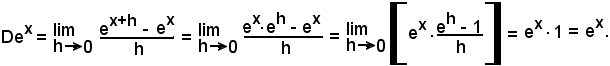
Quindi:
Dex = ex.
Nota bene
Per la dimostrazione suddetta, sono stati effettuati in sequenza i seguenti passaggi, partendo da Dex:
a)-si è applicata la definizione di derivata;
b-si è tenuto conto che ex+h = ex·eh;
Regole di derivazione delle operazioni tra funzioni
1)-Considerazioni generali
1^) Tutte le funzioni che saranno considerate in seguito s'intenderanno definite nello stesso intervallo, che è quello comune agl'intervalli in cui ciascuna funzione è definita per proprio conto.
2^) Tutte le funzioni avranno derivata, e quindi saranno continue, in uno stesso punto generico x.
3^) Nel punto considerato, la funzione figurante al denominatore sarà diversa da zero.
4^) Si ricordi che date due funzioni y1 = f1(x) e y2 = f2(x), una loro combinazione lineare è data da
y = αf1(x) + βf2(x),
con α, β costanti arbitrarie.
2)-Derivata della combinazione lineare di due o più funzioni.
Teorema - La derivata di una combinazione lineare di due o più funzioni è uguale alla combinazione lineare, secondo le stesse costanti, delle derivate delle singole funzioni:
(1) D[αf1(x) + βf2(x)] = αDf1(x) + βDf2(x) = αf'1(x) + βf'2(x).

come volevasi dimostrare.
Casi particolari
1°) Se α = β = 1, la (1) diventa:
D[f1(x) + f2(x)] = Df1(x) + Df2(x) = f'1(x) + f'2(x),
cioè: la derivata della somma di due o più funzioni è ugiuale alla somma delle derivate delle singole funzioni.
2°) Se α = 1 e β = -1, la (1) diventa:
D[f1(x) - f2(x)] = Df1(x) - Df2(x) = f'1(x) - f'2(x),
cioè: la derivata della differenza di due funzioni è ugiuale alla differenza delle derivate delle singole funzioni.
3)-Derivata del prodotto di due funzioni
Teorema - La derivata del prodotto di due funzioni è uguale alla derivata della 1^ funzione per la seconda non derivata più la 1^ funzione per la derivata della 2^:
D[f1(x)·f2(x)] = f'1(x)·f2(x) + f1(x)·f'2(x).
Infatti:
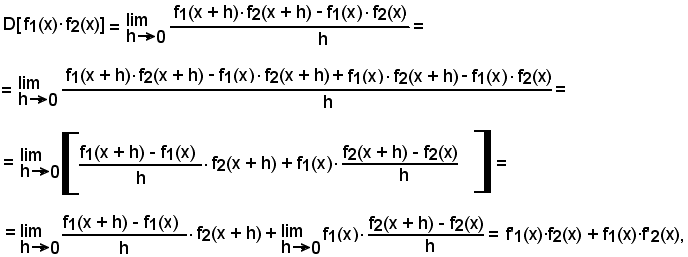
come volevasi dimostrare.
Nota bene
f1(x )·f2(x + h).
4)-Derivata del prodotto di tre funzioni
Si ottiene applicando due volte la regola 3).
D[f1(x)·f2(x)·f3(x)] = D{[f1(x)·f2(x)]·f3(x)} = D[f'1(x)·f2(x)]·f3(x) + f'1(x)·f'2(x)·Df3(x) = [f'1(x)·f2(x) +
f1(x)·f'2(x)]·f3(x) + f1(x)·f2(x)·f'3(x) = f'1(x)·f2(x)·f'3(x) + f1(x)·f'2(x)·f3(x) + f1(x)·f2(x)·f'3(x).
cioè:
-la derivata del prodotto di tre o più funzioni è uguale alla somma dei prodotti della derivata di ciascuna funzione per tutte le altre non derivate.
5)-Derivata del prodotto di una costante per una funzione
Si ottiene applicando sempre la regola 3).
D[k·f(x)] = (Dk)·f(x) + k·Df(x) = k·Df(x),
essendo Dk = 0,
cioè:
-una costante moltiplicativa passa inalterata in derivazione.
6)-Derivata del quoziente di due funzioni
Teorema - La derivata del quoziente di due funzioni è uguale ad una frazione che ha per numeratore il prodotto tra la derivata della funzione dividendo e quella divisore, non derivata, diminuito del prodotto tra la funzione dividendo e la derivata di quella divisore e per denominatore il quadrato della funzione divisore:
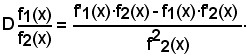
Infatti:
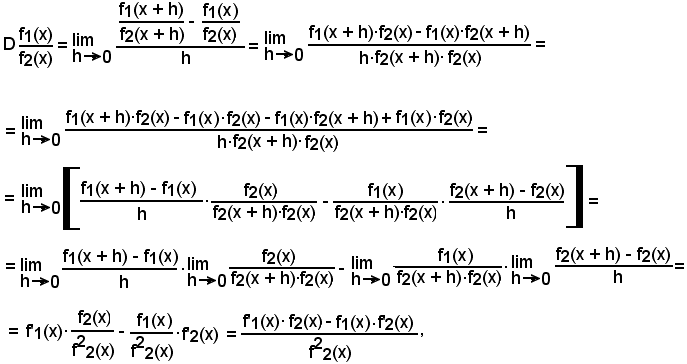
come volevasi dimostrare.
Nota bene
1)-Nella dimostrazione suddetta, al terzo passaggio, si è sottratto e aggiunto al numeratore
f1(x )·f2(x) e poi si sono scisse le frazioni.
2)-La dimostrazione suddetta si può effettuare anche considerando
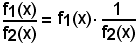
e applicando la regola di derivazione del prodotto e quella della derivata inversa della funzione che segue.
7)-Derivata della inversa di una funzione
Teorema - La derivata della inversa di una funzione è uguale ad una frazione che ha per numeratore la derivata, cambiata di segno, della funzione e per denominatore il quadrato della stessa funzione:
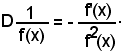
Infatti:
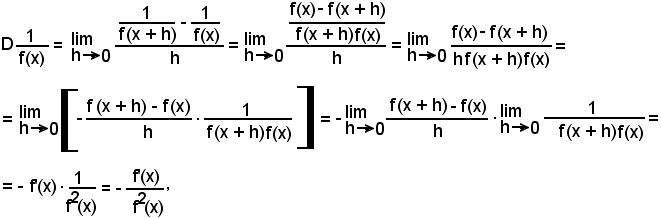
come volevasi dimostrare.
Nota bene
1)-La dimostrazione suddetta si può effettuare anche applicando il teorema della derivata di un quoziente, si ha:
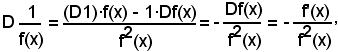
essendo D1 = 0.
2)-Per quanto detto in 5), si ha:
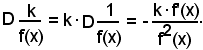
3)-Si rammenta che, in precedenza, si è trovato
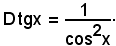
Allo stesso risultato si perviene considerando
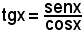
e applicando la regola di derivazione del quoziente di due funzioni, cioè:
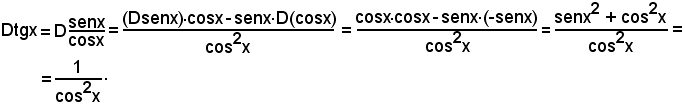
4)-Analogamente, si perviene allo stesso risultato, considerando
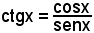
e applicando la regola di derivazione del quoziente di due funzioni, cioè:
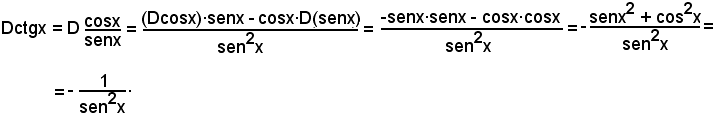
5)-Sapendo che è anche
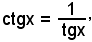
applicando la regola di derivazione dell'inversa di una funzione, si ha:
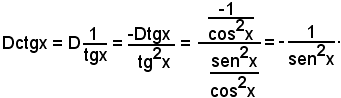
6)-Particolarmente importante per le numerose applicazioni è
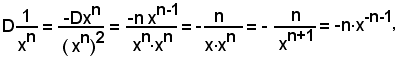
cioè:
-la regola di derivazione della potenza della variabile, data per l'esponente intero positivo nella formula gia vista, cioè in
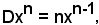
vale anche per l'esponente intero negativo.
Significato geometrico del rapporto incrementale e della derivata prima della funzione in un punto
1)-Premesse
Il concetto di derivata di una funzione di una variabile è uno dei più importanti della matematica. La parte della matematica, basata su tale concetto, è chiamata calcolo differenziale.
Il primo problema che dette origine al calcolo differenziale fu quello geometrico della ricerca della tangente ad una curva in un suo punto.
Sussessivamente se ne presentò un altro di natura fisica: quello del calcolo della velocità di un punto in moto, che sarà trattato.
2)-Retta tangente in un punto ad una curva
Nella geometria elementare sono state date le seguenti definizioni:
1^)-la tangente ad una circonferenza è la retta che ha in comune con essa un solo punto;
2^)-la tangente ad una circonferenza è la posizione limite a cui tende la retta secante TT1 quando

3^)-la tangente in un punto della circonferenza è la perpendicolare al raggio passante per il punto di contatto. Quest'ultima proprietà consente di tracciare subito la tangente in qualsiasi punto della circonferenza.
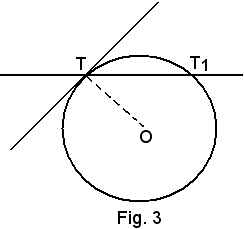
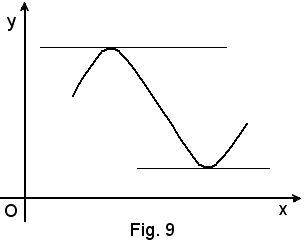
Si osservi che la 1^) definizione non è estendibile quando al posto della circonferenza si considera una qualsiasi altra curva, come ad esempio quella della figura seguente:
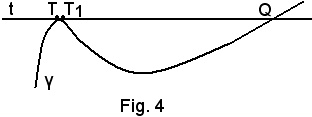
La retta t non incontra la curva γ nel solo punto T e quindi, in base alla 1^) definizione non è tangente alla curva. La retta t, invece, è ugualmente considerata come tangente nel punto T, intendendo in tal modo ritenerla come la posizione limite raggiunta dalla retta TT1 quando T1 tende a T.
La 2^) definizione è, pertanto, più utile ed anche più generale della precedente e risponde meglio di quella ai risultati cui la stessa intuizione fa pervenire.
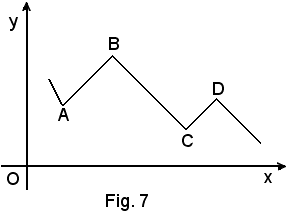
E' bene tuttavia precisare che con ciò non si è inteso dire che in ogni punto di una qualsiasi curva esista un'unica tangente o, addirittura, esista una tangente. Infatti, se si considera la curva γ della fig. 5 o della fig. 6, nel punto T, detto punto angoloso, esistono due rette t e t' tangenti alla curva.
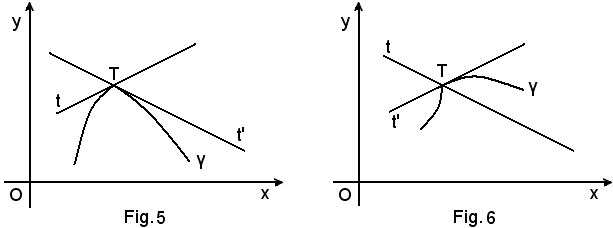
Ed ancora, se si considera la linea spezzata della fig, 7, si può vedere che pur essendo la linea continua nei vertici A, B, C, D la tangente addirittura non esiste.
Dagli esempi fatti, scaturisce con sufficiente evidenza che la sola continuità di una funzione non consente di attibuire alla curva che rappresenta la funzione tutte le proprietà viste per le curve più comuni.
L'esistenza della tangente ad una curva in un suo punto è data dal seguente teorema:
-condizione necessaria e sufficiente affinchè esista la tangente ad una curva in un suo punto è che in tale punto la funzione, che la curva rappresenta, abbia la derivata.
3)-Coefficiente angolare ed equazione della tangente ad una curva in un suo punto
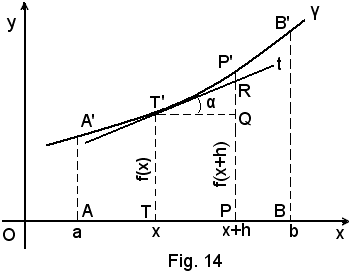
Sia y = f(x) una funzione derivabile in (a, b) e sia γ l'arco di curva che essa rappresenta in detto intervallo. Si sa che nel punto x0 il rapporto incrementale della funzione è:
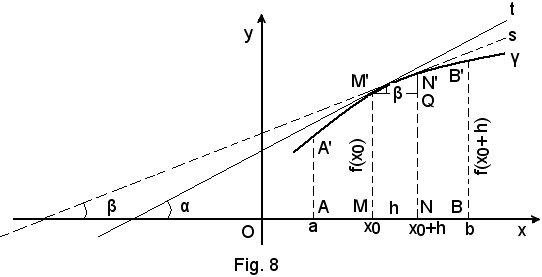
Poichè in figura è
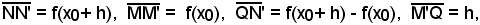
la (1) diventa
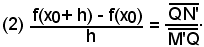
Poichè ancora, dal triangolo rettangolo M'QN', per una nota formula della trigonometria, è
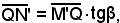
ossia
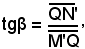
la (2) si può scrivere
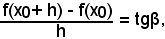
cioè:
-il rapporto incrementale di una funzione in un punto è uguale alla tangente trigonometrica dell'angolo che la secante alla curva, passante per i suoi punti, corrispondenti a quelli presi sull'intervallo, forma con la direzione positiva dell'asse x, in quanto è:
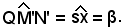
Più semplicemente, in base a note nozioni di geometria analitica, si può dire che:
-il rapporto incrementale di una funzione in un punto è uguale al coefficiente angolare della retta secante la curva nei suoi punti corrispondenti a quelli presi sull'intervallo.
Allora la derivata della funzione, esistente per ipotesi nel punto x0, come è noto è:
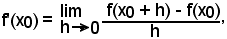
ma quando h tende a zero, N tende ad M sull'intervallo e sulla curva N' tende ad M', ossia la secante s diventa tangente t alla curva, nel punto M' ed ancora tgβ tende a tgα, per cui si ha:
(3) f'(x0) = tgα,
cioè:
-la derivata di una funzione in un punto è uguale al coefficiente angolare della retta tangente alla curva, che rappresenta la funzione, nel suo punto corrispondente a quello preso sull'intervallo.
Si ricordi che se M'[x0, y0 = f(x0)] è un punto di una curva, l'equazione del fascio di rette passanti per tale punto è data da:
y - y0 = m(x - x0),
dalla quale, al variare del parametro m, si hanno le infinite rette del fascio.
Quella tangente alla curva nello stesso punto si avrà sostituendo ad m il coefficiente angolare dato dalla (3), pertanto la sua equazione è:
(4) y - y0 = f'(x0)·(x - x0).
Esempi
1°)-Scrivere l'equazione della tangente alla parabola di equazione y = 2x2 - 3x + 1, nel punto di ascissa x0 = 2.
Si calcola dapprima y0 = f(x0) = f(2) = 3, e poi il fascio di rette passanti per il punto dato, che ha
y - 3 = m(x - 2).
2°)-Scrivere l'equazione della tangente alla curva di equazione
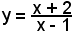
nel suo punto di ascissa x0 = 2.
Essendo
l'equazione del fascio di rette passanti per il punto (2, 4) diventa:
y - 4 = m(x - 2)
1)-Rapporto incrementale di una funzione
Sia y = f(x) una funzione definita in un intervallo (a, b) aperto o chiuso, limitato o illimitato e sia γ la curva da essa rappresentata.
Considerato un punto x0 di (a, b), sia y0 = f(x0) il valore che la funzione assume in esso.
Incrementando positivamente x0 di una quantità h = Δx0, si ottiene alla sua destra il punto x0 + h oppure x0 + Δx0.
Incrementando negativamente x0 di una quantità -h = -Δx0, si ottiene alla sua sinistra il punto x0 - h oppure x0 - Δx0.
Siano f(x0 + h) e f(x0 - h) i valori della funzione in questi due nuovi punti.

Le differenze
si chiamano, rispettivamente, incremento destro e sinistro della funzione.
I rapporti
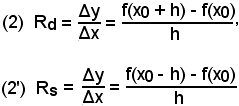
Per come è stato considerato, ognuno dei rapporti incrementali Rd e Rs diventa, a sua volta, una funzione dell'incremento h dato a x0. Il limite di Rd per l'incremento
Analogamente, il limite di Rs per
Quando accade che
f'(x0 +) = f'(x0 -),
cioè
il valore determinato, finito e comune dei due limiti, si chiama derivata della funzione nel punto x0.
Quindi:
-la derivata prima della funzione in un punto è il limite, per l'incremento della variabile tendente a zero, comune e finito, quando esiste, dei due rapporti incrementali.
2)-Osservazioni
1^) Dire che esiste f'(x0) significa, per quanto detto, che è f'(x0 +) = f'(x0 -). Si badi però che l'esistenza della f'(x0 +) e della f'(x0 -) non implica l'esistenza della f'(x0), perchè potrebbe essere f'(x0 +) ≠ f'(x0 -).
2^) Se il punto x0 coincide con un estremo dell'intervallo (a, b) di esistenza della funzione, si può considerare solo il Rd, se x0 = a oppure il Rs, se x0 = b, e quindi per la funzione si ha, rispettivamente, solo la derivata a destra o quella a sinistra del punto. Si parla ugualmente solo di derivata a destra o a sinistra di un punto, quando è f'(x0 +) ≠ f'x0 -).
3^) Una funzione che ammette la derivata in un punto dell'intervallo di esistenza, si dice derivabile in tale punto.
Se poi la funzione ha derivata in tutti i punti dell'intervallo, che può essere anche tutto l'asse x, la funzione si dice derivabile nell'intervallo.
4^) La derivata prima di una funzione in un punto x0 si indica con uno dei seguenti simboli:
e, quindi, la derivata prima di una funzione in un punto generico dell'intervallo si indica con uno dei seguenti simboli
quest'ultimo da leggere, per ora, "derivata di y rispetto alla variabile x" e non diversamente.
5^) Per le funzioni che solitamente si considerano è sempre
e quindi, per avere la derivata della funzione, si calcola uno solo dei limiti, e solitamente, per comodità e abitudine, quello di Rd.
Pertanto si scrive:
6^) Si osservi che se si calcolasse il
ponendo 0 al posto di h, si avrebbe la forma indeterminata
Ciò dice che il numeratore e il denominatore, ossia l'incremento Δy della funzione è quello della Δx = h della variabile indipendente sono due infinitesimi.
Poichè per definizione la derivata è il valore finito del limite, l'esistenza della derivata esprime che i due infinitesimi suddetti sono dello stesso ordine.
7^) Se fosse
in base a quanto detto, non esisterebbe la f'(x0); tuttavia si suol dire che esiste la derivata impropria della funzione nel punto x0.
3)-Derivabilità e continuità
Teorema - Se una funzione y = f(x) è derivabile in un punto x0, è anche continua in x0.
Infatti, essendo y = f(x) derivabile in x0, è noto che
Allora, potendo scrivere
considerando il limite per
Quindi, dire che
significa
cioè è dimostrata la continuità della funzione nel punto x0.
Non vale il teorema inverso, ossia non è sempre vero che se una funzione è continua in un punto è in esso anche derivabile, pertanto si dice che:
-la continuità di una funzione in un punto è condizione solo necessaria, ma non anche sufficiente, per la derivabilità della stessa nel punto considerato.
Da ciò segue che la condizione di derivabilità di una funzione è più restrittiva della continuità.
Derivata delle funzioni elementari
Per avere la derivata di una funzione occorre formare sempre il rapporto incrementale della funzione relativo al punto che si vuole e che può anche essere quello generico e calcolare il suo limite finito per
1^) Derivata della variabile indipendente:
Quindi:
Dx = 1.
2^) Derivata della potenza ad esponente intero positivo della variabile indipendente:
y = xn.
Ricordando che
da cui
e che
si considera
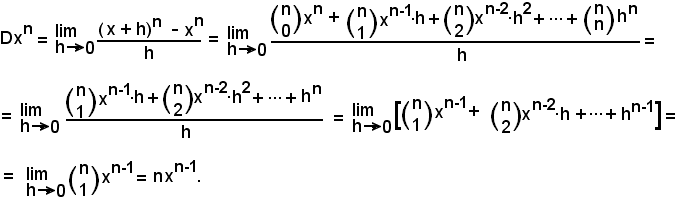
Quindi:
Dxn = nxn-1.
Nota bene
La terzultima espressione delle uguaglianze suddette si è ottenuta dalla precedente dividendo numeratore e denominatore per h, mentre la penultima si è ottenuta dalla precedente tenendo conto che tutti i termini dal secondo in poi tendono a zero per h tendente a zero.
Si osservi ora che per n = 1 la derivata suddetta diventa Dx = 1, vista in precedenza.
3^) Derivata di una costante:
Tenendo presente che y = k rappresenta la parallela all'asse x alla distanza k da esso, si ha:
Quindi:
Dk = 0.

4^) Derivata della radice quadrata della variabile indipendente:
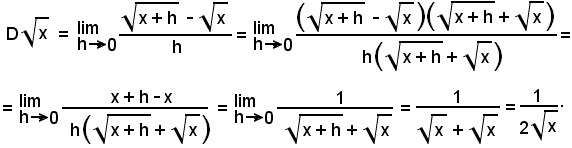
Quindi:
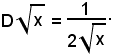
Nota bene
La terza espressione delle uguaglianze suddette si è ottenuta dalla precedente moltiplicando il numeratore e il denominatore per
e poi si è sviluppato e semplificato.
5^) Derivata del logaritmo neperiano della variabile indipendente:
y = logx.
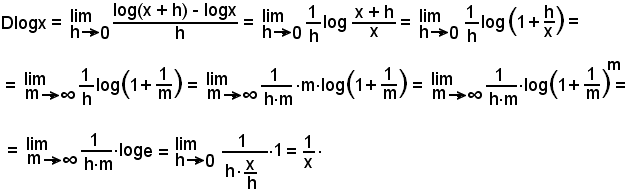
Quindi:
Nota bene
Per la dimostrazione suddetta, sono stati effettuati in sequenza i seguenti passaggi, partendo da Dlogx:
a)-si è applicata la definizione di derivata;
b)-si è applicato il teorema del logaritmo di un quoziente;
c)-si è considerata la forma equivalente;
d)-si è posto
ossia
e osservato che per
e)-si è moltiplicato e diviso per m;
f)-si è applicato il teorema del logaritmo di una potenza;
g)-si è tenuto conto che
e che loge = 1, inoltre si è sostituito ad m il valore espresso dalla (1);
h)-si è ottenuto il risultato.
6^) Derivata della funzione:
y = senx.
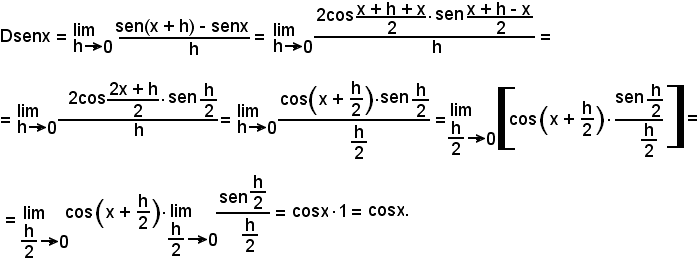
Quindi:
Dsenx = cosx.
Nota bene
Per la dimostrazione suddetta, sono stati effettuati in sequenza i seguenti passaggi, partendo da Dsenx:
a)-si è applicata la definizione di derivata;
b)-si è applicata la formula di prostaferesi
al numeratore;
c)-si è semplificato;
d)-si è considerata la forma equivalente;
e)-si è osservato che
f)-si è applicato il teorema del limite di un prodotto;
g)-si è tenuto conto che il limite del rapporto tra il seno di un arco e l'arco stesso, misurato in radianti, quando questo tende a zero, è uguale ad uno, cioè:

h)-si è ottenuto il risultato.
7^) Derivata della funzione:
y = cosx.
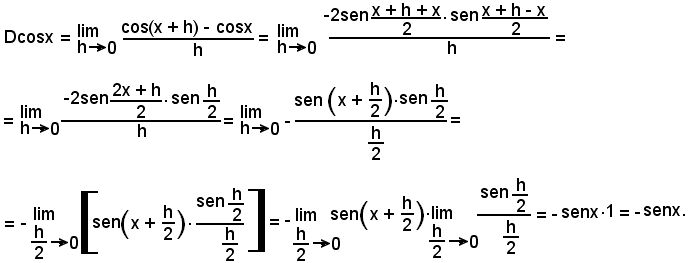
Quindi:
Dcosx = -senx.
Nota bene
Per la dimostrazione suddetta, sono stati effettuati in sequenza i seguenti passaggi, partendo da Dcosx:
a)-si è applicata la definizione di derivata;
b)-si è applicata la formula di prostaferesi
al numeratore e si è seguito lo stesso ragionamento della 6).
8^) Derivata della funzione:
y = tgx.
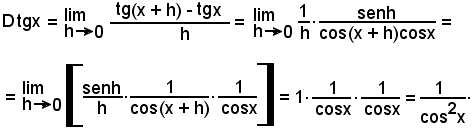
Quindi:
Nota bene
Per la dimostrazione suddetta, sono stati effettuati in sequenza i seguenti passaggi, partendo da Dtgx:
a)-si è applicata la definizione di derivata;
b)-si è applicata la formula di prostaferesi
al numeratore; il resto è ovvio.
9^) Derivata della funzione:
y = ctgx.
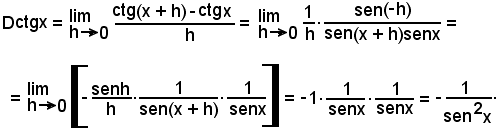
Quindi:
Nota bene
Per la dimostrazione suddetta, sono stati effettuati in sequenza i seguenti passaggi, partendo da Dctgx:
a)-si è applicata la definizione di derivata;
b)-si è applicata la formula di prostaferesi
al numeratore;
c)-si è tenuto conto che sen(-h) = -senh;
il resto è ovvio.
10^) Derivata della funzione:
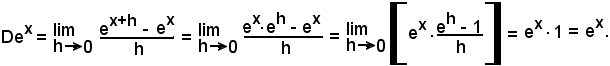
Quindi:
Dex = ex.
Nota bene
Per la dimostrazione suddetta, sono stati effettuati in sequenza i seguenti passaggi, partendo da Dex:
a)-si è applicata la definizione di derivata;
b-si è tenuto conto che ex+h = ex·eh;
c)-si è tenuto conto, come è noto, che
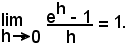
Regole di derivazione delle operazioni tra funzioni
1)-Considerazioni generali
1^) Tutte le funzioni che saranno considerate in seguito s'intenderanno definite nello stesso intervallo, che è quello comune agl'intervalli in cui ciascuna funzione è definita per proprio conto.
2^) Tutte le funzioni avranno derivata, e quindi saranno continue, in uno stesso punto generico x.
3^) Nel punto considerato, la funzione figurante al denominatore sarà diversa da zero.
4^) Si ricordi che date due funzioni y1 = f1(x) e y2 = f2(x), una loro combinazione lineare è data da
y = αf1(x) + βf2(x),
con α, β costanti arbitrarie.
2)-Derivata della combinazione lineare di due o più funzioni.
Teorema - La derivata di una combinazione lineare di due o più funzioni è uguale alla combinazione lineare, secondo le stesse costanti, delle derivate delle singole funzioni:
(1) D[αf1(x) + βf2(x)] = αDf1(x) + βDf2(x) = αf'1(x) + βf'2(x).

come volevasi dimostrare.
Casi particolari
1°) Se α = β = 1, la (1) diventa:
D[f1(x) + f2(x)] = Df1(x) + Df2(x) = f'1(x) + f'2(x),
cioè: la derivata della somma di due o più funzioni è ugiuale alla somma delle derivate delle singole funzioni.
2°) Se α = 1 e β = -1, la (1) diventa:
D[f1(x) - f2(x)] = Df1(x) - Df2(x) = f'1(x) - f'2(x),
cioè: la derivata della differenza di due funzioni è ugiuale alla differenza delle derivate delle singole funzioni.
3)-Derivata del prodotto di due funzioni
Teorema - La derivata del prodotto di due funzioni è uguale alla derivata della 1^ funzione per la seconda non derivata più la 1^ funzione per la derivata della 2^:
Infatti:
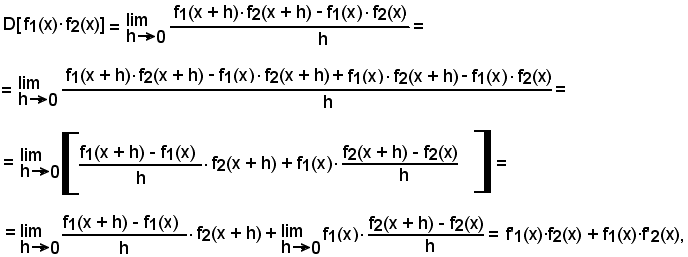
come volevasi dimostrare.
Nota bene
Nella dimostrazione suddetta, al secondo passaggio, si è sottratto e aggiunto al numeratore
f1(x )·f2(x + h).
4)-Derivata del prodotto di tre funzioni
Si ottiene applicando due volte la regola 3).
D[f1(x)·f2(x)·f3(x)] = D{[f1(x)·f2(x)]·f3(x)} = D[f'1(x)·f2(x)]·f3(x) + f'1(x)·f'2(x)·Df3(x) = [f'1(x)·f2(x) +
f1(x)·f'2(x)]·f3(x) + f1(x)·f2(x)·f'3(x) = f'1(x)·f2(x)·f'3(x) + f1(x)·f'2(x)·f3(x) + f1(x)·f2(x)·f'3(x).
cioè:
-la derivata del prodotto di tre o più funzioni è uguale alla somma dei prodotti della derivata di ciascuna funzione per tutte le altre non derivate.
5)-Derivata del prodotto di una costante per una funzione
Si ottiene applicando sempre la regola 3).
D[k·f(x)] = (Dk)·f(x) + k·Df(x) = k·Df(x),
essendo Dk = 0,
cioè:
-una costante moltiplicativa passa inalterata in derivazione.
6)-Derivata del quoziente di due funzioni
Teorema - La derivata del quoziente di due funzioni è uguale ad una frazione che ha per numeratore il prodotto tra la derivata della funzione dividendo e quella divisore, non derivata, diminuito del prodotto tra la funzione dividendo e la derivata di quella divisore e per denominatore il quadrato della funzione divisore:
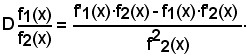
Infatti:
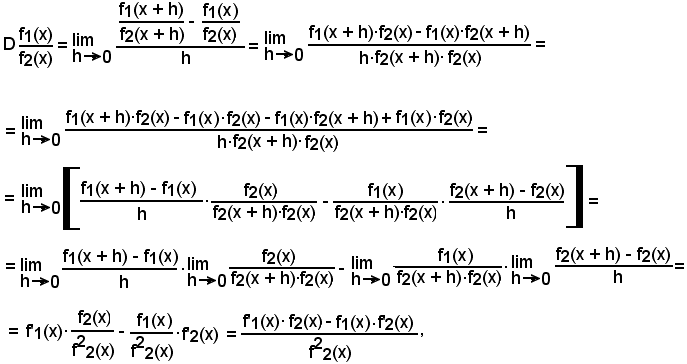
come volevasi dimostrare.
Nota bene
1)-Nella dimostrazione suddetta, al terzo passaggio, si è sottratto e aggiunto al numeratore
f1(x )·f2(x) e poi si sono scisse le frazioni.
2)-La dimostrazione suddetta si può effettuare anche considerando
e applicando la regola di derivazione del prodotto e quella della derivata inversa della funzione che segue.
7)-Derivata della inversa di una funzione
Teorema - La derivata della inversa di una funzione è uguale ad una frazione che ha per numeratore la derivata, cambiata di segno, della funzione e per denominatore il quadrato della stessa funzione:
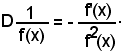
Infatti:
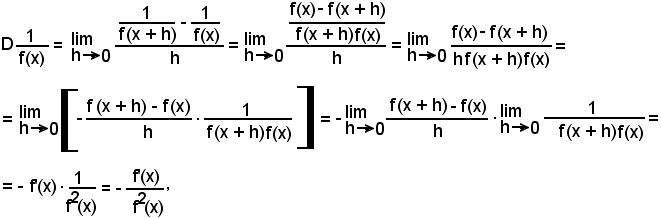
come volevasi dimostrare.
Nota bene
1)-La dimostrazione suddetta si può effettuare anche applicando il teorema della derivata di un quoziente, si ha:
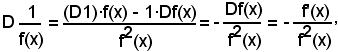
essendo D1 = 0.
2)-Per quanto detto in 5), si ha:
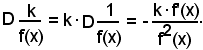
Allo stesso risultato si perviene considerando
e applicando la regola di derivazione del quoziente di due funzioni, cioè:
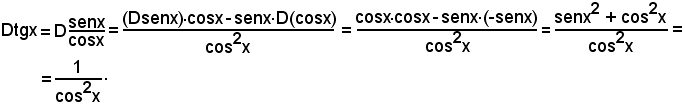
4)-Analogamente, si perviene allo stesso risultato, considerando
e applicando la regola di derivazione del quoziente di due funzioni, cioè:
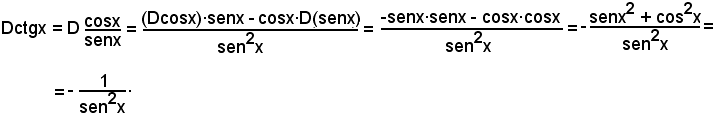
5)-Sapendo che è anche
applicando la regola di derivazione dell'inversa di una funzione, si ha:
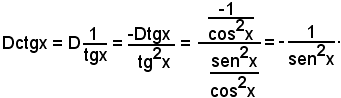
6)-Particolarmente importante per le numerose applicazioni è
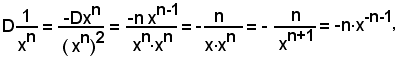
cioè:
-la regola di derivazione della potenza della variabile, data per l'esponente intero positivo nella formula gia vista, cioè in
vale anche per l'esponente intero negativo.
Significato geometrico del rapporto incrementale e della derivata prima della funzione in un punto
1)-Premesse
Il concetto di derivata di una funzione di una variabile è uno dei più importanti della matematica. La parte della matematica, basata su tale concetto, è chiamata calcolo differenziale.
Il primo problema che dette origine al calcolo differenziale fu quello geometrico della ricerca della tangente ad una curva in un suo punto.
Sussessivamente se ne presentò un altro di natura fisica: quello del calcolo della velocità di un punto in moto, che sarà trattato.
2)-Retta tangente in un punto ad una curva
Nella geometria elementare sono state date le seguenti definizioni:
1^)-la tangente ad una circonferenza è la retta che ha in comune con essa un solo punto;
2^)-la tangente ad una circonferenza è la posizione limite a cui tende la retta secante TT1 quando
3^)-la tangente in un punto della circonferenza è la perpendicolare al raggio passante per il punto di contatto. Quest'ultima proprietà consente di tracciare subito la tangente in qualsiasi punto della circonferenza.

Si osservi che la 1^) definizione non è estendibile quando al posto della circonferenza si considera una qualsiasi altra curva, come ad esempio quella della figura seguente:

La retta t non incontra la curva γ nel solo punto T e quindi, in base alla 1^) definizione non è tangente alla curva. La retta t, invece, è ugualmente considerata come tangente nel punto T, intendendo in tal modo ritenerla come la posizione limite raggiunta dalla retta TT1 quando T1 tende a T.
La 2^) definizione è, pertanto, più utile ed anche più generale della precedente e risponde meglio di quella ai risultati cui la stessa intuizione fa pervenire.
E' bene tuttavia precisare che con ciò non si è inteso dire che in ogni punto di una qualsiasi curva esista un'unica tangente o, addirittura, esista una tangente. Infatti, se si considera la curva γ della fig. 5 o della fig. 6, nel punto T, detto punto angoloso, esistono due rette t e t' tangenti alla curva.
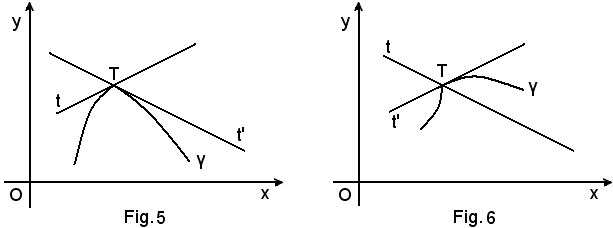
Ed ancora, se si considera la linea spezzata della fig, 7, si può vedere che pur essendo la linea continua nei vertici A, B, C, D la tangente addirittura non esiste.

Dagli esempi fatti, scaturisce con sufficiente evidenza che la sola continuità di una funzione non consente di attibuire alla curva che rappresenta la funzione tutte le proprietà viste per le curve più comuni.
L'esistenza della tangente ad una curva in un suo punto è data dal seguente teorema:
-condizione necessaria e sufficiente affinchè esista la tangente ad una curva in un suo punto è che in tale punto la funzione, che la curva rappresenta, abbia la derivata.
3)-Coefficiente angolare ed equazione della tangente ad una curva in un suo punto
Sia y = f(x) una funzione derivabile in (a, b) e sia γ l'arco di curva che essa rappresenta in detto intervallo. Si sa che nel punto x0 il rapporto incrementale della funzione è:

Poichè in figura è
la (1) diventa
Poichè ancora, dal triangolo rettangolo M'QN', per una nota formula della trigonometria, è
ossia
la (2) si può scrivere
cioè:
-il rapporto incrementale di una funzione in un punto è uguale alla tangente trigonometrica dell'angolo che la secante alla curva, passante per i suoi punti, corrispondenti a quelli presi sull'intervallo, forma con la direzione positiva dell'asse x, in quanto è:
Più semplicemente, in base a note nozioni di geometria analitica, si può dire che:
-il rapporto incrementale di una funzione in un punto è uguale al coefficiente angolare della retta secante la curva nei suoi punti corrispondenti a quelli presi sull'intervallo.
Allora la derivata della funzione, esistente per ipotesi nel punto x0, come è noto è:
ma quando h tende a zero, N tende ad M sull'intervallo e sulla curva N' tende ad M', ossia la secante s diventa tangente t alla curva, nel punto M' ed ancora tgβ tende a tgα, per cui si ha:
(3) f'(x0) = tgα,
cioè:
-la derivata di una funzione in un punto è uguale al coefficiente angolare della retta tangente alla curva, che rappresenta la funzione, nel suo punto corrispondente a quello preso sull'intervallo.
Si ricordi che se M'[x0, y0 = f(x0)] è un punto di una curva, l'equazione del fascio di rette passanti per tale punto è data da:
y - y0 = m(x - x0),
dalla quale, al variare del parametro m, si hanno le infinite rette del fascio.
Quella tangente alla curva nello stesso punto si avrà sostituendo ad m il coefficiente angolare dato dalla (3), pertanto la sua equazione è:
(4) y - y0 = f'(x0)·(x - x0).
Esempi
1°)-Scrivere l'equazione della tangente alla parabola di equazione y = 2x2 - 3x + 1, nel punto di ascissa x0 = 2.
Si calcola dapprima y0 = f(x0) = f(2) = 3, e poi il fascio di rette passanti per il punto dato, che ha
y - 3 = m(x - 2).
Volendo la retta tangente alla curva nel punto, dev'essere
Essendo
sostituendo nell'equazione del fascio, si ha l'equazione richiesta della tangente, cioè:
y - 3 = 5(x - 2),
ossia
y = 5x - 7, in forma ridotta,
oppure
5x - y - 7 = 0, in forma generale.
m = f'(2).
Essendo
f'(x) = 4x - 3
e f'(2) = 5, coefficiente della tangente,
e f'(2) = 5, coefficiente della tangente,
sostituendo nell'equazione del fascio, si ha l'equazione richiesta della tangente, cioè:
y - 3 = 5(x - 2),
ossia
y = 5x - 7, in forma ridotta,
oppure
5x - y - 7 = 0, in forma generale.
2°)-Scrivere l'equazione della tangente alla curva di equazione
nel suo punto di ascissa x0 = 2.
Essendo
y0 = f(x0) = f(2) = 4,
l'equazione del fascio di rette passanti per il punto (2, 4) diventa:
y - 4 = m(x - 2)
e l'equazione della tangente è:
y - 4 = f'(2)·(x - 2).
Poichè
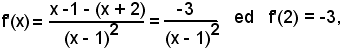
l'equazione richiesta è
y - 4 = -3(x - 2),
ossia
y = -3x + 10, in forma esplicita,
oppure
3x + y - 10 = 0, in forma implicita.
Nota bene
Se in un punto (x0) è f'(x0) = 0, la tangente alla curva in x0 risulta parallela all'asse x.
Derivate successive o di ordine superiore
1)-Definizioni e simbolismi
Poichè
l'equazione richiesta è
y - 4 = -3(x - 2),
ossia
y = -3x + 10, in forma esplicita,
oppure
3x + y - 10 = 0, in forma implicita.

Nota bene
Se in un punto (x0) è f'(x0) = 0, la tangente alla curva in x0 risulta parallela all'asse x.
Derivate successive o di ordine superiore
1)-Definizioni e simbolismi
Sia
y = f(x) una funzione derivabile in (a, b) e sia y' = f'(x) la sua
derivata. Se tale funzione è a sua volta derivabile in (a, b),
la sua derivata, detta seconda o del 2° ordine rispetto alla y =
f(x), si indicherà con uno dei seguenti simboli:
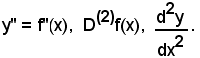
Analogamente, se la funzione y'' = f''(x) è nuovamente derivabile in (a, b), la sua derivata, detta terza o del 3° ordine, si indicherà con uno dei seguenti simboli:
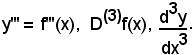
In modo analogo si può procedere e, pertanto si possono considerare, purchè esistano, le derivate di qualsiasi ordine.
2)- Casi notevoli di derivate successive
1°)-Un polinomio intero di grado n in x
y = a0xn + a1xn-1 + a2xn-2 + ... + an-1x + an
ha derivate fino all'ordine n + 1.
E'
D(n)y = a0·n!
e quindi
D(n+1)y = 0.
Esempio:
y = f(x) = ax3 + bx2+ cx + d,
Df(x) = 3ax2 + 2bx+ c,
D(2)f(x) = 2·3ax + 2b,
D(3)f(x) = 1·2·3a = 3!a,
D(4)f(x) = 0.
2°)-La funzione y = ex ha derivate di qualsiasi ordine.
Si è visto che
D ex = ex,
quindi:
D(2)ex = Dex = ex,
e in generale
D(n)ex = ex,
per qualsiasi n.
3°)-Tenendo presente che
Dsenx = cosx e Dcosx = - senx,
si ha:
Dsenx = cosx,
D(2)senx = Dcosx = -senx,
D(3)senx = D(2)cosx = D(-senx) = -cosx,
D(4)senx = D(3)cosx = D(2)(-senx) = D(-cosx) = senx,
D(5)senx = D(4)cosx = D(3)(- senx) = D(2)(-cosx) = Dsenx = cosx,
cioè:
-la funzione y = senx ha derivate di qualsiasi ordine; esse riproducono ciclicamente la funzione con periodo quattro.
Pertanto, indicando con n un numero naturale, si ha:
D(4n)senx = senx,
D(4n+1)senx = Dsenx = cosx,
D(4n+2)senx = D(2)senx = -senx,
D(4n+3)senx = D(3)senx = -cosx,
D(4n+4)senx = D(4)senx = senx.
Esempi:
D(23)senx = D(3)senx = -cosx,
D(37)senx = Dsenx = cosx.
4°)-Analogamente si ha:
Dcosx = -senx,
D(2)cosx = D(-senx) = -cosx,
D(3)cosx = D(2)(-senx) = D(-cosx) = senx,
D(4)cosx = D(3)(-senx) = D(2)(-cosx) = Dsenx = cosx,
vale, quindi, per la funzione y = cosx quanto detto per la funzione y = senx.
Significato fisico del rapporto incrementale e della derivata prima e seconda di una funzione
1)-Moto rettilineo vario: velocità media e istantanea
Si consideri un punto P mobile su una retta, si indichi con t il tempo e con s lo spazio o segmenti, che P percorre. E' noto che s dipende da t, per cui si può scrivere che s = s(t).
Ciò significa che dando un incremento h, ovviamente positivo, alla variabile t, ossia considerando il tempo t + h, lo spazio percorso sarà s(t + h). Ricordando, dalla cinematica, che la velocità media di un punto è il rapporto tra lo spazio percorso e l'intervallo di tempo impiegato, si ha:
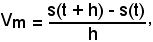
cioè:
-il rapporto incrementale della funzione s = s(t), della variabile tempo, è uguale alla velocità media del punto che si muove di moto rettilineo vario.
Passando al limite per h tendente a zero, si ha:
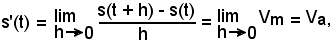
cioè:
-la derivata prima della stessa funzione s = s(t) è uguale alla velocità istantanea del punto mobile.
2)-Accelerazione media e vera
cioè:
-la derivata seconda della funzione s = s(t) è uguale all'accelerazione vera, o istantanea, del punto mobile.
3)-Secondo principio fondamentale della meccanica
Il secondo principio fondamentale della meccanica, detto principio di Galileo Galilei, esprime la relazione tra la forza F applicata ad un corpo di massa m, libero di muoversi, e l'accelerazione a da essa prodotta, cioè:
F = m·a,
che per quanto detto in 1) e 2), si può scrivere:
F = m·V'(t) = ms''·(t).
Funzioni composte e loro derivazione
1)-Concetto di funzione composta o funzione di funzione
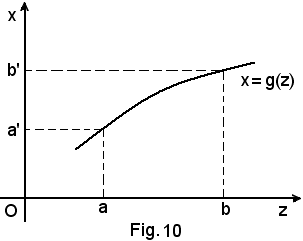
Sia
(1) x = g(z)
una funzione della variabile z, definita in un certo intervallo (a, b) e sia (a', b') il suo campo di variabilità, ossia quando z varia in (a, b) i valori della x risultano appartenenti all'intervallo (a', b').
Si consideri ora l'altra funzione
(2) y = f(x),
in cui la x è proprio la (1).
Ciò significa che per ogni x di (a', b') viene a corrispondere un valore di y in un altro certo intervallo (a'', b''), che è il campo di esistenza della y. Allora, dire che ad ogni z di (a, b) corrisponde un valore della x in (a', b') e ad x di (a', b' ) corrisponde un valore della y in (a'', b''), è come dire che ad ogni valore della z corrisponde un valore di y tramite x.
Questa dipendenza o relazione tra le variabili y e z tramite un'altra variabile o funzione, è quella che si chiama funzione composta o funzione di funzione e si indica con
(3) y = f[g(z)],
mentre
x = g(z)
si chiama funzione componente o funzione intermedia.
2)-Derivata di una funzione composta
Siano
y = f(x) e x = g(z)
due funzioni tali che variando la x nell'intervallo (a, b), la funzione x = g(z) assuma valori che appartengono allo stesso campo di esistenza della prima funzione. Queste condizioni, per quanto detto in (1), definiscono la funzione composta o funzione di funzione
y = f[g(x)],
della quale si vuole trovare la regola di derivazione.
A tale scopo, vale il seguente teorema:
-la funzione y = f[g(x)], definita come composta delle funzioni y = f(x) ed x = g(z), entrambe derivabili, è anch'essa derivabile e la derivata, rispetto alla variabile indipendente z, è uguale al prodotto delle derivate di ciascuna funzione componente rispetto alla propria variabile, come se questa fosse quella indipendente.
Cioè:
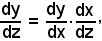
oppure
y'(z) = y'(x)·x'(z).
Una dimostrazione non rigorosa del teorema è data dalle seguenti considerazioni:
sia Δz l'incremento della variabile indipendente z, Δx quello corrispondente alla funzione x, la quale, a sua volta, è la variabile della funzione y e quindi sia Δy l'incremento subito dalla y in corrispondenza di quello di Δx subito dalla x. Il rapporto incrementale della y, pensata come funzione della variabile z, si può scrivere
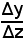
e questo, a sua volta, può essere scritto, dividendo e moltiplicando, quindi non alterando, per l'incremento Δx subito dalla x in corrispondenza di quello Δz dato alla z, come segue:
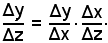
Considerando il limite di ambo i membri per Δz tendente a zero, si ha:
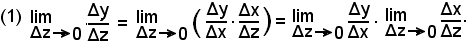
Poichè le funzioni componenti sono per ipotesi derivabili, ricordando che per definizione di derivata gl'incrementi della variabile indipendente e della funzione sono infinitesimi dello stesso ordine, cioè:
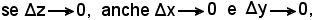
la (1) si può scrivere
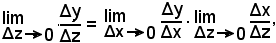
da cui segue
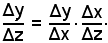
Il teorema è così dimostrato.
3)-Estensione del teorema
Il teorema vale identicamente nel caso di più funzioni componenti.
Cioè se
y = f(x), x = g(z) e z = ψ(t)
sono funzioni derivabili e tali da definire la funzione composta y di t
y = f{g[ψ(t)]},
la derivata di quest'ultima, rispetto alla variabile indipendente t, è:
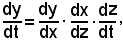
oppure
y'(t) = y'(x)·x'(z)·z'(t).
3)-Esempi
La y è il quadrato, 1^ funzione componente, del seno, 2^ funzione componente, della variabile x. Avendosi due funzioni, la derivata richiesta si presenterà come prodotto di due fattori, ognuno dei quali, come è stato detto nel teorema, è la derivata di ciascuna funzione componente rispetto alla propria variabile, come se fosse indipendente.
Si ha:
y'(x) = 2·senx·cosx.
La 1^ funzione componente è il cubo del coseno,
la 2^ funzione componente è il coseno dell'arco,
la 3^ funzione componente è 7x,
quindi
y'(x) = 3cos27x·(-sen7x)·7 = -21cos27x·sen7x.
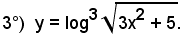
La 1^ funzione componente è il cubo del logaritmo,
la 2^ funzione componente è il logaritmo,
la 3^ funzione componente è la radice quadrata,
la 4^ funzione componente è (3x2 + 5),
quindi:
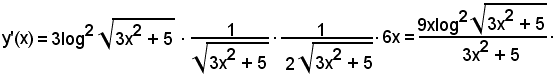
Funzioni inverse e loro derivazione
Sia y = f(x) una funzione continua nell'intervallo chiuso (a, b) e siano m e M, rispettivamente, i valori minimo e massimo che essa assume nell'intervallo.
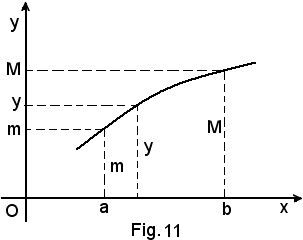
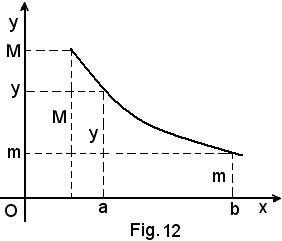
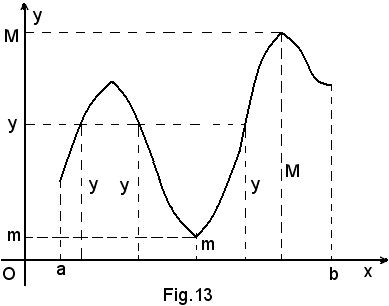
Ad ogni valore x della variabile indipendente nell'intervallo (a, b) corrisponde uno ed un solo valore di y per la funzione nell'intervallo (m, M), ma non sempre accade il viceversa, come accade nella Fig. 13: al valore y in (m, M) corrispondono, infatti, 3 valori della x in (a, b).
Se invece la funzione y = f(x) è sempre crescente, Fig. 11 o sempre decrescente, Fig. 12, ossia, come si dice, è monotona in (a, b), allora accade che ad ogni valore di x corrisponde un solo valore di y e viceversa ad ogni valore di y corrisponde il precedente valore di x.
Questa relazione, che permette di passare dalla variabile y alla variabile x è, a sua volta, una nuova funzione
x = g(y),
che è detta funzione inversa della y = f(x) data. Algebricamente, data la y = f(x), la funzione inversa si ottiene, quando è possibile, ricavando la x dalla y = f(x).
Esempio
Se
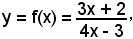
essa è definita in
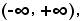
ad eccezione di
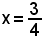
ed è sempre decrescente; successivamente si ha:
4xy - 3y = 3x + 2,
x(4y - 3) = 3y + 2,
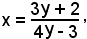
che è la funzione inversa, anch'essa definita in
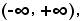
ad eccezione del punto y = 3/4, sempre decrescente.
Si badi, però, che non sempre la funzione inversa di una funzione monodroma, ad un solo valore, è anch'essa monodroma.
Infatti, se y = x2 è la funzione monodroma, crescente per x > 0 e decrescente per x < 0, le funzioni inverse
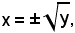
che si ottengono, non sono più monodrome.
Così da y = senx per 0 ≤ x ≤ π, si ha come funzione inversa x = arcseny, che è addirittura infinitivoca e infinitiforme.
Dagli esempi fatti, seguono le seguenti proprietà:
1^) La funzione inversa di una funzione monodroma è anch'essa monodroma solo se la funzione data è sempre crescente o sempre decrescente.
2^) La funzione inversa di una funzione monodroma non sempre crescente o non sempre decrescente può essere monodroma, polidroma o, addirittura, infinitivoca.
2)-Derivata delle funzioni inverse
Teorema - Se y = f(x) e x = g(y) sono due funzioni l'una inversa dell'altra e ciascuna con derivata sempre diversa da zero, si ha
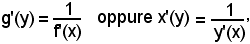
cioè:
-la derivata della funzione inversa è uguale all'inversa della derivata della funzione data.
Infatti, essendo per ipotesi y = f(x) con x = g(y), si può dire che la y è funzione di se se stessa tramite la x. Per il teorema della funzione composta, allora si ha:
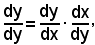
e poichè
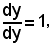
si può scrivere
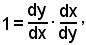
da cui
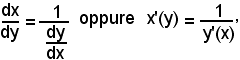
come volevasi dimostrare.
Nota bene
Si badi a non confondere la funzione inversa di una data funzione con l'inversa
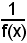
della funzione stessa, per la quale si ha:
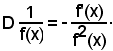
3)-Derivata di alcune funzioni inverse notevoli
1° Si consideri la funzione
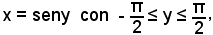
nel quale intervallo la funzione data è sempre crescente e, pertanto, ammette come funzione inversa
y = arcsenx
definita, a sua volta, nell'intervallo chiuso (-1, 1).
Avendosi
x'(y) = cosy
è
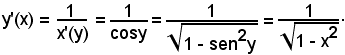
Dunque:
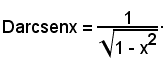
2° Si consideri la funzione
x = cosy con 0 ≤ y ≤ π
nel quale intervallo la funzione data è sempre decrescente e, pertanto, ammette la funzione inversa
y = arccosx
definita, a sua volta, nell'intervallo chiuso (-1, 1).
Avendosi
x'(y) = -seny
è
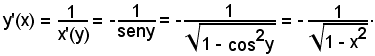
Dunque:
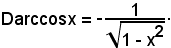
3° Si consideri la funzione
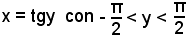
nel quale intervallo la funzione data è sempre crescente e, pertanto, ammette la funzione inversa
y = arctgx
definita, a sua volta, in
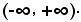
Avendosi
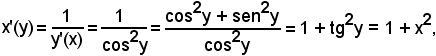
è
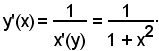
Dunque:
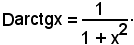
4° Si consideri la funzione
y = ctgx con 0 < y < π
nel quale intervallo aperto la funzione data è sempre decrescente e, pertanto, ammette la funzione inversa
y = arcctgx
definita, a sua volta, in
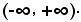
è
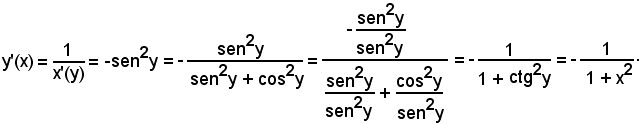
Dunque:
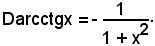
5° Si consideri la funzione
y = ex,
sempre crescente per x > 0 e sempre decrescente per x < 0.
La sua funzione inversa è
y = logy.
Poichè
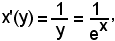
è
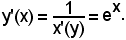
Dunque:
Dex = ex.
Quest'ultimo risultato è stato trovato in precedenza.
Altre derivate di funzioni notevoli
1)-Derivata della funzione y = xα, con x > 0 e α reale qualsiasi
Per α > 0 intero, si è visto che
Dxα = α·xα-1 e Dx-α·x-α-1.
La regola di derivazione della potenza è applicabile ugualmente per α reale qualsiasi.
Infatti, considerato
y = xα
e considerati i logaritmi neperiani dei due membri:
logy = logxα = α·logx,
cioè
logy = α·logx,
derivando ambo i membri e tenendo presente che, essendo y = xα, il 1° membro risulta essere una funzione composta, si ha:
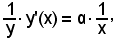
cioè
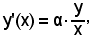
ma
y = xα,
dunque
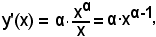
come volevasi dimostrare.
2)-Derivata della potenza con esponente razionale
Da
y = xα,
se
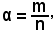
si ha
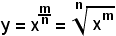
e quindi
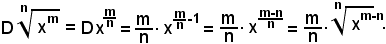
Nota bene
1° Se
cioè
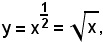
si ha
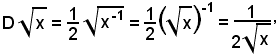
cioè si ritrova il risultato ottenuto in precedenza.
2° Se
m =1 e n > 1,
si ha la funzione,
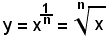
e quindi
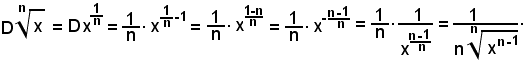
Nota bene
Nel quarto passaggio si è tenuto conto che 1 - n < 0.
Esempio
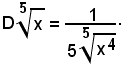
3)-Derivata della funzione esponenziale y = ax.
Da
y = ax
prendendo i logaritmi neperiani dei due membri ed applicando il teorema del logaritmo della potenza, si ha:
logy = x·loga.
Derivando ambo i membri e tenendo presente che il 1° membro è una funzione composta, si ha:
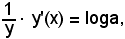
da cui
y'(x) = = y·loga
e, quindi, poichè y = ax,
Dax= y'(x) = ax·loga.
4)-Derivata della funzione logaritmica y = logax.Sapendo che
logax = logx·logae,
derivando ambo i membri, si ha:
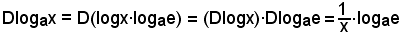
e poichè
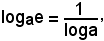
si ha anche
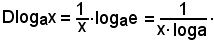
Elenco delle derivate notevoli
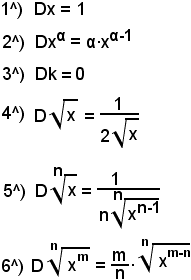
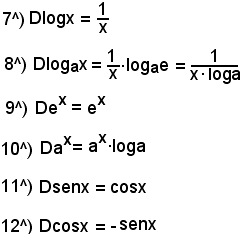

Elenco generalizzato delle derivate notevoli
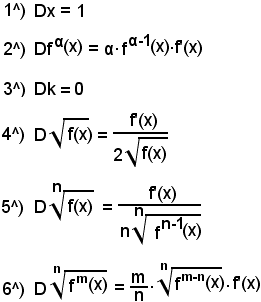

Differenziazione
1)-Differenziale di una funzione
Se y = f(x) è una funzione derivabile in un intervallo (a, b), si sa che
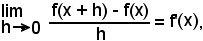
e pertanto, almeno in generale, è:
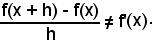
Tale relazione di disuguaglianza può essere scritta sotto forma di uguaglianza, come segue:
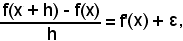
ove ε tende a zero quando h tende a zero, ossia ε è un infinitesimo dello stesso ordine come h.
Si ha allora:
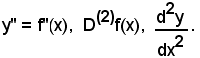
Analogamente, se la funzione y'' = f''(x) è nuovamente derivabile in (a, b), la sua derivata, detta terza o del 3° ordine, si indicherà con uno dei seguenti simboli:
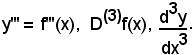
In modo analogo si può procedere e, pertanto si possono considerare, purchè esistano, le derivate di qualsiasi ordine.
2)- Casi notevoli di derivate successive
1°)-Un polinomio intero di grado n in x
y = a0xn + a1xn-1 + a2xn-2 + ... + an-1x + an
ha derivate fino all'ordine n + 1.
E'
e quindi
D(n+1)y = 0.
Esempio:
y = f(x) = ax3 + bx2+ cx + d,
Df(x) = 3ax2 + 2bx+ c,
D(2)f(x) = 2·3ax + 2b,
D(3)f(x) = 1·2·3a = 3!a,
D(4)f(x) = 0.
2°)-La funzione y = ex ha derivate di qualsiasi ordine.
Si è visto che
quindi:
D(2)ex = Dex = ex,
e in generale
D(n)ex = ex,
per qualsiasi n.
3°)-Tenendo presente che
Dsenx = cosx e Dcosx = - senx,
si ha:
Dsenx = cosx,
D(2)senx = Dcosx = -senx,
D(3)senx = D(2)cosx = D(-senx) = -cosx,
D(4)senx = D(3)cosx = D(2)(-senx) = D(-cosx) = senx,
D(5)senx = D(4)cosx = D(3)(- senx) = D(2)(-cosx) = Dsenx = cosx,
cioè:
-la funzione y = senx ha derivate di qualsiasi ordine; esse riproducono ciclicamente la funzione con periodo quattro.
Pertanto, indicando con n un numero naturale, si ha:
D(4n)senx = senx,
D(4n+1)senx = Dsenx = cosx,
D(4n+2)senx = D(2)senx = -senx,
D(4n+3)senx = D(3)senx = -cosx,
D(4n+4)senx = D(4)senx = senx.
Esempi:
D(23)senx = D(3)senx = -cosx,
D(37)senx = Dsenx = cosx.
4°)-Analogamente si ha:
Dcosx = -senx,
D(4)cosx = D(3)(-senx) = D(2)(-cosx) = Dsenx = cosx,
vale, quindi, per la funzione y = cosx quanto detto per la funzione y = senx.
Significato fisico del rapporto incrementale e della derivata prima e seconda di una funzione
1)-Moto rettilineo vario: velocità media e istantanea
Si consideri un punto P mobile su una retta, si indichi con t il tempo e con s lo spazio o segmenti, che P percorre. E' noto che s dipende da t, per cui si può scrivere che s = s(t).
Ciò significa che dando un incremento h, ovviamente positivo, alla variabile t, ossia considerando il tempo t + h, lo spazio percorso sarà s(t + h). Ricordando, dalla cinematica, che la velocità media di un punto è il rapporto tra lo spazio percorso e l'intervallo di tempo impiegato, si ha:
cioè:
-il rapporto incrementale della funzione s = s(t), della variabile tempo, è uguale alla velocità media del punto che si muove di moto rettilineo vario.
Passando al limite per h tendente a zero, si ha:
cioè:
-la derivata prima della stessa funzione s = s(t) è uguale alla velocità istantanea del punto mobile.
2)-Accelerazione media e vera
Ricordando che l'accelerazione è la variazione di velocità rispetto al tempo, si ha:
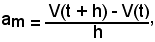
quindi
-il rapporto incrementale della funzione V = V(t) è uguale all'accelerazione media del punto mobile.
Infine è:
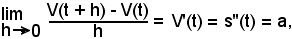
quindi
-il rapporto incrementale della funzione V = V(t) è uguale all'accelerazione media del punto mobile.
Infine è:
cioè:
-la derivata seconda della funzione s = s(t) è uguale all'accelerazione vera, o istantanea, del punto mobile.
3)-Secondo principio fondamentale della meccanica
Il secondo principio fondamentale della meccanica, detto principio di Galileo Galilei, esprime la relazione tra la forza F applicata ad un corpo di massa m, libero di muoversi, e l'accelerazione a da essa prodotta, cioè:
che per quanto detto in 1) e 2), si può scrivere:
F = m·V'(t) = ms''·(t).
Funzioni composte e loro derivazione
1)-Concetto di funzione composta o funzione di funzione
Sia
(1) x = g(z)
una funzione della variabile z, definita in un certo intervallo (a, b) e sia (a', b') il suo campo di variabilità, ossia quando z varia in (a, b) i valori della x risultano appartenenti all'intervallo (a', b').

Si consideri ora l'altra funzione
(2) y = f(x),
in cui la x è proprio la (1).
Ciò significa che per ogni x di (a', b') viene a corrispondere un valore di y in un altro certo intervallo (a'', b''), che è il campo di esistenza della y. Allora, dire che ad ogni z di (a, b) corrisponde un valore della x in (a', b') e ad x di (a', b' ) corrisponde un valore della y in (a'', b''), è come dire che ad ogni valore della z corrisponde un valore di y tramite x.
Questa dipendenza o relazione tra le variabili y e z tramite un'altra variabile o funzione, è quella che si chiama funzione composta o funzione di funzione e si indica con
(3) y = f[g(z)],
mentre
si chiama funzione componente o funzione intermedia.
2)-Derivata di una funzione composta
Siano
y = f(x) e x = g(z)
due funzioni tali che variando la x nell'intervallo (a, b), la funzione x = g(z) assuma valori che appartengono allo stesso campo di esistenza della prima funzione. Queste condizioni, per quanto detto in (1), definiscono la funzione composta o funzione di funzione
y = f[g(x)],
della quale si vuole trovare la regola di derivazione.
A tale scopo, vale il seguente teorema:
-la funzione y = f[g(x)], definita come composta delle funzioni y = f(x) ed x = g(z), entrambe derivabili, è anch'essa derivabile e la derivata, rispetto alla variabile indipendente z, è uguale al prodotto delle derivate di ciascuna funzione componente rispetto alla propria variabile, come se questa fosse quella indipendente.
Cioè:
oppure
y'(z) = y'(x)·x'(z).
Una dimostrazione non rigorosa del teorema è data dalle seguenti considerazioni:
sia Δz l'incremento della variabile indipendente z, Δx quello corrispondente alla funzione x, la quale, a sua volta, è la variabile della funzione y e quindi sia Δy l'incremento subito dalla y in corrispondenza di quello di Δx subito dalla x. Il rapporto incrementale della y, pensata come funzione della variabile z, si può scrivere
e questo, a sua volta, può essere scritto, dividendo e moltiplicando, quindi non alterando, per l'incremento Δx subito dalla x in corrispondenza di quello Δz dato alla z, come segue:
Considerando il limite di ambo i membri per Δz tendente a zero, si ha:
Poichè le funzioni componenti sono per ipotesi derivabili, ricordando che per definizione di derivata gl'incrementi della variabile indipendente e della funzione sono infinitesimi dello stesso ordine, cioè:
la (1) si può scrivere
da cui segue
Il teorema è così dimostrato.
3)-Estensione del teorema
Il teorema vale identicamente nel caso di più funzioni componenti.
Cioè se
sono funzioni derivabili e tali da definire la funzione composta y di t
y = f{g[ψ(t)]},
la derivata di quest'ultima, rispetto alla variabile indipendente t, è:
oppure
y'(t) = y'(x)·x'(z)·z'(t).
3)-Esempi
1°) y = sen2x.
La y è il quadrato, 1^ funzione componente, del seno, 2^ funzione componente, della variabile x. Avendosi due funzioni, la derivata richiesta si presenterà come prodotto di due fattori, ognuno dei quali, come è stato detto nel teorema, è la derivata di ciascuna funzione componente rispetto alla propria variabile, come se fosse indipendente.
Si ha:
y'(x) = 2·senx·cosx.
2°) y = cos37x.
La 1^ funzione componente è il cubo del coseno,
la 2^ funzione componente è il coseno dell'arco,
la 3^ funzione componente è 7x,
quindi
y'(x) = 3cos27x·(-sen7x)·7 = -21cos27x·sen7x.
La 1^ funzione componente è il cubo del logaritmo,
la 2^ funzione componente è il logaritmo,
la 3^ funzione componente è la radice quadrata,
la 4^ funzione componente è (3x2 + 5),
quindi:
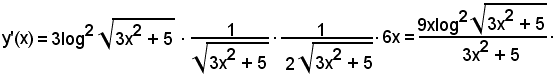
Funzioni inverse e loro derivazione
Sia y = f(x) una funzione continua nell'intervallo chiuso (a, b) e siano m e M, rispettivamente, i valori minimo e massimo che essa assume nell'intervallo.



Ad ogni valore x della variabile indipendente nell'intervallo (a, b) corrisponde uno ed un solo valore di y per la funzione nell'intervallo (m, M), ma non sempre accade il viceversa, come accade nella Fig. 13: al valore y in (m, M) corrispondono, infatti, 3 valori della x in (a, b).
Se invece la funzione y = f(x) è sempre crescente, Fig. 11 o sempre decrescente, Fig. 12, ossia, come si dice, è monotona in (a, b), allora accade che ad ogni valore di x corrisponde un solo valore di y e viceversa ad ogni valore di y corrisponde il precedente valore di x.
Questa relazione, che permette di passare dalla variabile y alla variabile x è, a sua volta, una nuova funzione
x = g(y),
che è detta funzione inversa della y = f(x) data. Algebricamente, data la y = f(x), la funzione inversa si ottiene, quando è possibile, ricavando la x dalla y = f(x).
Esempio
Se
essa è definita in
ad eccezione di
ed è sempre decrescente; successivamente si ha:
4xy - 3y = 3x + 2,
x(4y - 3) = 3y + 2,
che è la funzione inversa, anch'essa definita in
ad eccezione del punto y = 3/4, sempre decrescente.
Si badi, però, che non sempre la funzione inversa di una funzione monodroma, ad un solo valore, è anch'essa monodroma.
Infatti, se y = x2 è la funzione monodroma, crescente per x > 0 e decrescente per x < 0, le funzioni inverse
che si ottengono, non sono più monodrome.
Così da y = senx per 0 ≤ x ≤ π, si ha come funzione inversa x = arcseny, che è addirittura infinitivoca e infinitiforme.
Dagli esempi fatti, seguono le seguenti proprietà:
1^) La funzione inversa di una funzione monodroma è anch'essa monodroma solo se la funzione data è sempre crescente o sempre decrescente.
2^) La funzione inversa di una funzione monodroma non sempre crescente o non sempre decrescente può essere monodroma, polidroma o, addirittura, infinitivoca.
2)-Derivata delle funzioni inverse
Teorema - Se y = f(x) e x = g(y) sono due funzioni l'una inversa dell'altra e ciascuna con derivata sempre diversa da zero, si ha
cioè:
-la derivata della funzione inversa è uguale all'inversa della derivata della funzione data.
Infatti, essendo per ipotesi y = f(x) con x = g(y), si può dire che la y è funzione di se se stessa tramite la x. Per il teorema della funzione composta, allora si ha:
e poichè
si può scrivere
da cui
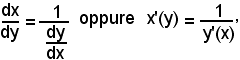
come volevasi dimostrare.
Nota bene
Si badi a non confondere la funzione inversa di una data funzione con l'inversa
della funzione stessa, per la quale si ha:
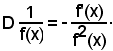
3)-Derivata di alcune funzioni inverse notevoli
1° Si consideri la funzione
nel quale intervallo la funzione data è sempre crescente e, pertanto, ammette come funzione inversa
y = arcsenx
definita, a sua volta, nell'intervallo chiuso (-1, 1).
Avendosi
x'(y) = cosy
è
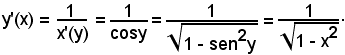
Dunque:
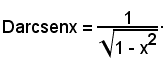
2° Si consideri la funzione
x = cosy con 0 ≤ y ≤ π
nel quale intervallo la funzione data è sempre decrescente e, pertanto, ammette la funzione inversa
y = arccosx
definita, a sua volta, nell'intervallo chiuso (-1, 1).
Avendosi
x'(y) = -seny
è
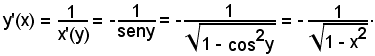
Dunque:
3° Si consideri la funzione
nel quale intervallo la funzione data è sempre crescente e, pertanto, ammette la funzione inversa
y = arctgx
definita, a sua volta, in
Avendosi
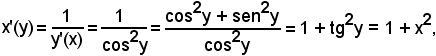
è
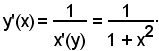
Dunque:
4° Si consideri la funzione
y = ctgx con 0 < y < π
nel quale intervallo aperto la funzione data è sempre decrescente e, pertanto, ammette la funzione inversa
y = arcctgx
definita, a sua volta, in
Avendosi
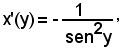
è
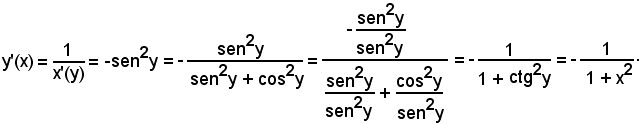
Dunque:
5° Si consideri la funzione
y = ex,
sempre crescente per x > 0 e sempre decrescente per x < 0.
La sua funzione inversa è
y = logy.
Poichè
è
Dunque:
Dex = ex.
Quest'ultimo risultato è stato trovato in precedenza.
Altre derivate di funzioni notevoli
1)-Derivata della funzione y = xα, con x > 0 e α reale qualsiasi
Per α > 0 intero, si è visto che
Dxα = α·xα-1 e Dx-α·x-α-1.
La regola di derivazione della potenza è applicabile ugualmente per α reale qualsiasi.
Infatti, considerato
y = xα
e considerati i logaritmi neperiani dei due membri:
logy = logxα = α·logx,
cioè
logy = α·logx,
derivando ambo i membri e tenendo presente che, essendo y = xα, il 1° membro risulta essere una funzione composta, si ha:
cioè
ma
y = xα,
dunque
come volevasi dimostrare.
2)-Derivata della potenza con esponente razionale
Da
y = xα,
se
si ha
e quindi
Nota bene
1° Se
m =1 e n = 2,
cioè
si ha
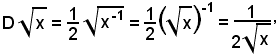
cioè si ritrova il risultato ottenuto in precedenza.
2° Se
m =1 e n > 1,
si ha la funzione,
e quindi
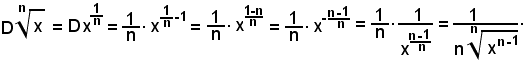
Nota bene
Nel quarto passaggio si è tenuto conto che 1 - n < 0.
Esempio
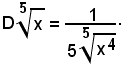
3)-Derivata della funzione esponenziale y = ax.
Da
y = ax
prendendo i logaritmi neperiani dei due membri ed applicando il teorema del logaritmo della potenza, si ha:
logy = x·loga.
Derivando ambo i membri e tenendo presente che il 1° membro è una funzione composta, si ha:
da cui
y'(x) = = y·loga
e, quindi, poichè y = ax,
Dax= y'(x) = ax·loga.
4)-Derivata della funzione logaritmica y = logax.
derivando ambo i membri, si ha:
e poichè
si ha anche
Elenco delle derivate notevoli
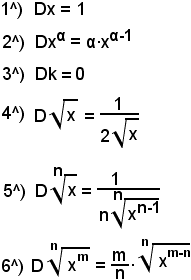
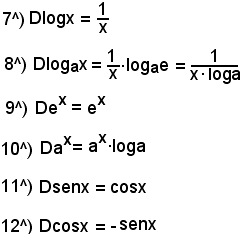

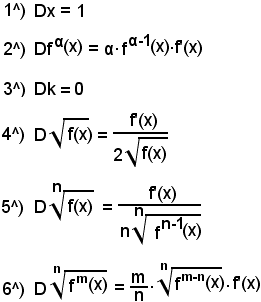


Differenziazione
1)-Differenziale di una funzione
Se y = f(x) è una funzione derivabile in un intervallo (a, b), si sa che
e pertanto, almeno in generale, è:
ove ε tende a zero quando h tende a zero, ossia ε è un infinitesimo dello stesso ordine come h.
Si ha allora:
f(x + h) - f(x) = f'(x)·h + ε·h
e, ricordando che
f(x + h) - f(x) = Δy,
la relazione precedente diventa
Δy = f'(x)·h + ε·h,
cioè:
-l'incremento Δy di una funzione si può scomporre nella somma di due infinitesimi, il 1° f'(x)·h, del 1° ordine, è detto infinitesimo, principale, ed il 2° ε·h, di ordine superiore al 1°, giacchè sia h che ε tendono a zero.
L'infinitesimo principale, si chiama differenziale della funzione e si scrive:
(1) dy = f'(x)·h.
Concetto differenziale
Il differenziale di una funzione è l'infinitesimo del 1° ordine o infinitesimo principale dei due in cui si può scomporre l'incremento della funzione.
Valore del differenziale di una funzione
E' dato dal prodotto della derivata della funzione per l'incremento h della variabile indipendente.
Alla (1) si usa dare una forma diversa, osservando che se
f(x) = x
la (1) dà
dx = 1·h = h,
cioè:
-il differenziale della variabile indipendente è uguale all'incremento che si dà alla stessa.
La (1) si può allora scrivere:
(2) dy = f'(x)·dx,
che è la forma più usata per scrivere il differenziale di una funzione.
e, ricordando che
la relazione precedente diventa
Δy = f'(x)·h + ε·h,
cioè:
-l'incremento Δy di una funzione si può scomporre nella somma di due infinitesimi, il 1° f'(x)·h, del 1° ordine, è detto infinitesimo, principale, ed il 2° ε·h, di ordine superiore al 1°, giacchè sia h che ε tendono a zero.
L'infinitesimo principale, si chiama differenziale della funzione e si scrive:
(1) dy = f'(x)·h.
Concetto differenziale
Il differenziale di una funzione è l'infinitesimo del 1° ordine o infinitesimo principale dei due in cui si può scomporre l'incremento della funzione.
Valore del differenziale di una funzione
E' dato dal prodotto della derivata della funzione per l'incremento h della variabile indipendente.
Alla (1) si usa dare una forma diversa, osservando che se
f(x) = x
la (1) dà
dx = 1·h = h,
cioè:
-il differenziale della variabile indipendente è uguale all'incremento che si dà alla stessa.
La (1) si può allora scrivere:
(2) dy = f'(x)·dx,
che è la forma più usata per scrivere il differenziale di una funzione.
Dalla (2) si ha
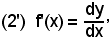
cioè
-la derivata di una funzione è uguale al rapporto tra il differenziale della stessa e il differenziale della variabile indipendente.
Nota bene
1°) Si è visto in precedenza che
uno dei simboli con cui si indicava la derivata di una funzione, è, invece, un vero rapporto.
2°) Da quanto detto, segue che il differenziale di una funzione dipende dal punto x, nel quale si calcola la derivata, e dall'incremento h.
3°) Una funzione derivabile in un punto è ivi differenziabile.
Significato geometrico del differenziale di una funzione
Sia y = f(x) una funzione derivabile in (a, b), γ l'arco di curva da essa rappresentata in detto intervallo e sia T'[x, f(x)] un punto di γ .
Se ad x si dà l'incremento h, al punto incrementato P(x+h, 0) di (a, b) corrisponderà sulla curva il punto P'[x+h, f(x+h)]. Poichè per ipotesi la y = f(x) è derivabile nel punto x di (a, b) si avrà in T' la tangente t. Considerata da T' la parallela all'asse x, si indichino, rispettivamente, con Q ed R i suoi punti d'incontro e della tangente t con PP'. Dal triangolo rettangolo T'QR, si ha:
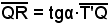
poichè
tgα = f'(x)
e
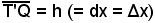
pertanto
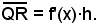
Sapendo che è
dy = f'(x)·h,
si deduce
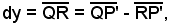
cioè:
-il differenziale della funzione è uguale all'incremento che subisce l'ordinata di un punto della tangente, in corrispondenza dell'incremento dato all'ascissa del punto iniziale.
Dalla Fig. 14 e dalle considerazioni precedenti, infine, si ha
cioè:
-la differenza tra l'incremento e il differenziale della funzione è geometricamente rappresentata dal segmento intercetto tra la curva e la tangente.
Ciò porta alle seguenti altre considerazioni:
1^)-sostituire il differenziale all'incremento di una funzione, significa sostituire nell'intervallo (x, x+h), la tangente nel punto di ascissa x alla curva;
2^)-quanto più piccolo è l'incremento h dato alla variabile x, tanto più piccola sarà la differenza Δy - dy e, quindi, tanto più piccolo sarà l'errore che si commette considerando la tangente invece che la curva, nell'intervallo (x, x+h).
3)-Regole di differenziazione
Poichè per calcolare il differenziale di una funzione basta moltiplicare la derivata della stessa per l'incremento h = dx della variabile indipendente, ossia non si ha bisogno di una nuova regola, parimenti non se ne ha bisogno per differenziare la funzione che si ottiene come risultato delle operazioni che si possono effettuare con due o più funzioni. In seguito si scriveranno le formule relative alle operazioni, già viste per le derivate; gli enunciati delle stesse saranno evidenti e, comunque, si otterranno da quelli delle corrispondenti regole delle derivate con la sola sostituzione del termine differenziale al posto di derivata:
1^ d [f1(x) + f2(x)] = df1(x) + df2(x) = f'1'(x)dx + f2'(x)dx,
2^ d [f1(x) · f2(x)] = f2(x)·df1(x) + f1(x)·df2(x),
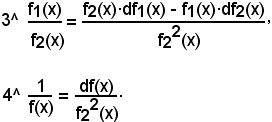
Elenco dei differenziali notevoli
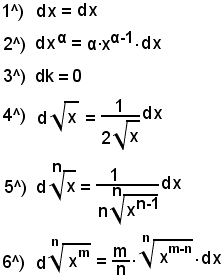
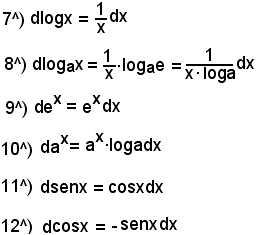
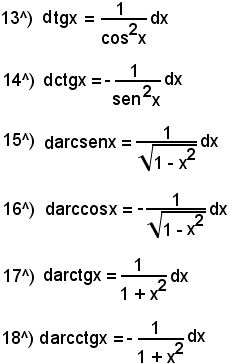
Funzioni crescenti e decrescenti
Premessa
D'ora in poi la funzione y = f(x) si considererà sempre non solo definita limitata e derivabile in un intervallo (a, b) finito o infinito, ma anche dotata in esso delle derivate successive limitate e continue.
1)-Funzione crescente in un punto e in un intervallo
Considerato il punto x0 di (a, b) ed un suo conveniente intorno (x0-h, x0+h), sempre appartenente ad (a, b), si dice che la funzione è crescente nel punto x0, quando per ogni
x0 - h < x < x0 + h,
si verifica
Definizione - Una funzione si dice crescente in un punto x0 quando, per ogni punto del considerato intorno di x0, il valore che la funzione ha in x0 risulta maggiore di tutti quelli che la f(x) assume nei punti dell'intorno sinistro di x0, e minore di tutti quelli che assume nei punti dell'intorno destro di x0.
Una funzione si dice crescente in un intervallo se lo è in ogni suo punto.
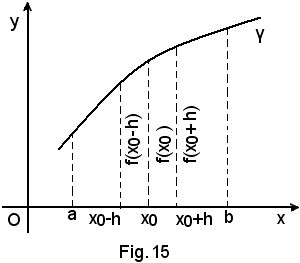
Si osservi che la (1) è equivalente al sistema di disequazioni
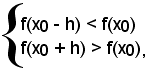
a sua volta equivalente a
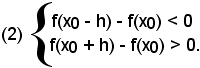
Dalle (2) segue
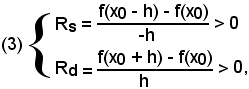
cioè:
-un punto x0 in cui una funzione è crescente, i rapporti incrementali sinistro e destro della funzione risultano positivi.
Inversamente, ricordando che il quoziente è positivo quando dividendo e divisore sono concordi, dalle (3) si torna alle (2), ossia alle (1).
Si è così dimostrato il teorema:
-condizione necessaria e sufficiente affinchè una funzione sia crescente in un punto x0 è che siano positivi i rapporti incrementali sinistro e destro della funzione, relativi al punto x0.
2)-Criterio per il riconoscimento della crescenza di una funzione in un punto
Una funzione si dice decrescente in un intervallo se lo è in ogni suo punto.
Per il teorema enunciato, per dire che in un punto x0 la funzione è crescente, basterebbe considerare Rs e Rd e vedere se sono entrambi positivi.
Più comodo è però il criterio stabilito dal seguente teorema:
-condizione sufficiente affinchè una funzione sia crescente in un punto x0, è che sia positiva la derivata della funzione calcolata nel punto.
Infatti, avendosi:
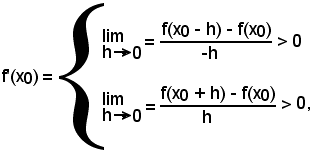
per il teorema della permanenza del segno, dire che
f'(x0) > 0,
cioè
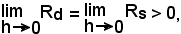
significa che è
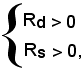
e poichè in Rd è h > 0, dev'essere
f(x0 + h) - f(x0) > 0,
cioè
(1) f(x0) < f(x0 + h).
Inoltre, essendo in Rs > 0, -h < 0, dev'essere
f(x0 - h) - f(x0) < 0
cioè
(2) f(x0 - h) < f(x0).
Da (1) e (2) segue:
f(x0 - h) < f(x0) < f(x0 + h),
ossia la funzione è crescente nel punto x0.
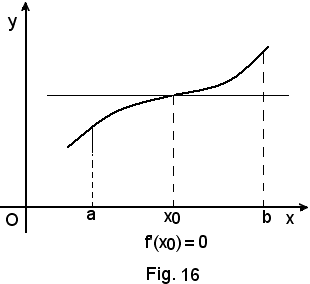
La condizione stabilita dal teorema non è anche necessaria, in quanto, come risulta dalla Fig.16, pur essendo la funzione crescente nel punto x0, la funzione crescente è f'(x) = 0, poichè la tangente alla curva è parallela all'asse x. In seguito si preciserà la natura di tale punto x0.Il precedente teorema è perciò invertibile solo parzialmente, ossia vale il seguente:
-se in un punto x0 la funzione è crescente ed ammette derivata determinata, questa derivata è positiva o nulla, cioè
3)-Funzione decrescente in un punto e in un intervallo
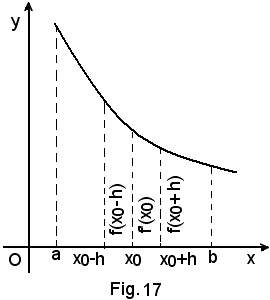
Si ha, cioè:
(1) f (x0 - h) > f(x0) > f(x0 + h).
Analogamente a quanto visto in 1), si ha che la (1) è equivalente al sistema di equazioni
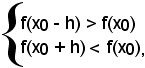
a sua volta equivalente a
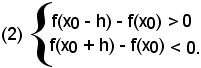
Dalle (2) segue:
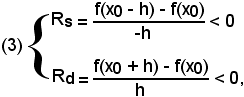
cioè:
-in un punto x0 in cui una funzione è decrescente, i rapporti incrementali sinistro e destro della funzione risultano negativi. Poichè dalle (3) si torna alle (2) e alla (1), ricordando che un quoziente è negativo quando dividendo e divisore sono discordi, resta dimostrato il teorema:
-condizione necessaria e sufficiente affinchè una funzione sia decrescente in un punto x0 è che siano negativi i rapporti incrementali sinistro e destro della funzione, relativi al punto x0.
2)-Criterio per il riconoscimento della decrescenza di una funzione in un punto
Più conveniente dell'esame di Rs e Rd è il seguente teorema:
-condizione sufficiente affinchè una funzione sia decrescente in un punto x0, è che sia negativa la derivata della funzione calcolata nel punto.
La dimostrazione è del tutto analoga a quella vista per una funzione crescente in un punto e si tralascia. Per effetto della stessa considerazione fatta in (2), e risultante dalla Fig. 18, il teorema è invertibile solo parzialmente, ossia vale il seguente:
-se in un punto x0 la funzione è decrescente ed ammette derivata determinata, tale derivata è negativa o nulla, cioè
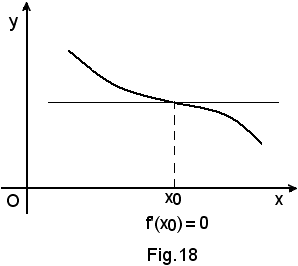
Massimi e minimi
1)-Punto di massimo e valore massimo di una funzione
Definizione - Un punto x0 si dice di massimo per la funzione y = f(x) quando il valore che la funzione ha in esso è più grande di tutti quelli che assume nel conveniente intorno (x0-h, x0+h) di x0, cioè:
(1) f(x0 - h) < f(x0) > f(x0 + h).
f(x0), in tal caso, si dice valore massimo o massimo della funzione.
Si badi che il massimo di una funzione in un punto è da considerare relativamente all'intorno preso del punto e, perciò, si chiama massimo relativo.
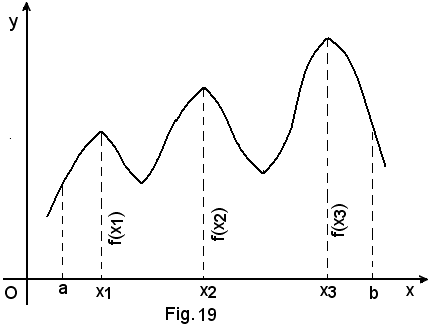
Se invece il valore f(x0) fosse il massimo della funzione per qualsiasi intorno del punto x0, allora si chiamerebbe massimo assoluto. Esso coincide con il massimo relativo, se la funzione non ha altri massimi, ma è il massimo dei massimi relativi nel caso in cui la funzione ammetta più massimi relativi.
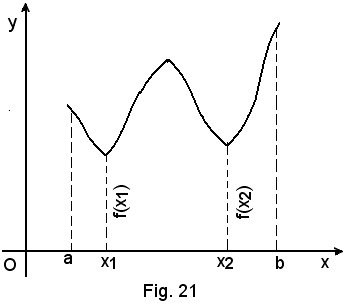
Per la curva e la funzione della Fig. 19, f(x1), f(x2), f(x3) sono massimi relativi a convenienti intorni di ciascuno dei punti x1, x2, x3; f(x3) è il massimo assoluto della funzione in (a, b) in quanto risulta:
f(x3) > f(x2) > f(x1).
La (1) equivale al sistema di disequazioni:
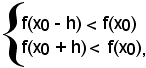
a sua volta equivalente a
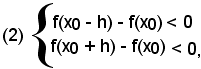
Dalle (2) segue:
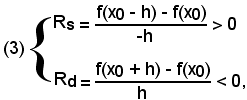
cioè:
-se in un punto x0 la funzione ha un massimo, in quel punto si ha Rs > 0 e Rd < 0.
Per quanto detto sulle funzioni crescenti e decrescenti, segue:
-un punto x0 è di massimo per una funzione, quando questa è crescente nell'intorno sinistro di x0 ed è decrescente nell'intorno destro di x0.
Da questa considerazione e dalle ipotesi della continuità delle derivate della funzione, segue ancora:
-se in un punto x0 una funzione ha un massimo, risulta: f'(x0) = 0.
Si vedrà che l'annullarsi della derivata prima di una funzione in un punto è condizione solo necessaria, e non anche sufficiente, per dire che il punto è di massimo.
2)-Punto di minimo e valore minimo di una funzione
Definizione - Un punto x0 si dice di minimo per la funzione y = f(x) quando il valore che la funzione ha in esso è più piccolo di tutti quelli che assume nel conveniente intorno (x0-h, x0+h) di x0, cioè:
(1) f(x0 - h) > f(x0) < f(x0 + h).
f(x0), in tal caso, si dice valore minimo o minimo della funzione.
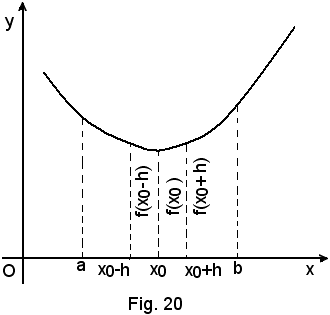
Come il massimo, anche il minimo di una funzione in un punto è da considerare relativamente all'intorno preso del punto e, perciò, si chiama minimo relativo.
Il minimo dei minimi della funzione in (a, b) si chiama minimo assoluto.
Per la curva e la funzione della Fig. 21, f(x1), f(x2) sono minimi relativi a convenienti intorni di ciascuno dei punti x1 e x2;
f(x1) è il minimo assoluto della funzione in (a, b).
La (1) equivale al sistema di disequazioni:
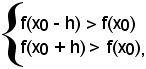
a sua volta equivalente a
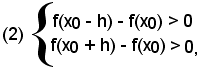
dalle quali segue
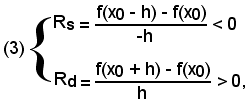
cioè:
-se in un punto x0 la funzione ha un minimo, in quel punto si ha Rs < 0 e Rd > 0.
Per quanto detto sulle funzioni crescenti e decrescenti, segue:
-un punto x0 è di minimo per una funzione, quando questa è decrescente nell'intorno sinistro di x0 ed è crescente nell'intorno destro di x0.
Da questa considerazione e dalle ipotesi della continuità delle derivate della funzione, si ha:
-se in un punto x0 una funzione ha un minimo, risulta: f'(x0) = 0.
Basterebbe questo risultato per avere conferma di quanto detto per il massimo e che ora, si potrà generalizzare come segue:
-l'annullarsi della derivata prima di una funzione in un punto è condizione solo necessaria, ma non anche sufficiente, per dire che il punto è di massimo o di minimo.
Ciò vuol dire che:
-se x0 è un punto di massimo o di minimo, in x0 è f'(x0) = 0, ma non viceversa.
Quindi:
-i punti di massimo o di minimo di una funzione sono da ricercarsi fra i valori che annullano la derivata della funzione, ossia tra le radici dell'equazione f'(x) = 0.
Tuttavia, poichè la condizione f'(x) = 0 è solo necessaria perchè x0 sia punto di massimo o di minimo, significa che esistono altri punti in cui si annulla ugualmente la derivata della funzione, e quindi questi punti sono anche radici dell'equazione f'(x) = 0 senza però che siano di massimo o di minimo.
Retta tangente ad una curva in cui è f'(x) = 0. Punti di flesso
Tenendo presente il significato geometrico di derivata di una funzione in un punto, si sa che nei punti in cui è f'(x) = 0 la retta tangente alla curva è parallela all'asse x.
Pertanto, da quanto detto in precedenza, si può dire che:
-nei punti di massimo o di minimo di una funzione, la tangente alla curva che rappresenta la funzione, è parallela all'asse x.
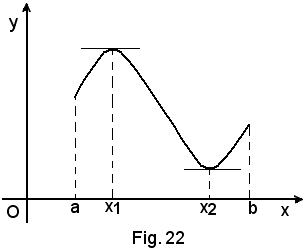
Si è già detto che vi sono altri punti, oltre quelli di massimo e di minimo in cui è f'(x) = 0, quindi vi sono altri punti in cui la tangente è ancora parallela all'asse x.
Mentre per i punti di massimo e di minimo, come si vede nella Fig. 22, esistono convenienti intorni nei quali la curva giace tutta da una parte, semipiano, rispetto alla tangente, che è parallela all'asse x, per i punti delle Fig. 23 e Fig. 24, la tangente alla curva, parallela all'asse x, taglia la curva in due rami e pertanto in qualsiasi intorno dei punti la curva giace sempre in semipiani opposti.
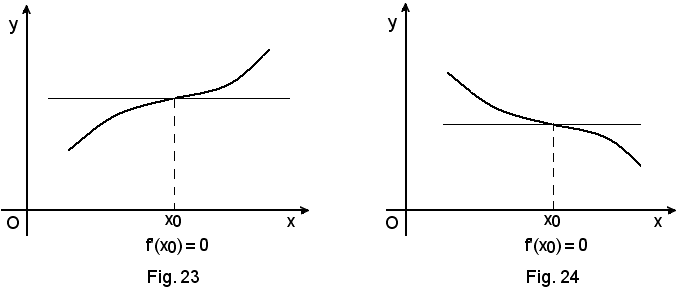
Questi punti, in cui la tangente alla curva è parallela all'asse x e quindi f'(x) = 0, ma non dotati di alcun intorno nel quale la curva giaccia tutta in uno stesso semipiano si dicono punti di flesso. Di tali punti di flesso si parlerà in seguito.
Determinazione dei punti di massimo o di minimo
1° Teorema - Data una funzione y = f(x), soddisfacente alle ipotesi della premessa fatta prima di trattare le funzioni crescenti e decrescenti, cioè y = f(x) dev'essere sempre non solo definita limitata e derivabile in un intervallo (a, b) finito o infinito, ma anche dotata in esso delle derivate successive limitate e continue, se in un punto x0 è f'(x0) = 0 e f'' < 0, x0 è un punto di massimo per la funzione.
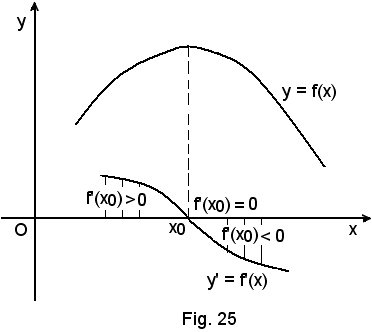
Infatti, si consideri la funzione y' = f'(x), la cui curva rappresentatrice passa per il punto x0, in quanto per ipotesi è f'(x0) = 0. La stessa curva risulta essere decrescente in x0, essendo ancora per ipotesi f''(x0) < 0, ricordando che la D2f(x) = D[Df(x)] e pertanto la curva avrà l'andamento della Fig. 25. Avere tale andamento, significa che a sinistra di x0 è f'(x) > 0, e pertanto la y = f(x) risulta ivi crescente, e a destra di x0 è f'(x) < 0, e pertanto la y = f(x) risulta ivi decrescente.
Da tutto ciò e dalla continuità della y' = f'(x), ammessa per ipotesi, si deduce, come si vede dalla Fig. 25 che x0 è un punto di massimo.
Teorema - Data una funzione y = f(x), soddisfacente alle stesse ipotesi del teorema 1, se in un punto x0 è f'(x0) = 0 e f'' > 0, x0 è un punto di minimo per la funzione.
Infatti, si consideri ancora la funzione y' = f'(x), la cui curva rappresentatrice passa per il punto x0, in quanto per ipotesi è f'(x0) = 0. La stessa curva risulta essere crescente in x0, essendo ancora per ipotesi f''(x0) > 0, e pertanto la curva avrà l'andamento della Fig. 26. Avere tale andamento, significa che a sinistra di x0 è f'(x) < 0, e pertanto la y = f(x) risulta ivi decrescente, e a destra di x0 è f'(x) > 0, e pertanto la y = f(x) risulta ivi crescente.
Da tutto ciò, e dalla continuità della y' = f'(x) ammessa per ipotesi, si deduce, come si vede dalla Fig. 26, che x0 è un punto di minimo.
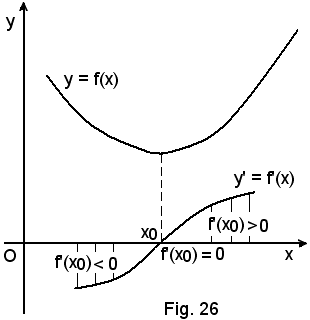
Nulla però si è detto se in x0 è f''(x0) = 0. La natura di questi punti si precisa subito.
Allora, per effettuare la ricerca dei punti di massimo e di minimo, detti anche punti estremanti, di una funzione, si calcola la derivata della stessa e si considera l'equazione f'(x) = 0.
Le radici di tale equazione possono essere punto di massimo o di minimo o, di altra natura, singolari.
Per precisare la loro natura, si calcola la derivata seconda della funzione ed in questa si sostituiscono una alla volta le radici dell'equazione f'(x) = 0.
Effettuata la sostituzione, se risulta f''(x) < 0, il numero sostituito rappresenta l'ascissa di un punto di massimo; se invece risulta f''(x) > 0, il numero sostituito rappresenta l'ascissa di un punto di minimo; infine, se risulta f''(x) = 0, ma nello stesso punto è f'''(x) ≠ 0, il numero sostituito rappresenta l'ascissa di un punto di flesso.
Nota bene
Solitamente, per le funzioni che si tratteranno, saranno sufficienti le condizioni suddette per stabilire la natura dei punti in cui la f'(x) = 0, tuttavia, si precisa che:
-se in un punto x0 è f''(x0) = 0 ed anche f'''(x0) = 0, basta effettuare le derivate successive della funzione e calcolare il valore di ciascuna sempre in x0.
Quando capita che la 1^ derivata che non si annulla in x0 è di ordine dispari, la funzione ha in x0 un flesso; se invece detta derivata è di ordine pari, x0 è un punto di massimo o di minimo, sempre relativo, a seconda del valore negativo o positivo di tale derivata.
Esempi di ricerca dei punti estremanti di una funzione e degl'intervalli di crescenza o decrescenza della stessa
1) y = mx + n, equazione di una retta con m ≠ 0 e n ≠0.
Essendo y'(x) = m ≠ 0 sempre, la funzione non ha punti estremanti.
Se m < 0, la linea retta è crescente.
Se m < 0, la linea retta è decrescente su tutto l'asse reale
2) y = ax2 + bx + c, equazione di una parabola con a ≠ 0.
Essendo
y'(x) = 2ax + b,
dall'equazione
2ax + b = 0
si ha la radice
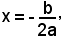
la quale può essere l'ascissa un punto di massimo o di minimo o di flesso per la curva.
Essendo
y''(x) = 2a ≠ 0,
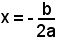
è l'ascissa di un punto di massimo o di minimo, e precisamente:
se a < 0, ascissa di un punto di massimo;
se a > 0, ascissa di un punto di minimo.
Si ricorda dalla geometria analitica che -b/2a è l'ascissa del vertice della parabola e tale punto risulta essere un massimo o un minimo per la curva a seconda che questa rivolga la concavità verso il semiasse -y, a < 0, o verso il semiasse +y, a > 0.
Il valore massimo o minimo della funzione è quello che la funzione assume nel punto corrispondente e, quindi, si ottiene sostituendo nella funzione l'ascissa di quello.
Nell'esempio:
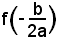
è uguale al valore massimo se a >0,
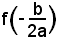
è uguale al valore minimo se a > 0,
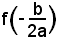
è l'ordinata del vertice.
Infine, la funzione è crescente nell'intervallo in cui risulta f'(x) = 2ax + b > 0 e decrescente in quello in cui risulta f'(x) = 2ax + b < 0.
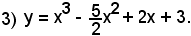
Si ha:
f'(x) = 3x2 - 5x + 2
e, quindi, si considera l'equazione
y'(x) = 0,
cioè
3x2 - 5x + 2 = 0,
le cui radici sono
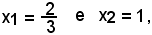
che possono essere punti di massimo o di minimo o di flesso.
Essendo
f''(x) = 6x - 5
e
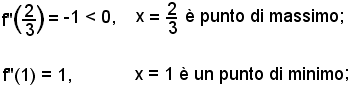
inoltre è

Infine, poichè
f'(x) = 3x2 - 5x + 2 > 0
per
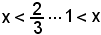
esternamente all'intervallo
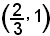
la funzione è crescente e nello stesso intervallo è, invece, decrescente.

Si ha:
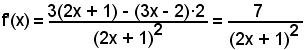
quindi, si considera l'equazione
f'(x) = 0,
cioè
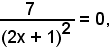
che è impossibile e, pertanto, non vi sono punti estremanti.
Poichè
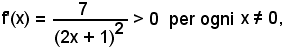
la curva è sempre crescente.

Si ha:
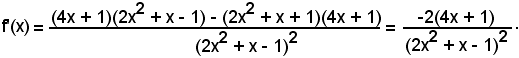
Si considera allora l'equazione
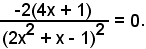
cioè
-la derivata di una funzione è uguale al rapporto tra il differenziale della stessa e il differenziale della variabile indipendente.
Nota bene
1°) Si è visto in precedenza che
uno dei simboli con cui si indicava la derivata di una funzione, è, invece, un vero rapporto.
2°) Da quanto detto, segue che il differenziale di una funzione dipende dal punto x, nel quale si calcola la derivata, e dall'incremento h.
3°) Una funzione derivabile in un punto è ivi differenziabile.
Significato geometrico del differenziale di una funzione
Sia y = f(x) una funzione derivabile in (a, b), γ l'arco di curva da essa rappresentata in detto intervallo e sia T'[x, f(x)] un punto di γ .

Se ad x si dà l'incremento h, al punto incrementato P(x+h, 0) di (a, b) corrisponderà sulla curva il punto P'[x+h, f(x+h)]. Poichè per ipotesi la y = f(x) è derivabile nel punto x di (a, b) si avrà in T' la tangente t. Considerata da T' la parallela all'asse x, si indichino, rispettivamente, con Q ed R i suoi punti d'incontro e della tangente t con PP'. Dal triangolo rettangolo T'QR, si ha:
poichè
tgα = f'(x)
e
pertanto
Sapendo che è
dy = f'(x)·h,
si deduce
cioè:
-il differenziale della funzione è uguale all'incremento che subisce l'ordinata di un punto della tangente, in corrispondenza dell'incremento dato all'ascissa del punto iniziale.
Dalla Fig. 14 e dalle considerazioni precedenti, infine, si ha
Δy - dy = RP',
cioè:
-la differenza tra l'incremento e il differenziale della funzione è geometricamente rappresentata dal segmento intercetto tra la curva e la tangente.
Ciò porta alle seguenti altre considerazioni:
1^)-sostituire il differenziale all'incremento di una funzione, significa sostituire nell'intervallo (x, x+h), la tangente nel punto di ascissa x alla curva;
2^)-quanto più piccolo è l'incremento h dato alla variabile x, tanto più piccola sarà la differenza Δy - dy e, quindi, tanto più piccolo sarà l'errore che si commette considerando la tangente invece che la curva, nell'intervallo (x, x+h).
3)-Regole di differenziazione
Poichè per calcolare il differenziale di una funzione basta moltiplicare la derivata della stessa per l'incremento h = dx della variabile indipendente, ossia non si ha bisogno di una nuova regola, parimenti non se ne ha bisogno per differenziare la funzione che si ottiene come risultato delle operazioni che si possono effettuare con due o più funzioni. In seguito si scriveranno le formule relative alle operazioni, già viste per le derivate; gli enunciati delle stesse saranno evidenti e, comunque, si otterranno da quelli delle corrispondenti regole delle derivate con la sola sostituzione del termine differenziale al posto di derivata:
1^ d [f1(x) + f2(x)] = df1(x) + df2(x) = f'1'(x)dx + f2'(x)dx,
2^ d [f1(x) · f2(x)] = f2(x)·df1(x) + f1(x)·df2(x),
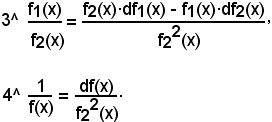
Elenco dei differenziali notevoli
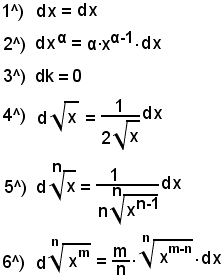
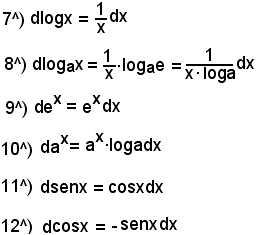
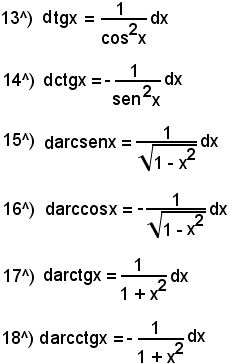
Funzioni crescenti e decrescenti
Premessa
D'ora in poi la funzione y = f(x) si considererà sempre non solo definita limitata e derivabile in un intervallo (a, b) finito o infinito, ma anche dotata in esso delle derivate successive limitate e continue.
1)-Funzione crescente in un punto e in un intervallo
Considerato il punto x0 di (a, b) ed un suo conveniente intorno (x0-h, x0+h), sempre appartenente ad (a, b), si dice che la funzione è crescente nel punto x0, quando per ogni
x0 - h < x < x0 + h,
si verifica
(1) f (x0 - h) < f(x0) < f(x0 + h).
Definizione - Una funzione si dice crescente in un punto x0 quando, per ogni punto del considerato intorno di x0, il valore che la funzione ha in x0 risulta maggiore di tutti quelli che la f(x) assume nei punti dell'intorno sinistro di x0, e minore di tutti quelli che assume nei punti dell'intorno destro di x0.
Una funzione si dice crescente in un intervallo se lo è in ogni suo punto.

Si osservi che la (1) è equivalente al sistema di disequazioni
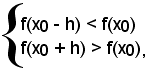
a sua volta equivalente a
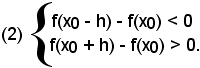
Dalle (2) segue
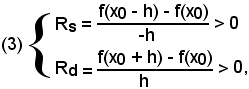
cioè:
-un punto x0 in cui una funzione è crescente, i rapporti incrementali sinistro e destro della funzione risultano positivi.
Inversamente, ricordando che il quoziente è positivo quando dividendo e divisore sono concordi, dalle (3) si torna alle (2), ossia alle (1).
Si è così dimostrato il teorema:
-condizione necessaria e sufficiente affinchè una funzione sia crescente in un punto x0 è che siano positivi i rapporti incrementali sinistro e destro della funzione, relativi al punto x0.
2)-Criterio per il riconoscimento della crescenza di una funzione in un punto
Una funzione si dice decrescente in un intervallo se lo è in ogni suo punto.
Per il teorema enunciato, per dire che in un punto x0 la funzione è crescente, basterebbe considerare Rs e Rd e vedere se sono entrambi positivi.
Più comodo è però il criterio stabilito dal seguente teorema:
-condizione sufficiente affinchè una funzione sia crescente in un punto x0, è che sia positiva la derivata della funzione calcolata nel punto.
Infatti, avendosi:
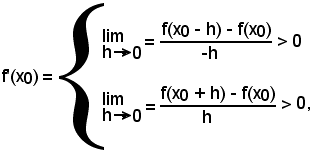
per il teorema della permanenza del segno, dire che
f'(x0) > 0,
cioè
significa che è
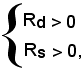
e poichè in Rd è h > 0, dev'essere
f(x0 + h) - f(x0) > 0,
cioè
(1) f(x0) < f(x0 + h).
Inoltre, essendo in Rs > 0, -h < 0, dev'essere
f(x0 - h) - f(x0) < 0
cioè
(2) f(x0 - h) < f(x0).
Da (1) e (2) segue:
f(x0 - h) < f(x0) < f(x0 + h),
ossia la funzione è crescente nel punto x0.
La condizione stabilita dal teorema non è anche necessaria, in quanto, come risulta dalla Fig.16, pur essendo la funzione crescente nel punto x0, la funzione crescente è f'(x) = 0, poichè la tangente alla curva è parallela all'asse x. In seguito si preciserà la natura di tale punto x0.
-se in un punto x0 la funzione è crescente ed ammette derivata determinata, questa derivata è positiva o nulla, cioè
f'(x) ≥ 0.

3)-Funzione decrescente in un punto e in un intervallo
Definizione - Una funzione si dice decrescente in un punto x0 quando, per ogni punto del conveniente intorno (x0-h, x0+h) di x0, il valore che la funzione ha in x0 risulta minore di tutti quelli che assume nei punti dell'intorno sinistro di x0, e maggiore di tutti quelli che assume nei punti dell'intorno destro di x0.

Si ha, cioè:
Una funzione si dice decrescente in un intervallo se lo è in ogni suo punto.
Analogamente a quanto visto in 1), si ha che la (1) è equivalente al sistema di equazioni
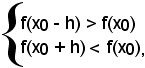
a sua volta equivalente a
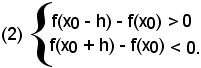
Dalle (2) segue:
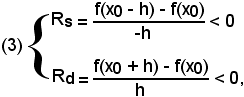
cioè:
-in un punto x0 in cui una funzione è decrescente, i rapporti incrementali sinistro e destro della funzione risultano negativi. Poichè dalle (3) si torna alle (2) e alla (1), ricordando che un quoziente è negativo quando dividendo e divisore sono discordi, resta dimostrato il teorema:
-condizione necessaria e sufficiente affinchè una funzione sia decrescente in un punto x0 è che siano negativi i rapporti incrementali sinistro e destro della funzione, relativi al punto x0.
2)-Criterio per il riconoscimento della decrescenza di una funzione in un punto
Più conveniente dell'esame di Rs e Rd è il seguente teorema:
-condizione sufficiente affinchè una funzione sia decrescente in un punto x0, è che sia negativa la derivata della funzione calcolata nel punto.
La dimostrazione è del tutto analoga a quella vista per una funzione crescente in un punto e si tralascia. Per effetto della stessa considerazione fatta in (2), e risultante dalla Fig. 18, il teorema è invertibile solo parzialmente, ossia vale il seguente:
-se in un punto x0 la funzione è decrescente ed ammette derivata determinata, tale derivata è negativa o nulla, cioè
f'(x) ≤ 0.

Massimi e minimi
1)-Punto di massimo e valore massimo di una funzione
Definizione - Un punto x0 si dice di massimo per la funzione y = f(x) quando il valore che la funzione ha in esso è più grande di tutti quelli che assume nel conveniente intorno (x0-h, x0+h) di x0, cioè:
(1) f(x0 - h) < f(x0) > f(x0 + h).
f(x0), in tal caso, si dice valore massimo o massimo della funzione.
Si badi che il massimo di una funzione in un punto è da considerare relativamente all'intorno preso del punto e, perciò, si chiama massimo relativo.
Se invece il valore f(x0) fosse il massimo della funzione per qualsiasi intorno del punto x0, allora si chiamerebbe massimo assoluto. Esso coincide con il massimo relativo, se la funzione non ha altri massimi, ma è il massimo dei massimi relativi nel caso in cui la funzione ammetta più massimi relativi.
Per la curva e la funzione della Fig. 19, f(x1), f(x2), f(x3) sono massimi relativi a convenienti intorni di ciascuno dei punti x1, x2, x3; f(x3) è il massimo assoluto della funzione in (a, b) in quanto risulta:

La (1) equivale al sistema di disequazioni:
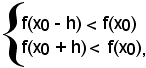
a sua volta equivalente a
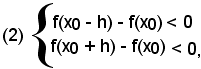
Dalle (2) segue:
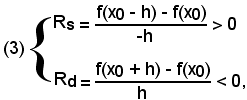
cioè:
-se in un punto x0 la funzione ha un massimo, in quel punto si ha Rs > 0 e Rd < 0.
Per quanto detto sulle funzioni crescenti e decrescenti, segue:
-un punto x0 è di massimo per una funzione, quando questa è crescente nell'intorno sinistro di x0 ed è decrescente nell'intorno destro di x0.
Da questa considerazione e dalle ipotesi della continuità delle derivate della funzione, segue ancora:
-se in un punto x0 una funzione ha un massimo, risulta: f'(x0) = 0.
Si vedrà che l'annullarsi della derivata prima di una funzione in un punto è condizione solo necessaria, e non anche sufficiente, per dire che il punto è di massimo.
2)-Punto di minimo e valore minimo di una funzione
Definizione - Un punto x0 si dice di minimo per la funzione y = f(x) quando il valore che la funzione ha in esso è più piccolo di tutti quelli che assume nel conveniente intorno (x0-h, x0+h) di x0, cioè:
(1) f(x0 - h) > f(x0) < f(x0 + h).
f(x0), in tal caso, si dice valore minimo o minimo della funzione.

Come il massimo, anche il minimo di una funzione in un punto è da considerare relativamente all'intorno preso del punto e, perciò, si chiama minimo relativo.
Il minimo dei minimi della funzione in (a, b) si chiama minimo assoluto.
Per la curva e la funzione della Fig. 21, f(x1), f(x2) sono minimi relativi a convenienti intorni di ciascuno dei punti x1 e x2;
f(x1) è il minimo assoluto della funzione in (a, b).

La (1) equivale al sistema di disequazioni:
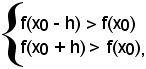
a sua volta equivalente a
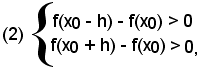
dalle quali segue
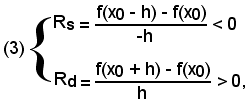
cioè:
-se in un punto x0 la funzione ha un minimo, in quel punto si ha Rs < 0 e Rd > 0.
Per quanto detto sulle funzioni crescenti e decrescenti, segue:
-un punto x0 è di minimo per una funzione, quando questa è decrescente nell'intorno sinistro di x0 ed è crescente nell'intorno destro di x0.
Da questa considerazione e dalle ipotesi della continuità delle derivate della funzione, si ha:
-se in un punto x0 una funzione ha un minimo, risulta: f'(x0) = 0.
Basterebbe questo risultato per avere conferma di quanto detto per il massimo e che ora, si potrà generalizzare come segue:
-l'annullarsi della derivata prima di una funzione in un punto è condizione solo necessaria, ma non anche sufficiente, per dire che il punto è di massimo o di minimo.
Ciò vuol dire che:
-se x0 è un punto di massimo o di minimo, in x0 è f'(x0) = 0, ma non viceversa.
Quindi:
-i punti di massimo o di minimo di una funzione sono da ricercarsi fra i valori che annullano la derivata della funzione, ossia tra le radici dell'equazione f'(x) = 0.
Tuttavia, poichè la condizione f'(x) = 0 è solo necessaria perchè x0 sia punto di massimo o di minimo, significa che esistono altri punti in cui si annulla ugualmente la derivata della funzione, e quindi questi punti sono anche radici dell'equazione f'(x) = 0 senza però che siano di massimo o di minimo.
Retta tangente ad una curva in cui è f'(x) = 0. Punti di flesso
Tenendo presente il significato geometrico di derivata di una funzione in un punto, si sa che nei punti in cui è f'(x) = 0 la retta tangente alla curva è parallela all'asse x.
Pertanto, da quanto detto in precedenza, si può dire che:
-nei punti di massimo o di minimo di una funzione, la tangente alla curva che rappresenta la funzione, è parallela all'asse x.

Si è già detto che vi sono altri punti, oltre quelli di massimo e di minimo in cui è f'(x) = 0, quindi vi sono altri punti in cui la tangente è ancora parallela all'asse x.
Mentre per i punti di massimo e di minimo, come si vede nella Fig. 22, esistono convenienti intorni nei quali la curva giace tutta da una parte, semipiano, rispetto alla tangente, che è parallela all'asse x, per i punti delle Fig. 23 e Fig. 24, la tangente alla curva, parallela all'asse x, taglia la curva in due rami e pertanto in qualsiasi intorno dei punti la curva giace sempre in semipiani opposti.
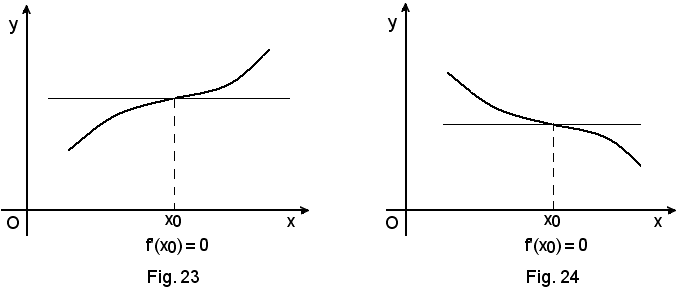
Questi punti, in cui la tangente alla curva è parallela all'asse x e quindi f'(x) = 0, ma non dotati di alcun intorno nel quale la curva giaccia tutta in uno stesso semipiano si dicono punti di flesso. Di tali punti di flesso si parlerà in seguito.
Determinazione dei punti di massimo o di minimo
1° Teorema - Data una funzione y = f(x), soddisfacente alle ipotesi della premessa fatta prima di trattare le funzioni crescenti e decrescenti, cioè y = f(x) dev'essere sempre non solo definita limitata e derivabile in un intervallo (a, b) finito o infinito, ma anche dotata in esso delle derivate successive limitate e continue, se in un punto x0 è f'(x0) = 0 e f'' < 0, x0 è un punto di massimo per la funzione.

Infatti, si consideri la funzione y' = f'(x), la cui curva rappresentatrice passa per il punto x0, in quanto per ipotesi è f'(x0) = 0. La stessa curva risulta essere decrescente in x0, essendo ancora per ipotesi f''(x0) < 0, ricordando che la D2f(x) = D[Df(x)] e pertanto la curva avrà l'andamento della Fig. 25. Avere tale andamento, significa che a sinistra di x0 è f'(x) > 0, e pertanto la y = f(x) risulta ivi crescente, e a destra di x0 è f'(x) < 0, e pertanto la y = f(x) risulta ivi decrescente.
Da tutto ciò e dalla continuità della y' = f'(x), ammessa per ipotesi, si deduce, come si vede dalla Fig. 25 che x0 è un punto di massimo.
Teorema - Data una funzione y = f(x), soddisfacente alle stesse ipotesi del teorema 1, se in un punto x0 è f'(x0) = 0 e f'' > 0, x0 è un punto di minimo per la funzione.
Infatti, si consideri ancora la funzione y' = f'(x), la cui curva rappresentatrice passa per il punto x0, in quanto per ipotesi è f'(x0) = 0. La stessa curva risulta essere crescente in x0, essendo ancora per ipotesi f''(x0) > 0, e pertanto la curva avrà l'andamento della Fig. 26. Avere tale andamento, significa che a sinistra di x0 è f'(x) < 0, e pertanto la y = f(x) risulta ivi decrescente, e a destra di x0 è f'(x) > 0, e pertanto la y = f(x) risulta ivi crescente.
Da tutto ciò, e dalla continuità della y' = f'(x) ammessa per ipotesi, si deduce, come si vede dalla Fig. 26, che x0 è un punto di minimo.

Nulla però si è detto se in x0 è f''(x0) = 0. La natura di questi punti si precisa subito.
Allora, per effettuare la ricerca dei punti di massimo e di minimo, detti anche punti estremanti, di una funzione, si calcola la derivata della stessa e si considera l'equazione f'(x) = 0.
Le radici di tale equazione possono essere punto di massimo o di minimo o, di altra natura, singolari.
Per precisare la loro natura, si calcola la derivata seconda della funzione ed in questa si sostituiscono una alla volta le radici dell'equazione f'(x) = 0.
Effettuata la sostituzione, se risulta f''(x) < 0, il numero sostituito rappresenta l'ascissa di un punto di massimo; se invece risulta f''(x) > 0, il numero sostituito rappresenta l'ascissa di un punto di minimo; infine, se risulta f''(x) = 0, ma nello stesso punto è f'''(x) ≠ 0, il numero sostituito rappresenta l'ascissa di un punto di flesso.
Nota bene
Solitamente, per le funzioni che si tratteranno, saranno sufficienti le condizioni suddette per stabilire la natura dei punti in cui la f'(x) = 0, tuttavia, si precisa che:
-se in un punto x0 è f''(x0) = 0 ed anche f'''(x0) = 0, basta effettuare le derivate successive della funzione e calcolare il valore di ciascuna sempre in x0.
Quando capita che la 1^ derivata che non si annulla in x0 è di ordine dispari, la funzione ha in x0 un flesso; se invece detta derivata è di ordine pari, x0 è un punto di massimo o di minimo, sempre relativo, a seconda del valore negativo o positivo di tale derivata.
Esempi di ricerca dei punti estremanti di una funzione e degl'intervalli di crescenza o decrescenza della stessa
1) y = mx + n, equazione di una retta con m ≠ 0 e n ≠0.
Essendo y'(x) = m ≠ 0 sempre, la funzione non ha punti estremanti.
Se m < 0, la linea retta è crescente.
Se m < 0, la linea retta è decrescente su tutto l'asse reale
2) y = ax2 + bx + c, equazione di una parabola con a ≠ 0.
Essendo
dall'equazione
2ax + b = 0
si ha la radice
la quale può essere l'ascissa un punto di massimo o di minimo o di flesso per la curva.
Essendo
è l'ascissa di un punto di massimo o di minimo, e precisamente:
se a < 0, ascissa di un punto di massimo;
se a > 0, ascissa di un punto di minimo.
Si ricorda dalla geometria analitica che -b/2a è l'ascissa del vertice della parabola e tale punto risulta essere un massimo o un minimo per la curva a seconda che questa rivolga la concavità verso il semiasse -y, a < 0, o verso il semiasse +y, a > 0.
Il valore massimo o minimo della funzione è quello che la funzione assume nel punto corrispondente e, quindi, si ottiene sostituendo nella funzione l'ascissa di quello.
Nell'esempio:
è uguale al valore massimo se a >0,
è uguale al valore minimo se a > 0,
è l'ordinata del vertice.
Infine, la funzione è crescente nell'intervallo in cui risulta f'(x) = 2ax + b > 0 e decrescente in quello in cui risulta f'(x) = 2ax + b < 0.
Si ha:
f'(x) = 3x2 - 5x + 2
e, quindi, si considera l'equazione
y'(x) = 0,
cioè
3x2 - 5x + 2 = 0,
le cui radici sono
che possono essere punti di massimo o di minimo o di flesso.
Essendo
f''(x) = 6x - 5
e
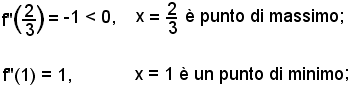
inoltre è

Infine, poichè
f'(x) = 3x2 - 5x + 2 > 0
per
esternamente all'intervallo
la funzione è crescente e nello stesso intervallo è, invece, decrescente.
Si ha:
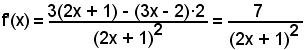
quindi, si considera l'equazione
f'(x) = 0,
cioè
che è impossibile e, pertanto, non vi sono punti estremanti.
Poichè
la curva è sempre crescente.

Si ha:
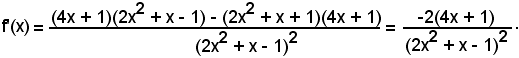
Si considera allora l'equazione
Dopo
aver osservato che sono da scartare i valori x = -1 e x = 1/2, per i
quali si annulla il denominatore, la radice dell'equazione è x =
-1/4.
Essendo
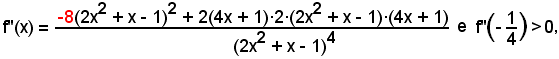
si ha che:

è l'ordinata minima o il valore minimo della funzione.
Nota bene
Si badi che, nelle funzioni razionali fratte, per la determinazione del segno della f''(x0) basta esaminare il segno del solo 1° fattore del 1° termine del numeratore, in rosso nell'esempio, per ovvie considerazioni algebriche.
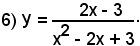
Si ha:
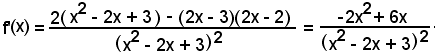
L'equazione f'(x) = 0 è:
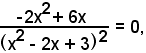
il cui denominatore è sempre diverso da zero e le cui radici sono
x1 = 0 e x2 = 3,
punti di massimo, di minimo o di flesso.
Essendo:
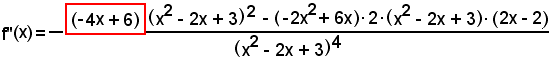
se
f''(0) > 0, è x = 0 punto di minimo della funzione,
f''(3) < 0, è x = 3 punto di massimo della funzione,
ed infine
f(0) = -1, è il valore minimo della funzione,
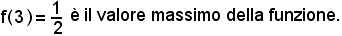
Asintoti di una curva e loro ricerca
1)-Definizione - Si chiama asintoto di una curva, quella retta alla quale la curva si avvicina sempre più toccandola però solo all'infinito.
Dalla definizione precedente, segue:
-un asintoto di una curva è una tangente in un punto improprio, all'infinito, della curva.
2)-Asintoto verticale
Come è noto, dire che
significa che la retta x = x0 è un asintoto verticale della curva.
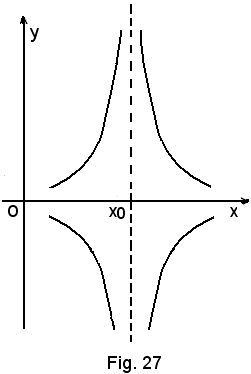
In particolare se y = f(x) è una funzione razionale fratta, si ha
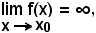
quando il suo denominatore tende a zero, ossia quando la variabile tende ad una radice dell'equazione che si ottiene uguagliando il denominatore a zero. Quindi, sempre per le funzioni razionali fratte, si può dire che:
-L'equazione complessiva degli asintoti verticali è il denominatore della frazione uguagliato a zero.
Esempi
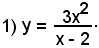
L'equazione dell'asintoto verticale è
x = 2,
in quanto
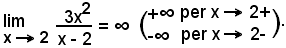
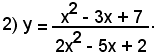
Le radici dell'equazione
2x2 - 5x + 2 =0
sono x = 1/2 e x = 2, pertanto, le rette di equazione
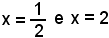
sono gli asintoti verticali della curva che rappresenta la funzione, e che ha altri asintoti, quelli orizzontali che saranno trattati di seguito.
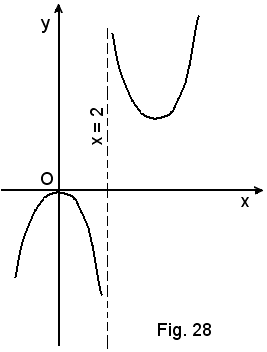
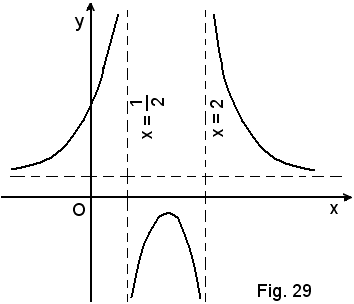
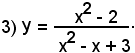
L'equazione è razionale fratta, ma l'equazione
x2 - x + 3
è impossibile nel campo reale e quindi la curva che rappresenta la funzione non ha asintoti verticali.
4) y = tgx.
Essendo in (0, 2π)
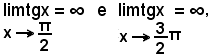
le rette di equazione
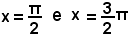
sono asintoti della curva, tangentoide.
Asintoto orizzontale
Come è noto, dire che
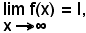
significa che la retta y = l è asintoto orizzontale della curva; pertanto l'equazione dell'asintoto orizzontale di una curva y = f(x) è
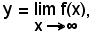
Esempi
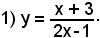
L'equazione dell'asintoto orizzontale della curva è
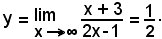
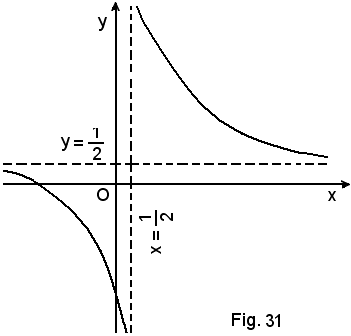
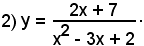
Poichè
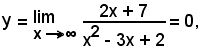
l'asse x è asintoto orizzontale per la curva. Si osservi che la curva ha due asintoti verticali di equazioni
x = 1 e x = 2.
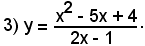
Poichè
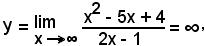
la curva non ha asintoto orizzontale.
Asintoto obliquo
Nel caso in cui risulti
se la curva di equazione y = f(x) ha un asintoto, questo, per quanto detto in 2) ed in 3), non può essere nè verticale nè orizzontale, risulterà allora obliquo rispetto agli assi cartesiani e la sua equazione sarà pertanto della forma:
y = mx + n.
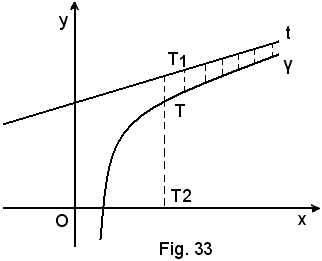
Come si vede nella Fig. 33, affinchè la retta t sia asintoto della curva γ, dev'essere:

ossia
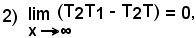
essendo T2T1 l'ordinata y di un punto della t e quindi y = mx + n, e T2T1 l'ordinata y di un punto della γ e quindi x = f(x).
La 2) si può allora scrivere come segue:
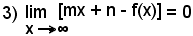
e, dividendo tutto per x,
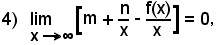
ma poichè
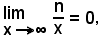
affinchè la 4) sia verificata si deve avere
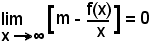
e quindi
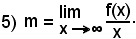
Sostituendo la 5) nella 3), si ha:
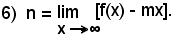
In conclusione, l'eventuale asintoto obliquo della funzione è una retta di equazione
y = mx + n,
per la quale è

Si potrebbe dimostrare, ma si tralascia, che se esistono finiti i limiti 7) e 8) la curva è dotata di asintoto obliquo, la cui equazione è
y = mx + n,
con m ed n aventi i valori dati proprio dalla 7) e dalla 8).
E' ovvio che se anche uno solo dei due limiti 7) e 8) esiste, ma non è finito oppure non esiste addirittura, la curva non possiede asintoti obliqui.
Nota bene
L'esistenza dell'asintoto obliquo di una curva, rappresentatrice di una funzione razionale fratta, può essere ammessa subito, se si verifica la seguente condizione:
-il grado del numeratore è di un'unità maggiore di quello del denominatore.
Ciò significa che esistono finiti i limiti 7) e 8).
Esempi
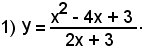
Essendo
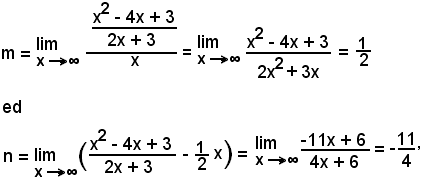
l'asintoto obliquo della curva è la retta di equazione
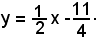
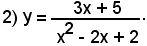
Essendo
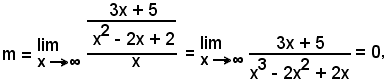
la curva non ha asintoto obliquo.
Essendo
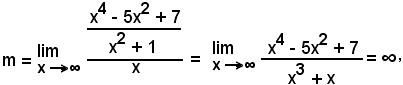
la curva non ha asintoto obliquo.
Essendo
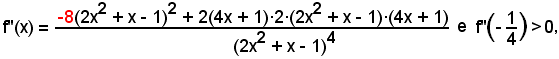
si ha che:

è l'ordinata minima o il valore minimo della funzione.
Nota bene
Si badi che, nelle funzioni razionali fratte, per la determinazione del segno della f''(x0) basta esaminare il segno del solo 1° fattore del 1° termine del numeratore, in rosso nell'esempio, per ovvie considerazioni algebriche.
Si ha:
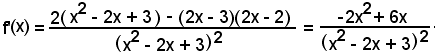
L'equazione f'(x) = 0 è:
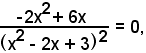
il cui denominatore è sempre diverso da zero e le cui radici sono
x1 = 0 e x2 = 3,
punti di massimo, di minimo o di flesso.
Essendo:
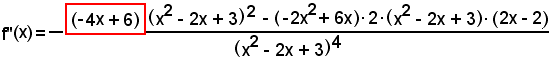
se
f''(0) > 0, è x = 0 punto di minimo della funzione,
f''(3) < 0, è x = 3 punto di massimo della funzione,
ed infine
f(0) = -1, è il valore minimo della funzione,
Asintoti di una curva e loro ricerca
1)-Definizione - Si chiama asintoto di una curva, quella retta alla quale la curva si avvicina sempre più toccandola però solo all'infinito.
Dalla definizione precedente, segue:
-un asintoto di una curva è una tangente in un punto improprio, all'infinito, della curva.
2)-Asintoto verticale
Come è noto, dire che
significa che la retta x = x0 è un asintoto verticale della curva.

In particolare se y = f(x) è una funzione razionale fratta, si ha
quando il suo denominatore tende a zero, ossia quando la variabile tende ad una radice dell'equazione che si ottiene uguagliando il denominatore a zero. Quindi, sempre per le funzioni razionali fratte, si può dire che:
-L'equazione complessiva degli asintoti verticali è il denominatore della frazione uguagliato a zero.
Esempi
L'equazione dell'asintoto verticale è
x = 2,
in quanto
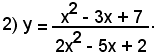
Le radici dell'equazione
2x2 - 5x + 2 =0
sono x = 1/2 e x = 2, pertanto, le rette di equazione
sono gli asintoti verticali della curva che rappresenta la funzione, e che ha altri asintoti, quelli orizzontali che saranno trattati di seguito.


L'equazione è razionale fratta, ma l'equazione
x2 - x + 3
è impossibile nel campo reale e quindi la curva che rappresenta la funzione non ha asintoti verticali.
4) y = tgx.
Essendo in (0, 2π)
le rette di equazione
sono asintoti della curva, tangentoide.
Asintoto orizzontale
Come è noto, dire che
significa che la retta y = l è asintoto orizzontale della curva; pertanto l'equazione dell'asintoto orizzontale di una curva y = f(x) è

Esempi
L'equazione dell'asintoto orizzontale della curva è

Poichè
l'asse x è asintoto orizzontale per la curva. Si osservi che la curva ha due asintoti verticali di equazioni
x = 1 e x = 2.

Poichè
la curva non ha asintoto orizzontale.
Asintoto obliquo
Nel caso in cui risulti
se la curva di equazione y = f(x) ha un asintoto, questo, per quanto detto in 2) ed in 3), non può essere nè verticale nè orizzontale, risulterà allora obliquo rispetto agli assi cartesiani e la sua equazione sarà pertanto della forma:
y = mx + n.

Come si vede nella Fig. 33, affinchè la retta t sia asintoto della curva γ, dev'essere:
ossia
essendo T2T1 l'ordinata y di un punto della t e quindi y = mx + n, e T2T1 l'ordinata y di un punto della γ e quindi x = f(x).
La 2) si può allora scrivere come segue:
e, dividendo tutto per x,
ma poichè
affinchè la 4) sia verificata si deve avere
e quindi
Sostituendo la 5) nella 3), si ha:
In conclusione, l'eventuale asintoto obliquo della funzione è una retta di equazione
per la quale è

Si potrebbe dimostrare, ma si tralascia, che se esistono finiti i limiti 7) e 8) la curva è dotata di asintoto obliquo, la cui equazione è
con m ed n aventi i valori dati proprio dalla 7) e dalla 8).
E' ovvio che se anche uno solo dei due limiti 7) e 8) esiste, ma non è finito oppure non esiste addirittura, la curva non possiede asintoti obliqui.
Nota bene
L'esistenza dell'asintoto obliquo di una curva, rappresentatrice di una funzione razionale fratta, può essere ammessa subito, se si verifica la seguente condizione:
-il grado del numeratore è di un'unità maggiore di quello del denominatore.
Ciò significa che esistono finiti i limiti 7) e 8).
Esempi
Essendo
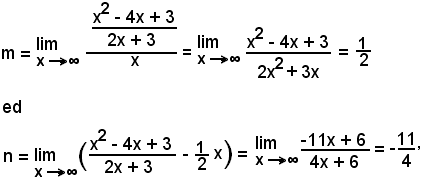
l'asintoto obliquo della curva è la retta di equazione
Essendo
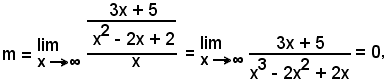
la curva non ha asintoto obliquo.
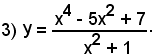
Essendo
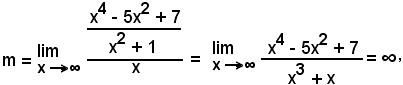
la curva non ha asintoto obliquo.