MIKY & GENNY
FUNZIONI ---> INDICE
1)-Concetto generale di funzione
Il concetto di funzione è già noto dalla matematica elementare; ora lo si vuole esporre in generale per intendere bene la definizione data da Dirichlet.
Quando i valori di una variabile y dipendono comunque da quelli di una variabile x, in modo che ad ogni valore di x, x compreso, ad esempio in un intervallo, corrispondono uno o più valori di y, si dice che y dipende o è in funzione di x in quell'intervallo.
Le espressioni
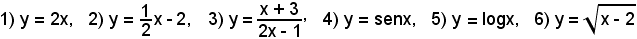
sono esempi di funzione, in quanto i valori della variabile y si ottengono in corrispondenza di quelli che si assegnano ad x e, pertanto, dipendono da quelli. Ciascuno degli esempi fatti esprime un legame fra y ed x, rappresentato dall'espressione analitica. Ma, per il concetto di funzione, non è necessario che vi sia una tale espressione, ossia non sempre esiste un'espressione analitica che rappresenti il legame esistente fra le due variabili y ed x, come accade per le funzioni derivanti dallo studio di fatti sperimentali.
7) La pressione atmosferica y, in un dato luogo, è funzione del tempo x;
8) la temperatura y, misurata da un termometro, è ancora funzione del tempo x;
9) il volume y di un gas a temperatura costante è funzione della pressione x (legge di Boyle e Mariotte);
10) l'area y di un rettangolo, avente una data base, è funzione dell'altezza x;
11) l'area y di un quadrato è funzione del lato x.
La legge o legame che vincola i valori di y a quelli di x può essere di natura qualsiasi: fisica, geometrica, analitica, demografica, ecc.
Nel concetto di funzione non vi è altro, insomma, che il concetto di corrispondenza tra y ed x, o il concetto di dipendenza dei valori di y rispetto a quelli assegnati ad x.
Non è però detto che alla variabile x si possano sempre dare valori del tutto arbitrari.
Infatti, negli esempi 7), 8), 9), 10), 11), x non può mai avere valori negativi; nell'esempio 3), x non può assumere valore 1/2, in quanto annullando il denominatore della funzione, fa perdere di significato alla stessa; nell'esempio 6), se si vuol rimanere nel campo dei numeri reali, occorre che sia x ≥ 2.
Ancora, per quanto si sa dalla trigonometria, l'espressione y = tgx fa corrispondere alla y dei valori, purchè quelli di x siano diversi dai multipli dispari di π/2.
Insomma, occorre pensare che il legame che permette di determinare il valore, o i valori, di y in corrispondenza di quello assegnato ad x, si ha, talvolta, solo quando alla stessa x si attribuiscono non tutti, ma solo dei convenienti valori o, meglio ancora, dei valori appartenenti ad un certo insieme che può essere, o no, tutto l'intervallo.
L'insieme dei valori che si potranno attribuire ad x, per avere in corrispondenza quelli di y, si chiama campo di esistenza o di definizione della funzione y.
Si è ora in grado di intendere perfettamente la seguente definizione dovuta a Dirichlet:
-si dice che una variabile y è in funzione della variabile indipendente x, definita in un certo insieme A di valori, quando ad ogni x appartenente ad A, corrispondono, con una legge prefissata, uno o più valori di y.
Si scrive:
y = f(x), oppure y = f(x, y) = 0,
in cui "f", o un'altra lettera qualsiasi, è il simbolo dell'operazione o relazione che associa, ad ogni dato valore di x appartenente all'insieme A, il valore, o i valori, corrispondenti di y.
Se ad ogni valore di x appartenente ad A corrisponde un solo valore di y, si dice che y è una funzione univoca o uniforme o monodroma di x; se ad un valore di x appartenente all'insieme A corrispondono più valori di y, si dice che y è una funzione polidroma; infine, una funzione è detta infinitivoca, se ad un x appartenente all'insieme A corrispondono infiniti valori di y.
Tipi di funzioni
Tra i tipi di funzioni definite analiticamente, ossia mediante un'espressione analitica, si distinguono:
a)-le funzioni razionali, intere o fratte;
b)-le funzioni irrazionali;
c)-le funzioni algrebriche;
d)-le funzioni trascendenti.
a)-Una funzione si dice razionale intera se tale è l'espressione analitica di f(x) che la definisce, ad esempio:
y = f(x) = a0xm + a1xm-1 + a2xm-2 + ... + am-1x + am.
Le funzioni di questo tipo sono definite per
 ≤ x ≤
≤ x ≤ 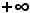 .
.
a')-Una funzione si dice razionale fratta quando f(x) è, o può ridursi, al quoziente di funzioni razionali intere, polinomi, ad esempio:
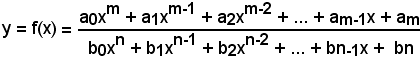
è una funzione definita per tutti i valori reali di x ad eccezione di quelli che annullano il denominatore.
b)-Una funzione si dice irrazionale quando la variabile indipendente compare sotto un segno di estrazione di radice oltre che, eventualmente, in operazioni razionali.
c)-Una funzione si dice algebrica se la relazione tra y ed x è rappresentata o rappresentabile da un'equazione razionale intera nelle due variabili y ed x, pertanto riducibile sempre ad un polinomio intero in x ed y, uguagliato a zero, cioè:
P(x, y) = 0.
Ogni funzione algebrica data da un'equazione intera di grado superiore al 1° è polidroma e, come si vedrà, la sua rappresentazione grafica è costituita da punti reali in numero minore o uguale al grado della stessa equazione.
Tutte le funzioni razionali sono algebriche e ad un solo ramo; esse. infatti, sono della forma:
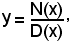
con N(x) e D(x) polinomi.
Dall'espressione precedente si ha l'equazione in x ed y seguente:
D(x)·y - N(x) = 0.
Le funzioni irrazionali sono anche algebriche, in quanto si dimostra che la relazione fra x ed y può essere ricondotta ad un'equazione intera che però, in generale, viene ad essere l'insieme della funzione data e di tutte quelle che si introducono con le elevazioni a potenza.
Esempio
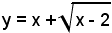
diventa successivamente:
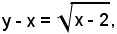
cioè
(y - x)2 = x - 2,
o anche
x2 + y2 - 2xy - x + 2 = 0.
d)-Tutte le funzioni non algebriche si dicono trascendenti; esse sono del tipo seguente:
y = senx, y = cosx, y = tgx, y = logx, y = ax, y = arcsenx, ecc.
Funzioni esplicite ed implicite
Si è già detto di indicare la relazione tra la variabile dipendente o funzione y e la variabile indipendente x con le notazioni dovute ad Eulero:
(1) y = f(x), (2) f(x, y) = 0.
Nel 1° caso si dice di avere la funzione in forma esplicita, intentendo con ciò che si conoscono nell'ordine tutte le operazioni che si devono effettuare su x per avere i valori di y. Quando è data la funzione in forma esplicita, il valore y0 della variabile dipendente che corrisponde ad un certo valore x0 attribuito a quella indipendente, è indicato con:
y0 = f(x0).
Nel 2° caso si dice di avere la funzione in forma implicita, intentendo con ciò che la relazione fra y ed x è espressa da un'equazione in dette variabili.
Esempi di funzioni implicite visti in geometria analitica:
3x + 2y + 4 = 0, equazione della retta;
x2 + y2 = 9, equazione della circonferenza;
x2 + y2 - 6x - 8y + 9 = 0, equazione della circonferenza;
4x2 + 9y2 = 36, equazione dell'ellisse;
16x2 - 9y2 = 144, equazione dell'iperbole;
xy = k, equazione dell'iperbole.
Per passare dalla forma implicita a quella esplicita, occorre, quando è possibile, risolvere l'equazione rispetto ad y.
Così, ad esempio, dalla funzione implicita
x2 + y2 = 9
si hanno le funzioni implicite
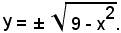
Rappresentazione numerica delle funzioni
Si abbia una funzione y = f(x) con x appartenente ad un insieme A.
Se di essa non si ha espressione mediante formule o, pur avendola, detta espressione non è comoda, si potrà dare in ogni caso una rappresentazione sensibile della relazione di dipendenza dei valori della y rispetto a quelli attribuiti alla x nell'insieme A, ricorrendo a tavole numeriche, cioè a tabelle che danno, per un certo numero più o meno grande di valori della variabile x, i valori corrispondenti della y.
Ad esempio, tali sono le tavole logaritmiche numeriche e trigonometriche; nel caso di due variabili intere che assumano i valori interi da 1 a 10, la tavola pitagorica dà il prodotto dei due numeri.
In generale, tutte le tabelle riportano le osservazioni dedotte da esperienze o statistiche.
Una tavola numerica è detta a semplice entrata quando è riferita ad una funzione di sola variabile indipendente; a doppia entrata quando è riferita a funzioni di due variabili indipendenti e così via.
Rappresentazione geometrica o grafica delle funzioni
Sia y = f(x) una funzione reale della variabile x definita in un intervallo finito o infinito, aperto o chiuso, ]a, b[, [a, b], dell'asse x, cioè l'insieme A dei numeri reali compresi in detto intervallo, se finito, o eventualmente su tutto l'asse reale, se l'intervallo è infinito, cioè ,
,  .
.
Per vedere l'andamento e quindi conoscere le caratteristiche delle funzione, si usa il seguente procedimento:
-si considera un certo numero di valori
x1, x2, x3, ... xn,
che possono essere attribuiti alla variabile x e, per ognuno di essi, si ricava il corrispondente della variabile, cioè
y1 = f(x1), y2 = f(x2), y3 = f(x3), ... yn = f(xn).
Quindi si considerano le coppie di numeri
(x1, y1 ), (x2, y2), (x3, y3), ... (xn, yn),
le quali quali, come è noto, si possono porre in corrispondenza biunivoca con i punti
P1, P2, P3, ... Pn
di un piano, mediante un riferimento di assi cartesiani ortogonali.
La linea congiungente i punti P1, P2, P3, ... Pn si chiama immagine geometrica o diagramma o rappresentazione grafica della funzione y = f(x).
Nel prosieguo, l'insieme A sarà sempre un intervallo finito o infinito dell'asse x ed i punti P1, P2, P3, ... Pn costituiranno sempre una linea piana, cioè giacente nel piano xOy considerato.
La funzione y = f(x), sarà detta equazione della linea.
Poichè in pratica non è possibile segnare nel piano tutti i punti P della linea, se ne segnano solo alcuni. Tanto più grande è il numero dei punti segnati e quanto più vicini sono gli stessi, tanto più la linea che congiunge tali punti rispecchierà l'andamento effettivo della funzione; ossia, tanto maggiore sarà l'approssimazione della linea tracciata sul piano all'altra che idealmente rappresenta la funzione data.
Esempi
Tenendo presenti le nozioni di geometria analitica e di trigonometria, si ricorda che:
1°) l'equazione y = mx + n rappresenta rette;
2°) l'equazione
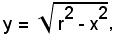
con r2 - x2 ≥ 0, cioè -r ≤ x ≤ r, rappresenta la semicirconferenza di centro O e raggio r situata nel I e II quadrante, mentre
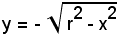
rappresenta l'altra semicirconferenza di centro O e raggio r situata nel III e IV quadrante.
3°) l'equazione
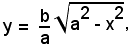
con a2 - x2 ≥ 0, cioè -a ≤ x ≤ a, rappresenta la semiellisse di centro O e semiassi a e b, situata nel I e II quadrante, mentre
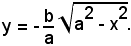
rappresenta l'altra semiellisse.
4°) l'equazione y = senx rappresenta la sinusoide.
Nota bene
a)-A seconda che una funzione sia monodroma o polidroma, si ha che una retta del piano, parallela all'asse y, incontra la linea rappresentatrice della funzione, rispettivamente in uno o più punti.
b)-Il problema inverso, cioè di determinare la funzione y = f(x), una volta assegnata una certa linea del piano, non è semplice nè sempre possibile.
Funzioni limitate e illimitate
Sia y = f(x) una funzione definita in un insieme A, cioè per ogni x appartenente ad A e sia B l'insieme di tutti i valori assunti da y in corrispondenza di quelli assegnati ad x in A, segue che:
1)-se B è limitato superiormente, anche la funzione è limitata superiormente,
2)-se B è limitato inferiormente, anche la funzione è limitata inferiormente,
3)-se B è limitato superiormente ed inferiormente, la funzione è limitata.
Sia k un certo numero reale positivo, le seguenti relazioni indicano che:
a) f(x) ≥ k, se la funzione è limitata superiormente,
b) -k ≤ f(x), se la funzione è limitata inferiormente,
c) -k ≤ f(x) ≤ k, oppure |f(x)| ≤ k, se la funzione è limitata.
Una funzione non limitata si dice illimitata.
Il concetto di funzione è già noto dalla matematica elementare; ora lo si vuole esporre in generale per intendere bene la definizione data da Dirichlet.
Quando i valori di una variabile y dipendono comunque da quelli di una variabile x, in modo che ad ogni valore di x, x compreso, ad esempio in un intervallo, corrispondono uno o più valori di y, si dice che y dipende o è in funzione di x in quell'intervallo.
Le espressioni
sono esempi di funzione, in quanto i valori della variabile y si ottengono in corrispondenza di quelli che si assegnano ad x e, pertanto, dipendono da quelli. Ciascuno degli esempi fatti esprime un legame fra y ed x, rappresentato dall'espressione analitica. Ma, per il concetto di funzione, non è necessario che vi sia una tale espressione, ossia non sempre esiste un'espressione analitica che rappresenti il legame esistente fra le due variabili y ed x, come accade per le funzioni derivanti dallo studio di fatti sperimentali.
7) La pressione atmosferica y, in un dato luogo, è funzione del tempo x;
8) la temperatura y, misurata da un termometro, è ancora funzione del tempo x;
9) il volume y di un gas a temperatura costante è funzione della pressione x (legge di Boyle e Mariotte);
10) l'area y di un rettangolo, avente una data base, è funzione dell'altezza x;
11) l'area y di un quadrato è funzione del lato x.
La legge o legame che vincola i valori di y a quelli di x può essere di natura qualsiasi: fisica, geometrica, analitica, demografica, ecc.
Nel concetto di funzione non vi è altro, insomma, che il concetto di corrispondenza tra y ed x, o il concetto di dipendenza dei valori di y rispetto a quelli assegnati ad x.
Non è però detto che alla variabile x si possano sempre dare valori del tutto arbitrari.
Infatti, negli esempi 7), 8), 9), 10), 11), x non può mai avere valori negativi; nell'esempio 3), x non può assumere valore 1/2, in quanto annullando il denominatore della funzione, fa perdere di significato alla stessa; nell'esempio 6), se si vuol rimanere nel campo dei numeri reali, occorre che sia x ≥ 2.
Ancora, per quanto si sa dalla trigonometria, l'espressione y = tgx fa corrispondere alla y dei valori, purchè quelli di x siano diversi dai multipli dispari di π/2.
Insomma, occorre pensare che il legame che permette di determinare il valore, o i valori, di y in corrispondenza di quello assegnato ad x, si ha, talvolta, solo quando alla stessa x si attribuiscono non tutti, ma solo dei convenienti valori o, meglio ancora, dei valori appartenenti ad un certo insieme che può essere, o no, tutto l'intervallo.
L'insieme dei valori che si potranno attribuire ad x, per avere in corrispondenza quelli di y, si chiama campo di esistenza o di definizione della funzione y.
Si è ora in grado di intendere perfettamente la seguente definizione dovuta a Dirichlet:
-si dice che una variabile y è in funzione della variabile indipendente x, definita in un certo insieme A di valori, quando ad ogni x appartenente ad A, corrispondono, con una legge prefissata, uno o più valori di y.
Si scrive:
y = f(x), oppure y = f(x, y) = 0,
in cui "f", o un'altra lettera qualsiasi, è il simbolo dell'operazione o relazione che associa, ad ogni dato valore di x appartenente all'insieme A, il valore, o i valori, corrispondenti di y.
Se ad ogni valore di x appartenente ad A corrisponde un solo valore di y, si dice che y è una funzione univoca o uniforme o monodroma di x; se ad un valore di x appartenente all'insieme A corrispondono più valori di y, si dice che y è una funzione polidroma; infine, una funzione è detta infinitivoca, se ad un x appartenente all'insieme A corrispondono infiniti valori di y.
Tipi di funzioni
Tra i tipi di funzioni definite analiticamente, ossia mediante un'espressione analitica, si distinguono:
a)-le funzioni razionali, intere o fratte;
b)-le funzioni irrazionali;
c)-le funzioni algrebriche;
d)-le funzioni trascendenti.
a)-Una funzione si dice razionale intera se tale è l'espressione analitica di f(x) che la definisce, ad esempio:
y = f(x) = a0xm + a1xm-1 + a2xm-2 + ... + am-1x + am.
Le funzioni di questo tipo sono definite per
a')-Una funzione si dice razionale fratta quando f(x) è, o può ridursi, al quoziente di funzioni razionali intere, polinomi, ad esempio:
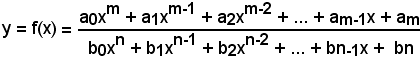
è una funzione definita per tutti i valori reali di x ad eccezione di quelli che annullano il denominatore.
b)-Una funzione si dice irrazionale quando la variabile indipendente compare sotto un segno di estrazione di radice oltre che, eventualmente, in operazioni razionali.
c)-Una funzione si dice algebrica se la relazione tra y ed x è rappresentata o rappresentabile da un'equazione razionale intera nelle due variabili y ed x, pertanto riducibile sempre ad un polinomio intero in x ed y, uguagliato a zero, cioè:
Ogni funzione algebrica data da un'equazione intera di grado superiore al 1° è polidroma e, come si vedrà, la sua rappresentazione grafica è costituita da punti reali in numero minore o uguale al grado della stessa equazione.
Tutte le funzioni razionali sono algebriche e ad un solo ramo; esse. infatti, sono della forma:
con N(x) e D(x) polinomi.
Dall'espressione precedente si ha l'equazione in x ed y seguente:
Le funzioni irrazionali sono anche algebriche, in quanto si dimostra che la relazione fra x ed y può essere ricondotta ad un'equazione intera che però, in generale, viene ad essere l'insieme della funzione data e di tutte quelle che si introducono con le elevazioni a potenza.
Esempio
diventa successivamente:
cioè
o anche
d)-Tutte le funzioni non algebriche si dicono trascendenti; esse sono del tipo seguente:
Funzioni esplicite ed implicite
Si è già detto di indicare la relazione tra la variabile dipendente o funzione y e la variabile indipendente x con le notazioni dovute ad Eulero:
(1) y = f(x), (2) f(x, y) = 0.
Nel 1° caso si dice di avere la funzione in forma esplicita, intentendo con ciò che si conoscono nell'ordine tutte le operazioni che si devono effettuare su x per avere i valori di y. Quando è data la funzione in forma esplicita, il valore y0 della variabile dipendente che corrisponde ad un certo valore x0 attribuito a quella indipendente, è indicato con:
Nel 2° caso si dice di avere la funzione in forma implicita, intentendo con ciò che la relazione fra y ed x è espressa da un'equazione in dette variabili.
Esempi di funzioni implicite visti in geometria analitica:
3x + 2y + 4 = 0, equazione della retta;
x2 + y2 = 9, equazione della circonferenza;
x2 + y2 - 6x - 8y + 9 = 0, equazione della circonferenza;
4x2 + 9y2 = 36, equazione dell'ellisse;
16x2 - 9y2 = 144, equazione dell'iperbole;
xy = k, equazione dell'iperbole.
Per passare dalla forma implicita a quella esplicita, occorre, quando è possibile, risolvere l'equazione rispetto ad y.
Così, ad esempio, dalla funzione implicita
si hanno le funzioni implicite
Rappresentazione numerica delle funzioni
Si abbia una funzione y = f(x) con x appartenente ad un insieme A.
Se di essa non si ha espressione mediante formule o, pur avendola, detta espressione non è comoda, si potrà dare in ogni caso una rappresentazione sensibile della relazione di dipendenza dei valori della y rispetto a quelli attribuiti alla x nell'insieme A, ricorrendo a tavole numeriche, cioè a tabelle che danno, per un certo numero più o meno grande di valori della variabile x, i valori corrispondenti della y.
Ad esempio, tali sono le tavole logaritmiche numeriche e trigonometriche; nel caso di due variabili intere che assumano i valori interi da 1 a 10, la tavola pitagorica dà il prodotto dei due numeri.
In generale, tutte le tabelle riportano le osservazioni dedotte da esperienze o statistiche.
Una tavola numerica è detta a semplice entrata quando è riferita ad una funzione di sola variabile indipendente; a doppia entrata quando è riferita a funzioni di due variabili indipendenti e così via.
Rappresentazione geometrica o grafica delle funzioni
Sia y = f(x) una funzione reale della variabile x definita in un intervallo finito o infinito, aperto o chiuso, ]a, b[, [a, b], dell'asse x, cioè l'insieme A dei numeri reali compresi in detto intervallo, se finito, o eventualmente su tutto l'asse reale, se l'intervallo è infinito, cioè
Per vedere l'andamento e quindi conoscere le caratteristiche delle funzione, si usa il seguente procedimento:
-si considera un certo numero di valori
x1, x2, x3, ... xn,
che possono essere attribuiti alla variabile x e, per ognuno di essi, si ricava il corrispondente della variabile, cioè
Quindi si considerano le coppie di numeri
le quali quali, come è noto, si possono porre in corrispondenza biunivoca con i punti
P1, P2, P3, ... Pn
di un piano, mediante un riferimento di assi cartesiani ortogonali.
La linea congiungente i punti P1, P2, P3, ... Pn si chiama immagine geometrica o diagramma o rappresentazione grafica della funzione y = f(x).
Nel prosieguo, l'insieme A sarà sempre un intervallo finito o infinito dell'asse x ed i punti P1, P2, P3, ... Pn costituiranno sempre una linea piana, cioè giacente nel piano xOy considerato.
La funzione y = f(x), sarà detta equazione della linea.
Poichè in pratica non è possibile segnare nel piano tutti i punti P della linea, se ne segnano solo alcuni. Tanto più grande è il numero dei punti segnati e quanto più vicini sono gli stessi, tanto più la linea che congiunge tali punti rispecchierà l'andamento effettivo della funzione; ossia, tanto maggiore sarà l'approssimazione della linea tracciata sul piano all'altra che idealmente rappresenta la funzione data.
Esempi
Tenendo presenti le nozioni di geometria analitica e di trigonometria, si ricorda che:
1°) l'equazione y = mx + n rappresenta rette;
2°) l'equazione
con r2 - x2 ≥ 0, cioè -r ≤ x ≤ r, rappresenta la semicirconferenza di centro O e raggio r situata nel I e II quadrante, mentre
rappresenta l'altra semicirconferenza di centro O e raggio r situata nel III e IV quadrante.
3°) l'equazione
con a2 - x2 ≥ 0, cioè -a ≤ x ≤ a, rappresenta la semiellisse di centro O e semiassi a e b, situata nel I e II quadrante, mentre
rappresenta l'altra semiellisse.
4°) l'equazione y = senx rappresenta la sinusoide.
Nota bene
a)-A seconda che una funzione sia monodroma o polidroma, si ha che una retta del piano, parallela all'asse y, incontra la linea rappresentatrice della funzione, rispettivamente in uno o più punti.
b)-Il problema inverso, cioè di determinare la funzione y = f(x), una volta assegnata una certa linea del piano, non è semplice nè sempre possibile.
Funzioni limitate e illimitate
Sia y = f(x) una funzione definita in un insieme A, cioè per ogni x appartenente ad A e sia B l'insieme di tutti i valori assunti da y in corrispondenza di quelli assegnati ad x in A, segue che:
1)-se B è limitato superiormente, anche la funzione è limitata superiormente,
2)-se B è limitato inferiormente, anche la funzione è limitata inferiormente,
3)-se B è limitato superiormente ed inferiormente, la funzione è limitata.
Sia k un certo numero reale positivo, le seguenti relazioni indicano che:
a) f(x) ≥ k, se la funzione è limitata superiormente,
b) -k ≤ f(x), se la funzione è limitata inferiormente,
c) -k ≤ f(x) ≤ k, oppure |f(x)| ≤ k, se la funzione è limitata.
Una funzione non limitata si dice illimitata.