INTEGRALI DEFINITI ---> INDICE
1)-Premessa
Il problema che storicamente ha condotto al concetto di integrale definito è quello della determinazione dell'area di una data superficie piana limitata da contorni curvilinei (quadratura delle superfici) e del volume di un dato solido (cubatura dei solidi). Questo problema ha le sue origini nel metodo di esaustione, che fu introdotto in forma sistematica nella geometria da Eudosso da Cnido nel IV secolo a. C.
2)-Quadratura di una superficie piana
Si rammenta dalla geometria elementare che:
a)-dopo aver fissato un quadrato U come unità di misura, è stata definita l'area di un qualsiasi altro quadrato Q, rispetto ad U;
b)-dopo aver trattato la teoria dell'equivalenza, è stata definita e calcolata l'area di un poligono P come area del quadrato ad esso equivalente;
c)-è stata definita e calcolata l'area del cerchio come il maggior valore dell'area di ogni poligono convesso inscritto e minore dell'area di ogni poligono convesso ad esso circoscritto.
Si dimostra anche che tale numero esiste ed è unico come elemento separatore delle classi contigue, oppure come limite comune delle due successioni convergenti
(1) a3, a4, a5, ... an, ...
(2) A3, A4, A5, ... An, ...
formate, rispettivamente, dalle aree dei poligoni suddetti.
Tale definizione dell'area del cerchio suggerisce un criterio generale per la definizione dell'area di una regione piana qualsiasi, cioè a contorni curvilinei qualsiasi:
-l'area A di una regione piana qualsiasi S è il numero che, esistente finito ed unico, risulta maggiore o uguale all'area di un poligono contenuto in S, cioè costituito tutto da punti di S, e minore o uguale all'area di un poligono contenente S, cioè che contiene tutti i punti di S.
Definire e calcolare l'area di una superficie piana, costituisce il problema della quadratura di una superficie.
3)-Quadratura di un trapezoide
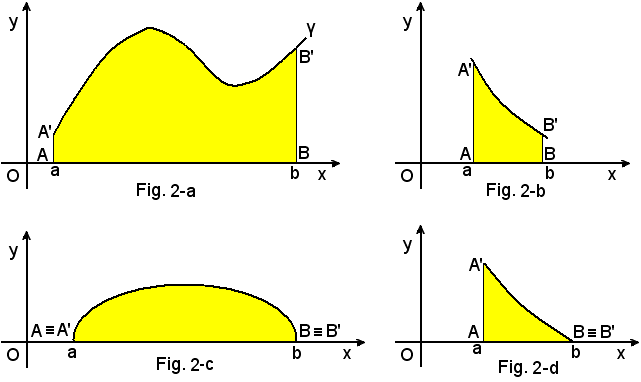
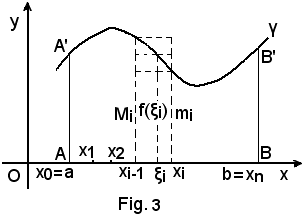
Si consideri una funzione y = f(x), definita in un intervallo (a, b), ed ivi sempre continua e non negativa, e sia γ la curva che la rappresenta nel sistema di assi cartesiani ortogonali nella seguente figura.
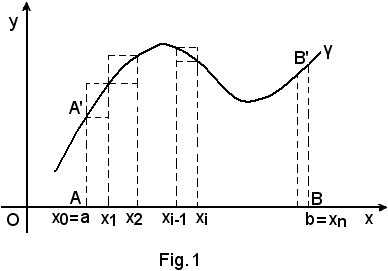
La regione piana, limitata inferiormente dall'intervallo chiuso (a, b) considerato sull'asse x, superiormente dall'arco A'B' della curva γ e lateralmente dai segmenti di lunghezza f(a) ed f(b) appartenenti alle rette x = a ed x = b, si chiama trapezoide, in quanto è una deformazione di un trapezio, che sarebbe tale se i punti A' e B' fossero uniti da un segmento invece che da una linea curva.
Ci si propone di dimostrare che il trapezoide indicato è quadrabile, e di indicare un metodo per calcolare la sua area.
Pertanto, si divida l'intervallo (a, b), rappresentato dal segmento AB, in un numero n qualsiasi di parti, non necessariamente uguali, mediante i punti di ascisse
(3) x0 = a, x1, x2, ... xi-1, xi, ... xn = b
e si indichino rispettivamente con
(4) δ1, δ2, ... δi-1, δi, ... δn
le misure dei nuovi intervalli ottenuti, cioè sia, in ordine
x1 - x0 = δ1, x2 - x1 = δ2, xi - xi-1 = δi, ... xn - xn-1 = δn.
Si indichino ancora, rispettivamente, con
(5) m1, m2, ... mi-1, mi, ... mn
(6) M1, M2, ... Mi-1, Mi, ... Mn
i minimi ed i massimi che la funzione y = f(x) assume nei singoli intervalli δ1; quindi si formino prima i rettangoli di base δ1 e altezza m1 e poi i rettangoli di base δ1 e altezza M1.
Tutti i primi rettangoli costituiscono una figura chiamata plurirettangolo o scaloide contenuto nel trapezoide, mentre i secondi costituiscono il plurirettangolo o scaloide contenente il trapezoide.
L'area del plurirettangolo o scaloide contenuto nel trapezoide è:
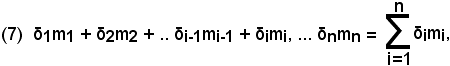
mentre quella del plurirettangolo o scaloide contenente il trapezoide è
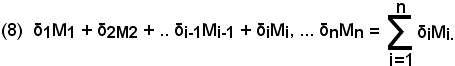
Indicando con T il trapezoide, evidentemente risulta
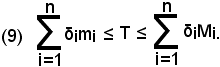
Aumentando indefinitamente i punti x1 di divisione dell'intervallo (a, b), ovvero facendo tendere n all'infinito, la lunghezza δ1 delle singole parti tende a zero, per cui la (9) diventa
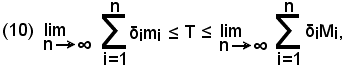
oppure
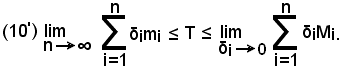
Poichè la funzione considerata è continua e non negativa in (a, b), si verifica, e si omette la dimostrazione del teorema, che
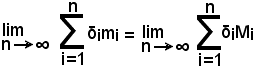
e quindi, per il teorema del confronto dei limiti, si ha
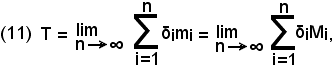
ossia:
-il trapezoide considerato è quadrabile e la sua area T è il limite comune a cui tendono gli scaloidi contenuti e contenenti il trapezoide allorchè n tende ad infinito oppure δi tende a zero.
In seguito si vedrà una regola mediante la quale si perverrà, apparentemente in modo diverso, al calcolo di T, ossia dei due limiti della (11) ed in base alla quale si scriverà:
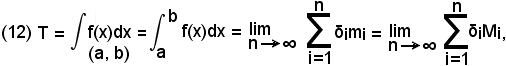
o solamente
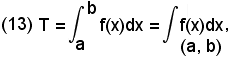
in cui il nuovo algoritmo scritto si legge integrale definito da a a b di f(x)dx.
La (7) e la (8) si chiamano anche somme integrali, rispettivamente, per difetto e per eccesso.
4)-Nota bene
1°)-Siccome non è stata posta altra condizione al modo di suddividere (a, b) in parti, oltre quella della crescenza indefinita del loro numero, ossia quella della tendenza a zero della parte di massima lunghezza, a maggior ragione tutte le altre tenderanno a zero. Ovviamente, si sarebbe potuto suddividere (a, b) in n parti uguali, per cui la lunghezza di ciascuna di esse sarebbe stata
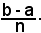
In tal caso, allorchè n tende ad infinito, tutte le lunghezze tendono simultaneamente a zero.
2°)-Per ipotesi y = f(x) è continua e non negativa, pertanto l'arco A'B' della curva γ in (a, b) può essere uno di quelli delle figure seguenti ed il trapezoide la parte in rosso.
5)-Integrale definito come limite di somme integrali generalizzate
Alla definizione di integrale definito si può pervenire anche come segue:
-diviso (a, b) in parti uguali, ma non necessariamente, siano
(1) ξ, ξ2, ... ξi, ... ξn
n punti a piacere presi rispettivamente in ciascuna delle n parti in cui è stata diviso (a, b), e siano
(2) f(ξ1), f(ξ2), ... f(ξi), ... f(ξn)
i valori assunti dalla funzione y = f(x) in ciascuno di essi.
Essendo chiaramente
(3) mi ≤ f(ξi) ≤ Mi,
è anche
(4) δimi ≤ δif(ξi) ≤ δiMi
e quindi
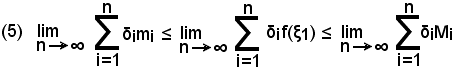
e poichè i due limiti estremi sono uguali, sempre per il teorema del confronto si ha
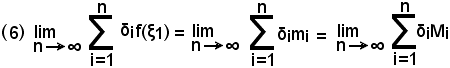
e in definitiva:
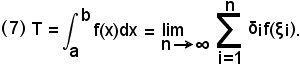
6)-Nota bene
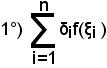
si chiama somma integrale generalizzata.
2°) La formazione della somma integrale generalizzata è senz'altro più immediata e più semplice delle altre due per difetto e per eccesso, in quanto in ciascun intervallo (xi-1, xi) non occorre più calcolare il minimo mi ed il massimo Mi, ma prendere un opportuno valore f(ξi) della funzione.
e pertanto, in
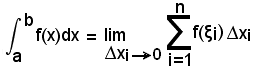
f(x)dx è un prodotto effettivo, come già detto in precedenza, e rappresenta f(ξi)∆xi.
6°) Essendo l'integrale definito l'area di un trapezoide, ossia il limite di una delle somme integrali, esso è un numero e non più una delle funzioni primitive di quella integranda, ma la totalità.
Proprietà dell'integrale definito
1^ In 3), per la quadratura di un trapezoide, si è supposto che la funzione fosse continua e non negativa in (a, b) e, pertanto, si è pervenuti all'area del trapezoide
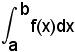
o anche
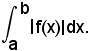
Se
invece la funzione y = f(x) è sempre continua in (a, b), ma
negativa o nulla, cioè non positiva, si dimostra che il
trapezoide è ancora quadrabile e la sua area è
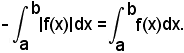
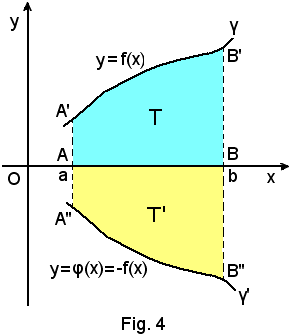
Infatti, nell'ipotesi fatta, basterà considerare in (a, b) la funzione φ(x) = -f(x), la cui curva γ' rappresentatrice sarà simmetrica di γ rispetto all'asse x. Anche il trapezoide relativo a γ' risulta simmetrico di T rispetto all'asse x e poichè si ha, evidentemente, per le somme integrali generalizzate
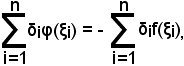
si avrà anche
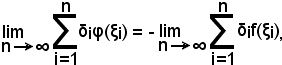
ossia
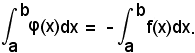
Da ciò segue che:
-l'integrale definito dà l'area del trapezoide in valore e segno, secondo il riferimento cartesiano.
2^ La definizione di integrale definito è stata data in (a, b) con a < b, tuttavia si pone:
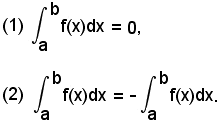
La (1) sarà spiegata allorchè si vedrà come si calcola un integrale definito, per quanto è intuitivo che, nel caso limite in cui l'intervallo è ridotto al solo punto a, il trapezoide non esiste.
Con la (2) si ha che:
-allorchè si scambiano fra loro gli estremi di integrazione, l'integrale definito conserva il valore assoluto ma cambia segno.
Scambiando infatti i due estremi di integrazione, si ha che:
sono rappresentati dallo stesso trapezoide T, alla cui area però sono da attribuire segni opposti in relazione ai due versi di orientamento dell'intervallo (a, b).
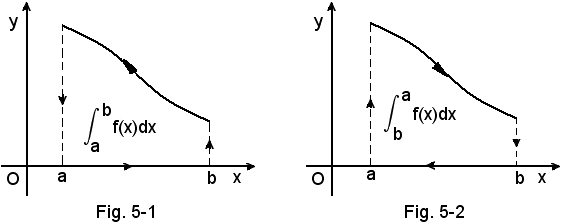
Analiticamente si ha:
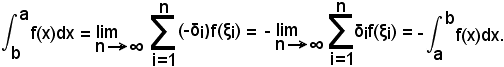
3^ Se c'è un punto qualsiasi di (a, b), si ha:
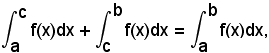
cioè: la somma di due integrali definiti della stessa funzione integranda, ed i cui termini di integrazione indicano intervalli consecutivi, è uguale ad un unico integrale definito, della stessa funzione, i cui estremi di integrazione sono il primo e l'ultimo di quelli precedenti.
Infatti, si ha:
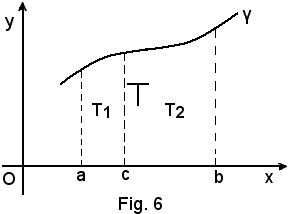
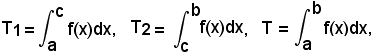
e poichè
T1 + T2 = T,
segue
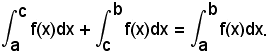
4^ Se f1(x), f2(x), ... fn(x) sono funzioni continue in uno stesso intervallo (a, b), si ha:
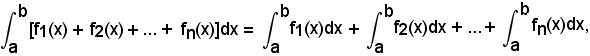
cioè: l'integrale definito della somma di funzioni è uguale alla somma deg'integrali definiti delle singole funzioni.
Infatti, si ha:
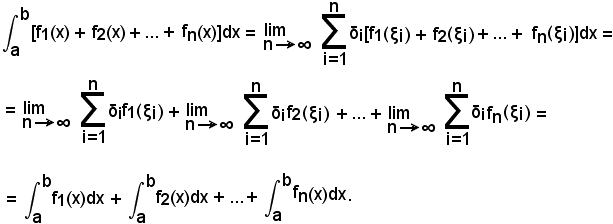
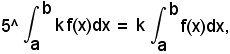
cioè: una costante moltiplicativa passa inalterata fuori dal segno d'integrale definito.
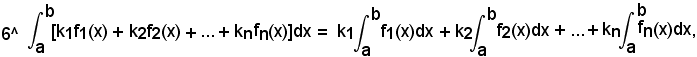
cioè: l'integrale definito di una combinazione lineare di funzioni è uguale alla combinazione lineare, secondo le stesse costanti, degl'integrali definiti delle singole funzioni.
Tale proprietà è conseguenza delle precedenti 4^ e 5^.
7^ Poichè l'integrale definito è rappresentato dal valore dell'area del trapezoide, allorchè sono dati la funzione integranda e l'intervallo, esso non dipende dalla variabile indipendente e quindi, per la sua indicazione, può essere usata una lettera qualsiasi, cioè si ha:
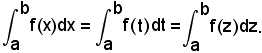
Calcolo dell'integrale definito
1)-L'integrale definito come funzione del suo estremo superiore
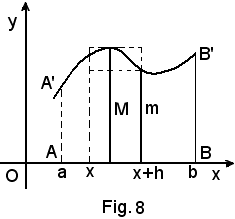
Sia y = f(x) una funzione continua in (a, b) e X un punto di ascissa x, interno a tale intervallo.
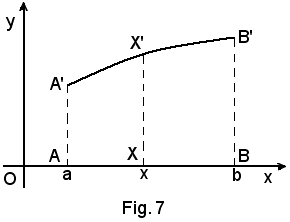
Al variare di x in (a, b) varia il trapezoide AXX'A', e quindi la sua area, ossia varia
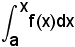
che, pertanto, diventa funzione di x, cioè del suo estremo superiore.
Si scriverà:
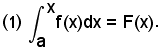
Non si deve confondere la variabile della funzione, che per quanto detto in precedenza si sarebbe potuta indicare con un'altra lettera, con quella che indica l'estremo superiore variabile. Questa nuova funzione F(x), così ottenuta, si chiama funzione integrale; essa è chiaramente definita in (a, b) ed è anche continua in (a, b). Basterà, perciò, dimostrare che:
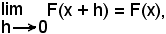
avendo posto
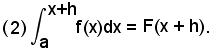
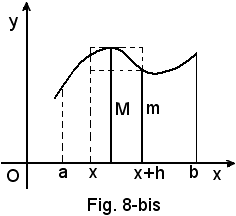
Tenendo presente il significato geometrico della funzione integrale F(x), e quindi di F(x + h), si ha:
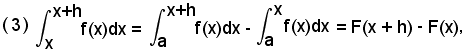
ed allora, indicando con m e M, rispettivamente, il valore minimo e quello massimo della funzione y = f(x) in (x, x+h), si ha
(4) hm < F(x + h) - F(x) < hM.
Quando h tende a zero, per effetto della continuità della funzione y = f(x), si ha:
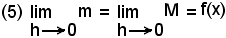
e
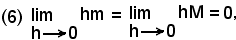
per il teorema del confronto, segue
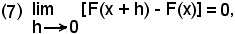
cioè
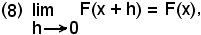
ciò che dimostra la continuità della funzione integrale.
2)-Teorema fondamentale del calcolo integrale o di Torricelli
Se la funzione integranda è continua, la funzione integrale è una sua primitiva.
Con le stesse notazioni del paragrafo precedente, considerate la (3) e la (4), si dividono tutti i membri per h > 0 e si ottiene:
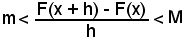
e tenendo presente la (5) e la continuità della F(x), si perviene a
f(x) < F'(x) < f(x),
cioè
F'(x) = f(x)
come volevasi dimostrare, quindi
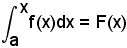
con
F'(x) = f(x),
ossia l'integrale definito con l'estremo superiore variabile si ritiene come un integrale indefinito; la sua funzione integrale diventa una primitiva di quella integranda, pertanto, tenendo presente il primo teorema sulle funzioni primitive, si può scrivere
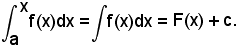3)-Calcolo dell'integrale definito
Il teorema di Torricelli permette di calcolare l'integrale definito di una funzione mediante quello indefinito della stessa e permette di evitare il calcolo del limite delle somme integrali viste in (3) e (5).
Infatti, si consideri
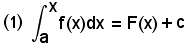
e, supposto prima
x = a,
si ha:
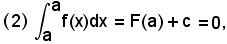
da cui
(3) c = -F(a).
Si supponga ora nella (1)
x = b,
si ha:
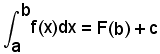
e, per la (3), risulta
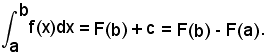
Si scriverà:
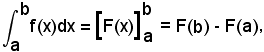
cioè: per calcolare l'integrale definito di una data funzione, si troverà prima una primitiva dell'integranda, ossia si risolverà come se si trattasse di un integrale indefinito, e quindi si limiterà tale primitiva nell'intervallo avente per estremi quelli di integrazione. Limitare una primitiva, o in generale una funzione in un intervallo, significa sostituire ordinatamente al posto della sua variabile l'estremo superiore e poi quello inferiore, e quindi fare la differenza dei valori così ottenuti.
Nota bene
Poichè il calcolo di un integrale definito ha bisogno, come si è detto, della risoluzione dell'integrale indefinito, per tale motivo sono stati studiati prima gl'integrali indefiniti nonostante storicamente e concettualmente fossero successivi.
Generalizzazione del significato geometrico dell'integrale definito
Da quanto visto nelle proprietà precedenti, poichè le aree dei trapezoidi, calcolate per mezzo degl'integrali definiti, sono anche negative, si impone una generalizzazione del concetto di area, ossia del significato geometrico dell'integrale definito.
A tale scopo, si considerino i vari casi che si possono avere e cioè:
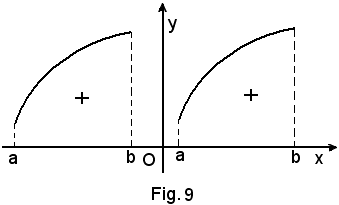
a) y = f(x) > 0, grafico della funzione nel I e nel II quadrante, ed a < b, si ha:
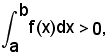
in quanto risultano positive le somme integrali, e quindi il loro limite.
b) y = f(x) > 0 ed a > b, si ha
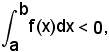
in quanto le somme integrali sono negative, essendo ciascun ∆xi < 0, mentre f(ξi) > 0.
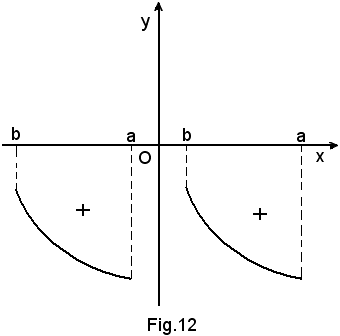
c) y = f(x) < 0, ed a > b, grafico della funzione nel III e nel IV quadrante, ed a < b, si ha:
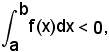
in quanto le somme integrali sono negative, essendo ciascun ∆xi > 0, mentre f(ξi) < 0.
d) y = f(x) < 0, ed a < b, si ha:
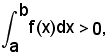
in quanto le somme integrali sono positive, essendo ciascun ∆xi < 0, mentre f(ξi) < 0.
Dai quattro casi esposti trova giustificazione la seguente regola sul segno dell'area del trapezoide.
L'area di un trapezoide è positiva o negativa a seconda che il trapezoide resti alla sinistra o alla destra di chi percorra l'intervallo d'integrazione dall'estremo superiore a quello inferiore.
e) Se allora, in un intervallo (a, b), la funzione y = f(x) assume tanto valori positivi quanto negativi, ossia attraverso l'asse x le ascisse dei punti d'incontro sono le radici dell'equazione f(x) = 0 e la funzione ha, per esempio, l'andamento della seguente figura,
l'integrale
può risultare tanto positivo quanto negativo, o addirittura nullo, in quanto dà la somma algebrica delle aree dei seguenti trapezoidi:
Il problema che storicamente ha condotto al concetto di integrale definito è quello della determinazione dell'area di una data superficie piana limitata da contorni curvilinei (quadratura delle superfici) e del volume di un dato solido (cubatura dei solidi). Questo problema ha le sue origini nel metodo di esaustione, che fu introdotto in forma sistematica nella geometria da Eudosso da Cnido nel IV secolo a. C.
2)-Quadratura di una superficie piana
Si rammenta dalla geometria elementare che:
a)-dopo aver fissato un quadrato U come unità di misura, è stata definita l'area di un qualsiasi altro quadrato Q, rispetto ad U;
b)-dopo aver trattato la teoria dell'equivalenza, è stata definita e calcolata l'area di un poligono P come area del quadrato ad esso equivalente;
c)-è stata definita e calcolata l'area del cerchio come il maggior valore dell'area di ogni poligono convesso inscritto e minore dell'area di ogni poligono convesso ad esso circoscritto.
Si dimostra anche che tale numero esiste ed è unico come elemento separatore delle classi contigue, oppure come limite comune delle due successioni convergenti
(1) a3, a4, a5, ... an, ...
(2) A3, A4, A5, ... An, ...
formate, rispettivamente, dalle aree dei poligoni suddetti.
Tale definizione dell'area del cerchio suggerisce un criterio generale per la definizione dell'area di una regione piana qualsiasi, cioè a contorni curvilinei qualsiasi:
-l'area A di una regione piana qualsiasi S è il numero che, esistente finito ed unico, risulta maggiore o uguale all'area di un poligono contenuto in S, cioè costituito tutto da punti di S, e minore o uguale all'area di un poligono contenente S, cioè che contiene tutti i punti di S.
Definire e calcolare l'area di una superficie piana, costituisce il problema della quadratura di una superficie.
3)-Quadratura di un trapezoide
Si consideri una funzione y = f(x), definita in un intervallo (a, b), ed ivi sempre continua e non negativa, e sia γ la curva che la rappresenta nel sistema di assi cartesiani ortogonali nella seguente figura.
La regione piana, limitata inferiormente dall'intervallo chiuso (a, b) considerato sull'asse x, superiormente dall'arco A'B' della curva γ e lateralmente dai segmenti di lunghezza f(a) ed f(b) appartenenti alle rette x = a ed x = b, si chiama trapezoide, in quanto è una deformazione di un trapezio, che sarebbe tale se i punti A' e B' fossero uniti da un segmento invece che da una linea curva.
Ci si propone di dimostrare che il trapezoide indicato è quadrabile, e di indicare un metodo per calcolare la sua area.
Pertanto, si divida l'intervallo (a, b), rappresentato dal segmento AB, in un numero n qualsiasi di parti, non necessariamente uguali, mediante i punti di ascisse
(3) x0 = a, x1, x2, ... xi-1, xi, ... xn = b
e si indichino rispettivamente con
(4) δ1, δ2, ... δi-1, δi, ... δn
le misure dei nuovi intervalli ottenuti, cioè sia, in ordine
x1 - x0 = δ1, x2 - x1 = δ2, xi - xi-1 = δi, ... xn - xn-1 = δn.
Si indichino ancora, rispettivamente, con
(5) m1, m2, ... mi-1, mi, ... mn
(6) M1, M2, ... Mi-1, Mi, ... Mn
i minimi ed i massimi che la funzione y = f(x) assume nei singoli intervalli δ1; quindi si formino prima i rettangoli di base δ1 e altezza m1 e poi i rettangoli di base δ1 e altezza M1.
Tutti i primi rettangoli costituiscono una figura chiamata plurirettangolo o scaloide contenuto nel trapezoide, mentre i secondi costituiscono il plurirettangolo o scaloide contenente il trapezoide.
L'area del plurirettangolo o scaloide contenuto nel trapezoide è:
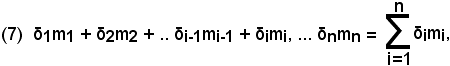
mentre quella del plurirettangolo o scaloide contenente il trapezoide è
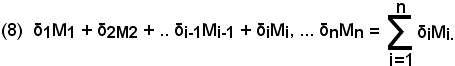
Indicando con T il trapezoide, evidentemente risulta
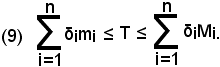
Aumentando indefinitamente i punti x1 di divisione dell'intervallo (a, b), ovvero facendo tendere n all'infinito, la lunghezza δ1 delle singole parti tende a zero, per cui la (9) diventa
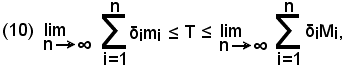
oppure
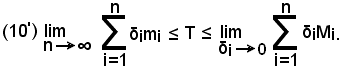
Poichè la funzione considerata è continua e non negativa in (a, b), si verifica, e si omette la dimostrazione del teorema, che
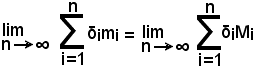
e quindi, per il teorema del confronto dei limiti, si ha
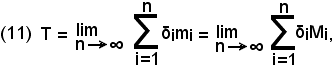
ossia:
-il trapezoide considerato è quadrabile e la sua area T è il limite comune a cui tendono gli scaloidi contenuti e contenenti il trapezoide allorchè n tende ad infinito oppure δi tende a zero.
In seguito si vedrà una regola mediante la quale si perverrà, apparentemente in modo diverso, al calcolo di T, ossia dei due limiti della (11) ed in base alla quale si scriverà:
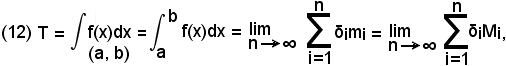
o solamente
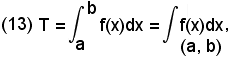
in cui il nuovo algoritmo scritto si legge integrale definito da a a b di f(x)dx.
La (7) e la (8) si chiamano anche somme integrali, rispettivamente, per difetto e per eccesso.
4)-Nota bene
1°)-Siccome non è stata posta altra condizione al modo di suddividere (a, b) in parti, oltre quella della crescenza indefinita del loro numero, ossia quella della tendenza a zero della parte di massima lunghezza, a maggior ragione tutte le altre tenderanno a zero. Ovviamente, si sarebbe potuto suddividere (a, b) in n parti uguali, per cui la lunghezza di ciascuna di esse sarebbe stata
In tal caso, allorchè n tende ad infinito, tutte le lunghezze tendono simultaneamente a zero.
2°)-Per ipotesi y = f(x) è continua e non negativa, pertanto l'arco A'B' della curva γ in (a, b) può essere uno di quelli delle figure seguenti ed il trapezoide la parte in rosso.
5)-Integrale definito come limite di somme integrali generalizzate
Alla definizione di integrale definito si può pervenire anche come segue:
-diviso (a, b) in parti uguali, ma non necessariamente, siano
(1) ξ, ξ2, ... ξi, ... ξn
n punti a piacere presi rispettivamente in ciascuna delle n parti in cui è stata diviso (a, b), e siano
i valori assunti dalla funzione y = f(x) in ciascuno di essi.
Essendo chiaramente
(3) mi ≤ f(ξi) ≤ Mi,
è anche
(4) δimi ≤ δif(ξi) ≤ δiMi
e quindi
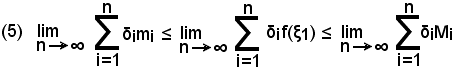
e poichè i due limiti estremi sono uguali, sempre per il teorema del confronto si ha
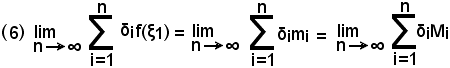
e in definitiva:
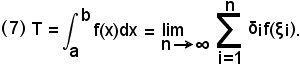
6)-Nota bene
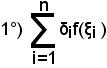
si chiama somma integrale generalizzata.
2°) La formazione della somma integrale generalizzata è senz'altro più immediata e più semplice delle altre due per difetto e per eccesso, in quanto in ciascun intervallo (xi-1, xi) non occorre più calcolare il minimo mi ed il massimo Mi, ma prendere un opportuno valore f(ξi) della funzione.
3°) Questo nuovo modo con il quale è stato definito l'integrale, giustifica il simbolo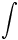 
adottato per rappresentarlo. Tale simbolo è da considerare una S deformata, essendo l'iniziale della parola somma.
4°) A tal punto permane la difficoltà di calcolare il limite (7).
Il calcolo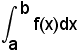
può essere talvolta facilitato allorchè si prendano come punti ξi gli estremi sinistri o destri degl'intervalli parziali (xi-1, xi).
5°) Se i δi vengono indicati con ∆xi perchè in effetti le lunghezze δi sono gl'incrementi dati ai punti xi-1 per avere i punti xi, la somma generalizzata diventa
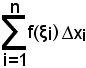
adottato per rappresentarlo. Tale simbolo è da considerare una S deformata, essendo l'iniziale della parola somma.4°) A tal punto permane la difficoltà di calcolare il limite (7).
Il calcolo
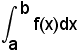può essere talvolta facilitato allorchè si prendano come punti ξi gli estremi sinistri o destri degl'intervalli parziali (xi-1, xi).5°) Se i δi vengono indicati con ∆xi perchè in effetti le lunghezze δi sono gl'incrementi dati ai punti xi-1 per avere i punti xi, la somma generalizzata diventa
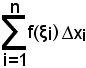
e pertanto, in
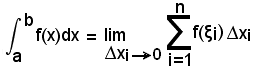
f(x)dx è un prodotto effettivo, come già detto in precedenza, e rappresenta f(ξi)∆xi.
6°) Essendo l'integrale definito l'area di un trapezoide, ossia il limite di una delle somme integrali, esso è un numero e non più una delle funzioni primitive di quella integranda, ma la totalità.
Proprietà dell'integrale definito
1^ In 3), per la quadratura di un trapezoide, si è supposto che la funzione fosse continua e non negativa in (a, b) e, pertanto, si è pervenuti all'area del trapezoide
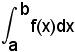
o anche
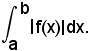
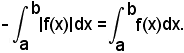
Infatti, nell'ipotesi fatta, basterà considerare in (a, b) la funzione φ(x) = -f(x), la cui curva γ' rappresentatrice sarà simmetrica di γ rispetto all'asse x. Anche il trapezoide relativo a γ' risulta simmetrico di T rispetto all'asse x e poichè si ha, evidentemente, per le somme integrali generalizzate
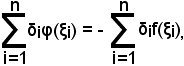
si avrà anche
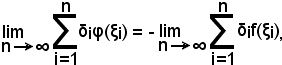
ossia
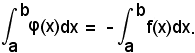
Da ciò segue che:
-l'integrale definito dà l'area del trapezoide in valore e segno, secondo il riferimento cartesiano.
2^ La definizione di integrale definito è stata data in (a, b) con a < b, tuttavia si pone:
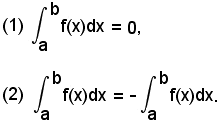
La (1) sarà spiegata allorchè si vedrà come si calcola un integrale definito, per quanto è intuitivo che, nel caso limite in cui l'intervallo è ridotto al solo punto a, il trapezoide non esiste.
Con la (2) si ha che:
-allorchè si scambiano fra loro gli estremi di integrazione, l'integrale definito conserva il valore assoluto ma cambia segno.
Scambiando infatti i due estremi di integrazione, si ha che:
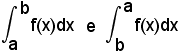
sono rappresentati dallo stesso trapezoide T, alla cui area però sono da attribuire segni opposti in relazione ai due versi di orientamento dell'intervallo (a, b).
Analiticamente si ha:
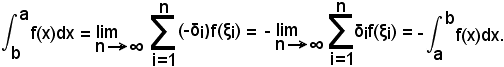
3^ Se c'è un punto qualsiasi di (a, b), si ha:
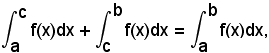
cioè: la somma di due integrali definiti della stessa funzione integranda, ed i cui termini di integrazione indicano intervalli consecutivi, è uguale ad un unico integrale definito, della stessa funzione, i cui estremi di integrazione sono il primo e l'ultimo di quelli precedenti.
Infatti, si ha:
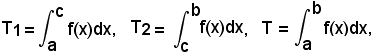
e poichè
segue
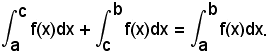
4^ Se f1(x), f2(x), ... fn(x) sono funzioni continue in uno stesso intervallo (a, b), si ha:
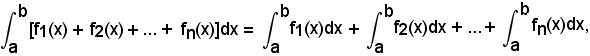
cioè: l'integrale definito della somma di funzioni è uguale alla somma deg'integrali definiti delle singole funzioni.
Infatti, si ha:
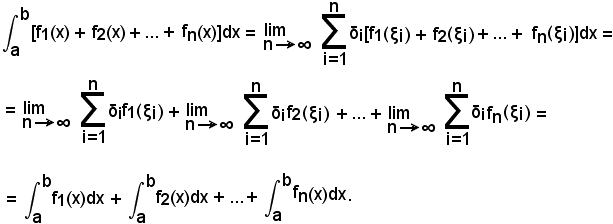
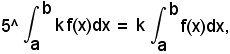
cioè: una costante moltiplicativa passa inalterata fuori dal segno d'integrale definito.
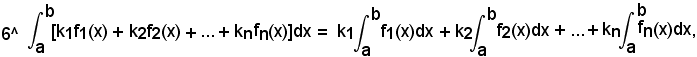
cioè: l'integrale definito di una combinazione lineare di funzioni è uguale alla combinazione lineare, secondo le stesse costanti, degl'integrali definiti delle singole funzioni.
Tale proprietà è conseguenza delle precedenti 4^ e 5^.
7^ Poichè l'integrale definito è rappresentato dal valore dell'area del trapezoide, allorchè sono dati la funzione integranda e l'intervallo, esso non dipende dalla variabile indipendente e quindi, per la sua indicazione, può essere usata una lettera qualsiasi, cioè si ha:
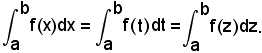
Calcolo dell'integrale definito
1)-L'integrale definito come funzione del suo estremo superiore
Sia y = f(x) una funzione continua in (a, b) e X un punto di ascissa x, interno a tale intervallo.
Al variare di x in (a, b) varia il trapezoide AXX'A', e quindi la sua area, ossia varia
che, pertanto, diventa funzione di x, cioè del suo estremo superiore.
Si scriverà:
Non si deve confondere la variabile della funzione, che per quanto detto in precedenza si sarebbe potuta indicare con un'altra lettera, con quella che indica l'estremo superiore variabile. Questa nuova funzione F(x), così ottenuta, si chiama funzione integrale; essa è chiaramente definita in (a, b) ed è anche continua in (a, b). Basterà, perciò, dimostrare che:
avendo posto
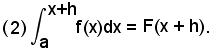
Tenendo presente il significato geometrico della funzione integrale F(x), e quindi di F(x + h), si ha:
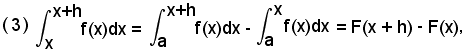
ed allora, indicando con m e M, rispettivamente, il valore minimo e quello massimo della funzione y = f(x) in (x, x+h), si ha
(4) hm < F(x + h) - F(x) < hM.
Quando h tende a zero, per effetto della continuità della funzione y = f(x), si ha:
e
per il teorema del confronto, segue
cioè
ciò che dimostra la continuità della funzione integrale.
2)-Teorema fondamentale del calcolo integrale o di Torricelli
Se la funzione integranda è continua, la funzione integrale è una sua primitiva.
Con le stesse notazioni del paragrafo precedente, considerate la (3) e la (4), si dividono tutti i membri per h > 0 e si ottiene:
e tenendo presente la (5) e la continuità della F(x), si perviene a
f(x) < F'(x) < f(x),
cioè
F'(x) = f(x)
come volevasi dimostrare, quindi
con
F'(x) = f(x),
ossia l'integrale definito con l'estremo superiore variabile si ritiene come un integrale indefinito; la sua funzione integrale diventa una primitiva di quella integranda, pertanto, tenendo presente il primo teorema sulle funzioni primitive, si può scrivere
Il teorema di Torricelli permette di calcolare l'integrale definito di una funzione mediante quello indefinito della stessa e permette di evitare il calcolo del limite delle somme integrali viste in (3) e (5).
Infatti, si consideri
e, supposto prima
x = a,
si ha:
da cui
(3) c = -F(a).
Si supponga ora nella (1)
x = b,
si ha:
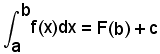
e, per la (3), risulta
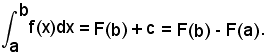
Si scriverà:
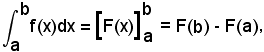
cioè: per calcolare l'integrale definito di una data funzione, si troverà prima una primitiva dell'integranda, ossia si risolverà come se si trattasse di un integrale indefinito, e quindi si limiterà tale primitiva nell'intervallo avente per estremi quelli di integrazione. Limitare una primitiva, o in generale una funzione in un intervallo, significa sostituire ordinatamente al posto della sua variabile l'estremo superiore e poi quello inferiore, e quindi fare la differenza dei valori così ottenuti.
Nota bene
Poichè il calcolo di un integrale definito ha bisogno, come si è detto, della risoluzione dell'integrale indefinito, per tale motivo sono stati studiati prima gl'integrali indefiniti nonostante storicamente e concettualmente fossero successivi.
Generalizzazione del significato geometrico dell'integrale definito
Da quanto visto nelle proprietà precedenti, poichè le aree dei trapezoidi, calcolate per mezzo degl'integrali definiti, sono anche negative, si impone una generalizzazione del concetto di area, ossia del significato geometrico dell'integrale definito.
A tale scopo, si considerino i vari casi che si possono avere e cioè:
a) y = f(x) > 0, grafico della funzione nel I e nel II quadrante, ed a < b, si ha:
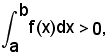
in quanto risultano positive le somme integrali, e quindi il loro limite.
b) y = f(x) > 0 ed a > b, si ha
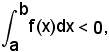
in quanto le somme integrali sono negative, essendo ciascun ∆xi < 0, mentre f(ξi) > 0.
c) y = f(x) < 0, ed a > b, grafico della funzione nel III e nel IV quadrante, ed a < b, si ha:
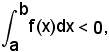
in quanto le somme integrali sono negative, essendo ciascun ∆xi > 0, mentre f(ξi) < 0.
d) y = f(x) < 0, ed a < b, si ha:
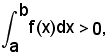
in quanto le somme integrali sono positive, essendo ciascun ∆xi < 0, mentre f(ξi) < 0.
Dai quattro casi esposti trova giustificazione la seguente regola sul segno dell'area del trapezoide.
L'area di un trapezoide è positiva o negativa a seconda che il trapezoide resti alla sinistra o alla destra di chi percorra l'intervallo d'integrazione dall'estremo superiore a quello inferiore.
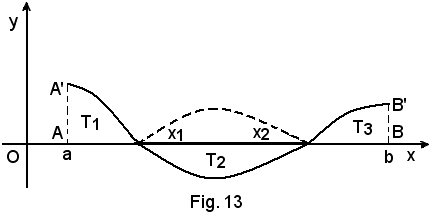
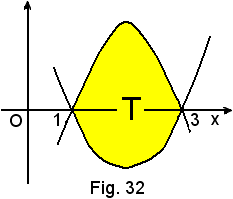
e) Se allora, in un intervallo (a, b), la funzione y = f(x) assume tanto valori positivi quanto negativi, ossia attraverso l'asse x le ascisse dei punti d'incontro sono le radici dell'equazione f(x) = 0 e la funzione ha, per esempio, l'andamento della seguente figura,
l'integrale
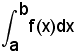può risultare tanto positivo quanto negativo, o addirittura nullo, in quanto dà la somma algebrica delle aree dei seguenti trapezoidi:T1 (A1 > 0), T2 (A2 < 0), T3 (A3 < 0).
Nel caso in cui si richieda l'area complessiva della regione piana limitata dalla curva di equazione y = f(x) in (a, b), detta area è limitata lateralmente sempre dalle rette di equazione x = a ed x = b, ossia si richieda l'area, indipendentemente dai segni delle sue singole parti componenti, allora non è possibile calcolare un unico integrale definito, ma trovati, come in Fig. 13, i sottointervalli (a, x1), (x1, x2), (x2, b), in cui la funzione non cambia segno, la sua area richiesta è:
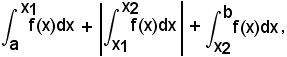
il che equivale a sostituire ai trapezoidi situati al di sotto dell'asse x i simmetrici rispetto allo stesso asse.
Esempi
1°)-Calcolare l'area della regione piana limitata superiormente dalla linea di equazione
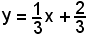
nell'intervallo (1, 4).
Si ha:
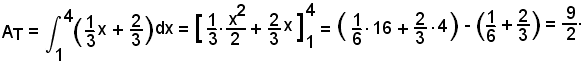
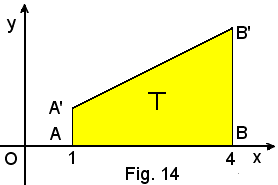
2°)-Calcolare l'area della regione piana limitata superiormente dalla linea di equazione
y = x2 - 4x + 5
nell'intervallo
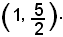
Si ha:
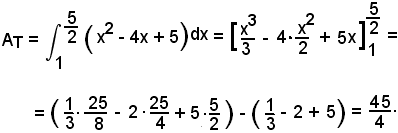
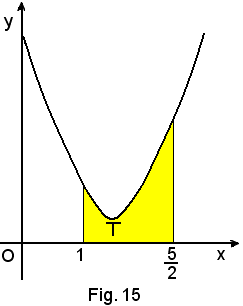
3°)-Calcolare l'area della regione piana limitata superiormente dalla linea di equazione
y = x3 + x
nell'intervallo (0,2).
Si ha:
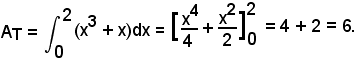
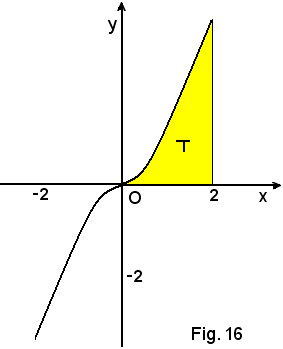
4°)-Calcolare l'area della regione piana limitata superiormente dalla linea di equazione
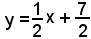
nell'intervallo (-5, -1).
Si hanno due casi:
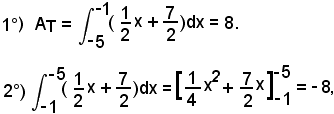
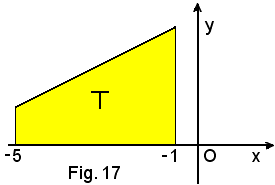
5°)-Calcolare l'area della regione piana limitata dalla linea di equazione
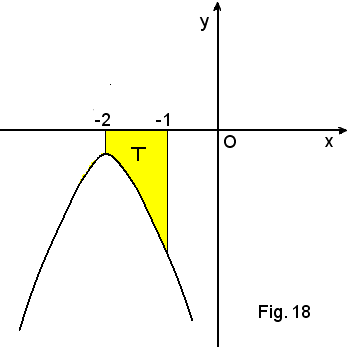
y = -x2 - 4x - 5
nell'intervallo (-2, -1).
Si hanno due casi:
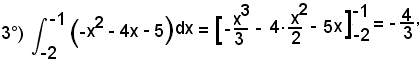
6°)-Calcolare l'area della regione piana (segmento parabolico) limitata dalla parabola di equazione
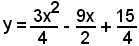
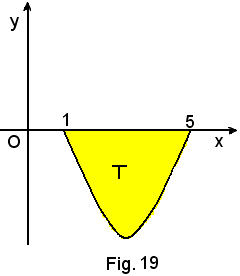
e dall'asse x.
Si osserva prima che la parabola interseca l'asse x nei punti di ascissa 1 e 5, pertanto si deve calcolare l'area del segmento parabolico nell'intervallo (1, 5).
Si hanno due casi:
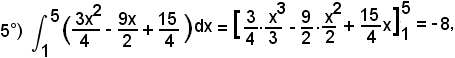
7°)-Calcolare l'area della regione piana limitata dalla linea di equazione
y = senx
negl'intervalli (0, π), (π, 2π), (0, 2π).
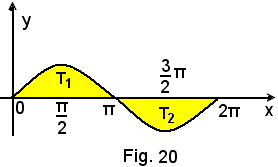
Nell'intervallo (0, π) si ha:
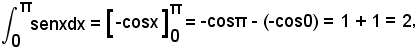
quindi
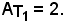
Nell'intervallo (π, 2π) si ha:
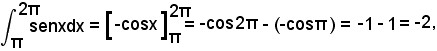
quindi
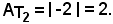
Nell'intervallo (0, 2π) si ha:
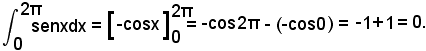
Infine l'area totale è data da:
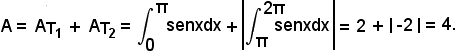
8°)-Calcolare l'area della regione piana limitata dalla linea di equazione
y = x3 - 3x2 + 2x
negl'intervalli (0, 1), (1, 2), (0, 2).
L'andamento della linea di equazione y = x3 - 3x2 + 2x è rappresentato dalla curva γ nella figura seguente.
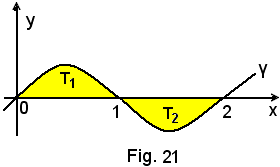Nell'intervallo (0, 1) si ha:
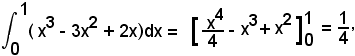
quindi
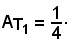
Nell'intervallo (1, 2) si ha:
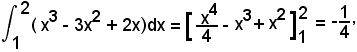
quindi
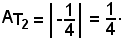
Nell'intervallo (0, 2) si ha:
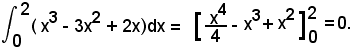
Infine l'area totale nell'intervallo (0, 2) è data da:
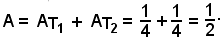
Quadrature notevoli
1)-Area del trapezoide limitato dalla parabola y = ax2 in (0, x0).
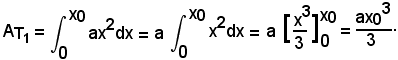
Osservando che è
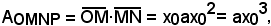
si ha:
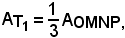
da cui segue
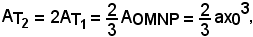
per il teorema di Archimede.
2)-Area del trapezoide limitato dall'iperbole particolare y = k/x in (x1, x2).
Supposto k > 0 e considerato il ramo d'iperbole equilatera del I quadrante, si ha:
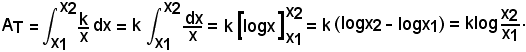
Nota bene
Se k = 1, x1 = 1, x2 = a, si ha
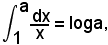
cioè: il logaritmo naturale o neperiano di un numero esprime l'area del trapezoide limitato dall'iperbole particolare y = 1/x oppure xy = 1 nell'intervallo in cui il primo estremo è 1 ed il secondo è il numero dato.
Da qui il motivo per cui i logaritmi naturali o neperiani sono chiamati anche iperbolici.
Valore medio di una funzione in un intervallo
Sia y = f(x) una funzione integrabile in un intervallo (a, b). Dividendo l'intervallo in n parti uguali, la lunghezza di ciascuna di esse è, come noto:
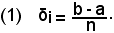
Se allora si considera la somma integrale generalizzata
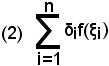
per la (1), diventa
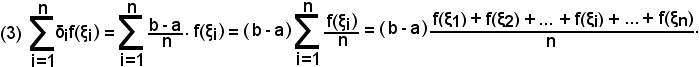
Sapendo che
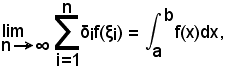
per la (3) si ha:
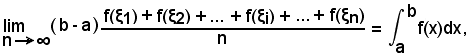
ossia
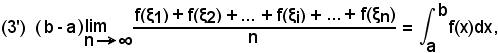
ed ancora
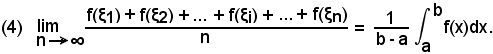
Il quoziente
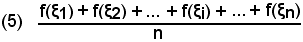
costituisce la media aritmetica degli n valori dati alla funzione in (a, b), cioè uno per ciascun sottointervallo δi di (a, b).
Posto allora
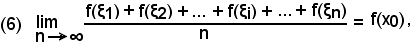
la (4) diventa
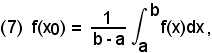
cioè: il valore medio di una funzione in un intervallo (a, b) si ottiene dividendo l'integrale definito della funzione in quell'intervallo per la lunghezza dello stesso intervallo.
Esempi
1°) Il valore medio della funzione y = x2 nell'intervallo (2, 4) è:
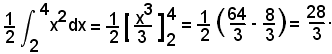
2°) Il valore medio della funzione y = 2x2 -3x + 1 nell'intervallo (1, 4) è:
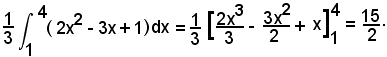
3°) Il valore medio della funzione y = senx nell'intervallo (0, π) è:
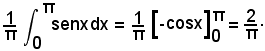
Dalla (7), liberando dal denominatore, si ha
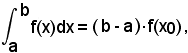
cioè: l'integrale definito di una funzione continua è uguale alla lunghezza dell'intervallo in cui è stato calcolato per il valore che la funzione integranda assume in un conveniente punto di questo intervallo.
Oppure, in base al significato geometrico di integrale definito:
-il valore medio di una funzione continua in un intervallo (a, b) è l'altezza del rettangolo che ha per base l'intervallo (a, b) ed è equivalente al trapezoide
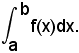
Calcolo dell'area di una superficie limitata da due linee o da una linea chiusa
1)-Le due linee sono situate al di sopra dell'asse x.
Si consideri la superficie S limitata dagli archi di linee, curve o rette di equazione
y1 = f1(x), y2 = f2(x).
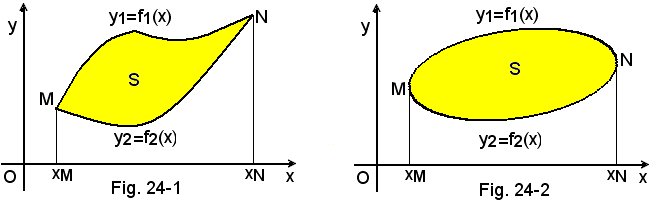
Da evidenti considerazioni geometriche l'area A di S, AS, è uguale alla differenza delle aree dei trapezoidi aventi per base l'intervallo (xN, xM), in cui M ed N sono i punti d'incontro delle due linee. Inoltre sono limitati superiormente dagli archi MN appartenenti, rispettivamente, alle linee di equazione y1 = f1(x) e y2 = f2(x), con f1(x) > f2(x).
Quindi si ha:
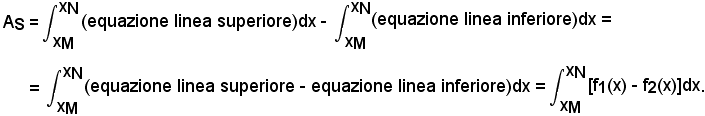
Nota bene
Si vedrà in seguito il caso in cui i due archi MN appartengono ad una stessa linea di equazione implicita f(x, y) = 0.
Esempi
1°)-Calcolare l'area della regione piana limitata dalle due parabole di equazioni:
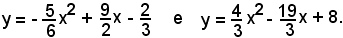
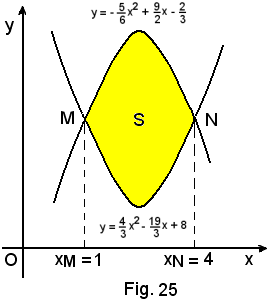
Dopo aver rappresentato graficamente le due parabole, ed aver trovato i loro punti d'intersezione (1, 3) e (4, 4), si calcola l'area della superficie S evidenziata in giallo nella figura suddetta.
Si ha:
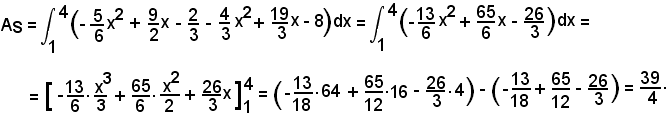
L'unità di misura delle superfici è il quadrato di lato uguale all'unità di misura convenuta per le lunghezze nel sistema cartesiano.
2°)-Calcolare l'area della sezione piana limitata dalle rette di equazioni:
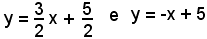
nell'intervallo (1, 3).
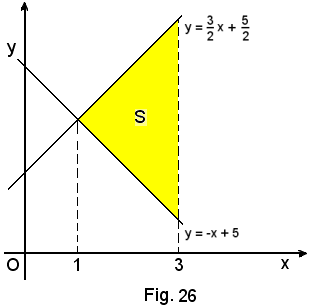
Si ha:
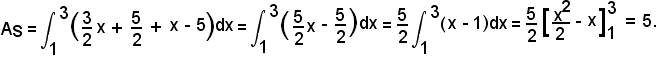
2)-Le due linee sono situate al di sotto dell'asse x.
L'area A della regione piana S limitata dai due archi MN appartenenti alle linee di equazioni
y1 = f1(x), y2 = f2(x),
con f1(x) < f2(x) < 0, è:
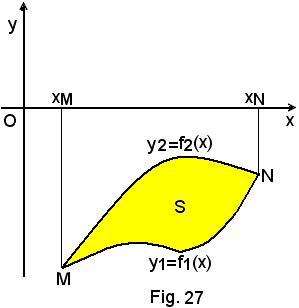
Esempi
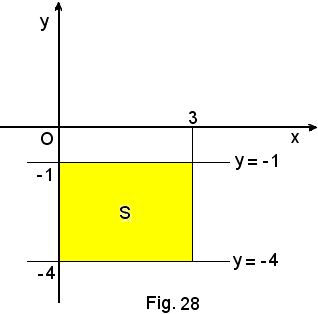
1°)-Calcolare l'area della striscia di piano limitata dalle rette di equazioni
y = -4 e y = -1,
nell'intervallo (0, 3).
Essendo
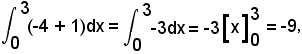
l'area richiesta è
AS = |-9| = 9.
2°)-Calcolare l'area della regione piana limitata, rispettivamente dalla parabola e dalla retta di equazioni:
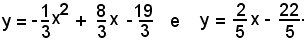
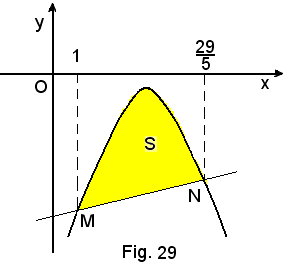
Dopo aver trovato le coordinate dei punti d'intersezione tra parabola e retta:
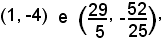
l'area A della superficie S è il valore assoluto di
3°)-Calcolare l'area della regione piana limitata tra le due parabole di equazioni:
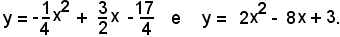
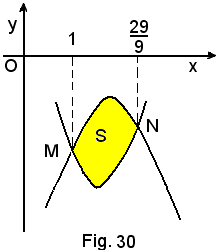
Dopo aver trovato i punti d'intersezione M e N tra le due parabole, le cui ascisse sono xM = 1 e xN = 29/9, l'area A di S è il valore assoluto di:
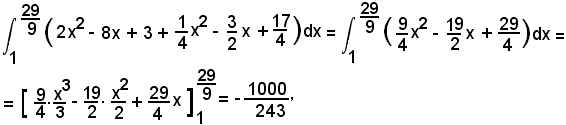
quindi
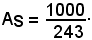
3)-Una delle due linee è situata una al di sopra e l'altra al di sotto dell'asse x.
Per l'area della regione piana, limitata dai due archi MN appartenenti rispettivamente alle linee di equazioni:
y1 = f1(x) > 0 e y2 = f2(x) > 0,
essendo
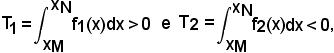
si ha
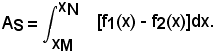
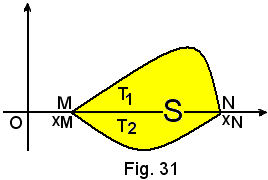
Dopo aver trovato le coordinate dei punti d'intersezione delle due parabole:
(1, 0) e (3, 0),
l'area richiesta è
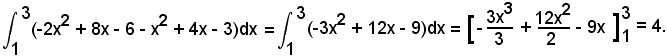
2°)-Calcolare l'area della regione piana limitata, rispettivamente, dalla retta e dalla cubica di equazioni:
y = -4x + 4 e y = -x3 + 2x2 + x - 2.
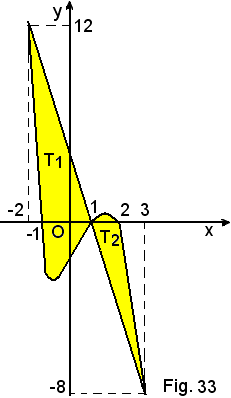
Dopo aver trovato i punti d'intersezione della retta con la cubica, le cui coordinate sono
(-2, 12), (1, 0) e (3, -8),
si ha:
per cui
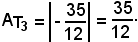
Allora l'area richiesta è:
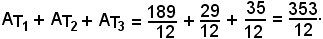
4)-Superficie limitata da una linea chiusa
a)-Area del cerchio di centro O e raggio r.
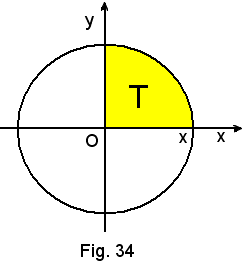
In tal caso l'equazione implicita della circonferenza è:
x2 + y2 = r2.
Esplicitando rispetto ad y, risulta:
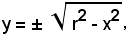
in cui il segno + vale per la semicirconferenza situata nel I e nel II quadrante, e quello - per la semicirconferenza situata nel III e nel IV quadrante.
Per calcolare l'area del cerchio, basta calcolare quella di un quadrante, ad esempio T, e moltiplicarla per 4.
Si ha:
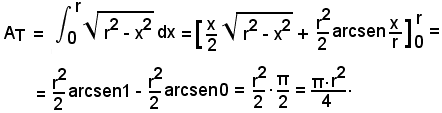
L'area del cerchio è:
A = 4·AT = πr2,
come già noto dalla geometria.
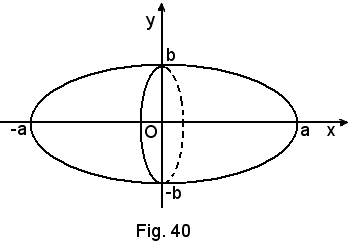
b)-Area dell'ellisse di centro O e semiassi a e b.
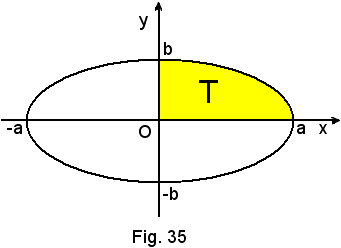
L'equazione implicita dell'ellisse è:
b2x2 + a2y2 = a2b2,
oppure
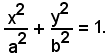
Esplicitando rispetto ad y, risulta:
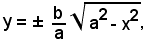
in cui il segno + vale per la semiellisse posta al di sopra dell'asse x, e quello - per quella posta al di sotto dello stesso asse. Per calcolare l'area dell'ellisse, basta calcolare quella di un quadrante, ad esempio T, e moltiplicarla per 4.
Si ha:
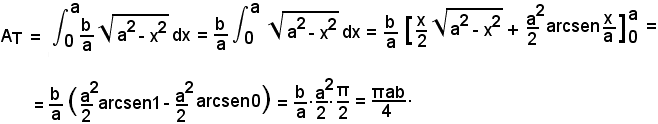
L'area dell'ellisse è:
A = 4·AT =πab.
Se a = b, si ha l'area del cerchio.
Nota bene
Se la circonferenza e l'ellisse non si trovano nelle suddette posizioni, conviene effettuare un opportuno movimento degli assi cartesiani per riportarsi ai casi considerati.
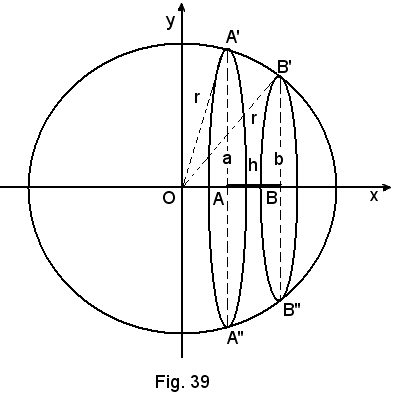
Teorema di Cavalieri
Se due superfici piane sono comprese fra due rette parallele, sulle quali hanno almeno un punto e sono uguali, o stanno in un rapporto k, e le corde sono in esse determinate da una qualsiasi retta parallela alle prime due, le due figure piane sono equivalenti, o stanno sullo stesso rapporto k.
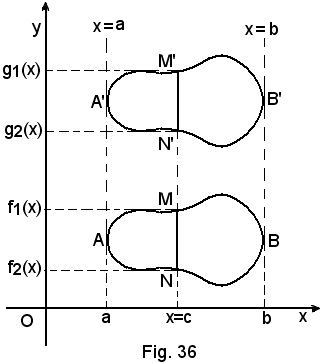
Siano f(x, y) = 0 e g(x, y) = 0 le equazioni implicite delle linee chiuse γ e γ' limitanti le superfici S1 e S2, e si supponga di aver esplicitato tali equazioni, rispetto alla y, in modo che l'arco superiore di γ abbia equazione y1 = f1(x) e quello inferiore y2 = f2(x), così che l'arco superiore di γ' abbia equazione y3 = g1(x) e quello inferiore y4 = g2(x). Per semplicità, si supponga che le due curve siano comprese, tangenti, alle rette di equazioni x = a, x = b, come nella figura suddetta, nei punti A, A', B, B'. Sia x = c una parallela alle precedenti rette, compresa nella striscia di piano da quelle limitata, e secante γ e γ' rispettivamente nei punti M, N, M', N'. Se, per ipotesi,
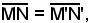
cioè:
f1(x) - f2(x) = g1(x) - g2(x),
sarà anche
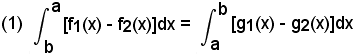
ed ancora, se per ipotesi,
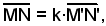
cioè
f1(x) - f2(x) = k·[g1(x) - g2(x)],
sarà anche
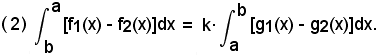
La (1) e la (2) dimostrano il teorema.
Applicazioni geometriche degl'integrali definiti
1)-Volume di un solido di rotazione.
Si consideri l'arco A'B' di una curva γ, la cui equazione y = f(x) si suppone continua in (a, b), unitamente alla sua derivata.
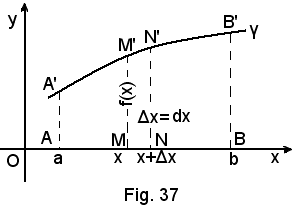
Se si fa ruotare l'arco A'B' intorno all'asse x in modo che, durante il movimento, ogni punto dell'arco mantenga costante la sua distanza dall'asse x, si sa dalla geometria elementare che ogni punto di A'B' descrive una circonferenza di raggio uguale alla distanza f(x) del punto dall'asse x, e posta in un piano normale al suddetto asse.
Il trapezoide ABB'A' descrive un solido detto di rotazione dal movimento che si fa compiere alla figura piana. Considerando uno degli n trapezoidi elementari visti in precedenza, di base
(x, x+Δx),
ossia Δx = dx e altezza f(x), allorchè n tende ad infinito, ciascuno dei suddetti trapezoidi si potrà considerare un rettangolo di base Δx ed altezza f(x).
Quando la figura piana ABB'A' ruota intorno all'asse x, ruoterà ciascuno dei suddetti rettangoli, generando un cilindro il cui volume è:
π·f2(x)·Δx,
pertanto il volume generato dall'intero trapezoide ABB'A' intorno all'asse x sarà
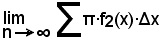
e quindi, indicando con Vs il volume del solido, si avrà
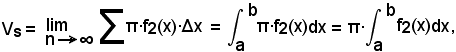
che è la formula per calcolare il volume di un qualsiasi solido ottenuto dalla rotazione di una figura piana intorno all'asse x.
2)-Volume del cono.
E' noto dalla geometria che il cono è generato dalla rotazione completa di un triangolo rettangolo intorno ad un cateto.
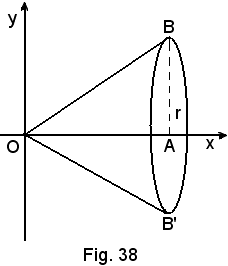
Sia AOB il triangolo rettangolo, in cui
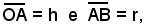
per cui la retta OB ha per equazione
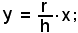
si avrà
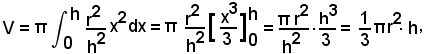
formula nota dalla geometria.
3)-Volume della sfera.
E' noto dalla geometria che la sfera è generata dalla rotazione completa di un semicerchio intorno al proprio diametro.
Sia
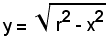
l'equazione della semicirconferenza superiore all'asse x; si ha:
4)-Volume del segmento sferico a due basi.
Siano
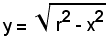
l'equazione della semicirconferenza superiore all'asse x, a e b i raggi delle basi del segmento sferico,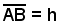
la sua altezza ed x1, x2 le ascisse dei punti A e B.
Si ha:
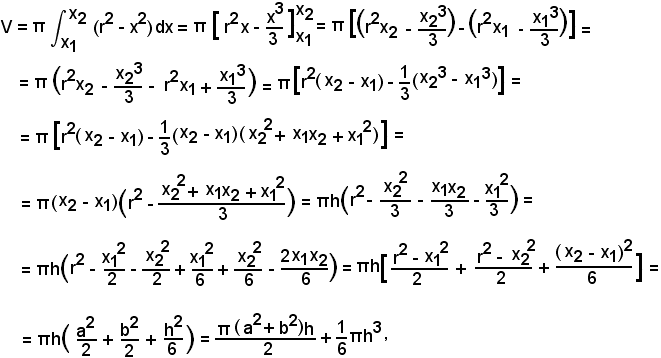
formula nota dalla geometria.
Nota bene
Durante i passaggi effettuati, si è tenuto conto che:
1) x1 - x2 = h;
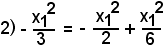
ed analogamente per x2;3) r2 - x12 = a2 e r2 - x22 = b2.
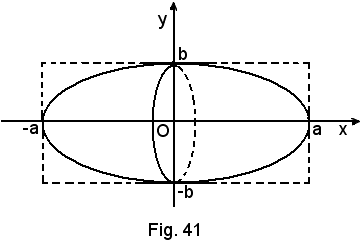
5)-Volume dell'ellissoide.
L'ellissoide è generato dalla rotazione completa di una semiellisse intorno ad un suo diametro, ad esempio, come nella figura suddetta, dalla semiellisse superiore all'asse x, avente per equazione:
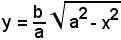
intorno allo stesso asse.
Si ha:
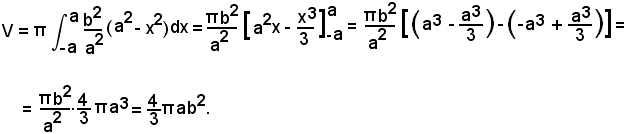
Nota bene
Se a = b = r, si torna alla sfera.
6)-Volume del tronco di cono.
Il tronco di cono è generato dalla rotazione di un trapezio.
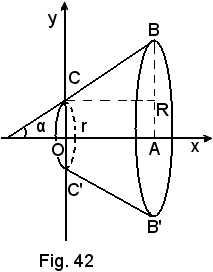
Si indichi
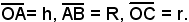
La retta CB, come noto, ha un'equazione del tipo
y = mx + n
e, in tal caso è
Quindi, l'equazione della retta CB, generatrice della superficie laterale del solido richiesto è:
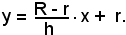
Si ha:
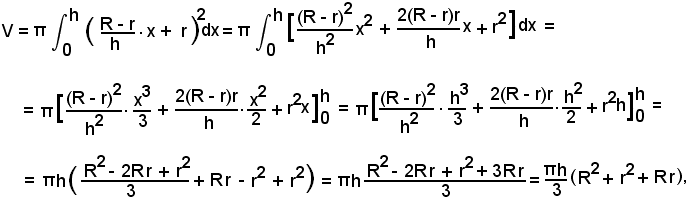
formula nota dalla geometria.
6)-Volume del toro.
Il toro è generato dalla rotazione di un cerchio intorno ad una retta, dall'asse x nella figura seguente, giacente nel suo stesso piano e non secante il cerchio.
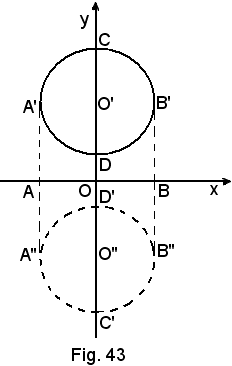
Si supponga che il cerchio abbia la posizione tracciata nella figura suddetta, pertanto, la sua equazione è del tipo:
x2 + y2 - 2βy + β2 - r2 = 0,
mentre quella dell'arco A'CB' è
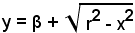
e quella dell'arco A'DB' è
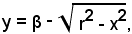
in cui β è l'ordinata del centro O'.
Il volume del toro è dato dalla differenza dei volumi dei solidi generati, nella rotazione completa, rispettivamente dai trapezoidi AA'CB'B e AA'DB'B, quindi:
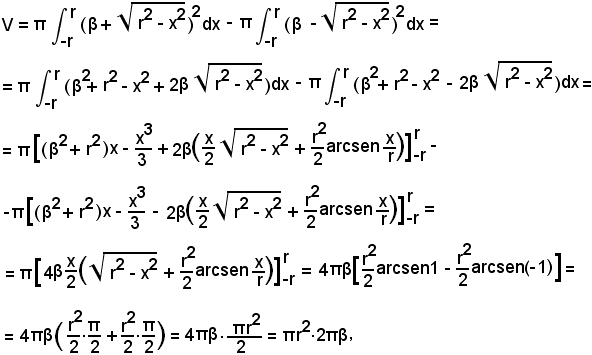
formula nota dalla geometria: il volume del toro è uguale al prodotto dell'area del cerchio che lo genera per la lunghezza della circonferenza descritta, nella rotazione, dal centro dello stesso cerchio.
Baricentro di una figura piana omogenea
Si consideri la figura piana ABB'A', limitata superiormente dall'arco A'B' appartenente alla curva di equazione y = f(x), e siano a e b le ascisse dei punti A e B e (x0, y0) le coordinate del baricentro G della figura che si suppone omogenea, ossia di uguale densità d in tutte le sue parti.
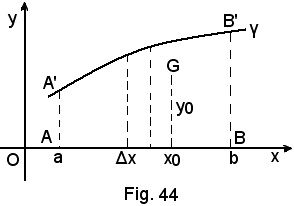
Si sa dalla fisica che G è il punto di applicazione della forza peso P che, in uno stesso luogo, è data dal prodotto della superficie per la densità della stessa, quindi:
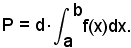
Si ricordi ancora il teorema di Varignon: il momento di una forza rispetto ad un punto è dato dalla somma algebrica dei momenti delle forze componenti quella data. Pertanto, se si considera la forza P come risultante di tutte le forze pi, peso di ciascuna striscia in cui la figura ABB'A' è divisa dalle parallele all'asse y passanti per i punti xi, xi + Δxi, potendosi ognuna di dette strisce considerare come un rettangolo di base Δxi e altezza f(xi), si avrà:
Pi = f(xi)Δxid,
quindi
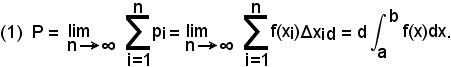
Il momento della forza P, considerata parallela ad y, rispetto ad O, diventa allora P·x0 e per la (1):
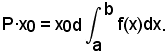
La somma dei momenti delle pi rispetto ad O è:
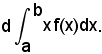
Per il teorema di Varignon, deve quindi aversi:
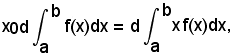
da cui si ricava
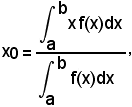
ascissa di G.
Analogamente, considerando la P parallela all'asse x, dai momenti rispetto ad O e dalla considerazione che il baricentro è situato a metà ordinata della relativa striscia, si ha:
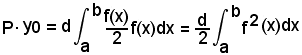
e quindi, ancora analogamente a quanto sopra,
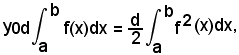
da cui
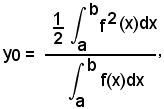
ordinata di G.
Volume di un generico solido di rotazione
Per calcolare il volume di un qualsiasi solido di rotazione, ci si serve del teorema di Guldino e Cavalieri:
-il volume del solido ottenuto dalla rotazione completa di una superficie piana intorno ad una retta giacente nello stesso piano e non secante la superficie, è uguale al prodotto dell'area della superficie per la lunghezza della circonferenza descritta nella rotazione dal baricentro della superficie.
Applicazioni
Con tale teorema si può calcolare:
1)-il volume del toro.
Infatti, essendo l'area del cerchio πr2, detta β l'ordinata del centro, si ha:
V = πr2·2πβ,
formula già trovata;
2)-il volume del solido generato in una rotazione completa da un'ellisse di semiassi a e b, essendo πab l'area di tale ellisse e indicando con β l'ordinata del baricentro, centro, dell'ellisse è:
V = πab·2πβ.
Nel caso in cui si richieda l'area complessiva della regione piana limitata dalla curva di equazione y = f(x) in (a, b), detta area è limitata lateralmente sempre dalle rette di equazione x = a ed x = b, ossia si richieda l'area, indipendentemente dai segni delle sue singole parti componenti, allora non è possibile calcolare un unico integrale definito, ma trovati, come in Fig. 13, i sottointervalli (a, x1), (x1, x2), (x2, b), in cui la funzione non cambia segno, la sua area richiesta è:
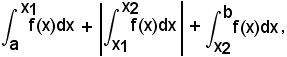
il che equivale a sostituire ai trapezoidi situati al di sotto dell'asse x i simmetrici rispetto allo stesso asse.
Esempi
1°)-Calcolare l'area della regione piana limitata superiormente dalla linea di equazione
nell'intervallo (1, 4).
Si ha:
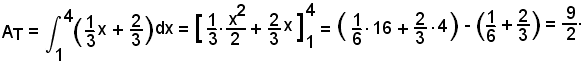
2°)-Calcolare l'area della regione piana limitata superiormente dalla linea di equazione
y = x2 - 4x + 5
nell'intervallo
Si ha:
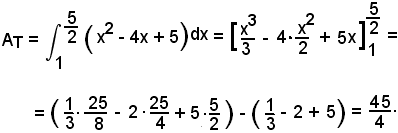
3°)-Calcolare l'area della regione piana limitata superiormente dalla linea di equazione
y = x3 + x
nell'intervallo (0,2).
Si ha:
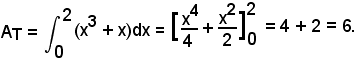
4°)-Calcolare l'area della regione piana limitata superiormente dalla linea di equazione
nell'intervallo (-5, -1).
Si hanno due casi:
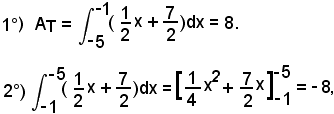
per cui
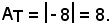
5°)-Calcolare l'area della regione piana limitata dalla linea di equazione
y = -x2 - 4x - 5
nell'intervallo (-2, -1).
Si hanno due casi:
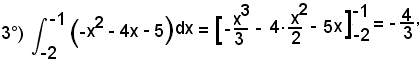
per cui
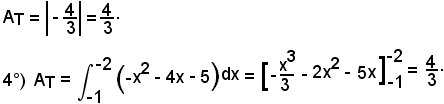
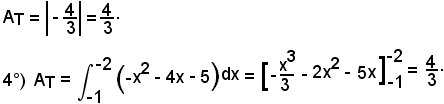
6°)-Calcolare l'area della regione piana (segmento parabolico) limitata dalla parabola di equazione
e dall'asse x.
Si osserva prima che la parabola interseca l'asse x nei punti di ascissa 1 e 5, pertanto si deve calcolare l'area del segmento parabolico nell'intervallo (1, 5).
Si hanno due casi:
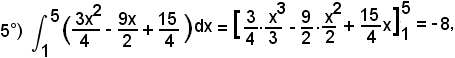
per cui
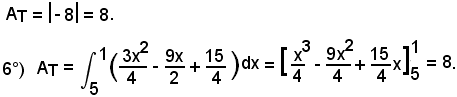
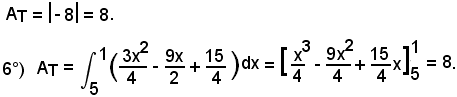
7°)-Calcolare l'area della regione piana limitata dalla linea di equazione
y = senx
negl'intervalli (0, π), (π, 2π), (0, 2π).
Nell'intervallo (0, π) si ha:
quindi
Nell'intervallo (π, 2π) si ha:
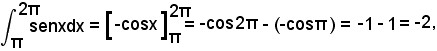
quindi
Nell'intervallo (0, 2π) si ha:
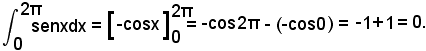
Infine l'area totale è data da:
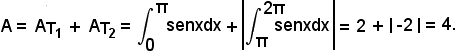
8°)-Calcolare l'area della regione piana limitata dalla linea di equazione
y = x3 - 3x2 + 2x
negl'intervalli (0, 1), (1, 2), (0, 2).
L'andamento della linea di equazione y = x3 - 3x2 + 2x è rappresentato dalla curva γ nella figura seguente.
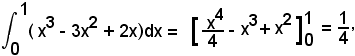
quindi
Nell'intervallo (1, 2) si ha:
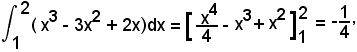
quindi
Nell'intervallo (0, 2) si ha:
Infine l'area totale nell'intervallo (0, 2) è data da:
Quadrature notevoli
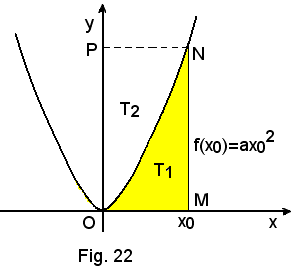
1)-Area del trapezoide limitato dalla parabola y = ax2 in (0, x0).
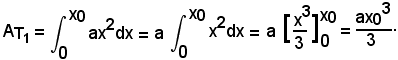
Osservando che è
da cui segue
per il teorema di Archimede.
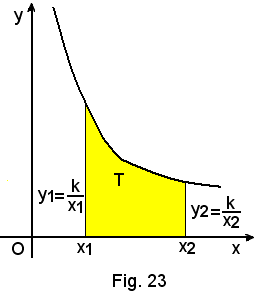
2)-Area del trapezoide limitato dall'iperbole particolare y = k/x in (x1, x2).
Supposto k > 0 e considerato il ramo d'iperbole equilatera del I quadrante, si ha:
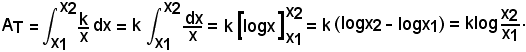
Nota bene
Se k = 1, x1 = 1, x2 = a, si ha
cioè: il logaritmo naturale o neperiano di un numero esprime l'area del trapezoide limitato dall'iperbole particolare y = 1/x oppure xy = 1 nell'intervallo in cui il primo estremo è 1 ed il secondo è il numero dato.
Da qui il motivo per cui i logaritmi naturali o neperiani sono chiamati anche iperbolici.
Valore medio di una funzione in un intervallo
Sia y = f(x) una funzione integrabile in un intervallo (a, b). Dividendo l'intervallo in n parti uguali, la lunghezza di ciascuna di esse è, come noto:
Se allora si considera la somma integrale generalizzata
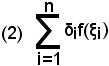
per la (1), diventa
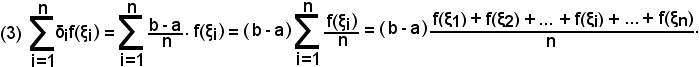
Sapendo che
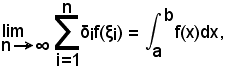
per la (3) si ha:
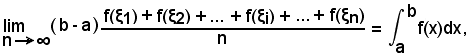
ossia
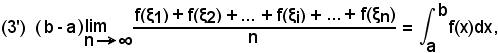
ed ancora
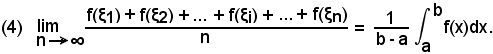
Il quoziente
costituisce la media aritmetica degli n valori dati alla funzione in (a, b), cioè uno per ciascun sottointervallo δi di (a, b).
Posto allora
la (4) diventa
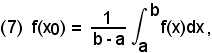
cioè: il valore medio di una funzione in un intervallo (a, b) si ottiene dividendo l'integrale definito della funzione in quell'intervallo per la lunghezza dello stesso intervallo.
Esempi
1°) Il valore medio della funzione y = x2 nell'intervallo (2, 4) è:
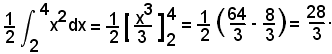
2°) Il valore medio della funzione y = 2x2 -3x + 1 nell'intervallo (1, 4) è:
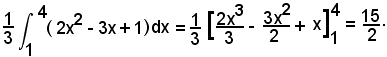
3°) Il valore medio della funzione y = senx nell'intervallo (0, π) è:
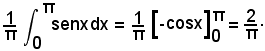
Dalla (7), liberando dal denominatore, si ha
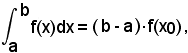
cioè: l'integrale definito di una funzione continua è uguale alla lunghezza dell'intervallo in cui è stato calcolato per il valore che la funzione integranda assume in un conveniente punto di questo intervallo.
Oppure, in base al significato geometrico di integrale definito:
-il valore medio di una funzione continua in un intervallo (a, b) è l'altezza del rettangolo che ha per base l'intervallo (a, b) ed è equivalente al trapezoide
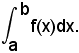
Calcolo dell'area di una superficie limitata da due linee o da una linea chiusa
1)-Le due linee sono situate al di sopra dell'asse x.
Si consideri la superficie S limitata dagli archi di linee, curve o rette di equazione
y1 = f1(x), y2 = f2(x).
Da evidenti considerazioni geometriche l'area A di S, AS, è uguale alla differenza delle aree dei trapezoidi aventi per base l'intervallo (xN, xM), in cui M ed N sono i punti d'incontro delle due linee. Inoltre sono limitati superiormente dagli archi MN appartenenti, rispettivamente, alle linee di equazione y1 = f1(x) e y2 = f2(x), con f1(x) > f2(x).
Quindi si ha:
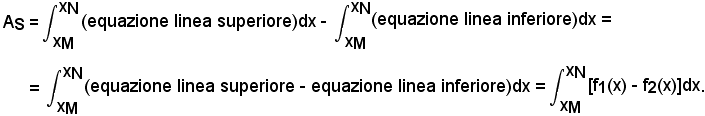
Nota bene
Si vedrà in seguito il caso in cui i due archi MN appartengono ad una stessa linea di equazione implicita f(x, y) = 0.
Esempi
1°)-Calcolare l'area della regione piana limitata dalle due parabole di equazioni:
Dopo aver rappresentato graficamente le due parabole, ed aver trovato i loro punti d'intersezione (1, 3) e (4, 4), si calcola l'area della superficie S evidenziata in giallo nella figura suddetta.
Si ha:
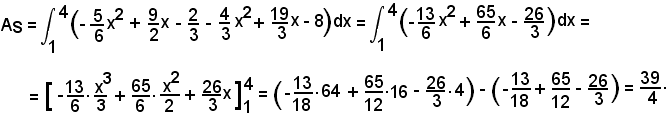
L'unità di misura delle superfici è il quadrato di lato uguale all'unità di misura convenuta per le lunghezze nel sistema cartesiano.
2°)-Calcolare l'area della sezione piana limitata dalle rette di equazioni:
nell'intervallo (1, 3).
Si ha:
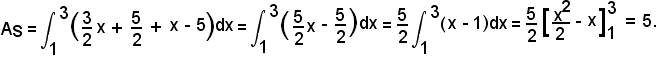
2)-Le due linee sono situate al di sotto dell'asse x.
L'area A della regione piana S limitata dai due archi MN appartenenti alle linee di equazioni
y1 = f1(x), y2 = f2(x),
con f1(x) < f2(x) < 0, è:
Esempi
1°)-Calcolare l'area della striscia di piano limitata dalle rette di equazioni
y = -4 e y = -1,
nell'intervallo (0, 3).
Essendo
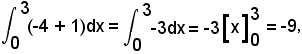
l'area richiesta è
AS = |-9| = 9.
2°)-Calcolare l'area della regione piana limitata, rispettivamente dalla parabola e dalla retta di equazioni:
Dopo aver trovato le coordinate dei punti d'intersezione tra parabola e retta:
l'area A della superficie S è il valore assoluto di
3°)-Calcolare l'area della regione piana limitata tra le due parabole di equazioni:
Dopo aver trovato i punti d'intersezione M e N tra le due parabole, le cui ascisse sono xM = 1 e xN = 29/9, l'area A di S è il valore assoluto di:
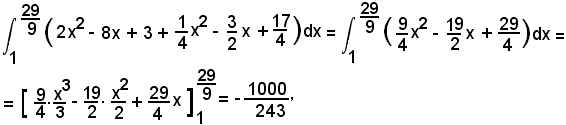
quindi
3)-Una delle due linee è situata una al di sopra e l'altra al di sotto dell'asse x.
Per l'area della regione piana, limitata dai due archi MN appartenenti rispettivamente alle linee di equazioni:
y1 = f1(x) > 0 e y2 = f2(x) > 0,
essendo
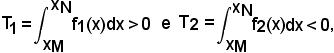
si ha
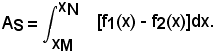
Esempi
1°)-Calcolare l'area della regione piana limitata dalle due parabole di equazioni:
y = - 2x2 + 8x - 6 e y = x2 - 4x + 3.
1°)-Calcolare l'area della regione piana limitata dalle due parabole di equazioni:
y = - 2x2 + 8x - 6 e y = x2 - 4x + 3.
Dopo aver trovato le coordinate dei punti d'intersezione delle due parabole:
(1, 0) e (3, 0),
l'area richiesta è
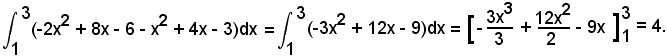
2°)-Calcolare l'area della regione piana limitata, rispettivamente, dalla retta e dalla cubica di equazioni:
y = -4x + 4 e y = -x3 + 2x2 + x - 2.
Dopo aver trovato i punti d'intersezione della retta con la cubica, le cui coordinate sono
(-2, 12), (1, 0) e (3, -8),
si ha:
per cui
Allora l'area richiesta è:
4)-Superficie limitata da una linea chiusa
a)-Area del cerchio di centro O e raggio r.
In tal caso l'equazione implicita della circonferenza è:
x2 + y2 = r2.
Esplicitando rispetto ad y, risulta:
in cui il segno + vale per la semicirconferenza situata nel I e nel II quadrante, e quello - per la semicirconferenza situata nel III e nel IV quadrante.
Per calcolare l'area del cerchio, basta calcolare quella di un quadrante, ad esempio T, e moltiplicarla per 4.
Si ha:
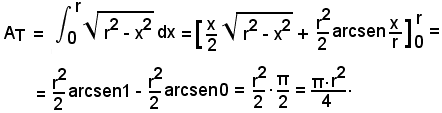
L'area del cerchio è:
A = 4·AT = πr2,
come già noto dalla geometria.
b)-Area dell'ellisse di centro O e semiassi a e b.
L'equazione implicita dell'ellisse è:
b2x2 + a2y2 = a2b2,
oppure
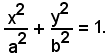
Esplicitando rispetto ad y, risulta:
in cui il segno + vale per la semiellisse posta al di sopra dell'asse x, e quello - per quella posta al di sotto dello stesso asse. Per calcolare l'area dell'ellisse, basta calcolare quella di un quadrante, ad esempio T, e moltiplicarla per 4.
Si ha:
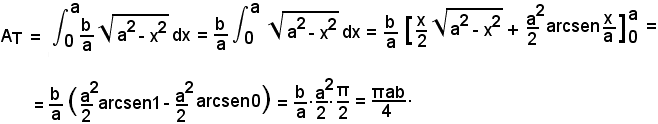
L'area dell'ellisse è:
A = 4·AT =πab.
Se a = b, si ha l'area del cerchio.
Nota bene
Se la circonferenza e l'ellisse non si trovano nelle suddette posizioni, conviene effettuare un opportuno movimento degli assi cartesiani per riportarsi ai casi considerati.
Teorema di Cavalieri
Se due superfici piane sono comprese fra due rette parallele, sulle quali hanno almeno un punto e sono uguali, o stanno in un rapporto k, e le corde sono in esse determinate da una qualsiasi retta parallela alle prime due, le due figure piane sono equivalenti, o stanno sullo stesso rapporto k.
Siano f(x, y) = 0 e g(x, y) = 0 le equazioni implicite delle linee chiuse γ e γ' limitanti le superfici S1 e S2, e si supponga di aver esplicitato tali equazioni, rispetto alla y, in modo che l'arco superiore di γ abbia equazione y1 = f1(x) e quello inferiore y2 = f2(x), così che l'arco superiore di γ' abbia equazione y3 = g1(x) e quello inferiore y4 = g2(x). Per semplicità, si supponga che le due curve siano comprese, tangenti, alle rette di equazioni x = a, x = b, come nella figura suddetta, nei punti A, A', B, B'. Sia x = c una parallela alle precedenti rette, compresa nella striscia di piano da quelle limitata, e secante γ e γ' rispettivamente nei punti M, N, M', N'. Se, per ipotesi,
cioè:
f1(x) - f2(x) = g1(x) - g2(x),
sarà anche
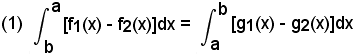
ed ancora, se per ipotesi,
cioè
f1(x) - f2(x) = k·[g1(x) - g2(x)],
sarà anche
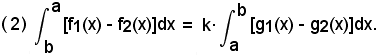
La (1) e la (2) dimostrano il teorema.
Applicazioni geometriche degl'integrali definiti
1)-Volume di un solido di rotazione.
Si consideri l'arco A'B' di una curva γ, la cui equazione y = f(x) si suppone continua in (a, b), unitamente alla sua derivata.
Se si fa ruotare l'arco A'B' intorno all'asse x in modo che, durante il movimento, ogni punto dell'arco mantenga costante la sua distanza dall'asse x, si sa dalla geometria elementare che ogni punto di A'B' descrive una circonferenza di raggio uguale alla distanza f(x) del punto dall'asse x, e posta in un piano normale al suddetto asse.
Il trapezoide ABB'A' descrive un solido detto di rotazione dal movimento che si fa compiere alla figura piana. Considerando uno degli n trapezoidi elementari visti in precedenza, di base
(x, x+Δx),
ossia Δx = dx e altezza f(x), allorchè n tende ad infinito, ciascuno dei suddetti trapezoidi si potrà considerare un rettangolo di base Δx ed altezza f(x).
Quando la figura piana ABB'A' ruota intorno all'asse x, ruoterà ciascuno dei suddetti rettangoli, generando un cilindro il cui volume è:
π·f2(x)·Δx,
pertanto il volume generato dall'intero trapezoide ABB'A' intorno all'asse x sarà
e quindi, indicando con Vs il volume del solido, si avrà
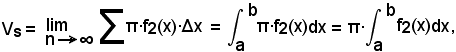
che è la formula per calcolare il volume di un qualsiasi solido ottenuto dalla rotazione di una figura piana intorno all'asse x.
2)-Volume del cono.
E' noto dalla geometria che il cono è generato dalla rotazione completa di un triangolo rettangolo intorno ad un cateto.
Sia AOB il triangolo rettangolo, in cui
per cui la retta OB ha per equazione
si avrà
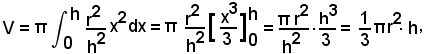
formula nota dalla geometria.
3)-Volume della sfera.
E' noto dalla geometria che la sfera è generata dalla rotazione completa di un semicerchio intorno al proprio diametro.
Sia
l'equazione della semicirconferenza superiore all'asse x; si ha:
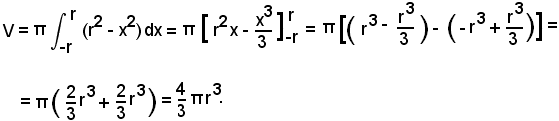
4)-Volume del segmento sferico a due basi.
Siano
l'equazione della semicirconferenza superiore all'asse x, a e b i raggi delle basi del segmento sferico,
la sua altezza ed x1, x2 le ascisse dei punti A e B.Si ha:
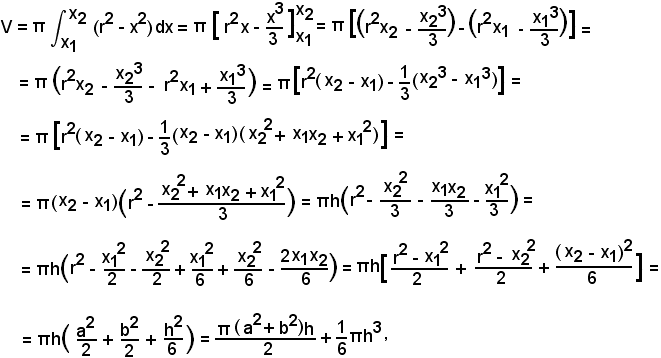
formula nota dalla geometria.
Nota bene
Durante i passaggi effettuati, si è tenuto conto che:
1) x1 - x2 = h;
ed analogamente per x2;
5)-Volume dell'ellissoide.
L'ellissoide è generato dalla rotazione completa di una semiellisse intorno ad un suo diametro, ad esempio, come nella figura suddetta, dalla semiellisse superiore all'asse x, avente per equazione:
intorno allo stesso asse.
Si ha:
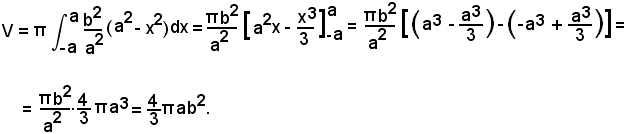
Nota bene
Se a = b = r, si torna alla sfera.
6)-Volume del tronco di cono.
Il tronco di cono è generato dalla rotazione di un trapezio.
Si indichi
La retta CB, come noto, ha un'equazione del tipo
y = mx + n
e, in tal caso è
Quindi, l'equazione della retta CB, generatrice della superficie laterale del solido richiesto è:
Si ha:
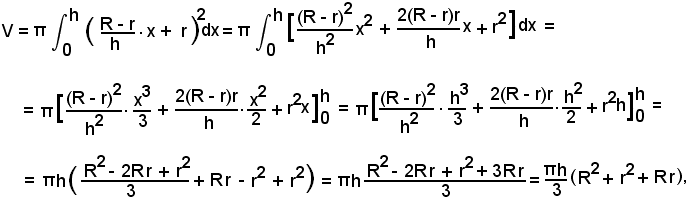
formula nota dalla geometria.
6)-Volume del toro.
Il toro è generato dalla rotazione di un cerchio intorno ad una retta, dall'asse x nella figura seguente, giacente nel suo stesso piano e non secante il cerchio.
Si supponga che il cerchio abbia la posizione tracciata nella figura suddetta, pertanto, la sua equazione è del tipo:
x2 + y2 - 2βy + β2 - r2 = 0,
mentre quella dell'arco A'CB' è
e quella dell'arco A'DB' è
in cui β è l'ordinata del centro O'.
Il volume del toro è dato dalla differenza dei volumi dei solidi generati, nella rotazione completa, rispettivamente dai trapezoidi AA'CB'B e AA'DB'B, quindi:
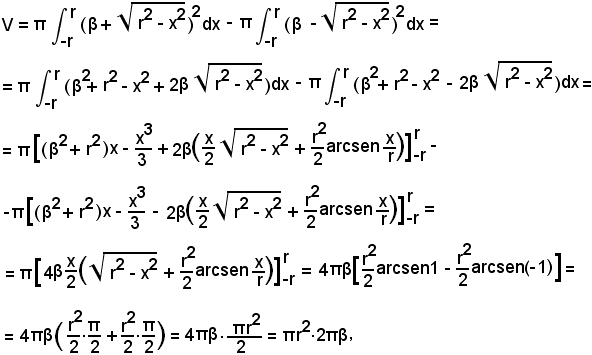
formula nota dalla geometria: il volume del toro è uguale al prodotto dell'area del cerchio che lo genera per la lunghezza della circonferenza descritta, nella rotazione, dal centro dello stesso cerchio.
Baricentro di una figura piana omogenea
Si consideri la figura piana ABB'A', limitata superiormente dall'arco A'B' appartenente alla curva di equazione y = f(x), e siano a e b le ascisse dei punti A e B e (x0, y0) le coordinate del baricentro G della figura che si suppone omogenea, ossia di uguale densità d in tutte le sue parti.
Si sa dalla fisica che G è il punto di applicazione della forza peso P che, in uno stesso luogo, è data dal prodotto della superficie per la densità della stessa, quindi:
Si ricordi ancora il teorema di Varignon: il momento di una forza rispetto ad un punto è dato dalla somma algebrica dei momenti delle forze componenti quella data. Pertanto, se si considera la forza P come risultante di tutte le forze pi, peso di ciascuna striscia in cui la figura ABB'A' è divisa dalle parallele all'asse y passanti per i punti xi, xi + Δxi, potendosi ognuna di dette strisce considerare come un rettangolo di base Δxi e altezza f(xi), si avrà:
Pi = f(xi)Δxid,
quindi
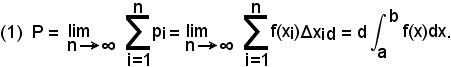
Il momento della forza P, considerata parallela ad y, rispetto ad O, diventa allora P·x0 e per la (1):
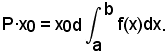
La somma dei momenti delle pi rispetto ad O è:
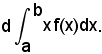
Per il teorema di Varignon, deve quindi aversi:
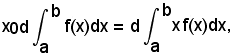
da cui si ricava
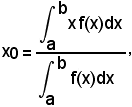
ascissa di G.
Analogamente, considerando la P parallela all'asse x, dai momenti rispetto ad O e dalla considerazione che il baricentro è situato a metà ordinata della relativa striscia, si ha:
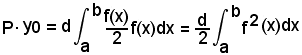
e quindi, ancora analogamente a quanto sopra,
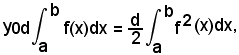
da cui
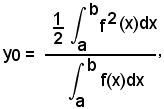
ordinata di G.
Volume di un generico solido di rotazione
Per calcolare il volume di un qualsiasi solido di rotazione, ci si serve del teorema di Guldino e Cavalieri:
-il volume del solido ottenuto dalla rotazione completa di una superficie piana intorno ad una retta giacente nello stesso piano e non secante la superficie, è uguale al prodotto dell'area della superficie per la lunghezza della circonferenza descritta nella rotazione dal baricentro della superficie.
Applicazioni
Con tale teorema si può calcolare:
1)-il volume del toro.
Infatti, essendo l'area del cerchio πr2, detta β l'ordinata del centro, si ha:
V = πr2·2πβ,
formula già trovata;
2)-il volume del solido generato in una rotazione completa da un'ellisse di semiassi a e b, essendo πab l'area di tale ellisse e indicando con β l'ordinata del baricentro, centro, dell'ellisse è:
V = πab·2πβ.