MIKY & GENNY
INTEGRALI INDEFINITI ---> INDICE
1)-Premessa
Nella teoria delle derivate si è visto che se
DF(x) = f(x),
è anche
in cui C è una costante arbitraria.
Ciò significa che esistono infinite funzioni, tutte differenti per una costante additiva, che hanno la stessa derivata.
Teorema - Se f(x) è una funzione continua in un intervallo chiuso (a, b), esiste sempre in (a, b) un'altra funzione F(x), di cui f(x) è la derivata.
Si omette la dimostrazione.
Inoltre, ricordando che tutte le funzioni che si considerano nella matematica elementare sono continue, tale teorema vale per tutte le funzioni.
2)-Integrale indefinito
Definizione 1 - Si chiama integrale indefinito di una funzione f(x) nell'intervallo chiuso (a, b), un'altra funzione F(x), tale che la sua derivata in (a, b) sia f(x).
Scrivere
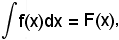
significa
Definizione 2 - Si chiama integrale indefinito di una funzione f(x) nell'intervallo chiuso (a, b), un'altra funzione F(x), tale che il suo differenziale in (a, b) sia f(x)dx.
Scrivere
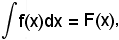
significa
dF(x) = f(x)dx.
Per la definizione 1 l'integrale indefinito si presenta come l'operazione inversa della derivazione e per la definizione 2 si presenta come l'operazione inversa della differenziazione.
F(x) si chiama integrale indefinito o funzione primitiva di f(x); f(x) si chiama funzione integranda.
Il simbolo
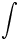
è una deformazione della lettera s, iniziale della parola somma, per i motivi che saranno visti in seguito.
3)-Teoremi sulla funzione primitiva
1°)-Se F(x) è una funzione primitiva di f(x) anche F(x) + C è una funzione primitiva di f(x); oppure di funzioni primitive di una stessa funzione integranda ne esistono infinite e tutte differiscono per una costante.
Cioè se
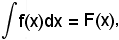
è anche
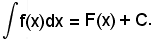
Infatti:
D[F(x) + C] = DF(x) + DC = f(x).
2°)-Se F1(x) e F2(x) sono due funzioni primitive di una stessa funzione f(x), esse differiscono per una costante.
Cioè se
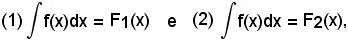
deve aversi:
F1(x) - F2(x) = C.
Infatti, per la definizione 1, la (1) e la (2) esprimono che:
DF1(x) = f(x) e DF2(x) = f(x)
e, quindi, sottraendo membro a membro
DF1(x) - DF2(x) = 0,
ossia
D[F1(x) - F2(x)] = 0,
da cui, per quanto è noto sulla derivata di una costante, si ha
F1(x) - F2(x) = C.
4)-Osservazioni e considerazioni geometriche
1^)-Da quanto detto è opportuno osservare che, mentre l'operazione di derivazione conduce sempre ad un unico risultato, nel senso che la derivata di una funzione, quando esiste è unica, l'operazione di integrazione indefinita ha invece infinite soluzioni.
Pertanto, se prima si integra e poi si deriva una funzione, si ha la stessa funzione:
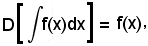
invece, se prima si deriva e poi si integra una funzione, si ottiene una funzione che, rispetto alla data, è aumentata di una costante arbitraria,
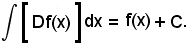
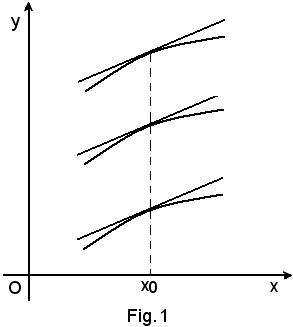
2^)-Geometricamente,
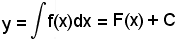
rappresenta tutte le infinite linee che si ottengono da quella di equazione y = F(x), con una sola traslazione dell'asse x e tutte le linee hanno tangenti parallele fra loro nei punti di uguale ascissa x0, in quanto il coefficiente angolare di tali rette è sempre
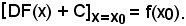
5)-Proprietà dell'integrale indefinito
Teorema - Se f1(x), f2(x) ... fn(x) sono funzioni, di ciascuna delle quali si conosce un integrale indefinito, ossia una funzione primitiva, rispettivamente
F1(x), F2(x) ... Fn(x),
si ha che l'integrale indefinito di una combinazione lineare delle f(x) è uguale alla combinazione lineare degl'integrali delle singole f(x), ossia alla combinazione lineare delle funzioni primitive F(x), sempre secondo le stesse costanti.
αf1(x) + βf2(x) + ... + νfn(x),
per dimostrare che è
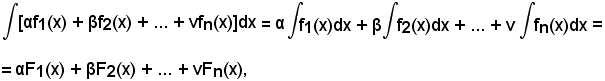
basta far vedere che è
D[αF1(x) + βF2(x) + ... + νFn(x)] = αf1(x) + βf2(x) + ... + νfn(x),
e ciò risulta evidente dai teoremi sulle derivate e dalla definizione di integrale indefinito, per le ipotesi
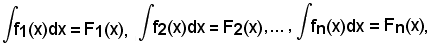
ossia
DF1(x) = f1(x), DF2(x) = f2(x), ..., DFn(x) = fn(x).
Dal teorema dimostrato seguono i seguenti casi particolari:
1°)-Se
α = β = ... = ν = |1|,
si ha:
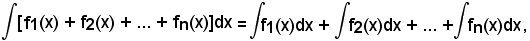
cioè
-l'integrale della somma di due funzioni è uguale alla somma degl'integrali delle singole funzioni.
2°)-Se
α ≠ 0 = e β = γ = ... = ν = 0, si ha:
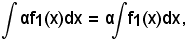
cioè
-una costante moltiplicativa passa inalterata in integrazione come in derivazione.
6)-Integrali immediati
In base a quanto detto ed a quanto è stato visto per le derivate, è possibile indicare il seguente elenco di integrali immediati:
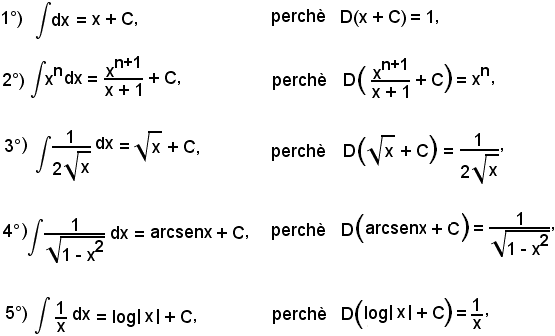

Nota bene
1)-Al tipo 2°) si riporta il seguente
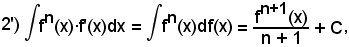
dopo aver osservato che
df(x) = f'(x)dx
e che n è un qualsiasi numero positivo o negativo.
2)-Al tipo 5°) si riporta il seguente
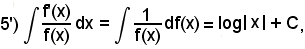
dopo aver ancora osservato che
df(x) = f'(x)dx.
7)-Esempi
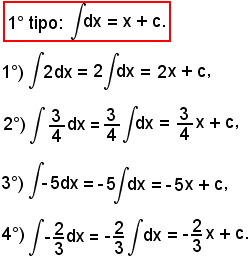
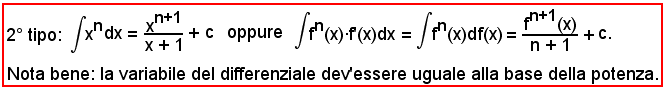
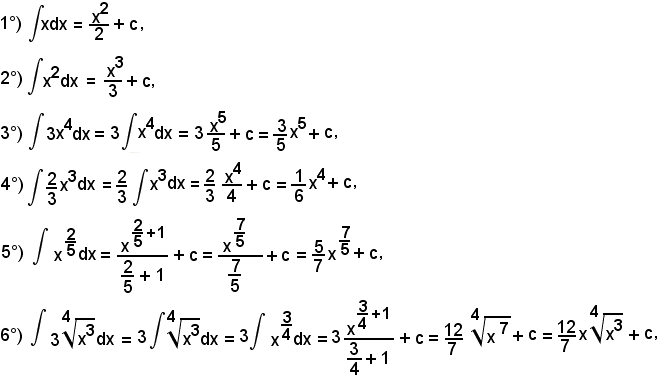
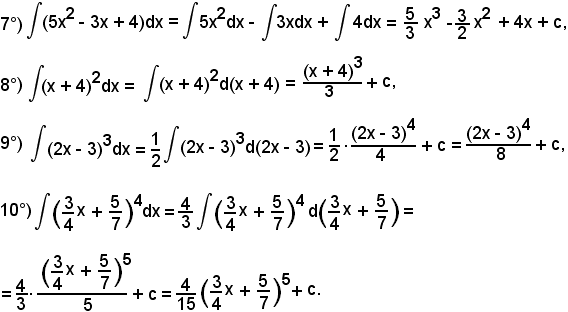
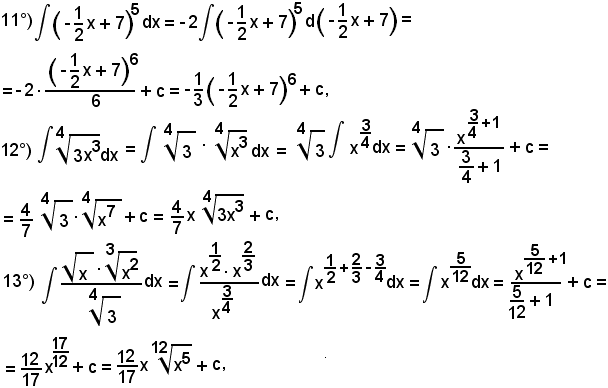
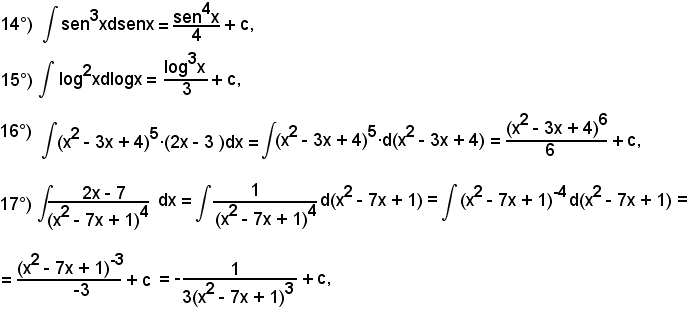
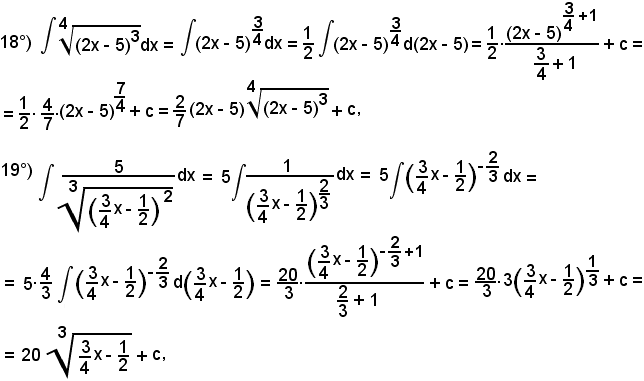

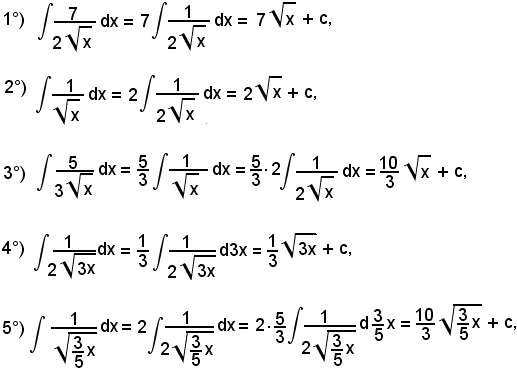
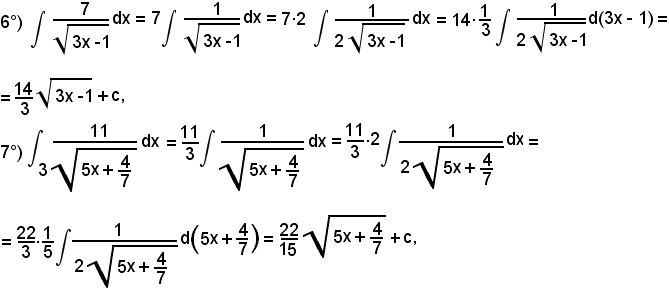
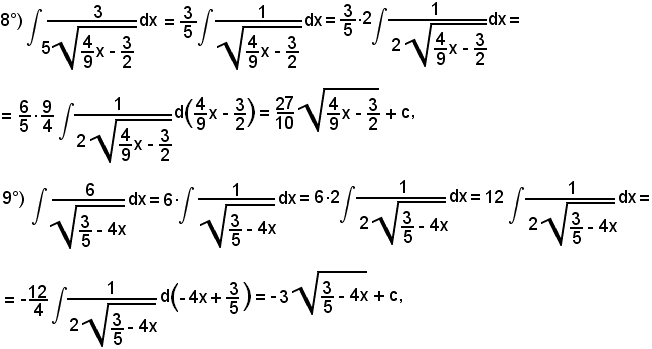
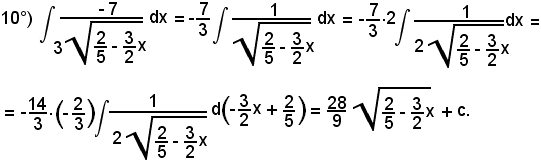

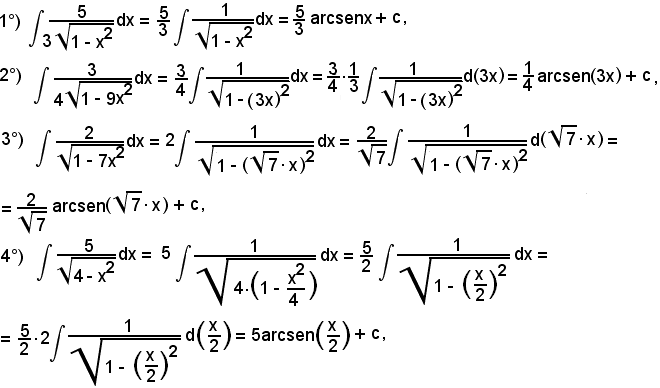
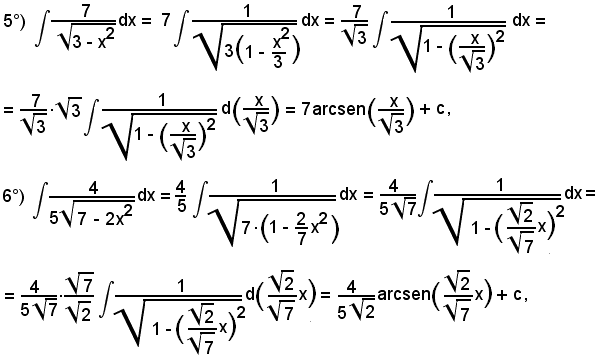
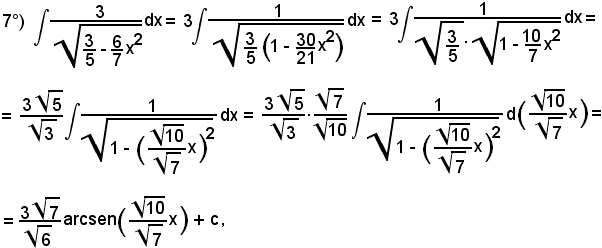
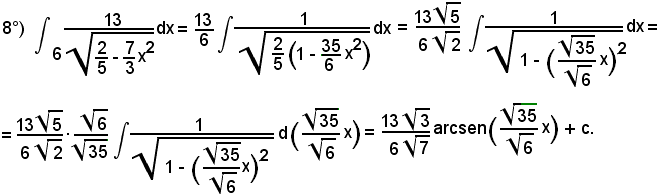

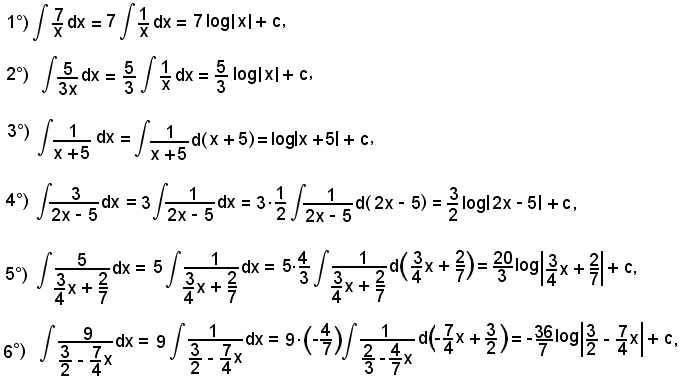
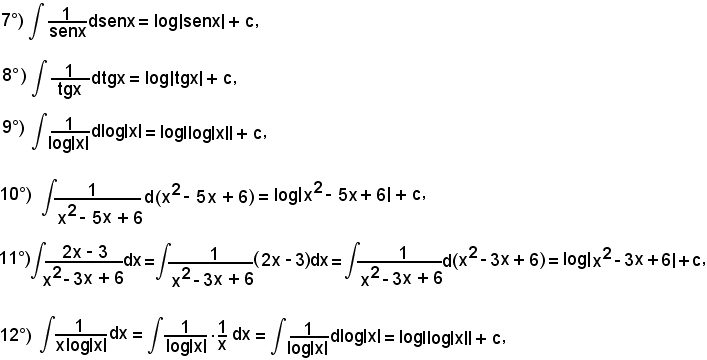
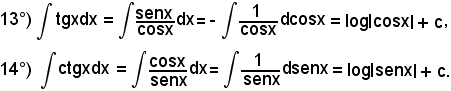

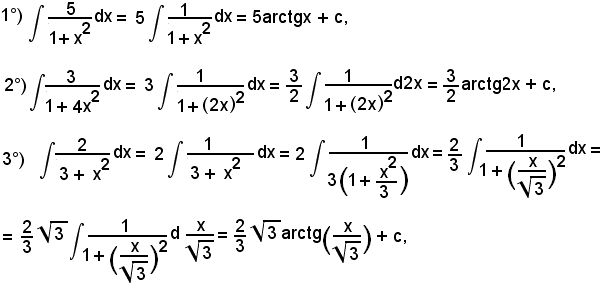
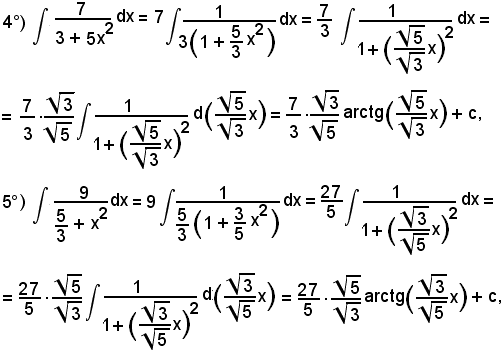
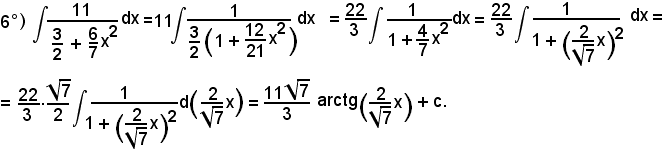

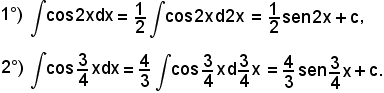

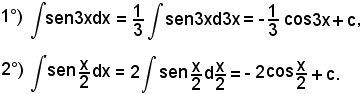
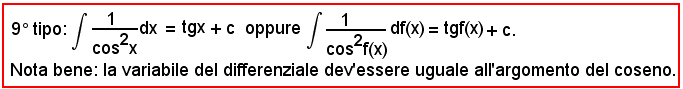
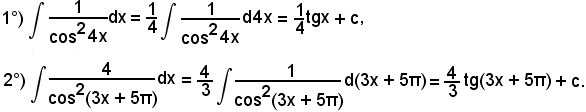

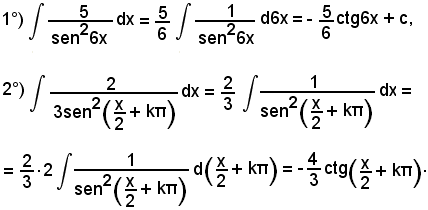

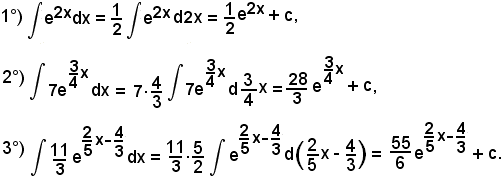
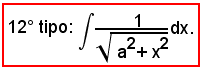
L'integrale proposto appartiene al 5° tipo; infatti, dividendo e moltiplicando la frazione integranda per
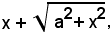
si ha:
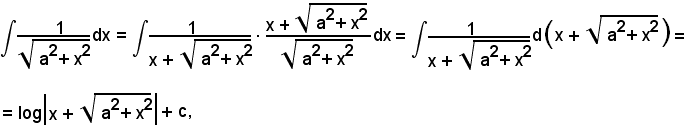
tenendo presente che
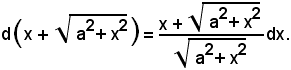
Nella teoria delle derivate si è visto che se
DF(x) = f(x),
è anche
D[F(x) + C] = f(x),
in cui C è una costante arbitraria.
Ciò significa che esistono infinite funzioni, tutte differenti per una costante additiva, che hanno la stessa derivata.
Teorema - Se f(x) è una funzione continua in un intervallo chiuso (a, b), esiste sempre in (a, b) un'altra funzione F(x), di cui f(x) è la derivata.
Si omette la dimostrazione.
Inoltre, ricordando che tutte le funzioni che si considerano nella matematica elementare sono continue, tale teorema vale per tutte le funzioni.
2)-Integrale indefinito
Definizione 1 - Si chiama integrale indefinito di una funzione f(x) nell'intervallo chiuso (a, b), un'altra funzione F(x), tale che la sua derivata in (a, b) sia f(x).
Scrivere
significa
DF(x) = f(x).
Definizione 2 - Si chiama integrale indefinito di una funzione f(x) nell'intervallo chiuso (a, b), un'altra funzione F(x), tale che il suo differenziale in (a, b) sia f(x)dx.
Scrivere
significa
dF(x) = f(x)dx.
Per la definizione 1 l'integrale indefinito si presenta come l'operazione inversa della derivazione e per la definizione 2 si presenta come l'operazione inversa della differenziazione.
F(x) si chiama integrale indefinito o funzione primitiva di f(x); f(x) si chiama funzione integranda.
Il simbolo
è una deformazione della lettera s, iniziale della parola somma, per i motivi che saranno visti in seguito.
3)-Teoremi sulla funzione primitiva
1°)-Se F(x) è una funzione primitiva di f(x) anche F(x) + C è una funzione primitiva di f(x); oppure di funzioni primitive di una stessa funzione integranda ne esistono infinite e tutte differiscono per una costante.
Cioè se
è anche
Infatti:
2°)-Se F1(x) e F2(x) sono due funzioni primitive di una stessa funzione f(x), esse differiscono per una costante.
Cioè se
deve aversi:
Infatti, per la definizione 1, la (1) e la (2) esprimono che:
DF1(x) = f(x) e DF2(x) = f(x)
e, quindi, sottraendo membro a membro
DF1(x) - DF2(x) = 0,
ossia
D[F1(x) - F2(x)] = 0,
da cui, per quanto è noto sulla derivata di una costante, si ha
F1(x) - F2(x) = C.
4)-Osservazioni e considerazioni geometriche
1^)-Da quanto detto è opportuno osservare che, mentre l'operazione di derivazione conduce sempre ad un unico risultato, nel senso che la derivata di una funzione, quando esiste è unica, l'operazione di integrazione indefinita ha invece infinite soluzioni.
Pertanto, se prima si integra e poi si deriva una funzione, si ha la stessa funzione:
invece, se prima si deriva e poi si integra una funzione, si ottiene una funzione che, rispetto alla data, è aumentata di una costante arbitraria,
2^)-Geometricamente,
rappresenta tutte le infinite linee che si ottengono da quella di equazione y = F(x), con una sola traslazione dell'asse x e tutte le linee hanno tangenti parallele fra loro nei punti di uguale ascissa x0, in quanto il coefficiente angolare di tali rette è sempre

5)-Proprietà dell'integrale indefinito
Teorema - Se f1(x), f2(x) ... fn(x) sono funzioni, di ciascuna delle quali si conosce un integrale indefinito, ossia una funzione primitiva, rispettivamente
F1(x), F2(x) ... Fn(x),
si ha che l'integrale indefinito di una combinazione lineare delle f(x) è uguale alla combinazione lineare degl'integrali delle singole f(x), ossia alla combinazione lineare delle funzioni primitive F(x), sempre secondo le stesse costanti.
Infatti, dette α, β, ... ν, n costanti e considerata la combinazione lineare delle f(x):
αf1(x) + βf2(x) + ... + νfn(x),
per dimostrare che è
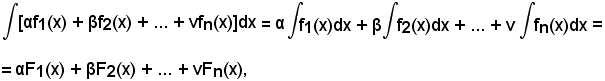
basta far vedere che è
D[αF1(x) + βF2(x) + ... + νFn(x)] = αf1(x) + βf2(x) + ... + νfn(x),
e ciò risulta evidente dai teoremi sulle derivate e dalla definizione di integrale indefinito, per le ipotesi
ossia
DF1(x) = f1(x), DF2(x) = f2(x), ..., DFn(x) = fn(x).
Dal teorema dimostrato seguono i seguenti casi particolari:
1°)-Se
si ha:
cioè
-l'integrale della somma di due funzioni è uguale alla somma degl'integrali delle singole funzioni.
2°)-Se
α ≠ 0 = e β = γ = ... = ν = 0, si ha:
cioè
-una costante moltiplicativa passa inalterata in integrazione come in derivazione.
6)-Integrali immediati
In base a quanto detto ed a quanto è stato visto per le derivate, è possibile indicare il seguente elenco di integrali immediati:
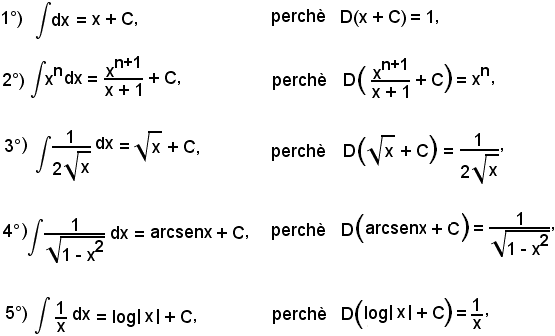

Nota bene
1)-Al tipo 2°) si riporta il seguente
dopo aver osservato che
df(x) = f'(x)dx
e che n è un qualsiasi numero positivo o negativo.
2)-Al tipo 5°) si riporta il seguente
dopo aver ancora osservato che
df(x) = f'(x)dx.
7)-Esempi
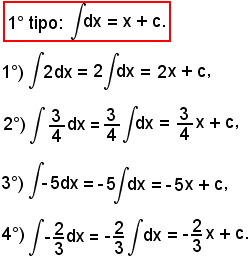
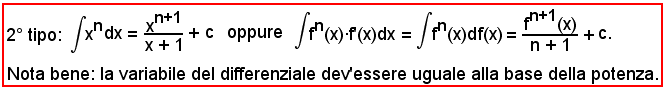
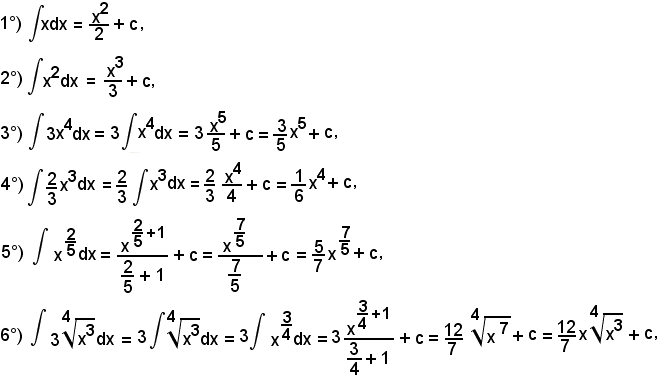
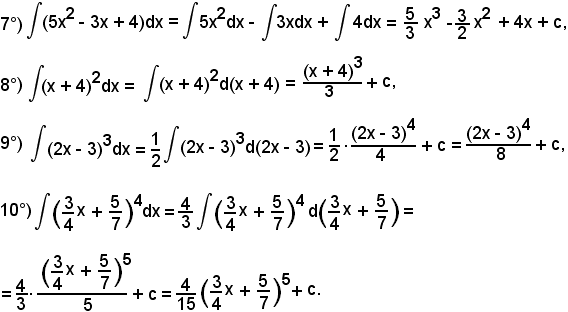
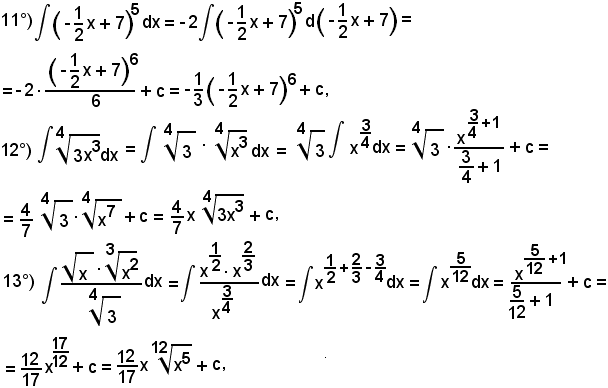
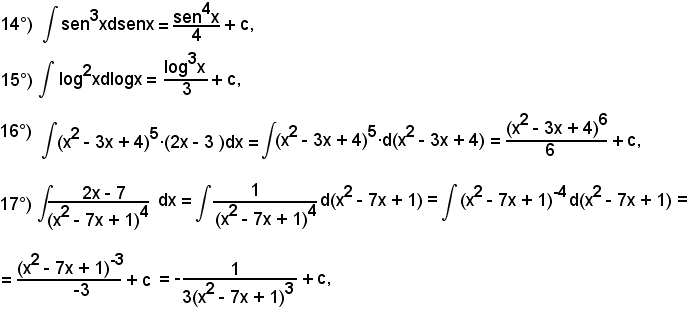
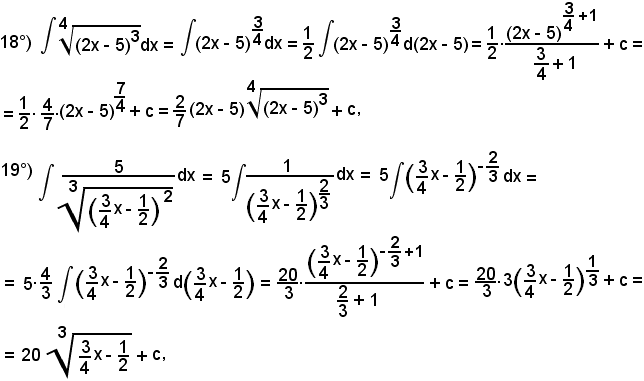

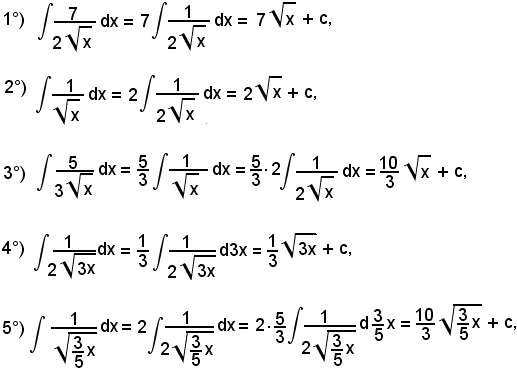
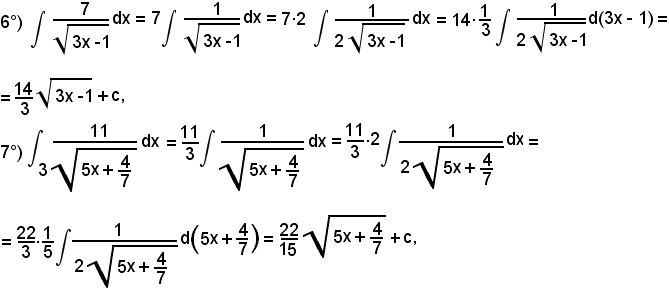
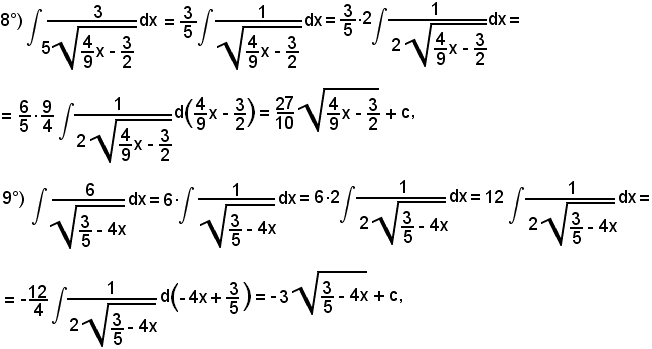
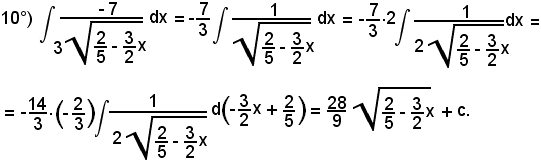

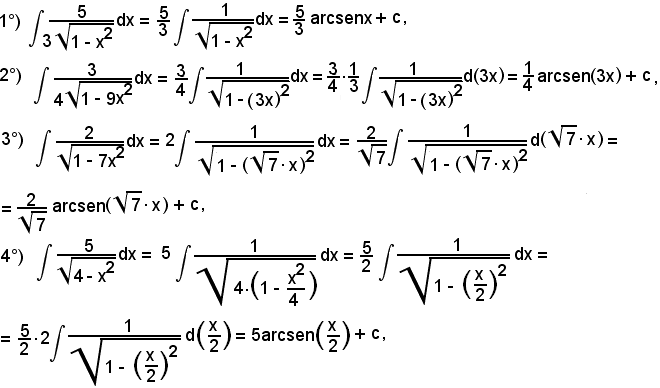
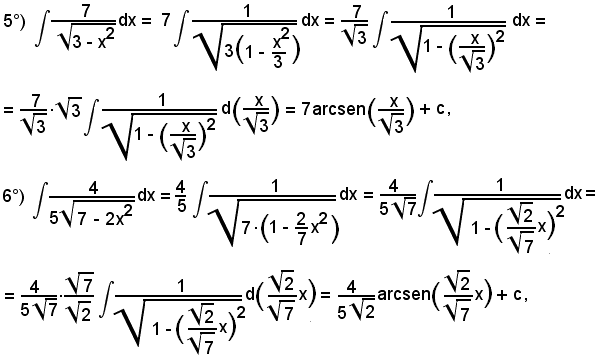
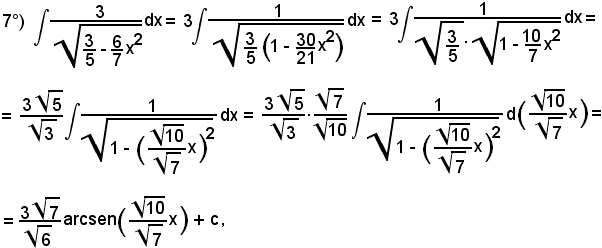
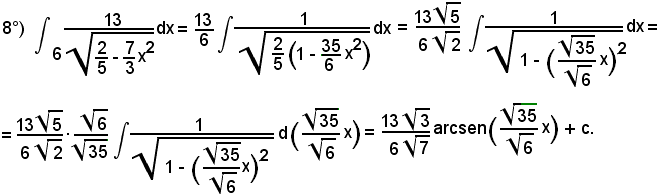

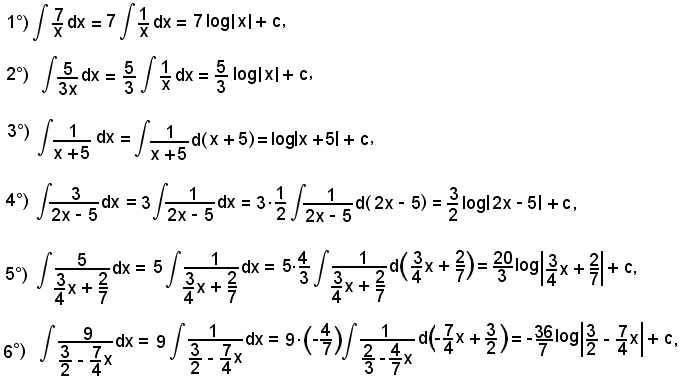
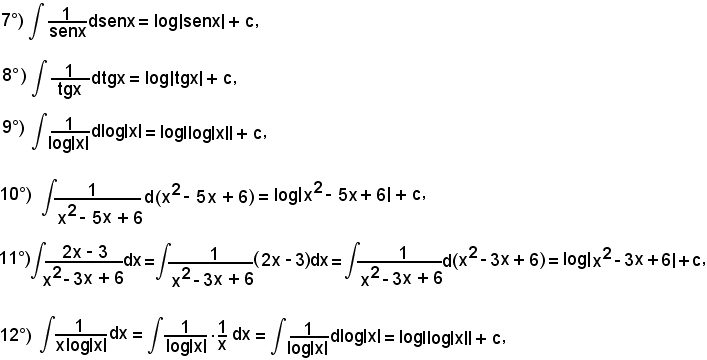
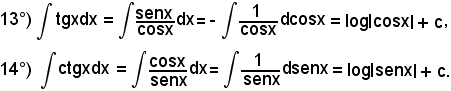

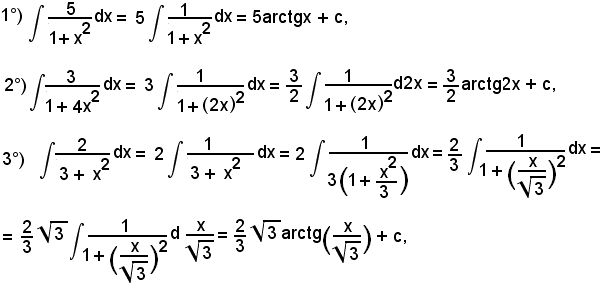
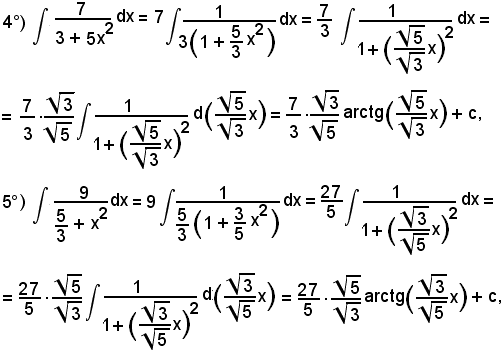
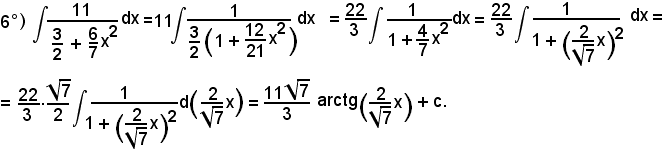

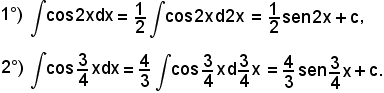

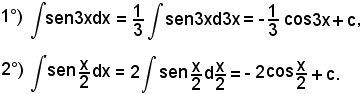
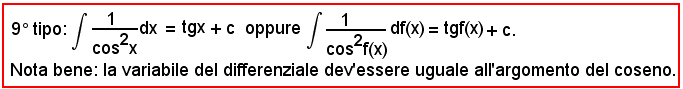
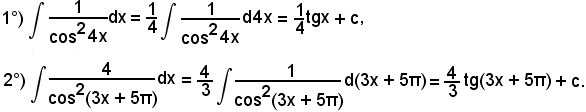

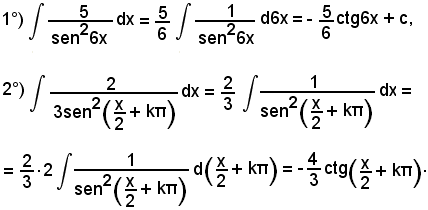

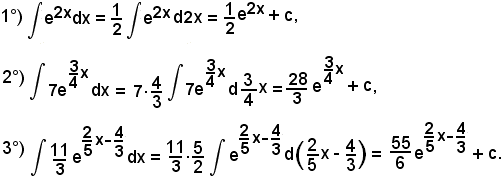
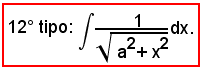
L'integrale proposto appartiene al 5° tipo; infatti, dividendo e moltiplicando la frazione integranda per
si ha:
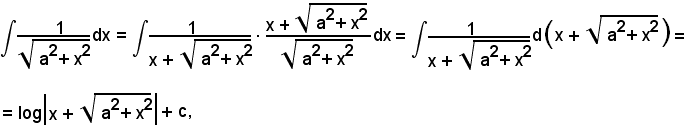
tenendo presente che