MIKY & GENNY
METODI DI INTEGRAZIONE ---> INDICE
1)-Considerazioni generali
Non vi sono dei metodi generali che permettono di calcolare l'integrale di una qualsiasi funzione però, come è stato illustrato negli esempi, si possono eseguire degli artifici per riportare l'integrale proposto ad uno dei tipi immediati, per poi trasformarlo in un altro più facilmente calcolabile. Gli artifici di calcolo, a cui si fa più comunemente ricorso, sono i seguenti:
a)-integrazione per parti,
b)-integrazione per decomposizione,
c)-integrazione per sostituzione.
2)-Integrazione per parti
Siano
due funzioni derivabili che, per brevità, saranno indicate in seguito soltanto con u e v.
Il differenziale del loro prodotto è:
d(u·v) = u·dv + v·du
e quindi
u·dv = d(u·v) - v·du.
Integrando ambo i membri di tale uguaglianza e applicando al 2° membro il teorema della somma, a meno di una costante additiva, si ha:
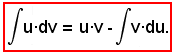
Questa è la formula dell'integrazione per parti.
Posto
u = fattore finito e dv = fattore differenziale,
essa esprime la seguente regola di integrazione:
meno l'integrale dell'integrale del fattore differenziale (v) per il differenziale del fattore finito (du).
L'integrazione per parti si applica soprattutto quando la funzione integranda è trascendente o è il prodotto di una funzione algebrica per una funzione trascendente.
3)-Esempi di integrazione per parti
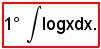
Posto
u = logx e dv = dx,
si ha:
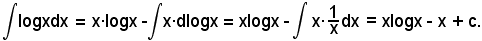

Posto
u = arctgx e dv = dx,
si ha:
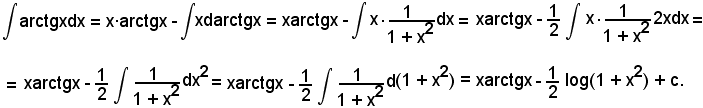

Posto
u = arcsenx e dv = dx,
si ha:
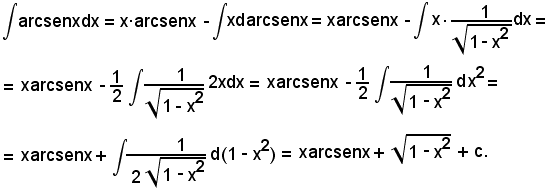
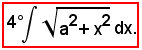
Posto
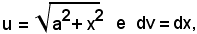
si ha:
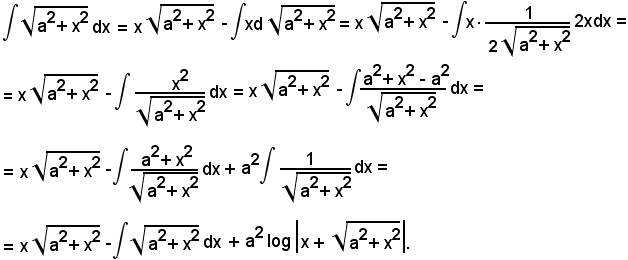
Si è quindi trovato:
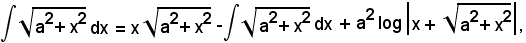
per cui
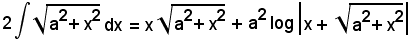
e, in definitiva,
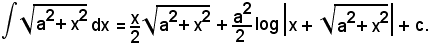
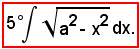
Posto
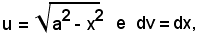
si ha:
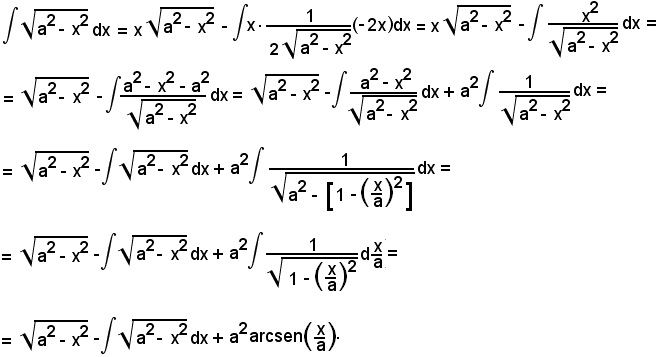
Si è quindi trovato:
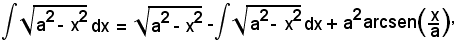
per cui
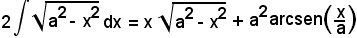
e, in definitiva,
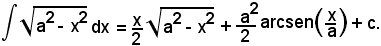
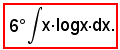
In teoria, si potrebbero effettuare le seguenti tre posizioni:
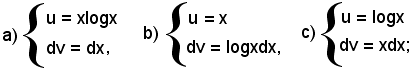
di esse, in generale, non si devono considerare convenienti quelle in cui l'integrale del fattore differenziale non è immediato o noto e quelle il cui integrale del suddetto fattore differenziale conduce ad un fattore di grado maggiore di quello che compare nella data funzione integranda.
Si è detto in generale, giacchè in taluni casi, e precisamente quelli in cui il fattore finito è un logaritmo o un arcotangente, che l'elevamento di grado suddetto viene ad essere compensato o eliminato allorchè si fa il differenziale del fattore finito.
In base alla posizione a), si ha:
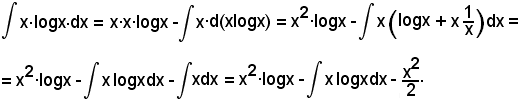
Si è quindi trovato:
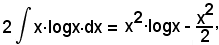
per cui
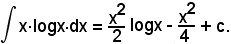
La posizione b) non conviene, per i motivi suddetti; si tralascia lo sviluppo con la posizione c).

Delle tre possibili posizioni
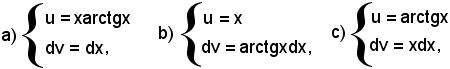
la b) è chiaramente non conveniente, in quanto
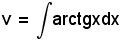
richiederebbe un'altra integrazione per parti. In base alla posizione a), si ha:
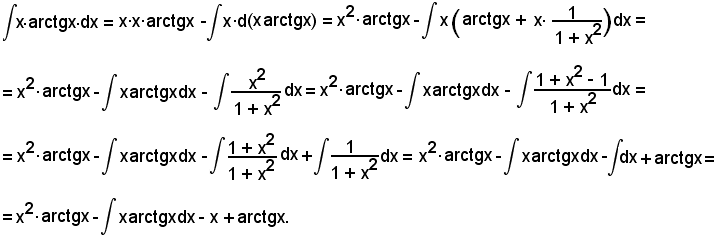
Si è quindi trovato:
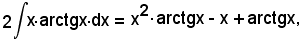
per cui
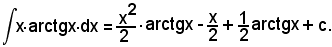
Si tralascia lo sviluppo con la posizione c).

Delle tre possibili posizioni
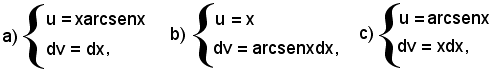
per quanto già detto nell'esempio precedente, la b) non è conveniente, In base alla posizione a), si ha:
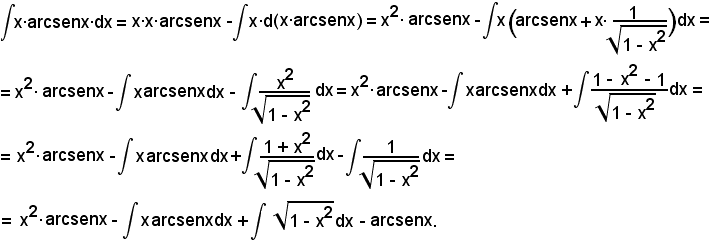
Si è quindi trovato:

e, dopo aver osservato che l'integrale figurante nel 2° membro è quello del 5° esempio per a = 1, sostituendo la funzione primitiva trovata in precedenza, si ha
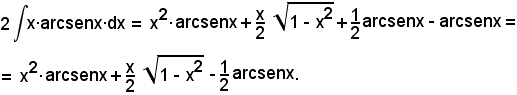
In definitiva:
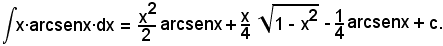
E' bene notare che, nell'integrazione per parti dell'integrale dato, è stato necessario effettuare ancora l'integrazione per parti di un altro integrale. La posizione che porta a ciò in generale è sconveniente nel senso che, applicandola, si perviene ad un altro integrale non immediato, o per lo meno non noto per precedente calcolo, pertanto si tralascia. In base alla posizione c), si ha:
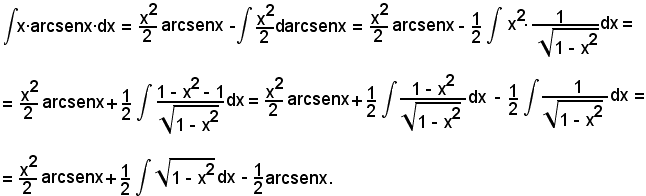
Come si può osservare, anche con la posizione c) si è pervenuti allo stesso risultato di prima, e ciò spiega perchè nella nota precedente si è detto in generale di tralasciare la posizione considerata.
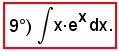
Delle tre possibili posizioni
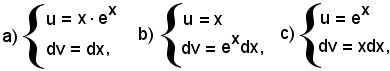
la a) e la c) non sono convenienti in quanto fanno pervenire ad un altro integrale più complesso di quello dato. In base alla posizione b), si ha:
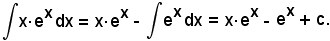
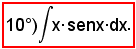
Delle tre possibili posizioni
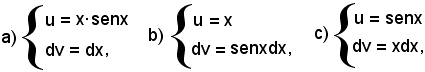
la a) e la c) non sono convenienti. In base alla posizione b), si ha:
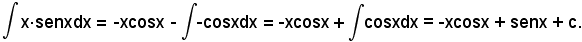
E' analogo al precedente, quindi posto
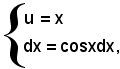
si ha:
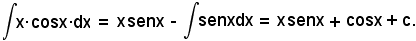
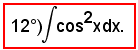
Posto
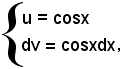
si ha:
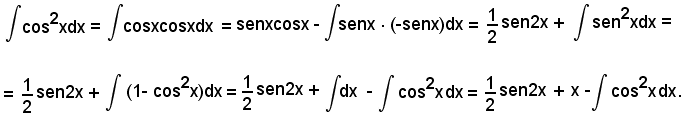
Quindi, si è ottenuto:

da cui
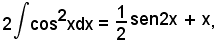
o anche
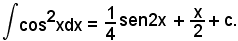
Posto
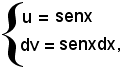
si ha:
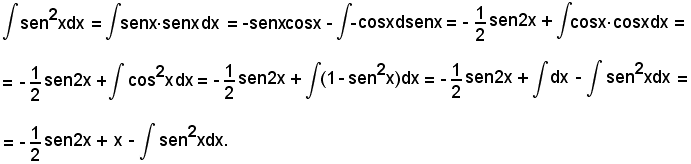
Quindi, si è ottenuto:

da cui
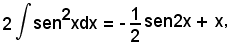
o anche
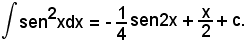
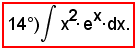
Posto
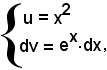
si ha:
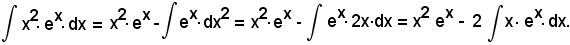
Si osserva ora che l'ultimo integrale ottenuto è il 9°), e quindi in tale esempio, come spesso accade, è necessaria un'altra, o anche più, integrazione per parti per calcolare quello proposto.
4)-Integrazione per decomposizione
Consiste nel decomporre la funzione integranda in una somma algebrica di altre funzioni e, quindi, nel trasformare l'integrale proposto in una somma di integrali di altre funzioni, le cui primitive siano note, o per lo meno più facilmente calcolabili. Inoltre, tale metodo trova un'importante applicazione nella ricerca degl'integrali delle funzioni razionali.
5)-Esempi di integrazione per decomposizione

Applicando la formula di bisezione, si ha:
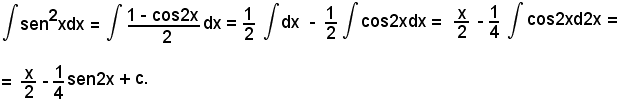
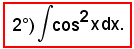
Applicando la formula di bisezione, si ha:
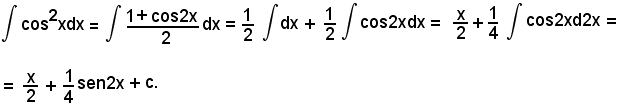
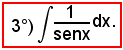
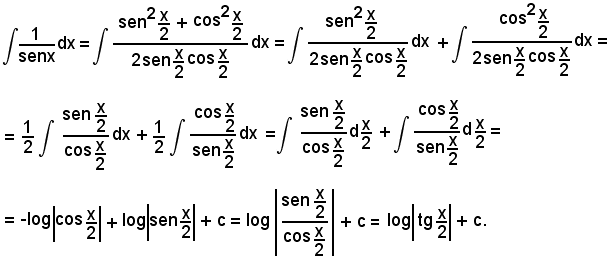
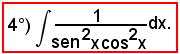
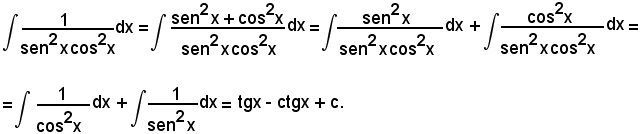
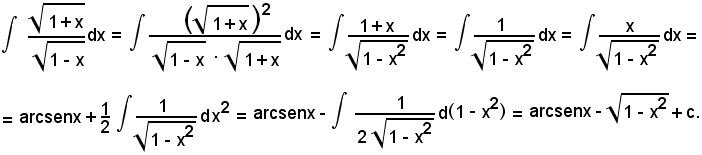
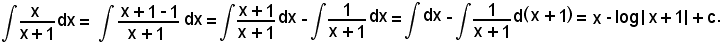
6)-Integrazione delle funzioni razionali
Si considerino due polinomi nella stessa variabile x, primi fra loro, cioè senza fattori comuni:
(1) N(x) = a0xm + a1xm-1 + a2xm-2 + ... + am-1x + am,
Se
x1, x2, ..., xn
sono le n radici reali e distinte della (7) o della (7'), si sa, dall'algebra elementare, che vale la decomposizione
(8) D(x) = (x - x1)(x - x2)(x - 3) ... (x - xn).
Si può dimostrare inoltre, ma si omette la dimostrazione, che vale la seguente scomposizione in somma:
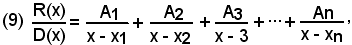
ove le n frazioni del 2° membro hanno per denominatore, ciascuna e ordinatamente, uno dei fattori di 1° grado della (8), e per numeratore le n costanti
A1, A2, A3..., An
che si possono determinare in vari modi, tra i quali il seguente.
Liberando la (9) dai denominatori, si ha:
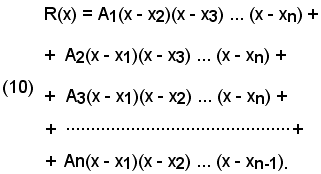
Ponendo di seguito in ambo i membri della (10)
x = x1, x = x2, x = x3, ... x = xn,
si ricavano rispettivamente i valori di
A1, A2, A3..., An.
Considerando ora l'integrale di ambo i membri della (9), si ha:
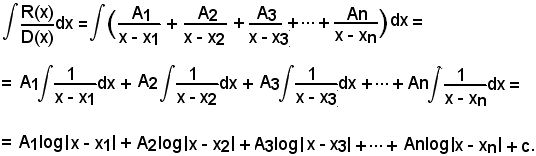
Quindi, dopo aver seguito il procedimento suddetto, è stato effettuato il calcolo dell'integrale del tipo (6).
Esempi
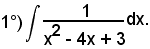
Essendo
x2 - 4x + 3 = (x - 1)(x - 3),
vale la seguente scomposizione in somma:
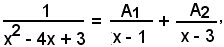
da cui, liberando dai denominatori, si ha:
1 = A1(x - 3) + A2(x - 1);
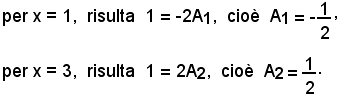
Pertanto:
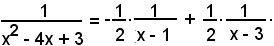
Considerando l'integrale di ambo i membri, si ha:
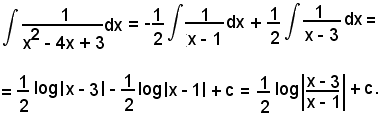
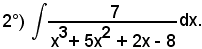
Essendo
x3+ 5x2 + 2x - 8 = (x - 1)(x + 2)(x + 4),
vale la seguente scomposizione in somma:
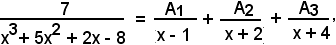
da cui, liberando dai denominatori, si ha:
7 = A1(x + 2)(x + 4) + A2(x - 1)(x + 4) + A3(x - 1)(x + 2);

Pertanto:
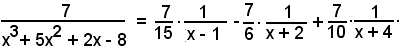
Considerando l'integrale di ambo i membri, si ha:
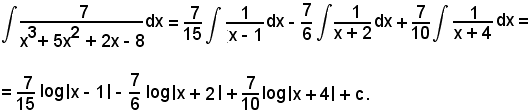
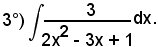
Essendo
2x2 - 3x + 1 = (2x - 1)(x - 1),
vale la seguente scomposizione in somma:
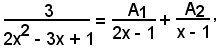
da cui, liberando dai denominatori, si ha:
3 = A1(x - 1) + A2(2x - 1);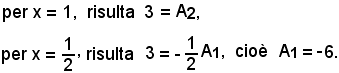
Pertanto:
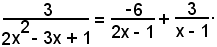
Considerando l'integrale di ambo i membri, si ha:
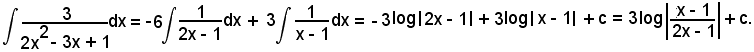
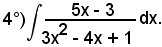
Essendo
3x2 - 4x + 1 = (3x - 1)(x - 1),
vale la seguente scomposizione in somma:
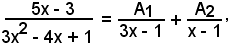
da cui, liberando dai denominatori, si ha
5x - 3 = A1(x - 1 ) + A2(3x - 1);
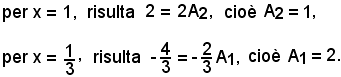
Pertanto:
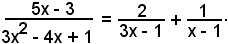
Considerando l'integrale di ambo i membri, si ha:
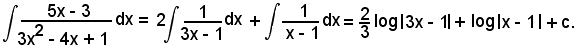
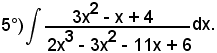
Essendo
2x3 - 3x2 - 11x + 6 = (2x - 1)(x + 2)(x - 3),
vale la seguente scomposizione in somma:
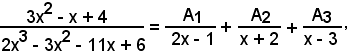
da cui, liberando dai denominatori, si ha:
3x2 - x + 4 = A1(x + 2)(x - 3) + A2(2x - 1)(x - 3) + A3(2x - 1)(x + 2);

Pertanto:
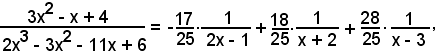
Considerando l'integrale di ambo i membri, si ha:
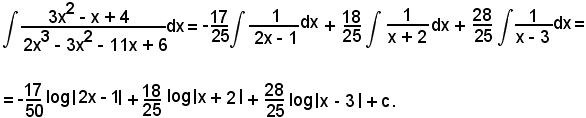
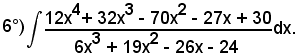
Effettuando la divisione, la funzione integranda diventa
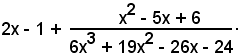
Quindi, si ha:
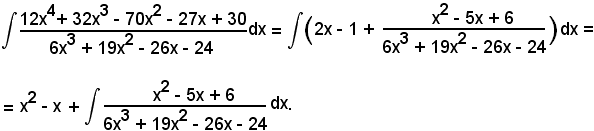
Per calcolare quest'ultimo integrale, si procede come negli esempi precedenti.
Essendo
6x3 + 19x2 - 26x - 24 = (3x + 2)(2x - 3)(x + 4),
vale la seguente scomposizione in somma
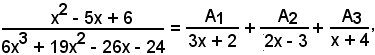
da cui, liberando dai denominatori, si ha:
x2 - 5x + 6 = A1(2x - 3)(x + 4) + A2(3x + 2)(x + 4) + A3(3x + 2)(2x - 3);
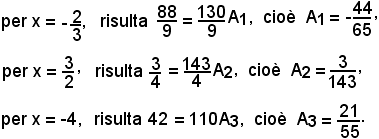
Pertanto:
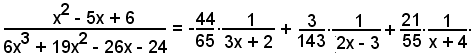
Considerando l'integrale di ambo i membri, si ha:
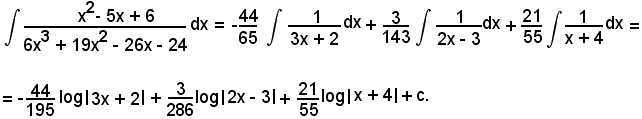
Pertanto, l'integrale proposto diventa:
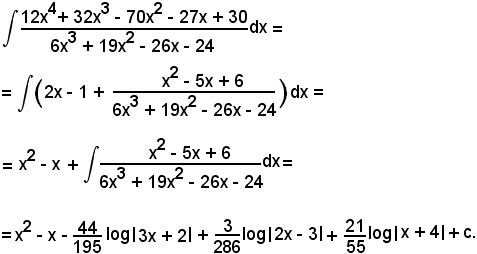
b)-l'equazione D(x) = 0 ha radici reali multiple
Considerata l'equazione di grado n:
D(x) = b0xn + b1n-1 + b2xn-2 + ... + bn-1x + bn = 0,
le sue radici siano, ad esempio, quattro e cioè
x1 di molteplicità α,
x2 di molteplicità β,
x3 di molteplicità γ,
x4 di molteplicità δ,
in cui, come è noto dall'algebra, dev'essere α + β + γ + δ = n, grado dell'equazione D(x) = 0.Si può dimostrare inoltre, ma si omette la dimostrazione, che vale la seguente scomposizione
in somma:
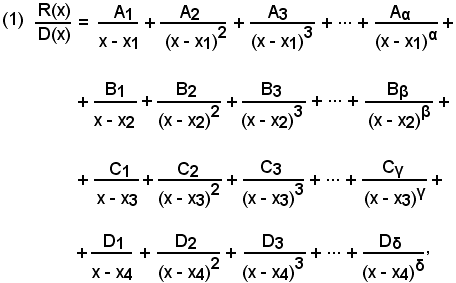
in cui

sono n costanti da determinare come segue:
si libera la (1) dai denominatori e, dopo aver ugualmente ordinato i due membri rispetto all'incognita, per il principio di identità dei polinomi, deve aversi quella dei coefficienti delle incognite di pari esponente dei due membri. Tali uguaglianze costituiranno un sistema nelle incognite (2) che, risolto, darà i valori delle costanti.
Esempi
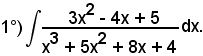
Poichè l'equazione
D(x) = x3 + 5x2 + 8x + 4 = 0
ammette le radici x1 = -1 e x2 = x3 = -2,
per cui è
x3 + 5x2 + 8x + 4 = (x + 1)(x + 2)2,
e vale la seguente scomposizione in somma:
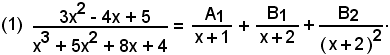
Liberando dai denominatori, si ha:
3x2 - 4x + 5 = A1(x + 2)2 + B1(x + 1)(x + 2) + B2(x + 1) = A1x2 + 4A1x + 4A1 + B1x2 + 3B1x + 2B1 + B2x + B2 = (A1 + B1)x2 + (4A1 + 3B1+ B2)x + (4A1 + B1+ B2)
e quindi, per il principio di identità dei polinomi, dev'essere
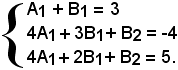
Le soluzioni di tale sistema sono:
A1 = 12, B1= -9, B2 = -25,
pertanto la (1) diventa
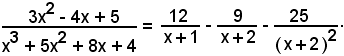
Quindi:
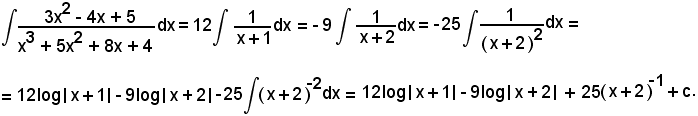
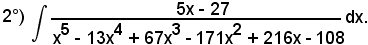
L'equazione
D(x) = x5 - 13x4 + 67x3 - 171x2 + 216x - 108 = 0
ha per radici
x1 = x2 = 2 e x3 = x4 = x5 = 3,
per cui è
x5 - 13x4 + 67x3 - 171x2 + 216x - 108 = (x - 2)2(x - 3)3
e vale la seguente scomposizione in somma:
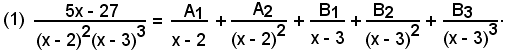
Liberando dai denominatori, si ha:
5x - 27 = A1(x - 2)(x - 3)3 + A2(x - 3)3 + B1(x - 2)2(x - 3)3 + B2(x - 2)2(x - 3) + B3(x - 2)2.
Sviluppando, ordinando e raccogliendo i fattori comuni nel 2° membro, si perviene all'uguaglianza
5x - 27 = (A1 + B1)x4 + (-11A1 + A2 - 10B1 + B2)x3 + (45A1 - 9A2 + 37B1 - 7B2 + B3)x2 +
+ (-81A1 + 27A2 - 60B1 + 16B2 - 4B3)x + (54A1 - 27A2 + 36B1 - 12B2 + 4B3),
per il verificarsi della quale, deve aversi

Le soluzioni di tale sistema sono:
A1 = 46, A2 = 17, B1 = -46, B2 = 29, B3 = -12,
pertanto la (1) diventa
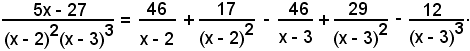
Quindi:
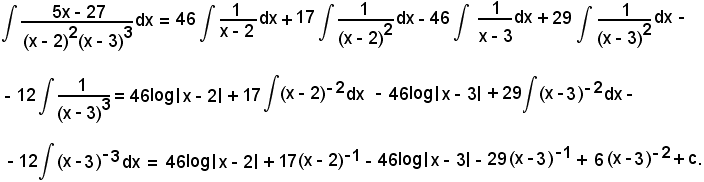
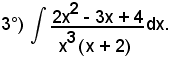
Poichè l'equazione
D(x) = x3(x - 2) = 0
ammette le radici
x1 = x2 = x3 = 0 e x4 = -2,
vale la seguente scomposizione in somma:
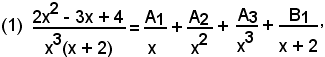
da cui
2x2 - 3x + 4 = A1x2(x + 2) + A2x(x + 2) + A3(x + 2) + B1x3.
Sviluppando, ordinando e raccogliendo i fattori comuni nel 2° membro, si perviene alla seguente uguaglianza:
2x2 - 3x + 4 = (A1 + B1)x3 + (2A1 + A2)x2 + (2A2 +A3)x + 2A3,
per il verificarsi della quale, deve aversi
Le soluzioni di tale sistema sono:
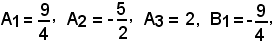
pertanto la (1) diventa
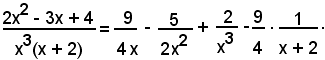
Quindi:
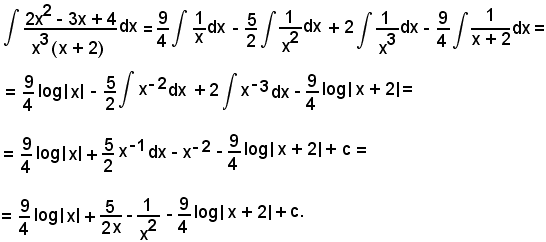
c)-l'equazione D(x) = 0 ha radici complesse
Ci si limita a considerare i seguenti due tipi:
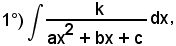
in cui k è una costante e l'equazione
D(x) = ax2 + bx + c = 0,
avendo il discriminante negativo, non ha radici reali.
E' noto, dall'algebra elementare, che può aversi la seguente trasformazione:
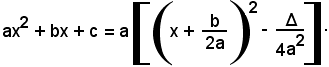
Pertanto risulta
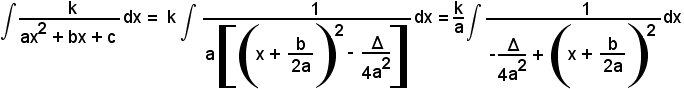
e l'integrale a cui si è pervenuti è del tipo 6°), cioè
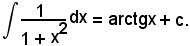
Esempi
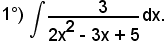
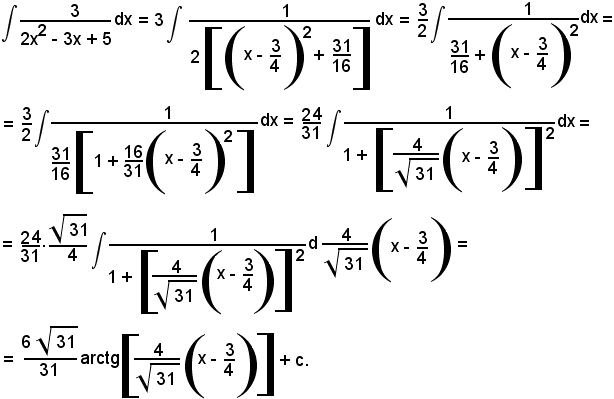
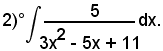
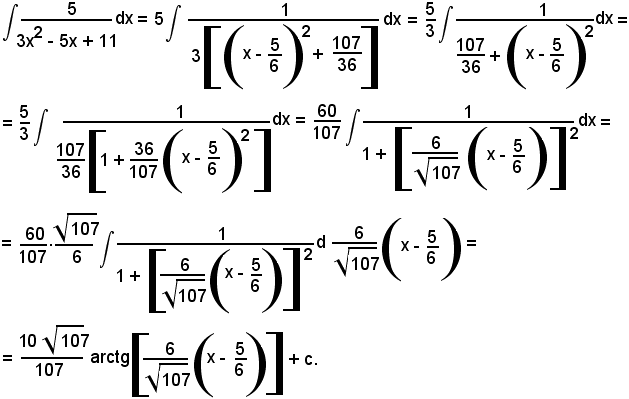
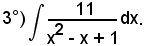
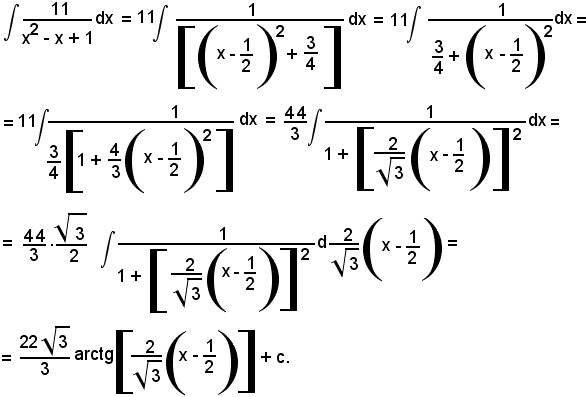
Osservando che si può scrivere
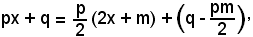
l'integrale proposto diventa
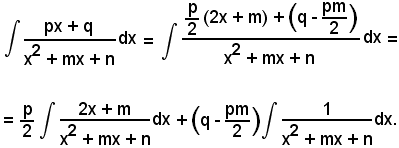
Esempi
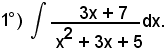
Poichè si può scrivere
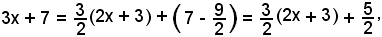
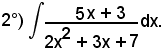
Poichè si può scrivere
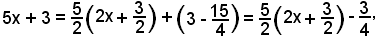
si ha:
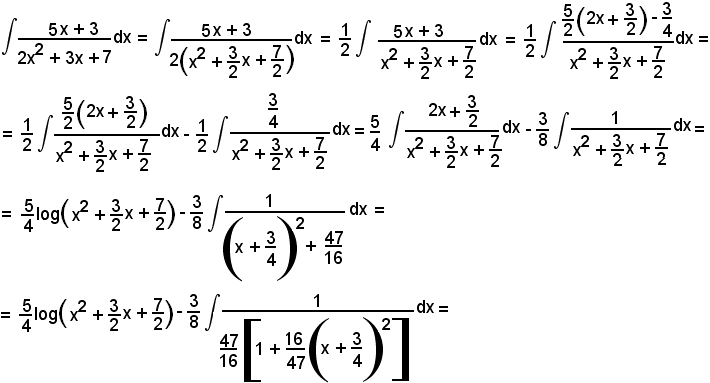
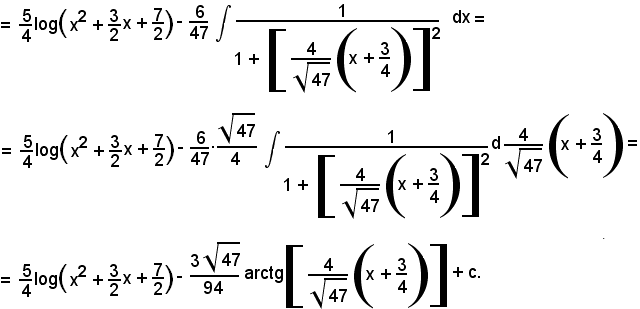
7)-Integrazione per sostituzione
Un altro artificio molto utile per trasformare la funzione integranda in un'altra che appartenga a tipi di cui si conosca la primitiva, consiste nel cambiare la variabile con un'altra legata a quella da un'opportuna relazione.
Si voglia calcolare
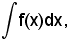
in cui f(x) sia una funzione continua in un intervallo (a, b), e si supponga di conoscere una funzione F(x) primitiva della f(x), cioè tale che si possa scrivere
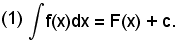
Nella F(x) si ponga x = g(t), in cui g(t) sia una funzione nella nuova variabile t, derivabile e continua in un certo intervallo (a', b'), in modo che quando la t varia con continuità in (a', b'), la x varia con continuità in (a, b). In tal modo la F(x) diventa una funzione composta della t tramite x, cioè F(x) = F[g(t)], ed è noto che
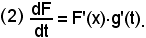
Dall'ipotesi F'(x) = f(x), si ha che f(x) = F[g(t)] è una funzione primitiva di f(x)·g'(t), e quindi l'integrale (1) diventa
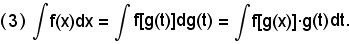
Quest'ultimo integrale, talvolta, risulta appartenente ad uno dei tipi già noti; una volta calcolato, e ammesso che la funzione x = g(x), basterà sostituire a t questa φ(x), per avere la funzione primitiva di quella integranda inizialmente proposta.
Nota bene
1)-Quando furono date le definizioni di integrale indefinito, furono fatte alcune considerazioni sulla precisione e sulla comodità delle stesse funzioni. In entrambi i casi, però, per indicare l'integrale indefinito, si scrisse;
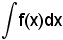
e non solo
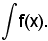
Si vuole ora mostrare che il fattore dx, se è comodo per la risoluzione di alcuni tipi di integrali, è addirittura necessario nell'integrazione per sostituzione.
Esempi
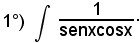
Si ha:
Si ha:
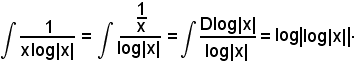
In ciascuno dei due esempi visti il fattore dx non è risultato necessario, in quanto senza di esso si è pervenuti ugualmente alla determinazione di una primitiva della funzione integranda proposta. La necessarietà dell'uso del fattore dx è proprio data dalla formula (3).
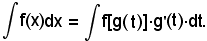
Infatti la sostituzione x = g(t), mentre trasforma la f(x) in f[g(t)], trasforma anche dx in g'(t)·dt e, pertanto, poichè g'(t)·dt è effettivamente un prodotto, anche f(x)·dx è tale, ossia dx è proprio un fattore e non un simbolo.
2)-Non vi sono regole per stabilire la sostituzione più conveniente, in quanto essa dipende dalla pratica di calcolo che si possiede.
9)-Esempi di integrazione per sostituzione
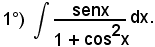
Posto
cosx = t,
per cui
dcosx = dt,
cioè
-senxdx = dt,
sostituendo si ha:
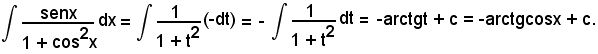
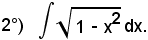
Posto
x = sent,
ossia
t = arcsenx,
si ha
dx = dsent = cost·dt
e sostituendo si ha:
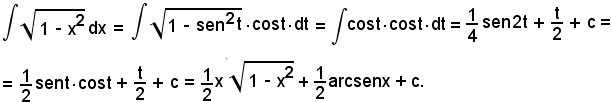
L'integrale precedente è un caso particolare del seguente.
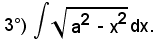
Posto
x = a·sent,
da cui
si ha:
dx = a·cost·dt
e sostituendo, risulta
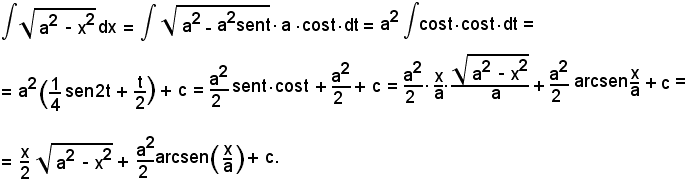
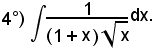
Posto
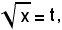
si ha:
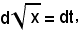
cioè
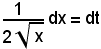
e sostituendo
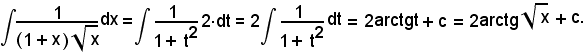
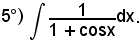
Posto
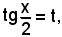
per cui
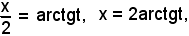
si ha:
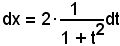
e, ricordando la formula parametrica
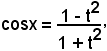
sostituendo si ha
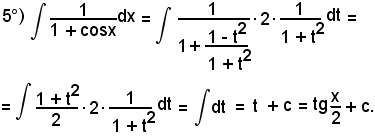
Posto
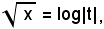
per cui
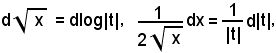
cioè
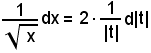
e, sostituendo, si ha
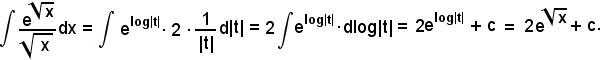
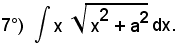
Posto
x2 + a2 = t,
per cui
d(x2 + a2) = dt,
cioè
2xdx = dt,
sostituendo, si ha:
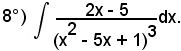
Posto
x2 - 5x + 1 = t,
per cui
d(x2 - 5x + 1) = dt,
cioè
(2x - 5)dx = dt,
sostituendo, si ha:
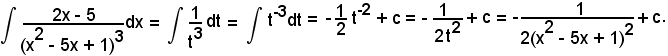
10)-Integrazione di alcune funzioni irrazionali
Il metodo di integrazione per sostituzione viene applicato per il calcolo di alcuni tipi di integrali di funzioni irrazionali. Infatti, per opportune sostituzioni, ci si riporta ad integrali di funzioni razionali della nuova variabile. Ci si limita a considerare i seguenti tipi:
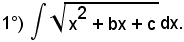
Con la sostituzione
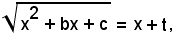
quadrando ambo i membri, si ha:
x2 + bx + c = x2 + 2xt + t2,
ossia
bx + c = 2xt + t2,
da cui
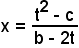 e
e
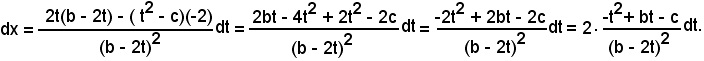
e
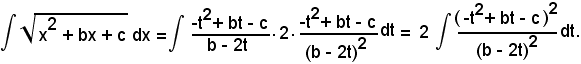
In tal modo la funzione integranda è diventata razionale.
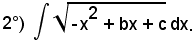
Affinchè la funzione
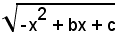
abbia valori reali, dev'essere
-x2 + bx + c ≥ 0.
Se α e β sono le radici dell'equazione associata, nell'intervallo (α, β), risulta -x2 + bx + c ≥ 0 ed è anche
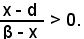
Si consideri allora la posizione
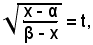
dalla quale, dopo aver quadrato ambo i membri, si ha:
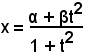
e
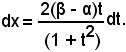
Si può allora scrivere:
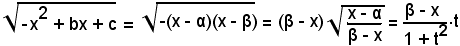
e quindi si ha
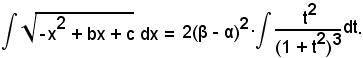
In tal modo la funzione integranda è diventata razionale.
Non vi sono dei metodi generali che permettono di calcolare l'integrale di una qualsiasi funzione però, come è stato illustrato negli esempi, si possono eseguire degli artifici per riportare l'integrale proposto ad uno dei tipi immediati, per poi trasformarlo in un altro più facilmente calcolabile. Gli artifici di calcolo, a cui si fa più comunemente ricorso, sono i seguenti:
a)-integrazione per parti,
b)-integrazione per decomposizione,
c)-integrazione per sostituzione.
2)-Integrazione per parti
Siano
u = u(x) e v = v(x)
due funzioni derivabili che, per brevità, saranno indicate in seguito soltanto con u e v.
Il differenziale del loro prodotto è:
d(u·v) = u·dv + v·du
e quindi
u·dv = d(u·v) - v·du.
Integrando ambo i membri di tale uguaglianza e applicando al 2° membro il teorema della somma, a meno di una costante additiva, si ha:
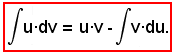
Questa è la formula dell'integrazione per parti.
Posto
u = fattore finito e dv = fattore differenziale,
essa esprime la seguente regola di integrazione:
-l'integrale
di un fattore finito(u) per un fattore differenziale (dv) è
uguale al fattore finito (u) per il fattore differenziale
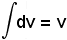
meno l'integrale dell'integrale del fattore differenziale (v) per il differenziale del fattore finito (du).
L'integrazione per parti si applica soprattutto quando la funzione integranda è trascendente o è il prodotto di una funzione algebrica per una funzione trascendente.
3)-Esempi di integrazione per parti
Posto
u = logx e dv = dx,
si ha:
Posto
u = arctgx e dv = dx,
si ha:
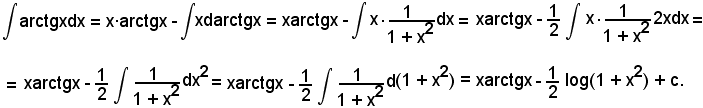

Posto
u = arcsenx e dv = dx,
si ha:
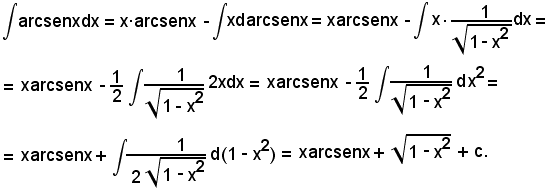
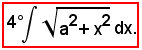
Posto
si ha:
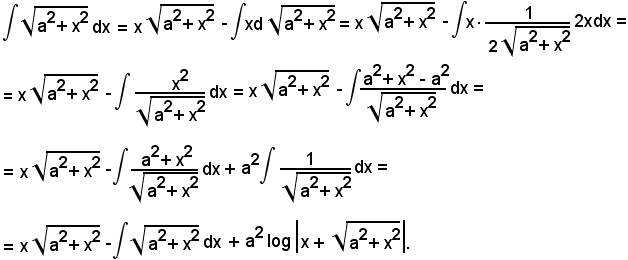
Si è quindi trovato:
per cui
e, in definitiva,
Posto
si ha:
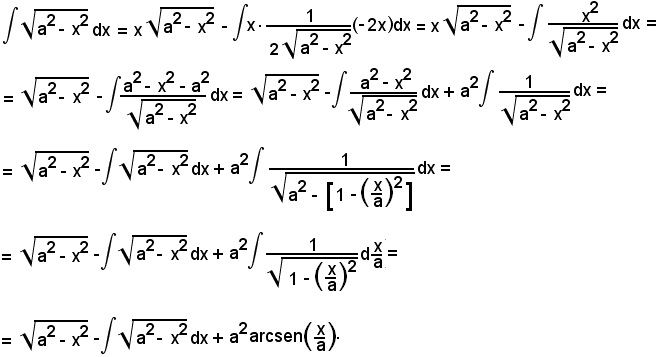
Si è quindi trovato:
per cui
e, in definitiva,
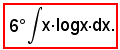
In teoria, si potrebbero effettuare le seguenti tre posizioni:
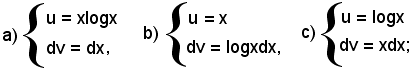
di esse, in generale, non si devono considerare convenienti quelle in cui l'integrale del fattore differenziale non è immediato o noto e quelle il cui integrale del suddetto fattore differenziale conduce ad un fattore di grado maggiore di quello che compare nella data funzione integranda.
Si è detto in generale, giacchè in taluni casi, e precisamente quelli in cui il fattore finito è un logaritmo o un arcotangente, che l'elevamento di grado suddetto viene ad essere compensato o eliminato allorchè si fa il differenziale del fattore finito.
In base alla posizione a), si ha:
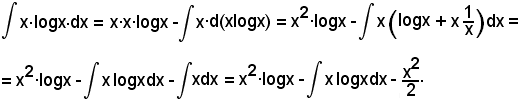
Si è quindi trovato:
per cui
La posizione b) non conviene, per i motivi suddetti; si tralascia lo sviluppo con la posizione c).

Delle tre possibili posizioni
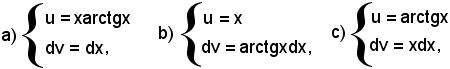
la b) è chiaramente non conveniente, in quanto
richiederebbe un'altra integrazione per parti. In base alla posizione a), si ha:
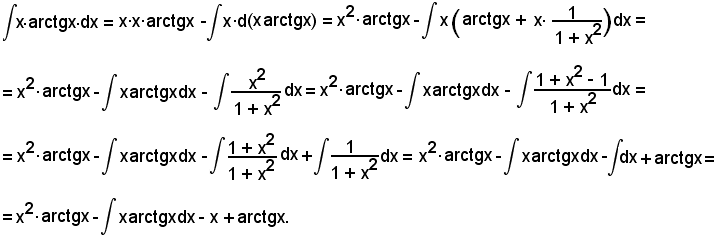
Si è quindi trovato:
per cui
Si tralascia lo sviluppo con la posizione c).

Delle tre possibili posizioni
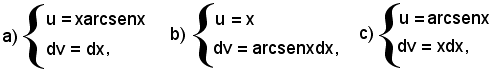
per quanto già detto nell'esempio precedente, la b) non è conveniente, In base alla posizione a), si ha:
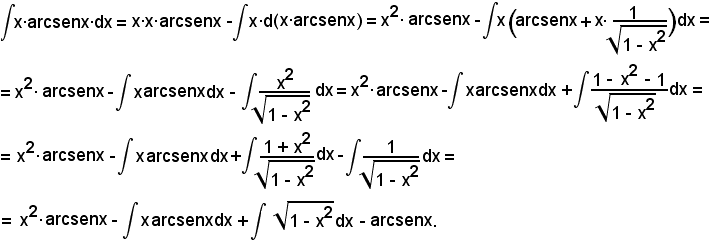
Si è quindi trovato:
e, dopo aver osservato che l'integrale figurante nel 2° membro è quello del 5° esempio per a = 1, sostituendo la funzione primitiva trovata in precedenza, si ha
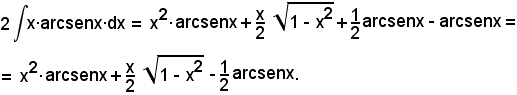
In definitiva:
E' bene notare che, nell'integrazione per parti dell'integrale dato, è stato necessario effettuare ancora l'integrazione per parti di un altro integrale. La posizione che porta a ciò in generale è sconveniente nel senso che, applicandola, si perviene ad un altro integrale non immediato, o per lo meno non noto per precedente calcolo, pertanto si tralascia. In base alla posizione c), si ha:
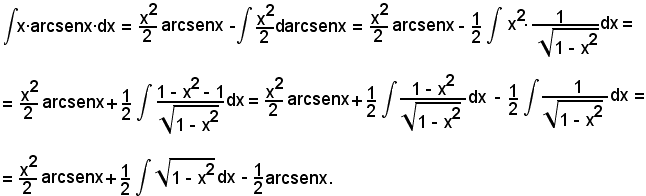
Come si può osservare, anche con la posizione c) si è pervenuti allo stesso risultato di prima, e ciò spiega perchè nella nota precedente si è detto in generale di tralasciare la posizione considerata.
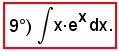
Delle tre possibili posizioni
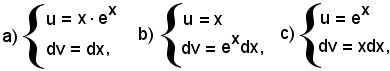
la a) e la c) non sono convenienti in quanto fanno pervenire ad un altro integrale più complesso di quello dato. In base alla posizione b), si ha:
Delle tre possibili posizioni
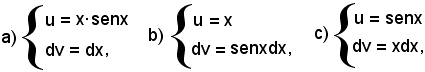
la a) e la c) non sono convenienti. In base alla posizione b), si ha:
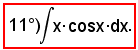
E' analogo al precedente, quindi posto
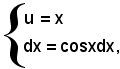
si ha:
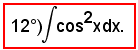
Posto
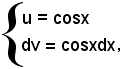
si ha:
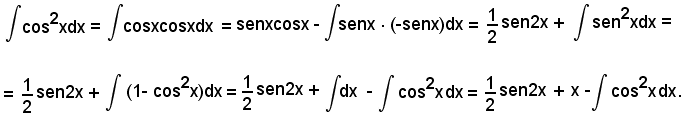
Quindi, si è ottenuto:
da cui
o anche

Posto
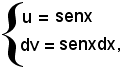
si ha:
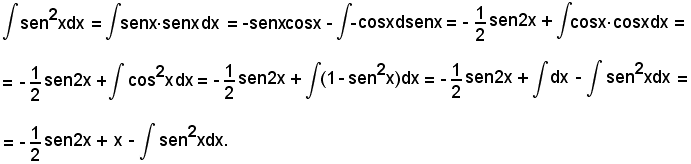
Quindi, si è ottenuto:
da cui
o anche
Posto
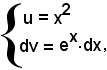
si ha:
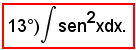
Si osserva ora che l'ultimo integrale ottenuto è il 9°), e quindi in tale esempio, come spesso accade, è necessaria un'altra, o anche più, integrazione per parti per calcolare quello proposto.
4)-Integrazione per decomposizione
Consiste nel decomporre la funzione integranda in una somma algebrica di altre funzioni e, quindi, nel trasformare l'integrale proposto in una somma di integrali di altre funzioni, le cui primitive siano note, o per lo meno più facilmente calcolabili. Inoltre, tale metodo trova un'importante applicazione nella ricerca degl'integrali delle funzioni razionali.
5)-Esempi di integrazione per decomposizione
Applicando la formula di bisezione, si ha:
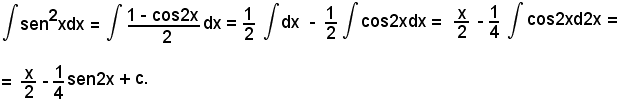
Applicando la formula di bisezione, si ha:
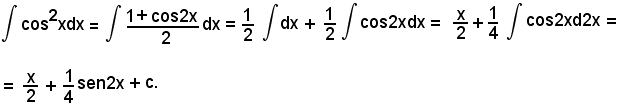
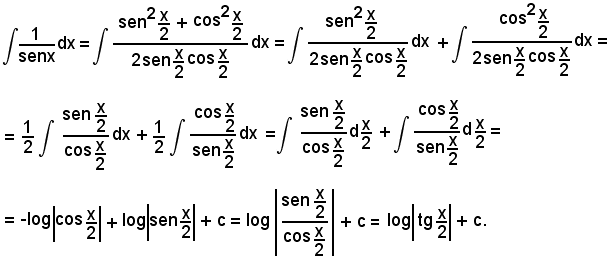
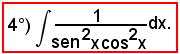
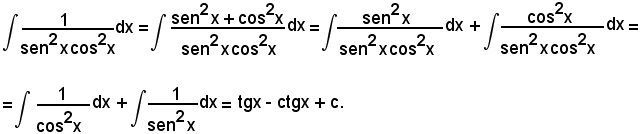
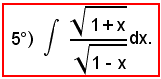
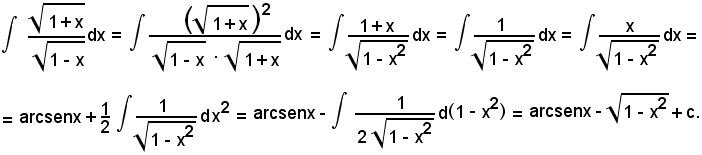
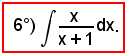
6)-Integrazione delle funzioni razionali
Si considerino due polinomi nella stessa variabile x, primi fra loro, cioè senza fattori comuni:
(1) N(x) = a0xm + a1xm-1 + a2xm-2 + ... + am-1x + am,
(2) D(x) = b0xn + b1 n-1 + b2xn-2 + ... + bn-1x + bn.
Una funzione razionale fratta è data dal loro rapporto:
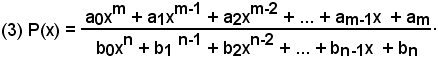
Se m > n, la frazione P(x) si dice impropria, mentre se m < n si dice propria. Quando la frazione è impropria, ed anche quando m = n, si può effettuare la divisione tra N(x) e D(x) e, indicando con Q(x) il polinomio quoziente, di grado m - n, e con R(x) l'eventuale polinomio resto, di grado minore di n, si ha:
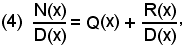
cioè la funzione
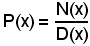
risulta scomposta nella somma di una funzione intera Q(x) e di una funzione razionale fratta propria
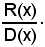
Considerando l'integrale indefinito di ambo i membri della (4), si ha:
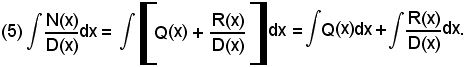
Poichè è noto il calcolo di
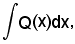
resta da vedere come effettuare quello di
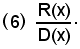
A tal punto, è bene evidenziare che, per l'integrazione delle funzioni razionali fratte, si ridurrà sempre ad un integrale del tipo (6), ovvero ad una funzione integranda frazione propria.
Si distinguono ora i seguenti casi:
a)-l'equazione D(x) = 0 ha radici tutte reali e distinte;
b)-l'equazione D(x) = 0 ha radici tutte reali ma non tutte distinte;
c)-l'equazione D(x) = 0 non ha radici reali.
a)-l'equazione D(x) = 0 ha radici tutte reali e distinte
Considerata l'equazione di grado n,
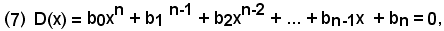
dividendo ambo i membri per b0, diverso da zero, la si trasformi nell'altra equivalente, avente il 1° coefficiente uguale ad uno:
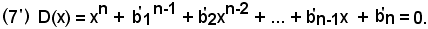
Una funzione razionale fratta è data dal loro rapporto:
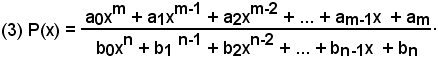
Se m > n, la frazione P(x) si dice impropria, mentre se m < n si dice propria. Quando la frazione è impropria, ed anche quando m = n, si può effettuare la divisione tra N(x) e D(x) e, indicando con Q(x) il polinomio quoziente, di grado m - n, e con R(x) l'eventuale polinomio resto, di grado minore di n, si ha:
cioè la funzione
risulta scomposta nella somma di una funzione intera Q(x) e di una funzione razionale fratta propria
Considerando l'integrale indefinito di ambo i membri della (4), si ha:
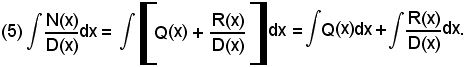
Poichè è noto il calcolo di
resta da vedere come effettuare quello di
A tal punto, è bene evidenziare che, per l'integrazione delle funzioni razionali fratte, si ridurrà sempre ad un integrale del tipo (6), ovvero ad una funzione integranda frazione propria.
Si distinguono ora i seguenti casi:
a)-l'equazione D(x) = 0 ha radici tutte reali e distinte;
b)-l'equazione D(x) = 0 ha radici tutte reali ma non tutte distinte;
c)-l'equazione D(x) = 0 non ha radici reali.
a)-l'equazione D(x) = 0 ha radici tutte reali e distinte
Considerata l'equazione di grado n,
dividendo ambo i membri per b0, diverso da zero, la si trasformi nell'altra equivalente, avente il 1° coefficiente uguale ad uno:
Se
x1, x2, ..., xn
sono le n radici reali e distinte della (7) o della (7'), si sa, dall'algebra elementare, che vale la decomposizione
(8) D(x) = (x - x1)(x - x2)(x - 3) ... (x - xn).
Si può dimostrare inoltre, ma si omette la dimostrazione, che vale la seguente scomposizione in somma:
ove le n frazioni del 2° membro hanno per denominatore, ciascuna e ordinatamente, uno dei fattori di 1° grado della (8), e per numeratore le n costanti
A1, A2, A3..., An
che si possono determinare in vari modi, tra i quali il seguente.
Liberando la (9) dai denominatori, si ha:
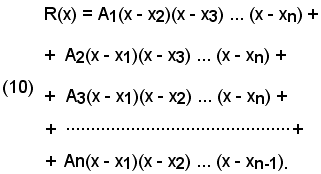
Ponendo di seguito in ambo i membri della (10)
x = x1, x = x2, x = x3, ... x = xn,
si ricavano rispettivamente i valori di
A1, A2, A3..., An.
Considerando ora l'integrale di ambo i membri della (9), si ha:
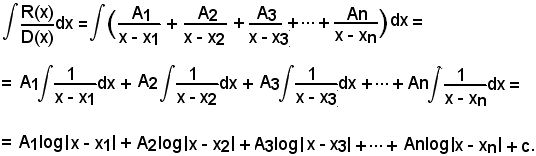
Quindi, dopo aver seguito il procedimento suddetto, è stato effettuato il calcolo dell'integrale del tipo (6).
Esempi
Essendo
x2 - 4x + 3 = (x - 1)(x - 3),
vale la seguente scomposizione in somma:
da cui, liberando dai denominatori, si ha:
1 = A1(x - 3) + A2(x - 1);
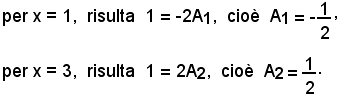
Pertanto:
Considerando l'integrale di ambo i membri, si ha:
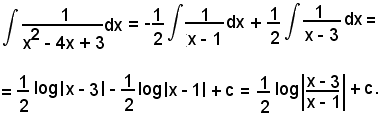
Essendo
x3+ 5x2 + 2x - 8 = (x - 1)(x + 2)(x + 4),
vale la seguente scomposizione in somma:
da cui, liberando dai denominatori, si ha:
7 = A1(x + 2)(x + 4) + A2(x - 1)(x + 4) + A3(x - 1)(x + 2);

Pertanto:
Considerando l'integrale di ambo i membri, si ha:
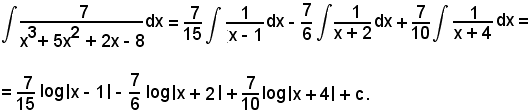
Essendo
2x2 - 3x + 1 = (2x - 1)(x - 1),
vale la seguente scomposizione in somma:
da cui, liberando dai denominatori, si ha:
3 = A1(x - 1) + A2(2x - 1);
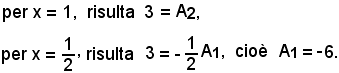
Pertanto:
Considerando l'integrale di ambo i membri, si ha:
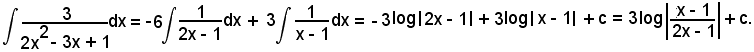
Essendo
3x2 - 4x + 1 = (3x - 1)(x - 1),
vale la seguente scomposizione in somma:
da cui, liberando dai denominatori, si ha
5x - 3 = A1(x - 1 ) + A2(3x - 1);
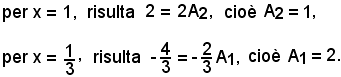
Pertanto:
Considerando l'integrale di ambo i membri, si ha:
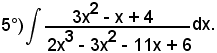
Essendo
2x3 - 3x2 - 11x + 6 = (2x - 1)(x + 2)(x - 3),
vale la seguente scomposizione in somma:
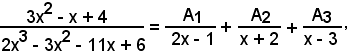
da cui, liberando dai denominatori, si ha:
3x2 - x + 4 = A1(x + 2)(x - 3) + A2(2x - 1)(x - 3) + A3(2x - 1)(x + 2);

Pertanto:
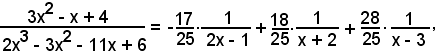
Considerando l'integrale di ambo i membri, si ha:
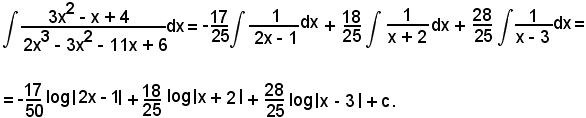
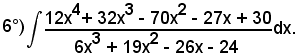
Effettuando la divisione, la funzione integranda diventa
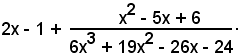
Quindi, si ha:
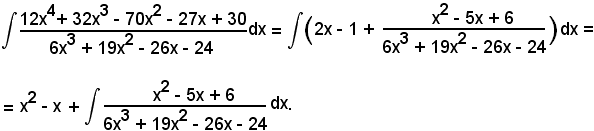
Per calcolare quest'ultimo integrale, si procede come negli esempi precedenti.
Essendo
6x3 + 19x2 - 26x - 24 = (3x + 2)(2x - 3)(x + 4),
vale la seguente scomposizione in somma
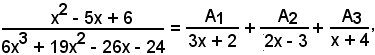
da cui, liberando dai denominatori, si ha:
x2 - 5x + 6 = A1(2x - 3)(x + 4) + A2(3x + 2)(x + 4) + A3(3x + 2)(2x - 3);
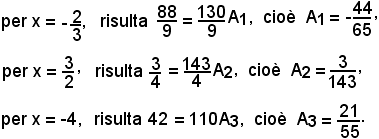
Pertanto:
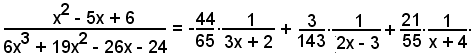
Considerando l'integrale di ambo i membri, si ha:
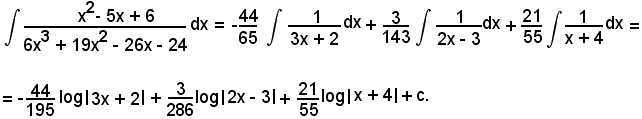
Pertanto, l'integrale proposto diventa:
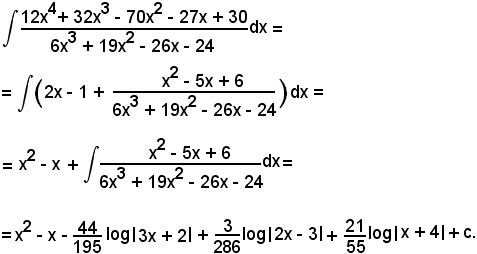
b)-l'equazione D(x) = 0 ha radici reali multiple
Considerata l'equazione di grado n:
le sue radici siano, ad esempio, quattro e cioè
x1 di molteplicità α,
x2 di molteplicità β,
x3 di molteplicità γ,
x4 di molteplicità δ,
in cui, come è noto dall'algebra, dev'essere α + β + γ + δ = n, grado dell'equazione D(x) = 0.
in somma:
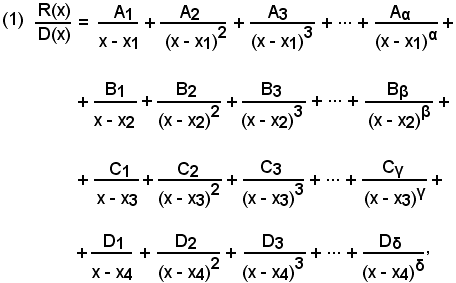
in cui

sono n costanti da determinare come segue:
si libera la (1) dai denominatori e, dopo aver ugualmente ordinato i due membri rispetto all'incognita, per il principio di identità dei polinomi, deve aversi quella dei coefficienti delle incognite di pari esponente dei due membri. Tali uguaglianze costituiranno un sistema nelle incognite (2) che, risolto, darà i valori delle costanti.
Esempi
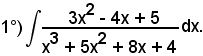
Poichè l'equazione
D(x) = x3 + 5x2 + 8x + 4 = 0
ammette le radici x1 = -1 e x2 = x3 = -2,
per cui è
x3 + 5x2 + 8x + 4 = (x + 1)(x + 2)2,
e vale la seguente scomposizione in somma:
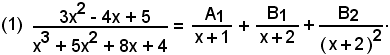
Liberando dai denominatori, si ha:
3x2 - 4x + 5 = A1(x + 2)2 + B1(x + 1)(x + 2) + B2(x + 1) = A1x2 + 4A1x + 4A1 + B1x2 + 3B1x + 2B1 + B2x + B2 = (A1 + B1)x2 + (4A1 + 3B1+ B2)x + (4A1 + B1+ B2)
e quindi, per il principio di identità dei polinomi, dev'essere
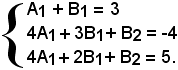
Le soluzioni di tale sistema sono:
A1 = 12, B1= -9, B2 = -25,
pertanto la (1) diventa
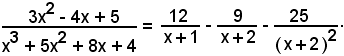
Quindi:
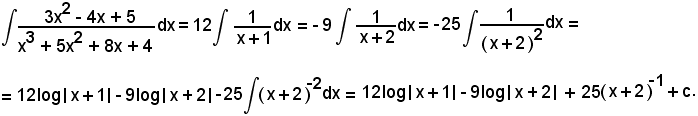
L'equazione
D(x) = x5 - 13x4 + 67x3 - 171x2 + 216x - 108 = 0
ha per radici
x1 = x2 = 2 e x3 = x4 = x5 = 3,
per cui è
x5 - 13x4 + 67x3 - 171x2 + 216x - 108 = (x - 2)2(x - 3)3
e vale la seguente scomposizione in somma:
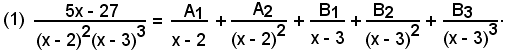
Liberando dai denominatori, si ha:
5x - 27 = A1(x - 2)(x - 3)3 + A2(x - 3)3 + B1(x - 2)2(x - 3)3 + B2(x - 2)2(x - 3) + B3(x - 2)2.
Sviluppando, ordinando e raccogliendo i fattori comuni nel 2° membro, si perviene all'uguaglianza
5x - 27 = (A1 + B1)x4 + (-11A1 + A2 - 10B1 + B2)x3 + (45A1 - 9A2 + 37B1 - 7B2 + B3)x2 +
+ (-81A1 + 27A2 - 60B1 + 16B2 - 4B3)x + (54A1 - 27A2 + 36B1 - 12B2 + 4B3),
per il verificarsi della quale, deve aversi

Le soluzioni di tale sistema sono:
A1 = 46, A2 = 17, B1 = -46, B2 = 29, B3 = -12,
pertanto la (1) diventa
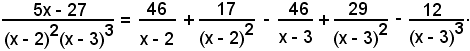
Quindi:
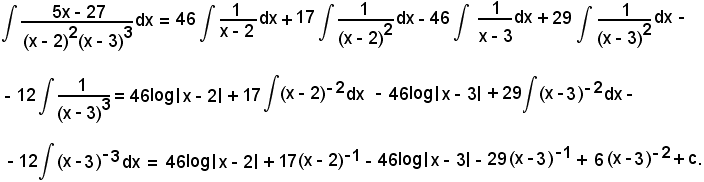
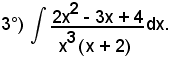
Poichè l'equazione
D(x) = x3(x - 2) = 0
ammette le radici
x1 = x2 = x3 = 0 e x4 = -2,
vale la seguente scomposizione in somma:
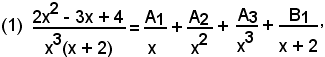
da cui
2x2 - 3x + 4 = A1x2(x + 2) + A2x(x + 2) + A3(x + 2) + B1x3.
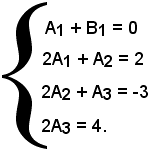
Sviluppando, ordinando e raccogliendo i fattori comuni nel 2° membro, si perviene alla seguente uguaglianza:
2x2 - 3x + 4 = (A1 + B1)x3 + (2A1 + A2)x2 + (2A2 +A3)x + 2A3,
per il verificarsi della quale, deve aversi

Le soluzioni di tale sistema sono:
pertanto la (1) diventa
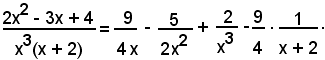
Quindi:
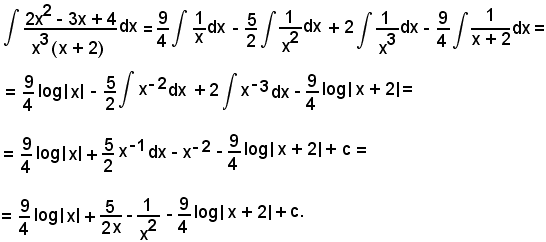
c)-l'equazione D(x) = 0 ha radici complesse
Ci si limita a considerare i seguenti due tipi:
in cui k è una costante e l'equazione
D(x) = ax2 + bx + c = 0,
avendo il discriminante negativo, non ha radici reali.
E' noto, dall'algebra elementare, che può aversi la seguente trasformazione:
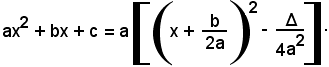
Pertanto risulta
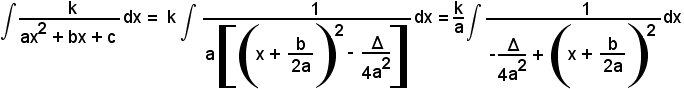
e l'integrale a cui si è pervenuti è del tipo 6°), cioè
Esempi
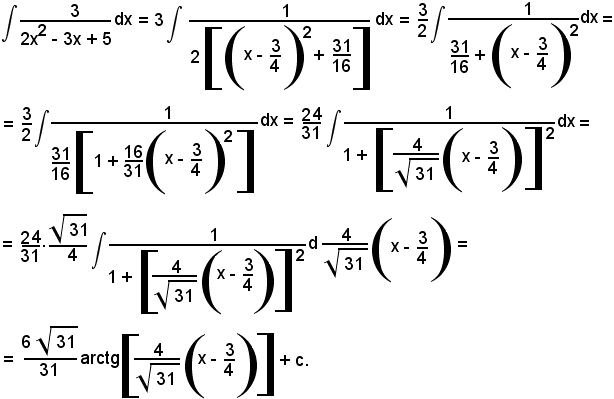
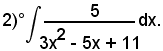

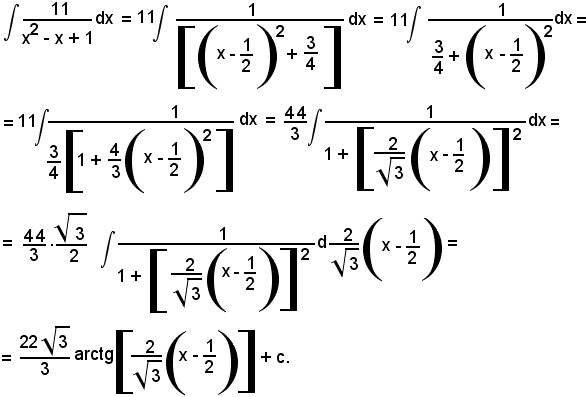
Osservando che si può scrivere
l'integrale proposto diventa
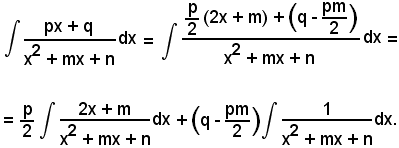
Esempi
Poichè si può scrivere
si ha:
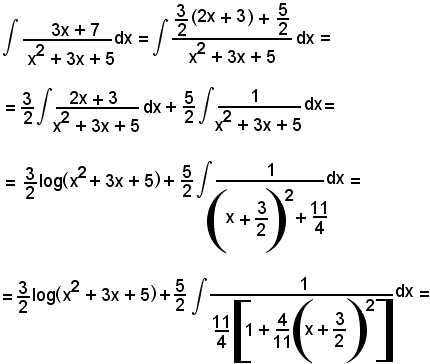
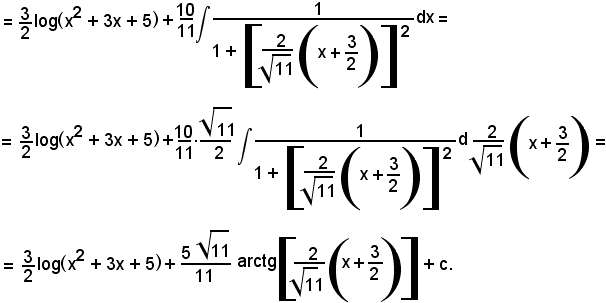
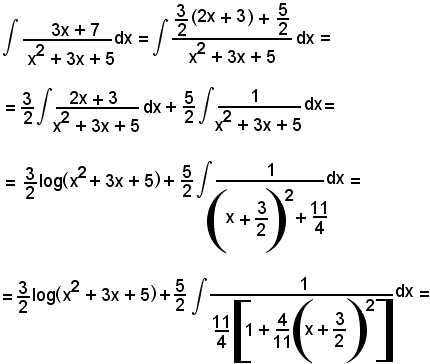
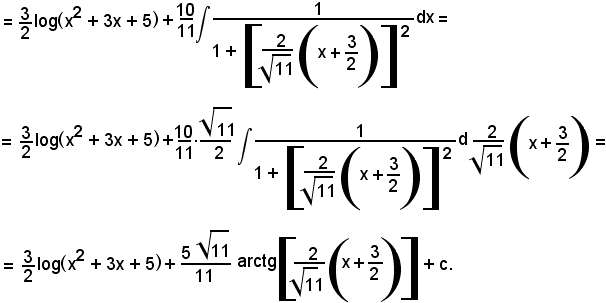
Poichè si può scrivere
si ha:
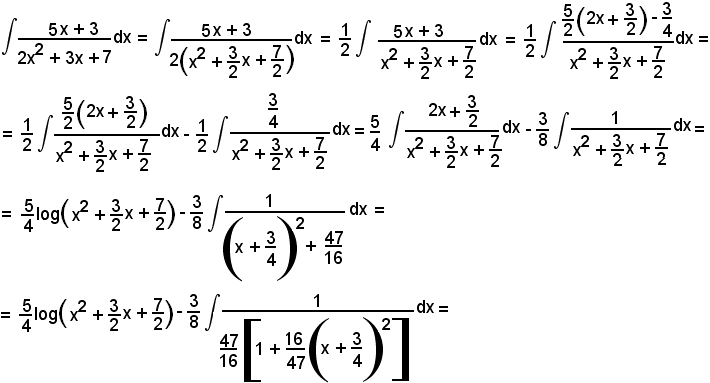
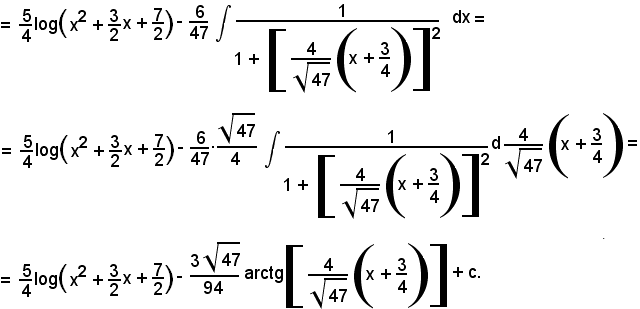
7)-Integrazione per sostituzione
Un altro artificio molto utile per trasformare la funzione integranda in un'altra che appartenga a tipi di cui si conosca la primitiva, consiste nel cambiare la variabile con un'altra legata a quella da un'opportuna relazione.
Si voglia calcolare
in cui f(x) sia una funzione continua in un intervallo (a, b), e si supponga di conoscere una funzione F(x) primitiva della f(x), cioè tale che si possa scrivere
Nella F(x) si ponga x = g(t), in cui g(t) sia una funzione nella nuova variabile t, derivabile e continua in un certo intervallo (a', b'), in modo che quando la t varia con continuità in (a', b'), la x varia con continuità in (a, b). In tal modo la F(x) diventa una funzione composta della t tramite x, cioè F(x) = F[g(t)], ed è noto che
Dall'ipotesi F'(x) = f(x), si ha che f(x) = F[g(t)] è una funzione primitiva di f(x)·g'(t), e quindi l'integrale (1) diventa
Quest'ultimo integrale, talvolta, risulta appartenente ad uno dei tipi già noti; una volta calcolato, e ammesso che la funzione x = g(x), basterà sostituire a t questa φ(x), per avere la funzione primitiva di quella integranda inizialmente proposta.
Nota bene
1)-Quando furono date le definizioni di integrale indefinito, furono fatte alcune considerazioni sulla precisione e sulla comodità delle stesse funzioni. In entrambi i casi, però, per indicare l'integrale indefinito, si scrisse;
e non solo
Si vuole ora mostrare che il fattore dx, se è comodo per la risoluzione di alcuni tipi di integrali, è addirittura necessario nell'integrazione per sostituzione.
Esempi
Si ha:
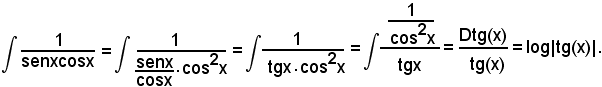
Si ha:
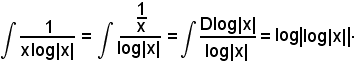
In ciascuno dei due esempi visti il fattore dx non è risultato necessario, in quanto senza di esso si è pervenuti ugualmente alla determinazione di una primitiva della funzione integranda proposta. La necessarietà dell'uso del fattore dx è proprio data dalla formula (3).
Infatti la sostituzione x = g(t), mentre trasforma la f(x) in f[g(t)], trasforma anche dx in g'(t)·dt e, pertanto, poichè g'(t)·dt è effettivamente un prodotto, anche f(x)·dx è tale, ossia dx è proprio un fattore e non un simbolo.
2)-Non vi sono regole per stabilire la sostituzione più conveniente, in quanto essa dipende dalla pratica di calcolo che si possiede.
9)-Esempi di integrazione per sostituzione
Posto
cosx = t,
per cui
dcosx = dt,
cioè
-senxdx = dt,
sostituendo si ha:
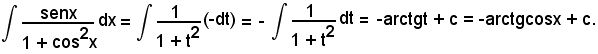
Posto
x = sent,
ossia
t = arcsenx,
si ha
dx = dsent = cost·dt
e sostituendo si ha:
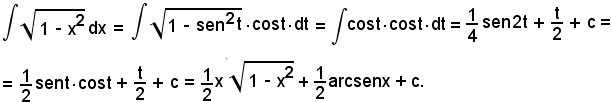
L'integrale precedente è un caso particolare del seguente.
Posto
x = a·sent,
da cui
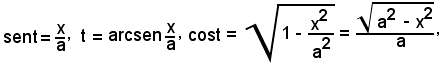
si ha:
dx = a·cost·dt
e sostituendo, risulta
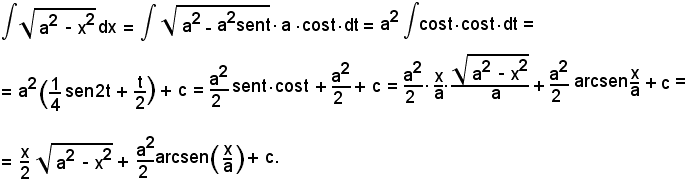
Posto
si ha:
cioè
e sostituendo
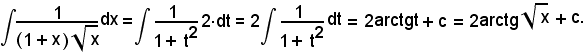
Posto
per cui
si ha:
e, ricordando la formula parametrica
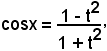
sostituendo si ha
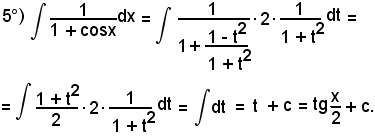
Posto
per cui
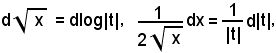
cioè
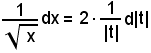
e, sostituendo, si ha
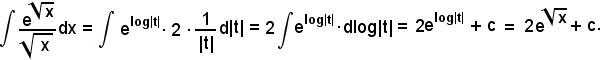
Posto
x2 + a2 = t,
per cui
d(x2 + a2) = dt,
cioè
2xdx = dt,
sostituendo, si ha:
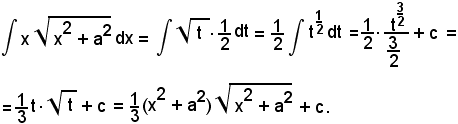
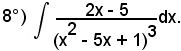
Posto
x2 - 5x + 1 = t,
per cui
d(x2 - 5x + 1) = dt,
cioè
(2x - 5)dx = dt,
sostituendo, si ha:
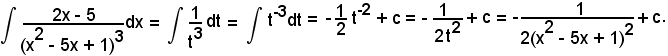
10)-Integrazione di alcune funzioni irrazionali
Il metodo di integrazione per sostituzione viene applicato per il calcolo di alcuni tipi di integrali di funzioni irrazionali. Infatti, per opportune sostituzioni, ci si riporta ad integrali di funzioni razionali della nuova variabile. Ci si limita a considerare i seguenti tipi:
Con la sostituzione
quadrando ambo i membri, si ha:
x2 + bx + c = x2 + 2xt + t2,
ossia
bx + c = 2xt + t2,
da cui
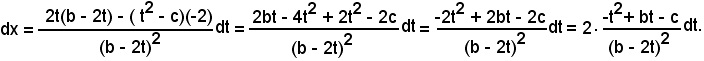
Quindi risulta:
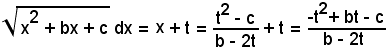
e
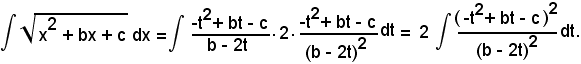
In tal modo la funzione integranda è diventata razionale.
Affinchè la funzione
abbia valori reali, dev'essere
-x2 + bx + c ≥ 0.
Se α e β sono le radici dell'equazione associata, nell'intervallo (α, β), risulta -x2 + bx + c ≥ 0 ed è anche
Si consideri allora la posizione
dalla quale, dopo aver quadrato ambo i membri, si ha:
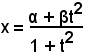
e
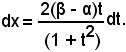
e quindi si ha
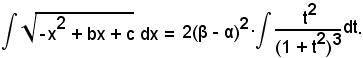
In tal modo la funzione integranda è diventata razionale.