MIKY & GENNY
NUMERI COMPLESSI ---> INDICE
Genesi dei numeri
E' opportuno ricordare le successive estensioni dei campi di numeri fatte nel corso dell'algebra, per pervenire al concetto di numero reale e, soprattutto, ricordare il perchè di tali estensioni.
Numeri naturali
Nel campo dei numeri naturali, rimanevano non sempre possibili le operazioni di sottrazione, nel caso del minuendo minore del sottraendo, e di divisione, nel caso in cui il divisore non era esattamente contenuto nel dividendo.
Per rendere sempre possibile l'operazione di divisione, escluso il caso del divisore zero, si passò al campo dei numeri razionali assoluti.
Numeri razionali assoluti
In tale campo, i suoi numeri naturali risultavano particolari numeri razionali assoluti, quali le frazioni apparenti.
Per rendere sempre possibile l'operazione di sottrazione, si passò al campo dei numeri razionali relativi.
Numeri razionali relativi
In tale campo, i precedenti numeri, razionali assoluti e naturali, risultavano particolari numeri razionali relativi e positivi.
Per rendere sempre possibile, almeno in alcuni casi, l'operazione di estrazione di radice, si passò al campo dei numeri reali relativi.
Numeri reali relativi
In tale campo, erano compresi tutti i numeri precedenti, sempre, come casi particolari, reali razionali.
Si badi che si è parlato sempre di estensione del campo dei numeri e non di introduzione di un campo totalmente nuovo, non solo perchè i numeri costituenti un certo campo erano sempre casi particolari di quelli costituenti il nuovo campo, ma anche perchè, ogni volta, venivano mantenute inalterate le definizioni delle quattro operazioni fondamentali dell'aritmetica, e ciascuna di esse conservava le proprietà formali, commutativa e associativa dell'addizione e della sottrazione, distributiva della moltiplicazione rispetto alla somma e alla differenza indicate.
Il campo più esteso dei numeri, noto fino a questo momento, è quello dei numeri reali, con i quali, tuttavia, non è possibile l'estrazione di radice con indice pari dai numeri negativi.
Per rendere possibile quest'altra operazione, si effettua una nuova estensione del campo dei numeri, introducendo i numeri complessi, i quali, si badi, costituiscono il campo completo dei numeri rispondenti alle esigenze dell'analisi matematica, in quanto è stato dimostrato che ogni ulteriore estensione di detto campo farebbe perdere qualcuna delle proprietà formali delle operazioni fondamentali, ad esempio la proprietà commutativa della moltiplicazione.
Unità immaginaria - Numeri complessi
Siano a e b due numeri reali e sia j un nuovo simbolo da chiamare unità immaginaria.
Le espressioni del tipo
(1) a + bj
cessano di essere puramente simboliche ed acquistano significato preciso purchè si stabilisca di seguire le seguenti convenzioni:
a)-siano considerate come se fossero dei veri e propri binomi di quantità reali,
b)-si possano eseguire con esse le quattro operazioni fondamentali dell'algebra e ciascuna con le stesse note regole,
c)-quando in un risultato ottenuto da un'operazione si presenta l'altro simbolo j2, al suo posto si consideri -1.
Rispettate le suddette convenzioni, le espressioni della forma (1) si chiamano numeri complessi.
I numeri reali a e b si chiamano coefficienti, e più precisamente a si chiama parte reale e b coefficiente dell'unità immaginaria.
Il numero reale
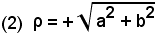
si chiama modulo del numero complesso.
Il numero
(3) a - bj
avente la stessa parte reale e lo stesso coefficiente dell'unità immaginaria di (1), ma cambiato di segno, si chiama numero complesso e coniugato di (1).
Risulta immediato che due numeri complessi e coniugati hanno lo stesso modulo.
Uguaglianza di due numeri complessi
Si vuole vedere quando sussiste l'uguaglianza
(4) a + bj = a' + b'j.
Avendo convenuto di operare sulle espressioni (1) come se se lo si facesse sui polinomi, la (4) si può scrivere:
(5) a - a' = (b' - b)j
ed elevando ambo i membri al quadrato, risulta
(6) (a - a')2 = (b - b')2j2
e per la convenzione c) di 2), si ha
(6') (a - a')2 = -(b' - b)2,
che esprime un'uguaglianza fra due numeri reali di segno opposto e, pertanto, vera solo se entrambi i numeri reali sono nulli, cioè dev'essere
(7) a = a', b = b',
quindi:
-due numeri complessi sono uguali, quando hanno uguali le parti reali ed uguali i coefficienti dell'unità immaginaria.
Nota bene
Quando due numeri complessi sono disuguali non è possibile stabilire fra loro i concetti di maggiore e minore.
Operazioni fondamentali tra numeri complessi
E' possibile, senza ulteriori convenzioni, porre le regole ed enunciare le proprietà valide per le operazioni fra numeri complessi.
1)-Sempre in base alle regole valide per le operazioni fra polinomi, segue:
cioè:-la somma di due numeri complessi coniugati è il numero reale doppio della parte reale di uno di essi.
2)-Per il prodotto si ha:
(9) (a + bj)·(a' + b'j) = aa' + ab'j + a'bj + bb'j2 = aa' + ab'j + a'bj - bb' = (aa - bb') + (ab' + a'b)j.
In particolare:
(9') (a + bj)·(a - bj) = a2 + b2,
cioè:-il prodotto di due numeri complessi coniugati è il numero reale somma dei quadrati della parte reale e del coefficiente dell'unità immaginaria di uno di essi, quadrato del modulo.
2)-Per il quoziente si ha:
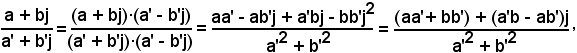
quindi, in definitiva
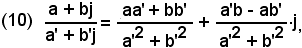
Nota bene
Nel primo passaggio si è moltiplicato numeratore e denominatore per il complesso e coniugato del denominatore.
Numeri reali puri
a)-Così come sono stati introdotti, i numeri complessi estendono il campo dei numeri reali, i quali vengono ad essere contenuti nei numeri complessi e, precisamente, si ottengono da quelli quando si suppone uguale a zero il coefficiente dell'unità immaginaria.
Nel caso in cui si suppone a = 0, i numeri complessi diventano della forma:
(11) bj
e vengono chiamati numeri immaginari puri;
b)-dalla (9') si ha:
a2 + b2 = (a + bj)·(a - bj),
che esprime la regola di scomposizione in fattori della somma di due quadrati, non scomponibile nel campo dei numeri reali.
Il numero complesso nella forma algebrica come coppia di numeri reali
1)-L'espressione
a + bj
si chiama anche forma algebrica del numero complesso.
Essa è perfettamente individuata dalla coppia ordinata di numeri reali (a, b), per cui si usa anche la seguente indicazione:
(12) a + bj = (a, b).
2)-Nuova indicazione dell'uguaglianza e delle operazioni tra numeri complessi.
L'uguaglianza e le operazioni tra numeri complessi sono allora sinteticamente espresse dalle seguenti formule:
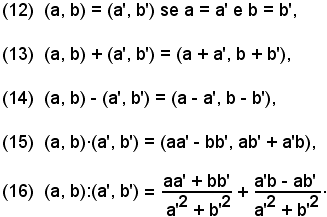
Potenza dell'unità immaginaria
Casi particolari
a)-Il numero complesso (a, 0) è il numero reale a, cioe:
(17) (a, 0) = a.
a')-In particolare:
(17') (1, 0) = 1.
b)-Il numero complesso (0, b) è il numero complesso puro bj, cioe:
(18) (0, b) = bj.
b')-In particolare:
(18') (0, 1) = j.
c)-da quanto detto, deriva:
(19) (0, 0) = 0,
cioè il numero complesso zero è quello che ha a = b = 0.
d)-dalla convenzione fatta in precedenza, e come caso particolare della (15), si ha:
(20) j2 = (0, 1)·(0, 1) = -1
e tenendo presente la proprietà associativa del prodotto, risulta
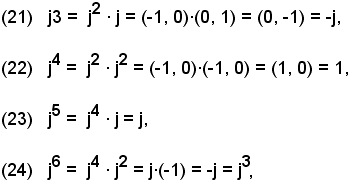
e così via.
Cioè:
-le successive potenze dell'unità immaginaria si ripetono periodicamente di quattro in quattro.
Reciproco e potenza ad esponente negativo di un numero complesso
Si definisce reciproco di un numero complesso (a, b) ≠ (0, 0) il numero:
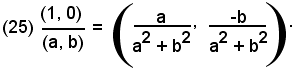
Dopo di ciò, il quoziente di due numeri complessi può essere ottenuto anche come prodotto del 1° per il reciproco del 2°.
Si definisce potenza ad esponente intero negativo -n del numero complesso (a, b) il reciproco di (a, b)n, cioè:
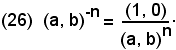
Per definizione si pone ancora:
(27) (a, b)0= (1, 0) = 1.
Quindi le regole per il calcolo con le potenze dei numeri complessi, si estendono al caso di esponenti interi di qualsiasi segno.
Rappresentazione geometrica di un numero complesso
1)-In modo del tutto analogo a quanto fatto per i numeri reali, Gauss stabilì una rappresentazione geometrica dei numeri complessi, prendendo come base della rappresentazione un piano, chiamato appunto piano di Gauss, invece di una retta, come fu fatto per i numero reali. Si considerino in un piano due assi ortogonali, vedi figura seguente:
-il 1°, asse delle a, detto anche asse reale,
-il 2°, asse delle b, detto anche asse immaginario.
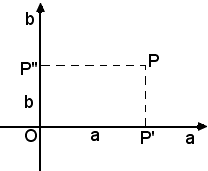
Dato il numero complesso a + bj, si segni sul piano il punto P avente per coordinate i due numeri reali a e b; il punto P lo si assume come rappresentante del numero complesso a + bj e lo si chiama punto immagine del numero complesso.
Segue subito che:
-ad ogni numero complesso corrisponde sempre uno ed un solo punto del piano e, viceversa, ad ogni punto del piano corrisponde uno ed un solo numero complesso.
In tal modo, resta stabilita una corrispondenza biunivoca tra i punti del piano, a distanza finita, ed i numeri complessi finiti, cioè aventi per modulo un numero finito.
Il modulo ρ di un numero complesso è rappresentato, geometricamente, dal segmento orientato, vettore, OP, per cui tutti i numeri complessi aventi uno stesso modulo sono i punti di una circonferenza di centro O e raggio uguale al modulo.
2)-I punti 1, j, -1, -j sono quelli d'incontro della circonferenza di raggio 1 con gli assi coordinati, vedi figura seguente.
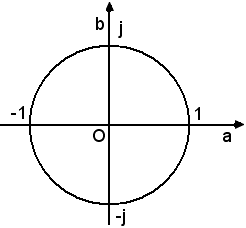
3)-I numeri complessi aventi parti reali uguali, sono rappresentati da due punti situati su una retta perpendicolare all'asse reale, vedi figura seguente:
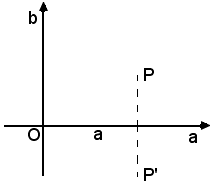
4)-Due numeri complessi aventi uguali i coefficienti delle unità immaginarie, sono rappresentati da due punti situati su una retta perpendicolare all'asse immaginario, vedi figura seguente:
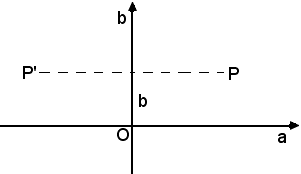
5)-Due numeri complessi coniugati sono rappresentati da due punti situati simmetricamente rispetto all'asse reale, vedi figura seguente:
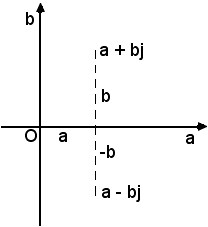
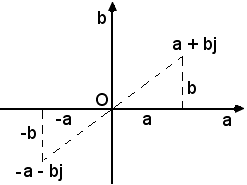
6)-Due numeri complessi uguali e di segno opposto, cioè aventi parti reali e coefficienti dell'unità immaginaria rispettivamente uguali e di segno opposto, sono rappresentati da due punti simmetrici rispetto all'origine, vedi figura seguente:
Forma trigonometrica di un numero complesso
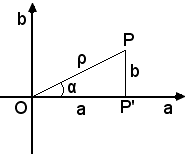
Sia P il punto immagine del numero complesso a + bj ed α l'angolo che il vettore OP forma con la direzione positiva dell'asse reale; α si chiama argomento del numero complesso, vedi figura seguente:
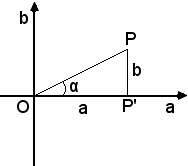
Dal triangolo rettangolo OP'P, per note formule della trigonometria, si ha:
(28) a = ρcosα, b = ρsenα,
per cui si ha l'identità
(29) a + bj = ρ(cosα + jsenα),
che indica la trasformazione di un numero complesso dalla forma algebrica a + bj a quella trigonometrica
(29') ρ(cosα + jsenα).
Detta forma trigonometrica di un numero complesso risulta particolarmente utile e significativa per esprimere e calcolare prodotti, potenze ed estrazioni di radici dei numeri complessi.
Si noti che: assegnare il modulo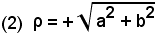e l'argomento α, di
un numero complesso, non è sufficiente a determinare, in modo
unico, lo stesso numero, perchè, come si sa dalla trigonometria,
archi differenti di un multiplo intero di circonferenza hanno le stesse
funzioni, quindi è:
b = ρsenα = sen(α + 2kπ).
In particolare, l'argomento di un numero reale è zero o un multiplo intero di 2π.
Due numeri complessi coniugati hanno lo stesso modulo e argomenti la cui somma è 2π o un multiplo intero di esso.
Operazioni dei numeri complessi in forma trigonometrica
[ρ(cosα + jsenα)]·[ρ'(cosβ + jsenβ)] = ρ·ρ'·(cosα + jsenα)·(cosβ + jsenβ) =
= ρ·ρ'·(cosαcosβ + jcosαsenβ + jsenαcosβ + j2senαsenβ) =
= ρ·ρ'·[(cosαcosβ - senαsenβ) + j·(senαcosβ + cosαsenβ)] =
= ρ·ρ'·[cos(α + β) + j·sen(α + β)],
cioè
(30) [ρ(cosα + jsenα)]·[ρ'(cosβ + jsenβ)] = ρ·ρ'·[cos(α + β) + j·sen(α + β)].
Quindi:
-il prodotto di due numeri complessi in forma trigonometrica è un altro numero complesso, nella stessa forma, che ha per modulo il prodotto dei moduli e per argomento la somma degli argomenti.
Esempio
2)-Potenza
Se si suppongono uguali gli n fattori di un prodotto di numeri complessi, si ha ha la potenza ennesima di uno di essi, espressa nella formula dovuta a Moivre:
(31) [ρ·(cosα + jsenα)n] = ρn·(cosα + jsenα),
ossia:
-la potenza di un numero complesso in forma trigonometrica è un altro numero complesso, nella stessa forma, che ha per modulo la potenza del modulo e per argomento quello del numero complesso dato moltiplicato per l'esponente della potenza.
3)-Quoziente
Per il quoziente di due numeri complessi in forma trigonometrica si ha:
cioè
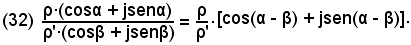
ossia:
-il quoziente di un numero complesso nella forma trigonometrica è un altro numero complesso, nella stessa forma, che ha per modulo il quoziente dei moduli e per argomento la differenza degli argomenti.
Radici nme di un numero complesso
1)-Nel campo dei numeri complessi l'operazione di estrazione di radice è sempre possibile e ogni numero complesso ammette tante radici quante sono le unità dell'indice della stessa radice.
2)-Dato un numero complesso ρ·(cosα + jsenα), estrarre da esso la sua radice nma, significa trovare quell'altro numero complesso, di modulo r e argomento x incognite, che elevato alla potenza nma dia quello dato.
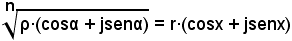
significa:
[r·(cosα + jsenα)]n = ρ·(cosx + jsenx).
Applicando la formula di Moivre (31), si ha:
rn·(cosnx + jsennx) = ρ·(cosα + jsenα),
dalla quale segue che dev'essere
rn = ρ,
cioè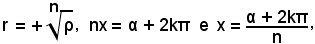
con k = 0, 1, 2, ... (n - 1), in corrispondenza dei quali valori di k si ottengono le n radici nme del numero complesso.
Dunque è:
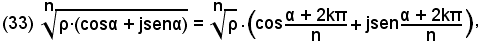
con k = 0, 1, 2, ... (n - 1).
Esempi
1°)-Calcolare:
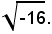
Poichè -16 = 16·(cosπ + jsenπ), è:
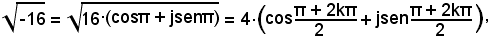
con k = 0, 1.
Per k = 0, si ha:
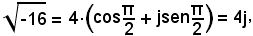
per k = 1, si ha:
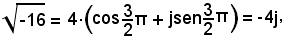
quindi
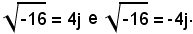
2°)-Calcolare:
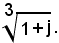
Poichè
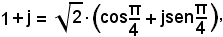
è:
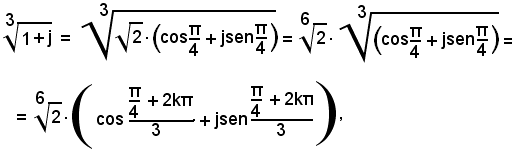
con k = 0, 1, 2.
Per k = 0, si ha:
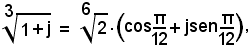
per k = 1, si ha:
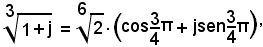
per k = 2, si ha:
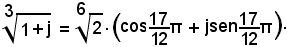
Cenni di calcolo vettoriale
1)-Grandezze scalari
Vengono chiamate scalari quelle grandezze che sono completamente individuate da un numero positivo o negativo.
Ad esempio, una lunghezza, un volume, la temperatura, la carica elettrica, ecc.
La misura di una grandezza scalare è naturalmente riferita ad una prefissata unità.
Grandezze vettoriali
Vengono chiamate grandezze vettoriali quelle altre entità delle quali si fa uso continuo nella fisica, che sono caratterizzatie, oltre che da un valore numerico, anche da una direzione e da un verso o senso.
Ad esempio, le forze, la velocità, l'accelerazione, ecc.
2)-Rappresentazione di una grandezza vettoriale - Vettori
E' opportuno ricordare le successive estensioni dei campi di numeri fatte nel corso dell'algebra, per pervenire al concetto di numero reale e, soprattutto, ricordare il perchè di tali estensioni.
Numeri naturali
Nel campo dei numeri naturali, rimanevano non sempre possibili le operazioni di sottrazione, nel caso del minuendo minore del sottraendo, e di divisione, nel caso in cui il divisore non era esattamente contenuto nel dividendo.
Per rendere sempre possibile l'operazione di divisione, escluso il caso del divisore zero, si passò al campo dei numeri razionali assoluti.
Numeri razionali assoluti
In tale campo, i suoi numeri naturali risultavano particolari numeri razionali assoluti, quali le frazioni apparenti.
Per rendere sempre possibile l'operazione di sottrazione, si passò al campo dei numeri razionali relativi.
Numeri razionali relativi
In tale campo, i precedenti numeri, razionali assoluti e naturali, risultavano particolari numeri razionali relativi e positivi.
Per rendere sempre possibile, almeno in alcuni casi, l'operazione di estrazione di radice, si passò al campo dei numeri reali relativi.
Numeri reali relativi
In tale campo, erano compresi tutti i numeri precedenti, sempre, come casi particolari, reali razionali.
Si badi che si è parlato sempre di estensione del campo dei numeri e non di introduzione di un campo totalmente nuovo, non solo perchè i numeri costituenti un certo campo erano sempre casi particolari di quelli costituenti il nuovo campo, ma anche perchè, ogni volta, venivano mantenute inalterate le definizioni delle quattro operazioni fondamentali dell'aritmetica, e ciascuna di esse conservava le proprietà formali, commutativa e associativa dell'addizione e della sottrazione, distributiva della moltiplicazione rispetto alla somma e alla differenza indicate.
Il campo più esteso dei numeri, noto fino a questo momento, è quello dei numeri reali, con i quali, tuttavia, non è possibile l'estrazione di radice con indice pari dai numeri negativi.
Per rendere possibile quest'altra operazione, si effettua una nuova estensione del campo dei numeri, introducendo i numeri complessi, i quali, si badi, costituiscono il campo completo dei numeri rispondenti alle esigenze dell'analisi matematica, in quanto è stato dimostrato che ogni ulteriore estensione di detto campo farebbe perdere qualcuna delle proprietà formali delle operazioni fondamentali, ad esempio la proprietà commutativa della moltiplicazione.
Unità immaginaria - Numeri complessi
Siano a e b due numeri reali e sia j un nuovo simbolo da chiamare unità immaginaria.
Le espressioni del tipo
(1) a + bj
cessano di essere puramente simboliche ed acquistano significato preciso purchè si stabilisca di seguire le seguenti convenzioni:
a)-siano considerate come se fossero dei veri e propri binomi di quantità reali,
b)-si possano eseguire con esse le quattro operazioni fondamentali dell'algebra e ciascuna con le stesse note regole,
c)-quando in un risultato ottenuto da un'operazione si presenta l'altro simbolo j2, al suo posto si consideri -1.
Rispettate le suddette convenzioni, le espressioni della forma (1) si chiamano numeri complessi.
I numeri reali a e b si chiamano coefficienti, e più precisamente a si chiama parte reale e b coefficiente dell'unità immaginaria.
Il numero reale
si chiama modulo del numero complesso.
Il numero
(3) a - bj
avente la stessa parte reale e lo stesso coefficiente dell'unità immaginaria di (1), ma cambiato di segno, si chiama numero complesso e coniugato di (1).
Risulta immediato che due numeri complessi e coniugati hanno lo stesso modulo.
Uguaglianza di due numeri complessi
Si vuole vedere quando sussiste l'uguaglianza
Avendo convenuto di operare sulle espressioni (1) come se se lo si facesse sui polinomi, la (4) si può scrivere:
(5) a - a' = (b' - b)j
ed elevando ambo i membri al quadrato, risulta
(6) (a - a')2 = (b - b')2j2
e per la convenzione c) di 2), si ha
(6') (a - a')2 = -(b' - b)2,
che esprime un'uguaglianza fra due numeri reali di segno opposto e, pertanto, vera solo se entrambi i numeri reali sono nulli, cioè dev'essere
(7) a = a', b = b',
quindi:
-due numeri complessi sono uguali, quando hanno uguali le parti reali ed uguali i coefficienti dell'unità immaginaria.
Nota bene
Quando due numeri complessi sono disuguali non è possibile stabilire fra loro i concetti di maggiore e minore.
Operazioni fondamentali tra numeri complessi
E' possibile, senza ulteriori convenzioni, porre le regole ed enunciare le proprietà valide per le operazioni fra numeri complessi.
1)-Sempre in base alle regole valide per le operazioni fra polinomi, segue:
(8) (a + bj) + (a' + b'j) = a + bj + a' - b'j = (a + a') + (b + b'j),
(8') (a + bj) - (a' + b'j) = a + bj - a' - b'j = (a - a') + (b - b'j),
cioè:
(8'') (a + bj) + (a - bj) = 2a,
(8') (a + bj) - (a' + b'j) = a + bj - a' - b'j = (a - a') + (b - b'j),
cioè:
-la somma algebrica di due numeri complessi è un numero
complesso che ha per parte reale e per coefficiente dell'unità
immaginaria, rispettivamente, la somma algebrica delle parti reali e
dei coefficienti dell'unità immaginaria dei due numeri complessi dati.
In particolare:
In particolare:
(8'') (a + bj) + (a - bj) = 2a,
cioè:
2)-Per il prodotto si ha:
(9) (a + bj)·(a' + b'j) = aa' + ab'j + a'bj + bb'j2 = aa' + ab'j + a'bj - bb' = (aa - bb') + (ab' + a'b)j.
In particolare:
(9') (a + bj)·(a - bj) = a2 + b2,
cioè:
2)-Per il quoziente si ha:
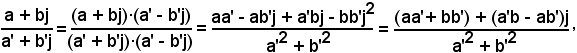
quindi, in definitiva
Nota bene
Nel primo passaggio si è moltiplicato numeratore e denominatore per il complesso e coniugato del denominatore.
Numeri reali puri
a)-Così come sono stati introdotti, i numeri complessi estendono il campo dei numeri reali, i quali vengono ad essere contenuti nei numeri complessi e, precisamente, si ottengono da quelli quando si suppone uguale a zero il coefficiente dell'unità immaginaria.
Nel caso in cui si suppone a = 0, i numeri complessi diventano della forma:
(11) bj
e vengono chiamati numeri immaginari puri;
b)-dalla (9') si ha:
a2 + b2 = (a + bj)·(a - bj),
che esprime la regola di scomposizione in fattori della somma di due quadrati, non scomponibile nel campo dei numeri reali.
Il numero complesso nella forma algebrica come coppia di numeri reali
1)-L'espressione
a + bj
si chiama anche forma algebrica del numero complesso.
Essa è perfettamente individuata dalla coppia ordinata di numeri reali (a, b), per cui si usa anche la seguente indicazione:
(12) a + bj = (a, b).
2)-Nuova indicazione dell'uguaglianza e delle operazioni tra numeri complessi.
L'uguaglianza e le operazioni tra numeri complessi sono allora sinteticamente espresse dalle seguenti formule:
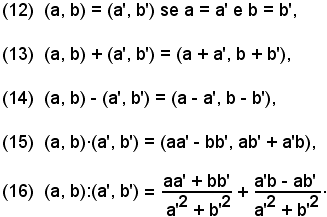
Potenza dell'unità immaginaria
Casi particolari
a)-Il numero complesso (a, 0) è il numero reale a, cioe:
(17) (a, 0) = a.
a')-In particolare:
(17') (1, 0) = 1.
b)-Il numero complesso (0, b) è il numero complesso puro bj, cioe:
(18) (0, b) = bj.
b')-In particolare:
(18') (0, 1) = j.
c)-da quanto detto, deriva:
(19) (0, 0) = 0,
cioè il numero complesso zero è quello che ha a = b = 0.
d)-dalla convenzione fatta in precedenza, e come caso particolare della (15), si ha:
(20) j2 = (0, 1)·(0, 1) = -1
e tenendo presente la proprietà associativa del prodotto, risulta
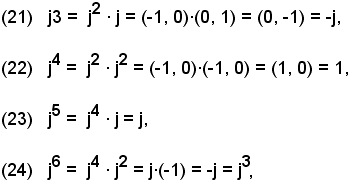
e così via.
Cioè:
-le successive potenze dell'unità immaginaria si ripetono periodicamente di quattro in quattro.
Reciproco e potenza ad esponente negativo di un numero complesso
Si definisce reciproco di un numero complesso (a, b) ≠ (0, 0) il numero:
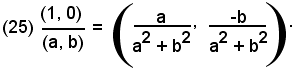
Dopo di ciò, il quoziente di due numeri complessi può essere ottenuto anche come prodotto del 1° per il reciproco del 2°.
Si definisce potenza ad esponente intero negativo -n del numero complesso (a, b) il reciproco di (a, b)n, cioè:
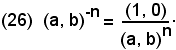
Per definizione si pone ancora:
(27) (a, b)0= (1, 0) = 1.
Quindi le regole per il calcolo con le potenze dei numeri complessi, si estendono al caso di esponenti interi di qualsiasi segno.
Rappresentazione geometrica di un numero complesso
1)-In modo del tutto analogo a quanto fatto per i numeri reali, Gauss stabilì una rappresentazione geometrica dei numeri complessi, prendendo come base della rappresentazione un piano, chiamato appunto piano di Gauss, invece di una retta, come fu fatto per i numero reali. Si considerino in un piano due assi ortogonali, vedi figura seguente:
-il 1°, asse delle a, detto anche asse reale,
-il 2°, asse delle b, detto anche asse immaginario.
Dato il numero complesso a + bj, si segni sul piano il punto P avente per coordinate i due numeri reali a e b; il punto P lo si assume come rappresentante del numero complesso a + bj e lo si chiama punto immagine del numero complesso.
Segue subito che:
-ad ogni numero complesso corrisponde sempre uno ed un solo punto del piano e, viceversa, ad ogni punto del piano corrisponde uno ed un solo numero complesso.
In tal modo, resta stabilita una corrispondenza biunivoca tra i punti del piano, a distanza finita, ed i numeri complessi finiti, cioè aventi per modulo un numero finito.
Il modulo ρ di un numero complesso è rappresentato, geometricamente, dal segmento orientato, vettore, OP, per cui tutti i numeri complessi aventi uno stesso modulo sono i punti di una circonferenza di centro O e raggio uguale al modulo.
2)-I punti 1, j, -1, -j sono quelli d'incontro della circonferenza di raggio 1 con gli assi coordinati, vedi figura seguente.
3)-I numeri complessi aventi parti reali uguali, sono rappresentati da due punti situati su una retta perpendicolare all'asse reale, vedi figura seguente:
4)-Due numeri complessi aventi uguali i coefficienti delle unità immaginarie, sono rappresentati da due punti situati su una retta perpendicolare all'asse immaginario, vedi figura seguente:
5)-Due numeri complessi coniugati sono rappresentati da due punti situati simmetricamente rispetto all'asse reale, vedi figura seguente:
6)-Due numeri complessi uguali e di segno opposto, cioè aventi parti reali e coefficienti dell'unità immaginaria rispettivamente uguali e di segno opposto, sono rappresentati da due punti simmetrici rispetto all'origine, vedi figura seguente:
Forma trigonometrica di un numero complesso
Sia P il punto immagine del numero complesso a + bj ed α l'angolo che il vettore OP forma con la direzione positiva dell'asse reale; α si chiama argomento del numero complesso, vedi figura seguente:
Dal triangolo rettangolo OP'P, per note formule della trigonometria, si ha:
(28) a = ρcosα, b = ρsenα,
per cui si ha l'identità
(29) a + bj = ρ(cosα + jsenα),
che indica la trasformazione di un numero complesso dalla forma algebrica a + bj a quella trigonometrica
(29') ρ(cosα + jsenα).
Detta forma trigonometrica di un numero complesso risulta particolarmente utile e significativa per esprimere e calcolare prodotti, potenze ed estrazioni di radici dei numeri complessi.
Si noti che: assegnare il modulo
e l'argomento α, di
un numero complesso, non è sufficiente a determinare, in modo
unico, lo stesso numero, perchè, come si sa dalla trigonometria,
archi differenti di un multiplo intero di circonferenza hanno le stesse
funzioni, quindi è:a = ρcosα = cos(α + 2kπ),
b = ρsenα = sen(α + 2kπ).
In particolare, l'argomento di un numero reale è zero o un multiplo intero di 2π.
Due numeri complessi coniugati hanno lo stesso modulo e argomenti la cui somma è 2π o un multiplo intero di esso.
Operazioni dei numeri complessi in forma trigonometrica
1)-Prodotto
Per il prodotto di due numeri complessi in forma trigonometrica si ha:
Per il prodotto di due numeri complessi in forma trigonometrica si ha:
[ρ(cosα + jsenα)]·[ρ'(cosβ + jsenβ)] = ρ·ρ'·(cosα + jsenα)·(cosβ + jsenβ) =
= ρ·ρ'·(cosαcosβ + jcosαsenβ + jsenαcosβ + j2senαsenβ) =
= ρ·ρ'·[(cosαcosβ - senαsenβ) + j·(senαcosβ + cosαsenβ)] =
= ρ·ρ'·[cos(α + β) + j·sen(α + β)],
cioè
(30) [ρ(cosα + jsenα)]·[ρ'(cosβ + jsenβ)] = ρ·ρ'·[cos(α + β) + j·sen(α + β)].
Quindi:
-il prodotto di due numeri complessi in forma trigonometrica è un altro numero complesso, nella stessa forma, che ha per modulo il prodotto dei moduli e per argomento la somma degli argomenti.
Esempio
[ρ·(cosα + jsenα)]·[ρ'·(cosβ + jsenβ)]·[ρ''·(cosγ + jsenγ)] = ρ·ρ'·ρ''·[cos(α + β + γ) + j·sen(α + β + γ)].
2)-Potenza
Se si suppongono uguali gli n fattori di un prodotto di numeri complessi, si ha ha la potenza ennesima di uno di essi, espressa nella formula dovuta a Moivre:
ossia:
-la potenza di un numero complesso in forma trigonometrica è un altro numero complesso, nella stessa forma, che ha per modulo la potenza del modulo e per argomento quello del numero complesso dato moltiplicato per l'esponente della potenza.
3)-Quoziente
Per il quoziente di due numeri complessi in forma trigonometrica si ha:
cioè
ossia:
-il quoziente di un numero complesso nella forma trigonometrica è un altro numero complesso, nella stessa forma, che ha per modulo il quoziente dei moduli e per argomento la differenza degli argomenti.
Radici nme di un numero complesso
1)-Nel campo dei numeri complessi l'operazione di estrazione di radice è sempre possibile e ogni numero complesso ammette tante radici quante sono le unità dell'indice della stessa radice.
2)-Dato un numero complesso ρ·(cosα + jsenα), estrarre da esso la sua radice nma, significa trovare quell'altro numero complesso, di modulo r e argomento x incognite, che elevato alla potenza nma dia quello dato.
significa:
[r·(cosα + jsenα)]n = ρ·(cosx + jsenx).
Applicando la formula di Moivre (31), si ha:
rn·(cosnx + jsennx) = ρ·(cosα + jsenα),
dalla quale segue che dev'essere
rn = ρ,
cioè
con k = 0, 1, 2, ... (n - 1), in corrispondenza dei quali valori di k si ottengono le n radici nme del numero complesso.
Dunque è:
con k = 0, 1, 2, ... (n - 1).
Esempi
1°)-Calcolare:
Poichè -16 = 16·(cosπ + jsenπ), è:
con k = 0, 1.
Per k = 0, si ha:
per k = 1, si ha:
quindi
2°)-Calcolare:
Poichè
è:
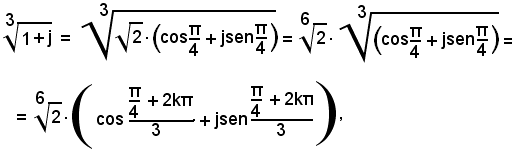
con k = 0, 1, 2.
Per k = 0, si ha:
per k = 1, si ha:
per k = 2, si ha:
Cenni di calcolo vettoriale
1)-Grandezze scalari
Vengono chiamate scalari quelle grandezze che sono completamente individuate da un numero positivo o negativo.
Ad esempio, una lunghezza, un volume, la temperatura, la carica elettrica, ecc.
La misura di una grandezza scalare è naturalmente riferita ad una prefissata unità.
Grandezze vettoriali
Vengono chiamate grandezze vettoriali quelle altre entità delle quali si fa uso continuo nella fisica, che sono caratterizzatie, oltre che da un valore numerico, anche da una direzione e da un verso o senso.
Ad esempio, le forze, la velocità, l'accelerazione, ecc.
2)-Rappresentazione di una grandezza vettoriale - Vettori
La
rappresentazione geometrica di due numeri complessi, vista in
precedenza, consente di pervenire alle considerazioni che seguono e che
hanno analogia con la rappresentazione geometrica dei numeri relativi, ossia con la posizione di un sistema di coordinate ascisse.
Infatti, si ricordi che quando su una retta sono fissati un punto origine O, un'unità di misura, segmento unitario Ou = 1 ed un verso, il numero x corrispondente ad un qualsiasi punto P della retta orientata, retta sostegno, non è altro che la misura del segmento orientato, con verso, cioè segno, OP.
Si ricordi inoltre che il numero complesso (a, b) = a + bj = ρ(cosα + jsenα) determina un certo punto P, punto immagine, che, a sua volta, considerato come estremo del segmento di origine O, determina il segmento orientato o vettore
.
Dunque, un vettore è caratterizzato da:
a)-un numero positivo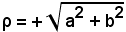
, detto modulo o intensità;
b)-una direzione, retta a cui appartiene il segmento OP;
c)-un verso, o senso, indicato dalla freccia < o >.
Tuttavia, bisogna tenere presente che due segmenti orientati o vettori si considerano uguali non quando hanno solo lo stesso modulo e lo stesso verso, ma anche la stessa direzione, mentre i segmenti orientati o vettori aventi lo stesso modulo e lo stesso verso, e non anche la stessa direzione, si dicono equipollenti.
Pertanto, quando si parla di vettore, senza aggiungere altro, o come è più preciso dire quando si parla di vettore libero, s'intende riferirsi ad uno qualsiasi dei suddetti vettori equipollenti.
In altri termini, il vettore libero è quell'entità definita per astrazione, che ha i caratteri comuni, misura, direzione e verso, a tutti gli equipollenti ad un dato sistema orientato.
Da quanto detto, segue che:
-un vettore è solo rappresentato da un segmento orientato ma non è confondibile con esso.
Quando invece, oltre ai suddetti termini caratteristici, si conviene di considerare dato anche il punto origine del vettore, questo si chiama vettore localizzato e, allora, è identificato dal segmento orientato.
Si conviene indicare un vettore, libero o localizzato con una lettera scritta in grassetto o tra parentesi:
u = (u), w = (w), ecc.,
mentre il suo modulo è indicato dalla stessa lettera scritta in corsivo o senza parentesi o ancora con
modu, |u|.
Un vettore di modulo unitario si chiama versore.
3)-Definizione- Prodotto di un vettore per un numero reale
Il prodotto di un vettore u per un numero reale k è l'altro vettore che ha:
a)-la stessa direzione di u;
b)-lo stesso verso, o quello opposto ad u, a seconda che k sia maggiore oppure minore di zero;
c)-modulo uguale a k·|u|.
Se in particolare k = -1, si ottiene il vettore di verso opposto a quello dato e lo si indica con -u.
Interpretazione vettoriale della somma e del prodotto di due numeri complessi
1)-Somma
Siano P e P' i punti immagine dei due numeri complessi (a, b) e (a', b') e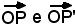
i vettori applicati che essi individuano.
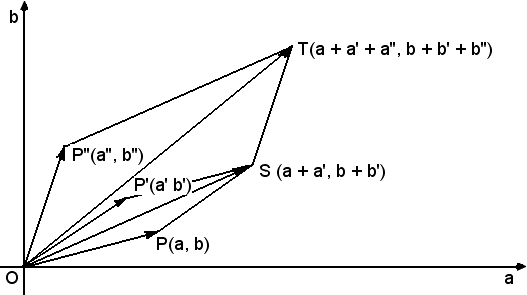
Costruito il parallelogramma OPTP', la sua diagonale, uscente dal punto O origine comune, individua il vettore
detto somma o risultante dei due dati, in quanto il punto T è il
punto immagine del numero complesso (a + a', b + b') = (a, b) + (a',
b').
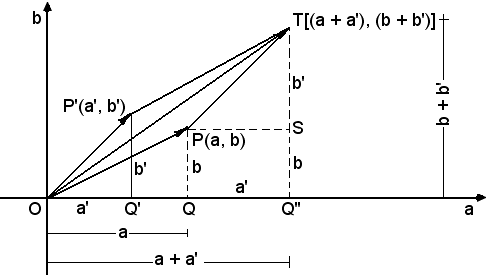
Infatti, dalla figura suddetta e dalla considerazione che
sono equipollenti, si ha:
OQ' = QQ'' = a',
OP = Q''S = b,
Q'P' = ST = b',
quindi
OQ'' = OQ + QQ'' = a + a',
Q''T = Q''S + ST = b + b',
cioè
T = (a + a', b + b'),
come volevasi dimostrare.
Nel caso di più numeri complessi, ossia di più vettori applicati nello stesso punto, basta applicare successivamente la regola del parallelogramma vista, che, come è noto dalla fisica, equivale alla costruzione del poligono delle forze.
Prodotto
a)-E' noto che il prodotto dei due numeri complessi, in forma trigonometrica è espresso dalla formula:
[ρ(cosα + jsenα)]·[ρ'(cosβ + jsenβ)] = ρ·ρ'·[cos(α + β) + jsen(α + β)].
Dalla stessa formula risulta che il vettore applicato, immagine del prodotto di due numeri complessi di moduli ρ e ρ' e argomenti α e β, ha per modulo il prodotto ρ·ρ' dei moduli ed è inclinato sull'asse reale di un angolo di ampiezza α + β, ossia si ottiene facendo ruotare la direzione del 1° vettore di un angolo uguale all'argomento β del secondo vettore.
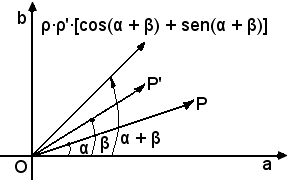
b)-Non altrettanto immediata è l'interpretazione del prodotto di due numeri complessi quando si parte dalla forma algebrica, ossia dalle coordinate cartesiane dei loro punti immagine. Tale trattazione è propria della meccanica e non dell'analisi matematica, per cui si tralascia.
Infatti, si ricordi che quando su una retta sono fissati un punto origine O, un'unità di misura, segmento unitario Ou = 1 ed un verso, il numero x corrispondente ad un qualsiasi punto P della retta orientata, retta sostegno, non è altro che la misura del segmento orientato, con verso, cioè segno, OP.
Si ricordi inoltre che il numero complesso (a, b) = a + bj = ρ(cosα + jsenα) determina un certo punto P, punto immagine, che, a sua volta, considerato come estremo del segmento di origine O, determina il segmento orientato o vettore
.Dunque, un vettore è caratterizzato da:
a)-un numero positivo
, detto modulo o intensità;b)-una direzione, retta a cui appartiene il segmento OP;
c)-un verso, o senso, indicato dalla freccia < o >.
Tuttavia, bisogna tenere presente che due segmenti orientati o vettori si considerano uguali non quando hanno solo lo stesso modulo e lo stesso verso, ma anche la stessa direzione, mentre i segmenti orientati o vettori aventi lo stesso modulo e lo stesso verso, e non anche la stessa direzione, si dicono equipollenti.
Pertanto, quando si parla di vettore, senza aggiungere altro, o come è più preciso dire quando si parla di vettore libero, s'intende riferirsi ad uno qualsiasi dei suddetti vettori equipollenti.
In altri termini, il vettore libero è quell'entità definita per astrazione, che ha i caratteri comuni, misura, direzione e verso, a tutti gli equipollenti ad un dato sistema orientato.
Da quanto detto, segue che:
-un vettore è solo rappresentato da un segmento orientato ma non è confondibile con esso.
Quando invece, oltre ai suddetti termini caratteristici, si conviene di considerare dato anche il punto origine del vettore, questo si chiama vettore localizzato e, allora, è identificato dal segmento orientato.
Si conviene indicare un vettore, libero o localizzato con una lettera scritta in grassetto o tra parentesi:
u = (u), w = (w), ecc.,
mentre il suo modulo è indicato dalla stessa lettera scritta in corsivo o senza parentesi o ancora con
Un vettore di modulo unitario si chiama versore.
3)-Definizione- Prodotto di un vettore per un numero reale
Il prodotto di un vettore u per un numero reale k è l'altro vettore che ha:
a)-la stessa direzione di u;
b)-lo stesso verso, o quello opposto ad u, a seconda che k sia maggiore oppure minore di zero;
c)-modulo uguale a k·|u|.
Se in particolare k = -1, si ottiene il vettore di verso opposto a quello dato e lo si indica con -u.
Interpretazione vettoriale della somma e del prodotto di due numeri complessi
1)-Somma
Siano P e P' i punti immagine dei due numeri complessi (a, b) e (a', b') e
i vettori applicati che essi individuano.Costruito il parallelogramma OPTP', la sua diagonale, uscente dal punto O origine comune, individua il vettore
detto somma o risultante dei due dati, in quanto il punto T è il
punto immagine del numero complesso (a + a', b + b') = (a, b) + (a',
b').Infatti, dalla figura suddetta e dalla considerazione che
sono equipollenti, si ha:OQ' = QQ'' = a',
OP = Q''S = b,
Q'P' = ST = b',
quindi
OQ'' = OQ + QQ'' = a + a',
Q''T = Q''S + ST = b + b',
cioè
T = (a + a', b + b'),
come volevasi dimostrare.
Nel caso di più numeri complessi, ossia di più vettori applicati nello stesso punto, basta applicare successivamente la regola del parallelogramma vista, che, come è noto dalla fisica, equivale alla costruzione del poligono delle forze.
Prodotto
a)-E' noto che il prodotto dei due numeri complessi, in forma trigonometrica è espresso dalla formula:
Dalla stessa formula risulta che il vettore applicato, immagine del prodotto di due numeri complessi di moduli ρ e ρ' e argomenti α e β, ha per modulo il prodotto ρ·ρ' dei moduli ed è inclinato sull'asse reale di un angolo di ampiezza α + β, ossia si ottiene facendo ruotare la direzione del 1° vettore di un angolo uguale all'argomento β del secondo vettore.
b)-Non altrettanto immediata è l'interpretazione del prodotto di due numeri complessi quando si parte dalla forma algebrica, ossia dalle coordinate cartesiane dei loro punti immagine. Tale trattazione è propria della meccanica e non dell'analisi matematica, per cui si tralascia.