MIKY & GENNY
PRINCIPI FONDAMENTALI, PROPRIETA' E DISEQUAZIONI ---> INDICE
Principi fondamentali
Quando due numeri relativi a e b non sono uguali, significa che uno di essi è maggiore oppure minore dell'altro e si scrive rispettivamente:
(1) a > b, (1') a < b.
Le relazioni scritte si chiamano disuguaglianze ed esprimono che:
-nel caso (1), la differenza a - b è un numero positivo,
-nel caso (1'), la differenza a - b è un numero negativo.
Le disuguaglianze (1) e (1') sono rispettivamente equivalenti alle seguenti:
(2) a - b > 0, (2') a - b < 0.
ProprietàSe a, b, c, m sono numeri reali, valgono le seguenti proposizioni:
1)-se a > b, segue b < a e viceversa (principio di simmetria);
2)-se a > b, b = c, segue a > c e viceversa (principio di sostituzione);
3)-se a > b, segue a + m > b + m e viceversa (principio di addizione);
4)-se ab > 0, segue a > 0 e b > 0 oppure a < 0 e b < 0 e viceversa;
da ab < 0, segue a > 0 e b < 0 oppure a < 0 e b > 0 e viceversa (principio dei segni);
5)-se m > 0, a > b, segue am > bm e viceversa, inoltre se m < 0, a > b, segue am < bm e viceversa (principio di moltiplicazione);
6)-se a > b, c > d, segue ac > bd quando b e c sono positivi, oppure quando sono positivi a e d. Infatti, nel primo caso, essendo c > 0, da a > b segue ac > bc e poichè b > 0, da c > d segue bc > bd. Dunque, ac > bc > bd per cui ac > bd. Lo stesso risultato si ottiene nel secondo caso.
7)-se a, b sono due numeri positivi ed n è intero positivo, da a > b segue an > bn.
Infatti, scrivendo n volte la relazione a > b e moltiplicando membro a membro, per la (6) si ha an > bn. Viceversa, da an > bn non sempre si deduce a > b. Ciò si ottiene se a e b sono entrambi positivi, giacchè in tal caso, non potendo essere a = b, perchè risulterebbe an = bn, nè a < b perchè in base alla proposizione sopra dimostrata si avrebbe an < bn, rimane a > b.
Esempio
Da (-4)2 > 22 non si ha -4 > 2 perchè i numeri -4 e 2 non sono entrambi positivi.
Precisamente, da an > bn non si deduce a > b se n è pari, mentre se n è dispari, si ha ugualmente a > b.
Infatti, se n è dispari, si ha l'identità:
an - bn = (a - b)(an-1 + an-2 b + an-3 b2 + ... + bn-1)
e il polinomio
è positivo per qualsiasi valore di a e b, per cui da
cioè da
segue
cioè
come volevasi dimostrare.
8)-se a > b ed i numeri a e b hanno lo stesso segno, si ha:
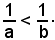
Infatti, la differenza

essendo ab > 0, sempre per aver supposto a e b concordi, mentre b - a < 0 perchè per ipotesi a > b.
Disequazioni
Definizione - Si chiama disequazione o inequazione una relazione del tipo
(1) A > B, (1') A < B,
dove A e B sono due espressioni (funzioni) contenenti una o più variabili.
Risolvere una disequazione significa determinare le eventuali soluzioni, cioè quei valori delle variabili per i quali la (1) o la (1') è verificata.
Equazione associata ad una disequazioneDefinizione
- Si chiama equazione associata ad una disequazione quella che si
ottiene sostituendo il segno di uguaglianza a quello di disuguaglianza
nella (1) o nella (1').
Disequazioni equiverse
Definizione - Si chiamano disequazioni equiverse due disequazioni del tipo
(2) A > B e C > D; oppure (2') A < B e C < D.
Disequazioni controverse
Definizione - Si chiamano disequazioni controverse due disequazioni del tipo
(3) A > B e C < D; oppure (3') A < B e C > D.
Disequazione conseguenza di un'altra disequazione
Definizione - Si chiama disequazione conseguenza di un'altra disequazione, quando ogni soluzione della prima è anche soluzione della seconda.
Disequazioni equivalenti
Definizione - Due disequazioni si dicono equivalenti quando ciascuna di esse è conseguenza dell'altra.
Nel seguito ci si occuperà delle disequazioni ad una sola variabile o incognita e quindi del tipo:
(4) A(x) > 0, (4') A(x) < 0.
Riduzioni di disequazioni
Applicando alle disequazioni le proprietà viste in precedenza, si hanno i seguenti teoremi.
Teorema 1 - Scambiando i membri di una disequazione, se ne ottiene un'altra controversa alla prima.
Da

si ha:

Teorema 2 (principio di sostituzione) - Se ad entrambi o ad uno solo dei due membri di una disequazione si sostituisce un'espressione uguale, si ottiene una disequazione equivalente ed equiversa alla data.
Da

si ha:

In virtù di questo principio, in ciascuno dei due membri di una disequazione, si possono eseguire le operazioni indicate.
Teorema 3 (principio di addizione) - Se ad entrambi i membri di una disequazione si aggiunge una stessa espressione, si ottiene una disequazione equivalente a quella data.
Da

si ha:

In base a tale principio si può trasportare un termine da un menbro all'altro di una disequazione, purchè lo si cambi di segno, così come si faceva nelle equazioni.
Teorema 4 (principio dei segni)- La disequazione
A(x) · B(x) > 0
è equivalente ai sistemi
 mentre
mentre
A(x) · B(x) < 0
è equivalente ai sistemi

Teorema 5 (principio della moltiplicazione) - Moltiplicando ambo i membri di una disequazione per un'espressione numericamente diversa da zero e di segno determinato, si ha una disequazione equivalente ed equiversa o controversa alla data, a seconda che l'espressione moltiplicatrice sia positiva o negativa per qualsiasi valore attribuito alla variabile in essa contenuta.
Cioè se è la disequazione data e M(x) è l'epressione sempre maggiore di zero o sempre minore di zero, si ha:
è la disequazione data e M(x) è l'epressione sempre maggiore di zero o sempre minore di zero, si ha:

Se invece, l'espressione M(x) assume per valori assegnati alla variabile x tanto valori positivi che negativi, non solo la disequazione A(x) > 0 non è equivalente nè alla A(x) · M(x) > 0 nè alla A(x) · M(x) < 0, ma non si può neppure dire che le siano conseguenza della A(x) > 0.
siano conseguenza della A(x) > 0.
Infatti, per essere soddisfatta la disequazione
(1) A(x) · M(x) > 0,
occorre che siano soddisfatti i sistemi di disequazioni:

e le soluzioni del sistema (2) non sono, in generale, tutte quelle che soddisfano la A(x) > 0, ovvero la moltiplicazione ha fatto perdere delle soluzioni alla disequazione A(x) > 0; per contro ha fatto acquistare alla stessa disequazione tutte le soluzioni del sistema (3). Quindi A(x) · M(x) > 0 non è equivalente alla A(x) > 0.
Risoluzione delle disequazioni razionali intere di 1° grado

dove A(x) è un polinomio in x.
Se tale polinomio è di 1° grado, si ha la disequazione del tipo

equivalente alla

a sua volta equivalente alla

a seconda che a > 0, oppure a < 0.
Poichè x = -b/a è la radice dell'equazione ax + b =0, associata alla disequazione data, le soluzioni di quest'ultima sono tutti i valori di x che soddisfano la (4) o la (4').
Scomposizione in fattori del trinomio di 2° grado
Si ricordi che l'equazione di 2° grado
ax2 + bx + c = 0,
avente il discriminante
Δ = b2 - 4ac > 0,
ammette radici reali date dalla formula risolutiva

avendo indicato con ciò x1 < x2.
Nel caso in cui Δ = 0, la radice reale doppia sarà indicata con
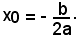
Inoltre è noto che le radici dell'equazione di 2° grado godono delle seguenti proprietà:
1)-la loro somma è uguale al secondo coefficiente, cambiato di segno, diviso il primo:

2)-il loro prodotto è uguale al termine noto, con lo stesso segno, diviso il primo coefficiente:

3)-considerando il trinomio di 2° grado:
A(x) = ax2 + bx + c,
nell'ipotesi che l'equazione da esso ottenuta uguagliandolo a zero ammetta radici reali e distinte, cioè sia Δ > 0, senza alterarlo, lo si può trasformare come segue:

Dunque, si ha:
A(x) = ax2 + bx + c = a(x - x1)(x - x2),
cioè un trinomio di 2° grado, avente Δ > 0, si scompone nel prodotto di tre fattori, il 1° uguale al primo coefficiente, il 2° uguale alla differenza tra l'incognita e la prima radice, il 3° uguale alla differenza tra l'incognita e la seconda radice.
Nota bene
Durante la trasformazione sono stati effettuati i seguenti passaggi:
-si è messo in evidenza il cofficiente a,
-si è effettuata la sostituzione delle espressioni ottenute dalle proprietà delle radici,
-si è sviluppato il contenuto della parentesi interna,
-si sono raccolti, a gruppi di termini, i fattori comuni,
-si è raccolto ancora il fattore comune x - x1.
4)-Nel caso in cui Δ = 0, per cui x1 = x2 = x0, la formula precedente diventa:
A(x) = ax2 + bx + c = a(x - x0)(x - x0) = a(x - x0)2.
5)-Nel caso in cui Δ < 0, non esistono radici reali per l'equazione A(x) = 0 e il trinomio si trasforma come segue:

Dunque, in tal caso, si ha:

Nota bene
Durante la trasformazione sono stati effettuati i seguenti passaggi:
-si è messo in evidenza il cofficiente a,
-si è moltiplicato per 2 il numeratore ed il denominatore della frazione b/a e aggiunto e sottratto b2/4a2.
Segno del trinomio di secondo grado avente Δ > 0
1)-Si consideri il trinomio tipico di 2° grado:
A(x) = ax2 + bx + c.
Nel caso in cui Δ > 0, per quanto detto in precedenza, si può considerare scomposto in fattori:
A(x) = ax2 + bx + c = a(x - x1)(x - x2),
dove x1 e x2, x1 < x2, sono le radici dell'equazione A(x) =0.
Riportati i numeri x1 e x2 su una retta orientata, in base ad un fissato sistema di coordinate ascisse

il segmento di origine x1 ed estremo x2, si chiama intervallo delle radici.
Si vuole vedere quale segno assume il trinomio A(x) quando la variabile x varia rispetto all'intervallo delle radici, cioè quando si danno alla x valori esterni, a sinistra e a destra dell'intervallo, oppure interni ad esso o, addirittura, si supponga x = x1 e x = x2, cioè x coincidente con gli estrtemi dell'intervallo.
Distinguendo tutti i casi possibili, si vedrà quali di essi, portando ad identiche conclusioni, potranno essere raggruppati.
2)-x esterna a sinistra dell'intervallo:
x < x1 < x2.
In tal caso è:
x - x1 < 0, x - x2 < 0
ed il prodotto di tali fattori è maggiore di zero.
Quindi in:
A(x) = ax2 + bx + c = a(x - x1)(x - x2),
se a > 0, sarà A(x) > 0,
se a < 0, sarà A(x) < 0,
ossia per
x < x1 < x2
il trinomio ha lo stesso segno di quello del 1° coefficiente.3)-x esterna a destra dell'intervallo:
x > x2 > x1.
In tal caso è:
x - x1 > 0, x - x2 > 0
e quindi ancora
4)-x interna all'intervallo:
x1 < x < x2.
In tal caso è:
x - x1 > 0, x - x2 < 0,
per cui
(x - x1)(x - x2) < 0,
e quindi in
A(x) = a(x - x1)(x - x2)
se a > 0, sarà A(x) < 0,
se a < 0, sarà A(x) > 0,
ossia per
x1 < x < x2,
il trinomio ha segno contrario a quello del primo coefficiente.
Viceversa, un trinomio A(x), avente Δ > 0, assume segno contrario a quello del primo coefficiente per valori della variabile interni all'intervallo delle radici dell'equazione A(x) = 0.
In formula:
a·A(x) < 0, per x1 < x < x2.
5)-se x = x1 oppure x = x2 in
A(x) = ax2 + bx + c = a(x - x1)(x - x2),
annullandosi uno dei fattori, è nullo tutto il prodotto, cioè è
A(x) = 0,
e quindi, per valori della x uguali ad una delle radici, il trinomio si annulla.
Viceversa, un trinomio A(x), avente Δ > 0, si annulla per valori della variabile uguali ad una delle radici dell'equazione A(x) = 0.
In formula:
a·A(x) = 0, per x = x1, oppure x = x2.
6)-Riepilogo
Per i trinomi aventi Δ > 0 possono quindi verificarsi tutti i casi e cioè:
a)-possono assumere lo stesso segno di quello del 1° coefficiente:
a·A(x) > 0, per x < x1 .... < x2 < x;
b)-possono assumere il segno contrario a quello del 1° coefficiente:
a·A(x) < 0, per x1 < x < x2;
c)-possono annullarsi:
a·A(x) = 0, per x = x1 e per x = x2;
Segno del trinomio di secondo grado avente Δ = 0
1)-Si consideri il trinomio tipico di 2° grado
A(x) = ax2 + bx + c.
Quando Δ = 0, come già visto, lo si può considerare scomposto in fattori come segue:
A(x) = ax2 + bx + c = a(x - x0)2.
In questo caso, sulla retta orientata, si riporta il solo punto di ascissa x0:

e si fa variare la x rispetto ad esso; ciò significa condiderare i casi in cui è
x < x0, x > x0, x = x0.
2)-Se x < x0, è x - x0 < 0; se x > x0, x - x0 > 0, ma in entrambi i casi è
(x - x0)2 > 0,
e quindi in
A(x) = ax2 + bx + c = a(x - x0)2,
ossia per x ≠ x0, x < x0 oppure x > x0, il trinomio ha lo stesso segno di quello del 1° coefficiente.
Viceversa, un trinomio A(x), avente Δ = 0, assume lo stesso segno di quello del 1° coefficiente per valori della variabile diversi dalla radice dell'equazione A(x) = 0.
In formula:
a·A(x) > 0, per x ≠ x0.
3)-Se x = x0, è x - x0 = 0; e quindi anche
A(x) = ax2 + bx + c = a(x - x0)2 = 0,
cioè per il valore della variabile uguale alla radice il trinomio si annulla.
Viceversa, un trinomio A(x), avente Δ = 0, si annulla, se la variabile diventa uguale alla radice dell'equazione A(x) = 0.
In formula:
a·A(x) = 0, per x = x0.
4)-Non essendosi trovato il caso in cui il trinomio assume il segno contrario a quello del 1° coefficiente, significa che detto caso per i trinomi aventi Δ = 0 è impossibile, cioè:
a·A(x) < 0 impossibile, se Δ = 0.
Segno del trinomio di secondo grado avente Δ < 0
1)-Si consideri il trinomio A(x) nel caso in cui sia Δ < 0 e quindi, per quanto già visto, risulta:

Non essendovi radici reali nell'equazione A(x) = 0, non vi è alcun riferimento per i valori della variabile x, è ciò significa che per qualsiasi valore della variabile accade che l'espressione nella parentesi quadra assume sempre valori positivi, in quanto il 1° termine, essendo un quadrato è sempre positivo o nullo ed il 2° termine -Δ/4a2 è anch'esso sempre positivo, proprio perchè il numeratore della frazione è Δ < 0 per ipotesi, per cui -Δ > 0 e il denominatore è sempre positivo essendo un quadrato.
Quindi, se l'espressione suddetta è sempre positiva, sarà:
a·A(x) > 0, se a > 0;
a·A(x) < 0, se a < 0,
ossia, per qualsiasi valore della x, il trinomio ha sempre lo stesso segno di quello del 1° coefficiente.
Viceversa, un trinomio A(x), avente Δ < 0, assume sempre lo stesso segno di quello del 1° coefficiente per qualsiasi valore della variabile.
In formula:
a·A(x) > 0, per qualsiasi x.
Non si possono verificare altri casi, cioè:
a·A(x) < 0, impossibile;
a·A(x) = 0, impossibile.
Risoluzione delle disequazioni razionali intere di 2° grado
1)-Una disequazione intera di 2° grado si presenta nella forma tipica:

dove a, b, c sono numeri reali, dei quali, senz'altro, a ≠ 0.
Si può considerare addirittura a > 0 in quanto, se così non fosse, basterebbe, come è noto, cambiare tutti i segni ed il verso della disequazione per riportarsi ad un'altra equivalente alla data ed avente a > 0.
2)-La risoluzione di una disequazione, del tipo

consiste nel trovare i valori della variabile per cui è
ax2 + bx + c = > 0,
ossia, il trinomio, 1° membro, assume lo stesso segno di quello del 1° coefficiente, oppure è
ax2 + bx + c = < 0,
ossia, il trinomio, 1° membro, assume il segno contrario a quello del 1° coefficiente.
Pertanto, la risoluzione di una disequazione di 2° grado è, in tal modo, riportata alla ricerca del segno del trinomio, 1° membro, rispetto a quello del suo 1° coefficiente.
Esempi
1°) 2x2 - 3x + 1 = > 0.
Si vuole che il trinomio assuma lo stesso segno del 1° coefficiente.
Poichè risulta
Δ = 9 - 8 = 1 > 0,
le radici reali e distinte dell'equazione associata, sono:

e quindi
2x2 - 3x + 1 > 0,
per

2°) 2x2 - 5x + 3 = < 0.
Si vuole che il trinomio assuma il segno contrario del 1° coefficiente.
Poichè risulta
Δ = 25 - 24 = 1 > 0,
le radici reali e distinte dell'equazione associata, sono:

e quindi
2x2 - 5x + 3 = < 0
per

3°) 4x2 - 4x + 1 > 0.
Si vuole che il trinomio assuma lo stesso segno del 1° coefficiente.
Poichè risulta

la radice reale doppia dell'equazione associata, è:

e quindi
4x2 - 4x + 1 > 0
per

4°) 4x2 - 12x + 9 < 0.
Si vuole che il trinomio assuma il segno contrario a quello del 1° coefficiente.
Poichè risulta

la radice reale doppia dell'equazione associata, è:

e quindi
4x2 - 12 + 9 < 0
è impossibile.
5°) x2 - 3x + 7 > 0.
Si vuole che il trinomio assuma lo stesso segno di quello del 1° coefficiente.
Poichè risulta
Δ = 9 - 28 = -19 < 0,
l'equazione associata non ha radici reali e quindi è
x2 - 3x + 7 > 0
per qualsiasi valore di x.
6°) x2 - 2x + 9 < 0.
Si vuole che il trinomio assuma segno contrario di quello del 1° coefficiente.
Poichè risulta

l'equazione associata non ha radici reali e quindi
x2 - 2x + 9 < 0
è impossibile.
7°) 3x2 - 10x + 3 > 0.
Poichè risulta

le radici reali e distinte dell'equazione associata, sono:

La disequazione è soddisfatta per valori della variabile esterni all'intervallo delle radici, cioè:

8°) x2 - 5x + 2 < 0.
Poichè risulta
Δ = 25 - 8 = 17 > 0,
le radici reali e distinte dell'equazione associata, sono:

La disequazione è soddisfatta per valori della variabile interni all'intervallo delle radici, cioè:

9°) x2 - 6x + 9 > 0.
Poichè risulta

le radici reali e coincidenti dell'equazione associata, sono:
x1 = x2 = x0 = 3.
La disequazione è soddisfatta per tutti i valori della x diversi da 3, cioè per tutti i punti della retta escluso quello di ascissa 3:

10°) x2 - 8x + 16 < 0.
Poichè risulta

x0 = 4.
La disequazione è impossibile.
Forme miste di disequazioni
Le forme A(x) ≥ 0 oppure A(x) ≤ 0 si chiamano forme miste di disequazioni e significano che sono da considerare, contemporaneamente, le soluzioni delle disequazioni e delle equazioni ad esse associate, ossia le soluzioni dei sistemi misti:

Esempi
1°) x2 - 7x + 6 ≥ 0.
Poichè risulta
Δ = 49 - 24 = 25 > 0,
le radici reali e distinte dell'equazione associata, sono:

La disequazione è soddisfatta da:

2°) 2x2 - 3x - 2 ≤ 0.
Poichè risulta
Δ = 9 + 16 = 25 > 0,
le radici reali e distinte dell'equazione associata, sono:

La disequazione è soddisfatta da:

Sistemi di disequazioni
1)-Generalità
Il sistema di disequazioni è costituito da due o più disequazioni nella stessa incognita.
Risolverlo significa trovare, se esistono, le soluzioni comuni a tutte le disequazioni.
Nel caso in cui non esistano tali soluzioni comuni, il sistema si dice impossibile e le disequazioni si dicono incompatibili.
Per risolvere un sistema di disequazioni, si devono risolvere le singole disequazioni e poi si devono confrontare le condizioni soddisfacenti a ciascuna di esse, per trovare quelle altre condizioni soddisfacenti contemporaneamente tutte le disequazioni del sistema.
Per la ricerca delle condizioni comuni è molto utile riferirsi alla rappresentazione già usata negli esempi 7°, 8° e 9° precedenti.
Le soluzioni del sistema sono date, in tal modo, da quei valori dell'incognita i cui punti immagine, nel sistema di coordinate ascisse, si trovano negl'intervalli comuni a tutte le condizioni trovate, tante quante sono le disequazioni del sistema.
2)-Esempi di risoluzione di sistemi di disequazioni intere

e nel sistema coordinate ascisse, si ha:


e nel sistema coordinate ascisse, si ha:


e nel sistema coordinate ascisse, si ha:


è equivalente a

e nel sistema coordinate ascisse, si ha:


è equivalente a

e nel sistema coordinate ascisse, si ha:

cioè, il sistema è impossibile.

e nel sistema coordinate ascisse, si ha:

Disequazioni razionali frazionarie
1)-Generalità
Una disequazione si dice frazionaria o fratta quando l'incognita compare al denominatore della frazione.
Queste disequazioni sono del tipo:

avendo indicato con N(x) e D(x), rispettivamente numeratore e denominatore della (1) e della (1'), due polinomi nella variabile x. Poichè una frazione è positiva quando i suoi termini sono concordi, la (1) diventa equivalente ai due sistemi

le cui soluzioni sono quelle della (1).
Analogamente, sapendo che una frazione è negativa quando i suoi termini sono discordi, la (1') diventa equivalente ai due sistemi

Pertanto la risoluzione delle disequazioni razionali fratte si riporta a quella dei sistemi di disequazioni.
2)-Esempi di risoluzione di disequazioni razionali fratte

è equivalente ai due sistemi:

quindi:


è equivalente ai due sistemi:

quindi:


è equivalente ai due sistemi:



è equivalente ai due sistemi:

Il primo sistema è perciò soddisfatto per:


Si comincia con i seguenti calcoli:



equivalente a

a sua volta equivalente ai due sistemi:


Altre disequazioni risolvibili mediante sistemi
Sono quelle della forma:
(1) A(x)·B(x) > 0, (1') A(x)·B(x) < 0,
ove A(x) e B(x) indicano sempre espressioni razionali intere, polinomi, nella variabile x.
La (1), per il principio dei segni, è equivalente ai sistemi:

la cui risoluzione è nota.
La (1'), per lo stesso principio, è equivalente ai sistemi:

la cui risoluzione è anch'essa nota.
Nota bene
Per quanto detto in precedenza, si ha l'equivalenza, rispettivamente, tra le disequazioni:

(1°) (2x + 1)(3x - 2) > 0.
La disequazione è equivalente ai sistemi.

(2°) (4x - 3)(2x - 1) < 0.
La disequazione è equivalente ai sistemi:

Disequazioni irrazionali
Generalità
Si chiamano disequazioni irrazionali quelle del tipo:

con n intero positivo e A(x), B(x) espressioni razionali della variabile x.
Nei tipi suddetti, si è supposto il radicale positivo, perchè, nel caso contrario, lo si farebbe diventare tale, cambiando, come è noto, il segno di ambo i membri della disequazione e il verso della stessa. Per la risoluzione di tali disequazioni si devono tenere presenti i principi fondamentali delle disuguaglianze.
Teorema - Per n intero positivo dispari, le disequazioni

sono equivalenti.
Infatti, si passa dalla (1) alla (1') elevando al quadrato ambo i membri alla potenza nma e poichè è dispari, l'elevamento a potenza non altera il segno della disequazione.
Esempi

La disequazione è equivalente a:
(x + 2)3 > x3 + 4x2 + 7x + 6,
x3+ 6x2 + 12x + 8 > x3 + 4x2 + 7x + 6,
2x2 + 5x + 2 > 0.
Le radici dell'equazione associata a quest'ultima disequazione sono x = -2, x = -1/2 e, pertanto, la disequazione proposta è soddisfatta per
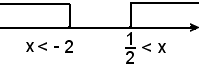

La disequazione è equivalente a:
(x + 1)3 < x3 + 2x2 + 5x + 4,
x3+ 3x2 + 3x + 1 < x3 + 2x2 + 5x + 4,
x2 - 2 x - 3 < 0.
Le radici dell'equazione associata a quest'ultima disequazione sono x = -1, x = 3 e, pertanto, la disequazione proposta è soddisfatta per

Teorema - Per n intero positivo pari, la disequazione

è equivalente al sistema:

le cui disequazioni costituiscono le condizioni verificate per le quali è soddisfatta la (1).
Infatti, la B(x) ≥ 0 deriva dalla realtà del radicale ed essa comporta che sia anche

Infine, essendo i due membri della (1) non negativi, è lecito elevarli alla stessa potenza nma, per cui An(x) < B(x).
Esempi

La disequazione è equivalente al sistema:

La prima disequazione mista è soddisfatta per

la seconda per x > 1, la terza per x > 5/3.
Unificando le condizioni, si ha:

La disequazione proposta è quindi verificata per:


La disequazione è equivalente al sistema:

La prima disequazione mista è soddisfatta per

la seconda per x > 1,
la terza per

Unificando le condizioni, si ha:

Non essendovi condizioni comuni alle tre disequazioni, ossia non essendovi valori della variabile soddisfacenti simultaneamente le tre disequazioni del sistema, la disequazione proposta, equivalente al sistema, è impossibile.
Teorema - Se n è intero positivo pari, la disequazione

è equivalente a ciascuno dei sistemi:

Infatti, la realtà del radicale comporta la condizione B(x) ≥ 0 e, quindi, l'altra

Allora nella (1), essendo il 2° membro positivo, si può avere che il 1° membro sia negativo è cioè il sistema:

e si può avere che il 1° membro sia anch'esso positivo e, quindi, elevando ambo i membri alla potenza nma, si ha il sistema

Esempi

La disequazione è equivalente a ciascuno dei due sistemi

La disequazione proposta è, dunque, soddisfatta per
x ≤ 1 ... 5 < x.

La disequazione è equivalente a ciascuno dei due sistemi

La disequazione proposta è, dunque, soddisfatta per
x ≤ -7.
Quando due numeri relativi a e b non sono uguali, significa che uno di essi è maggiore oppure minore dell'altro e si scrive rispettivamente:
(1) a > b, (1') a < b.
Le relazioni scritte si chiamano disuguaglianze ed esprimono che:
-nel caso (1), la differenza a - b è un numero positivo,
-nel caso (1'), la differenza a - b è un numero negativo.
Le disuguaglianze (1) e (1') sono rispettivamente equivalenti alle seguenti:
(2) a - b > 0, (2') a - b < 0.
Proprietà
1)-se a > b, segue b < a e viceversa (principio di simmetria);
2)-se a > b, b = c, segue a > c e viceversa (principio di sostituzione);
3)-se a > b, segue a + m > b + m e viceversa (principio di addizione);
4)-se ab > 0, segue a > 0 e b > 0 oppure a < 0 e b < 0 e viceversa;
da ab < 0, segue a > 0 e b < 0 oppure a < 0 e b > 0 e viceversa (principio dei segni);
5)-se m > 0, a > b, segue am > bm e viceversa, inoltre se m < 0, a > b, segue am < bm e viceversa (principio di moltiplicazione);
6)-se a > b, c > d, segue ac > bd quando b e c sono positivi, oppure quando sono positivi a e d. Infatti, nel primo caso, essendo c > 0, da a > b segue ac > bc e poichè b > 0, da c > d segue bc > bd. Dunque, ac > bc > bd per cui ac > bd. Lo stesso risultato si ottiene nel secondo caso.
7)-se a, b sono due numeri positivi ed n è intero positivo, da a > b segue an > bn.
Infatti, scrivendo n volte la relazione a > b e moltiplicando membro a membro, per la (6) si ha an > bn. Viceversa, da an > bn non sempre si deduce a > b. Ciò si ottiene se a e b sono entrambi positivi, giacchè in tal caso, non potendo essere a = b, perchè risulterebbe an = bn, nè a < b perchè in base alla proposizione sopra dimostrata si avrebbe an < bn, rimane a > b.
Esempio
Da (-4)2 > 22 non si ha -4 > 2 perchè i numeri -4 e 2 non sono entrambi positivi.
Precisamente, da an > bn non si deduce a > b se n è pari, mentre se n è dispari, si ha ugualmente a > b.
Infatti, se n è dispari, si ha l'identità:
an - bn = (a - b)(an-1 + an-2 b + an-3 b2 + ... + bn-1)
e il polinomio
an-1 + an-2 b + an-3 b2 + ... + bn-1
è positivo per qualsiasi valore di a e b, per cui da
an > bn > 0,
cioè da
an > bn
segue
a - b > 0,
cioè
a > b,
come volevasi dimostrare.
8)-se a > b ed i numeri a e b hanno lo stesso segno, si ha:
Infatti, la differenza
essendo ab > 0, sempre per aver supposto a e b concordi, mentre b - a < 0 perchè per ipotesi a > b.
Disequazioni
Definizione - Si chiama disequazione o inequazione una relazione del tipo
(1) A > B, (1') A < B,
dove A e B sono due espressioni (funzioni) contenenti una o più variabili.
Risolvere una disequazione significa determinare le eventuali soluzioni, cioè quei valori delle variabili per i quali la (1) o la (1') è verificata.
Equazione associata ad una disequazione
Disequazioni equiverse
Definizione - Si chiamano disequazioni equiverse due disequazioni del tipo
(2) A > B e C > D; oppure (2') A < B e C < D.
Disequazioni controverse
Definizione - Si chiamano disequazioni controverse due disequazioni del tipo
(3) A > B e C < D; oppure (3') A < B e C > D.
Disequazione conseguenza di un'altra disequazione
Definizione - Si chiama disequazione conseguenza di un'altra disequazione, quando ogni soluzione della prima è anche soluzione della seconda.
Disequazioni equivalenti
Definizione - Due disequazioni si dicono equivalenti quando ciascuna di esse è conseguenza dell'altra.
Nel seguito ci si occuperà delle disequazioni ad una sola variabile o incognita e quindi del tipo:
(4) A(x) > 0, (4') A(x) < 0.
Riduzioni di disequazioni
Applicando alle disequazioni le proprietà viste in precedenza, si hanno i seguenti teoremi.
Teorema 1 - Scambiando i membri di una disequazione, se ne ottiene un'altra controversa alla prima.
Da
si ha:
Teorema 2 (principio di sostituzione) - Se ad entrambi o ad uno solo dei due membri di una disequazione si sostituisce un'espressione uguale, si ottiene una disequazione equivalente ed equiversa alla data.
Da
si ha:
In virtù di questo principio, in ciascuno dei due membri di una disequazione, si possono eseguire le operazioni indicate.
Teorema 3 (principio di addizione) - Se ad entrambi i membri di una disequazione si aggiunge una stessa espressione, si ottiene una disequazione equivalente a quella data.
Da
si ha:
In base a tale principio si può trasportare un termine da un menbro all'altro di una disequazione, purchè lo si cambi di segno, così come si faceva nelle equazioni.
Teorema 4 (principio dei segni)- La disequazione
A(x) · B(x) > 0
è equivalente ai sistemi

A(x) · B(x) < 0
è equivalente ai sistemi

Teorema 5 (principio della moltiplicazione) - Moltiplicando ambo i membri di una disequazione per un'espressione numericamente diversa da zero e di segno determinato, si ha una disequazione equivalente ed equiversa o controversa alla data, a seconda che l'espressione moltiplicatrice sia positiva o negativa per qualsiasi valore attribuito alla variabile in essa contenuta.
Cioè se

Se invece, l'espressione M(x) assume per valori assegnati alla variabile x tanto valori positivi che negativi, non solo la disequazione A(x) > 0 non è equivalente nè alla A(x) · M(x) > 0 nè alla A(x) · M(x) < 0, ma non si può neppure dire che le
Infatti, per essere soddisfatta la disequazione
occorre che siano soddisfatti i sistemi di disequazioni:

e le soluzioni del sistema (2) non sono, in generale, tutte quelle che soddisfano la A(x) > 0, ovvero la moltiplicazione ha fatto perdere delle soluzioni alla disequazione A(x) > 0; per contro ha fatto acquistare alla stessa disequazione tutte le soluzioni del sistema (3). Quindi A(x) · M(x) > 0 non è equivalente alla A(x) > 0.
Risoluzione delle disequazioni razionali intere di 1° grado
In base ai teoremi visti, è possibile risolvere le disequazioni intere, ossia quelle della forma
dove A(x) è un polinomio in x.
Se tale polinomio è di 1° grado, si ha la disequazione del tipo
equivalente alla
a sua volta equivalente alla
a seconda che a > 0, oppure a < 0.
Poichè x = -b/a è la radice dell'equazione ax + b =0, associata alla disequazione data, le soluzioni di quest'ultima sono tutti i valori di x che soddisfano la (4) o la (4').
Scomposizione in fattori del trinomio di 2° grado
Si ricordi che l'equazione di 2° grado
ax2 + bx + c = 0,
avente il discriminante
Δ = b2 - 4ac > 0,
ammette radici reali date dalla formula risolutiva

avendo indicato con ciò x1 < x2.
Nel caso in cui Δ = 0, la radice reale doppia sarà indicata con
Inoltre è noto che le radici dell'equazione di 2° grado godono delle seguenti proprietà:
1)-la loro somma è uguale al secondo coefficiente, cambiato di segno, diviso il primo:
2)-il loro prodotto è uguale al termine noto, con lo stesso segno, diviso il primo coefficiente:
3)-considerando il trinomio di 2° grado:
A(x) = ax2 + bx + c,
nell'ipotesi che l'equazione da esso ottenuta uguagliandolo a zero ammetta radici reali e distinte, cioè sia Δ > 0, senza alterarlo, lo si può trasformare come segue:

Dunque, si ha:
A(x) = ax2 + bx + c = a(x - x1)(x - x2),
cioè un trinomio di 2° grado, avente Δ > 0, si scompone nel prodotto di tre fattori, il 1° uguale al primo coefficiente, il 2° uguale alla differenza tra l'incognita e la prima radice, il 3° uguale alla differenza tra l'incognita e la seconda radice.
Nota bene
Durante la trasformazione sono stati effettuati i seguenti passaggi:
-si è messo in evidenza il cofficiente a,
-si è effettuata la sostituzione delle espressioni ottenute dalle proprietà delle radici,
-si è sviluppato il contenuto della parentesi interna,
-si sono raccolti, a gruppi di termini, i fattori comuni,
-si è raccolto ancora il fattore comune x - x1.
4)-Nel caso in cui Δ = 0, per cui x1 = x2 = x0, la formula precedente diventa:
A(x) = ax2 + bx + c = a(x - x0)(x - x0) = a(x - x0)2.
5)-Nel caso in cui Δ < 0, non esistono radici reali per l'equazione A(x) = 0 e il trinomio si trasforma come segue:

Dunque, in tal caso, si ha:

Nota bene
Durante la trasformazione sono stati effettuati i seguenti passaggi:
-si è messo in evidenza il cofficiente a,
-si è moltiplicato per 2 il numeratore ed il denominatore della frazione b/a e aggiunto e sottratto b2/4a2.
Segno del trinomio di secondo grado avente Δ > 0
1)-Si consideri il trinomio tipico di 2° grado:
A(x) = ax2 + bx + c.
Nel caso in cui Δ > 0, per quanto detto in precedenza, si può considerare scomposto in fattori:
A(x) = ax2 + bx + c = a(x - x1)(x - x2),
dove x1 e x2, x1 < x2, sono le radici dell'equazione A(x) =0.
Riportati i numeri x1 e x2 su una retta orientata, in base ad un fissato sistema di coordinate ascisse
il segmento di origine x1 ed estremo x2, si chiama intervallo delle radici.
Si vuole vedere quale segno assume il trinomio A(x) quando la variabile x varia rispetto all'intervallo delle radici, cioè quando si danno alla x valori esterni, a sinistra e a destra dell'intervallo, oppure interni ad esso o, addirittura, si supponga x = x1 e x = x2, cioè x coincidente con gli estrtemi dell'intervallo.
Distinguendo tutti i casi possibili, si vedrà quali di essi, portando ad identiche conclusioni, potranno essere raggruppati.
2)-x esterna a sinistra dell'intervallo:
x < x1 < x2.
In tal caso è:
x - x1 < 0, x - x2 < 0
ed il prodotto di tali fattori è maggiore di zero.
Quindi in:
A(x) = ax2 + bx + c = a(x - x1)(x - x2),
se a > 0, sarà A(x) > 0,
se a < 0, sarà A(x) < 0,
ossia per
x < x1 < x2
il trinomio ha lo stesso segno di quello del 1° coefficiente.
In tal caso è:
x - x1 > 0, x - x2 > 0
e quindi ancora
(x - x1)(x - x2) > 0,
per cui in
A(x) = ax2 + bx + c = a(x - x1)(x - x2),
se a > 0, sarà A(x) > 0,
se a < 0, sarà A(x) < 0,
se a < 0, sarà A(x) < 0,
dunque, sia per x < x1 < x2 che per x > x2 > x1,
cioè per valori della variabile esterni, a sinistra e a destra,
all'intervallo delle radici, il trinomio ha lo stesso segno di quello
del primo coefficiente.
Viceversa, un trinomio A(x), avente Δ > 0, assume lo stesso segno di quello del primo coefficiente per valori della variabile esterni all'intervallo delle radici dell'equazione A(x) = 0.
In formula:
a·A(x) > 0, per x < x1 .... < x2 < x.
Viceversa, un trinomio A(x), avente Δ > 0, assume lo stesso segno di quello del primo coefficiente per valori della variabile esterni all'intervallo delle radici dell'equazione A(x) = 0.
In formula:
a·A(x) > 0, per x < x1 .... < x2 < x.
x1 < x < x2.
In tal caso è:
x - x1 > 0, x - x2 < 0,
per cui
(x - x1)(x - x2) < 0,
e quindi in
A(x) = a(x - x1)(x - x2)
se a > 0, sarà A(x) < 0,
se a < 0, sarà A(x) > 0,
ossia per
x1 < x < x2,
il trinomio ha segno contrario a quello del primo coefficiente.
Viceversa, un trinomio A(x), avente Δ > 0, assume segno contrario a quello del primo coefficiente per valori della variabile interni all'intervallo delle radici dell'equazione A(x) = 0.
In formula:
a·A(x) < 0, per x1 < x < x2.
5)-se x = x1 oppure x = x2 in
A(x) = ax2 + bx + c = a(x - x1)(x - x2),
annullandosi uno dei fattori, è nullo tutto il prodotto, cioè è
e quindi, per valori della x uguali ad una delle radici, il trinomio si annulla.
Viceversa, un trinomio A(x), avente Δ > 0, si annulla per valori della variabile uguali ad una delle radici dell'equazione A(x) = 0.
In formula:
a·A(x) = 0, per x = x1, oppure x = x2.
6)-Riepilogo
Per i trinomi aventi Δ > 0 possono quindi verificarsi tutti i casi e cioè:
a)-possono assumere lo stesso segno di quello del 1° coefficiente:
b)-possono assumere il segno contrario a quello del 1° coefficiente:
c)-possono annullarsi:
a·A(x) = 0, per x = x1 e per x = x2;
Segno del trinomio di secondo grado avente Δ = 0
1)-Si consideri il trinomio tipico di 2° grado
Quando Δ = 0, come già visto, lo si può considerare scomposto in fattori come segue:
A(x) = ax2 + bx + c = a(x - x0)2.
In questo caso, sulla retta orientata, si riporta il solo punto di ascissa x0:
e si fa variare la x rispetto ad esso; ciò significa condiderare i casi in cui è
x < x0, x > x0, x = x0.
2)-Se x < x0, è x - x0 < 0; se x > x0, x - x0 > 0, ma in entrambi i casi è
(x - x0)2 > 0,
e quindi in
A(x) = ax2 + bx + c = a(x - x0)2,
se a > 0, sarà A(x) > 0;
se a < 0, sarà A(x) < 0,
ossia per x ≠ x0, x < x0 oppure x > x0, il trinomio ha lo stesso segno di quello del 1° coefficiente.
Viceversa, un trinomio A(x), avente Δ = 0, assume lo stesso segno di quello del 1° coefficiente per valori della variabile diversi dalla radice dell'equazione A(x) = 0.
In formula:
3)-Se x = x0, è x - x0 = 0; e quindi anche
cioè per il valore della variabile uguale alla radice il trinomio si annulla.
Viceversa, un trinomio A(x), avente Δ = 0, si annulla, se la variabile diventa uguale alla radice dell'equazione A(x) = 0.
In formula:
a·A(x) = 0, per x = x0.
4)-Non essendosi trovato il caso in cui il trinomio assume il segno contrario a quello del 1° coefficiente, significa che detto caso per i trinomi aventi Δ = 0 è impossibile, cioè:
a·A(x) < 0 impossibile, se Δ = 0.
Segno del trinomio di secondo grado avente Δ < 0
1)-Si consideri il trinomio A(x) nel caso in cui sia Δ < 0 e quindi, per quanto già visto, risulta:

Non essendovi radici reali nell'equazione A(x) = 0, non vi è alcun riferimento per i valori della variabile x, è ciò significa che per qualsiasi valore della variabile accade che l'espressione nella parentesi quadra assume sempre valori positivi, in quanto il 1° termine, essendo un quadrato è sempre positivo o nullo ed il 2° termine -Δ/4a2 è anch'esso sempre positivo, proprio perchè il numeratore della frazione è Δ < 0 per ipotesi, per cui -Δ > 0 e il denominatore è sempre positivo essendo un quadrato.
Quindi, se l'espressione suddetta è sempre positiva, sarà:
a·A(x) > 0, se a > 0;
a·A(x) < 0, se a < 0,
ossia, per qualsiasi valore della x, il trinomio ha sempre lo stesso segno di quello del 1° coefficiente.
Viceversa, un trinomio A(x), avente Δ < 0, assume sempre lo stesso segno di quello del 1° coefficiente per qualsiasi valore della variabile.
In formula:
a·A(x) > 0, per qualsiasi x.
Non si possono verificare altri casi, cioè:
a·A(x) < 0, impossibile;
a·A(x) = 0, impossibile.
Risoluzione delle disequazioni razionali intere di 2° grado
1)-Una disequazione intera di 2° grado si presenta nella forma tipica:
dove a, b, c sono numeri reali, dei quali, senz'altro, a ≠ 0.
Si può considerare addirittura a > 0 in quanto, se così non fosse, basterebbe, come è noto, cambiare tutti i segni ed il verso della disequazione per riportarsi ad un'altra equivalente alla data ed avente a > 0.
2)-La risoluzione di una disequazione, del tipo
consiste nel trovare i valori della variabile per cui è
ax2 + bx + c = > 0,
ossia, il trinomio, 1° membro, assume lo stesso segno di quello del 1° coefficiente, oppure è
ax2 + bx + c = < 0,
ossia, il trinomio, 1° membro, assume il segno contrario a quello del 1° coefficiente.
Pertanto, la risoluzione di una disequazione di 2° grado è, in tal modo, riportata alla ricerca del segno del trinomio, 1° membro, rispetto a quello del suo 1° coefficiente.
Esempi
1°) 2x2 - 3x + 1 = > 0.
Si vuole che il trinomio assuma lo stesso segno del 1° coefficiente.
Poichè risulta
Δ = 9 - 8 = 1 > 0,
le radici reali e distinte dell'equazione associata, sono:

e quindi
2x2 - 3x + 1 > 0,
per
2°) 2x2 - 5x + 3 = < 0.
Si vuole che il trinomio assuma il segno contrario del 1° coefficiente.
Poichè risulta
Δ = 25 - 24 = 1 > 0,
le radici reali e distinte dell'equazione associata, sono:

e quindi
2x2 - 5x + 3 = < 0
per
3°) 4x2 - 4x + 1 > 0.
Si vuole che il trinomio assuma lo stesso segno del 1° coefficiente.
Poichè risulta
la radice reale doppia dell'equazione associata, è:
e quindi
per
4°) 4x2 - 12x + 9 < 0.
Si vuole che il trinomio assuma il segno contrario a quello del 1° coefficiente.
Poichè risulta
la radice reale doppia dell'equazione associata, è:
e quindi
4x2 - 12 + 9 < 0
è impossibile.
5°) x2 - 3x + 7 > 0.
Si vuole che il trinomio assuma lo stesso segno di quello del 1° coefficiente.
Poichè risulta
Δ = 9 - 28 = -19 < 0,
l'equazione associata non ha radici reali e quindi è
x2 - 3x + 7 > 0
per qualsiasi valore di x.
6°) x2 - 2x + 9 < 0.
Si vuole che il trinomio assuma segno contrario di quello del 1° coefficiente.
Poichè risulta
l'equazione associata non ha radici reali e quindi
x2 - 2x + 9 < 0
è impossibile.
7°) 3x2 - 10x + 3 > 0.
Poichè risulta
le radici reali e distinte dell'equazione associata, sono:

La disequazione è soddisfatta per valori della variabile esterni all'intervallo delle radici, cioè:

8°) x2 - 5x + 2 < 0.
Poichè risulta
Δ = 25 - 8 = 17 > 0,
le radici reali e distinte dell'equazione associata, sono:

La disequazione è soddisfatta per valori della variabile interni all'intervallo delle radici, cioè:

9°) x2 - 6x + 9 > 0.
Poichè risulta
le radici reali e coincidenti dell'equazione associata, sono:
La disequazione è soddisfatta per tutti i valori della x diversi da 3, cioè per tutti i punti della retta escluso quello di ascissa 3:
Poichè risulta
x0 = 4.
La disequazione è impossibile.
Forme miste di disequazioni
Le forme A(x) ≥ 0 oppure A(x) ≤ 0 si chiamano forme miste di disequazioni e significano che sono da considerare, contemporaneamente, le soluzioni delle disequazioni e delle equazioni ad esse associate, ossia le soluzioni dei sistemi misti:

Esempi
1°) x2 - 7x + 6 ≥ 0.
Poichè risulta
Δ = 49 - 24 = 25 > 0,
le radici reali e distinte dell'equazione associata, sono:

La disequazione è soddisfatta da:
Poichè risulta
Δ = 9 + 16 = 25 > 0,
le radici reali e distinte dell'equazione associata, sono:

La disequazione è soddisfatta da:

Sistemi di disequazioni
1)-Generalità
Il sistema di disequazioni è costituito da due o più disequazioni nella stessa incognita.
Risolverlo significa trovare, se esistono, le soluzioni comuni a tutte le disequazioni.
Nel caso in cui non esistano tali soluzioni comuni, il sistema si dice impossibile e le disequazioni si dicono incompatibili.
Per risolvere un sistema di disequazioni, si devono risolvere le singole disequazioni e poi si devono confrontare le condizioni soddisfacenti a ciascuna di esse, per trovare quelle altre condizioni soddisfacenti contemporaneamente tutte le disequazioni del sistema.
Per la ricerca delle condizioni comuni è molto utile riferirsi alla rappresentazione già usata negli esempi 7°, 8° e 9° precedenti.
Le soluzioni del sistema sono date, in tal modo, da quei valori dell'incognita i cui punti immagine, nel sistema di coordinate ascisse, si trovano negl'intervalli comuni a tutte le condizioni trovate, tante quante sono le disequazioni del sistema.
2)-Esempi di risoluzione di sistemi di disequazioni intere

e nel sistema coordinate ascisse, si ha:


e nel sistema coordinate ascisse, si ha:


e nel sistema coordinate ascisse, si ha:


è equivalente a

e nel sistema coordinate ascisse, si ha:


è equivalente a

e nel sistema coordinate ascisse, si ha:

cioè, il sistema è impossibile.

e nel sistema coordinate ascisse, si ha:

Disequazioni razionali frazionarie
1)-Generalità
Una disequazione si dice frazionaria o fratta quando l'incognita compare al denominatore della frazione.
Queste disequazioni sono del tipo:
avendo indicato con N(x) e D(x), rispettivamente numeratore e denominatore della (1) e della (1'), due polinomi nella variabile x. Poichè una frazione è positiva quando i suoi termini sono concordi, la (1) diventa equivalente ai due sistemi

le cui soluzioni sono quelle della (1).
Analogamente, sapendo che una frazione è negativa quando i suoi termini sono discordi, la (1') diventa equivalente ai due sistemi

Pertanto la risoluzione delle disequazioni razionali fratte si riporta a quella dei sistemi di disequazioni.
2)-Esempi di risoluzione di disequazioni razionali fratte
è equivalente ai due sistemi:

quindi:
è equivalente ai due sistemi:

quindi:
è equivalente ai due sistemi:

Il primo sistema è perciò soddisfatto per:

è equivalente ai due sistemi:

Il primo sistema è perciò soddisfatto per:
Si comincia con i seguenti calcoli:

equivalente a

a sua volta equivalente ai due sistemi:


Altre disequazioni risolvibili mediante sistemi
Sono quelle della forma:
(1) A(x)·B(x) > 0, (1') A(x)·B(x) < 0,
ove A(x) e B(x) indicano sempre espressioni razionali intere, polinomi, nella variabile x.
La (1), per il principio dei segni, è equivalente ai sistemi:

la cui risoluzione è nota.
La (1'), per lo stesso principio, è equivalente ai sistemi:

la cui risoluzione è anch'essa nota.
Nota bene
Per quanto detto in precedenza, si ha l'equivalenza, rispettivamente, tra le disequazioni:
Esempi
(1°) (2x + 1)(3x - 2) > 0.
La disequazione è equivalente ai sistemi.

(2°) (4x - 3)(2x - 1) < 0.
La disequazione è equivalente ai sistemi:

Disequazioni irrazionali
Generalità
Si chiamano disequazioni irrazionali quelle del tipo:
con n intero positivo e A(x), B(x) espressioni razionali della variabile x.
Nei tipi suddetti, si è supposto il radicale positivo, perchè, nel caso contrario, lo si farebbe diventare tale, cambiando, come è noto, il segno di ambo i membri della disequazione e il verso della stessa. Per la risoluzione di tali disequazioni si devono tenere presenti i principi fondamentali delle disuguaglianze.
Teorema - Per n intero positivo dispari, le disequazioni
sono equivalenti.
Infatti, si passa dalla (1) alla (1') elevando al quadrato ambo i membri alla potenza nma e poichè è dispari, l'elevamento a potenza non altera il segno della disequazione.
Esempi
La disequazione è equivalente a:
(x + 2)3 > x3 + 4x2 + 7x + 6,
x3+ 6x2 + 12x + 8 > x3 + 4x2 + 7x + 6,
2x2 + 5x + 2 > 0.
Le radici dell'equazione associata a quest'ultima disequazione sono x = -2, x = -1/2 e, pertanto, la disequazione proposta è soddisfatta per

La disequazione è equivalente a:
(x + 1)3 < x3 + 2x2 + 5x + 4,
x3+ 3x2 + 3x + 1 < x3 + 2x2 + 5x + 4,
x2 - 2 x - 3 < 0.
Le radici dell'equazione associata a quest'ultima disequazione sono x = -1, x = 3 e, pertanto, la disequazione proposta è soddisfatta per
Teorema - Per n intero positivo pari, la disequazione
è equivalente al sistema:

le cui disequazioni costituiscono le condizioni verificate per le quali è soddisfatta la (1).
Infatti, la B(x) ≥ 0 deriva dalla realtà del radicale ed essa comporta che sia anche
Infine, essendo i due membri della (1) non negativi, è lecito elevarli alla stessa potenza nma, per cui An(x) < B(x).
Esempi
La disequazione è equivalente al sistema:

La prima disequazione mista è soddisfatta per
la seconda per x > 1, la terza per x > 5/3.
Unificando le condizioni, si ha:

La disequazione proposta è quindi verificata per:
La disequazione è equivalente al sistema:

La prima disequazione mista è soddisfatta per

la seconda per x > 1,
la terza per

Unificando le condizioni, si ha:

Non essendovi condizioni comuni alle tre disequazioni, ossia non essendovi valori della variabile soddisfacenti simultaneamente le tre disequazioni del sistema, la disequazione proposta, equivalente al sistema, è impossibile.
Teorema - Se n è intero positivo pari, la disequazione
è equivalente a ciascuno dei sistemi:

Infatti, la realtà del radicale comporta la condizione B(x) ≥ 0 e, quindi, l'altra
Allora nella (1), essendo il 2° membro positivo, si può avere che il 1° membro sia negativo è cioè il sistema:

e si può avere che il 1° membro sia anch'esso positivo e, quindi, elevando ambo i membri alla potenza nma, si ha il sistema

Esempi
La disequazione è equivalente a ciascuno dei due sistemi

La disequazione proposta è, dunque, soddisfatta per
La disequazione è equivalente a ciascuno dei due sistemi

La disequazione proposta è, dunque, soddisfatta per