MIKY & GENNY
STUDIO DELLE CURVE E COMPLEMENTI ---> INDICE
1)-Proprietà delle curve
Studiare le curve significa trovare le loro caratteristiche o proprietà e tracciare la linea che ne indichi l'andamento con sufficiente approssimazione. Per tale studio conviene trovare nell'ordine quanto segue:
1°)-il campo di esistenza delle funzioni,
2°)-gli eventuali punti d'incontro con gli assi coordinati,
3°)-gli eventuali punti estremanti delle curve ed i valori, ordinate, delle stesse in essi,
4°)-gli eventuali asintoti delle curve,
5°)-qualora fossero necessari, i punti delle curve servendosi delle equazioni delle stesse, y = f(x),
6°)-gli eventuali intervalli in cui le curve sono crescenti o decrescenti, nel caso in cui tutti gli elementi trovati in precedenza non risultassero sufficienti per tracciare i grafici.
Gli esempi seguenti mostreranno, in generale, una volta in possesso degli elementi suddetti, come si sia in grado di rappresentare graficamente le curve.
2)-Esempi di studio delle curve
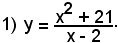
1°)-il campo di esistenza della curva è
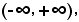
ad eccezione del punto x = 2.
2°)-I punti d'incontro con l'asse x sono dati da
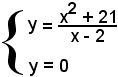
e, dal confronto delle due equazioni, si ha
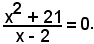
Quest'ultima è un'equazione frazionaria, per cui x = 2 è un valore che annulla il denominatore, quindi è da scartare tra le radici. Liberando dal denominatore, si ha l'equazione
x2 + 21 = 0,
che è impossibile nel campo reale e, quindi, la curva non ha punti d'incontro con l'asse x.
I punti d'incontro con l'asse y sono dati da
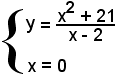
e, per sostituzione, si ha
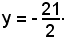
Quindi la curva interseca l'asse y nel punto di coordinate
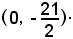
3°)-ricerca dei punti estremanti;
essendo:
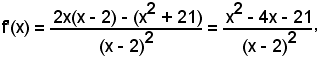
f'(x) = 0
è
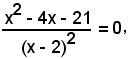
per la quale x = 2 è da scartare ancora tra le radici. Liberando il denominatore, si ha l'equazione
x2 - 4x - 21 = 0,
le cui radici sono
x1 = -3 e x2 = 7,
le quali sono le ascisse dei punti di massimo, di minimo o di flesso. Per precisare la natura di questi punti, si calcola la derivata seconda della funzione:
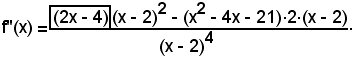
Ricordando che nelle equazioni razionali fratte il segno della f''(x) è dato dal segno del solo 1° fattore del 1° termine, si ha:
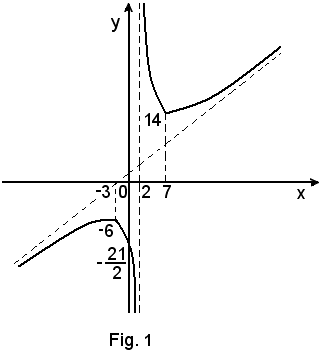
f''(-3) < 0, cioè x = -3 è un punto di massimo,
f''(7) > 0, cioè x = 7 è un punto di minimo e
f(-3) = -6 è l'ordinata massima,
f(7) = 14 è l'ordinata minima.
4°)-ricerca degli eventuali asintoti;
a) verticale, la sua equazione è
x - 2 = 0,
cioè
x = 2.
Si perviene a tale risultato ricordando che l'equazione dell'asintoto verticale è del tipo
y = mx + n,
nella quale
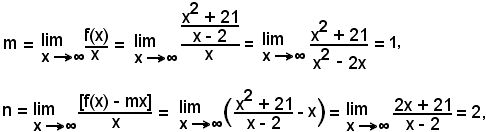
quindi
e pertanto le intercette di tale retta sugli assi sono:
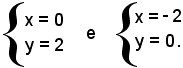
b) orizzontale, non esiste perchè
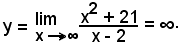
La curva ha, dunque, l'andamento della seguente figura:
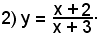
1°)-il campo di esistenza della curva è
ad eccezione del punto x = -3.
2°)-I punti d'incontro con l'asse x sono dati da
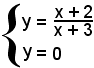
e, dal confronto delle due equazioni, si ha
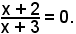
Quest'ultima è un'equazione frazionaria, per cui x = -3 è un valore che annulla il denominatore, quindi è da scartare tra le radici. Liberando dal denominatore, si ha l'equazione
x + 2 = 0,
cioè
x = -2.
Quindi la curva interseca l'asse x nel punto di coordinate (-2, 0).
I punti d'incontro con l'asse y sono dati da
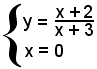
e, per sostituzione, si ha
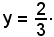
Quindi la curva interseca l'asse y nel punto di coordinate
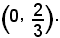
3°)-ricerca dei punti estremanti;
essendo:
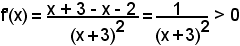
sempre, ad eccezione di x = -3, la curva è sempre crescente, e quindi non ha punti di massimo o di minimo.
4°)-ricerca degli eventuali asintoti;
a) verticale, la sua equazione è
x = -3.
b) orizzontale, è dato da
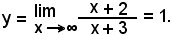
Altri punti
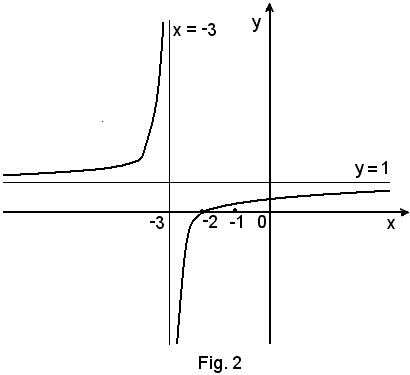
La curva ha, dunque, l'andamento della seguente figura:
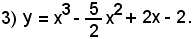
1°)-il campo di esistenza della curva è
essendo la funzione razionale intera, quindi essa è definita su tutto l'asse reale.
2°)-I punti d'incontro con l'asse x sono dati da

e, dal confronto delle due equazioni, si ha l'equazione di 3° grado seguente:
2x3 - 5x2 + 4x - 4 = 0.
Effettuando la ricerca delle radici razionali, si trova che l'unica radice è x = 2, perchè l'equazione che si ottiene abbassando di grado la precedente, dopo aver eseguito con la regola di Ruffini la divisione tra il polinomio 1° membro ed il binomio x - 2, è
2x2 - x + 2 = 0,
che non ha radici reali.
I punti d'incontro con l'asse y sono dati da
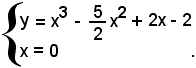
Quindi la curva interseca l'asse y nel punto di coordinate (0, -2).
3°)-ricerca dei punti estremanti;
essendo:
f'(x) = 3x2 - 5x + 2,
l'equazione da considerare è
3x2 - 5x + 2 = 0,
le cui radici sono
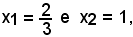
le quali sono le ascisse di punti di massimo, di minimo o di flesso.
Poichè
f''(x) = 6x - 5,

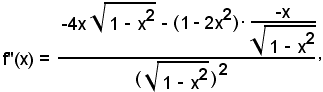
4°)-ricerca
degli eventuali asintoti; le curve rappresentatrici di
funzioni razionali intere non sono dotate di asintoti.
5°)-la curva è crescente per
f'(x) = 3x2 - 5x + 2 > 0,
ossia esternamente all'intervallo
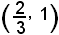
ed è decrescente per
f'(x) = 3x2 - 5x + 2 < 0,
ossia internamente allo stesso intervallo.
La curva ha, dunque, l'andamento della seguente figura:
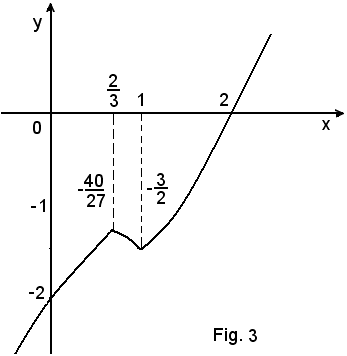
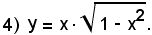
1°)-la funzione è irrazionale intera ed è definita in tutti i punti per cui è
1 - x2 ≥ 0,
ossia per tutte le
-1 ≤ x ≤ 1.
2°)-I punti d'incontro con l'asse x sono dati da
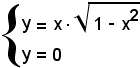
e, dal confronto delle due equazioni, si ha l'equazione seguente:
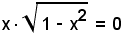
e quindi
x1 = 0, x2 = -1, x3 = 1.
I punti d'incontro con l'asse y sono dati da
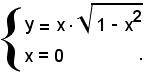
Quindi la curva interseca l'asse y nel punto di coordinate (0, 0).
3°)-ricerca dei punti estremanti;
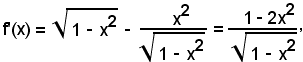
l'equazione da considerare è
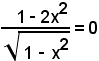
con x = ± 1 da scartare.
Liberando dal denominatore, si ha:
1 - x2 = 0
e, risolvendo tale equazione, risulta
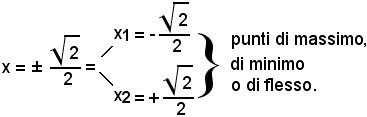
Poichè
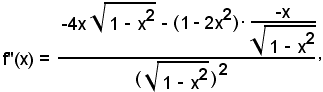

4°)-ricerca degli eventuali asintoti;
-la curva rappresentatrice di una funzione intera anche irrazionale non ha asintoti.
La curva ha, dunque, l'andamento della seguente figura:
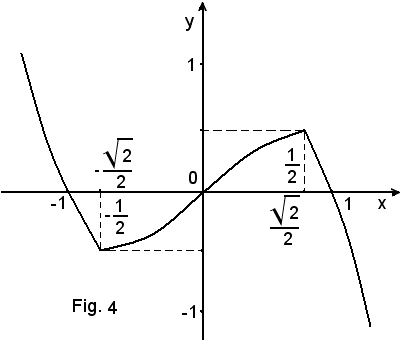
5) y = senx·cosx da studiare nell'intervallo (0, 2π).
1°)-il campo di esistenza delle funzioni trigonometriche è solitamente fornito dalla traccia dell'esercizio ed in tal caso è (0, 2π), quindi risulta:
0 ≤ x ≤ 2π.
2°)-I punti d'incontro con l'asse x sono dati da
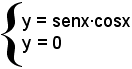
e, dal confronto delle due equazioni, si ha l'equazione seguente:
senx·cosx = 0,
ossia,

Risultano così trovati i punti d'incontro con l'asse x.
I punti d'incontro con l'asse y sono dati da
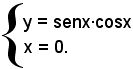
Quindi la curva interseca l'asse y nel punto di coordinate (0, 0).
3°)-ricerca dei punti estremanti;essendo:
f'(x) = cos2x - sen2x
l'equazione da risolvere è
cos2x - sen2x = 0,
quadratica omogenea, equivalente a
1 - tg2x = 0,
ossia
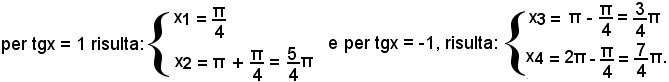
Risultano così trovate le ascisse dei punti di massimo, di minimo o di flesso.
Ora si ha:
f''(x) = -2coxsenx - 2senxcosx = -4senxcosx
e poichè

inoltre

4°)-ricerca degli eventuali asintoti; le funzioni trigonometriche in seno e coseno non hanno asintoti.La curva ha, dunque, l'andamento della seguente figura:

Altre applicazioni dei massimi e dei minimi
1° Problema - Tra tutti i rettangoli di dato perimetro 2p, determinare quello di area massima.
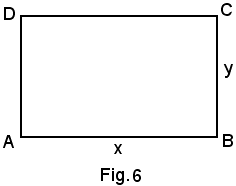
Indicando con x e y le dimensioni del rettangolo, si sa che
2x +2y = 2p,
ossia
x + y = p,
da cui
(1) y = p - x.
Inoltre, l'area del rettangolo è data da
S = x·y.
Sostituendo in quest'ultima uguaglianza la (1), si ha l'area espressa in funzione della sola variabile x, cioè:
S(x) = x (p - x) = -x2 + px,
della quale è richiesto il massimo.
e
S''(x) = -2 < 0
sempre, si ha che per x = p/2 il rettangolo assume area massima. Si noti che in corrispondenza di tale valore si ha anche y = p/2, ossia il rettangolo di area massima è il quadrato di lato p/2.
2° Problema - Tra tutti i rettangoli di dato perimetro 2p, determinare quello che ha la minima diagonale.
Con le stesse indicazioni precedenti si ha:
x + y = p,
da cui
(1) y = p - x.
Inoltre, la diagonale del rettangolo è data da
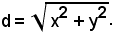
Sostituendo in quest'ultima uguaglianza la (1), la si esprime come funzione della sola variabile x, cioè:
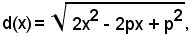
della quale è richiesto il minimo.
Si ha:
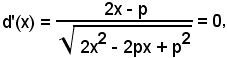
equazione frazionaria con denominatore sempre diverso da zero, dalla quale si ricava x = p/2.
Essendo poi
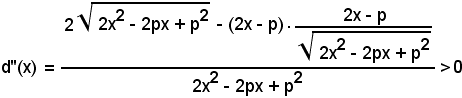
sempre per x = p/2, si ha il minimo della funzione d(x).
Poichè dalla (1) si ricava y = p/2, si ha:
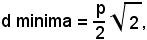
ossia il rettangolo di diagonale minima è il quadrato di lato p/2.
3° Problema - Tra tutti i triangoli isosceli inscritti in una circonferenza di raggio r, determinare quello di area massima.
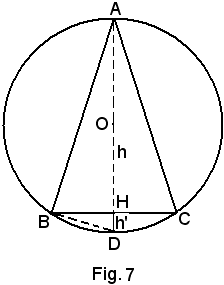

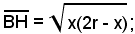
inoltre l'area in funzione di x è;
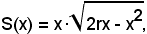
della quale è richiesto il massimo.
Si ha:
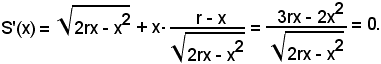
Le radici di questa equazione sono
x1 = 0,
non accettabile perchè annulla il denominatore, e
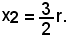
Essendo poi
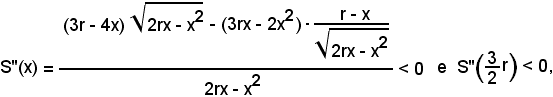
per x = (1/2)r si ha il triangolo richiesto, che è quello equilatero inscritto.
Complementi allo studio di una curva
1)-Concavità e convessità di una curva in un punto
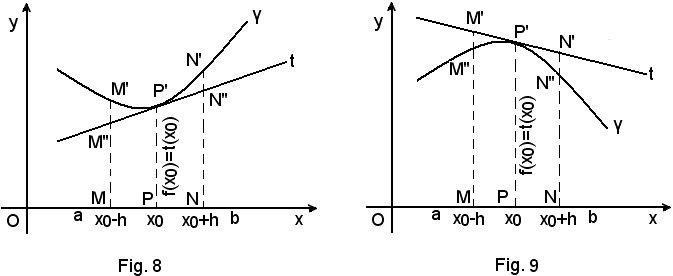
Sia P' il punto di γ avente ascissa x0 in (a, b) e t la retta tangente in P' a γ la cui equazione, funzione di x, si indichi, per brevità y = t(x).
Considerato un intorno (x0-h, x0+h) di x0 e detti M' ed N' i punti di γ aventi per ascissa, rispettivamente x0-h e x0+h ed M'' e N'' quelli di t aventi le stesse ascisse, si ha:
1^ definizione - la curva γ nel punto P', Fig. 8, rivolge la concavità verso la direzione positiva dell'asse y, quando tutti i punti di y, ad eccezione di P', aventi ascisse appartenenti al conveniente intorno considerato di x0, hanno ordinata maggiore dei corrispondenti punti della tangente t.
(1) f(x0 - h) > t(x0 - h), f(x0 + h) > t(x0 + h);
2^ definizione - la curva γ nel punto P', Fig. 9, rivolge la concavità verso il semiasse negativo dell'asse y, quando tutti i punti di γ, ad eccezione di P', aventi ascisse appartenenti al conveniente intorno considerato di x0, hanno ordinata minore dei corrispondenti punti della tangente t.
(2) f(x0 - h) < t(x0 - h), f(x0 + h) < t(x0 + h).
Considerato che è
f(x0) = t(x0),
pertanto si può scrivere tanto
P' [x0, f(x0)]
quanto
P' [x0, t(x0)],
e che f'(x0) è il coefficiente angolare della tangente t, la cui equazione è stata indicata per brevità con y = t(x). Il coefficiente angolare f'(x0) della t può anche essere scritto sotto la forma
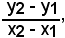
che assume quello della retta passante per i due punti (x1, y1) e (x2, y2), i quali in tal caso sono:
M'' = [x0-h, t(x0-h)] e P'[x0, t(x0)],
oppure
P'[x0, t(x0)] e N'' = [x0+h, t(x0+h)].
In ogni caso, si deve avere sempre lo stesso valore per il coefficiente angolare della t e quindi dev'essere:
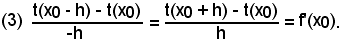
Teorema 1 - Nei punti in cui la curva rivolge la concavità verso il semiasse positivo y, si ha:
Rs < f'(x0) < Rd.
Infatti, tenendo sempre presente che
f(x0) = t(x0),
le (1) si possono scrivere
f(x0 - h) - f(x0) > t(x0 - h) - t(x0), f(x0 + h) - f(x0) > t(x0 + h) - t(x0)
e dividendo ambo i membri della 1^ disuguaglianza per -h, per cui si deve cambiare il verso, ed ambo i membri della 2^ per h, si ha:
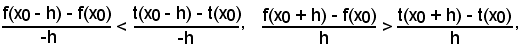
dalle quali, per la (3), si ha
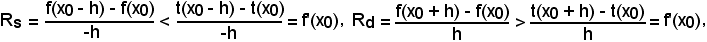
ossia
Rs < f'(x0) < Rd,
come volevasi dimostrare.
Teorema 2 - Nei punti in cui la curva rivolge la concavità verso il semiasse negativo delle y, si ha:
Infatti, scrivendo le (2) come segue
f(x0 - h) - f(x0) < t(x0 - h) - t(x0), f(x0 + h) - f(x0) < t(x0 + h) - t(x0)
e dividendo ambo i membri della 1^ disuguaglianza per -h ed ambo i membri della 2^ per h, si ha:
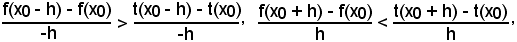
dalle quali, per la (3), si ha
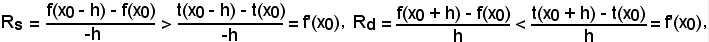
ossia
Rs > f'(x0) > Rd,
come volevasi dimostrare.
Punti di flesso o di inflessioneIn
precedenza è stata data la definizione di punto di flesso e si è visto che
in esso la curva, essendo tagliata dalla tangente, giace, rispetto a
questa, in semipiani opposti. In un punto x0 di flesso si è avuto inoltre f'(x0)
= 0 e, quindi, la tangente ed anche la secante alla curva risultavano
parallele all'asse x. Si precisa che la definizione di punto di
flesso o di inflessione data in precedenza vale per qualsiasi
inclinazione della tangente.
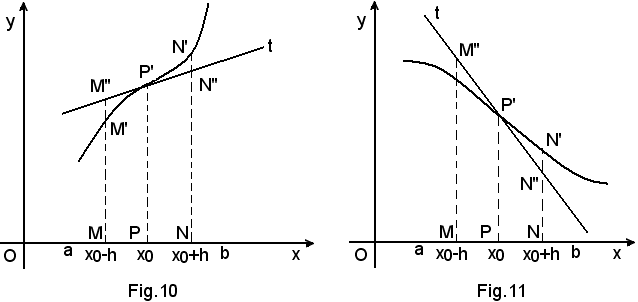
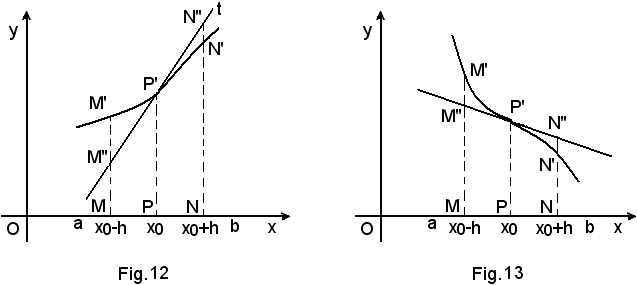
Come si vede nelle figure suddette, la tangente-secante alla curva non è più parallela all'asse x. Il punto P' delle figure 10 e 12 è detto flesso ascendente, in esso è:
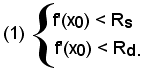
Il punto P' delle figure 11 e 13 è detto flesso discendente, in esso è:
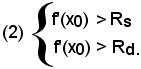
Viceversa, se in un punto x0 si vericano le (1), x0 è un punto di flesso ascendente e, se si verificano le (2), x0 è un punto di flesso discendente.
Teoremi sulle funzioni derivabili - Sviluppi in serie delle funzioni
1)-Teorema di Rolle-Dini
Se la funzione y = f(x) è:
a)-continua in un intervallo chiuso (a, b),
b)-derivabile in (a, b),
c)-con valori uguali negli estremi dell'intervallo f(b) = f(a),
esiste almeno un punto x0 interno ad (a, b) in cui si ha f'(x0).
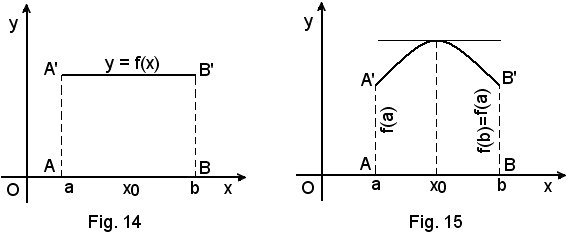
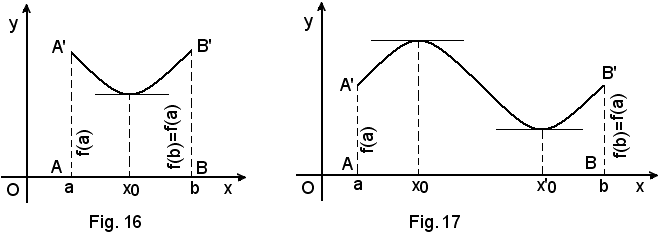
Infatti, essendo y = f(x) continua nell'intervallo chiuso (a, b), per il teorema di Weierstrass, essa ammette un massimo e un minimo assoluti. Se tali valori massimo e minimo sono assunti dalla funzione negli estremi a e b dell'intervallo, Fig. 14, per l'ipotesi f(a) = f(b), essi sono necessariamente uguali e quindi la funzione viene ad essere costante in (a, b), ed allora la sua derivata è nulla in tutti i punti di (a, b). Il teorema sarebbe perciò dimostrato addirittura per tutti i punti di (a, b). Se invece, il valore massimo o minimo viene assunto dalla funzione in un punto x0 interno ad (a, b), Fig. 15, Fig. 16 e Fig. 17, poichè la funzione è derivabile in (a, b) per ipotesi, per quanto si sa dalla teoria dei punti estremanti, risulta:
f'(x0) = 0,
e il teorema è ugualmente dimostrato.
Nota bene
1)-Il teorema ha il nome di due grandi matematici, rispettivamente francese ed italiano, in quanto fu enunciato dal primo nel 1691 ma solo nel caso in cui la funzione y = f(x) fosse razionale intera della x, polinomio, mentre in forma rigorosa e completa fu enunciato dal pisano Ulisse Dini nel 1878.
Studiare le curve significa trovare le loro caratteristiche o proprietà e tracciare la linea che ne indichi l'andamento con sufficiente approssimazione. Per tale studio conviene trovare nell'ordine quanto segue:
1°)-il campo di esistenza delle funzioni,
2°)-gli eventuali punti d'incontro con gli assi coordinati,
3°)-gli eventuali punti estremanti delle curve ed i valori, ordinate, delle stesse in essi,
4°)-gli eventuali asintoti delle curve,
5°)-qualora fossero necessari, i punti delle curve servendosi delle equazioni delle stesse, y = f(x),
6°)-gli eventuali intervalli in cui le curve sono crescenti o decrescenti, nel caso in cui tutti gli elementi trovati in precedenza non risultassero sufficienti per tracciare i grafici.
Gli esempi seguenti mostreranno, in generale, una volta in possesso degli elementi suddetti, come si sia in grado di rappresentare graficamente le curve.
2)-Esempi di studio delle curve
1°)-il campo di esistenza della curva è
ad eccezione del punto x = 2.
2°)-I punti d'incontro con l'asse x sono dati da
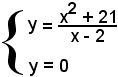
e, dal confronto delle due equazioni, si ha
Quest'ultima è un'equazione frazionaria, per cui x = 2 è un valore che annulla il denominatore, quindi è da scartare tra le radici. Liberando dal denominatore, si ha l'equazione
che è impossibile nel campo reale e, quindi, la curva non ha punti d'incontro con l'asse x.
I punti d'incontro con l'asse y sono dati da
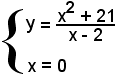
e, per sostituzione, si ha
Quindi la curva interseca l'asse y nel punto di coordinate
3°)-ricerca dei punti estremanti;
essendo:
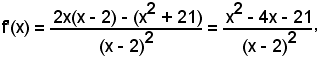
l'equazione
f'(x) = 0
è
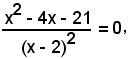
per la quale x = 2 è da scartare ancora tra le radici. Liberando il denominatore, si ha l'equazione
x2 - 4x - 21 = 0,
le cui radici sono
x1 = -3 e x2 = 7,
le quali sono le ascisse dei punti di massimo, di minimo o di flesso. Per precisare la natura di questi punti, si calcola la derivata seconda della funzione:
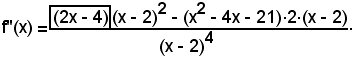
Ricordando che nelle equazioni razionali fratte il segno della f''(x) è dato dal segno del solo 1° fattore del 1° termine, si ha:
4°)-ricerca degli eventuali asintoti;
a) verticale, la sua equazione è
x - 2 = 0,
cioè
x = 2.
Si perviene a tale risultato ricordando che l'equazione dell'asintoto verticale è del tipo
y = mx + n,
nella quale
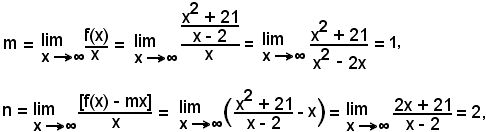
quindi
y = x + 2
e pertanto le intercette di tale retta sugli assi sono:

b) orizzontale, non esiste perchè
La curva ha, dunque, l'andamento della seguente figura:

1°)-il campo di esistenza della curva è
ad eccezione del punto x = -3.
2°)-I punti d'incontro con l'asse x sono dati da
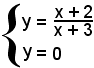
e, dal confronto delle due equazioni, si ha
Quest'ultima è un'equazione frazionaria, per cui x = -3 è un valore che annulla il denominatore, quindi è da scartare tra le radici. Liberando dal denominatore, si ha l'equazione
x + 2 = 0,
cioè
x = -2.
Quindi la curva interseca l'asse x nel punto di coordinate (-2, 0).
I punti d'incontro con l'asse y sono dati da
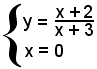
e, per sostituzione, si ha
Quindi la curva interseca l'asse y nel punto di coordinate
3°)-ricerca dei punti estremanti;
essendo:
sempre, ad eccezione di x = -3, la curva è sempre crescente, e quindi non ha punti di massimo o di minimo.
4°)-ricerca degli eventuali asintoti;
a) verticale, la sua equazione è
x = -3.
b) orizzontale, è dato da
Altri punti
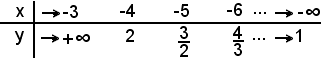
La curva ha, dunque, l'andamento della seguente figura:

1°)-il campo di esistenza della curva è
essendo la funzione razionale intera, quindi essa è definita su tutto l'asse reale.
2°)-I punti d'incontro con l'asse x sono dati da

e, dal confronto delle due equazioni, si ha l'equazione di 3° grado seguente:
2x3 - 5x2 + 4x - 4 = 0.
Effettuando la ricerca delle radici razionali, si trova che l'unica radice è x = 2, perchè l'equazione che si ottiene abbassando di grado la precedente, dopo aver eseguito con la regola di Ruffini la divisione tra il polinomio 1° membro ed il binomio x - 2, è
2x2 - x + 2 = 0,
che non ha radici reali.
Quindi la curva interseca l'asse x nel punto di coordinate (2, 0).
I punti d'incontro con l'asse y sono dati da
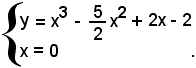
Quindi la curva interseca l'asse y nel punto di coordinate (0, -2).
3°)-ricerca dei punti estremanti;
essendo:
f'(x) = 3x2 - 5x + 2,
l'equazione da considerare è
3x2 - 5x + 2 = 0,
le cui radici sono
le quali sono le ascisse di punti di massimo, di minimo o di flesso.
Poichè

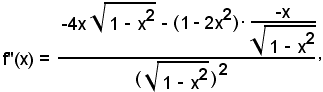
5°)-la curva è crescente per
ossia esternamente all'intervallo
ed è decrescente per
f'(x) = 3x2 - 5x + 2 < 0,
ossia internamente allo stesso intervallo.
La curva ha, dunque, l'andamento della seguente figura:

1°)-la funzione è irrazionale intera ed è definita in tutti i punti per cui è
1 - x2 ≥ 0,
ossia per tutte le
-1 ≤ x ≤ 1.
2°)-I punti d'incontro con l'asse x sono dati da
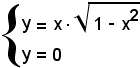
e, dal confronto delle due equazioni, si ha l'equazione seguente:
e quindi
x1 = 0, x2 = -1, x3 = 1.
I punti d'incontro con l'asse y sono dati da
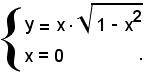
Quindi la curva interseca l'asse y nel punto di coordinate (0, 0).
3°)-ricerca dei punti estremanti;
essendo:
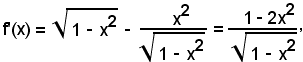
l'equazione da considerare è
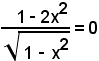
con x = ± 1 da scartare.
Liberando dal denominatore, si ha:
1 - x2 = 0
e, risolvendo tale equazione, risulta
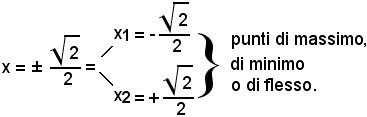
Poichè
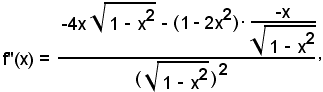

4°)-ricerca degli eventuali asintoti;
-la curva rappresentatrice di una funzione intera anche irrazionale non ha asintoti.
La curva ha, dunque, l'andamento della seguente figura:

5) y = senx·cosx da studiare nell'intervallo (0, 2π).
1°)-il campo di esistenza delle funzioni trigonometriche è solitamente fornito dalla traccia dell'esercizio ed in tal caso è (0, 2π), quindi risulta:
0 ≤ x ≤ 2π.
2°)-I punti d'incontro con l'asse x sono dati da
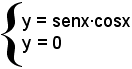
e, dal confronto delle due equazioni, si ha l'equazione seguente:
senx·cosx = 0,
ossia,

Risultano così trovati i punti d'incontro con l'asse x.
I punti d'incontro con l'asse y sono dati da
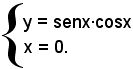
Quindi la curva interseca l'asse y nel punto di coordinate (0, 0).
3°)-ricerca dei punti estremanti;
f'(x) = cos2x - sen2x
l'equazione da risolvere è
cos2x - sen2x = 0,
quadratica omogenea, equivalente a
1 - tg2x = 0,
ossia
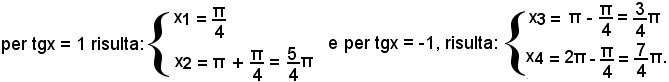
Risultano così trovate le ascisse dei punti di massimo, di minimo o di flesso.
Ora si ha:
e poichè

inoltre

4°)-ricerca degli eventuali asintoti; le funzioni trigonometriche in seno e coseno non hanno asintoti.

Altre applicazioni dei massimi e dei minimi
1° Problema - Tra tutti i rettangoli di dato perimetro 2p, determinare quello di area massima.

Indicando con x e y le dimensioni del rettangolo, si sa che
2x +2y = 2p,
ossia
x + y = p,
da cui
(1) y = p - x.
Inoltre, l'area del rettangolo è data da
S = x·y.
Sostituendo in quest'ultima uguaglianza la (1), si ha l'area espressa in funzione della sola variabile x, cioè:
S(x) = x (p - x) = -x2 + px,
della quale è richiesto il massimo.
Avendosi:
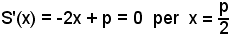
e
S''(x) = -2 < 0
sempre, si ha che per x = p/2 il rettangolo assume area massima. Si noti che in corrispondenza di tale valore si ha anche y = p/2, ossia il rettangolo di area massima è il quadrato di lato p/2.
2° Problema - Tra tutti i rettangoli di dato perimetro 2p, determinare quello che ha la minima diagonale.
Con le stesse indicazioni precedenti si ha:
x + y = p,
da cui
(1) y = p - x.
Inoltre, la diagonale del rettangolo è data da
Sostituendo in quest'ultima uguaglianza la (1), la si esprime come funzione della sola variabile x, cioè:
della quale è richiesto il minimo.
Si ha:
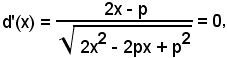
equazione frazionaria con denominatore sempre diverso da zero, dalla quale si ricava x = p/2.
Essendo poi
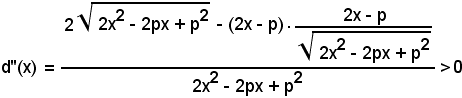
sempre per x = p/2, si ha il minimo della funzione d(x).
Poichè dalla (1) si ricava y = p/2, si ha:
ossia il rettangolo di diagonale minima è il quadrato di lato p/2.
3° Problema - Tra tutti i triangoli isosceli inscritti in una circonferenza di raggio r, determinare quello di area massima.

inoltre l'area in funzione di x è;
della quale è richiesto il massimo.
Si ha:
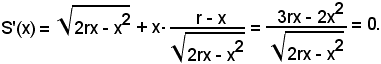
Le radici di questa equazione sono
x1 = 0,
non accettabile perchè annulla il denominatore, e
Essendo poi
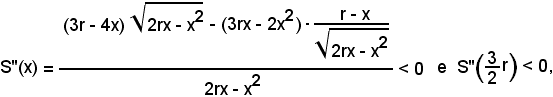
per x = (1/2)r si ha il triangolo richiesto, che è quello equilatero inscritto.
Complementi allo studio di una curva
1)-Concavità e convessità di una curva in un punto
Sia P' il punto di γ avente ascissa x0 in (a, b) e t la retta tangente in P' a γ la cui equazione, funzione di x, si indichi, per brevità y = t(x).
Considerato un intorno (x0-h, x0+h) di x0 e detti M' ed N' i punti di γ aventi per ascissa, rispettivamente x0-h e x0+h ed M'' e N'' quelli di t aventi le stesse ascisse, si ha:
1^ definizione - la curva γ nel punto P', Fig. 8, rivolge la concavità verso la direzione positiva dell'asse y, quando tutti i punti di y, ad eccezione di P', aventi ascisse appartenenti al conveniente intorno considerato di x0, hanno ordinata maggiore dei corrispondenti punti della tangente t.
(1) f(x0 - h) > t(x0 - h), f(x0 + h) > t(x0 + h);
2^ definizione - la curva γ nel punto P', Fig. 9, rivolge la concavità verso il semiasse negativo dell'asse y, quando tutti i punti di γ, ad eccezione di P', aventi ascisse appartenenti al conveniente intorno considerato di x0, hanno ordinata minore dei corrispondenti punti della tangente t.
(2) f(x0 - h) < t(x0 - h), f(x0 + h) < t(x0 + h).

Considerato che è
f(x0) = t(x0),
pertanto si può scrivere tanto
P' [x0, f(x0)]
quanto
P' [x0, t(x0)],
e che f'(x0) è il coefficiente angolare della tangente t, la cui equazione è stata indicata per brevità con y = t(x). Il coefficiente angolare f'(x0) della t può anche essere scritto sotto la forma
che assume quello della retta passante per i due punti (x1, y1) e (x2, y2), i quali in tal caso sono:
M'' = [x0-h, t(x0-h)] e P'[x0, t(x0)],
oppure
P'[x0, t(x0)] e N'' = [x0+h, t(x0+h)].
In ogni caso, si deve avere sempre lo stesso valore per il coefficiente angolare della t e quindi dev'essere:
Teorema 1 - Nei punti in cui la curva rivolge la concavità verso il semiasse positivo y, si ha:
Rs < f'(x0) < Rd.
Infatti, tenendo sempre presente che
f(x0) = t(x0),
le (1) si possono scrivere
f(x0 - h) - f(x0) > t(x0 - h) - t(x0), f(x0 + h) - f(x0) > t(x0 + h) - t(x0)
e dividendo ambo i membri della 1^ disuguaglianza per -h, per cui si deve cambiare il verso, ed ambo i membri della 2^ per h, si ha:
dalle quali, per la (3), si ha
ossia
Rs < f'(x0) < Rd,
come volevasi dimostrare.
Teorema 2 - Nei punti in cui la curva rivolge la concavità verso il semiasse negativo delle y, si ha:
Rd < f'(x0) < Rs.
Infatti, scrivendo le (2) come segue
f(x0 - h) - f(x0) < t(x0 - h) - t(x0), f(x0 + h) - f(x0) < t(x0 + h) - t(x0)
e dividendo ambo i membri della 1^ disuguaglianza per -h ed ambo i membri della 2^ per h, si ha:
dalle quali, per la (3), si ha
ossia
Rs > f'(x0) > Rd,
come volevasi dimostrare.
Punti di flesso o di inflessione


Come si vede nelle figure suddette, la tangente-secante alla curva non è più parallela all'asse x. Il punto P' delle figure 10 e 12 è detto flesso ascendente, in esso è:
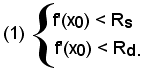
Il punto P' delle figure 11 e 13 è detto flesso discendente, in esso è:
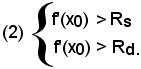
Viceversa, se in un punto x0 si vericano le (1), x0 è un punto di flesso ascendente e, se si verificano le (2), x0 è un punto di flesso discendente.
Teoremi sulle funzioni derivabili - Sviluppi in serie delle funzioni
1)-Teorema di Rolle-Dini
Se la funzione y = f(x) è:
a)-continua in un intervallo chiuso (a, b),
b)-derivabile in (a, b),
c)-con valori uguali negli estremi dell'intervallo f(b) = f(a),
esiste almeno un punto x0 interno ad (a, b) in cui si ha f'(x0).


Infatti, essendo y = f(x) continua nell'intervallo chiuso (a, b), per il teorema di Weierstrass, essa ammette un massimo e un minimo assoluti. Se tali valori massimo e minimo sono assunti dalla funzione negli estremi a e b dell'intervallo, Fig. 14, per l'ipotesi f(a) = f(b), essi sono necessariamente uguali e quindi la funzione viene ad essere costante in (a, b), ed allora la sua derivata è nulla in tutti i punti di (a, b). Il teorema sarebbe perciò dimostrato addirittura per tutti i punti di (a, b). Se invece, il valore massimo o minimo viene assunto dalla funzione in un punto x0 interno ad (a, b), Fig. 15, Fig. 16 e Fig. 17, poichè la funzione è derivabile in (a, b) per ipotesi, per quanto si sa dalla teoria dei punti estremanti, risulta:
f'(x0) = 0,
e il teorema è ugualmente dimostrato.
Nota bene
1)-Il teorema ha il nome di due grandi matematici, rispettivamente francese ed italiano, in quanto fu enunciato dal primo nel 1691 ma solo nel caso in cui la funzione y = f(x) fosse razionale intera della x, polinomio, mentre in forma rigorosa e completa fu enunciato dal pisano Ulisse Dini nel 1878.
2)-Un
altro matematico italiano, il gesuita Bonaventura Cavalieri, già
nel 1635 considerò lo stesso teorema nella sua interpretazione
geometrica:
-se un Arco A'B' di una curva, incontrato da una parallela all'asse y in non più di un punto, ha uguali le ordinate degli estremi yB' = yA', esiste almeno un punto sull'arco in cui la tangente è parallela all'asse x, quindi f'(x0) = 0.
2)-Teorema di Cauchy sugli accrescimenti finiti
Se y1 = f1(x) e y2 = f2(x) sono:
a)-due funzioni continue in un intervallo chiuso (a, b),
b)-derivabili in (a, b),
c)-tali che almeno y2 = f2(x) abbia valori disuguali negli estremi dell'intervallo f2(b) ≠ f2(a),
d)-la f'2(x) non si annulli in (a, b),
esiste un punto x0 interno ad (a, b) in cui sussiste la relazione
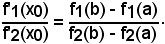
Infatti, considerata la funzione y = F(x) combinazione lineare delle due funzioni date secondo le costanti arbitrarie non nulle α e β, ugualmente continua in (a, b) e ivi derivabile:
y = F(x) = αf1(x) - βf2(x)
se si vuole trovare la relazione che lega le due costanti affinchè la y = F(x) soddisfi anche l'ipotesi c) del teorema di Rolle-Dini.
Essendo
F(b) = αf1(b) - βf2(b) e F(a) = αf1(a) - βf2(a),
affinchè sia
F(a) = F(b),
dev'essere
αf1(b) - βf2(b) = αf1(a) - βf2(a),
da cui
e, dividendo ambo i membri per
α[f2(b) - f2(a)] ≠ 0,
si ha:

Dunque, quando β e α sono vincolate dalla relazione (1), la y = F(x) soddisfa tutte le ipotesi del teorema di Rolle-Dini e, pertanto, per tale teorema, esiste un punto x0 di (a, b) in cui è
F'(x0) = 0.
Poichè
F'(x) = αf'1(x) - βf'2(x)
è
F'(x0) = αf'1(x0) - βf'2(x0) = 0,
da cui
αf'1(x0) = βf'2(x0)
e, dividendo ambo i membri per
αf'2(x0) ≠ 0,
si ha:
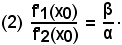
Dal confronto di (2) e (1), si ricava:
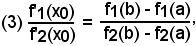
come volevasi dimostrare.
Nota bene
1)-Il teorema è detto degli accrescimenti finiti, perchè le differenze f1(b) - f1(a) e f2(b) - f2(a) sono gli accrescimenti o incrementi subiti, rispettivamente, dalle funzioni y1 = f1(x) e y2 = f2(x) quando si passa dal punto a al punto b nell'intervallo, ossia quando la variabile x subisce l'incremento b - a. La (3) allora esprime che:
-il rapporto tra gli accrescimenti delle due funzioni è uguale a quello della derivata delle stesse in un punto intermedio tra i due, iniziale e finale, assunti dalla variabile indipendente.
2)-Per b tendente ad a è:
f1(b) - f1(a) e f2(b) - f2(a)
Si consideri la (3) del teorema di Cauchy:
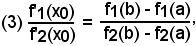
Si supponga ora che
y2 = f2(x) = x,
per cui
f'2(x) = 1
sempre e quindi anche
f'2(x0) = 1, f2(b) = b, f2(a) = a
e la (3) diventa
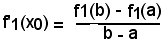
Se y1 = f1(x) la si indica y = f(x), si ha:
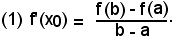
Il teorema è così dimostrato.
Nota storica
La forma analitica del teorema appena dimostrato fu enunciata da Lagrange nel 1801.
b)-Interpretazione geometrica della (1)
Sia A'B' l'arco di curva rappresentato dalla y = f(x) in (a, b). Per i significati geometrici di rapporto incrementale e derivata prima di una funzione in un punto, il teorema precedente si può esprimere nella seguente forma:
-dato un arco di curva e considerata la corsa passante per i suoi estremi, esiste sempre almeno un punto sull'arco, in cui la tangente risulta parallela alla corda.
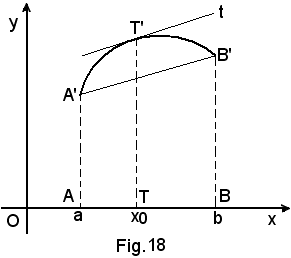
Nota beneLa forma geometrica del teorema appena dimostrato fu enunciata da Cavalieri nel 1635.
c)-Generalizzazione della (1)
Se si considera
a = x e b = x + h,
per cui
b - a = h,
la (1) diventa:
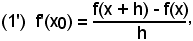
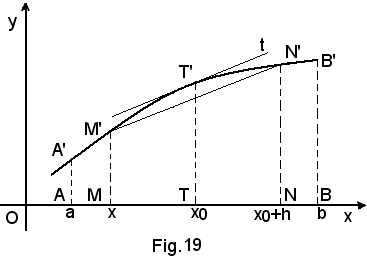
la cui interpretazione geometrica, identica a quella vista di Cavalieri, è chiaramente visibile nella seguente Fig. 19:
La (1') è da considerare la relazione fondamentale dell'analisi infinitesimale. Da essa infatti si ha:
f(x + h) - f(x)= f'(x0)·h,
ossia
che è lo sviluppo in serie, dovuto a Taylor, di una funzione limitatamente alla derivata prima della stessa la quale, come si nota, è calcolata nel punto x0 intermedio tra x e x + h.
Sviluppo in serie di TaylorLa (2) è un caso particolare della seguente formula, della quale si tralascia la dimostrazione:
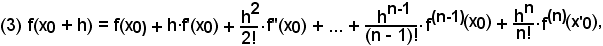
in cui l'ultima derivata è sempre calcolata in un punto x'0 intermedio tra x0 e x0 + h.
La (3) si chiama formula dello sviluppo in serie di Taylor di una funzione relativa al punto e permette di esprimere una qualsiasi funzione in somma di altre.
L'ultimo termine si chiama termine complementare della serie. Per quest'ultimo termine esistono varie forme, sulle quali però non è il caso di soffermarsi.
Sviluppo in serie di Mac-Laurin
Più utile e di più frequente applicazione è la formula dello sviluppo in serie di Mac-Laurin, che è la seguente:
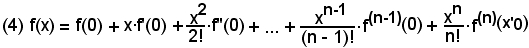
e che si ottiene dalla (3) ponendo prima
x = x0 + h,
per cui
h = x - x0,
quindi si ha:
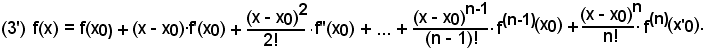
Ponendo ancora
x0 = 0,
cioè considerando lo sviluppo relativo al punto zero, risulta:
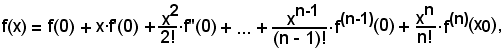
che è la (4).
6)-Esempi di sviluppi in serie di Mac-Laurin
1°)-Sviluppare in serie di Mac-Laurin la funzione y = senx.
Essendo
f(0) = sen0 = 0,
si ha:
f'(x) = cosx e f'(0) = cos0 = 1,
f''(x) = -senx e f''(0) = -sen0 = 0,
f'''(x) = -cosx e f'''(0) = -cos0 = -1,
fIV(x) = senx e fIV(0) = sen0 = 0.
Ricordando la periodicità delle derivate delle funzioni in oggetto, si ha la serie del seno:
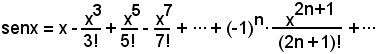
2°)-Sviluppare in serie di Mac-Laurin la funzione y = cosx.
f(0) = cos0 = 1,
si ha:
f'(x) = -senx e f'(0) = -sen0 = 0,
f''(x) = -cosx e f''(0) = -cos0 = -1,
f'''(x) = senx e f'''(0) = sen0 = 0,
fIV(x) = cosx e fIV(0) = cos0 = 1.
Ricordando la periodicità delle derivate delle funzioni in oggetto, si ha la serie del coseno:
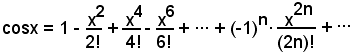
3°)-Sviluppare in serie di Mac-Laurin la funzione y = ex.
e0 = 1,
e ricordando che
Dex = ex
sempre, per cui
f'(0) = f''(0) = ... = e0 = 1,
si ha la serie esponenziale:
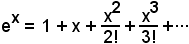
Nota bene
Lo sviluppo in serie di una funzione serve ad approssimare una funzione mediante un polinomio di grado determinato, e con l'ultimo termine, chiamato termine complementare, dare l'ordine di grandezza dell'errore che si commette con l'approssimazione fatta.
Teoremi di De L'Hospital
1°)-Siano y1 = f1(x) e y2 = f2(x) due funzioni:
a)-continue e derivabili nell'intervallo (a, b),
b)-che si annullano in uno stesso punto x0 di (a, b), cioè risulta f1(x0) = f2(x0) = 0,
c)-f'2(x) ≠ 0 in tutti i punti di (a, b), al più escluso x0,
se esiste
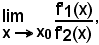
esiste anche
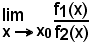
e si ha:
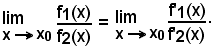
L'ipotesi c) assicura che y2 = f2(x) al più si annulla in x = x0, in quanto se si annullasse in un altro punto x0 + h, con h ≠ 0, per il teorema di Rolle-Dini, dovrebbe esistere almeno un punto ξ, compreso tra x0 e x0 + h, in cui sarebbe f'2(ξ) = 0 e ciò risulterebbe contro l'ipotesi c).
La funzione
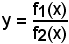
è, pertanto, definita in ogni punto x di (a, b), al più escluso x0,
Posto
a = x0, b = x, x0 = ξ (tra x e x0),
la formula che esprime il teorema di Cauchy, diventa:
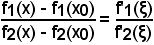
e poichè f1(x0) = f2(x0) = 0,
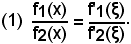
Allora, se x tende ad x0, anche ξ tende ad x0 e, dall'esistenza di
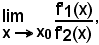
dalla (1) discende l'esistenza anche di
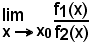
e di
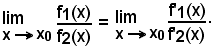
Il teorema è così dimostrato.
Tale teorema vale anche se all'ipotesi di continuità e dell'annullarsi delle due funzioni in x0, si sostituisce l'altra ipotesi che le due funzioni siano definite e continue per x ≠ x0, e infinitesime per x tendente ad x0, e ciò anche quando il punto x0 è all'infinito.
Infatti, posto
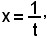
se esiste
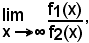
sarà
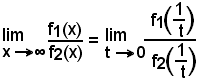
e si verifica che
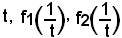
soddisfano in t = 0 e nell'intorno di tale punto le condizioni del teorema precedente.
2°)-Siano y1 = f1(x) e y2 = f2(x) due funzioni:
a)-derivabili in un intorno del punto x0, al più escluso x0,
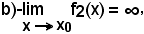
c)-f'2(x) ≠ 0 nell'intorno considerato, ad eccezione al più del punto x0,
allora, se esiste
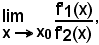
esiste anche
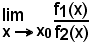
ed è
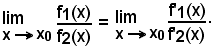
Si tralascia la dimostrazione di tale teorema.
I due teoremi suddetti di De L'Hospital si possono unificare nel seguente
3°)-teorema generale.
Se per x tendente ad x0, ove x0 è un punto al finito oppure all'infinito, le due funzioni y1 = f1(x) e y2 = f2(x) sono tali che si abbia contemporaneamente

allora, la ricerca del
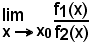
può essere ricondotta a quella del
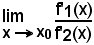
e, se quest'ultimo esiste, si ha:
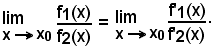
2)-Metodi per uscire dalle forme indeterminate dei limiti

Il teorema generale di De L'Hospital dà, in effetti, un metodo per la ricerca del limite di un'espressione che si presenta nella forma indeterminata 0/0, in quanto si ha:
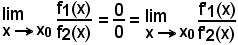
e, nel caso in cui si abbia ancora la stessa forma indeterminata, si applica nuovamente il teorema, ossia si considera
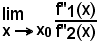
e così di seguito, fino ad uscire dalla indeterminazione.
Esempi
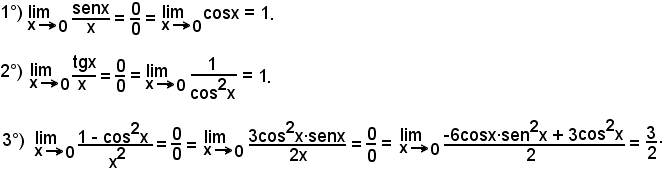

Quando è
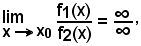
per le ipotesi sulle due funzioni, si può scrivere
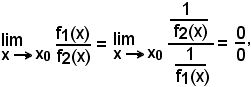
cioè si ritorna al 1° caso.
Esempio
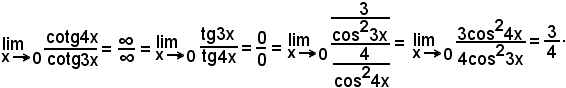
Nel caso in cui le funzioni siano due polinomi ed x tende ad si applica direttamente il 1° teorema.
si applica direttamente il 1° teorema.
Esempi
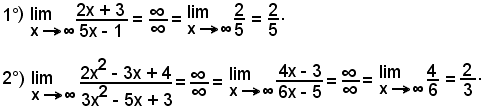

Quando è
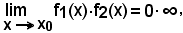
cioè quando
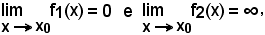
potendosi scrivere

ci si ritrova nuovamente nel caso 0/0.
Esempio
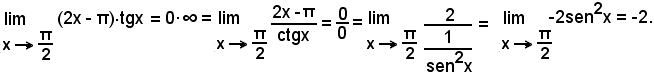

Quando è
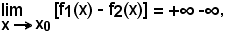
potendosi scrivere
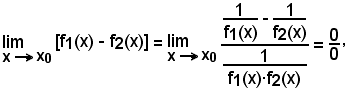
ci si ritrova ancora nel caso 0/0.
Esempio
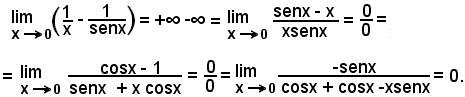
3)-Altre forme indeterminate
Sono le seguenti:
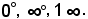
Esse si presentano alla ricerca di
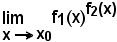
e precisamente si ha:
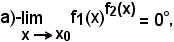
quando è
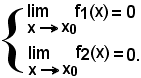
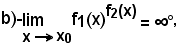
quando è
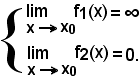
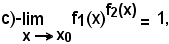
quando è
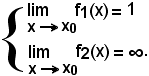
Premesso che la funzione
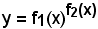
ha senso nel campo reale quando f1(x) > 0, prendendo i logaritmi neperiani di ambo i membri e applicando il teorema della potenza, si ha:

e, pertanto, si è portati alla ricerca del limite del 2° membro, che dà luogo in ciascuno dei casi a), b), c) visti, alla forma indeterminata
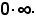
Una volta usciti da tale forma indeterminata, si torna al

passando dal logaritmo al numero per la continuità della funzione logaritmo.
Esempio
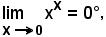
poichè da
y = xx,
essendo
logy = xlogx,
si ha:
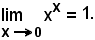
Nota bene
Per applicare correttamente i teoremi occorre, caso per caso, verificare se sono soddisfatte tutte le ipotesi in essi previste, in quanto può accadere che esista
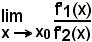
mentre non esista
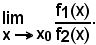
Inoltre, si deve osservare che la non applicabilità del teorema di De L'Hospital non significa, a priori, la non esistenza del limite richiesto.
Infatti:
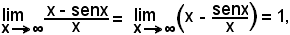
in quanto è
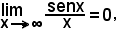
come rapporto di una quantità limitata,
-1 ≤ senx ≤ 1,
ad un'altra che tende ad , mentre se fosse stato applicato il teorema si sarebbe pervenuti a
, mentre se fosse stato applicato il teorema si sarebbe pervenuti a
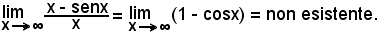
-se un Arco A'B' di una curva, incontrato da una parallela all'asse y in non più di un punto, ha uguali le ordinate degli estremi yB' = yA', esiste almeno un punto sull'arco in cui la tangente è parallela all'asse x, quindi f'(x0) = 0.
2)-Teorema di Cauchy sugli accrescimenti finiti
Se y1 = f1(x) e y2 = f2(x) sono:
a)-due funzioni continue in un intervallo chiuso (a, b),
b)-derivabili in (a, b),
c)-tali che almeno y2 = f2(x) abbia valori disuguali negli estremi dell'intervallo f2(b) ≠ f2(a),
d)-la f'2(x) non si annulli in (a, b),
esiste un punto x0 interno ad (a, b) in cui sussiste la relazione
Infatti, considerata la funzione y = F(x) combinazione lineare delle due funzioni date secondo le costanti arbitrarie non nulle α e β, ugualmente continua in (a, b) e ivi derivabile:
y = F(x) = αf1(x) - βf2(x)
se si vuole trovare la relazione che lega le due costanti affinchè la y = F(x) soddisfi anche l'ipotesi c) del teorema di Rolle-Dini.
Essendo
F(b) = αf1(b) - βf2(b) e F(a) = αf1(a) - βf2(a),
affinchè sia
F(a) = F(b),
dev'essere
αf1(b) - βf2(b) = αf1(a) - βf2(a),
da cui
α[f1(b) - f1(a)] = β[f2(b) - f2(a)]
e, dividendo ambo i membri per
α[f2(b) - f2(a)] ≠ 0,
si ha:
Dunque, quando β e α sono vincolate dalla relazione (1), la y = F(x) soddisfa tutte le ipotesi del teorema di Rolle-Dini e, pertanto, per tale teorema, esiste un punto x0 di (a, b) in cui è
F'(x0) = 0.
Poichè
F'(x) = αf'1(x) - βf'2(x)
è
da cui
αf'1(x0) = βf'2(x0)
e, dividendo ambo i membri per
αf'2(x0) ≠ 0,
si ha:
Dal confronto di (2) e (1), si ricava:
come volevasi dimostrare.
Nota bene
1)-Il teorema è detto degli accrescimenti finiti, perchè le differenze f1(b) - f1(a) e f2(b) - f2(a) sono gli accrescimenti o incrementi subiti, rispettivamente, dalle funzioni y1 = f1(x) e y2 = f2(x) quando si passa dal punto a al punto b nell'intervallo, ossia quando la variabile x subisce l'incremento b - a. La (3) allora esprime che:
-il rapporto tra gli accrescimenti delle due funzioni è uguale a quello della derivata delle stesse in un punto intermedio tra i due, iniziale e finale, assunti dalla variabile indipendente.
2)-Per b tendente ad a è:
f1(b) - f1(a) e f2(b) - f2(a)
tendono a zero, ossia gl'incrementi delle due funzioni diventano due infinitesimi.
Dalla (3) si può anche dire che:
-il rapporto tra gl'incrementi delle due funzioni eguaglia quello delle derivate delle stesse in un punto x0 anche nel caso in cui gl'incrementi diventano infinitesimi.
3)-Teorema del valore medio o di Lagrange e Cavalieri
a)-Forma analitica
Data una funzione y = f(x):
-continua in un intervallo chiuso (a, b),
-derivabile in tutto (a, b),
esiste un punto x0 di (a, b) in cui si ha:
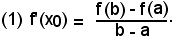
Dalla (3) si può anche dire che:
-il rapporto tra gl'incrementi delle due funzioni eguaglia quello delle derivate delle stesse in un punto x0 anche nel caso in cui gl'incrementi diventano infinitesimi.
3)-Teorema del valore medio o di Lagrange e Cavalieri
a)-Forma analitica
Data una funzione y = f(x):
-continua in un intervallo chiuso (a, b),
-derivabile in tutto (a, b),
esiste un punto x0 di (a, b) in cui si ha:
Si consideri la (3) del teorema di Cauchy:
Si supponga ora che
y2 = f2(x) = x,
per cui
f'2(x) = 1
sempre e quindi anche
f'2(x0) = 1, f2(b) = b, f2(a) = a
e la (3) diventa
Se y1 = f1(x) la si indica y = f(x), si ha:
Il teorema è così dimostrato.
Nota storica
La forma analitica del teorema appena dimostrato fu enunciata da Lagrange nel 1801.
b)-Interpretazione geometrica della (1)
Sia A'B' l'arco di curva rappresentato dalla y = f(x) in (a, b). Per i significati geometrici di rapporto incrementale e derivata prima di una funzione in un punto, il teorema precedente si può esprimere nella seguente forma:
-dato un arco di curva e considerata la corsa passante per i suoi estremi, esiste sempre almeno un punto sull'arco, in cui la tangente risulta parallela alla corda.

Nota bene
c)-Generalizzazione della (1)
Se si considera
a = x e b = x + h,
per cui
b - a = h,
la (1) diventa:
la cui interpretazione geometrica, identica a quella vista di Cavalieri, è chiaramente visibile nella seguente Fig. 19:

La (1') è da considerare la relazione fondamentale dell'analisi infinitesimale. Da essa infatti si ha:
f(x + h) - f(x)= f'(x0)·h,
ossia
(2) f(x + h) = f(x)+ f'(x0)·h,
che è lo sviluppo in serie, dovuto a Taylor, di una funzione limitatamente alla derivata prima della stessa la quale, come si nota, è calcolata nel punto x0 intermedio tra x e x + h.
Sviluppo in serie di Taylor
in cui l'ultima derivata è sempre calcolata in un punto x'0 intermedio tra x0 e x0 + h.
La (3) si chiama formula dello sviluppo in serie di Taylor di una funzione relativa al punto e permette di esprimere una qualsiasi funzione in somma di altre.
L'ultimo termine si chiama termine complementare della serie. Per quest'ultimo termine esistono varie forme, sulle quali però non è il caso di soffermarsi.
Sviluppo in serie di Mac-Laurin
Più utile e di più frequente applicazione è la formula dello sviluppo in serie di Mac-Laurin, che è la seguente:
e che si ottiene dalla (3) ponendo prima
x = x0 + h,
per cui
h = x - x0,
quindi si ha:
Ponendo ancora
x0 = 0,
cioè considerando lo sviluppo relativo al punto zero, risulta:
che è la (4).
6)-Esempi di sviluppi in serie di Mac-Laurin
1°)-Sviluppare in serie di Mac-Laurin la funzione y = senx.
Essendo
f(0) = sen0 = 0,
si ha:
f'(x) = cosx e f'(0) = cos0 = 1,
f''(x) = -senx e f''(0) = -sen0 = 0,
f'''(x) = -cosx e f'''(0) = -cos0 = -1,
fIV(x) = senx e fIV(0) = sen0 = 0.
Ricordando la periodicità delle derivate delle funzioni in oggetto, si ha la serie del seno:
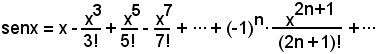
2°)-Sviluppare in serie di Mac-Laurin la funzione y = cosx.
Essendo
f(0) = cos0 = 1,
si ha:
f'(x) = -senx e f'(0) = -sen0 = 0,
f''(x) = -cosx e f''(0) = -cos0 = -1,
f'''(x) = senx e f'''(0) = sen0 = 0,
fIV(x) = cosx e fIV(0) = cos0 = 1.
Ricordando la periodicità delle derivate delle funzioni in oggetto, si ha la serie del coseno:
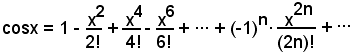
3°)-Sviluppare in serie di Mac-Laurin la funzione y = ex.
Essendo
e0 = 1,
e ricordando che
Dex = ex
sempre, per cui
f'(0) = f''(0) = ... = e0 = 1,
si ha la serie esponenziale:
Nota bene
Lo sviluppo in serie di una funzione serve ad approssimare una funzione mediante un polinomio di grado determinato, e con l'ultimo termine, chiamato termine complementare, dare l'ordine di grandezza dell'errore che si commette con l'approssimazione fatta.
Teoremi di De L'Hospital
1°)-Siano y1 = f1(x) e y2 = f2(x) due funzioni:
a)-continue e derivabili nell'intervallo (a, b),
b)-che si annullano in uno stesso punto x0 di (a, b), cioè risulta f1(x0) = f2(x0) = 0,
c)-f'2(x) ≠ 0 in tutti i punti di (a, b), al più escluso x0,
se esiste
esiste anche
e si ha:
L'ipotesi c) assicura che y2 = f2(x) al più si annulla in x = x0, in quanto se si annullasse in un altro punto x0 + h, con h ≠ 0, per il teorema di Rolle-Dini, dovrebbe esistere almeno un punto ξ, compreso tra x0 e x0 + h, in cui sarebbe f'2(ξ) = 0 e ciò risulterebbe contro l'ipotesi c).
La funzione
è, pertanto, definita in ogni punto x di (a, b), al più escluso x0,
Posto
a = x0, b = x, x0 = ξ (tra x e x0),
la formula che esprime il teorema di Cauchy, diventa:
e poichè f1(x0) = f2(x0) = 0,
Allora, se x tende ad x0, anche ξ tende ad x0 e, dall'esistenza di
dalla (1) discende l'esistenza anche di
e di
Il teorema è così dimostrato.
Tale teorema vale anche se all'ipotesi di continuità e dell'annullarsi delle due funzioni in x0, si sostituisce l'altra ipotesi che le due funzioni siano definite e continue per x ≠ x0, e infinitesime per x tendente ad x0, e ciò anche quando il punto x0 è all'infinito.
Infatti, posto
se esiste
sarà
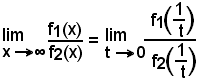
e si verifica che
soddisfano in t = 0 e nell'intorno di tale punto le condizioni del teorema precedente.
2°)-Siano y1 = f1(x) e y2 = f2(x) due funzioni:
a)-derivabili in un intorno del punto x0, al più escluso x0,
c)-f'2(x) ≠ 0 nell'intorno considerato, ad eccezione al più del punto x0,
allora, se esiste
esiste anche
ed è
Si tralascia la dimostrazione di tale teorema.
I due teoremi suddetti di De L'Hospital si possono unificare nel seguente
3°)-teorema generale.
Se per x tendente ad x0, ove x0 è un punto al finito oppure all'infinito, le due funzioni y1 = f1(x) e y2 = f2(x) sono tali che si abbia contemporaneamente

allora, la ricerca del
può essere ricondotta a quella del
e, se quest'ultimo esiste, si ha:
2)-Metodi per uscire dalle forme indeterminate dei limiti
Il teorema generale di De L'Hospital dà, in effetti, un metodo per la ricerca del limite di un'espressione che si presenta nella forma indeterminata 0/0, in quanto si ha:
e, nel caso in cui si abbia ancora la stessa forma indeterminata, si applica nuovamente il teorema, ossia si considera
e così di seguito, fino ad uscire dalla indeterminazione.
Esempi
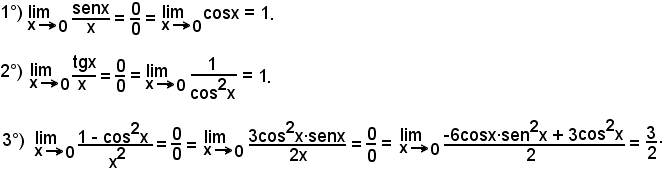
Quando è
per le ipotesi sulle due funzioni, si può scrivere
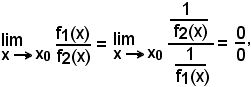
cioè si ritorna al 1° caso.
Esempio
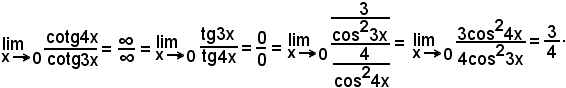
Nel caso in cui le funzioni siano due polinomi ed x tende ad
Esempi
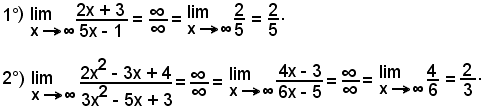
Quando è
cioè quando
potendosi scrivere

ci si ritrova nuovamente nel caso 0/0.
Esempio
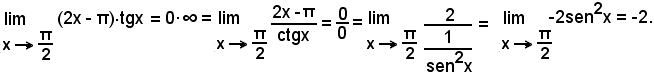
Quando è
potendosi scrivere
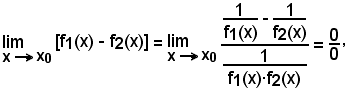
ci si ritrova ancora nel caso 0/0.
Esempio
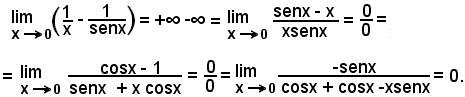
3)-Altre forme indeterminate
Sono le seguenti:
Esse si presentano alla ricerca di
e precisamente si ha:
quando è
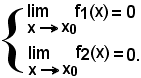
quando è
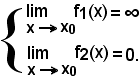
quando è
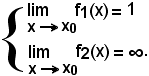
Premesso che la funzione
ha senso nel campo reale quando f1(x) > 0, prendendo i logaritmi neperiani di ambo i membri e applicando il teorema della potenza, si ha:
e, pertanto, si è portati alla ricerca del limite del 2° membro, che dà luogo in ciascuno dei casi a), b), c) visti, alla forma indeterminata
Una volta usciti da tale forma indeterminata, si torna al
passando dal logaritmo al numero per la continuità della funzione logaritmo.
Esempio
poichè da
y = xx,
essendo
logy = xlogx,
si ha:
Nota bene
Per applicare correttamente i teoremi occorre, caso per caso, verificare se sono soddisfatte tutte le ipotesi in essi previste, in quanto può accadere che esista
mentre non esista
Inoltre, si deve osservare che la non applicabilità del teorema di De L'Hospital non significa, a priori, la non esistenza del limite richiesto.
Infatti:
in quanto è
come rapporto di una quantità limitata,
-1 ≤ senx ≤ 1,
ad un'altra che tende ad