MIKY & GENNY
TEORIA DEGLI INSIEMI ---> INDICE
Concetto di insieme
1)-Del concetto di insieme, o aggregato, classe, famiglia, gruppo, totalità, unione, collezione, ecc., si è tentato di dare diverse definizioni, ma tutte sono risultate non solo logicamente non soddisfacenti, ma addirittura tali da presupporre in realtà lo stesso concetto che si voleva definire.
Giorgio Cantor, riconosciuto come il fondatore della teoria degli insiemi, nonostante che prima di lui si fossero occupati di questioni inerenti la suddetta teoria, i matematici Cauchy, Schwarz, Dedekind, dette la seguente definizione:
-l'insieme è una collezione di oggetti determinati e distinti concepita dal nostro pensiero come il tutto.
Non potendo ridurlo a nozioni più semplici, si dice che il concetto di insieme è primitivo, cioè è una nozione elementare o naturale del pensiero dell'uomo.
Senza avere la la pretesa di dare una definizione, si potrebbe intendere per insieme finito la riunione di un gruppo finito di elementi di natura qualsiasi, cioè di specie naturalmente diverse, come si vedrà negli esempi successivi.
Allora, un insieme di elementi si dirà infinito quando, considerato un qualsiasi insieme finito di quegli elementi, esiste sempre almeno un elemento, fra quelli assegnati, non appartenente all'insieme finito.
Si badi che il concetto di insieme infinito è di natura potenziale e non attuale.
Esempi di insiemi finiti
1)-i numeri interi minori di un dato numero, ad esempio di 100,
2)-gli alunni di una classe,
3)-le suppellettili di un'aula,
4)-i libri esistenti in una biblioteca,
5)-gli abitanti di una città,
6)-gli oggetti esistenti in un negozio,
7)-le lettere di un alfabeto,
8)-un quaderno, una penna, un libro, un fiore,
9)-le radici di una data equazione.
Esempi di insiemi infiniti
1)-l'insieme dei punti di un segmento o di una retta,
2)-l'insieme delle rette del piano o dello spazio,
3)-l'insieme dei numeri naturali,
4)-l'insieme delle equazioni,
5)-l'insieme dei numeri reali.
Dagli esempi dati, si osserva che nella formazione di un insieme non ci si è preoccupati della natura degli elementi costituenti l'insieme stesso.
La teoria degl'insiemi non si occupa della natura degli elementi, ma delle loro proprietà e delle loro relazioni logiche nel modo più astratto possibile, tanto che molti si chiesero se non si uscisse, in tal modo, dal campo della matematica, per entrare in quello della metafisica.
Per quanto siano evidenti gli addentellati di natura filosofica, riflettendo nel modo di procedere i concetti basilari ed i principi della logica, è bene affermare subito non solo il dominio della matematica ma anche l'importanza della teoria nella matematica.
In definitiva:
-un insieme si considera definito, quando è assegnata una legge mediante la quale è possibile stabilire se un dato elemento, indipendentemente dalla sua natura, appartiene o no all'insieme.
Definire un insieme, significa, dunque, assegnare tale legge o, come si dice, la proprietà caratteristica dell'insieme.
Per individuare un insieme finito si possono nominare uno per uno tutti gli elementi, ma per gl'insiemi infiniti, poichè non è possibile fare altrettanto, l'individuazione avviene mediante l'assegnazione della proprietà caratteristica.
2)-Notazioni
Gli elementi di un insieme, solitamente, vengono indicati con le lettere minuscole: a, b, c ..., oppure con a1, a2, a3 ..., e sono rappresentati graficamente con punti o crocette.
Tutto l'insieme viene indicato con una lettera maiuscola: A, B, C...
In generale, per designare insiemi i cui elementi siano rappresentati da simboli, si racchiudono gli elementi in una parentesi graffa. Quindi l'insieme delle cifre è:
{0, 1, 2, 3, 4, 5, 6, 7, 8, 9}
e ciascuna cifra è un elemento che appartiene a detto insieme.
Pertanto, si può scrivere:
A = {a, b, c ...}
e significa che l'insieme A ha per elementi a, b, c...
L'appartenenza di un elemento a ad un insieme A viene indicata con il simbolo ; quindi la scrittura
; quindi la scrittura

si legge "a appartiene ad A".
La non appartenenza viene indicata con la scrittura
a 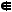 A
A
e si legge "a non appartiene ad A".
Un insieme può essere formato o contenere un solo elemento, il quale, si noti, non è identificabile con l'insieme stesso.
Si scrive:
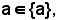
dove a è l'elemento e {a} l'insieme.
Concetto di ambiente
Si è detto che per individuare o assegnare un insieme finito o infinito occorre dare la proprietà caratteristica dell'insieme, ossia la legge mediante la quale sia possibile stabilire, senza equivoci, se un certo elemento appartiene o no all'insieme.
Poichè la natura degli elementi costituenti un insieme può essere affatto arbitraria, ad esempio:
A = {numeri interi, persone, astri}
risulta evidente che, perchè la proprietà abbia significato preciso, ossia non dia adito ad equivoci, è necessario che essa sia riferita a degli oggetti appartenenti ad un insieme più generale, ma in un certo senso già noto.
Un tale insieme più generale è chiamato ambiente.
Solitamente un ambiente è indicato con Ω.
Si osservi subito che ogni insieme, a sua volta, può essere assunto come ambiente, perchè, mediante l'assegnazione di proprietà significative, da esso possono essere dedotti nuovi insiemi.
Esempi
1)-l'insieme dei numeri interi ha per ambiente i numeri razionali,
2)-l'insieme dei numeri pari o dispari ha per ambiente i numeri interi,
3)-l'insieme dei numeri multipli di 4 ha per ambiente i numeri pari.
Insieme vuoto
Dato Ω, mediante l'enunciazione di una certa legge si ricaveranno certi insiemi di elementi aventi, appunto, quella legge come proprietà caratteristica.
Se in Ω non esiste alcun elemento soddisfacente alla proprietà caratteristica enunciata, si dirà ancora di avere un insieme, ovviamente particolare, in quanto non contenente alcun elemento e si chiamerà insieme vuoto e sarà indicato con: Ø,
L'insieme vuoto Ø viene ad avere, in sostanza, lo stesso valore che aveva lo zero in aritmetica e la stessa importanza.
Potenza di un insieme
Si ripete ancora una volta che, definire un insieme di numeri reali, significa assegnare almeno una legge mediante la quale si possa stabilire se un dato numero reale appartiene o no all'insieme.
Le difficoltà di concepire un tale insieme come un elemento o oggetto definito, sono in relazione con le difficoltà teoriche di concepire il "continuo lineare", ossia l'insieme di tutti i numeri reali.
Non è possibile chiarire del tutto questi concetti, in questa trattazione, in quanto si avrebbe bisogno di possedere altre nozioni e paricolarmente quella di potenza di un insieme o di un numero cardinale di un insieme.
Tuttavia si pensi che, in un certo qual modo la nozione di potenza è l'estensione, per gli insiemi infiniti, del concetto di numero cardinale che si possiede per gl'insiemi finiti, concetto che, intuitivamente, dà la numerosità del gruppo degli elementi considerati, a differenza del concetto di numero ordinale che sta ad indicare soltanto l'ordine naturale con cui gli elementi del gruppo si susseguono.
Si ritiene utile la conoscenza di quanto segue:
-si dice che due insiemi di elementi qualsiasi hanno la stessa potenza o numero cardinale, quando è possibile porre tra i loro elementi una corrispondenza biunivoca di modo che ad ogni elemento di uno dei due insiemi corrisponda uno ed un solo elemento dell'altro.
Ovviamente, se due insiemi A e B hanno ciascuno la stessa potenza di un terzo insieme C, A e B hanno la stessa potenza.
Invece di dire che due insiemi hanno la stessa potenza, si dice che le loro potenze sono uguali, cosicchè si sarebbe potuto esporre la proprietà precedente dicendo: due potenze uguali ad una terza sono uguali fra loro.
Due insiemi di un numero finito di elementi hanno la stessa potenza se sono formati dallo stesso numero di elementi, cioè se hanno lo stesso numero cardinale.
Ogni insieme di infiniti elementi ha una potenza superiore a quella di un qualsiasi insieme finito.
Tra gli insiemi infiniti, quelli i cui elementi si possono porre in corrispondenza biunivoca con i numeri interi 1, 2, 3, ... si dice che hanno la stessa potenza dell'insieme dei numeri e tale potenza si chiama "del numerabile".
Bisogna osservare che:
-se da un insieme numerabile si toglie, con una legge assegnata, un insieme di elementi in modo che l'insieme rimanente sia ancora formato da un numero infinito di elementi, quest'ultimo insieme ha ancora la potenza del numerabile.
Ovvero, l'assioma aritmetico che la parte è minore del tutto non ha l'analogo nella teoria degl'insiemi.
Un insieme non numerabile, quale è quello dei numeri reali, dicesi di avere la potenza del continuo, il continuo reale.
La potenza del continuo è ovviamente superiore a quella del numerabile.
Infatti, dell'insieme dei numeri reali, che si è detto avere la potenza del continuo, fa parte l'insieme dei numeri razionali che ha la potenza del numerabile.
Teorema - Togliendo od aggiungendo, con una legge assegnata, da un insieme non numerabile un insieme di elementi numerabile, si ottiene ancora un insieme non numerabile.
In altri termini, la potenza di un insieme non numerabile, in generale, non muta se si tolgono o si aggiungono ad esso, con leggi assegnate, insiemi con la potenza del numerabile.
Nota bene
Dal teorema enunciato, segue che:
a)-quando si studiano le potenze degli insiemi non numerabili, si possono abbandonare, senza inconvenienti, insiemi numerabili di elementi. Gli insiemi numerabili godono così, rispetto a quelli non numerabili, della stessa proprietà degli infinitesimi rispetto alle quantità finite;
b)-l'insieme dei numeri irrazionali di un dato intervallo ha la potenza del continuo, cioè la stessa potenza di tutti i punti dell'intervallo che costituiscono l'insieme dei numeri reali.
Questo perchè, si ripete, equivale ad aver tralasciato l'insieme dei numeri razionali che ha la potenza del numerabile;
c)-tutti gli insiemi finiti della teoria che si sta espandendo o hanno la potenza del numerabile o hanno la potenza del continuo.
Ciò, però, non porta ad escludere la possibilità dell'esistenza di insiemi di punti che non abbiano nè la potenza del numerabile nè quella del continuo; vale a dire:
-la questione se tale ipotesi porta a contraddizioni è rimasta insoluta.
In altri termini, si tratta di vedere se è possibile che esista una potenza intermedia tra il numerabile e il continuo.
E' opportuno ancora, almeno per informazione, dire che esistono insiemi non di numeri ma di funzioni, ad esempio l'insieme delle funzioni di variabile reale, che hanno una potenza superiore a quella del continuo.
Insieme di punti
Sapendo che è sempre possibile porre una corrispondenza biunivoca tra i numeri reali e i punti di una retta, corrispondenza che, come è noto, si realizza mediante un sistema di coordinate ascisse su una retta, oppure tra le coppie di numeri reali e i punti di un piano, corrispondenza che si realizza con il sistema di coordinate cartesiane nel piano; lo studio degli insiemi di numeri reali equivale a quello degli insiemi lineari di punti o degli insiemi a due dimensioni di punti del piano. Per questo si dice indifferentemente punto x e numero x oppure punto P e coppia (x, y), coordinate di P. In corrispondenza alla teoria gegli insiemi lineari, ad una dimensione, di punti e a quella degli insiemi piani, a due dimensioni, si può svolgere, parallelamente, una teoria degli insiemi di punti a tre o, in generale a p dimensioni.
Intervalli
Sia assegnata la retta r;

se a < b, si chiama intervallo chiuso l'insieme dei punti tali che:
a ≤ x ≤ b;
l'intervallo chiuso si indica con [a, b] e, rispettivamente, a e b si chiamano chiamano estremi dell'intervallo [a, b] e precisamente a 1° e b 2° estremo.
Si chiama intervallo aperto l'insieme dei punti tali che
a < x < b;
l'intervallo aperto si indica con ]a, b[ e, rispettivamente, a e b si chiamano chiamano estremi dell'intervallo ]a, b[.
Si chiama intervallo semiaperto o semichiuso l'insieme dei punti tali che
rispettivamente sia
1) a ≤ x < b e 2) a < x ≤ b;
l'intervallo semiaperto o semichiuso si indica con [a, b[, ed è valida la (1), cioè se è chiuso in a e aperto in b, oppure con ]a, b] ed è valida la (2), cioè se è aperto in a e chiuso in b.
I punti x < a e x > b si dicono esterni all'intervallo.
Il numero b - a si chiama ampiezza dell'intervallo.
Proprietà descrittive degli insiemi lineari di punti
Si consideri sulla retta r l'insieme dei punti in corrispondenza biunivoca con un assegnato insieme di numeri reali, secondo un sistema di coordinate ascisse fissato sulla stessa retta r; se esiste un punto β tale che nessun punto dell'insieme sia alla destra di β, si dice che l'insieme dato è limitato a destra.
Un punto b tale che nessun punto dell'insieme sia alla destra di b e tale che esistano punti dell'insieme interno all'intervallo [b - ε, b], qualunque sia il numero ε positivo, si dirà confine superiore o limite superiore dell'insieme.
Il punto b può appartenere o no all'insieme dato; se appartiene si dirà massimo dell'insieme; quindi, dire che b è il massimo dell'insieme, significa dire che b è l'estremo superiore dell'insieme ed è un punto dello stesso insieme.
Esempio
L'insieme:
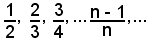
ha per confine superiore il numero 1, il quale però non appartenendo all'insieme non è un massimo.
Invece nell'insieme:
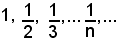
il confine superiore è 1, che è anche un massimo.
In modo perfettamente analogo si ha che se l'insieme è limitato a sinistra, vale a dire, se esiste un punto α tale che i punti dell'insieme dato siano alla sua destra, esisterà un punto a tale che nessun punto dell'insieme è alla sinistra di a e tale che a o è un punto dell'insieme oppure esistono punti dell'insieme interni ad ogni intervallo [a, a + ε], con ε > 0 arbitrario, a sarà chiamato confine o limite inferiore e nel caso appartenga all'insieme si dirà il minimo.
E' evidente che un insieme di numeri non può ammettere più di un confine inferiore.
Esempio
L'insieme
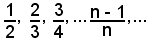
ha per confine inferiore 1, che è un minimo, mentre l'insieme
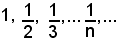
ha per confine inferiore 0, che non è un minimo.
Insieme lineare di punti limitato
Un insieme lineare di punti per cui esistono il confine superiore ed il confine inferiore si dice limitato.
Insieme lineare di punti illimitato a destra
Se non esiste alcun punto b tale che tutti i punti dell'insieme siano a sinistra di b, l'insieme si dirà illimitato a destra o anche che il suo confine superiore è +∞.
Insieme lineare di punti illimitato a sinistra
I simboli -∞ e +∞ stanno ad indicare soltanto che l'insieme dato è privo, rispettivamente, di limite inferiore e di limite superiore.
Essi non sono punti, ma qualche volta, impropriamente, si usano come tali.
Dire, dunque che +∞ è il confine superiore dell'insieme significa che, se a è un punto assegnato arbitrariamente sulla retta sostegno, esistono sempre punti x dell'insieme alla destra di a.
Analogamente, dire che che -∞ è il confine inferiore dell'insieme significa che, per ogni punto b assegnato arbitrariamente sulla retta sostegno, esistono punti dell'insieme alla sinistra di b.
Un insieme di numeri reali ammette sempre sia un confine superiore che uno inferiore.
Invece:
a)-l'insieme di numeri reali positivi è limitato a sinistra, ma non a destra;
b)-l'insieme di numeri reali negativi è limitato a destra, ma non a sinistra.
Quando l'insieme dato è limitato, l'intervallo [a, b] avente per estremo sinistro il confine inferiore o per estremo destro il confine superiore dell'insieme, sarà chiamato intervallo in cui esiste l'insieme o intervallo fondamentale dell'insieme.
3)-Nota bene
La distinzione fra insiemi lineari limitati ed insiemi lineari illimitati non è, come potrebbe sembrare a prima vista, sostanziale dato che si può porre, anzi in infiniti modi, una corrispondenza biunivoca fra i punti dell'insieme illimitato ed i punti di un insieme limitato, in modo che sia conservato l'ordine relativo con cui si susseguono i punti dell'insieme dato, e ciò non altera, sostanzialmente, la proprietà descrittiva dell'insieme.
Una tale corrispondenza è, ad esempio, data da:
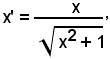
con il radicale considerato con il segno +.
L'interpretazione geometrica della corrispondenza risulta evidente dalla seguente figura seguente.
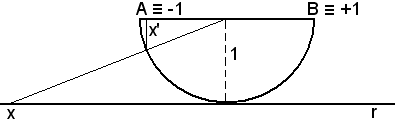
I punti della retta r, sostegno, vengono trasformati nei punti del segmento AB, cioè dell'intervallo [-1, +1] in modo che a -∞ corrisponde A = -1 ed a +∞ corrisponde B = +1 e l'ordine relativo è mantenuto.
In tal modo,ad ogni punto x dell'intervallo illimitato [-∞, +∞] corrisponde un punto x dell'intervallo aperto [-1, +1] e volendo completare la rappresentazione, si può far corrispondere agli estremi -1 e +1 del segmento [-1, +1] i punti impropri -∞ e +∞.
Intorno di un punto - Punto di accumulazione
Sia dato un punto x di un intervallo [a, b]:
a)-un intervallo [x - δ1, x + δ2], con δ1 e δ2 positivi, che giaccia completamente in [a, b] si chiama intorno completo o solo intorno del punto x, e può supporsi arbitrariamente piccolo, scegliendo δ1 e δ2 sufficientemente piccoli.
Un intervallo (x - δ, x ), appartenente sempre ad [a, b], si chiama intorno sinistro di x.
Un intervallo (x, x + δ), appartenente sempre ad [a, b], si chiama intorno destro di x.
Il numero δ1 + δ2, si chiama ampiezza dell'intorno di x.
Nel caso in cui sia δ1 = δ2, ossia l'intorno sinistro è uguale a quello destro di x, l'ampiezza dell'intorno completo simmetrico è 2δ.
L'intorno destro e sinistro hanno, quindi, ampiezza δ.
Gli estremi a e b dell'intervallo [a, b] possono avere soltanto intorni destro o sinistro, rispettivamente.
Un intorno del punto x può essere, come intervallo, aperto o chiuso.
b)-Sia A un insieme appartente all'intervallo [a, b].
Definizione - Un punto P di [a, b] si dice punto di accumulazione o punto limite dell'insieme A, se è tale che in ogni suo intorno esistono punti di A distinti da P.
La definizione posta equivale a:
-un punto P è un punto di accumulazione dell'insieme A, se in ogni suo intorno cadono sempre infiniti punti di A.
Un punto di accumulazione di un insieme può o no appartenere all'intervallo stesso.
E' fondamentale il seguente teorema di Bolzano Weierstrass:
-ogni insieme A limitato e infinito, ha almeno un punto di accumulazione.
Nell'enunciato dato è implicito che il teorema non è valido se l'insieme è illimitato.
Esempi
L'insieme lineare dei punti corrispondenti, mediante un sistema di coordinate ascisse, ai numeri 1, 2, 3, ... non hanno alcun punto limite.
Lo stesso dicasi dell'insieme corrispondente ai numeri -1, -2, -3, ...
Se a ciascuno di questi insiemi di punti si applica la trasformazione
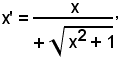
essi si trasformano, rispettivamente, nei due insiemi di punti:
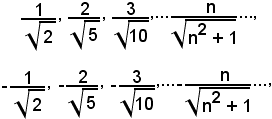
che hanno come punti di accumulazione, rispettivamente, 1 e -1, estremi dell'intervallo [-1, +1] degli x' e che non corrispondono a nessuno dei punti x del 1° e del 2° dei due numeri suddetti.
Se però si conviene di aggiungere all'insieme dei numeri reali i due numeri impropri -∞ e +∞, i cui corrispondenti nell'intervallo [-1, +1] saranno proprio i punti -1 e +1, potrà tutta la retta [-∞, +∞] essere riguardata come un intervallo chiuso e corrispondente all'intervallo finito chiuso [-1, +1] degli x'.
Allora il punto x = +∞ potrà essere considerato, nel senso esteso, come punto di accumulazione dell'insieme 1, 2, 3 ...; esso corrisponde al punto di accumulazione +1 dell'insieme
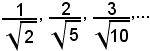
nell'intervallo [-1, +1].
Analogamente, il punto aggiunto -∞ corrisponderà al punto di accumulazione -1 dell'insieme
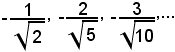
sempre nell'intervallo [-1, +1].
In tal modo, al ogni punto di accumulazione al finito di un insieme A' nell'intervallo [-∞, +∞] delle x, corrisponde un punto di accumulazione o limite dell'insieme corrispondente dei punti x' nell'intervallo [-1, +1].
Pertanto, risulta che, una volta aggiunti ai punti di una retta i punti impropri -∞ e +∞, in modo che essa divenga un intervallo chiuso, il teorema di esistenza di un punto di accumulazione continua a sussistere anche per gli insiemi illimitati.
D'altra parte, la differenza fra i due casi, insieme limitato e insieme illimitato, una volta fatta la convenzione di considerare come punti impropri -∞ e +∞, scompare quando si trasforma l'insieme illimitato in un insieme esistente nell'intervallo [-1, +1].
Si potrà, allora, chiamare intorno, rispettivamente, dei punti +∞ e -∞, ciascuno degl'intervalli [a, +∞] [-∞, a], dove a è un punto arbitrario della retta sostegno.
Notazioni
1)-Si ricordi che se α è un numero reale qualsiasi, con la scrittura |α|, che si legge valore assoluto di α, si intende indicare lo stesso numero α; se esso è positivo, risulta
mentre, se esso è negativo
2)-Detto α un numero reale positivo, la scrittura
equivale a:
-a ≤ x < +a.
Esempi
1°) |x| < 3 equivale a:
2°) |x| ≤ 2 equivale a:
3°) |x - 3| < 7 equivale a:
4°) |x - 2| ≤ 3 equivale a:
3)-Allora, in generale:
|x - x0| < δ
equivale a
-δ < x - x0 < δ
e quindi a
x0 - δ < x < x0 + δ.
Ciò significa che:
-il punto x appartiene all'intorno aperto ]x0 - δ, x0 + δ].
Ed ancora:
|x - x0| ≤ δ
equivale a
-δ ≤ x - x0 ≤ δ,
da cui
x0 - δ ≤ x ≤ x0 + δ.
Ciò significa che:
-il punto x appartiene all'intorno chiuso [x0 - δ, x0 + δ].
1)-Del concetto di insieme, o aggregato, classe, famiglia, gruppo, totalità, unione, collezione, ecc., si è tentato di dare diverse definizioni, ma tutte sono risultate non solo logicamente non soddisfacenti, ma addirittura tali da presupporre in realtà lo stesso concetto che si voleva definire.
Giorgio Cantor, riconosciuto come il fondatore della teoria degli insiemi, nonostante che prima di lui si fossero occupati di questioni inerenti la suddetta teoria, i matematici Cauchy, Schwarz, Dedekind, dette la seguente definizione:
-l'insieme è una collezione di oggetti determinati e distinti concepita dal nostro pensiero come il tutto.
Non potendo ridurlo a nozioni più semplici, si dice che il concetto di insieme è primitivo, cioè è una nozione elementare o naturale del pensiero dell'uomo.
Senza avere la la pretesa di dare una definizione, si potrebbe intendere per insieme finito la riunione di un gruppo finito di elementi di natura qualsiasi, cioè di specie naturalmente diverse, come si vedrà negli esempi successivi.
Allora, un insieme di elementi si dirà infinito quando, considerato un qualsiasi insieme finito di quegli elementi, esiste sempre almeno un elemento, fra quelli assegnati, non appartenente all'insieme finito.
Si badi che il concetto di insieme infinito è di natura potenziale e non attuale.
Esempi di insiemi finiti
1)-i numeri interi minori di un dato numero, ad esempio di 100,
2)-gli alunni di una classe,
3)-le suppellettili di un'aula,
4)-i libri esistenti in una biblioteca,
5)-gli abitanti di una città,
6)-gli oggetti esistenti in un negozio,
7)-le lettere di un alfabeto,
8)-un quaderno, una penna, un libro, un fiore,
9)-le radici di una data equazione.
Esempi di insiemi infiniti
1)-l'insieme dei punti di un segmento o di una retta,
2)-l'insieme delle rette del piano o dello spazio,
3)-l'insieme dei numeri naturali,
4)-l'insieme delle equazioni,
5)-l'insieme dei numeri reali.
Dagli esempi dati, si osserva che nella formazione di un insieme non ci si è preoccupati della natura degli elementi costituenti l'insieme stesso.
La teoria degl'insiemi non si occupa della natura degli elementi, ma delle loro proprietà e delle loro relazioni logiche nel modo più astratto possibile, tanto che molti si chiesero se non si uscisse, in tal modo, dal campo della matematica, per entrare in quello della metafisica.
Per quanto siano evidenti gli addentellati di natura filosofica, riflettendo nel modo di procedere i concetti basilari ed i principi della logica, è bene affermare subito non solo il dominio della matematica ma anche l'importanza della teoria nella matematica.
In definitiva:
-un insieme si considera definito, quando è assegnata una legge mediante la quale è possibile stabilire se un dato elemento, indipendentemente dalla sua natura, appartiene o no all'insieme.
Definire un insieme, significa, dunque, assegnare tale legge o, come si dice, la proprietà caratteristica dell'insieme.
Per individuare un insieme finito si possono nominare uno per uno tutti gli elementi, ma per gl'insiemi infiniti, poichè non è possibile fare altrettanto, l'individuazione avviene mediante l'assegnazione della proprietà caratteristica.
2)-Notazioni
Gli elementi di un insieme, solitamente, vengono indicati con le lettere minuscole: a, b, c ..., oppure con a1, a2, a3 ..., e sono rappresentati graficamente con punti o crocette.
Tutto l'insieme viene indicato con una lettera maiuscola: A, B, C...
In generale, per designare insiemi i cui elementi siano rappresentati da simboli, si racchiudono gli elementi in una parentesi graffa. Quindi l'insieme delle cifre è:
{0, 1, 2, 3, 4, 5, 6, 7, 8, 9}
e ciascuna cifra è un elemento che appartiene a detto insieme.
Pertanto, si può scrivere:
A = {a, b, c ...}
e significa che l'insieme A ha per elementi a, b, c...
L'appartenenza di un elemento a ad un insieme A viene indicata con il simbolo
si legge "a appartiene ad A".
La non appartenenza viene indicata con la scrittura
e si legge "a non appartiene ad A".
Un insieme può essere formato o contenere un solo elemento, il quale, si noti, non è identificabile con l'insieme stesso.
Si scrive:
dove a è l'elemento e {a} l'insieme.
Concetto di ambiente
Si è detto che per individuare o assegnare un insieme finito o infinito occorre dare la proprietà caratteristica dell'insieme, ossia la legge mediante la quale sia possibile stabilire, senza equivoci, se un certo elemento appartiene o no all'insieme.
Poichè la natura degli elementi costituenti un insieme può essere affatto arbitraria, ad esempio:
risulta evidente che, perchè la proprietà abbia significato preciso, ossia non dia adito ad equivoci, è necessario che essa sia riferita a degli oggetti appartenenti ad un insieme più generale, ma in un certo senso già noto.
Un tale insieme più generale è chiamato ambiente.
Solitamente un ambiente è indicato con Ω.
Si osservi subito che ogni insieme, a sua volta, può essere assunto come ambiente, perchè, mediante l'assegnazione di proprietà significative, da esso possono essere dedotti nuovi insiemi.
Esempi
1)-l'insieme dei numeri interi ha per ambiente i numeri razionali,
2)-l'insieme dei numeri pari o dispari ha per ambiente i numeri interi,
3)-l'insieme dei numeri multipli di 4 ha per ambiente i numeri pari.
Insieme vuoto
Dato Ω, mediante l'enunciazione di una certa legge si ricaveranno certi insiemi di elementi aventi, appunto, quella legge come proprietà caratteristica.
Se in Ω non esiste alcun elemento soddisfacente alla proprietà caratteristica enunciata, si dirà ancora di avere un insieme, ovviamente particolare, in quanto non contenente alcun elemento e si chiamerà insieme vuoto e sarà indicato con: Ø,
L'insieme vuoto Ø viene ad avere, in sostanza, lo stesso valore che aveva lo zero in aritmetica e la stessa importanza.
Potenza di un insieme
Si ripete ancora una volta che, definire un insieme di numeri reali, significa assegnare almeno una legge mediante la quale si possa stabilire se un dato numero reale appartiene o no all'insieme.
Le difficoltà di concepire un tale insieme come un elemento o oggetto definito, sono in relazione con le difficoltà teoriche di concepire il "continuo lineare", ossia l'insieme di tutti i numeri reali.
Non è possibile chiarire del tutto questi concetti, in questa trattazione, in quanto si avrebbe bisogno di possedere altre nozioni e paricolarmente quella di potenza di un insieme o di un numero cardinale di un insieme.
Tuttavia si pensi che, in un certo qual modo la nozione di potenza è l'estensione, per gli insiemi infiniti, del concetto di numero cardinale che si possiede per gl'insiemi finiti, concetto che, intuitivamente, dà la numerosità del gruppo degli elementi considerati, a differenza del concetto di numero ordinale che sta ad indicare soltanto l'ordine naturale con cui gli elementi del gruppo si susseguono.
Si ritiene utile la conoscenza di quanto segue:
-si dice che due insiemi di elementi qualsiasi hanno la stessa potenza o numero cardinale, quando è possibile porre tra i loro elementi una corrispondenza biunivoca di modo che ad ogni elemento di uno dei due insiemi corrisponda uno ed un solo elemento dell'altro.
Ovviamente, se due insiemi A e B hanno ciascuno la stessa potenza di un terzo insieme C, A e B hanno la stessa potenza.
Invece di dire che due insiemi hanno la stessa potenza, si dice che le loro potenze sono uguali, cosicchè si sarebbe potuto esporre la proprietà precedente dicendo: due potenze uguali ad una terza sono uguali fra loro.
Due insiemi di un numero finito di elementi hanno la stessa potenza se sono formati dallo stesso numero di elementi, cioè se hanno lo stesso numero cardinale.
Ogni insieme di infiniti elementi ha una potenza superiore a quella di un qualsiasi insieme finito.
Tra gli insiemi infiniti, quelli i cui elementi si possono porre in corrispondenza biunivoca con i numeri interi 1, 2, 3, ... si dice che hanno la stessa potenza dell'insieme dei numeri e tale potenza si chiama "del numerabile".
Bisogna osservare che:
-se da un insieme numerabile si toglie, con una legge assegnata, un insieme di elementi in modo che l'insieme rimanente sia ancora formato da un numero infinito di elementi, quest'ultimo insieme ha ancora la potenza del numerabile.
Ovvero, l'assioma aritmetico che la parte è minore del tutto non ha l'analogo nella teoria degl'insiemi.
Un insieme non numerabile, quale è quello dei numeri reali, dicesi di avere la potenza del continuo, il continuo reale.
La potenza del continuo è ovviamente superiore a quella del numerabile.
Infatti, dell'insieme dei numeri reali, che si è detto avere la potenza del continuo, fa parte l'insieme dei numeri razionali che ha la potenza del numerabile.
Teorema - Togliendo od aggiungendo, con una legge assegnata, da un insieme non numerabile un insieme di elementi numerabile, si ottiene ancora un insieme non numerabile.
In altri termini, la potenza di un insieme non numerabile, in generale, non muta se si tolgono o si aggiungono ad esso, con leggi assegnate, insiemi con la potenza del numerabile.
Nota bene
Dal teorema enunciato, segue che:
a)-quando si studiano le potenze degli insiemi non numerabili, si possono abbandonare, senza inconvenienti, insiemi numerabili di elementi. Gli insiemi numerabili godono così, rispetto a quelli non numerabili, della stessa proprietà degli infinitesimi rispetto alle quantità finite;
b)-l'insieme dei numeri irrazionali di un dato intervallo ha la potenza del continuo, cioè la stessa potenza di tutti i punti dell'intervallo che costituiscono l'insieme dei numeri reali.
Questo perchè, si ripete, equivale ad aver tralasciato l'insieme dei numeri razionali che ha la potenza del numerabile;
c)-tutti gli insiemi finiti della teoria che si sta espandendo o hanno la potenza del numerabile o hanno la potenza del continuo.
Ciò, però, non porta ad escludere la possibilità dell'esistenza di insiemi di punti che non abbiano nè la potenza del numerabile nè quella del continuo; vale a dire:
-la questione se tale ipotesi porta a contraddizioni è rimasta insoluta.
In altri termini, si tratta di vedere se è possibile che esista una potenza intermedia tra il numerabile e il continuo.
E' opportuno ancora, almeno per informazione, dire che esistono insiemi non di numeri ma di funzioni, ad esempio l'insieme delle funzioni di variabile reale, che hanno una potenza superiore a quella del continuo.
Insieme di punti
Sapendo che è sempre possibile porre una corrispondenza biunivoca tra i numeri reali e i punti di una retta, corrispondenza che, come è noto, si realizza mediante un sistema di coordinate ascisse su una retta, oppure tra le coppie di numeri reali e i punti di un piano, corrispondenza che si realizza con il sistema di coordinate cartesiane nel piano; lo studio degli insiemi di numeri reali equivale a quello degli insiemi lineari di punti o degli insiemi a due dimensioni di punti del piano. Per questo si dice indifferentemente punto x e numero x oppure punto P e coppia (x, y), coordinate di P. In corrispondenza alla teoria gegli insiemi lineari, ad una dimensione, di punti e a quella degli insiemi piani, a due dimensioni, si può svolgere, parallelamente, una teoria degli insiemi di punti a tre o, in generale a p dimensioni.
Intervalli
Sia assegnata la retta r;
se a < b, si chiama intervallo chiuso l'insieme dei punti tali che:
a ≤ x ≤ b;
l'intervallo chiuso si indica con [a, b] e, rispettivamente, a e b si chiamano chiamano estremi dell'intervallo [a, b] e precisamente a 1° e b 2° estremo.
Si chiama intervallo aperto l'insieme dei punti tali che
a < x < b;
l'intervallo aperto si indica con ]a, b[ e, rispettivamente, a e b si chiamano chiamano estremi dell'intervallo ]a, b[.
Si chiama intervallo semiaperto o semichiuso l'insieme dei punti tali che
rispettivamente sia
1) a ≤ x < b e 2) a < x ≤ b;
l'intervallo semiaperto o semichiuso si indica con [a, b[, ed è valida la (1), cioè se è chiuso in a e aperto in b, oppure con ]a, b] ed è valida la (2), cioè se è aperto in a e chiuso in b.
I punti x < a e x > b si dicono esterni all'intervallo.
Il numero b - a si chiama ampiezza dell'intervallo.
Proprietà descrittive degli insiemi lineari di punti
Si consideri sulla retta r l'insieme dei punti in corrispondenza biunivoca con un assegnato insieme di numeri reali, secondo un sistema di coordinate ascisse fissato sulla stessa retta r; se esiste un punto β tale che nessun punto dell'insieme sia alla destra di β, si dice che l'insieme dato è limitato a destra.
Un punto b tale che nessun punto dell'insieme sia alla destra di b e tale che esistano punti dell'insieme interno all'intervallo [b - ε, b], qualunque sia il numero ε positivo, si dirà confine superiore o limite superiore dell'insieme.
Il punto b può appartenere o no all'insieme dato; se appartiene si dirà massimo dell'insieme; quindi, dire che b è il massimo dell'insieme, significa dire che b è l'estremo superiore dell'insieme ed è un punto dello stesso insieme.
Esempio
L'insieme:
ha per confine superiore il numero 1, il quale però non appartenendo all'insieme non è un massimo.
Invece nell'insieme:
il confine superiore è 1, che è anche un massimo.
In modo perfettamente analogo si ha che se l'insieme è limitato a sinistra, vale a dire, se esiste un punto α tale che i punti dell'insieme dato siano alla sua destra, esisterà un punto a tale che nessun punto dell'insieme è alla sinistra di a e tale che a o è un punto dell'insieme oppure esistono punti dell'insieme interni ad ogni intervallo [a, a + ε], con ε > 0 arbitrario, a sarà chiamato confine o limite inferiore e nel caso appartenga all'insieme si dirà il minimo.
E' evidente che un insieme di numeri non può ammettere più di un confine inferiore.
Esempio
L'insieme
ha per confine inferiore 1, che è un minimo, mentre l'insieme
ha per confine inferiore 0, che non è un minimo.
Insieme lineare di punti limitato
Un insieme lineare di punti per cui esistono il confine superiore ed il confine inferiore si dice limitato.
Insieme lineare di punti illimitato a destra
Se non esiste alcun punto b tale che tutti i punti dell'insieme siano a sinistra di b, l'insieme si dirà illimitato a destra o anche che il suo confine superiore è +∞.
Insieme lineare di punti illimitato a sinistra
Se non esiste alcun punto a tale che ogni punto dell'insieme sia alla destra di a, l'insieme si dirà illimitato
a sinistra o anche che il suo confine inferiore è -∞.
I simboli -∞ e +∞ stanno ad indicare soltanto che l'insieme dato è privo, rispettivamente, di limite inferiore e di limite superiore.
Essi non sono punti, ma qualche volta, impropriamente, si usano come tali.
Dire, dunque che +∞ è il confine superiore dell'insieme significa che, se a è un punto assegnato arbitrariamente sulla retta sostegno, esistono sempre punti x dell'insieme alla destra di a.
Analogamente, dire che che -∞ è il confine inferiore dell'insieme significa che, per ogni punto b assegnato arbitrariamente sulla retta sostegno, esistono punti dell'insieme alla sinistra di b.
Un insieme di numeri reali ammette sempre sia un confine superiore che uno inferiore.
Invece:
a)-l'insieme di numeri reali positivi è limitato a sinistra, ma non a destra;
b)-l'insieme di numeri reali negativi è limitato a destra, ma non a sinistra.
Quando l'insieme dato è limitato, l'intervallo [a, b] avente per estremo sinistro il confine inferiore o per estremo destro il confine superiore dell'insieme, sarà chiamato intervallo in cui esiste l'insieme o intervallo fondamentale dell'insieme.
3)-Nota bene
La distinzione fra insiemi lineari limitati ed insiemi lineari illimitati non è, come potrebbe sembrare a prima vista, sostanziale dato che si può porre, anzi in infiniti modi, una corrispondenza biunivoca fra i punti dell'insieme illimitato ed i punti di un insieme limitato, in modo che sia conservato l'ordine relativo con cui si susseguono i punti dell'insieme dato, e ciò non altera, sostanzialmente, la proprietà descrittiva dell'insieme.
Una tale corrispondenza è, ad esempio, data da:
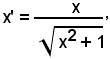
con il radicale considerato con il segno +.
L'interpretazione geometrica della corrispondenza risulta evidente dalla seguente figura seguente.

I punti della retta r, sostegno, vengono trasformati nei punti del segmento AB, cioè dell'intervallo [-1, +1] in modo che a -∞ corrisponde A = -1 ed a +∞ corrisponde B = +1 e l'ordine relativo è mantenuto.
In tal modo,ad ogni punto x dell'intervallo illimitato [-∞, +∞] corrisponde un punto x dell'intervallo aperto [-1, +1] e volendo completare la rappresentazione, si può far corrispondere agli estremi -1 e +1 del segmento [-1, +1] i punti impropri -∞ e +∞.
Intorno di un punto - Punto di accumulazione
Sia dato un punto x di un intervallo [a, b]:
a)-un intervallo [x - δ1, x + δ2], con δ1 e δ2 positivi, che giaccia completamente in [a, b] si chiama intorno completo o solo intorno del punto x, e può supporsi arbitrariamente piccolo, scegliendo δ1 e δ2 sufficientemente piccoli.
Un intervallo (x - δ, x ), appartenente sempre ad [a, b], si chiama intorno sinistro di x.
Un intervallo (x, x + δ), appartenente sempre ad [a, b], si chiama intorno destro di x.
Il numero δ1 + δ2, si chiama ampiezza dell'intorno di x.
Nel caso in cui sia δ1 = δ2, ossia l'intorno sinistro è uguale a quello destro di x, l'ampiezza dell'intorno completo simmetrico è 2δ.
L'intorno destro e sinistro hanno, quindi, ampiezza δ.
Gli estremi a e b dell'intervallo [a, b] possono avere soltanto intorni destro o sinistro, rispettivamente.
Un intorno del punto x può essere, come intervallo, aperto o chiuso.
b)-Sia A un insieme appartente all'intervallo [a, b].
Definizione - Un punto P di [a, b] si dice punto di accumulazione o punto limite dell'insieme A, se è tale che in ogni suo intorno esistono punti di A distinti da P.
La definizione posta equivale a:
-un punto P è un punto di accumulazione dell'insieme A, se in ogni suo intorno cadono sempre infiniti punti di A.
Un punto di accumulazione di un insieme può o no appartenere all'intervallo stesso.
E' fondamentale il seguente teorema di Bolzano Weierstrass:
-ogni insieme A limitato e infinito, ha almeno un punto di accumulazione.
Nell'enunciato dato è implicito che il teorema non è valido se l'insieme è illimitato.
Esempi
L'insieme lineare dei punti corrispondenti, mediante un sistema di coordinate ascisse, ai numeri 1, 2, 3, ... non hanno alcun punto limite.
Lo stesso dicasi dell'insieme corrispondente ai numeri -1, -2, -3, ...
Se a ciascuno di questi insiemi di punti si applica la trasformazione
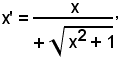
essi si trasformano, rispettivamente, nei due insiemi di punti:
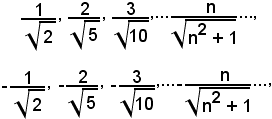
che hanno come punti di accumulazione, rispettivamente, 1 e -1, estremi dell'intervallo [-1, +1] degli x' e che non corrispondono a nessuno dei punti x del 1° e del 2° dei due numeri suddetti.
Se però si conviene di aggiungere all'insieme dei numeri reali i due numeri impropri -∞ e +∞, i cui corrispondenti nell'intervallo [-1, +1] saranno proprio i punti -1 e +1, potrà tutta la retta [-∞, +∞] essere riguardata come un intervallo chiuso e corrispondente all'intervallo finito chiuso [-1, +1] degli x'.
Allora il punto x = +∞ potrà essere considerato, nel senso esteso, come punto di accumulazione dell'insieme 1, 2, 3 ...; esso corrisponde al punto di accumulazione +1 dell'insieme
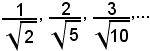
nell'intervallo [-1, +1].
Analogamente, il punto aggiunto -∞ corrisponderà al punto di accumulazione -1 dell'insieme
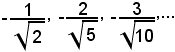
sempre nell'intervallo [-1, +1].
In tal modo, al ogni punto di accumulazione al finito di un insieme A' nell'intervallo [-∞, +∞] delle x, corrisponde un punto di accumulazione o limite dell'insieme corrispondente dei punti x' nell'intervallo [-1, +1].
Pertanto, risulta che, una volta aggiunti ai punti di una retta i punti impropri -∞ e +∞, in modo che essa divenga un intervallo chiuso, il teorema di esistenza di un punto di accumulazione continua a sussistere anche per gli insiemi illimitati.
D'altra parte, la differenza fra i due casi, insieme limitato e insieme illimitato, una volta fatta la convenzione di considerare come punti impropri -∞ e +∞, scompare quando si trasforma l'insieme illimitato in un insieme esistente nell'intervallo [-1, +1].
Si potrà, allora, chiamare intorno, rispettivamente, dei punti +∞ e -∞, ciascuno degl'intervalli [a, +∞] [-∞, a], dove a è un punto arbitrario della retta sostegno.
Notazioni
1)-Si ricordi che se α è un numero reale qualsiasi, con la scrittura |α|, che si legge valore assoluto di α, si intende indicare lo stesso numero α; se esso è positivo, risulta
|α| = +α,
mentre, se esso è negativo
|α| = -α.
2)-Detto α un numero reale positivo, la scrittura
|x| ≤ a
equivale a:
Esempi
1°) |x| < 3 equivale a:
-3 < x < 3.
2°) |x| ≤ 2 equivale a:
-2 ≤ x ≤ 2.
3°) |x - 3| < 7 equivale a:
-7 < x - 3 < 7
-4 < x < 10.
e quindi a
4°) |x - 2| ≤ 3 equivale a:
-3 ≤ x - 2 ≤ 3
-1 ≤ x ≤ 5.
e quindi a
3)-Allora, in generale:
equivale a
e quindi a
x0 - δ < x < x0 + δ.
Ciò significa che:
-il punto x appartiene all'intorno aperto ]x0 - δ, x0 + δ].
Ed ancora:
|x - x0| ≤ δ
equivale a
da cui
-il punto x appartiene all'intorno chiuso [x0 - δ, x0 + δ].