MIKY & GENNY
TEORIA DEI LIMITI DELLE FUNZIONI ---> INDICE
Concetto di limite delle funzioni
Premessa
Le successioni si possono considerare come particolari funzioni, ossia funzioni definite solo per valori interi e positivi della variabile, non esistendo, infatti, differenza formale nelle scritture
y = f(x) e y = f(n) = an,
con x = n = 1, 2, 3 ...
In precedenza sono stati esaminati i vari casi di limite delle successioni, ossia i primi esempi di tendenza al limite di una funzione. Ora si vuole mostrare come quei concetti introdotti per le successioni, ossia per particolari funzioni, possano estendersi ad una qualsiasi funzione reale della variabile reale y = f(x), tipo che sarà sempre considerato in seguito.
1)-Limite destro finito della funzione, per la variabile indipendente x tendente ad un valore finito x0.
Sia y = f(x) una funzione definita in un intervallo che abbia x0 come estremo sinistro, tenendo anche presente che nel punto x0 essa può anche non essere definita.
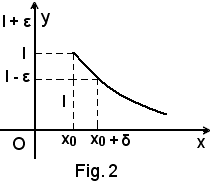
Definizione - Si dice che f(x), per x tendente ad x0 da destra, e si scrive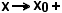
, ha per limite il numero finito l quando, per ogni numero ε > 0, piccolo a piacere, esiste in corrispondenza un intorno destro, ad esempio di ampiezza δ, del punto x0, tale che per tutti i punti x di tale intorno, risulti:
x0 < x < x0 + δ,
oppure
|x - x0| < δ,
al più escluso il punto x0, si abbia la relazione
l - ε < f(x) < l + ε,
oppure
Si scrive:
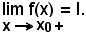
Osservazioni
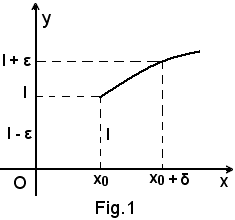
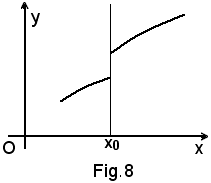
1°)-L'ampiezza δ dell'intorno destro del punto x0 dipende, in generale, dal numero ε > 0 considerato a piacere in quanto, come si vede nella Fig. 1, riportato l sull'asse y, a partire da esso si segnino i punti l - ε ed l + ε e da ciascuno di questi si consideri quella parallela all'asse x che incontri la curva. Dal punto così ottenuto sulla curva, si consideri la perpendicolare all'asse x: il punto ottenuto su questo asse è x0 + δ.
Appare chiaro che al variare di ε varia il punto x0 + δ, ossia il δ. L'intorno (x0, x0 + δ) così ottenuto è quello richiesto, in quanto, come si può vedere nella stessa figura, per ogni x appartenente ad esso, x0 < x < x0 + δ, i valori della funzione sono tutti compresi tra l ed l + ε ossia
Nel caso in cui la curva sia decrescente, come risulta dalla Fig. 2, per ogni x0 < x < x0 + δ si perviene a:
l - ε < f(x) < l + ε
e quindi, per comprendere i due casi, si dice: per tutte le x0 < x < x0 + δ, è
l - ε < f(x) < l + ε.
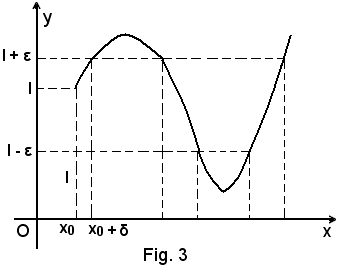
Nel caso in cui la curva sia intersecata più volte dalle parallele all'asse x, come risulta dalla Fig. 3, l'intorno destro di x0 che si deve considerare è minore di tutti quelli che si vengono a formare.
2°)-La definizione posta può essere data, rigorosamente, come segue:
-si dice che f(x) ha per limite il numero l per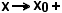, quando le x avvicinandosi indefinitamente al valore x0 da destra, attraverso tutti i valori abbastanza prossimi ad x0, ma rimanendo distinti da x0, i valori che assume la f(x) si avvicinano anch'essi indefinitamente ad l, ossia diventano e restano vicini ad l quanto si vuole.
2)-Limite sinistro finito della funzione, per la variabile indipendente x tendente ad un valore finito x0:
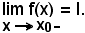
La definizione è del tutto analoga alla precedente, solo che, ovviamente, la f(x) dev'essere definita in un intorno sinistro del punto x0, ad eccezione al più del solo punto x0.
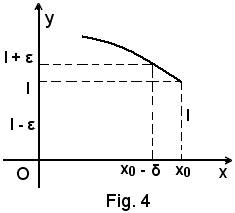
Le relazioni da verificare, rispetto alla Fig. 4, sono:
x0 - δ < x < x0,
l < f(x) < l + ε,
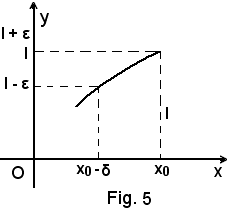
mentre, rispetto alla Fig. 5, sono:
x0 - δ < x < x0,
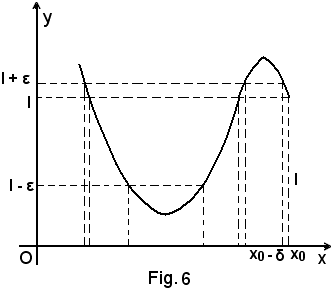
e, in generale, Fig. 6, per le osservazioni fatte in 1), sono
x0 - δ < x < x0,
l - ε < f(x) < l + ε.
3)-Limite finito della funzione, per la variabile indipendente x tendente ad un valore finito x0.
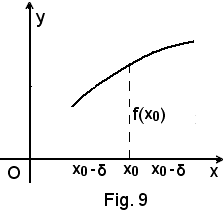
Sia y = f(x) una funzione definita in un intorno completo del punto x0, ad eccezione al più dello stesso punto x0.
Definizione - Si dice che è
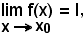
quando, per ogni ε > 0, piccolo a piacere, esiste un conveniente intorno, di ampiezza 2δ, del punto x0, tale che per tutti i i punti x di tale intorno, ad eccezione al più del solo punto x0,
x0 - δ < x < x0 + δ,
si abbia:
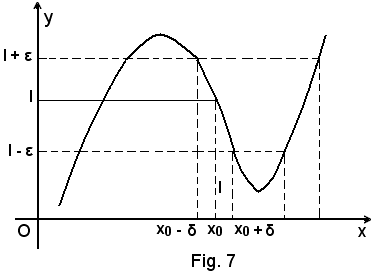
Osservazioni
1°)-La definizione comporta chiaramente l'esistenza dei limiti destro e sinistro della funzione rispetto al punto x0 ed ancora l'uguaglianza dei suddetti limiti. Come meglio si vedrà in seguito, l'esistenza dei due suddetti limiti non porta di conseguenza l'uguaglianza degli stessi. Nel caso in cui i due limiti destro e sinistro della funzione, rispetto al punto x0, siano disuguali, la definizione suddetta non ha senso.
2°)-Analogamente, quanto detto in 1) ed in 2) si può esprimere come segue:
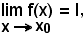
quando avvicinandosi le x ad x0 indefinitamente, assumendo tutti i valori abbastanza prossimi ad x0 tanto da destra, quanto da sinistra, ma rimanendo sempre dìstinte da x0, anche i valori che assume la f(x) si avvicinano indefinitamente al l, ossia diventano prima e restano poi vicini ad l quanto si vuole.
3°)-E' opportuno ancora insistere sulla precisazione che si è sempre fatta "per tutte le x dell'intorno di x0 ad eccezion fatta al più del solo punto x0" si è sempre fatta per i seguenti motivi:
-in generale lo studio di una funzione nell'intorno di un punto x0 si scinde in due parti e cioè, comportamento dalla funzione nel punto x0 e comportamento della funzione negli altri punti dell'intorno. Le due parti sono del tutto separate e distinte, per cui ognuna di esse può essere posta indipendentemente dall'altra, anzi anche quando l'altra non ha senso.
Il concetto di limite riguarda il comportamento della funzione negli altri punti dell'intorno del punto x0 e non proprio in questo.
Continuità e discontinuità di una funzione in un punto ed in un intervallo
Si consideri una funzione y = f(x) in un intorno completo di un punto x0.
Definizione - Si dice che la funzione è continua in x0, quando sono verificate le seguenti condizioni:
La funzione si dice continua in un intervallo finito o infinito, quando è continua in tutti i suoi punti.
Dalla definizione di continuità in un punto si ha che il calcolo di
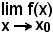
consiste nel sostituire nella funzione, alla variabile x, il valore a cui essa tende.
Si suole anche dire:
-una funzione è continua in un punto x0, se nel punto il limite della funzione è uguale alla funzione del limite:
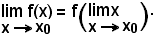
Esempi
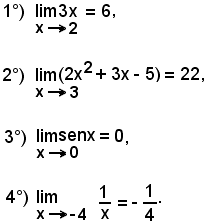
Le seguenti relazioni:
valgono identicamente quando è x0 = 0 oppure l = 0 od ancora x0 = 0 e l = f(x0) = 0.
Basterà per questo sostituire nelle singole relazioni che riguardano x0 ed l il numero zero, ma si tralascia l'estensione di tali concetti.
Proprietà delle funzioni continue
Le proprietà delle funzioni continue sono espresse dai seguenti teoremi, dei quali ci si limita a dare solo l'enunciato.
1°) Teorema del valore assoluto - Se f(x) è una funzione continua in un certo intervallo, anche |f(x)| è continua nello stesso intervallo.
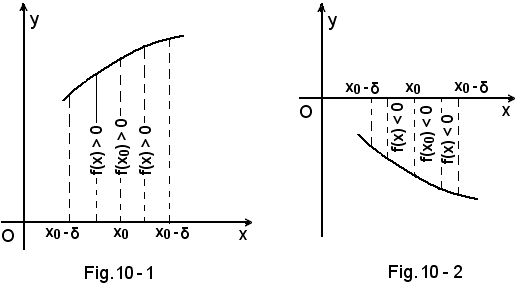
2°) Teorema della permanenza del segno - Se f(x) è continua in un certo intervallo ed in un punto x0 di questo e diverso da zero, per cui è f(x0) > 0 oppure f(x0) < 0, esiste un intorno completo di x0 in cui la funzione conserva il segno che ha nel punto.
Ciò è espresso nelle figure seguenti:
3°) Teorema delle operazioni razionali - La somma, la differenza, il prodotto ed il quoziente di funzioni continue in uno stesso intervallo è, a sua volta, una funzione continua nello stesso intervallo, salvo nei casi in cui perde di significato.
Più in generale, si può anche dire:
-le funzioni composte con un numero finito di operazioni razionali, potenze ad esponente reale, logaritmi, funzioni esponenziali e circolari, sono continue nei punti in cui sono definite.
4°) Teorema di Weierstrass - Se una funzione è continua in un certo intervallo chiuso [a, b], essa è nello stesso intervallo, limitata e dotata di massimo M e minimo m relativi.
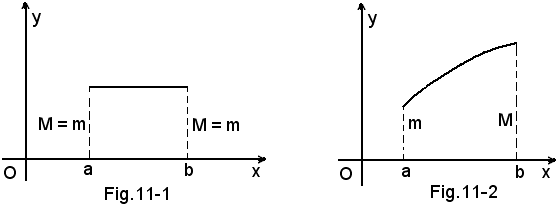
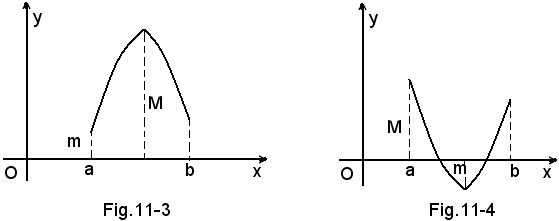
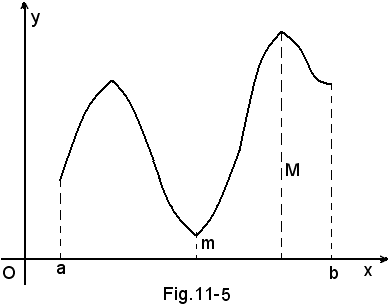
5°) Teorema - Se una funzione f(x) è continua e limitata in un intervallo chiuso [a, b] e negli estremi dell'intervallo assume valori di segno contrario, esiste in [a, b] almeno un punto x0 in cui la funzione si annulla (ciò avviene se x0 è radice dell'equazione f(x) = 0.
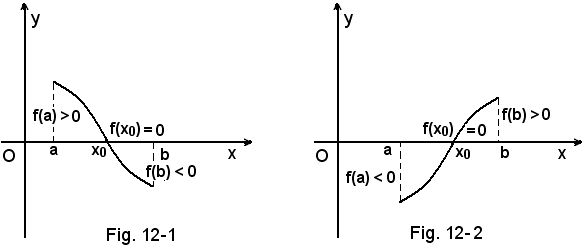
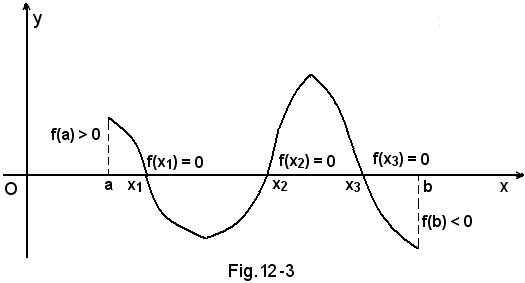
6°) Teorema - Se una funzione f(x) è continua e limitata in un intervallo chiuso [a, b] e tale da avere negli estremi dell'intervallo valori dello stesso segno, allora in [a, b] la funzione non si annulla mai o si annulla un numero pari di volte.
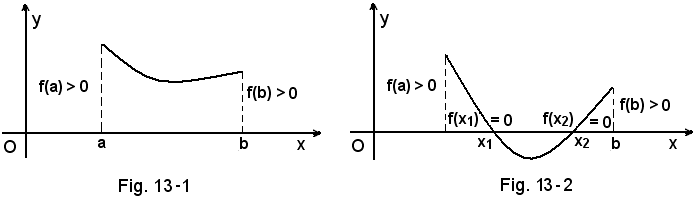
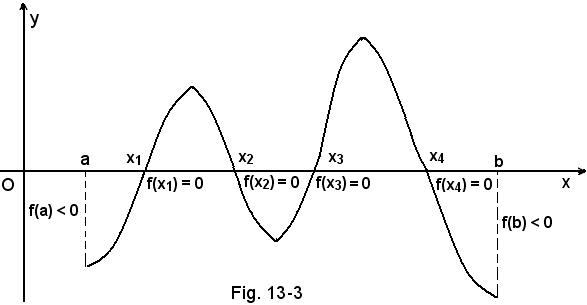
Il 5° ed il 6° teorema sono particolarmente importanti in quanto stabiliscono i criteri che permettono di dire se qualche radice dell'equaxione f(x) = 0 è o meno compresa tra due numeri reali dati a e b. In ciò consiste il problema della separazione delle radici di un'equazione a cui segue quello dell'approssimazione.
Discontinuità
1)-Concetto di funzione discontinua
Si ricorda che una funzione si dice continua in x0, quando sono verificate le seguenti condizioni:
Segue che se tali condizioni non sono verificate la funzione non è continua, o meglio, si dice discontinua. In tal modo la discontinuità sembrerebbe essere il carattere opposto della discontinuità, ma ciò non è esatto e pertanto occorre precisare meglio tale carattere di discontinuità.
Una funzione è discontinua in x0, o perchè esistendo
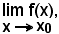
il valore di detto limite è diverso da f(x0) o perchè non esiste proprio il
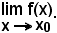
Nel 1° caso la discontinuità si dice di 1^ specie o eliminabile, in quanto basterebbe convenire, opportunamente, di dare alla f(x) un altro valore del punto x0 e cioè proprio il valore di
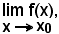
per ristabilire nel punto la continuità della funzione.
Nel caso in cui, invece, manca uno dei due limiti destro o sinistro o entrambi, la discontinuità si dice di 2^
specie e non è più eliminabile.
2)-Esempi di funzioni discontinue
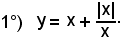
Se x > 0, risulta y = x + 1; tale equazione rappresenta la semiretta parallela alla 1^ bisettrice del punto di coordinate (0, 1).
Se x < 0, risulta y = x - 1; tale equazione rappresenta la semiretta parallela alla 2^ bisettrice del punto di coordinate (0, -1).
Si ha, pertanto, la seguente rappresentazione della funzione:
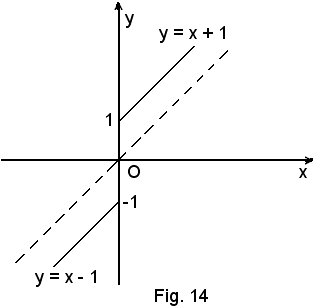
quindi è
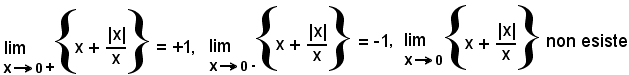
ed il punto zero è un punto di discontinuità di 1^ specie.
2°) y = C(x), oppure y = [x] oppure y = E(x):
Premessa
Le successioni si possono considerare come particolari funzioni, ossia funzioni definite solo per valori interi e positivi della variabile, non esistendo, infatti, differenza formale nelle scritture
y = f(x) e y = f(n) = an,
con x = n = 1, 2, 3 ...
In precedenza sono stati esaminati i vari casi di limite delle successioni, ossia i primi esempi di tendenza al limite di una funzione. Ora si vuole mostrare come quei concetti introdotti per le successioni, ossia per particolari funzioni, possano estendersi ad una qualsiasi funzione reale della variabile reale y = f(x), tipo che sarà sempre considerato in seguito.
1)-Limite destro finito della funzione, per la variabile indipendente x tendente ad un valore finito x0.
Sia y = f(x) una funzione definita in un intervallo che abbia x0 come estremo sinistro, tenendo anche presente che nel punto x0 essa può anche non essere definita.
Definizione - Si dice che f(x), per x tendente ad x0 da destra, e si scrive
, ha per limite il numero finito l quando, per ogni numero ε > 0, piccolo a piacere, esiste in corrispondenza un intorno destro, ad esempio di ampiezza δ, del punto x0, tale che per tutti i punti x di tale intorno, risulti:oppure
|x - x0| < δ,
al più escluso il punto x0, si abbia la relazione
l - ε < f(x) < l + ε,
oppure
|f(x) - l | < ε.
Si scrive:
Osservazioni
1°)-L'ampiezza δ dell'intorno destro del punto x0 dipende, in generale, dal numero ε > 0 considerato a piacere in quanto, come si vede nella Fig. 1, riportato l sull'asse y, a partire da esso si segnino i punti l - ε ed l + ε e da ciascuno di questi si consideri quella parallela all'asse x che incontri la curva. Dal punto così ottenuto sulla curva, si consideri la perpendicolare all'asse x: il punto ottenuto su questo asse è x0 + δ.
Appare chiaro che al variare di ε varia il punto x0 + δ, ossia il δ. L'intorno (x0, x0 + δ) così ottenuto è quello richiesto, in quanto, come si può vedere nella stessa figura, per ogni x appartenente ad esso, x0 < x < x0 + δ, i valori della funzione sono tutti compresi tra l ed l + ε ossia
l < f(x) < l + ε.
Nel caso in cui la curva sia decrescente, come risulta dalla Fig. 2, per ogni x0 < x < x0 + δ si perviene a:
l - ε < f(x) < l + ε
e quindi, per comprendere i due casi, si dice: per tutte le x0 < x < x0 + δ, è
l - ε < f(x) < l + ε.
Nel caso in cui la curva sia intersecata più volte dalle parallele all'asse x, come risulta dalla Fig. 3, l'intorno destro di x0 che si deve considerare è minore di tutti quelli che si vengono a formare.
2°)-La definizione posta può essere data, rigorosamente, come segue:
-si dice che f(x) ha per limite il numero l per
, quando le x avvicinandosi indefinitamente al valore x0 da destra, attraverso tutti i valori abbastanza prossimi ad x0, ma rimanendo distinti da x0, i valori che assume la f(x) si avvicinano anch'essi indefinitamente ad l, ossia diventano e restano vicini ad l quanto si vuole.2)-Limite sinistro finito della funzione, per la variabile indipendente x tendente ad un valore finito x0:
La definizione è del tutto analoga alla precedente, solo che, ovviamente, la f(x) dev'essere definita in un intorno sinistro del punto x0, ad eccezione al più del solo punto x0.
Le relazioni da verificare, rispetto alla Fig. 4, sono:
x0 - δ < x < x0,
l < f(x) < l + ε,
mentre, rispetto alla Fig. 5, sono:
x0 - δ < x < x0,
l - ε < f(x) < l,
e, in generale, Fig. 6, per le osservazioni fatte in 1), sono
x0 - δ < x < x0,
l - ε < f(x) < l + ε.
3)-Limite finito della funzione, per la variabile indipendente x tendente ad un valore finito x0.
Sia y = f(x) una funzione definita in un intorno completo del punto x0, ad eccezione al più dello stesso punto x0.
Definizione - Si dice che è
quando, per ogni ε > 0, piccolo a piacere, esiste un conveniente intorno, di ampiezza 2δ, del punto x0, tale che per tutti i i punti x di tale intorno, ad eccezione al più del solo punto x0,
x0 - δ < x < x0 + δ,
si abbia:
l - ε < f(x) < l + ε.
Osservazioni
1°)-La definizione comporta chiaramente l'esistenza dei limiti destro e sinistro della funzione rispetto al punto x0 ed ancora l'uguaglianza dei suddetti limiti. Come meglio si vedrà in seguito, l'esistenza dei due suddetti limiti non porta di conseguenza l'uguaglianza degli stessi. Nel caso in cui i due limiti destro e sinistro della funzione, rispetto al punto x0, siano disuguali, la definizione suddetta non ha senso.
2°)-Analogamente, quanto detto in 1) ed in 2) si può esprimere come segue:
quando avvicinandosi le x ad x0 indefinitamente, assumendo tutti i valori abbastanza prossimi ad x0 tanto da destra, quanto da sinistra, ma rimanendo sempre dìstinte da x0, anche i valori che assume la f(x) si avvicinano indefinitamente al l, ossia diventano prima e restano poi vicini ad l quanto si vuole.
3°)-E' opportuno ancora insistere sulla precisazione che si è sempre fatta "per tutte le x dell'intorno di x0 ad eccezion fatta al più del solo punto x0" si è sempre fatta per i seguenti motivi:
-in generale lo studio di una funzione nell'intorno di un punto x0 si scinde in due parti e cioè, comportamento dalla funzione nel punto x0 e comportamento della funzione negli altri punti dell'intorno. Le due parti sono del tutto separate e distinte, per cui ognuna di esse può essere posta indipendentemente dall'altra, anzi anche quando l'altra non ha senso.
Il concetto di limite riguarda il comportamento della funzione negli altri punti dell'intorno del punto x0 e non proprio in questo.
Continuità e discontinuità di una funzione in un punto ed in un intervallo
Si consideri una funzione y = f(x) in un intorno completo di un punto x0.
Definizione - Si dice che la funzione è continua in x0, quando sono verificate le seguenti condizioni:
La funzione si dice continua in un intervallo finito o infinito, quando è continua in tutti i suoi punti.
Dalla definizione di continuità in un punto si ha che il calcolo di
consiste nel sostituire nella funzione, alla variabile x, il valore a cui essa tende.
Si suole anche dire:
-una funzione è continua in un punto x0, se nel punto il limite della funzione è uguale alla funzione del limite:
Esempi
Le seguenti relazioni:
valgono identicamente quando è x0 = 0 oppure l = 0 od ancora x0 = 0 e l = f(x0) = 0.
Basterà per questo sostituire nelle singole relazioni che riguardano x0 ed l il numero zero, ma si tralascia l'estensione di tali concetti.
Proprietà delle funzioni continue
Le proprietà delle funzioni continue sono espresse dai seguenti teoremi, dei quali ci si limita a dare solo l'enunciato.
1°) Teorema del valore assoluto - Se f(x) è una funzione continua in un certo intervallo, anche |f(x)| è continua nello stesso intervallo.
2°) Teorema della permanenza del segno - Se f(x) è continua in un certo intervallo ed in un punto x0 di questo e diverso da zero, per cui è f(x0) > 0 oppure f(x0) < 0, esiste un intorno completo di x0 in cui la funzione conserva il segno che ha nel punto.
Ciò è espresso nelle figure seguenti:
3°) Teorema delle operazioni razionali - La somma, la differenza, il prodotto ed il quoziente di funzioni continue in uno stesso intervallo è, a sua volta, una funzione continua nello stesso intervallo, salvo nei casi in cui perde di significato.
Più in generale, si può anche dire:
-le funzioni composte con un numero finito di operazioni razionali, potenze ad esponente reale, logaritmi, funzioni esponenziali e circolari, sono continue nei punti in cui sono definite.
4°) Teorema di Weierstrass - Se una funzione è continua in un certo intervallo chiuso [a, b], essa è nello stesso intervallo, limitata e dotata di massimo M e minimo m relativi.
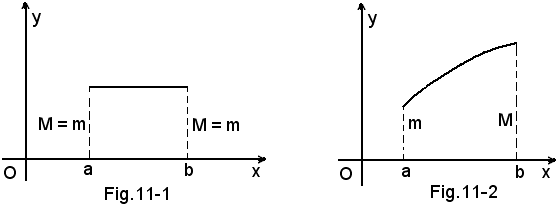
5°) Teorema - Se una funzione f(x) è continua e limitata in un intervallo chiuso [a, b] e negli estremi dell'intervallo assume valori di segno contrario, esiste in [a, b] almeno un punto x0 in cui la funzione si annulla (ciò avviene se x0 è radice dell'equazione f(x) = 0.
6°) Teorema - Se una funzione f(x) è continua e limitata in un intervallo chiuso [a, b] e tale da avere negli estremi dell'intervallo valori dello stesso segno, allora in [a, b] la funzione non si annulla mai o si annulla un numero pari di volte.
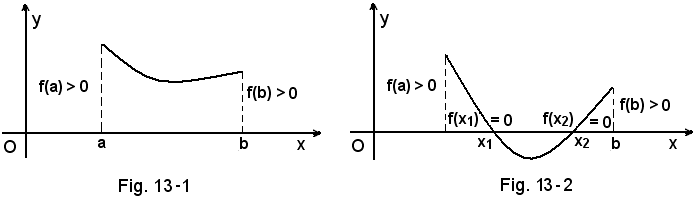
Il 5° ed il 6° teorema sono particolarmente importanti in quanto stabiliscono i criteri che permettono di dire se qualche radice dell'equaxione f(x) = 0 è o meno compresa tra due numeri reali dati a e b. In ciò consiste il problema della separazione delle radici di un'equazione a cui segue quello dell'approssimazione.
Discontinuità
1)-Concetto di funzione discontinua
Si ricorda che una funzione si dice continua in x0, quando sono verificate le seguenti condizioni:
Segue che se tali condizioni non sono verificate la funzione non è continua, o meglio, si dice discontinua. In tal modo la discontinuità sembrerebbe essere il carattere opposto della discontinuità, ma ciò non è esatto e pertanto occorre precisare meglio tale carattere di discontinuità.
Una funzione è discontinua in x0, o perchè esistendo
il valore di detto limite è diverso da f(x0) o perchè non esiste proprio il
Nel 1° caso la discontinuità si dice di 1^ specie o eliminabile, in quanto basterebbe convenire, opportunamente, di dare alla f(x) un altro valore del punto x0 e cioè proprio il valore di
per ristabilire nel punto la continuità della funzione.
2)-Esempi di funzioni discontinue
Se x > 0, risulta y = x + 1; tale equazione rappresenta la semiretta parallela alla 1^ bisettrice del punto di coordinate (0, 1).
Se x < 0, risulta y = x - 1; tale equazione rappresenta la semiretta parallela alla 2^ bisettrice del punto di coordinate (0, -1).
Si ha, pertanto, la seguente rappresentazione della funzione:
quindi è
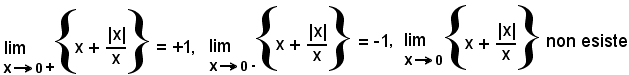
ed il punto zero è un punto di discontinuità di 1^ specie.
2°) y = C(x), oppure y = [x] oppure y = E(x):
si legge y uguale alla caratteristica di x, ossia parte intera del valore di x.
Per come è definita la funzione:
-se 0 < x < 1, cioè x = 0, ... è y = 0,
-se 1 < x < 2, cioè x = 1, ... è y = 1,
-se 2 < x < 3, cioè x = 2, ... è y = 2,
........................................................
........................................................
-se -1 < x < 0, cioè x = -0, ... è y = 0,
-se -2 < x < -1, cioè x = -1, ... è y = -1,
-se -3 < x < -2, cioè x = -2, ... è y = -2,
............................................................
............................................................
pertanto, si ha la seguente rappresentazione:
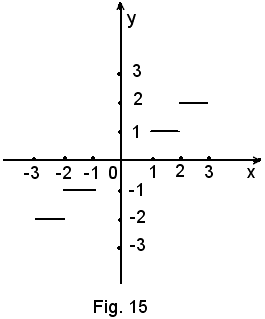
dalla quale risulta che tutti i punti di ascissa intera sono punti di discontinuità di 1^ specie per la funzione, ad eccezione del punto zero che è il punto di continuità, in quanto si ha
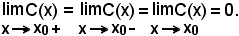
3°) y = M(x), da leggere y uguale mantissa della x, ossia parte decimale del valore della x.
Per come è definita la funzione:
-se 0 < x < 1, cioè x = 0, ..., è 0 < y < 1,
-se 1 < x < 2, cioè x = 1, ..., è sempre 0 < y < 1,
-se 2 < x < 3, cioè x = 2, ..., è sempre 0 < y < 1,
...........................................
...........................................
Invece:
-se -1 < x < 0, cioè x = -0, ..., è -1 < y < 0,
-se -2 < x < -1, cioè x = -1, ..., è sempre -1 < y < 0,
-se -3 < x < -2, cioè x = -2, ..., è sempre -1 < y < 0,
per cui si ha la seguente rappresentazione:
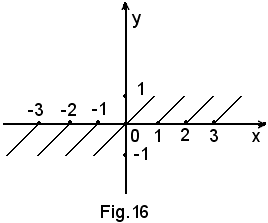
quindi, ancora tutti i punti di ascissa intera sono punti di discontinuità di 1^ specie, ad eccezione del punto O che è punto di continuità, in quanto è
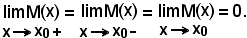
4°) La funzione di Dirichlet alla quale in (
, 
)
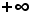si conviene di fare assumere il valore zero per ogni x irrazionale, ed
il valore 1 per ogni x razionale è discontinua per ogni valore
della x e la discontinuità è di 2^ specie, cioè non eliminabile.
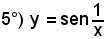
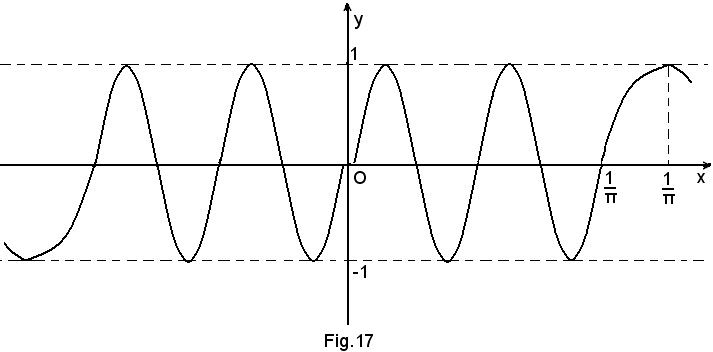
definita per ogni x ≠ 0.
Tale funzione assume il valore 0, cioè la curva incontra l'asse x, per
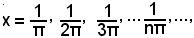
assume il valore 1 per
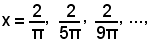
e valore -1 per
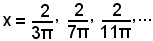
La curva rappresentatrice presenta, pertanto, infinite oscillazioni di ampiezza sempre uguale a 2 e le onde vanno infinitamente stringendosi allorchè x tende a zero (0+ e 0-). Pertanto, in qualsiasi intorno comunque piccolo di 0, si troveranno sempre dei punti in cui la funzione non ha limite, poichè i valori non diventano e non rimangono vicini, quanto si vuole, a nessun numero. E', pertanto, discontinua di 2^ specie.
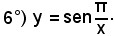
Tale funzione è analoga alla precedente.
Altri concetti di limite delle funzioni
1)-Limite infinito di una funzione per la variabile indipendente tendente all'infinito
Sia y = f(x) una funzione definita per tutti i valori della variabile x e quindi anche maggiori di un certo numero grande, ossia definita un un intorno di.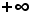
Si dice che è
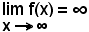
quando, per ogni numero k > 0 grande a piacere, esiste un valore x0 della variabile indipendente, tale che per tutte le x > x0, |f(x)| > k.
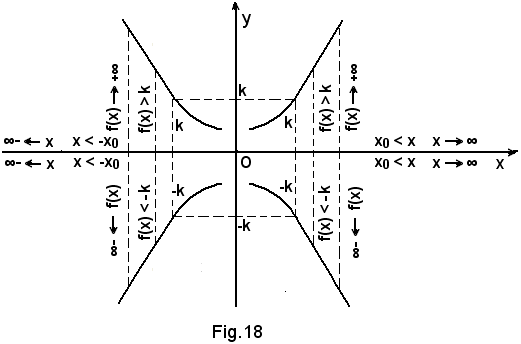
Poichè siano soddisfatte le condizioni richieste, la funzione deve avere l'andamento della figura seguente:
Osservazione
Il concetto esposto racchiude in sè i seguenti quattro limiti:
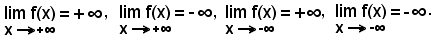
dei quali si tralasciano le ormai evidenti estensioni.
2)-Limite infinito di una funzione per la variabile indipendente tendente ad un valore finito
Si dice che
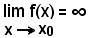
quando, per ogni numero k > 0 grande a piacere, esiste un conveniente intorno completo, di ampiezza 2δ, del punto x0, tale che per tutte le sue x:
x0 - δ < x < x0 + δ oppure |x - x0| < δ.
risulta:
|f(x)| > k.
Affinichè siano soddisfatte le condizioni richieste, la funzione deve avere l'andamento della figura seguente:
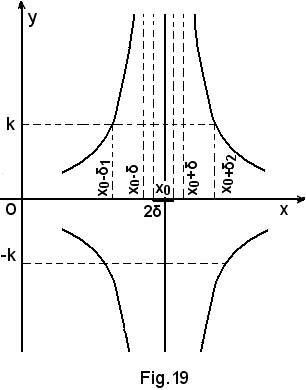
Osservazioni
1)-Il concetto esposto racchiude in sè i seguenti sei limiti:
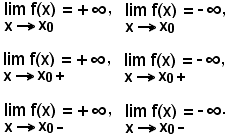
2)-Poichè x0 è un numero finito, può essere positivo, quello della Fig. 19, o negativo o, addirittura, può essere x0 = 0.
3)-Il concetto posto, interpretato geometricamente, esprime che la retta x0 = 0 è un asintoto verticale della curva rappresentatrice della funzione.
Nel caso in cui x0 = 0, l'asintoto è proprio l'asse y, cioè:
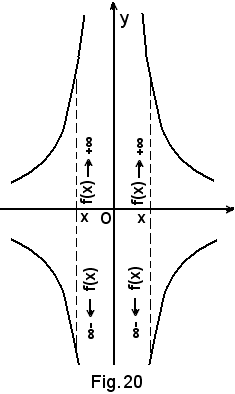
4)-La tangentoide fornisce un ulteriore esempio di funzione discontinua.
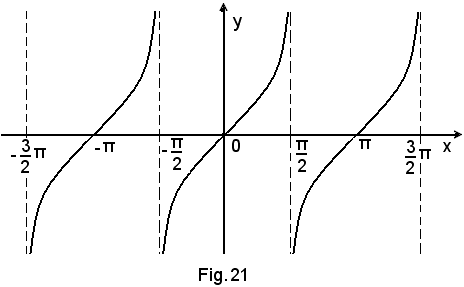
Si consideri la funzione y = tgx, si ha:
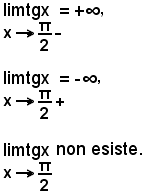
Analogamente si procede per
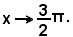
3)-Limite finito di una funzione per la variabile indipendente tendente all'infinitoSi dice che
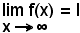
quando, per ogni numero ε > 0 piccolo a piacere, esiste un valore x0 della variabie indipendente tale che per tutte le sue |x| > x0, risulti
l - ε < f(x) < l + ε oppure |f(x) - l| < ε.
Affinchè siano soddisfatte le condizioni richieste, la funzione deve avere l'andamento della figura seguente:
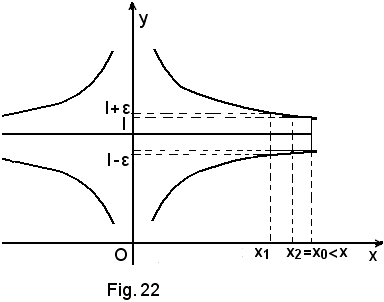
Osservazioni
1)-Il concetto esposto racchiude in sè i seguenti limiti:
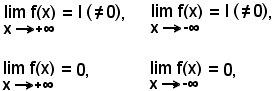
dei quali si tralasciano le ormai evidenti estensioni.
2)-Il concetto stesso, interpretato geometricamente, esprime che la retta y = 1 è un asintoto orizzontale della curva rappresentatrice della funzione.
3)-Nel caso in cui l = 0, l'asintoto coincide con l'asse x, cioè:
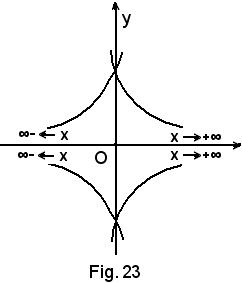
4)-Esempio di funzione discontinua
Si consideri l'iperbole equilatera, riferita ai suoi asintoti di equazione:
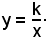
Si sa dalla geometria analitica che se k > 0 i due rami della curva giacciono rispettivamente nel I e III quadrante e se k < 0 nel II e IV.
Ci si limita a k > 0, pertanto la curva è la seguente:
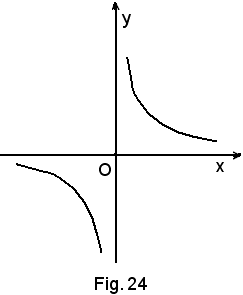
Si ha:
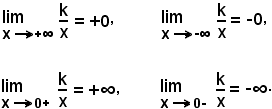
Riepilogo dei concetti di limite delle funzioni
In tutti i limiti suddetti può anche essere x0 = 0.
Per come è definita la funzione:
-se 0 < x < 1, cioè x = 0, ... è y = 0,
-se 1 < x < 2, cioè x = 1, ... è y = 1,
-se 2 < x < 3, cioè x = 2, ... è y = 2,
........................................................
........................................................
-se -1 < x < 0, cioè x = -0, ... è y = 0,
-se -2 < x < -1, cioè x = -1, ... è y = -1,
-se -3 < x < -2, cioè x = -2, ... è y = -2,
............................................................
............................................................
pertanto, si ha la seguente rappresentazione:
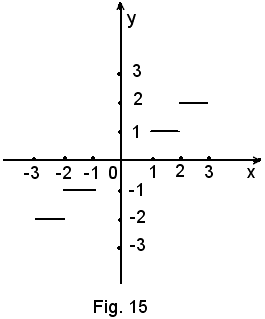
dalla quale risulta che tutti i punti di ascissa intera sono punti di discontinuità di 1^ specie per la funzione, ad eccezione del punto zero che è il punto di continuità, in quanto si ha
3°) y = M(x), da leggere y uguale mantissa della x, ossia parte decimale del valore della x.
Per come è definita la funzione:
-se 0 < x < 1, cioè x = 0, ..., è 0 < y < 1,
-se 1 < x < 2, cioè x = 1, ..., è sempre 0 < y < 1,
-se 2 < x < 3, cioè x = 2, ..., è sempre 0 < y < 1,
...........................................
...........................................
Invece:
-se -1 < x < 0, cioè x = -0, ..., è -1 < y < 0,
-se -2 < x < -1, cioè x = -1, ..., è sempre -1 < y < 0,
-se -3 < x < -2, cioè x = -2, ..., è sempre -1 < y < 0,
per cui si ha la seguente rappresentazione:
quindi, ancora tutti i punti di ascissa intera sono punti di discontinuità di 1^ specie, ad eccezione del punto O che è punto di continuità, in quanto è
4°) La funzione di Dirichlet alla quale in (
, )
si conviene di fare assumere il valore zero per ogni x irrazionale, ed
il valore 1 per ogni x razionale è discontinua per ogni valore
della x e la discontinuità è di 2^ specie, cioè non eliminabile.definita per ogni x ≠ 0.
Tale funzione assume il valore 0, cioè la curva incontra l'asse x, per
assume il valore 1 per
e valore -1 per
La curva rappresentatrice presenta, pertanto, infinite oscillazioni di ampiezza sempre uguale a 2 e le onde vanno infinitamente stringendosi allorchè x tende a zero (0+ e 0-). Pertanto, in qualsiasi intorno comunque piccolo di 0, si troveranno sempre dei punti in cui la funzione non ha limite, poichè i valori non diventano e non rimangono vicini, quanto si vuole, a nessun numero. E', pertanto, discontinua di 2^ specie.
Tale funzione è analoga alla precedente.
Altri concetti di limite delle funzioni
1)-Limite infinito di una funzione per la variabile indipendente tendente all'infinito
Sia y = f(x) una funzione definita per tutti i valori della variabile x e quindi anche maggiori di un certo numero grande, ossia definita un un intorno di
.Si dice che è
quando, per ogni numero k > 0 grande a piacere, esiste un valore x0 della variabile indipendente, tale che per tutte le x > x0, |f(x)| > k.
Poichè siano soddisfatte le condizioni richieste, la funzione deve avere l'andamento della figura seguente:
Osservazione
Il concetto esposto racchiude in sè i seguenti quattro limiti:
dei quali si tralasciano le ormai evidenti estensioni.
2)-Limite infinito di una funzione per la variabile indipendente tendente ad un valore finito
Si dice che
quando, per ogni numero k > 0 grande a piacere, esiste un conveniente intorno completo, di ampiezza 2δ, del punto x0, tale che per tutte le sue x:
x0 - δ < x < x0 + δ oppure |x - x0| < δ.
risulta:
|f(x)| > k.
Affinichè siano soddisfatte le condizioni richieste, la funzione deve avere l'andamento della figura seguente:
Osservazioni
1)-Il concetto esposto racchiude in sè i seguenti sei limiti:
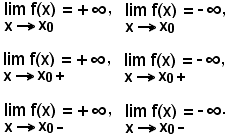
2)-Poichè x0 è un numero finito, può essere positivo, quello della Fig. 19, o negativo o, addirittura, può essere x0 = 0.
3)-Il concetto posto, interpretato geometricamente, esprime che la retta x0 = 0 è un asintoto verticale della curva rappresentatrice della funzione.
Nel caso in cui x0 = 0, l'asintoto è proprio l'asse y, cioè:
4)-La tangentoide fornisce un ulteriore esempio di funzione discontinua.
Si consideri la funzione y = tgx, si ha:
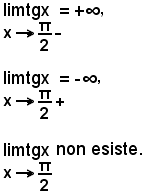
Analogamente si procede per
3)-Limite finito di una funzione per la variabile indipendente tendente all'infinito
quando, per ogni numero ε > 0 piccolo a piacere, esiste un valore x0 della variabie indipendente tale che per tutte le sue |x| > x0, risulti
l - ε < f(x) < l + ε oppure |f(x) - l| < ε.
Affinchè siano soddisfatte le condizioni richieste, la funzione deve avere l'andamento della figura seguente:
Osservazioni
1)-Il concetto esposto racchiude in sè i seguenti limiti:
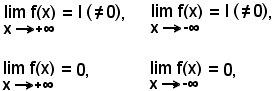
dei quali si tralasciano le ormai evidenti estensioni.
2)-Il concetto stesso, interpretato geometricamente, esprime che la retta y = 1 è un asintoto orizzontale della curva rappresentatrice della funzione.
3)-Nel caso in cui l = 0, l'asintoto coincide con l'asse x, cioè:
4)-Esempio di funzione discontinua
Si consideri l'iperbole equilatera, riferita ai suoi asintoti di equazione:
Si sa dalla geometria analitica che se k > 0 i due rami della curva giacciono rispettivamente nel I e III quadrante e se k < 0 nel II e IV.
Ci si limita a k > 0, pertanto la curva è la seguente:
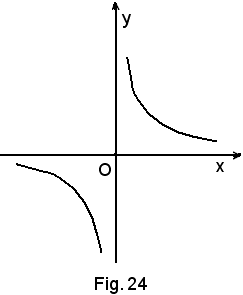
Si ha:
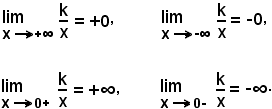
Riepilogo dei concetti di limite delle funzioni
In tutti i limiti suddetti può anche essere x0 = 0.
Teoremi fondamentali dei limiti delle funzioni
1)-Teorema dell'unicità del limite - Il limite di una funzione per la variabile indipendente tendente ad una valore x0, finito o infinito, è unico.
ll teorema si dimostra ragionando per assurdo.
Infatti, si supponga che possa essere:
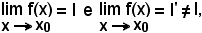
cioè per ogni ε > 0, piccolo a piacere, esiste un intorno completo, di ampiezza 2δ1, del punto x0 tale che per tutte le
x0 - δ1 < x < x0 + δ1
risulti
l - ε < f(x) < l + ε,
ossia
1)-Teorema dell'unicità del limite - Il limite di una funzione per la variabile indipendente tendente ad una valore x0, finito o infinito, è unico.
ll teorema si dimostra ragionando per assurdo.
Infatti, si supponga che possa essere:
x0 - δ1 < x < x0 + δ1
risulti
ossia
(1) |f(x) - l| < ε;
x0 - δ2 < x < x0 + δ2
risulti
l' - ε < f(x) < l' + ε,
ossia
Si pongano ora le condizioni, verificate le quali, siano contemporaneamente valide la (1) e la (2), cioè:
scelto un ε > 0, a piacere, sia δ il minore tra δ1 e δ2, per tutte le
x0 - δ < x < x0 + δ,
sarà anche
x0 - δ1 < x < x0 + δ1 e x0 - δ2 < x < x0 + δ2
e quindi
Allora, considerata l'identità:
l - l' = [f(x) - l'] - [f(x) - l],
successivamente si ha:
|l - l'| = [f(x) - l'] - [f(x)- l] < [f(x) - l'] + [f(x)- l] < ε + ε = 2ε,
e poichè ε è arbitrario, considerando
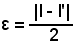
si avrebbe
|l - l'| < |l - l'|
e ciò è assurdo.
Siccome l'assurdo è derivato dall'aver supposto l'esistenza di due limiti diversi, e si è pervenuti ad un assurdo, si può concludere che quanto supposto non è vero, quindi esiste un solo limite.
Nota bene
Da ora in poi, ogni volta che si dimostrerà un teorema sui limiti riguardante due funzioni, dopo aver posto i due concetti inziali, si supporrà sempre "poste le condizioni per le quali essi valgono contemporaneamente".
2)-Teorema della limitazione
Se una funzione f(x) per x tendente a x0 ha un limite finito l, nel conveniente intorno considerato del punto x0, ad eccezione al più dello stesso punto x0, risulta:
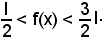
Infatti, dire
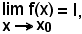
per il concetto di limite, in
x0 - δ < x < x0 + δ,
è
l - ε < f(x) < l + ε,
e poichè ε è a piacere, considerando
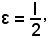
si ha:
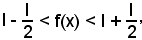
cioè
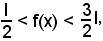
come volevasi dimostrare.
3)-Teorema della permanenza del segno
Se una funzione f(x) per x tendente a x0 ha un limite finito l diverso da zero, nel conveniente intorno considerato del punto x0, ad eccezione al più dello stesso punto x0, la funzione assume e conserva lo stesso segno del suo limite.
Infatti, se
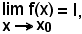
ossia per
x0 - δ < x < x0 + δ,
e
l - ε < f(x) < l + ε,
poichè ε è a piacere, lo si può considerare in modo che l - ε ed l + ε, e qundi i valori dalla f(x) compresi fra essi, abbiano lo stesso segno di l.
4)-Teorema del confronto
Se f1(x), f2(x), f3(x) sono tre funzioni definite in uno stesso intorno completo di un punto x0, ad eccezione al più dello stesso punto x0, e tali che in questo intorno sia sempre
f1(x) ≤ f2(x) ≤ f3(x),
se è
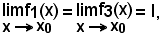
è anche
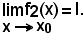
Infatti, poste le condizioni, verificate le quali valgono contemporaneamente
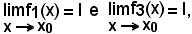
ossia
l - ε < f1(x) < l + ε e l - ε < f2(x) < l + ε,
dalla prima ipotesi, si ha allora:
l - ε < f1(x) ≤ f2(x) ≤ f3(x) < l + ε,
cioè
l - ε < f2(x) < l + ε,
il che significa che, per il concetto di limite
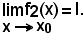
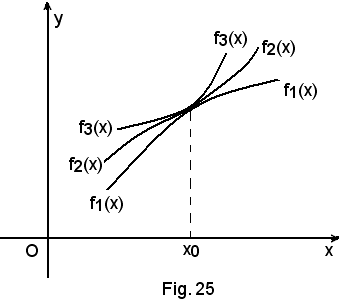
In tal modo resta dimostrato il teorema.
Nota bene
Il teorema è valido anche se è l = o l = , come si può facilmente verificare.
5)-Teorema dell'opposta
Cambiando di segno ad una funzione che per x tendente ad x0 ha un certo limite l, cambia il suo limite.
significa, nel conveniente intorno di x0,
l - ε < f(x) < l + ε,
da cui, cambiando i segni ed i versi, si ha:
-l - ε < -f(x) < -l + ε,
che significa
in tal modo resta dimostrato il teorema.
6)-Teorema della costante
Il limite di una costante è uguale alla stessa costante, a qualsiasi valore tenda la variabile indipendente.
Operazioni sui limiti finiti ed estensioni ai limiti infiniti
1)-Premesse
1^)-I teoremi enunciati per le successioni si estendono alle funzioni. In seguito ci si riferirà ai limiti ordinari, tralasciando le lievi modifiche da effettuare allorchè ci si vuol riferire, invece, ai limiti destro o sinistro.
2^)-Si avverte che nelle operazioni di somma, prodotto, quoziente e potenza si troveranno dei casi importanti che non rientrano nei calcoli ordinari, cioè si troveranno dei casi di indeterminazione, in quanto in essi, dalla sola conoscenza dei limiti delle funzioni, componenti l'operazione, non può dirsi subito com'è il limite della funzione risultato dell'operazione, giacchè tale limite può essere finito, infinito e può addirittura non esistere.
Si troveranno, inoltre, alcuni casi nei quali il limite potrà essere deciso senz'altro, In base a semplici ipotesi e considerazioni sulle funzioni componenti.
3^)-Si avverte infine in ciò segue che, le funzioni, due o più, che saranno considerate si intenderanno definite in uno stesso insieme, solitamente i punti di uno stesso intervallo, avente il punto, finito o infinito, cioè proprio o improprio, come punto di accumulazione.
2)-Limite di una somma
Se è
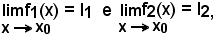
risulta:
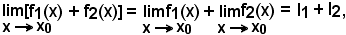
cioè il limite della somma di due o più funzioni è uguale alla somma dei limiti delle stesse.
x0 - δ < x < x0 + δ
varranno, contemporaneamente, le relazioni
l1 - ε < f1(x) < l1 + ε e l2 - ε < f2(x)) < l2 + ε,
ossia
Dimostrare che
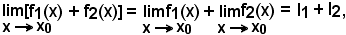
significa dimostrare che per ogni ε' > 0, piccolo a piacere, esiste un intorno completo del punto x0, tale che per tutte le sue x, eccettuato sempre al più lo stesso punto x0, vale la relazione:
Sussessivamente risulta:
|f1(x) + f2(x)| - (l1 + l2) = |f1(x) - l1 + f2 - l2(x)| ≤ |f1(x) - l1| + |f2 - l2(x)| < ε + ε = 2ε = ε',
in quanto, dato che ε si può considerare a piacere, lo si considera come segue:
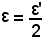
ed in tal modo il teorema è dimostrato.
Osservazioni1^)-Nel teorema dimostrato si è supposto che, in effetti, l1 e l2
siano numeri finiti, ma il teorema è valido anche nel caso in
cui le due funzioni abbiano, una o entrambe, limite infinito.
Tuttavia si precisa che:
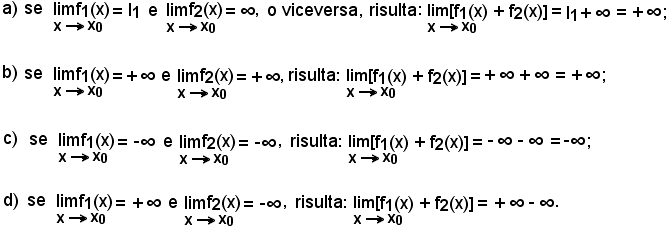
Nulla si può dire subito su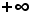 , che perciò costituisce il 1° caso di indeterminazione.
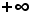
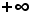Come si vedrà, occorre fare altre considerazioni, innanzitutto per vedere se la scrittura tra i simboli ha senso e, nel caso affermativo, per trovare il suo valore, cioè trovare se è un numero finito, anche zero, o o .
3)-Limite di una differenza
Se è
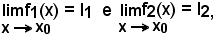
risulta:
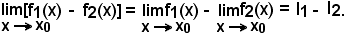
Infatti, per il teorema dell'opposta e per il teorema precedente, si ha:
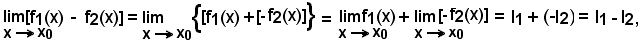
inoltre valgono le stesse osservazioni fatte in 2).
4)-Limite del prodotto
Se è
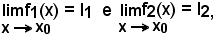
risulta:
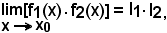
cioè, il limite di un prodotto è uguale al prodotto dei limiti.
Infatti, nelle solite condizioni di validità dei due concetti di limite, bisogna dimostrare che tutte le x del conveniente intorno completo di ampiezza 2δ del punto x0, eccettuato sempre al più lo stesso punto x0,
x0 - δ < x < x0 + δ
vale la relazione:
inoltre per ogni ε > 0, piccolo a piacere, lo stesso del precedente, esiste un intorno completo, di ampiezza 2δ2, del punto x0 tale che per tutte le
risulti
l' - ε < f(x) < l' + ε,
ossia
(2) |f(x) - l'| < ε.
Si pongano ora le condizioni, verificate le quali, siano contemporaneamente valide la (1) e la (2), cioè:
scelto un ε > 0, a piacere, sia δ il minore tra δ1 e δ2, per tutte le
x0 - δ < x < x0 + δ,
sarà anche
x0 - δ1 < x < x0 + δ1 e x0 - δ2 < x < x0 + δ2
e quindi
|f(x) - l| < ε e |f(x) - l'| < ε
Allora, considerata l'identità:
l - l' = [f(x) - l'] - [f(x) - l],
successivamente si ha:
|l - l'| = [f(x) - l'] - [f(x)- l] < [f(x) - l'] + [f(x)- l] < ε + ε = 2ε,
e poichè ε è arbitrario, considerando
si avrebbe
|l - l'| < |l - l'|
e ciò è assurdo.
Siccome l'assurdo è derivato dall'aver supposto l'esistenza di due limiti diversi, e si è pervenuti ad un assurdo, si può concludere che quanto supposto non è vero, quindi esiste un solo limite.
Nota bene
Da ora in poi, ogni volta che si dimostrerà un teorema sui limiti riguardante due funzioni, dopo aver posto i due concetti inziali, si supporrà sempre "poste le condizioni per le quali essi valgono contemporaneamente".
2)-Teorema della limitazione
Se una funzione f(x) per x tendente a x0 ha un limite finito l, nel conveniente intorno considerato del punto x0, ad eccezione al più dello stesso punto x0, risulta:
Infatti, dire
per il concetto di limite, in
è
l - ε < f(x) < l + ε,
e poichè ε è a piacere, considerando
si ha:
cioè
come volevasi dimostrare.
3)-Teorema della permanenza del segno
Se una funzione f(x) per x tendente a x0 ha un limite finito l diverso da zero, nel conveniente intorno considerato del punto x0, ad eccezione al più dello stesso punto x0, la funzione assume e conserva lo stesso segno del suo limite.
Infatti, se
ossia per
x0 - δ < x < x0 + δ,
e
l - ε < f(x) < l + ε,
poichè ε è a piacere, lo si può considerare in modo che l - ε ed l + ε, e qundi i valori dalla f(x) compresi fra essi, abbiano lo stesso segno di l.
4)-Teorema del confronto
Se f1(x), f2(x), f3(x) sono tre funzioni definite in uno stesso intorno completo di un punto x0, ad eccezione al più dello stesso punto x0, e tali che in questo intorno sia sempre
se è
è anche
Infatti, poste le condizioni, verificate le quali valgono contemporaneamente
ossia
l - ε < f1(x) < l + ε e l - ε < f2(x) < l + ε,
dalla prima ipotesi, si ha allora:
l - ε < f1(x) ≤ f2(x) ≤ f3(x) < l + ε,
cioè
l - ε < f2(x) < l + ε,
il che significa che, per il concetto di limite
In tal modo resta dimostrato il teorema.
Nota bene
Il teorema è valido anche se è l =
o l = , come si può facilmente verificare.5)-Teorema dell'opposta
Cambiando di segno ad una funzione che per x tendente ad x0 ha un certo limite l, cambia il suo limite.
Infatti, dire
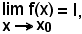
significa, nel conveniente intorno di x0,
l - ε < f(x) < l + ε,
da cui, cambiando i segni ed i versi, si ha:
-l - ε < -f(x) < -l + ε,
che significa
in tal modo resta dimostrato il teorema.
6)-Teorema della costante
Il limite di una costante è uguale alla stessa costante, a qualsiasi valore tenda la variabile indipendente.
Operazioni sui limiti finiti ed estensioni ai limiti infiniti
1)-Premesse
1^)-I teoremi enunciati per le successioni si estendono alle funzioni. In seguito ci si riferirà ai limiti ordinari, tralasciando le lievi modifiche da effettuare allorchè ci si vuol riferire, invece, ai limiti destro o sinistro.
2^)-Si avverte che nelle operazioni di somma, prodotto, quoziente e potenza si troveranno dei casi importanti che non rientrano nei calcoli ordinari, cioè si troveranno dei casi di indeterminazione, in quanto in essi, dalla sola conoscenza dei limiti delle funzioni, componenti l'operazione, non può dirsi subito com'è il limite della funzione risultato dell'operazione, giacchè tale limite può essere finito, infinito e può addirittura non esistere.
Si troveranno, inoltre, alcuni casi nei quali il limite potrà essere deciso senz'altro, In base a semplici ipotesi e considerazioni sulle funzioni componenti.
3^)-Si avverte infine in ciò segue che, le funzioni, due o più, che saranno considerate si intenderanno definite in uno stesso insieme, solitamente i punti di uno stesso intervallo, avente il punto, finito o infinito, cioè proprio o improprio, come punto di accumulazione.
2)-Limite di una somma
Se è
risulta:
cioè il limite della somma di due o più funzioni è uguale alla somma dei limiti delle stesse.
Infatti, per ogni ε > 0, piccolo a piacere, detta 2δ l'ampiezzadel minore dei due intorni completi del punto x0, trovati in corrispondenza di ε, per la validità di ciascuno dei concetti di limite, per tutte le
x0 - δ < x < x0 + δ
varranno, contemporaneamente, le relazioni
l1 - ε < f1(x) < l1 + ε e l2 - ε < f2(x)) < l2 + ε,
ossia
|f1(x) - l1| < ε oppure |f2(x) - l1|.
Dimostrare che
significa dimostrare che per ogni ε' > 0, piccolo a piacere, esiste un intorno completo del punto x0, tale che per tutte le sue x, eccettuato sempre al più lo stesso punto x0, vale la relazione:
|[f1(x) + f2(x)] - (l1 + l2|)| < ε'.
Sussessivamente risulta:
|f1(x) + f2(x)| - (l1 + l2) = |f1(x) - l1 + f2 - l2(x)| ≤ |f1(x) - l1| + |f2 - l2(x)| < ε + ε = 2ε = ε',
in quanto, dato che ε si può considerare a piacere, lo si considera come segue:
ed in tal modo il teorema è dimostrato.
Osservazioni
Tuttavia si precisa che:
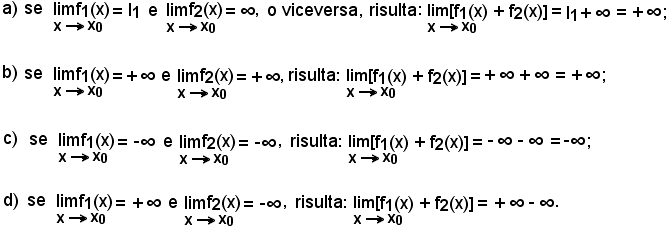
Nulla si può dire subito su
, che perciò costituisce il 1° caso di indeterminazione.Come si vedrà, occorre fare altre considerazioni, innanzitutto per vedere se la scrittura tra i simboli
ha senso e, nel caso affermativo, per trovare il suo valore, cioè trovare se è un numero finito, anche zero, o o .3)-Limite di una differenza
Se è
risulta:
Infatti, per il teorema dell'opposta e per il teorema precedente, si ha:
inoltre valgono le stesse osservazioni fatte in 2).
4)-Limite del prodotto
Se è
risulta:
cioè, il limite di un prodotto è uguale al prodotto dei limiti.
Infatti, nelle solite condizioni di validità dei due concetti di limite, bisogna dimostrare che tutte le x del conveniente intorno completo di ampiezza 2δ del punto x0, eccettuato sempre al più lo stesso punto x0,
x0 - δ < x < x0 + δ
vale la relazione:
|f1(x)·f2(x) - l1·l2| < ε' > 0,
con ε' piccolo a piacere.
Infatti, si ha:
per la validità di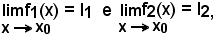
e per il teorema della limitazione, si ha:
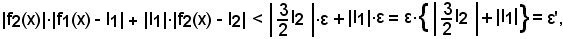
in quanto, essendo ε a piacere, si può considerare
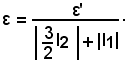
Il teorema è così dimostrato.
Osservazioni
Anche in questo teorema si è supposto che l1 e l2 siano numeri finiti, e quindi anche uno o entrambi zero. Se si ammette che uno di essi o entrambi diventino infiniti, si hanno i seguenti casi notevoli, che spesso si troveranno negli esercizi:
Cioè nulla si può dire subito sul risultato che costituisce il 2° caso di indeterminazione.
Da esso, come si vedrà, si potrà avere ancora un numero finito, anche 0, o infinito.
5)-Teorema dell'inversa
Se è
cioè: il limite dell'inversa di una funzione è uguale all'inverso del limite, supposto diverso da zero, della stessa.
Infatti, nell'ipotesi 1), per dimostrare la validità della 2), si deve dimostrare che per tutte le x del conveniente intorno completo, di ampiezza 2δ, del punto x0, eccettuato sempre al più lo stesso punto x0, si ha:
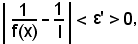
con ε' piccolo a piacere.
Infatti, successivamente si ha:
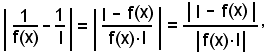
per la validità di 1) e per il teorema della limitazione, si ha:
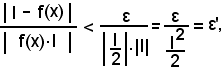
in quanto, essendo ε' a piacere, si può considerare
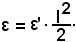
Osservazioni
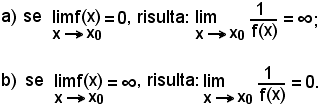
6)-Teorema del quoziente
Se
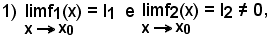
risulta
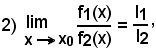
cioè: il limite del quoziente di due funzioni è uguale al quoziente dei limiti delle stesse.
Infatti, tenendo presente i due teoremi precedenti, si ha:
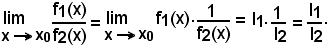
Osservazioni
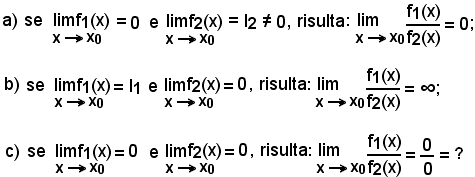
che costituisce il 3° caso di indeterminazione.
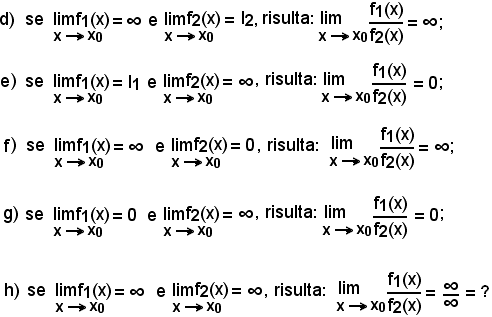
che costituisce il 4° caso di indeterminazione.
Valgono ancora i seguenti teoremi, dei quali ci si limita solo all'enunciato.
7)-Teorema della potenza
Se è
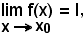
n un numero, risulta
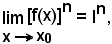
cioè: il limite della potenza di una funzione è uguale alla potenza del limite della stessa.
8)-Teorema del logaritmo
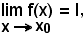
con n numero positivo, n ≠ 1, risulta
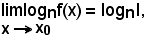
cioè: il limite del logaritmo di una funzione è uguale al logaritmo del limite della stessa.
Osservazioni
Infinitesimi ed infiniti - Confronto
1)-Definizione di infinitesimo - Si dice che una funzione f(x) per x tendente ad x0, o anche x = x0, è un infinitesimo o una funzione infinitesima, quando è:
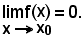
Esempi di infinitesimi
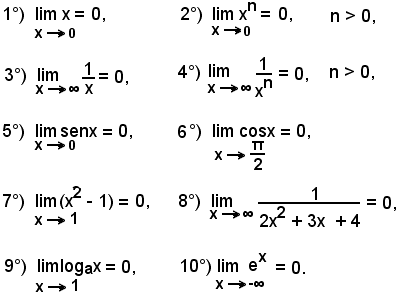
2)-Osservazioni
1^) Da
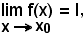
segue
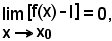
cioè: la funzione differenza fra la data ed il suo il limite per x tendente ad x0 qualsiasi è un infinitesimo.
2^) Negli esempi fatti si è visto che la tendenza a zero della funzione può aversi per:
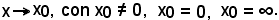
3)-Ordine di un infinitesimo
Nei primi esempi di 1), cioè
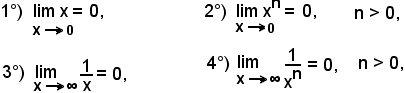
si è detto che è intuitivo che per
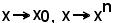
più rapidamente della stessa x, e così per
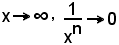
più rapidamente di
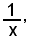
ossia nella tendenza a zero di una funzione, allorchè la variabile indipendente tende ad un valore x0 qualsiasi, vi può essere una maggiore o minore rapidità, o velocità, di approssimare e raggiungere il limite zero.
Questo carattere della funzione infinitesima si chiama ordine dell'infinitesimo.
Pertanto:
-due infinitesimi si diranno dello stesso ordine, quando raggiungeranno il limite zero con la stessa velocità;
-un infinitesimo si dirà di ordine superiore, o inferiore, ad un altro, quando raggiungerà il limite zero con maggiore, o minore, rapidità dell'altro.
Si tornerà fra poco su questi concetti per precisarli meglio e non nei casi particolari, come quelli visti negli esempi.
4)-Definizione di infinito - Si dice che una funzione per x tendente ad x0, o anche x = x0 è un infinito, quando è:
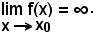
Esempi di infiniti
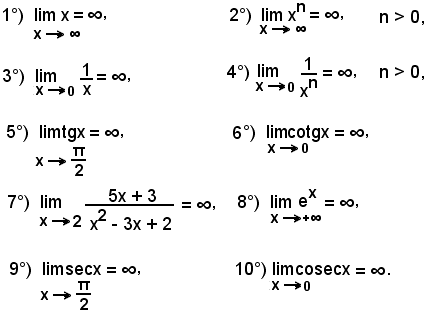
5)-Ordine di un infinito
Come per gli infinitesimi, l'ordine di un infinito è la maggiore o minore rapidità di approssimare e raggiungere il limite infinito.
Anche in tal caso risulta che:
-due infiniti si dicono dello stesso ordine quando raggiungono il limite infinito con la stessa rapidità;
-un infinito si dirà di ordine superiore o inferiore ad un altro, quando raggiungerà il limite infinito con rapidità maggiore o minore dell'altro.
Anche questi concetti saranno precisati, rigorosamente, tra poco.
6)-Osservazioni
1°) l'inverso di un infinitesimo è un infinito,
2°) l'inverso di un infinito è un infinitesimo,
3°) la somma di due infinitesimi è un infinitesimo,
4°) il prodotto di due infinitesimi è un infinitesimo,
5°) il prodotto di una costante per un infinitesimo è un infinitesimo,
6°) la somma di due infiniti dello stesso segno è un infinito,
7°) il prodotto di due infiniti è un infinito,
8°) il prodotto di una costante per un infinito è un infinito
Confronto di infinitesimi
Si abbiano i due infinitesimi
confrontarli significa vedere se sono dello stesso ordine e, nel caso contrario, vedere quale è di ordine superiore o inferiore.
Per effettuare il confronto due infinitesimi si considera il loro rapporto, che dà luogo al caso di indeterminazione:
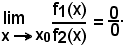
Applicando opportuni artifici di calcolo, da
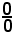
si pùo pervenire ad un numero diverso da zero, a zero ed a infinito.
Nel 1° caso significa che il rapporto, ed il suo limite, diventa, per x = x0, uguale ad un numero diverso da zero ed allora i due infinitesimi f1(x) e f2(x) si dicono dello stesso ordine.
Nel 2° caso significa che il rapporto diminuisce, per cui il suo limite è zero, e ciò accade quando il numeratore diminuisce più rapidamente del denominatore, quindi: l'infinitesimo f1(x) è di ordine superiore di f2(x).
Nel 3° caso significa che il rapporto aumenta, per cui il suo limite è infinito, e ciò accade quando il denominatore diminuisce più rapidamente del numeratore, quindi: l'infinitesimo f1(x) è di ordine inferiore di f2(x).
Confronto di infiniti
Si abbiano i due infiniti:
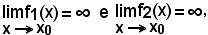
come per gli infinitesimi, confrontarli significa vedere se sono dello stesso ordine e, nel caso contrario, vedere quale è di ordine superiore o inferiore.
Per effettuare il confronto due infiniti si considera il loro rapporto, che dà luogo al caso di indeterminazione:
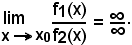
Applicando opportuni artifici di calcolo, si può pervenire ad un numero finito diverso da zero ed i due infiniti si diranno dello stesso ordine; a zero e l'infinito f1(x) al numeratore sarà di ordine inferiore all'altro f2(x); all'infinito e l'infinito f1(x) al numeratore sarà di ordine superiore all'altro f2(x).
Limiti notevoli delle funzioni
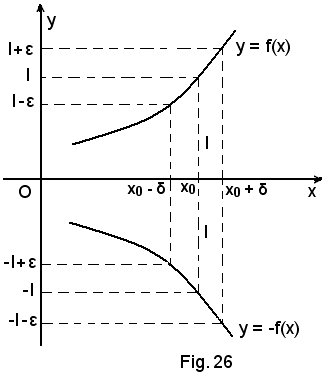
1) Il limite del rapporto fra il seno di un arco e l'arco stesso, misurato in radianti, quando questo tende a zero è uguale ad 1, cioè:
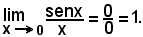
Limite destro
Poichè x tende a zero, non si altera la generalità della trattazione limitandosi a considerare un arco
piccolo e, comunque, del I quadrante.
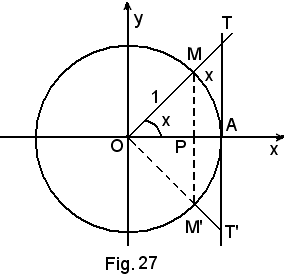
In riferimento alla Fig. 27, si sa dalla geometria elementare che risulta:
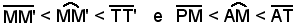
che, per le definizioni di funzioni circolari, significa
senx < x < tgx,
cioè
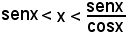
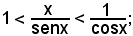
considerando gl'inversi
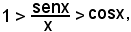
è anche
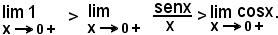
Essendo
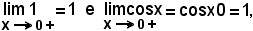
si ha:
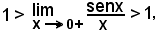
da cui, per il teorema del confronto, segue
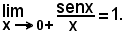
Limite sinistroSe l'arco x cambia segno, o verso, si ha:
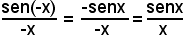
e quindi anche
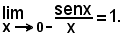
Dunque è, in ogni caso,
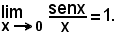
Osservazioni
1^) Poichè
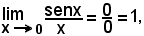
si ha che per x tendente a zero, il seno di un arco e l'arco stesso sono due infinitesimi dello stesso ordine.
2^) Per il teorema dell'inversa è anche:
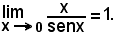
3^) Se l'arco non fosse misurato in radianti, si avrebbe:
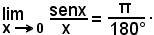
2) Il limite del rapporto fra la tangente di un arco e l'arco stesso, misurato in radianti, quando questo tende a zero è uguale ad 1.
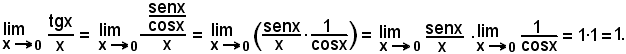
Quindi: si ha anche la tangente di un arco e l'arco, quando questo tende a zero sono due infinitesimi dello stesso ordine.
3) Risulta:
con x numero reale qualsiasi, positivo o negativo.
E' la generalizzazione, della quale si omette la dimostrazione del limite già visto:
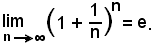
4) Risulta:
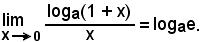
Infatti, posto
ed osservato che se
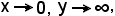
si ha:
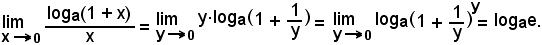
5) Risulta:
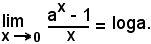
Infatti, posto
si ha:
ax = 1 + y
e
x = loga(1 + y).
Quindi, poichè se
allora si ha:
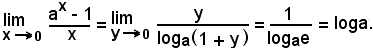
Nota bene
Se a = e, si ha:
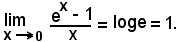
Metodi elementari per uscire da alcuni casi di indeterminazione
Come si è visto, nelle operazioni di somma, prodotto e quoziente, sono state trovate le seguenti forme di indeterminazione:
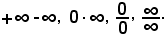
Si hanno inoltre i seguenti casi di indeterminazione:
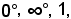
che si presentano quando si calcola
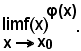
Precisamente, avendosi
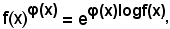
le ultime forme di indeterminazione corrispondono ai tre casi in cui l'esponente di e presenta la forma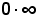
.
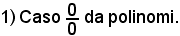
Si abbia
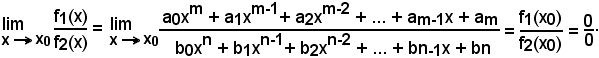
Per la continuità delle funzioni razionali, dire che i due polinomi numeratore e denominatore si sono annullati allorchè al posto della x è stato sostituito il valore numerico x0, significa, per quanto si sa dall'algebra elementare, che tutti polinomi sono divisibili per x - x0. Effettuata la divisione e scomposto ciascun polinomio nel prodotto del divisore (x - x0) per il quoziente Q1(x) e Q2(x) in ciascun caso trovato, polinomio ordinato allo stesso modo del dividendo e di un grado inferiore a quello, si ha:
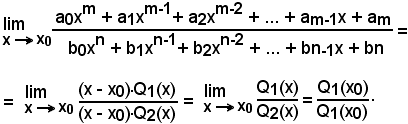
Osservazioni
1^ Se dal limite del quoziente di due polinomi, per x tendente ad x0, finito, si ha la forma indeterminata
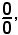
significa che entrambi i polinomi contengono il fattore comune x - x0, che va eliminato dal rapporto.
2^ Se è ancora
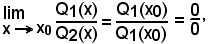
basta ripetere il procedimento fino ad uscire dalla forma indeterminata.
Esempi
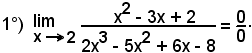
Effettuando la divisione di ciascun polinomio per x - 2, si hanno le seguenti scomposizioni:
x2 - 3x + 2 = (x - 2)(x + 2),
2x3 - 5x2 + 6x - 8 = (x - 2)(2x2 - x + 4),
per cui si può scrivere
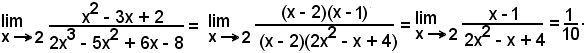
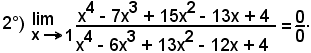
Essendo:
x4 - 7x3 + 15x2 - 13x + 4 = (x - 1)(x3 - 6x2 + 9x - 4),
x4 - 6x3 + 13x2 - 12x + 4 = (x - 1)(x3 - 5x2 + 8x - 4),
si può scrivere
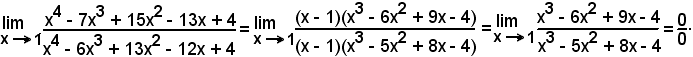
Essendo ancora:
x3 - 6x2 + 9x - 4 = (x - 1)(x2 - 5x + 4),
x3 - 5x2 + 8x - 4 = (x - 1)(x2 - 4x + 4),
si ha
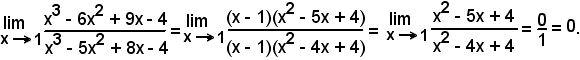
Dunque:
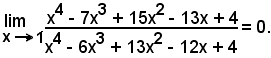
Si abbia:
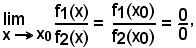
con f1(x) e f2(x) non più polinomi, ma altre funzioni dei tipi noti. Si cerca allora, ricorrendo ad artifici, di trasformare il rapporto f1(x)/f2(x) in un altro uguale ed il cui limite, sempre per x tendente ad x0, non sia più della forma indeterminata.
Nel caso in cui f1(x) e f2(x) siano espressioni contenenti funzioni circolari, applicando note formule della geometria, si trasforma per pervenire talvolta ad uno dei limiti notevoli:
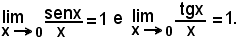
Gli esempi seguenti serviranno ad illustrare i criteri generali sopra esposti.
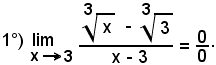
Essendo:
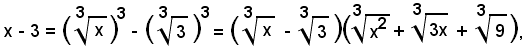si ha:
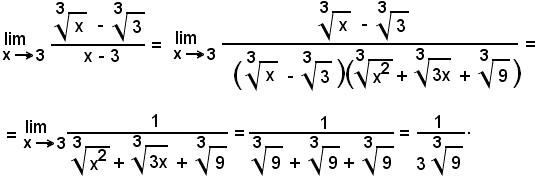
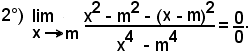
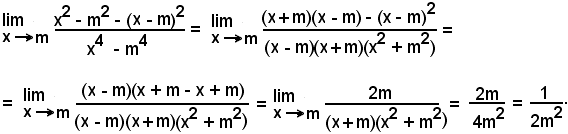
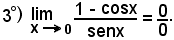
Moltiplicando numeratore e denominatore per 1 + cosx, si ha:
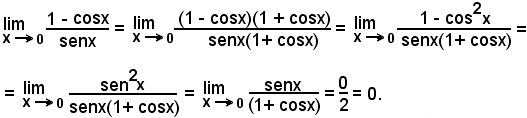
Moltiplicando e dividendo il numeratore per 3x e il denominatore per 5x, si ha:
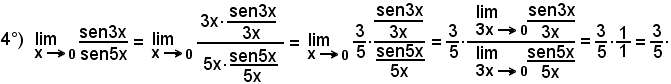
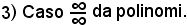
Si abbia:
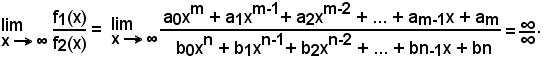
Si distinguono i tre casi
a) m = n, b) m > n, c) m < n
e si farà vedere che si perverrà rispettivamente al numero finito a0/b0, all'
, ed a zero.
Infatti:
-se m = n, basta dividere numeratore e denominatore per xm = xm, cioè per la variabile di maggior grado o esponente;
-se m > n oppure m < n, basta dividere numeratore e denominatore per la variabile al minore dei gradi tra numeratore e denominatore.
Esempi
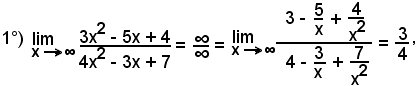
in quanto tutte le frazioni aventi la variabile al denominatore tendono a zero quando x tende ad.
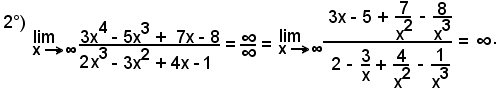
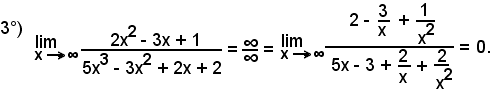
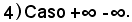
Moltiplicando e dividendo l'espressione per la stessa col segno di mezzo cambiato e fatte le opportune semplificazioni, si ricadrà nella forma indeterminata precedente
Esempi
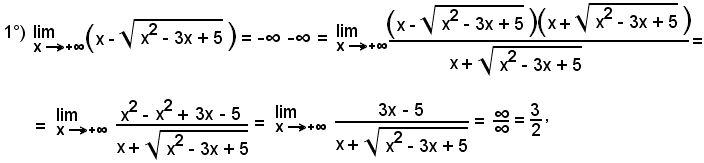
essendo numeratore e denominatore dello stesso grado.
Del resto si avrebbe:
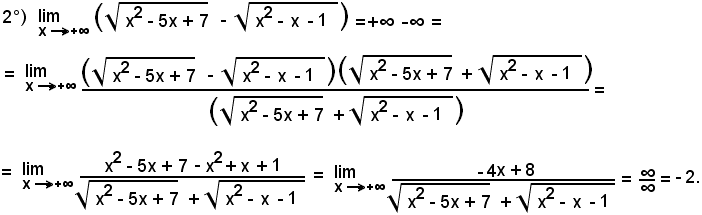
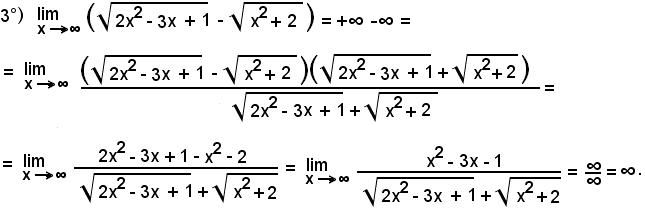
Si abbia:
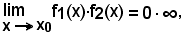
ossia
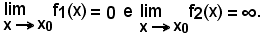
Mediante l'artificio seguente, si ha:
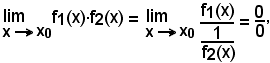
cioè si ricade nella 1^ forma indeterminata.
Esempio
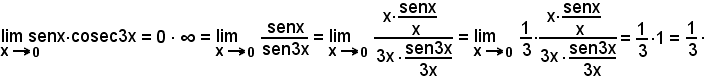
Nota bene
Un altro metodo, più generale, per uscire dalle forme indeterminate si vedrà nelle applicazioni dei teoremi di De L'Hospital, dopo aver trattato le derivate delle funzioni.
con ε' piccolo a piacere.
Infatti, si ha:
|f1(x)·f2(x) - l1·l2| = |f1(x)·f2(x) - f2(x)·l1 + f(x)2·l1 - l1·l2| ≤ |f2(x)·[f1(x) - l1]| + |l1·[f2(x) - l2]| =
= |f2(x)|·|f1(x) - l1| + |l1|·|f2(x) - l2|;
per la validità di
e per il teorema della limitazione, si ha:
in quanto, essendo ε a piacere, si può considerare
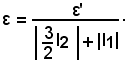
Il teorema è così dimostrato.
Osservazioni
Anche in questo teorema si è supposto che l1 e l2 siano numeri finiti, e quindi anche uno o entrambi zero. Se si ammette che uno di essi o entrambi diventino infiniti, si hanno i seguenti casi notevoli, che spesso si troveranno negli esercizi:
Cioè nulla si può dire subito sul risultato che costituisce il 2° caso di indeterminazione.
Da esso, come si vedrà, si potrà avere ancora un numero finito, anche 0, o infinito.
5)-Teorema dell'inversa
Se è
cioè: il limite dell'inversa di una funzione è uguale all'inverso del limite, supposto diverso da zero, della stessa.
Infatti, nell'ipotesi 1), per dimostrare la validità della 2), si deve dimostrare che per tutte le x del conveniente intorno completo, di ampiezza 2δ, del punto x0, eccettuato sempre al più lo stesso punto x0, si ha:
con ε' piccolo a piacere.
Infatti, successivamente si ha:
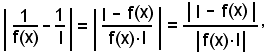
per la validità di 1) e per il teorema della limitazione, si ha:
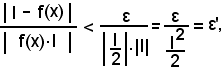
in quanto, essendo ε' a piacere, si può considerare
Osservazioni
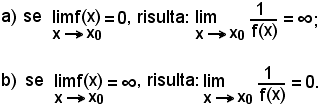
6)-Teorema del quoziente
Se
risulta
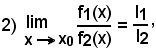
cioè: il limite del quoziente di due funzioni è uguale al quoziente dei limiti delle stesse.
Infatti, tenendo presente i due teoremi precedenti, si ha:
Osservazioni
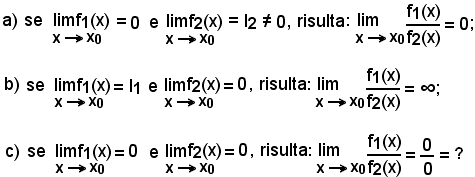
che costituisce il 3° caso di indeterminazione.
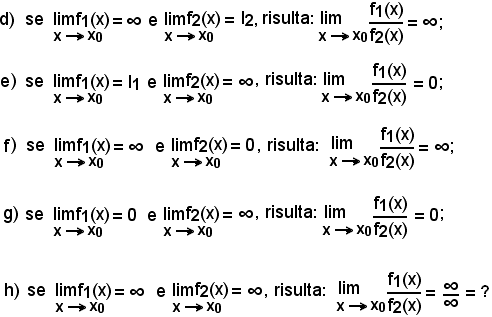
che costituisce il 4° caso di indeterminazione.
Valgono ancora i seguenti teoremi, dei quali ci si limita solo all'enunciato.
7)-Teorema della potenza
Se è
n un numero, risulta
cioè: il limite della potenza di una funzione è uguale alla potenza del limite della stessa.
8)-Teorema del logaritmo
Se è
con n numero positivo, n ≠ 1, risulta
cioè: il limite del logaritmo di una funzione è uguale al logaritmo del limite della stessa.
Osservazioni
Infinitesimi ed infiniti - Confronto
1)-Definizione di infinitesimo - Si dice che una funzione f(x) per x tendente ad x0, o anche x = x0, è un infinitesimo o una funzione infinitesima, quando è:
Esempi di infinitesimi
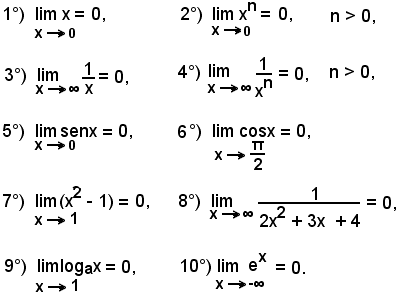
2)-Osservazioni
1^) Da
segue
cioè: la funzione differenza fra la data ed il suo il limite per x tendente ad x0 qualsiasi è un infinitesimo.
2^) Negli esempi fatti si è visto che la tendenza a zero della funzione può aversi per:
3)-Ordine di un infinitesimo
Nei primi esempi di 1), cioè
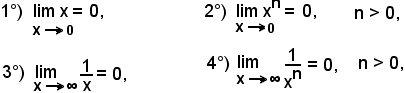
si è detto che è intuitivo che per
più rapidamente della stessa x, e così per
più rapidamente di
ossia nella tendenza a zero di una funzione, allorchè la variabile indipendente tende ad un valore x0 qualsiasi, vi può essere una maggiore o minore rapidità, o velocità, di approssimare e raggiungere il limite zero.
Questo carattere della funzione infinitesima si chiama ordine dell'infinitesimo.
Pertanto:
-due infinitesimi si diranno dello stesso ordine, quando raggiungeranno il limite zero con la stessa velocità;
-un infinitesimo si dirà di ordine superiore, o inferiore, ad un altro, quando raggiungerà il limite zero con maggiore, o minore, rapidità dell'altro.
Si tornerà fra poco su questi concetti per precisarli meglio e non nei casi particolari, come quelli visti negli esempi.
4)-Definizione di infinito - Si dice che una funzione per x tendente ad x0, o anche x = x0 è un infinito, quando è:
Esempi di infiniti
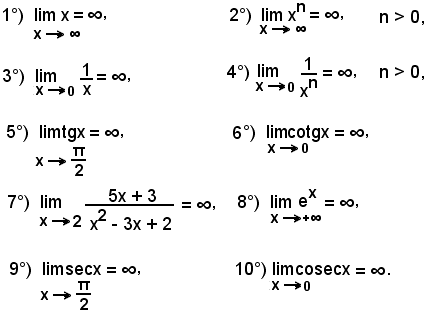
5)-Ordine di un infinito
Come per gli infinitesimi, l'ordine di un infinito è la maggiore o minore rapidità di approssimare e raggiungere il limite infinito.
Anche in tal caso risulta che:
-due infiniti si dicono dello stesso ordine quando raggiungono il limite infinito con la stessa rapidità;
-un infinito si dirà di ordine superiore o inferiore ad un altro, quando raggiungerà il limite infinito con rapidità maggiore o minore dell'altro.
Anche questi concetti saranno precisati, rigorosamente, tra poco.
6)-Osservazioni
1°) l'inverso di un infinitesimo è un infinito,
2°) l'inverso di un infinito è un infinitesimo,
3°) la somma di due infinitesimi è un infinitesimo,
4°) il prodotto di due infinitesimi è un infinitesimo,
5°) il prodotto di una costante per un infinitesimo è un infinitesimo,
6°) la somma di due infiniti dello stesso segno è un infinito,
7°) il prodotto di due infiniti è un infinito,
8°) il prodotto di una costante per un infinito è un infinito
Confronto di infinitesimi
Si abbiano i due infinitesimi
confrontarli significa vedere se sono dello stesso ordine e, nel caso contrario, vedere quale è di ordine superiore o inferiore.
Per effettuare il confronto due infinitesimi si considera il loro rapporto, che dà luogo al caso di indeterminazione:
Applicando opportuni artifici di calcolo, da
si pùo pervenire ad un numero diverso da zero, a zero ed a infinito.
Nel 1° caso significa che il rapporto, ed il suo limite, diventa, per x = x0, uguale ad un numero diverso da zero ed allora i due infinitesimi f1(x) e f2(x) si dicono dello stesso ordine.
Nel 2° caso significa che il rapporto diminuisce, per cui il suo limite è zero, e ciò accade quando il numeratore diminuisce più rapidamente del denominatore, quindi: l'infinitesimo f1(x) è di ordine superiore di f2(x).
Nel 3° caso significa che il rapporto aumenta, per cui il suo limite è infinito, e ciò accade quando il denominatore diminuisce più rapidamente del numeratore, quindi: l'infinitesimo f1(x) è di ordine inferiore di f2(x).
Confronto di infiniti
Si abbiano i due infiniti:
come per gli infinitesimi, confrontarli significa vedere se sono dello stesso ordine e, nel caso contrario, vedere quale è di ordine superiore o inferiore.
Per effettuare il confronto due infiniti si considera il loro rapporto, che dà luogo al caso di indeterminazione:
Applicando opportuni artifici di calcolo, si può pervenire ad un numero finito diverso da zero ed i due infiniti si diranno dello stesso ordine; a zero e l'infinito f1(x) al numeratore sarà di ordine inferiore all'altro f2(x); all'infinito e l'infinito f1(x) al numeratore sarà di ordine superiore all'altro f2(x).
Limiti notevoli delle funzioni
1) Il limite del rapporto fra il seno di un arco e l'arco stesso, misurato in radianti, quando questo tende a zero è uguale ad 1, cioè:
Limite destro
Poichè x tende a zero, non si altera la generalità della trattazione limitandosi a considerare un arco
piccolo e, comunque, del I quadrante.In riferimento alla Fig. 27, si sa dalla geometria elementare che risulta:
che, per le definizioni di funzioni circolari, significa
senx < x < tgx,
cioè
e dividendo per senx > 0, si ha:
considerando gl'inversi
è anche
Essendo
si ha:
da cui, per il teorema del confronto, segue
Limite sinistro
e quindi anche
Dunque è, in ogni caso,
Osservazioni
1^) Poichè
si ha che per x tendente a zero, il seno di un arco e l'arco stesso sono due infinitesimi dello stesso ordine.
2^) Per il teorema dell'inversa è anche:
3^) Se l'arco non fosse misurato in radianti, si avrebbe:
2) Il limite del rapporto fra la tangente di un arco e l'arco stesso, misurato in radianti, quando questo tende a zero è uguale ad 1.
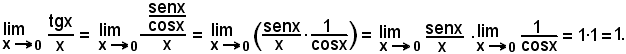
Quindi: si ha anche la tangente di un arco e l'arco, quando questo tende a zero sono due infinitesimi dello stesso ordine.
3) Risulta:
con x numero reale qualsiasi, positivo o negativo.
E' la generalizzazione, della quale si omette la dimostrazione del limite già visto:
4) Risulta:
Infatti, posto
ed osservato che se
si ha:
5) Risulta:
Infatti, posto
ax - 1 = y,
si ha:
e
x = loga(1 + y).
Quindi, poichè se
allora si ha:
Nota bene
Se a = e, si ha:
Metodi elementari per uscire da alcuni casi di indeterminazione
Come si è visto, nelle operazioni di somma, prodotto e quoziente, sono state trovate le seguenti forme di indeterminazione:
Si hanno inoltre i seguenti casi di indeterminazione:
che si presentano quando si calcola
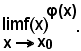
Precisamente, avendosi
le ultime forme di indeterminazione corrispondono ai tre casi in cui l'esponente di e presenta la forma
.Si abbia
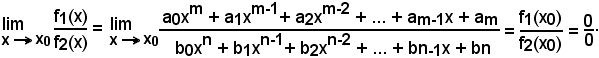
Per la continuità delle funzioni razionali, dire che i due polinomi numeratore e denominatore si sono annullati allorchè al posto della x è stato sostituito il valore numerico x0, significa, per quanto si sa dall'algebra elementare, che tutti polinomi sono divisibili per x - x0. Effettuata la divisione e scomposto ciascun polinomio nel prodotto del divisore (x - x0) per il quoziente Q1(x) e Q2(x) in ciascun caso trovato, polinomio ordinato allo stesso modo del dividendo e di un grado inferiore a quello, si ha:
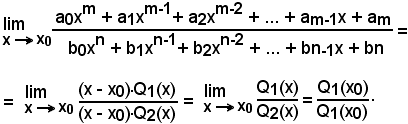
Osservazioni
1^ Se dal limite del quoziente di due polinomi, per x tendente ad x0, finito, si ha la forma indeterminata
significa che entrambi i polinomi contengono il fattore comune x - x0, che va eliminato dal rapporto.
2^ Se è ancora
basta ripetere il procedimento fino ad uscire dalla forma indeterminata.
Esempi
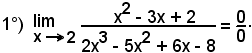
Effettuando la divisione di ciascun polinomio per x - 2, si hanno le seguenti scomposizioni:
x2 - 3x + 2 = (x - 2)(x + 2),
2x3 - 5x2 + 6x - 8 = (x - 2)(2x2 - x + 4),
per cui si può scrivere
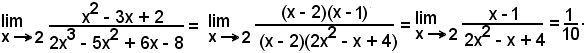
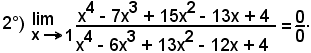
Essendo:
x4 - 7x3 + 15x2 - 13x + 4 = (x - 1)(x3 - 6x2 + 9x - 4),
x4 - 6x3 + 13x2 - 12x + 4 = (x - 1)(x3 - 5x2 + 8x - 4),
si può scrivere
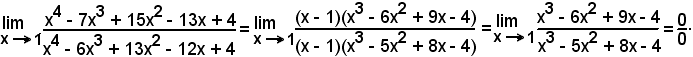
Essendo ancora:
x3 - 6x2 + 9x - 4 = (x - 1)(x2 - 5x + 4),
x3 - 5x2 + 8x - 4 = (x - 1)(x2 - 4x + 4),
si ha
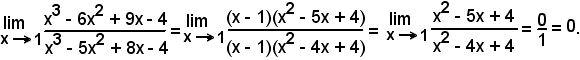
Dunque:
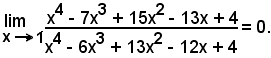
Si abbia:
con f1(x) e f2(x) non più polinomi, ma altre funzioni dei tipi noti. Si cerca allora, ricorrendo ad artifici, di trasformare il rapporto f1(x)/f2(x) in un altro uguale ed il cui limite, sempre per x tendente ad x0, non sia più della forma indeterminata.
Nel caso in cui f1(x) e f2(x) siano espressioni contenenti funzioni circolari, applicando note formule della geometria, si trasforma per pervenire talvolta ad uno dei limiti notevoli:
Gli esempi seguenti serviranno ad illustrare i criteri generali sopra esposti.
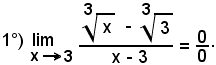
Essendo:
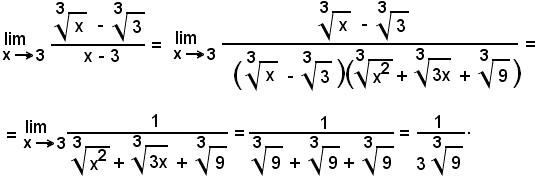
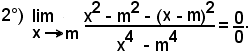
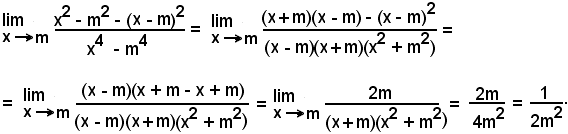
Moltiplicando numeratore e denominatore per 1 + cosx, si ha:
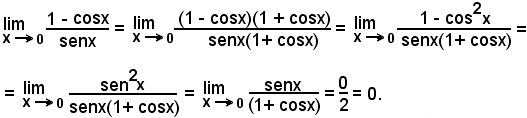
Moltiplicando e dividendo il numeratore per 3x e il denominatore per 5x, si ha:
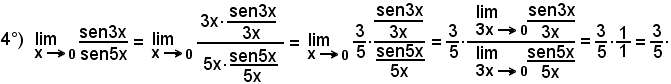
Si abbia:
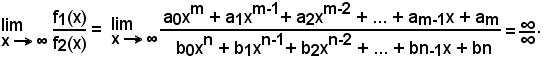
Si distinguono i tre casi
a) m = n, b) m > n, c) m < n
e si farà vedere che si perverrà rispettivamente al numero finito a0/b0, all'
, ed a zero.Infatti:
-se m = n, basta dividere numeratore e denominatore per xm = xm, cioè per la variabile di maggior grado o esponente;
-se m > n oppure m < n, basta dividere numeratore e denominatore per la variabile al minore dei gradi tra numeratore e denominatore.
Esempi
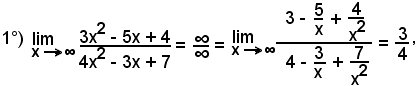
in quanto tutte le frazioni aventi la variabile al denominatore tendono a zero quando x tende ad
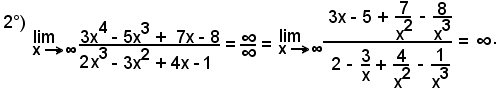
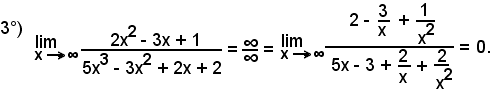
.Moltiplicando e dividendo l'espressione per la stessa col segno di mezzo cambiato e fatte le opportune semplificazioni, si ricadrà nella forma indeterminata precedente
Esempi
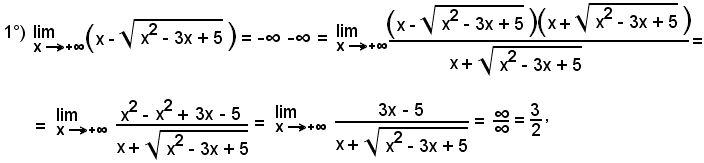
essendo numeratore e denominatore dello stesso grado.
Del resto si avrebbe:
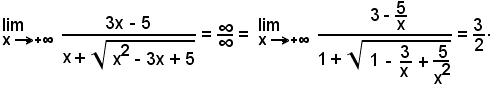
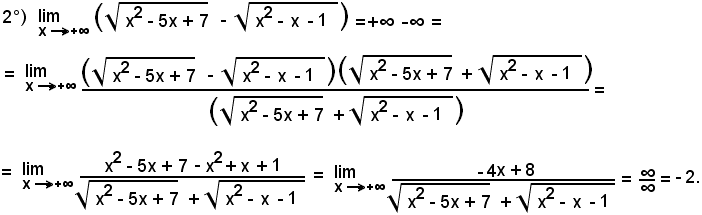
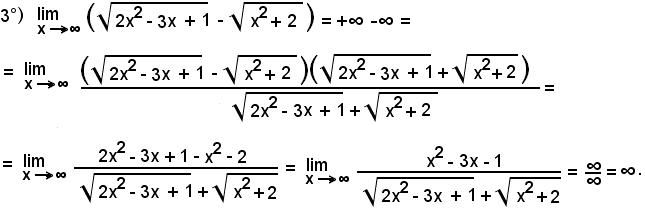
Si abbia:
ossia
Mediante l'artificio seguente, si ha:
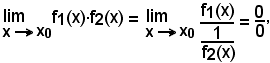
cioè si ricade nella 1^ forma indeterminata.
Esempio
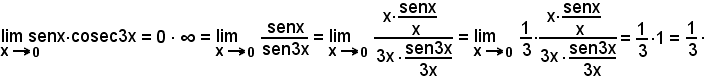
Nota bene
Un altro metodo, più generale, per uscire dalle forme indeterminate si vedrà nelle applicazioni dei teoremi di De L'Hospital, dopo aver trattato le derivate delle funzioni.