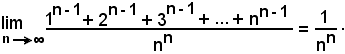MIKY & GENNY
TEORIA DEI LIMITI DELLE SUCCESSIONI ---> INDICE
1)-Successione divergente a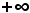 
Si dice che il limite di una successione an, per n tendente all'infinito, è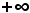, quando per ogni k > 0 grande a piacere è possibile determinare in sua corrispondenza un certo indice n0 tale che, per tutti gli indici n, da quello in poi (n ≥ n0), si verifichi che il valore dei termini della successione risulti maggiore di k.
Quindi:
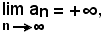
se per ogni k > 0, grande a piacere, esiste un n0 tale che per tutti gli n ≥ n0 risulti
(1) an > k.
Tale definizione è equivalente alla seguente:
-una successione an diverge a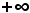 o ha limite 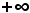, quando i suoi termini an, in valore, finiscono prima con il diventare e poi con il rimanere grandi quanto si vuole.
2)-Successione divergente a
Si dice che il limite di una successione an, per n tendente all'infinito, è quando per ogni k > 0, grande a piacere, è possibile determinare in sua corrispondenza un certo indice n0 tale che, per tutti gli indici n, da quello in poi (n ≥ n0), si verifichi che il valore dei termini della successione risulti minore di -k.
Quindi:
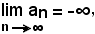
se per ogni k > 0, grande a piacere, esiste un n0 tale che per tutti gli n ≥ n0 risulti
(2) an < -k.
Tale definizione è equivalente alla seguente:
-una successione an diverge a o ha limite , quando i suoi termini an, in valore, finiscono prima con il diventare e poi con il rimanere piccoli negativi quanto si vuole.
3)-Successione divergente a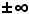
o solo 
Si dice che il limite di una successione an è quando, per ogni numero k > 0 grande a piacere, è possibile determinare in sua corrispondenza un certo indice n0 tale che, per tutti gli indici n, da quello in poi (n ≥ n0), si verifichi che il valore assoluto dei termini della successione risulti maggiore di k.
Quindi:
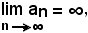
se per ogni k > 0 grande a piacere, esiste un n0 tale che per tutti gli n ≥ n0 risulti
(3) |an| > k.
Questa 3^ definizione, in effetti, è quella generale di successione divergente, nel senso che comprende le due precedenti come casi particolari.
Infatti:
a) se per si intende , vuol dire che gli an, almeno dall'indice n0 in poi, saranno positivi ed in tal caso la 3) si può scrivere
an > k,
che è la (1).
b) se per si intende , vuol dire che gli an, almeno dall'indice n0 in poi, saranno negativi ed in tal caso la 3), privata del segno di valore assoluto, si può scrivere
-an > k,
cioè
an < -k
che è la (2).
4)-Esempi di successioni divergenti
1°)-La serie dei numeri naturali è una successione divergente a:
2°)-L'opposta della serie dei numeri naturali è una successione divergente a:
3°)-La successione:
{(-1)n+1· n} = +1, -2, +3, -4, ...
è divergente, ma cambia infinite volte di segno.
5)-Successioni convergentiSi dice che il limite di una successione an è uguale ad un numero reale finito A quando, per ogni numero ε > 0 piccolo a piacere, è possibile determinare in sua corrispondenza un certo indice n0 tale che, per tutti gli indici n da quello in poi (n ≥ n0), si verifichi che il valore assoluto della differenza tra il valore dei termini an della successione ed il numero A risulti minore di ε.
Quindi:
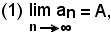
se per ogni ε > 0 piccolo a piacere, esiste un n0 tale che per tutti gli n ≥ n0 risulti
|an - A| < ε,
che è equivalente a
A - ε < an < A + ε.
Tale definizione è equivalente alla seguente:
-una successione an converge ad un numero finito A, o ha limite A, oppure, ancora, tende ad A, cioè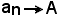
, quando i suoi termini an, finiscono prima con il diventare e poi con il rimanere vicini al numero A quanto si vuole.
6)-Esempi di successioni convergenti
1°)-La successione:
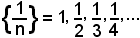
è convergente a zero, in quanto i suoi termini finiscono con il diventare e rimanere vicini allo zero quanto si vuole.
2°)-La successione:
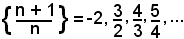
è convergente ad 1, in quanto i suoi termini finiscono con il diventare e rimanere vicini ad 1 quanto si vuole.
7)-Osservazioni
1°)-Occorre notare esplicitamente che, affinchè una successione,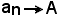
non basta che i suoi termini diventino vicini ad A quanto si vuole, ma
occorre anche che, una volta diventati vicini ad a, vi rimangano
sempre, cioè tutti a partire dall'indice n0 in poi.
Ad esempio, la successione:
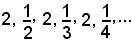
ottenuta interponendo il numero 2 fra i termini della successione
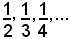
non converge più a zero, in quanto per qualsiasi n0 vi sono sì infiniti termini vicini allo zero quanto si vuole, ma ve ne sono altri infiniti, cioè tutti i numeri 2, che non sono vicini allo zero. Quindi, i termini della successione suddetta diventano vicini allo zero, ma non vi restano e pertanto zero non è il limite della successione. Con lo stesso ragionamento, si prova, ovviamente, che neppure 2 è il limite della successione.
2°)-Dire che tutti i termini an diventano e restano vicini ad A quanto si vuole, significa che nel prefissato intorno di A, almeno a partire da n0, cadano infiniti an e quindi A è un punto di accumulazione degli an.
3°)-Il fatto che i termini an debbano diventare vicini al numero A esprime, come del resto è intuitivo, che il concetto di limite è un concetto potenziale e non statico.
Carattere di una successione
Da quanto visto, si ha che una successione può presentare i tre seguenti casi o, come si dice, può avere i tre seguenti caratteri:
1°)-essere convergente, cioè il suo limite è finito,
2°)-essere divergente, cioè il suo limite è infinito,
3°)-essere indeterminata o oscillante, cioè non avere limite come, ad esempio, ciascuna delle due successioni seguenti
+1, -1, +1, -1, ...
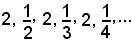
Teoremi sui limiti delle successioni
1)-Teorema dell'unicità del limite di una successione convergente - Una successione convergente non può avere due limiti diversi.
Il teorema si dimostra ragionando per assurdo.
Infatti, si supponga che la successione converga contemporaneamente ad A e A', cioè si supponga che:
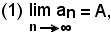
cioè per ogni ε > 0, piccolo a piacere, esiste un n1 tale che, per tutti gli n ≥ n1 risulti
(1) |an - A| < ε;
ed inoltre che
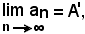
cioè per ogni ε > 0, piccolo a piacere, ed uguale a quello precedente, esiste un n2, tale che, per tutti gli n ≥ n2 risulti
Si dice che il limite di una successione an, per n tendente all'infinito, è
, quando per ogni k > 0 grande a piacere è possibile determinare in sua corrispondenza un certo indice n0 tale che, per tutti gli indici n, da quello in poi (n ≥ n0), si verifichi che il valore dei termini della successione risulti maggiore di k.Quindi:
se per ogni k > 0, grande a piacere, esiste un n0 tale che per tutti gli n ≥ n0 risulti
(1) an > k.
Tale definizione è equivalente alla seguente:
-una successione an diverge a
o ha limite , quando i suoi termini an, in valore, finiscono prima con il diventare e poi con il rimanere grandi quanto si vuole.2)-Successione divergente a
Si dice che il limite di una successione an, per n tendente all'infinito, è
quando per ogni k > 0, grande a piacere, è possibile determinare in sua corrispondenza un certo indice n0 tale che, per tutti gli indici n, da quello in poi (n ≥ n0), si verifichi che il valore dei termini della successione risulti minore di -k.Quindi:
se per ogni k > 0, grande a piacere, esiste un n0 tale che per tutti gli n ≥ n0 risulti
(2) an < -k.
Tale definizione è equivalente alla seguente:
-una successione an diverge a
o ha limite , quando i suoi termini an, in valore, finiscono prima con il diventare e poi con il rimanere piccoli negativi quanto si vuole.3)-Successione divergente a
o solo Si dice che il limite di una successione an è
quando, per ogni numero k > 0 grande a piacere, è possibile determinare in sua corrispondenza un certo indice n0 tale che, per tutti gli indici n, da quello in poi (n ≥ n0), si verifichi che il valore assoluto dei termini della successione risulti maggiore di k.Quindi:
se per ogni k > 0 grande a piacere, esiste un n0 tale che per tutti gli n ≥ n0 risulti
(3) |an| > k.
Questa 3^ definizione, in effetti, è quella generale di successione divergente, nel senso che comprende le due precedenti come casi particolari.
Infatti:
a) se per
si intende , vuol dire che gli an, almeno dall'indice n0 in poi, saranno positivi ed in tal caso la 3) si può scrivereche è la (1).
b) se per
si intende , vuol dire che gli an, almeno dall'indice n0 in poi, saranno negativi ed in tal caso la 3), privata del segno di valore assoluto, si può scrivere-an > k,
cioè
an < -k
che è la (2).
4)-Esempi di successioni divergenti
1°)-La serie dei numeri naturali è una successione divergente a
:{n} = 1, 2, 3, ... n, ...
2°)-L'opposta della serie dei numeri naturali è una successione divergente a
:{-n} = -1, -2, -3, ... -n, ...
3°)-La successione:
{(-1)n+1· n} = +1, -2, +3, -4, ...
è divergente, ma cambia infinite volte di segno.
5)-Successioni convergenti
Quindi:
se per ogni ε > 0 piccolo a piacere, esiste un n0 tale che per tutti gli n ≥ n0 risulti
|an - A| < ε,
che è equivalente a
A - ε < an < A + ε.
Tale definizione è equivalente alla seguente:
-una successione an converge ad un numero finito A, o ha limite A, oppure, ancora, tende ad A, cioè
, quando i suoi termini an, finiscono prima con il diventare e poi con il rimanere vicini al numero A quanto si vuole.6)-Esempi di successioni convergenti
1°)-La successione:
è convergente a zero, in quanto i suoi termini finiscono con il diventare e rimanere vicini allo zero quanto si vuole.
2°)-La successione:
è convergente ad 1, in quanto i suoi termini finiscono con il diventare e rimanere vicini ad 1 quanto si vuole.
7)-Osservazioni
1°)-Occorre notare esplicitamente che, affinchè una successione
,
non basta che i suoi termini diventino vicini ad A quanto si vuole, ma
occorre anche che, una volta diventati vicini ad a, vi rimangano
sempre, cioè tutti a partire dall'indice n0 in poi.Ad esempio, la successione:
ottenuta interponendo il numero 2 fra i termini della successione
non converge più a zero, in quanto per qualsiasi n0 vi sono sì infiniti termini vicini allo zero quanto si vuole, ma ve ne sono altri infiniti, cioè tutti i numeri 2, che non sono vicini allo zero. Quindi, i termini della successione suddetta diventano vicini allo zero, ma non vi restano e pertanto zero non è il limite della successione. Con lo stesso ragionamento, si prova, ovviamente, che neppure 2 è il limite della successione.
2°)-Dire che tutti i termini an diventano e restano vicini ad A quanto si vuole, significa che nel prefissato intorno di A, almeno a partire da n0, cadano infiniti an e quindi A è un punto di accumulazione degli an.
3°)-Il fatto che i termini an debbano diventare vicini al numero A esprime, come del resto è intuitivo, che il concetto di limite è un concetto potenziale e non statico.
Carattere di una successione
Da quanto visto, si ha che una successione può presentare i tre seguenti casi o, come si dice, può avere i tre seguenti caratteri:
1°)-essere convergente, cioè il suo limite è finito,
2°)-essere divergente, cioè il suo limite è infinito,
3°)-essere indeterminata o oscillante, cioè non avere limite come, ad esempio, ciascuna delle due successioni seguenti
Teoremi sui limiti delle successioni
1)-Teorema dell'unicità del limite di una successione convergente - Una successione convergente non può avere due limiti diversi.
Il teorema si dimostra ragionando per assurdo.
Infatti, si supponga che la successione converga contemporaneamente ad A e A', cioè si supponga che:
cioè per ogni ε > 0, piccolo a piacere, esiste un n1 tale che, per tutti gli n ≥ n1 risulti
(1) |an - A| < ε;
ed inoltre che
cioè per ogni ε > 0, piccolo a piacere, ed uguale a quello precedente, esiste un n2, tale che, per tutti gli n ≥ n2 risulti
(2) |an - A'| < ε.
Si pongano ora le condizioni, verificate le quali, siano contemporaneamente valide la (1) e la (2), cioè:
scelto un ε > 0, piccolo a piacere, e detto n0 l'indice maggiore tra n1 e n2, per tutti gli n ≥ n0 sarà certamente n ≥ n1 ed n ≥ n2 e quindi anche
Si pongano ora le condizioni, verificate le quali, siano contemporaneamente valide la (1) e la (2), cioè:
scelto un ε > 0, piccolo a piacere, e detto n0 l'indice maggiore tra n1 e n2, per tutti gli n ≥ n0 sarà certamente n ≥ n1 ed n ≥ n2 e quindi anche
|an - A| < ε e |an - A'| < ε.
Allora, considerata l'identità:
A - A' = (an - A') - (an - A),
successivamente si ha:
|A - A'| = |(an - A') - (an - A)| < |an - A'| + |an - A| < ε + ε = 2ε,
e poichè ε è arbitrario, considerando
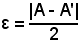
si avrebbe
|A - A'| < |A - A'|
e ciò è assurdo.
Siccome l'assurdo è derivato dall'aver supposto l'esistenza di due limiti diversi, e si è pervenuti ad un assurdo, si può concludere che quanto supposto non è vero, quindi esiste un solo limite.
2)-Teorema del valore assoluto
Se
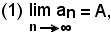
è anche
Infatti, dimostrare la (2), in base alla definizione di limite finito, equivale a dimostrare che:
||an | - |A|| < ε.
Poichè successivamente si ha:
||an | - |A|| ≤ |an - A| < ε,
per la (1), il teorema è dimostrato.
Nota bene
Non vale il teorema inverso. Infatti, considerata la successione:
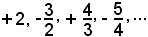
non ha alcun limite, mentre la successsione dei valori assoluti ha per limite 1.
3)-Inversa di una successione divergente o convergente a zero
Se è
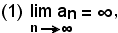
con tutti gli an ≠ 0, risulta:
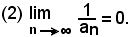
Infatti, basta osservare che per la (1) gli an diventano e restano grandi quanto si vuole e pertanto gl'inversi diventeranno e resteranno piccoli quanto si vuole.
4)-Coppia di successioni convergenti
Si dice che due successioni di numeri reali an e bn costituiscono una coppia di successioni convergenti, quando sono verificate le seguenti condizioni o proprietà:
1^)-la successione an non è decrescente, la bn non è crescente,
2^)-tutti gli an sono minori dei bn,
3^)-per ogni ε > 0 a piacere, esiste un n0 tale che, per tutti gli n ≥ n0, si abbia bn - an < ε.
Da quanto detto, si ha che:
-una coppia di successioni convergenti è una particolare coppia di classi contigue e quindi, come tra due successioni convergenti di due numeri reali, è sempre compreso un solo numero reale, detto elemento separatore.
Se α è tale numero, si ha:
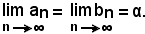
Nota bene
La lunghezza di una circonferenza e l'area del cerchio sono i limiti a cui tendono le coppie di successioni convergenti costituite rispettivamente dai perimetri pn e Pn dei poligoni inscritti e circoscritti e dalle aree sn e Sn degli stessi.
5)-Confronto di successioni - Teorema del confronto
Da quanto detto in precedenza, seguono le seguenti osservazioni:
1^)-data la successione an, sopprimendo in essa un qualsiasi numero finito di termini che precedono uno assegnato, si ha una nuova successione che ha lo stesso carattere e lo stesso limite di quella data;
2^)-se una successione an è convergente a zero, qualsiasi altra successione a'n, i cui termini siano in valore assoluto minori o uguali, ordinatamente, ai termini della successione data, è anche convergente a zero.
Infatti, da
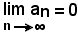
e dall'ipotesi a'n < an < ε, risulta
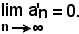
3^)-se una successione an è divergente, qualsiasi altra successione a'n, i cui termini siano in valore assoluto maggiori o uguali, ordinatamente, ai termini della successione data, è anche divergente.
Si può ora dimostrare il teorema del confronto:
-se an, bn, cn sono tre successioni tali che, per ogni valore di n tra i loro elementi, sussista ordinatamente la relazione
an < bn < cn,
si ha che
1)-se an e cn sono convergenti allo stesso numero, anche bn converge allo stesso numero,
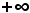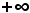2)-se an e cn, sono divergenti entrambe a o , anche bn diverge rispettivamente a o a .
Infatti, dire
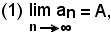
significa che:
per ogni ε > 0, piccolo a piacere un tale che, per tutti gli n ≥ n1 risulta
|an - A| < ε.
Analogamente,
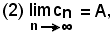
significa che:
per ogni ε > 0, piccolo a piacere, uguale al precedente, esiste un n2 tale che, per tutti gli n ≥ n2 risulta
|cn - A| < ε.
Poste le condizioni, come già visto, verificate le quali valgano contemporaneamente i due precedenti concetti, cioè:
scelto un ε > 0, piccolo a piacere, e considerato n0 maggiore sia di n1 che di n2, per tutti gli n ≥ n0 sarà certamente n ≥ n1 e n ≥ n2 e quindi contemporaneamente
|an - A| < ε e |cn - A| < ε,
ossia
A - ε < an < A + ε e A - ε < cn < A + ε.
Allora, dall'ipotesi
segue
A - ε < an < bn < cn< A + ε,
ossia:
A - ε < bn < A + ε,
che per il concetto di limite, equivale a:
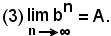
In tal modo è dimostrata la 1).
Si dimostra ora la 2).
Dire che
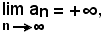
significa che:
per ogni k > 0, grande a piacere, esiste un n1 tale che, per tutti gli n ≥ n1, risulta
an > k.
Analogamente,
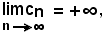
significa che:
per ogni k > 0, grande a piacere, uguale al precedente, esiste un n2 tale che, per tutti gli n ≥ n2, risulta
cn > k.
Allora, per ogni k > 0, grande a piacere, e per ogni n ≥ n0 ed n0 maggiore o uguale sia di n1 che di n2, sarà contemporaneamente
an > k e cn > k.
Dall'ipotesi
segue
k < an < bn,
ossia
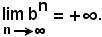
In tal modo è dimostrata la 2).
Del tutto identico è il casi in cui il limite di an e bn è.
Operazioni razionali delle successioni
Se an e bn sono due successioni:
-si chiamano somma, differenza, prodotto e quoziente di esse, le successioni aventi per termini generali, rispettivamente
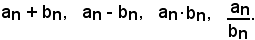
Pertanto, un'operazione razionale su due successioni si effettua eseguendo l'operazione sui termini di ugual posto, cioè corrispondenti, delle due successioni.
Naturalmente, per poter considerare la successione quoziente, tutti i bn, devono essere diversi da zero.
Operazioni razionali sui limiti finiti di successioni
Date due successioni convergenti an e bn, tali che:
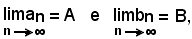
valgono i seguenti teoremi, dei quali si ometteranno le dimostrazioni, che in effetti sono casi particolari di quelle che saranno fatte negli stessi teoremi sulle funzioni.
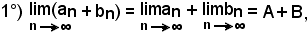
cioè: il limite della somma di due successioni convergenti è uguale alla somma dei limiti delle stesse.
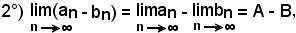
cioè: il limite della differenza di due successioni convergenti è uguale alla differenza dei limiti delle stesse.
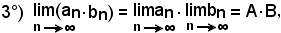
cioè: il limite del prodotto di due successioni convergenti è uguale al prodotto dei limiti delle stesse.
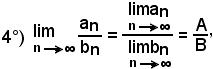
se bn ≠ 0 e B ≠ 0,
cioè: il limite del quoziente di due successioni convergenti è uguale al quoziente dei limiti delle stesse.
Sussistono anche i seguenti teoremi:
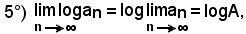
cioè: il limite del logaritmo, in qualsiasi base, di una successione convergente è uguale al logaritmo, nella stessa base del limite della stessa.
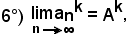
con k > 0, k =0, k < 0 e an ≠ 0, A ≠ 0 nell'ultimo caso,
cioè: il limite della potenza di una successione convergente è uguale alla potenza del limite della stessa.
Si può pertanto dire, salvo le condizioni particolari richieste dai teoremi, che:
-il limite di un'operazione tra successioni è uguale all'operazione tra i limiti delle stesse.
Si può ancora dire che:
il passaggio al limite, cioè l'operazione mediante la quale si determina il limite, è permutabile con qualsiasi altra operazione tra successioni, intendendo dire che o prima si effettua l'operazione tra successioni e quindi si calcola il limite della successione risultato, oppure prima si calcolano i limiti delle singole successioni e poi si effettua l'operazione su tali limiti, si perviene allo stesso risultato.
Limiti delle successioni monotone
Si ricorda che le successioni crescenti, non crescenti, decrescenti e non decrescenti si dicono monotone:
-crescente, quando
a1 < a2 < a3 < ... < an < ...
-non crescente, quando
a1 ≥ a2 ≥ a3 ≥ ... ≥ an ≥ ...
-decrescente, quando
a1 > a2 > a3 > ... > an > ...
-non decrescente, quando
a1≤ a2 ≤ a3 ≤ ... ≤ an ≤ ...
Valgono i seguenti teoremi:
1°)-una successione monotona non è mai indeterminata e quindi o è convergente o è divergente.
2°)-una successione monotona non decrescente approssima il suo limite per difetto; una non crescente lo approssima per eccesso.
Limiti notevoli di successioni
1)-Il numero "e".
Si vuole dimostrare che la successione:
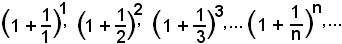
è convergente ed è
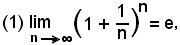
con 2 < e < 3, numero irrazionale.
Applicando la regola di sviluppo della potenza di un binomio data da Newton e poi semplificando, si ha:
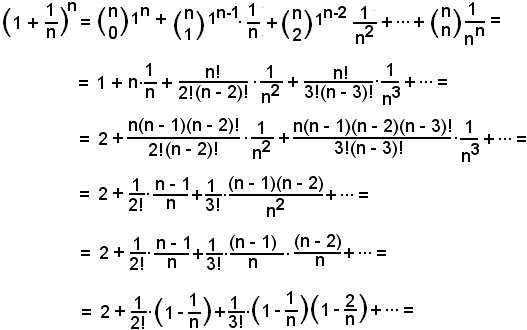
e poichè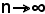
, le frazioni
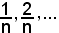
sono tutte proprie e al crescere di n, tendono a zero. Pertanto, le quantità in parentesi risultano essere numeri positivi, quindi, essendo
è
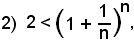
ossia che la successione
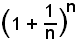
è limitata inferiormente.
Le stesse quantità suddette risultano, per la stessa osservazione fatta, numeri tutti minori di 1, per cui, se al posto di ciascuno di essi si pone 1, si ottiene un'espressione maggiorante della precedente, cioè:
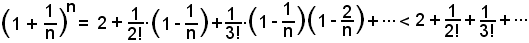
Si indica ora l'ultima quantità con
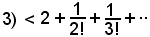
e poichè
avendo sommato membro a membro le quantità suddette, per cui risulta
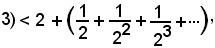
si ottiene un ulteriore maggiorante di
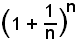
e quindi si potrà scrivere
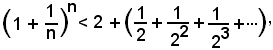
ove la somma nella parentesi del 2° membro è quella dei termini di una progressione geometrica di ragione q = 1/2.
Ricordando che una tale somma, limitata ai primi n termini della progressione il cui 1° termine sia a1 e la cui ragione sia q, è espressa dalla formula:
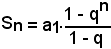
e, nel caso in esame, diventa
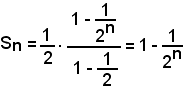
e si ha
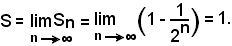
Allora è:
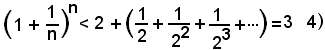
Da 2) e 4) segue:
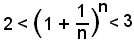
e, per il teorema del confronto,
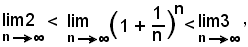
cioè in definitiva risulta
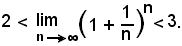
La relazione trovata esprime che:
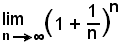
è uguale al numero reale la cui parte intera è 2. Le cifre decimali di questo numero sono infinite ed aperiodiche, per cui il numero è irrazionale, e poichè non è possibile scrivere tutte le sue infinite cifre decimali, lo si indica con la lettera "e".
Nota bene
a)-Volendo valori decimali approssimati di tale numero, basta calcolare successivamente le potenze:
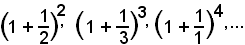
ma, per avere esatta la prima cifra decimale, occorre arrivare, con le ordinarie tavole logaritmiche, alla potenza
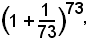
per cui, in pratica, per avere valori approssimati del numero "e", si ricorre ad altri metodi.
Per le applicazioni più frequenti è sufficiente conoscere il valore approssimato a meno di un decimiliardesimo, 10-10, che è il seguente:
e = 2,7182818284 ...
Il numero "e" è la base dei logaritmi naturali o iperbolici o neperiani, in onore al matematico scozzese Napier, che fu il primo a pubblicare tavole logaritmiche ed esporne la relativa teoria e l'uso.
b)-Nella dimostrazione fatta di è supposto n > 0 intero, ma si dimostra che è anche
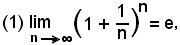
per n < 0.
Somma degli infiniti termini di una progressione geometricaDalla progressione illimitata:
a1, a2, a3, ..., an-1, an, ...
di ragione q, si considerino le seguenti somme parziali dei suoi termini:
S1 = a1,
S2 = a1 + a2,
S3 = a1 + a2 + a3,
.......................................................................
.......................................................................
Sn = a1 + a2 + a3 + ... + an-1 + an,
.......................................................................
.......................................................................
e la nuova successione
(1) S1, S2, S3, ... Sn, ...
Si vuole dimostrare che se è la ragione |q| < 1, la successione (1) è convergente ed è
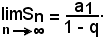
Infatti, ricordando dall'algebra la formula che esprime la somma dei primi n termini consecutivi della progressione:
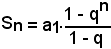
o anche equivalentemente
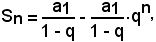
si ha:
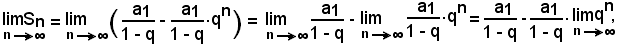
essendo
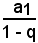
costante rispetto ad n.
Poichè |q| < 1, risulta:
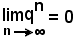
e quindi, in definitiva,
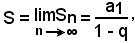
come volevasi dimostrare.
3)-Limiti notevoli di Cavalieri
a)-Si dimostra che:
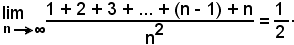
Infatti, ricordando che:
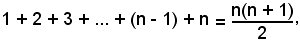
successivamente si ha:
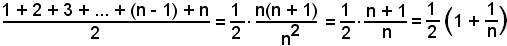
e quindi:
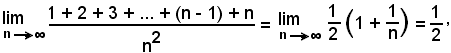
come volevasi dimostrare.
b)-Si dimostra che:
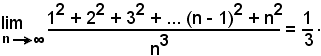
Infatti, ricordando che:
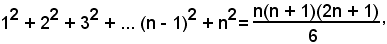
si ha:
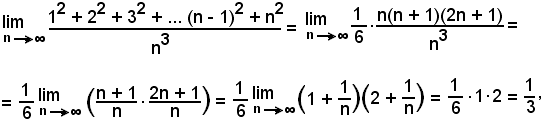
come volevasi dimostrare.
c)-In generale:
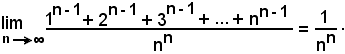
A - A' = (an - A') - (an - A),
successivamente si ha:
|A - A'| = |(an - A') - (an - A)| < |an - A'| + |an - A| < ε + ε = 2ε,
e poichè ε è arbitrario, considerando
si avrebbe
|A - A'| < |A - A'|
e ciò è assurdo.
Siccome l'assurdo è derivato dall'aver supposto l'esistenza di due limiti diversi, e si è pervenuti ad un assurdo, si può concludere che quanto supposto non è vero, quindi esiste un solo limite.
2)-Teorema del valore assoluto
Se
è anche
Infatti, dimostrare la (2), in base alla definizione di limite finito, equivale a dimostrare che:
||an | - |A|| < ε.
Poichè successivamente si ha:
||an | - |A|| ≤ |an - A| < ε,
per la (1), il teorema è dimostrato.
Nota bene
Non vale il teorema inverso. Infatti, considerata la successione:
non ha alcun limite, mentre la successsione dei valori assoluti ha per limite 1.
3)-Inversa di una successione divergente o convergente a zero
Se è
con tutti gli an ≠ 0, risulta:
Infatti, basta osservare che per la (1) gli an diventano e restano grandi quanto si vuole e pertanto gl'inversi diventeranno e resteranno piccoli quanto si vuole.
4)-Coppia di successioni convergenti
Si dice che due successioni di numeri reali an e bn costituiscono una coppia di successioni convergenti, quando sono verificate le seguenti condizioni o proprietà:
1^)-la successione an non è decrescente, la bn non è crescente,
2^)-tutti gli an sono minori dei bn,
3^)-per ogni ε > 0 a piacere, esiste un n0 tale che, per tutti gli n ≥ n0, si abbia bn - an < ε.
Da quanto detto, si ha che:
-una coppia di successioni convergenti è una particolare coppia di classi contigue e quindi, come tra due successioni convergenti di due numeri reali, è sempre compreso un solo numero reale, detto elemento separatore.
Se α è tale numero, si ha:
Nota bene
La lunghezza di una circonferenza e l'area del cerchio sono i limiti a cui tendono le coppie di successioni convergenti costituite rispettivamente dai perimetri pn e Pn dei poligoni inscritti e circoscritti e dalle aree sn e Sn degli stessi.
5)-Confronto di successioni - Teorema del confronto
Da quanto detto in precedenza, seguono le seguenti osservazioni:
1^)-data la successione an, sopprimendo in essa un qualsiasi numero finito di termini che precedono uno assegnato, si ha una nuova successione che ha lo stesso carattere e lo stesso limite di quella data;
2^)-se una successione an è convergente a zero, qualsiasi altra successione a'n, i cui termini siano in valore assoluto minori o uguali, ordinatamente, ai termini della successione data, è anche convergente a zero.
Infatti, da
e dall'ipotesi a'n < an < ε, risulta
3^)-se una successione an è divergente, qualsiasi altra successione a'n, i cui termini siano in valore assoluto maggiori o uguali, ordinatamente, ai termini della successione data, è anche divergente.
Si può ora dimostrare il teorema del confronto:
-se an, bn, cn sono tre successioni tali che, per ogni valore di n tra i loro elementi, sussista ordinatamente la relazione
si ha che
1)-se an e cn sono convergenti allo stesso numero, anche bn converge allo stesso numero,
2)-se an e cn, sono divergenti entrambe a
o , anche bn diverge rispettivamente a o a .Infatti, dire
significa che:
per ogni ε > 0, piccolo a piacere un tale che, per tutti gli n ≥ n1 risulta
|an - A| < ε.
Analogamente,
significa che:
per ogni ε > 0, piccolo a piacere, uguale al precedente, esiste un n2 tale che, per tutti gli n ≥ n2 risulta
Poste le condizioni, come già visto, verificate le quali valgano contemporaneamente i due precedenti concetti, cioè:
scelto un ε > 0, piccolo a piacere, e considerato n0 maggiore sia di n1 che di n2, per tutti gli n ≥ n0 sarà certamente n ≥ n1 e n ≥ n2 e quindi contemporaneamente
|an - A| < ε e |cn - A| < ε,
ossia
Allora, dall'ipotesi
an < bn < cn
segue
A - ε < an < bn < cn< A + ε,
ossia:
A - ε < bn < A + ε,
che per il concetto di limite, equivale a:
In tal modo è dimostrata la 1).
Si dimostra ora la 2).
Dire che
significa che:
per ogni k > 0, grande a piacere, esiste un n1 tale che, per tutti gli n ≥ n1, risulta
an > k.
Analogamente,
significa che:
per ogni k > 0, grande a piacere, uguale al precedente, esiste un n2 tale che, per tutti gli n ≥ n2, risulta
cn > k.
Allora, per ogni k > 0, grande a piacere, e per ogni n ≥ n0 ed n0 maggiore o uguale sia di n1 che di n2, sarà contemporaneamente
Dall'ipotesi
an < bn < cn,
segue
k < an < bn,
ossia
In tal modo è dimostrata la 2).
Del tutto identico è il casi in cui il limite di an e bn è
.Operazioni razionali delle successioni
Se an e bn sono due successioni:
-si chiamano somma, differenza, prodotto e quoziente di esse, le successioni aventi per termini generali, rispettivamente
Pertanto, un'operazione razionale su due successioni si effettua eseguendo l'operazione sui termini di ugual posto, cioè corrispondenti, delle due successioni.
Naturalmente, per poter considerare la successione quoziente, tutti i bn, devono essere diversi da zero.
Operazioni razionali sui limiti finiti di successioni
Date due successioni convergenti an e bn, tali che:
valgono i seguenti teoremi, dei quali si ometteranno le dimostrazioni, che in effetti sono casi particolari di quelle che saranno fatte negli stessi teoremi sulle funzioni.
cioè: il limite della somma di due successioni convergenti è uguale alla somma dei limiti delle stesse.
cioè: il limite della differenza di due successioni convergenti è uguale alla differenza dei limiti delle stesse.
cioè: il limite del prodotto di due successioni convergenti è uguale al prodotto dei limiti delle stesse.
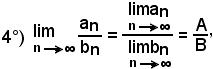
se bn ≠ 0 e B ≠ 0,
cioè: il limite del quoziente di due successioni convergenti è uguale al quoziente dei limiti delle stesse.
Sussistono anche i seguenti teoremi:
cioè: il limite del logaritmo, in qualsiasi base, di una successione convergente è uguale al logaritmo, nella stessa base del limite della stessa.
con k > 0, k =0, k < 0 e an ≠ 0, A ≠ 0 nell'ultimo caso,
cioè: il limite della potenza di una successione convergente è uguale alla potenza del limite della stessa.
Si può pertanto dire, salvo le condizioni particolari richieste dai teoremi, che:
-il limite di un'operazione tra successioni è uguale all'operazione tra i limiti delle stesse.
Si può ancora dire che:
il passaggio al limite, cioè l'operazione mediante la quale si determina il limite, è permutabile con qualsiasi altra operazione tra successioni, intendendo dire che o prima si effettua l'operazione tra successioni e quindi si calcola il limite della successione risultato, oppure prima si calcolano i limiti delle singole successioni e poi si effettua l'operazione su tali limiti, si perviene allo stesso risultato.
Limiti delle successioni monotone
Si ricorda che le successioni crescenti, non crescenti, decrescenti e non decrescenti si dicono monotone:
-crescente, quando
a1 < a2 < a3 < ... < an < ...
-non crescente, quando
a1 ≥ a2 ≥ a3 ≥ ... ≥ an ≥ ...
-decrescente, quando
a1 > a2 > a3 > ... > an > ...
-non decrescente, quando
a1≤ a2 ≤ a3 ≤ ... ≤ an ≤ ...
Valgono i seguenti teoremi:
1°)-una successione monotona non è mai indeterminata e quindi o è convergente o è divergente.
2°)-una successione monotona non decrescente approssima il suo limite per difetto; una non crescente lo approssima per eccesso.
Limiti notevoli di successioni
1)-Il numero "e".
Si vuole dimostrare che la successione:
è convergente ed è
con 2 < e < 3, numero irrazionale.
Applicando la regola di sviluppo della potenza di un binomio data da Newton e poi semplificando, si ha:
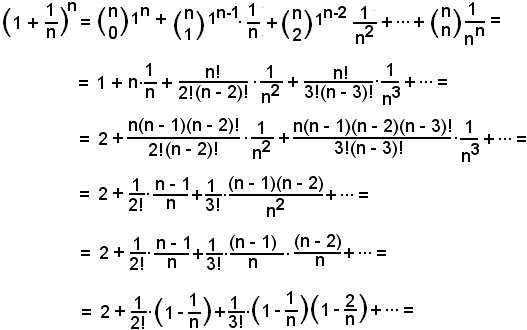
e poichè
, le frazionisono tutte proprie e al crescere di n, tendono a zero. Pertanto, le quantità in parentesi risultano essere numeri positivi, quindi, essendo
è
ossia che la successione
è limitata inferiormente.
Le stesse quantità suddette risultano, per la stessa osservazione fatta, numeri tutti minori di 1, per cui, se al posto di ciascuno di essi si pone 1, si ottiene un'espressione maggiorante della precedente, cioè:
Si indica ora l'ultima quantità con
e poichè
avendo sommato membro a membro le quantità suddette, per cui risulta
e quindi si potrà scrivere
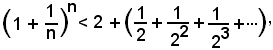
ove la somma nella parentesi del 2° membro è quella dei termini di una progressione geometrica di ragione q = 1/2.
Ricordando che una tale somma, limitata ai primi n termini della progressione il cui 1° termine sia a1 e la cui ragione sia q, è espressa dalla formula:
e, nel caso in esame, diventa
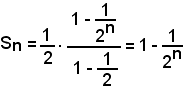
e si ha
Allora è:
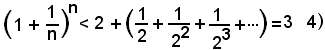
Da 2) e 4) segue:
e, per il teorema del confronto,
cioè in definitiva risulta
La relazione trovata esprime che:
è uguale al numero reale la cui parte intera è 2. Le cifre decimali di questo numero sono infinite ed aperiodiche, per cui il numero è irrazionale, e poichè non è possibile scrivere tutte le sue infinite cifre decimali, lo si indica con la lettera "e".
Nota bene
a)-Volendo valori decimali approssimati di tale numero, basta calcolare successivamente le potenze:
ma, per avere esatta la prima cifra decimale, occorre arrivare, con le ordinarie tavole logaritmiche, alla potenza
per cui, in pratica, per avere valori approssimati del numero "e", si ricorre ad altri metodi.
Per le applicazioni più frequenti è sufficiente conoscere il valore approssimato a meno di un decimiliardesimo, 10-10, che è il seguente:
e = 2,7182818284 ...
Il numero "e" è la base dei logaritmi naturali o iperbolici o neperiani, in onore al matematico scozzese Napier, che fu il primo a pubblicare tavole logaritmiche ed esporne la relativa teoria e l'uso.
b)-Nella dimostrazione fatta di è supposto n > 0 intero, ma si dimostra che è anche
per n < 0.
Somma degli infiniti termini di una progressione geometrica
di ragione q, si considerino le seguenti somme parziali dei suoi termini:
S1 = a1,
S2 = a1 + a2,
S3 = a1 + a2 + a3,
.......................................................................
.......................................................................
Sn = a1 + a2 + a3 + ... + an-1 + an,
.......................................................................
.......................................................................
e la nuova successione
(1) S1, S2, S3, ... Sn, ...
Si vuole dimostrare che se è la ragione |q| < 1, la successione (1) è convergente ed è
Infatti, ricordando dall'algebra la formula che esprime la somma dei primi n termini consecutivi della progressione:
o anche equivalentemente
si ha:
essendo
costante rispetto ad n.
Poichè |q| < 1, risulta:
e quindi, in definitiva,
come volevasi dimostrare.
3)-Limiti notevoli di Cavalieri
a)-Si dimostra che:
Infatti, ricordando che:
successivamente si ha:
e quindi:
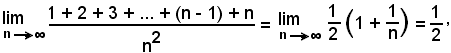
come volevasi dimostrare.
b)-Si dimostra che:
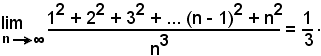
Infatti, ricordando che:
si ha:
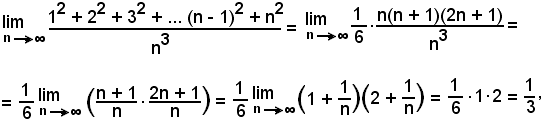
come volevasi dimostrare.
c)-In generale: