ELEMENTI PARTICOLARI DEGL'INSIEMI ---> INDICE
1)-Il più grande elemento di un insieme
Sia (E, ≤) un insieme ordinato e si consideri un elemento a E; si dice che a è il più grande elemento di E per la relazione d'ordine ≤, se si verifica che
E; si dice che a è il più grande elemento di E per la relazione d'ordine ≤, se si verifica che
 x
x E : x ≤ a.
E : x ≤ a.
Se esiste questo elemento a, esso è unico.
Infatti, supponendo che esistano a' ed a'', entrambi i più grandi elementi di E, relativamente ad a' ed a'' rispettivamente si ha:
(1) a' E
E 
 x
x E : x ≤ a',
E : x ≤ a',
(2) a'' E
E 
 x
x E : x ≤ a''.
E : x ≤ a''.
Poichè (1) e (2) valgono x
x E, data l'arbitrarietà di x, nella (1) si può sostituire a'' al posto di x e nella (2) a' al posto di x ottenendo:
E, data l'arbitrarietà di x, nella (1) si può sostituire a'' al posto di x e nella (2) a' al posto di x ottenendo:
a'' ≤ a' a' ≤ a''
a' ≤ a''  a' = a'',
a' = a'',
per l'assioma RO-2) di relazione d'ordine.
2)-Il più piccolo elemento di un insieme
Sia (E, ≤) un insieme ordinato e si consideri un elemento a E; si dice che a è il più piccolo elemento di E per la relazione d'ordine ≤, se si verifica che
E; si dice che a è il più piccolo elemento di E per la relazione d'ordine ≤, se si verifica che
 x
x E : a ≤ x .
E : a ≤ x .
Se esiste questo elemento a, esso è unico.
Infatti, supponendo che esistano a' ed a'', entrambi i più piccoli elementi di E, relativamente ad a' ed a'' rispettivamente si ha:
(1) a' E
E 
 x
x E : a' ≤ x,
E : a' ≤ x,
(2) a'' E
E 
 x
x E : a'' ≤ x.
E : a'' ≤ x.
Poichè (1) e (2) valgono x
x E, data l'arbitrarietà di x, nella (1) si può sostituire a'' al posto di x e nella (2) a' al posto di x ottenendo:
E, data l'arbitrarietà di x, nella (1) si può sostituire a'' al posto di x e nella (2) a' al posto di x ottenendo:
a' ≤ a'' a'' ≤ a'
a'' ≤ a'  a' = a'',
a' = a'',
per l'assioma RO-2) di relazione d'ordine.
Nota bene
1)-Se esistono il più piccolo elemento ed il più grande elemento di un insieme per la relazione d'ordine ≤, chiamati rispettivamente a'' ed a'', risulta:
a' ≤ a''.
2)-Chiaramente, a prende il nome di più grande elemento di E per ≤, in quanto si può avere un'ulteriore relazione d'ordine ≤' per la quale il più grande elemento non è lo stesso del più grande elemento per ≤.
3)-Analogamente, a si dice il più piccolo elemento di E per ≤, in quanto si può avere un'ulteriore relazione d'ordine ≤' per la quale il più piccolo elemento non è lo stesso del più piccolo elemento per ≤.
4)-Se A è una parte di E e se
a A
A 
 x
x A : x ≤A a,
A : x ≤A a,
in cui
x ≤A a x ≤ a,
x ≤ a,
si dice che a è il più grande elemento di A per ≤; lo stesso ragionamento è valido per il più piccolo elemento di A per ≤.
3)-Maggiorante di una parte di un insieme - parte di un insieme maggiorata
Si consideri una parte A dell'insieme E, non vuota: si dice che a E è maggiorante di A se
E è maggiorante di A se
 b
b A : b ≤ a.
A : b ≤ a.
Se esiste almeno un maggiorante, la parte A si dice maggiorata.
4)-Minorante di una parte di un insieme - parte di un insieme minorata
Si consideri una parte A dell'insieme E, non vuota: si dice che a E è minorante di A se
E è minorante di A se
 b
b A : a ≤ b.
A : a ≤ b.
Se esiste almeno un minorante, la parte A si dice minorata.
Nota bene
Si consideri una parte A dell'insieme E, non vuota, e la relazione ≤A; si afferma che
(x ≤A y) (x, y)
(x, y) A X A, (x ≤ y),
A X A, (x ≤ y),
cioè si vuole dimostrare che
1) (x ≤A y) (y ≤A z)
(y ≤A z)  x ≤A z,
x ≤A z,
2) (x ≤A y) (y ≤A x)
(y ≤A x)  x = y.
x = y.
Dimostrazione 1).
(x ≤A y) (y ≤A z)
(y ≤A z)  (x, y)
(x, y) A X A, (x ≤ y)
A X A, (x ≤ y)  (y, z)
(y, z) A X A, (y ≤ z)
A X A, (y ≤ z)  (x, z)
(x, z) A X A, (x ≤ z)
A X A, (x ≤ z) 
 x ≤A z.
x ≤A z.
Dimostrazione 2).
(x ≤A y) (y ≤A x)
(y ≤A x)  (x, y)
(x, y) A X A, (x ≤ y)
A X A, (x ≤ y)  (y, x)
(y, x) A X A, (y ≤ x)
A X A, (y ≤ x)  x = y.
x = y.
Se (A, ≤A) è un insieme ordinato ed a A, le seguenti due proposizioni sono equivalenti:
A, le seguenti due proposizioni sono equivalenti:
1) a è il più piccolo elemento per ≤A,
2) a A
A  x
x A : x ≤A a.
A : x ≤A a.
5)-Estremo superiore
Si consideri una parte A dell'insieme E, non vuota: si chiama estremo superiore di A, se esiste, il più piccolo dei maggioranti.
Se s è maggiorante di A, ossia
 b
b A : b ≤ s,
A : b ≤ s,
affinchè s sia estremo superiore di A, cioè
s = sup(A),
devono verificarsi le seguenti due condizioni:
1) l'insieme dei maggioranti è non vuoto,
2) se t è un ulteriore maggiorante risulta s ≤ t.
Nel caso in cui l'insieme A si riduce agli elementi x ed y, cioè
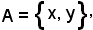
se esiste l'estremo superiore, esso si indica con
sup(x, y) = x v y.
5)-Estremo inferiore
Si consideri una parte A dell'insieme E, non vuota: si chiama estremo inferiore di A, se esiste, il più grande dei minoranti.
Se s è minorante di A, ossia
 b
b A : s ≤ b,
A : s ≤ b,
affinchè s sia estremo ineriore di A, cioè
s = inf(A),
devono verificarsi le seguenti due condizioni:
1) l'insieme dei minoranti è non vuoto,
2) se t è un ulteriore minorante risulta t ≤ s.
Nel caso in cui l'insieme A si riduce agli elementi x ed y, cioè
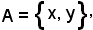
se esiste l'estremo inferiore, esso si indica con
inf(x, y) = x v y.
Nota bene
Ovviamente risulta che
inf(A) ≤ sup(A).
b) 1) x
x A : m ≤ x, 2) x
A : m ≤ x, 2) x E, m < x
E, m < x 
 a
a A
A  a < x.
a < x.
Relazioni di buon ordine
Si supponga che (E, ≤) sia un insieme ordinato; si dice che ≤ è una relazione di buon ordine sull'insieme E, quando ciascuna parte non vuota di E ha il più piccolo elemento per ≤, cioè:

Un insieme (E, ≤), in cui ≤ è una relazione di buon ordine, si chiama insieme ben ordinato.
Un esempio di insieme ben ordinato è dato dall'insieme dei numeri naturali (N, ≤).
Un esempio di insieme non ben ordinato è dato dall'insieme dei numeri reali.
Ovviamente, se (E, ≤) è un insieme ben ordinato, esso ha il più piccolo elemento per ≤; inoltre, se x ed y sono elementi di E, anche la parte formata dai soli elementi x ed y ha il più piccolo elemento per ≤, pertanto si può affermare che (E, ≤) è un insieme totalmente ordinato.
In generale non è vero il viceversa. Esempio tipico è (N, ≤).
Parte di un insieme ben ordinata
Una parte
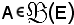
è ben ordinata per ≤, quando la relazione ≤A, indotta su A da ≤ è una relazione di buon ordine.
Si supponga che (E, ≤) sia un insieme ordinato; se una sua parte non vuota, ben ordinata per ≤, è dotata di estremo superiore, allora (E, ≤) si chiama insieme induttivo.
Sia (E, ≤) un insieme ordinato e si consideri un elemento a
Se esiste questo elemento a, esso è unico.
Infatti, supponendo che esistano a' ed a'', entrambi i più grandi elementi di E, relativamente ad a' ed a'' rispettivamente si ha:
(1) a'
(2) a''
Poichè (1) e (2) valgono
a'' ≤ a'
per l'assioma RO-2) di relazione d'ordine.
2)-Il più piccolo elemento di un insieme
Sia (E, ≤) un insieme ordinato e si consideri un elemento a
Se esiste questo elemento a, esso è unico.
Infatti, supponendo che esistano a' ed a'', entrambi i più piccoli elementi di E, relativamente ad a' ed a'' rispettivamente si ha:
(1) a'
(2) a''
Poichè (1) e (2) valgono
a' ≤ a''
per l'assioma RO-2) di relazione d'ordine.
Nota bene
1)-Se esistono il più piccolo elemento ed il più grande elemento di un insieme per la relazione d'ordine ≤, chiamati rispettivamente a'' ed a'', risulta:
a' ≤ a''.
2)-Chiaramente, a prende il nome di più grande elemento di E per ≤, in quanto si può avere un'ulteriore relazione d'ordine ≤' per la quale il più grande elemento non è lo stesso del più grande elemento per ≤.
3)-Analogamente, a si dice il più piccolo elemento di E per ≤, in quanto si può avere un'ulteriore relazione d'ordine ≤' per la quale il più piccolo elemento non è lo stesso del più piccolo elemento per ≤.
4)-Se A è una parte di E e se
a
in cui
x ≤A a
si dice che a è il più grande elemento di A per ≤; lo stesso ragionamento è valido per il più piccolo elemento di A per ≤.
3)-Maggiorante di una parte di un insieme - parte di un insieme maggiorata
Si consideri una parte A dell'insieme E, non vuota: si dice che a
Se esiste almeno un maggiorante, la parte A si dice maggiorata.
4)-Minorante di una parte di un insieme - parte di un insieme minorata
Si consideri una parte A dell'insieme E, non vuota: si dice che a
Se esiste almeno un minorante, la parte A si dice minorata.
Nota bene
Si consideri una parte A dell'insieme E, non vuota, e la relazione ≤A; si afferma che
(x ≤A y)
cioè si vuole dimostrare che
1) (x ≤A y)
2) (x ≤A y)
Dimostrazione 1).
(x ≤A y)
Dimostrazione 2).
(x ≤A y)
Se (A, ≤A) è un insieme ordinato ed a
1) a è il più piccolo elemento per ≤A,
2) a
5)-Estremo superiore
Si consideri una parte A dell'insieme E, non vuota: si chiama estremo superiore di A, se esiste, il più piccolo dei maggioranti.
Se s è maggiorante di A, ossia
affinchè s sia estremo superiore di A, cioè
s = sup(A),
devono verificarsi le seguenti due condizioni:
1) l'insieme dei maggioranti è non vuoto,
2) se t è un ulteriore maggiorante risulta s ≤ t.
Nel caso in cui l'insieme A si riduce agli elementi x ed y, cioè
se esiste l'estremo superiore, esso si indica con
sup(x, y) = x v y.
5)-Estremo inferiore
Si consideri una parte A dell'insieme E, non vuota: si chiama estremo inferiore di A, se esiste, il più grande dei minoranti.
Se s è minorante di A, ossia
affinchè s sia estremo ineriore di A, cioè
s = inf(A),
devono verificarsi le seguenti due condizioni:
1) l'insieme dei minoranti è non vuoto,
2) se t è un ulteriore minorante risulta t ≤ s.
Nel caso in cui l'insieme A si riduce agli elementi x ed y, cioè
se esiste l'estremo inferiore, esso si indica con
inf(x, y) = x v y.
Nota bene
Ovviamente risulta che
inf(A) ≤ sup(A).
Se A è una parte finita e non vuota dell'insieme E, totalmente ordinato dalla relazione ≤, ed m E, le seguenti due proposizioni sono equivalenti:
E, le seguenti due proposizioni sono equivalenti:
a) m = sup(A),
b) 1)  x
x A : x ≤ m, 2) x
A : x ≤ m, 2) x E, x < m
E, x < m 
 a
a A
A  x < a.
x < a.
Dimostrazione
a)  b)
b)
La a) esprime che m è il più piccolo dei maggioranti di A, per cui la 1) della b) è ovviamente vera.
Per dimostrare la 2) si ragiona per assurdo, cioè si suppone che
x E, x < m
E, x < m 
 a
a A : a ≤ x
A : a ≤ x
e quindi x, come m, risulta un maggiorante di A; ma, essendo x < m, si ha un maggiorante di A più piccolo di m, e ciò è assurdo per ipotesi. Siccome l'assurdo è derivato dall'aver supposto a ≤ x, si conclude che x < a.
b) a)
a)
La 1) della b) esprime che m è un maggiorante di A, si deve dimostrare che m è il più piccolo dei maggioranti di A.
Sia m' un altro maggiorante di A, per cui risulti:
 a
a A : a ≤ m',
A : a ≤ m',
si deve dimostrare che
m ≤ m'.
Ragionando per assurdo, si suppone che
m' < m,
e ciò contraddice l'ipotesi della 2) della b), poichè per essa si può asserire che
 a
a A
A  m' < a.
m' < a.
Ma ciò non è possibile, poichè m' è un maggiorante di A. Siccome l'assurdo è derivato dall'aver supposto m' ≤ m, si conclude che m ≤ m'. E' quindi dimostrato che m è il più piccolo dei maggioranti, e risulta m = sup(A).
e quindi x, come m, risulta un maggiorante di A; ma, essendo x < m, si ha un maggiorante di A più piccolo di m, e ciò è assurdo per ipotesi. Siccome l'assurdo è derivato dall'aver supposto a ≤ x, si conclude che x < a.
b)
La 1) della b) esprime che m è un maggiorante di A, si deve dimostrare che m è il più piccolo dei maggioranti di A.
Sia m' un altro maggiorante di A, per cui risulti:
si deve dimostrare che
m ≤ m'.
Ragionando per assurdo, si suppone che
m' < m,
e ciò contraddice l'ipotesi della 2) della b), poichè per essa si può asserire che
Ma ciò non è possibile, poichè m' è un maggiorante di A. Siccome l'assurdo è derivato dall'aver supposto m' ≤ m, si conclude che m ≤ m'. E' quindi dimostrato che m è il più piccolo dei maggioranti, e risulta m = sup(A).
In maniera del tutto analoga vale l'equivalenza delle seguenti due proposizioni:
a) m = inf(A),
b) 1)
Relazioni di buon ordine
Si supponga che (E, ≤) sia un insieme ordinato; si dice che ≤ è una relazione di buon ordine sull'insieme E, quando ciascuna parte non vuota di E ha il più piccolo elemento per ≤, cioè:

Un insieme (E, ≤), in cui ≤ è una relazione di buon ordine, si chiama insieme ben ordinato.
Un esempio di insieme ben ordinato è dato dall'insieme dei numeri naturali (N, ≤).
Un esempio di insieme non ben ordinato è dato dall'insieme dei numeri reali.
Ovviamente, se (E, ≤) è un insieme ben ordinato, esso ha il più piccolo elemento per ≤; inoltre, se x ed y sono elementi di E, anche la parte formata dai soli elementi x ed y ha il più piccolo elemento per ≤, pertanto si può affermare che (E, ≤) è un insieme totalmente ordinato.
In generale non è vero il viceversa. Esempio tipico è (N, ≤).
Parte di un insieme ben ordinata
Una parte
è ben ordinata per ≤, quando la relazione ≤A, indotta su A da ≤ è una relazione di buon ordine.
Si supponga che (E, ≤) sia un insieme ordinato; se una sua parte non vuota, ben ordinata per ≤, è dotata di estremo superiore, allora (E, ≤) si chiama insieme induttivo.