FUNZIONI E PROPRIETA' ---> INDICE
Si ricordano i seguenti concetti:
1)-Si chiama funzione, applicazione o trasformazione dell'insieme E nell'insieme F ogni applicazione f che abbia E come insieme di definizione ed F come insieme di variabilità, ed è indicata con
f : E  F,
F,
oppure con
f = (E, F, G),
in cui E, F e G sono, rispettivamente, l'insieme di definizione, l'insieme di variabilità ed il grafico, o la relazione funzionale dell'applicazione f.
2)-L'applicazione f : E F, dell'insieme E nell'insieme F, si dice surgettiva se f(E) = E, cioè:
F, dell'insieme E nell'insieme F, si dice surgettiva se f(E) = E, cioè:
(f surgettiva) (
( y
y F
F  x
x E
E  f(x) = y).
f(x) = y).
3)-L'applicazione f : E F, dell'insieme E nell'insieme F, si dice ingettiva se
F, dell'insieme E nell'insieme F, si dice ingettiva se
 x
x E
E  y
y E f(x) = f(y)
E f(x) = f(y)  x = y,
x = y,
cioè:
(f ingettiva) (
( x
x E
E  y
y E f(x) = f(y)
E f(x) = f(y)  x = y).
x = y).
4)-L'applicazione f : E F, dell'insieme E nell'insieme F, si dice bigettiva se è surgettiva e ingettiva, cioè:
F, dell'insieme E nell'insieme F, si dice bigettiva se è surgettiva e ingettiva, cioè:
(f bigettiva) (f surgettiva
(f surgettiva  f ingettiva).
f ingettiva).
5)-Siano assegnate due applicazioni:
f : E F e g : F
F e g : F  G.
G.
A partire da esse, si è considerata una nuova applicazione chiamata applicazione composta di f e g, tra elementi di E ed elementi di G, indicata con
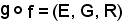 ,
,
che si legge g cerchietto f.Il valore che l'applicazione assume in x è il seguente:
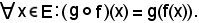
Proprietà delle applicazioni composte
Se
f : E F, g : F
F, g : F  G ed h : G
G ed h : G  H
H
sono tre applicazioni, si dimostra che:
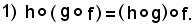
Infatti:
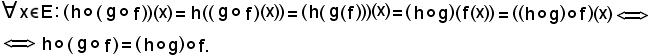
Se
f : E F
F
è un'applicazione dell'insieme E nell'insieme F, considerate le bigezioni canoniche, rispettivamente, dell'insieme E e dell'insieme F, cioè
iE : E E
E 
 x
x E: iE(x) = x ed iF : F
E: iE(x) = x ed iF : F  F
F 
 x
x E: iF(x) = x,
E: iF(x) = x,
si dimostra che:
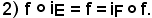
Infatti:
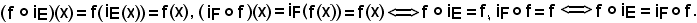
Siano
f : E F, g : F
F, g : F  G
G
due applicazioni e si indichi con h l'applicazione composta di f e g, cioè,

si dimostra che:
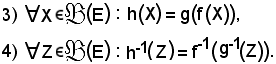
Dimostrazione 3): si considera un elemento
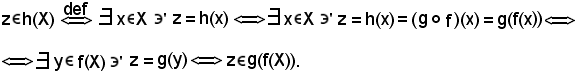
Dimostrazione 4): si considera un elemento
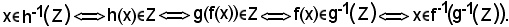
Caratterizzazione delle applicazioni surgettive1)-Sia
s : X  Y
Y
un'applicazione dell'insieme X nell'insieme Y, si dimostra che le seguenti tre proposizioni sono
equivalenti:
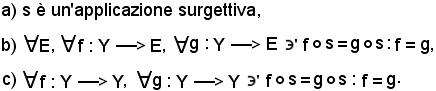
Cioè, si deve dimostrare che:
a) b)
b)  c)
c)  a).
a).
Dimostrazione a) b).
b).
Nell'ipotesi che s sia surgettiva, si deve dimostrare che
 y
y Y : f(y) = g(y).
Y : f(y) = g(y).
Allo scopo, si consideri l'elemento y Y, per la surgettività di s,
Y, per la surgettività di s,
 x
x X
X  s(x) = y,
s(x) = y,
quindi
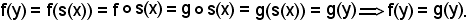
Dimostrazione b) c).
c).
E' immediata, in quanto essendo E un insieme qualsiasi, considerando nella b) E = Y, la c) è vera.
Dimostrazione c) a).
a).
Nell'ipotesi che sia vera la c), si deve dimostrare che s è surgettiva.
Supponiamo per assurdo che s non sia surgettiva, cioè
s(X) ≠ Y,
il che significa che non vi sono elementi di Y che hanno corrispondenza in X, quindi ha senso considerare il
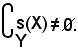
A tal punto si fissi l'attenzione su un arbitrario elemento
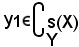
e su un elemento
y2 s(X),
s(X),
quindi
y1 ≠ y1
e si costruisca un'applicazione identica
f = iY : Y Y,
Y,
ed un'applicazione
g : Y Y
Y
così definita:
 y
y Y, y ≠ y1 : g(y) = y e
Y, y ≠ y1 : g(y) = y e  y1
y1 Y : g(y1) = y2.
Y : g(y1) = y2.
Per come sono state definite f e g, ovviamente
f ≠ g.
Si dimostra ora che:
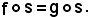
Allo scopo, basta dimostrare che le due applicazioni assumono lo stesso valore in x E:
E:
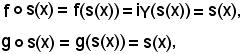
quindi
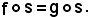
Siccome per ipotesi è vera la c), risulta
f = g
e ciò è assurdo, in quanto nello stesso tempo f è uguale e diversa da g.
Siccome l'assurdo è derivato dall'aver supposto f non surgettiva, si concludere che è tale.
2)-Siano assegnate le applicazioni f = (E, F, R) e g = (F, G S); per come sono state definite, è possibile considerare l'applicazione composta
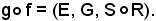
Si dimostra che se f e g sono applicazioni surgettive, anche l'applicazione composta è surgettiva, cioè:

Per dimostrare ciò, basta far vedere che

Infatti:
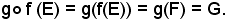
In tale dimostrazione si è tenuto conto che
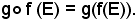
Infatti, poichè è noto che
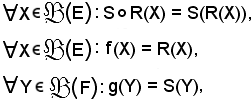
si ha
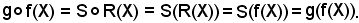
3)-Si considerino le applicazioni
pr1 : E X F  E
E 
 (x, y)
(x, y) E X F : pr1(x, y) = x,
E X F : pr1(x, y) = x,
pr2: E X F  E
E 
 (x, y)
(x, y) E X F : pr2(x, y) = y.
E X F : pr2(x, y) = y.
Si dimostra che pr1 e pr2, prima proiezione e seconda proiezione sono applicazioni surgettive.
Per quanto concerne la prima proiezione, si deve dimostrare che
 x
x E
E  z
z E X F
E X F  pr1(z) = x.
pr1(z) = x.
Infatti, considerato un elemento x E d un elemento y
E d un elemento y F, risulta (x, y)
F, risulta (x, y) E X F,
E X F,
quindi
pr1(x, y) = x.
Ponendo (x, y) = z, si ha:
pr1(z) = x.
Per la seconda proiezione la dimostrazione è analoga, cioè si deve dimostrare che:
 x
x E
E  z
z E X F
E X F  pr2(z) = x.
pr2(z) = x.
Infatti, considerato un elemento x E d un elemento y
E d un elemento y F, risulta (x, y)
F, risulta (x, y) E X F, quindi
E X F, quindi
pr2(x, y) = y.
Ponendo (x, y) = z, si ha:
pr2(z) = x.
Caratterizzazione delle applicazioni ingettive1)-Sia
s : X Y
Y
un'applicazione dell'insieme X nell'insieme Y, si dimostra che le seguenti tre proposizioni sono equivalenti:
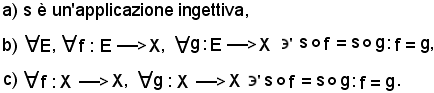
Cioè, si deve dimostrare che:
a) b)
b)  c)
c)  a),
a),
dopo aver osservato che nella proposizione b) le applicazioni composte rispettivamente di s ed f e di s e g hanno E come insieme di partenza ed Y come insieme di arrivo, cioè

mentre nella c) le applicazioni composte rispettivamente di s ed f e di s e g hanno X come insieme di partenza ed Y come insieme di arrivo, cioè

Dimostrazione a) b).
b).
Nell'ipotesi che s sia ingettiva, si deve dimostrare che
 x
x E : f(x) = g(x).
E : f(x) = g(x).
Allo scopo, si consideri l'elemento x E, per l'ingettività di s, si ha:
E, per l'ingettività di s, si ha:
s(f(x)) = s(g(x)) f(x) = g(x)
f(x) = g(x)  f = g.
f = g.
Dimostrazione b) c).
c).
E' immediata, in quanto essendo E un insieme qualsiasi, considerando nella b) X = E, la c) è vera.
Dimostrazione c) a).
a).
Nell'ipotesi che sia vera la c), si deve dimostrare che s è ingettiva,
cioè
 x1
x1 X,
X, x2
x2 X, s(x1) = s(x2)
X, s(x1) = s(x2)  x1 = x2.
x1 = x2.
Supponiamo per assurdo che s non lo sia, cioè
 x1
x1 X,
X, x2
x2 X, s(x1) = s(x2)
X, s(x1) = s(x2)  x1 ≠ x2.
x1 ≠ x2.
A tal punto si costruisca un'applicazione identica
f = iX : X X,
X,
ed un'applicazione
g : X X
X
così definita:
 x
x X, x ≠ x1, x ≠ x2, g(x) = x,
X, x ≠ x1, x ≠ x2, g(x) = x,
 x
x X, x = x1, g(x) = x2,
X, x = x1, g(x) = x2,
 x
x X, x = x2, g(x) = x1.
X, x = x2, g(x) = x1.
Per come sono state definite f e g, ovviamente
f ≠ g.
Si dimostra ora che: 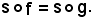
Allo scopo, basta dimostrare che le due applicazioni assumono lo stesso valore in x X, cioè:
X, cioè:
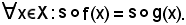
Infatti, se x = x1, si ha:
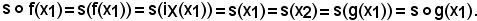
Se x = x2, si ha:
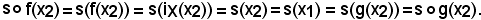
Se x ≠ x1, x ≠ x2, si ha:
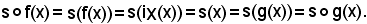
Nei tre casi visti, si ha:
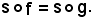
Siccome per ipotesi è vera la c), risulta
e ciò è assurdo, in quanto nello stesso tempo f è uguale e diversa da g.
Siccome l'assurdo è derivato dall'aver supposto f non ingettiva, si conclude che è tale.
2)-Siano assegnate le applicazioni f = (E, F, R) e g (F, G S); per come sono state definite, è possibile considerare l'applicazione composta
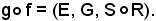
Si dimostra che se f e g sono applicazioni ingettive, anche l'applicazione composta è ingettiva, cioè:

Per dimostrare ciò, basta far vedere che
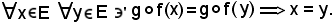
Infatti, siccome
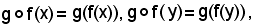
essendo
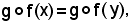
si ha:
g(f(x)) = g(f(x)).
Definizione di applicazione invertibile
Sia f un'applicazione di E in F di grafico G, cioè
f = (E, F, G),
e se esiste la sua inversa, univocamente determinata, g = (F, E, G-1), che gode delle seguenti proprietà:
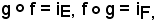
f si dice invertibile.
In altri termini:
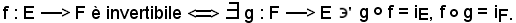
Caratterizzazione delle applicazioni invertibili
Sia f un'applicazione di E in F di grafico R, cioè
f = (E, F, R),
e sia g = (F, E, R-1) la sua inversa; si dimostra che:
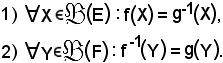
Dimostrazione 1)
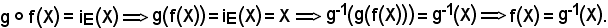
Dimostrazione 2)
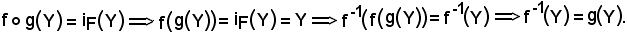
Caratterizzazione delle applicazioni bigettive1)-Si dimostra che le seguenti tre proposizioni sono equivalenti:
a) f : E F è invertibile,
F è invertibile,
b) f è bigettiva,
c) G-1è una relazione funzionale fra elementi di F ed elementi di E.
Cioè, si deve dimostrare che:
a) b)
b)  c)
c)  a).
a).
Dimostrazione a) b).
b).
Nell'ipotesi che f sia invertibile, si deve dimostrare che è bigettiva.
Si dimostra prima che f è surgettiva, cioè che
 y
y F
F  x
x E
E  f(x) = y.
f(x) = y.
Essendo f invertibile per ipotesi, si ha
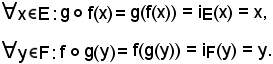
Inoltre, posto
x = g(y),
si ha:
y = iF(y) = f(g(x)) = f(x).
Si dimostra ora che
(f ingettiva) (
( x
x E
E  x'
x' E f(x) = f(x')
E f(x) = f(x')  x = x').
x = x').
Allo scopo, si considerano i due elementi
x E, x'
E, x' E
E  f(x) = f(x'),
f(x) = f(x'),
si deve dimostrare che
x = x'.
Infatti, tenendo conto che f è invertibile, si ha:
x = iE(x) = g(f(x) = g(f(x') = iE(x') x = x'.
x = x'.
Avendo dimostrato che f è surgettiva ed ingettiva, per definizione è bigettiva.
Dimostrazione b) c).
c).
Per definizione è noto che:
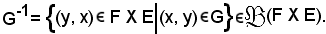
Si deve dimostrare che G-1 è una relazione funzionale fra elementi di F ed elementi di E, cioè
 y
y F : G-1≠
F : G-1≠
e si riduce ad un unico elemento.
Infatti, essendo per ipotesi bigettiva, per la sua surgettività
 y
y F
F  x
x E
E  f(x) = y
f(x) = y  (x, y)
(x, y) G
G  (y, x)
(y, x) G-1
G-1 x
x G-1(y)
G-1(y)  G-1(y)≠
G-1(y)≠ .
.
Si dimostra ora che G-1 si riduce ad un solo elemento; pertanto se ne considerano due e si dimostra che essi coincidono.
Siano essi
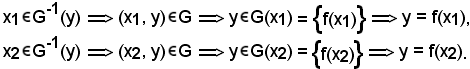
Poichè
f(x1) = f(x2),
data l'ingettività di f, risulta
x1 = x2.
E' quindi dimostrato che G-1 è una relazione funzionale.
Prima di dimostrare che c) a), si osserva quanto segue:
a), si osserva quanto segue:
si consideri una relazione G e la sua reciproca G-1.
Essendo
G E X F e G-1
E X F e G-1 F X E,
F X E,
si possono considerare le relazioni composte
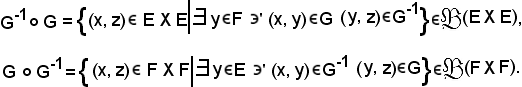
Si dimostra che:

Dimostrazione 1).
Si considera una coppia ordinata
(x, x) ΔE
ΔE  x
x E
E
e quindi
G(x) ≠ ,
,
allora si può prendere un elemento
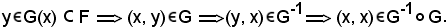
Dimostrazione 2).
G-1(x)≠ ,
,
allora si può prendere un elemento
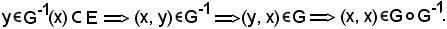
Dimostrazione 3).Si considera una coppia ordinata
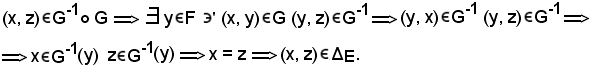
1)-Si chiama funzione, applicazione o trasformazione dell'insieme E nell'insieme F ogni applicazione f che abbia E come insieme di definizione ed F come insieme di variabilità, ed è indicata con
oppure con
f = (E, F, G),
in cui E, F e G sono, rispettivamente, l'insieme di definizione, l'insieme di variabilità ed il grafico, o la relazione funzionale dell'applicazione f.
2)-L'applicazione f : E
(f surgettiva)
3)-L'applicazione f : E
cioè:
(f ingettiva)
4)-L'applicazione f : E
(f bigettiva)
5)-Siano assegnate due applicazioni:
f : E
A partire da esse, si è considerata una nuova applicazione chiamata applicazione composta di f e g, tra elementi di E ed elementi di G, indicata con
che si legge g cerchietto f.
Proprietà delle applicazioni composte
Se
f : E
sono tre applicazioni, si dimostra che:
Infatti:
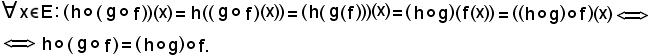
Se
f : E
è un'applicazione dell'insieme E nell'insieme F, considerate le bigezioni canoniche, rispettivamente, dell'insieme E e dell'insieme F, cioè
iE : E
si dimostra che:
Infatti:
Siano
f : E
due applicazioni e si indichi con h l'applicazione composta di f e g, cioè,
si dimostra che:
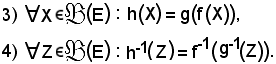
Dimostrazione 3): si considera un elemento
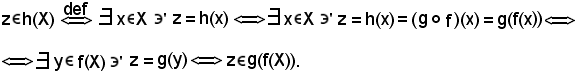
Dimostrazione 4): si considera un elemento
Caratterizzazione delle applicazioni surgettive
un'applicazione dell'insieme X nell'insieme Y, si dimostra che le seguenti tre proposizioni sono
equivalenti:
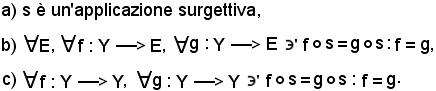
Cioè, si deve dimostrare che:
a)
Dimostrazione a)
Nell'ipotesi che s sia surgettiva, si deve dimostrare che
Allo scopo, si consideri l'elemento y
quindi
Dimostrazione b)
E' immediata, in quanto essendo E un insieme qualsiasi, considerando nella b) E = Y, la c) è vera.
Dimostrazione c)
Nell'ipotesi che sia vera la c), si deve dimostrare che s è surgettiva.
Supponiamo per assurdo che s non sia surgettiva, cioè
s(X) ≠ Y,
il che significa che non vi sono elementi di Y che hanno corrispondenza in X, quindi ha senso considerare il
A tal punto si fissi l'attenzione su un arbitrario elemento
e su un elemento
y2
quindi
y1 ≠ y1
e si costruisca un'applicazione identica
f = iY : Y
ed un'applicazione
g : Y
così definita:
Per come sono state definite f e g, ovviamente
Si dimostra ora che:
Allo scopo, basta dimostrare che le due applicazioni assumono lo stesso valore in x
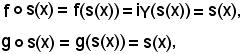
quindi
Siccome per ipotesi è vera la c), risulta
f = g
e ciò è assurdo, in quanto nello stesso tempo f è uguale e diversa da g.
Siccome l'assurdo è derivato dall'aver supposto f non surgettiva, si concludere che è tale.
2)-Siano assegnate le applicazioni f = (E, F, R) e g = (F, G S); per come sono state definite, è possibile considerare l'applicazione composta
Si dimostra che se f e g sono applicazioni surgettive, anche l'applicazione composta è surgettiva, cioè:
Per dimostrare ciò, basta far vedere che
Infatti:
In tale dimostrazione si è tenuto conto che
Infatti, poichè è noto che
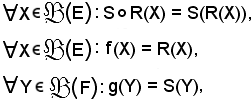
si ha
3)-Si considerino le applicazioni
Si dimostra che pr1 e pr2, prima proiezione e seconda proiezione sono applicazioni surgettive.
Per quanto concerne la prima proiezione, si deve dimostrare che
Infatti, considerato un elemento x
quindi
pr1(x, y) = x.
Ponendo (x, y) = z, si ha:
pr1(z) = x.
Per la seconda proiezione la dimostrazione è analoga, cioè si deve dimostrare che:
Infatti, considerato un elemento x
pr2(x, y) = y.
Ponendo (x, y) = z, si ha:
pr2(z) = x.
Caratterizzazione delle applicazioni ingettive
s : X
un'applicazione dell'insieme X nell'insieme Y, si dimostra che le seguenti tre proposizioni sono equivalenti:
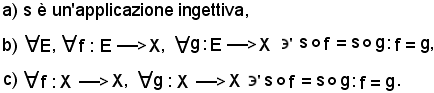
Cioè, si deve dimostrare che:
a)
dopo aver osservato che nella proposizione b) le applicazioni composte rispettivamente di s ed f e di s e g hanno E come insieme di partenza ed Y come insieme di arrivo, cioè
mentre nella c) le applicazioni composte rispettivamente di s ed f e di s e g hanno X come insieme di partenza ed Y come insieme di arrivo, cioè
Dimostrazione a)
Nell'ipotesi che s sia ingettiva, si deve dimostrare che
Allo scopo, si consideri l'elemento x
s(f(x)) = s(g(x))
Dimostrazione b)
E' immediata, in quanto essendo E un insieme qualsiasi, considerando nella b) X = E, la c) è vera.
Dimostrazione c)
Nell'ipotesi che sia vera la c), si deve dimostrare che s è ingettiva,
cioè
Supponiamo per assurdo che s non lo sia, cioè
A tal punto si costruisca un'applicazione identica
f = iX : X
ed un'applicazione
g : X
così definita:
Per come sono state definite f e g, ovviamente
f ≠ g.
Si dimostra ora che:
Allo scopo, basta dimostrare che le due applicazioni assumono lo stesso valore in x
Infatti, se x = x1, si ha:
Se x = x2, si ha:
Se x ≠ x1, x ≠ x2, si ha:
Nei tre casi visti, si ha:
Siccome per ipotesi è vera la c), risulta
f = g
e ciò è assurdo, in quanto nello stesso tempo f è uguale e diversa da g.
Siccome l'assurdo è derivato dall'aver supposto f non ingettiva, si conclude che è tale.
2)-Siano assegnate le applicazioni f = (E, F, R) e g (F, G S); per come sono state definite, è possibile considerare l'applicazione composta
Si dimostra che se f e g sono applicazioni ingettive, anche l'applicazione composta è ingettiva, cioè:
Per dimostrare ciò, basta far vedere che
Infatti, siccome
essendo
g(f(x)) = g(f(x)).
Ponendo
f(x) = u1 ed f(y) = u2,
si ha:
g(u1) = g(u1) u1 = u2
u1 = u2  f(x) = f(y)
f(x) = f(y)  x = y.
x = y.
3)-Siano f = (E, F, R) un'applicazione di E in F di grafico R e g = (E, E X F, R') un'applicazione di E in E X F di grafico R', ove
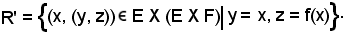
Si dimostra che l'applicazione g è ingettiva, cioè che
 x
x E
E  y
y E
E  g(x) = g(y)
g(x) = g(y)  x = y.
x = y.
Infatti,
4)-Si consideri la prima proiezione
pr1 : E X F  E
E 
 (x, y)
(x, y) E X F : pr1(x, y) = x,
E X F : pr1(x, y) = x,
si dimostra che la prima proiezione è ingettiva se l'insieme F si riduce ad un unico elemento, cioè:
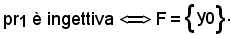
Supponendo per ipotesi che pr1 sia ingettiva, si prendano due elementi y1 F, y2
F, y2 F ed un elemento x
F ed un elemento x E. Si considerano ora le coppie ordinate (x, y1) e (x, y2) e, siccome per ipotesi pr1 è ingettiva, si ha:
E. Si considerano ora le coppie ordinate (x, y1) e (x, y2) e, siccome per ipotesi pr1 è ingettiva, si ha:
pr1(x, y1) = x e pr1(x, y2) = x pr1(x, y1) = pr1(x, y2)
pr1(x, y1) = pr1(x, y2)  (x, y1) = (x, y2)
(x, y1) = (x, y2)  y1 = y2 = y0.
y1 = y2 = y0.
E' quindi dimostrato che l'insieme F è formato dall'unico elemento y0.
Viceversa, supponendo che l'insieme F sia formato dall'unico elemento y0, la prima proiezione diventa
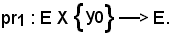
Si deve dimostrare che pr1 è ingettiva, cioè:
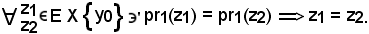
Infatti, presi
z1 = (x1, y0) e z2 = (x2 ,y0),
essendo
pr1(z1) = pr1(z2) pr1(x1, y0) = pr1(x2, y0)
pr1(x1, y0) = pr1(x2, y0)  x1 = x2,
x1 = x2,
f(x) = u1 ed f(y) = u2,
si ha:
g(u1) = g(u1)
3)-Siano f = (E, F, R) un'applicazione di E in F di grafico R e g = (E, E X F, R') un'applicazione di E in E X F di grafico R', ove
Si dimostra che l'applicazione g è ingettiva, cioè che
Infatti,
g(x) = (x, f(x)), g(y) = (y, f(y))  (x, f(x)) = (y, f(y))
(x, f(x)) = (y, f(y))  x = y.
x = y.
4)-Si consideri la prima proiezione
si dimostra che la prima proiezione è ingettiva se l'insieme F si riduce ad un unico elemento, cioè:
Supponendo per ipotesi che pr1 sia ingettiva, si prendano due elementi y1
pr1(x, y1) = x e pr1(x, y2) = x
E' quindi dimostrato che l'insieme F è formato dall'unico elemento y0.
Viceversa, supponendo che l'insieme F sia formato dall'unico elemento y0, la prima proiezione diventa
Si deve dimostrare che pr1 è ingettiva, cioè:
Infatti, presi
z1 = (x1, y0) e z2 = (x2 ,y0),
essendo
pr1(z1) = pr1(z2)
si ha
z1 = z2.
Definizione di applicazione invertibile
Sia f un'applicazione di E in F di grafico G, cioè
f = (E, F, G),
e se esiste la sua inversa, univocamente determinata, g = (F, E, G-1), che gode delle seguenti proprietà:
f si dice invertibile.
In altri termini:
Caratterizzazione delle applicazioni invertibili
Sia f un'applicazione di E in F di grafico R, cioè
f = (E, F, R),
e sia g = (F, E, R-1) la sua inversa; si dimostra che:
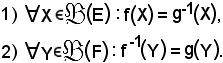
Dimostrazione 1)
Dimostrazione 2)
Caratterizzazione delle applicazioni bigettive
a) f : E
b) f è bigettiva,
c) G-1è una relazione funzionale fra elementi di F ed elementi di E.
Cioè, si deve dimostrare che:
a)
Dimostrazione a)
Nell'ipotesi che f sia invertibile, si deve dimostrare che è bigettiva.
Si dimostra prima che f è surgettiva, cioè che
Essendo f invertibile per ipotesi, si ha
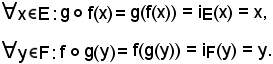
Inoltre, posto
x = g(y),
si ha:
y = iF(y) = f(g(x)) = f(x).
Si dimostra ora che
(f ingettiva)
Allo scopo, si considerano i due elementi
x
si deve dimostrare che
x = x'.
Infatti, tenendo conto che f è invertibile, si ha:
x = iE(x) = g(f(x) = g(f(x') = iE(x')
Avendo dimostrato che f è surgettiva ed ingettiva, per definizione è bigettiva.
Dimostrazione b)
Per definizione è noto che:
Si deve dimostrare che G-1 è una relazione funzionale fra elementi di F ed elementi di E, cioè
e si riduce ad un unico elemento.
Infatti, essendo per ipotesi bigettiva, per la sua surgettività
Si dimostra ora che G-1 si riduce ad un solo elemento; pertanto se ne considerano due e si dimostra che essi coincidono.
Siano essi
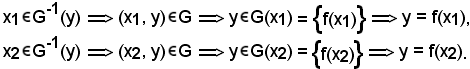
Poichè
f(x1) = f(x2),
data l'ingettività di f, risulta
x1 = x2.
E' quindi dimostrato che G-1 è una relazione funzionale.
Prima di dimostrare che c)
si consideri una relazione G e la sua reciproca G-1.
Essendo
G
si possono considerare le relazioni composte
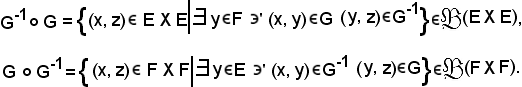
Si dimostra che:

Dimostrazione 1).
Si considera una coppia ordinata
(x, x)
e quindi
G(x) ≠
allora si può prendere un elemento
Dimostrazione 2).
Si considera una coppia ordinata
(x, x) ΔF
ΔF  x
x F
F
e quindi
(x, x)
e quindi
G-1(x)≠
allora si può prendere un elemento
Dimostrazione 3).
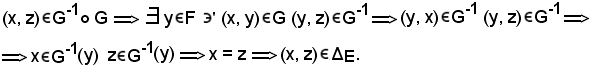
Dimostrazione 4).
Si considera una coppia ordinata
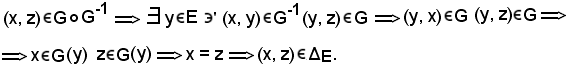
Dimostrazione c) a).
a).
Per ipotesi G-1è una relazione funzionale fra elementi di F ed elementi di E, cioè
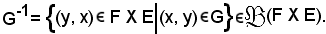
Si considera ora l'applicazione
g = (F, E, G-1)
e si dimostra che è l'inversa dell'applicazione f, cioè che
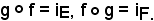
Infatti, siccome
iE = (E, E, ΔE),
affinchè risulti
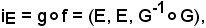
dev'essere
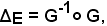
e ciò è vero per 1) e 3) della premessa.
Si considera una coppia ordinata
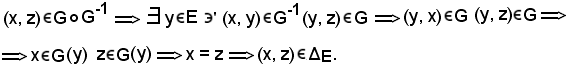
Dimostrazione c)
Per ipotesi G-1è una relazione funzionale fra elementi di F ed elementi di E, cioè
Si considera ora l'applicazione
g = (F, E, G-1)
e si dimostra che è l'inversa dell'applicazione f, cioè che
Infatti, siccome
iE = (E, E, ΔE),
affinchè risulti
dev'essere
e ciò è vero per 1) e 3) della premessa.
Infatti, siccome
iF = (F, F, ΔF),
affinchè risulti
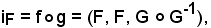
dev'essere
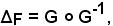
e ciò è vero per 2) e 4) della premessa.
2)-Siano f' : E F ed f'' : F
F ed f'' : F  G applicazioni bigettive e si consideri l'applicazione composta
G applicazioni bigettive e si consideri l'applicazione composta 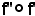 : E
: E  G, anch'essa bigettiva, della quale l'applicazione inversa è l'applicazione composta
G, anch'essa bigettiva, della quale l'applicazione inversa è l'applicazione composta 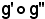 dell'applicazione g'' inversa di f'' e di g' inversa di f'; si deve dimostrare che:
dell'applicazione g'' inversa di f'' e di g' inversa di f'; si deve dimostrare che:
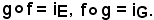
Posto
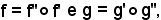
e ricordando che
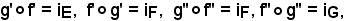
si ha:
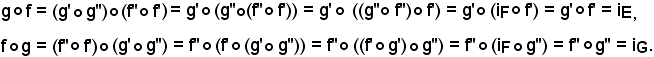
Applicazione inversa di una bigezione
Siccome ad ogni applicazione bigettiva si può associare l'applicazione inversa, si dimostrano i seguenti due lemmi, che saranno d'ausilio alla dimostrazione dell'equivalenza di due proposizioni seguenti.
Lemma 1
Se f : E F è un'applicazione dell'insieme E nell'insieme F, g' : F
F è un'applicazione dell'insieme E nell'insieme F, g' : F  E e g'' : F
E e g'' : F  E due applicazioni dell'insieme F nell'insieme E, iE ed iF le bigezioni canoniche di E in F, allora risulta:
E due applicazioni dell'insieme F nell'insieme E, iE ed iF le bigezioni canoniche di E in F, allora risulta:

e si ha
g' = g''.
Dimostrazione:
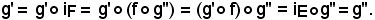
Lemma 2
Se f : E F è un'applicazione dell'insieme E nell'insieme F e se esiste un'applicazione g : F
F è un'applicazione dell'insieme E nell'insieme F e se esiste un'applicazione g : F  E tale che
E tale che
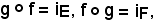
allora f è una bigezione di E in F, g è una bigezione di F in E e non esiste più di una bigezione di F in E che verifica le condizioni (1).
Dimostrazione
Sia y F e posto x = g(y), per la seconda delle condizioni (1), si ha:
F e posto x = g(y), per la seconda delle condizioni (1), si ha:
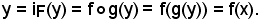
Essendo x E, f risulta surgettiva; inoltre considerati
E, f risulta surgettiva; inoltre considerati
x' E, x''
E, x'' E e f(x') = f(x''),
E e f(x') = f(x''),
per la prima delle condizioni (1), risulta:
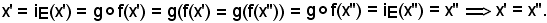
Quindi f, oltre ad essere surgettiva, è anche ingettiva, cioè una bigezione di E in F.
Scambiando ora l'ufficio di f con quello di g, dalle (1) segue che g è una bigezione di F in E.
Infatti, sia x E e posto y = f(x), per la prima delle condizioni (1), si ha:
E e posto y = f(x), per la prima delle condizioni (1), si ha:
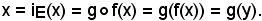
Essendo y F, g risulta surgettiva; inoltre considerati
F, g risulta surgettiva; inoltre considerati
y' E, y''
E, y'' E e g(y') = g(y''),
E e g(y') = g(y''),
per la seconda delle condizioni (1), risulta:
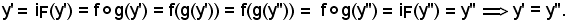
Quindi g, oltre ad essere surgettiva, è anche ingettiva, cioè una bigezione di F in E e, per il Lemma 1 è unica.
Sia f : E F un'applicazione bigettiva dell'insieme E nell'insieme F; l'unica applicazione bigettiva g : F
F un'applicazione bigettiva dell'insieme E nell'insieme F; l'unica applicazione bigettiva g : F  E, inversa di f, tale che
E, inversa di f, tale che
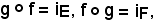
si chiama bigezione di f.
Quindi le applicazioni invertibili ammettono una ed una sola applicazione inversa.
Pertanto, si dimostra che le due seguemti proposizioni sono equivalenti:
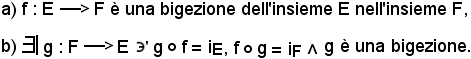
Dimostrazione a) b).
b).
Nell'ipotesi che f sia bigettiva, sia f = (E, F, G) l'applicazione di E in F avente grafico G.
Sia
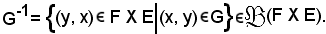
Si stabilisce ora che
 y
y F : G-1(y) = f-1(y).
F : G-1(y) = f-1(y).
Infatti,
x G-1(y)
G-1(y)  (y, x)
(y, x) G-1
G-1 (x, y)
(x, y) G
G  x
x E, y
E, y G(x)
G(x)  x
x E, y = f(x)
E, y = f(x)  x
x f-1(y).
f-1(y).
Poichè f è una bigezione, come è stato dimostrato, equivale a dire che G-1 è una relazione funzionale fra elementi di F ed elementi di E, quindi g = (F, E, G-1) è un'applicazione di F in E avente grafico G-1.
Si stabilisce ora che:
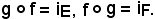
Infatti, sia x E e posto y = f(x), si ha:
E e posto y = f(x), si ha:
(x, y) G
G  (y, x)
(y, x) G-1
G-1 x = g(y),
x = g(y),
da cui
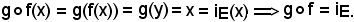
Analogamente, sia y F e posto X = g(y), si ha:
F e posto X = g(y), si ha:
(y, x) G-1
G-1 (x, y)
(x, y) G
G  y = f(x),
y = f(x),
da cui
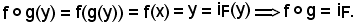
Avendo stabilito le due condizioni suddette, inoltre, per il Lemma 2 segue l'unicità e la bigettività di g, è dimostrato che a) b).
b).
Dimostrazione b) a).
a).
E' conseguenza del Lemma 2.
Ulteriori caratterizzazioni
1)-Si consideri l'applicazione
tx1x2 : E E,
E,
in cui
x1 E, x2
E, x2 E ed x1 ≠ x2,
E ed x1 ≠ x2,
così definita:
 x
x E:
E:
tx1x2(z) = z se z ≠ x1, z ≠ x2,
tx1x2(z) = x2 se z = x1,
tx1x2(z) = x1 se z = x2.
Si dimostra che tx1x2 è un'applicazione involutoria, cioè che tx1x2 deve avere se stessa per inversa. Esprimendo ciò simbolicamente, si deve dimostrare che:
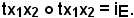
Infatti,
iF = (F, F, ΔF),
affinchè risulti
dev'essere
e ciò è vero per 2) e 4) della premessa.
2)-Siano f' : E
Posto
e ricordando che
si ha:
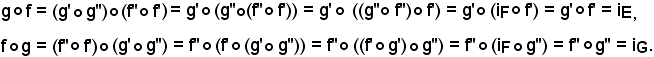
Applicazione inversa di una bigezione
Siccome ad ogni applicazione bigettiva si può associare l'applicazione inversa, si dimostrano i seguenti due lemmi, che saranno d'ausilio alla dimostrazione dell'equivalenza di due proposizioni seguenti.
Lemma 1
Se f : E
e si ha
g' = g''.
Dimostrazione:
Lemma 2
Se f : E
allora f è una bigezione di E in F, g è una bigezione di F in E e non esiste più di una bigezione di F in E che verifica le condizioni (1).
Dimostrazione
Sia y
Essendo x
x'
per la prima delle condizioni (1), risulta:
Quindi f, oltre ad essere surgettiva, è anche ingettiva, cioè una bigezione di E in F.
Scambiando ora l'ufficio di f con quello di g, dalle (1) segue che g è una bigezione di F in E.
Infatti, sia x
Essendo y
per la seconda delle condizioni (1), risulta:
Quindi g, oltre ad essere surgettiva, è anche ingettiva, cioè una bigezione di F in E e, per il Lemma 1 è unica.
Sia f : E
si chiama bigezione di f.
Quindi le applicazioni invertibili ammettono una ed una sola applicazione inversa.
Pertanto, si dimostra che le due seguemti proposizioni sono equivalenti:
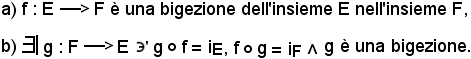
Dimostrazione a)
Nell'ipotesi che f sia bigettiva, sia f = (E, F, G) l'applicazione di E in F avente grafico G.
Sia
Si stabilisce ora che
Infatti,
x
Poichè f è una bigezione, come è stato dimostrato, equivale a dire che G-1 è una relazione funzionale fra elementi di F ed elementi di E, quindi g = (F, E, G-1) è un'applicazione di F in E avente grafico G-1.
Si stabilisce ora che:
Infatti, sia x
(x, y)
da cui
Analogamente, sia y
(y, x)
da cui
Avendo stabilito le due condizioni suddette, inoltre, per il Lemma 2 segue l'unicità e la bigettività di g, è dimostrato che a)
Dimostrazione b)
E' conseguenza del Lemma 2.
Ulteriori caratterizzazioni
1)-Si consideri l'applicazione
tx1x2 : E
in cui
x1
così definita:
tx1x2(z) = z se z ≠ x1, z ≠ x2,
tx1x2(z) = x2 se z = x1,
tx1x2(z) = x1 se z = x2.
Si dimostra che tx1x2 è un'applicazione involutoria, cioè che tx1x2 deve avere se stessa per inversa. Esprimendo ciò simbolicamente, si deve dimostrare che:
Infatti,
se z ≠ x1, z ≠ x2, si ha
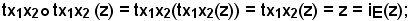
se z = x1, si ha
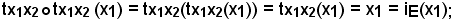
se z = x2, si ha
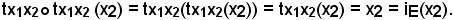
E' stato quindi dimostrato che tx1x2 è un'applicazione involutoria e si chiama trasposizione relativa agli elementi x1 ed x2 dell'insieme E.
Sotto forma di terna ordinata tx1x2 = (E, E, Rx1x2) ed il grafico ad essa relativa è:
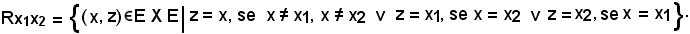
2)-Si supponga di avere i due insiemi prodotto EXF ed FXE e si considerino le applicazioni
tEXF : EXF FXE
FXE 
 (x, y)
(x, y) EXF: tEXF(x, y) = (y, x), cioè (y, x)
EXF: tEXF(x, y) = (y, x), cioè (y, x) FXE,
FXE,
tFXE : FXE EXF
EXF 
 (y, x)
(y, x) FXE: tFXE(y, x) = (x, y), cioè (x, y)
FXE: tFXE(y, x) = (x, y), cioè (x, y) EXF.
EXF.
Si dimostra che tEXF è invertibile, cioè che
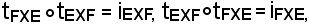
essendo
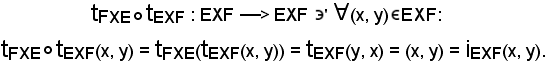
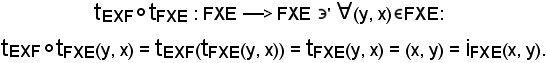
L'applicazione tEXF è quindi invertibile ed è chiamata applicazione trasposizione.
Se in particolare F = E, l'applicazione
tEXE : EXE EXE
EXE 
 (x, y)
(x, y) EXE:
EXE:

è involutoria, bigettiva ed è permutazione di E in E. Quindi,
tEXE TEXE
TEXE
cioè
TE = EE.
se z = x1, si ha
se z = x2, si ha
E' stato quindi dimostrato che tx1x2 è un'applicazione involutoria e si chiama trasposizione relativa agli elementi x1 ed x2 dell'insieme E.
Sotto forma di terna ordinata tx1x2 = (E, E, Rx1x2) ed il grafico ad essa relativa è:
2)-Si supponga di avere i due insiemi prodotto EXF ed FXE e si considerino le applicazioni
tEXF : EXF
tFXE : FXE
Si dimostra che tEXF è invertibile, cioè che
essendo
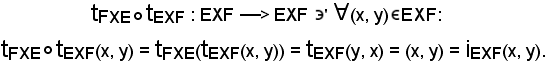
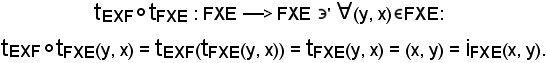
L'applicazione tEXF è quindi invertibile ed è chiamata applicazione trasposizione.
Se in particolare F = E, l'applicazione
tEXE : EXE
è involutoria, bigettiva ed è permutazione di E in E. Quindi,
tEXE
cioè
TE = EE.