FUNZIONI PARTICOLARI ---> INDICE
Siano (E, ≤), (E', ≤') due insiemi ordinati e, considerata la seguente applicazione
f : E E',
E',
f è crescente o isotona
 x
x E,
E,  y
y E, x < y : f(x) ≤' f(y).
E, x < y : f(x) ≤' f(y).
Nota bene
Se x = y, risulta f(x) = f(y).
f è decrescente o antitona
 x
x E,
E,  y
y E, x < y : f(y) ≤' f(x).
E, x < y : f(y) ≤' f(x).
f è strettamente crescente
 x
x E,
E,  y
y E, x < y : f(x) <' f(y).
E, x < y : f(x) <' f(y).
f è strettamente decrescente
 x
x E,
E,  y
y E, x < y : f(y) <' f(x).
E, x < y : f(y) <' f(x).
Se l'applicazione f rispecchia uno dei quattro casi suddetti, si chiama monotòna.
Si dimostra ora che:
-ogni applicazione costante di E in E' è un'applicazione crescente e decrescente.
Infatti, sia
f : E E'
E'
un'applicazione costante, cioè, fissato un elemento
a E',
E',  x
x E : f(x) = a.
E : f(x) = a.
Si verifica prima che f è crescente, cioè che
 x
x E,
E,  y
y E, x < y : f(x) ≤' f(y).
E, x < y : f(x) ≤' f(y).
Infatti risulta:
f(x) = a ≤' a' = f(y) f(x) ≤' f(y).
f(x) ≤' f(y).
Infine si verifica che f è decrescente, cioè che
 x
x E,
E,  y
y E, x < y : f(y) ≤' f(x).
E, x < y : f(y) ≤' f(x).
Infatti risulta:
f(x) = a ≤' a' = f(y) f(x) ≤' f(y).
f(x) ≤' f(y).
In generale, un'applicazione crescente e decrescente non è costante, però, con altre ipotesi lo è; pertanto si dimostra che:
(E, ≤) filtrante superiormente, crescente e decrescente f : E
f : E  E' è costante.
E' è costante.
Si deve dimostrare che f è costante, cioè che considerato un elemento a E con f(a)
E con f(a) E',
E',
 x
x E : f(x) = f(a).
E : f(x) = f(a).
Allo scopo, si prenda un elemento x E e siccome a
E e siccome a E ed E è filtrante superiormente, per definizione
E ed E è filtrante superiormente, per definizione
 z
z E
E  a ≤ z, x ≤ z.
a ≤ z, x ≤ z.
Siccome
f è crescente f(a) ≤' f(z), f(x) ≤' f(z),
f(a) ≤' f(z), f(x) ≤' f(z),
f è decrescente f(z) ≤' f(a), f(z) ≤' f(x),
f(z) ≤' f(a), f(z) ≤' f(x),
e quindi da
f(a) ≤' f(z), f(z) ≤' f(x) f(a) ≤' f(x),f(x) ≤' f(z), f(z) ≤' f(a)
f(a) ≤' f(x),f(x) ≤' f(z), f(z) ≤' f(a)  f(x) ≤' f(a),
f(x) ≤' f(a),
risulta
f(a) = f(x).
Siano (E, ≤), (E', ≤'), (E', ≤'') tre insiemi ordinati e si considerino le seguenti applicazioni:
f : E E', g : E'
E', g : E'  E'', g о f : E
E'', g о f : E  E''.
E''.
Si dimostra che se
(1) f e g sono strettamente crescenti g о f è strettamente crescente,
g о f è strettamente crescente,
(2) f e g sono crescenti g о f è crescente,
g о f è crescente,
(3) f e g sono strettamente decrescenti g о f è strettamente decrescente,
g о f è strettamente decrescente,
(4) f e g sono decrescenti g о f è decrescente.
g о f è decrescente.
Dimostrazione (1).
f è strettamente crescente, cioè fissati
x E, y
E, y E x < y
E x < y  f(x)
f(x) E', f(y)
E', f(y) E', f(x) ≤' f(y).
E', f(x) ≤' f(y).
f : E
si danno le seguenti definizioni:
f è crescente o isotona
Nota bene
Se x = y, risulta f(x) = f(y).
f è decrescente o antitona
f è strettamente crescente
f è strettamente decrescente
Se l'applicazione f rispecchia uno dei quattro casi suddetti, si chiama monotòna.
Si dimostra ora che:
-ogni applicazione costante di E in E' è un'applicazione crescente e decrescente.
Infatti, sia
f : E
un'applicazione costante, cioè, fissato un elemento
a
Si verifica prima che f è crescente, cioè che
Infatti risulta:
f(x) = a ≤' a' = f(y)
Infine si verifica che f è decrescente, cioè che
Infatti risulta:
f(x) = a ≤' a' = f(y)
In generale, un'applicazione crescente e decrescente non è costante, però, con altre ipotesi lo è; pertanto si dimostra che:
(E, ≤) filtrante superiormente, crescente e decrescente
Si deve dimostrare che f è costante, cioè che considerato un elemento a
Allo scopo, si prenda un elemento x
Siccome
f è crescente
f è decrescente
e quindi da
f(a) ≤' f(z), f(z) ≤' f(x)
risulta
f(a) = f(x).
Siano (E, ≤), (E', ≤'), (E', ≤'') tre insiemi ordinati e si considerino le seguenti applicazioni:
f : E
Si dimostra che se
(1) f e g sono strettamente crescenti
(2) f e g sono crescenti
(3) f e g sono strettamente decrescenti
(4) f e g sono decrescenti
Dimostrazione (1).
f è strettamente crescente, cioè fissati
x
g è strettamente crescente, cioè fissati
f(x) E', f(y)
E', f(y) E' f(x) ≤' f(y)
E' f(x) ≤' f(y)  g(f(x))
g(f(x)) E'', g(f(y))
E'', g(f(y)) E'', g(f(x)) ≤'' g(f(y))
E'', g(f(x)) ≤'' g(f(y))  g о f(x) ≤'' g о f(y).
g о f(x) ≤'' g о f(y).
In tal modo è dimostrata la (1), cioè che g о f è strettamente crescente; (2), (3) e (4) si dimostrano analogamente.
Sia (E, ≤) un insieme ordinato e si consideri la bigezione canonica
iE : E E.
E.
Si vuol vedere se iE è monotòna e, allo scopo, si dimostra che è strettamente crescente.
Infatti, considerati due elementi
x E, y
E, y E x < y
E x < y  iE(x) = x < y = iE(y)
iE(x) = x < y = iE(y)  iE(x) < iE(y).
iE(x) < iE(y).
Siccome iE è bigettiva, e quindi invertibile, ed essendo iE stessa la la sua inversa, quest'ultima è anche strettamente crescente.
Tutto ciò è un prototipo di quanto è chiamato isomorfismo secondo la seguente definizione:
-isomorfismo di E in E' per ≤ e ≤' è ogni applicazione bigettiva di E in E' strettamente crescente insieme alla sua inversa.
Quando esiste un isomorfismo di E in E', (E, ≤) e (E', ≤') si dicono isomorfi per l'ordine e tale circostanza si indica con
(E, ≤) ≈ (E', ≤').
Siano (E, ≤), (E', ≤'), (E', ≤'') tre insiemi ordinati, si dimostra che:
(E, ≤) ≈ (E', ≤'), (E', ≤') ≈ (E'', ≤'') (E, ≤) ≈ (E'', ≤'').
(E, ≤) ≈ (E'', ≤'').
Allo scopo, basta dimostrare che, essendo f e g bigettive e strettamente crescenti insieme alle loro inverse, anche g о f è strettamente crescente insieme alla sua inversa.
Infatti, g о f : E E'', essendo composta di due applicazioni strettamente crescenti, è anch'essa strettamente crescente, inoltre l'applicazione inversa di g о f, essendo composta dalle inverse di f e g a loro volta strettamente crescenti, è anche strettamente crescente, quindi risulta
E'', essendo composta di due applicazioni strettamente crescenti, è anch'essa strettamente crescente, inoltre l'applicazione inversa di g о f, essendo composta dalle inverse di f e g a loro volta strettamente crescenti, è anche strettamente crescente, quindi risulta
(E, ≤) ≈ (E'', ≤'').
Si dimostra inoltre, in modo ovvio, che:
(E, ≤) ≈ (E', ≤') (E', ≤') ≈ (E, ≤),
(E', ≤') ≈ (E, ≤),
ed anche
(E, ≤) ≈ (E, ≤),
in quanto esiste iE.
Dunque, l'isomorfismo gode delle stesse proprietà delle relazioni di equavalenza.
Sia (E, ≤) un insieme totalmente ordinato, (E', ≤') un insieme ordinato, ed
f : E E'
E'  (1) f(E) = E', (2)
(1) f(E) = E', (2)  x
x E,
E,  y
y E, x < y : f(x) <' f(y);
E, x < y : f(x) <' f(y);
si dimostra che:
a) f è un isomorfismo di E in E' per ≤ e ≤'.
b) ≤' è una relazione di totale ordine.
Dimostrazione a).
Affinchè f sia un isomorfismo, basta dimostrare che f è bigettiva e che la sua inversa sia strettamente crescente.
Siccome per ipotesi f è surgettiva, affinchè sia bigettiva, basta dimostrare che sia anche ingettiva, cioè
 x
x E,
E,  y
y E, x ≠ y : f(x) ≠ f(y).
E, x ≠ y : f(x) ≠ f(y).
Essendo E totalmente ordinato, e tenendo conto che x ≠ y, risulta
x < y v y < x.
Per la crescenza di f, risulta
x < y f(x) <' f(y)
f(x) <' f(y)  f(x) ≠ f(y);
f(x) ≠ f(y);
se invece
y < x f(y) <' f(x)
f(y) <' f(x)  f(y) ≠ f(x).
f(y) ≠ f(x).
Pertanto la f è ingettiva.
Essendo f bigettiva, ha senso considerare la sua inversa, chiamata
g : E' E
E  g о f = iE, f о g = iE'.
g о f = iE, f о g = iE'.
Si dimostra che g è anch'essa strettamente crescente, cioè considerati
x' E', y'
E', y' E', x' < y'
E', x' < y'  g(x') < g(y').
g(x') < g(y').
Essendo
x' E', y'
E', y' E'
E'  g(x')
g(x') E, g(y')
E, g(y') E,
E,
ed E totalmente ordinato da ≤, risulta
g(x') ≤ g(y'),
oppure
g(y') ≤ g(x').
Inoltre, g è bigettiva ed x' <' y', per cui
(1) g(x') < g(y') v (2) g(y') < g(x').
La (1) dimostra quanto asserito. Si vede ora se sussiste la (2).
f(g(y')) <' f(g(x')).
Siccome
f(g(y')) = f о g(y') = iE'(y') = y',
f(g(x')) = f о g(x') = iE'(x') = x',
cioè
y' <' x',
e ciò non può essere, perchè si è supposto che
x' <' y'.
In tal modo si è dimostrato che f è un isomorfismo di E in E' per ≤ e ≤'.
Dimostrazione b).
Si dimostra che ≤' è una relazione di totale ordine.
Infatti, siano
x' E', y'
E', y' E'
E' 
 x
x E, y
E, y E
E  f(x) = x', f(y) = y',
f(x) = x', f(y) = y',
ed essendo E totalmente ordinato, risulta
x ≤ y v y ≤ x.
Se
x ≤ y,
per la stretta crescenza della f, si ha
f(x) ≤' f(y) x' ≤' y'.
x' ≤' y'.
Analogamente, si dimostra che
y' ≤' x',
pertanto resta dimostrato che ≤' è una relazione di totale ordine.
Nota bene
Avendo dimostrato che una relazione di buon ordine è una relazione di totale ordine, il teorema ora dimostrato sussiste ugualmente; solo nell'ipotesi che ≤ sia una relazione di buon ordine, tale risulterà anche ≤', cioè occorre dimostrare che:
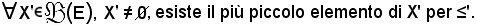
Chiaramente risulta
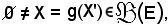
essendo ≤ una relazione di buon ordine su E,
 m
m X
X 
 x
x X : m ≤ x.
X : m ≤ x.
Si consideri ora
f(m) = m';
essendo
f(m) X'
X'  m'
m' X'.
X'.
Si dimostra ora che m' è il più piccolo elemento di X' per ≤'.
Scelto ad arbitrio
x' X'
X' 
 x
x E
E  f(x) = x';
f(x) = x';
inoltre
x' X'
X'  g(x')
g(x') X,
X,
allora, essendo m il più piccolo elemento di X, risulta
m ≤ g(x').
Tenendo conto della crescenza di f,
m ≤ g(x') f(m) ≤' f(g(x')) = f о g(x') = iE'(x') = x',
f(m) ≤' f(g(x')) = f о g(x') = iE'(x') = x',
cioè
f(m) ≤' x' m' ≤' x'.
m' ≤' x'.
Quindi ≤' è una relazione di buon ordine.
Corollario
Se è assegnato un insieme totalmente ordinato o bene ordinato ed un isomorfismo di tale insieme in un altro insieme ordinato, quest'ultimo è un insieme bene ordinato.
Siano (E, ≤) un insieme ordinato, E' un altro insieme ed
f : E E'
E'
un'applicazione bigettiva.
Si dimostra che esiste una ed una sola relazione d'ordine ≤' su E' in modo tale che f sia un isomorfismo di E in E', cioè:

Si indichi con
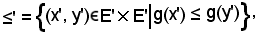
cioè
 x'
x' E',
E',  y'
y' E' x' ≤' y'
E' x' ≤' y'  g(x') ≤ g(y').
g(x') ≤ g(y').
Si dimostra ora che è una relazione d'ordine.
Allo scopo, si deve verificare che:
(1) x' E', y'
E', y' E', z'
E', z' E' x' ≤' y', y' ≤' z'
E' x' ≤' y', y' ≤' z'  x' ≤' z'.
x' ≤' z'.
(2) x' E', y'
E', y' E' x' ≤' y', y' ≤' x'
E' x' ≤' y', y' ≤' x'  x' = y'.
x' = y'.
Dimostrazione (1).
x' E', y'
E', y' E', z'
E', z' E' x' ≤' y', y' ≤' z'
E' x' ≤' y', y' ≤' z'  g(x') ≤ g(y'), g(y') ≤ g(z')
g(x') ≤ g(y'), g(y') ≤ g(z')  g(x') ≤ g(z')
g(x') ≤ g(z')  x' ≤' z'.
x' ≤' z'.
Dimostrazione (2).
x' E', y'
E', y' E' x' ≤' y', y' ≤' x'
E' x' ≤' y', y' ≤' x'  g(x') ≤ g(y'), g(y') ≤ g(x')
g(x') ≤ g(y'), g(y') ≤ g(x')  g(x') = g(y'),
g(x') = g(y'),
e per la bigettività di f, si ha:
f(g(x')) = f(g(y'))
ed inoltre, tenendo conto che
f(g(x')) = f о g(x') = iE'(x') = x' e f(g(y')) = f о g(y') = iE'(y') = y' x' = y'.
x' = y'.
In tal modo resta provata l'esistenza della relazione d'ordine ≤'; si prova ora l'unicità.
Allo scopo, basta riconoscere che, considerata l'ulteriore relazione d'ordine ≤'', risulta
≤' = ≤'',
cioè
≤' relazione d'ordine su E, ≤'' relazione d'ordine su E ≤'' = ≤''.
≤'' = ≤''.
Si dimostra prima che:
≤' ≤''.
≤''.
Infatti, si consideri
(x'', y') ≤'
≤'  x' ≤' y'
x' ≤' y'  g(x') ≤ g(y')
g(x') ≤ g(y')
e, siccome ≤'' è una relazione d'ordine su E, si ha:
x' = f(g(x')) ≤'' f(g(y')) = y' x' ≤'' y'
x' ≤'' y'  (x'', y')
(x'', y') ≤''.
≤''.
Per ≤'' si dimostra, analogamente che:
≤'' ≤'.
≤'.
Si dimostra ora che f è un isomorfismo, cioè che f è strettamente crescente insieme alla sua inversa g.
Siano ora
x E, y
E, y E, x < y
E, x < y  x ≠ y
x ≠ y  f(x) ≠ f(y),
f(x) ≠ f(y),
essendo f bigettiva e quindi ingettiva.Ora per dimostrare che
f(x) ≤' f(y),
per come è stata definita ≤', basta dimostrare che
g(f(x)) < g(f(y)),
e ciò è già vero, in quanto
g(f(x)) = x, g(f(y)) = y,
vale a dire che
x < y.
La relazione ≤' così costruita su E' si dice ottenuta per trasporto di ≤ su E' per f.
Nota bene
Se ≤ è una relazione di totale ordine, anche ≤' è tale, e lo stesso dicasi se ≤ è una relazione di buon ordine.
Tra le assunzioni fondamentali della "Teoria degl'insiemi" figurano le seguenti:
a) Assioma della scelta, b) Teorema di Zermelo, c) Teorema di Zorn.
L'assioma della scelta esprime:
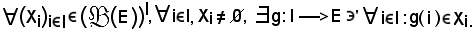
Il teorema di Zermelo esprime:

Il teorema di Zorn esprime:
se (E, ≤) è un insieme ordinato induttivo,
 x0
x0 E,
E,  m
m E, massimale per ≤
E, massimale per ≤  x0 ≤ m.
x0 ≤ m.
Si riconosce che dall'assioma della scelta consegue il teorema di Zermelo, e da questi quello di Zorn, e da quest'ultimo l'assioma della scelta, cioè:
a) b)
b)  c)
c)  a).
a).
Per facilitare tali dimostrazioni, si premettono alcuni lemmi.
Lemma 1
Si consideri l'insieme ordinato (E, ≤) e l'applicazione
f : E E
E 
 x
x E : x ≤ f(x).
E : x ≤ f(x).
Si fissi x0 E e si indichi con
E e si indichi con
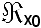
l'insieme delle parti K di E che verifichi le condizioni KI, KII, KIII, cioè:
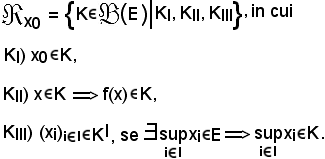
A tal punto, si dimostra quanto segue:
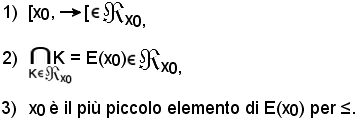
Dimostrazione 1).
Allo scopo, è necessario che essa verifichi KI), KII) e KIII), cioè:
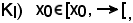
e ciò è vero, in quanto
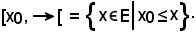
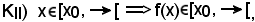
pertanto, si ha:
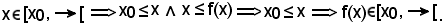
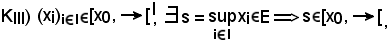
e ciò è vero, perchè:
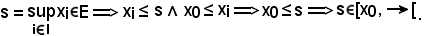
In tal modo è dimostrata la 1).
Dimostrazione 2).
Allo scopo, è necessario che essa verifichi KI), KII) e KIII):
KI) è verificato, in quanto si ha:
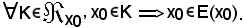
KII) è verificato, in quanto si ha:
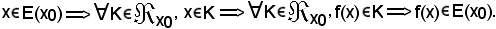
KIII) è verificato, in quanto, considerata la famiglia
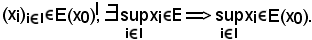
Infatti:
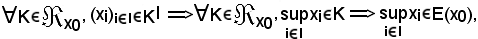
perchè per K è valida KIII).
Dimostrazione 3).
Si deve dimostrare che x0 è il più piccolo elemento di E(x0), cioè un minorante degli elementi di E(x0).
Infatti:
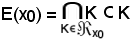
e, scegliendo come K l'intervallo
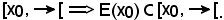
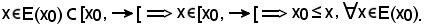
Pertanto resta dimostrato il lemma 1).
Nota bene
Si dimostra anche che:
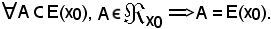
Ciò rappresenta il principio di induzione completa.Infatti, siccome per ipotesi risulta che
A E(x0),
E(x0),
ed essendo noto che
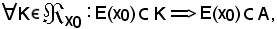
è dimostrato quanto asserito.
Lemma 2
Si considerino l'insieme ordinato (E, ≤), l'applicazione f : E E ed x0
E ed x0 E.
E.
Supponendo per ipotesi che
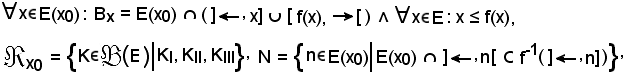
si dimostra:
1) n
n N : Bn = E(x0); 2) N = E(x0).
N : Bn = E(x0); 2) N = E(x0).
Dimostrazione 1).
E' ovvio che:
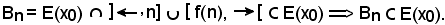
Per il principio d'induzione completa, affinchè risulti Bn = E(x0), bisogna dimostrare che:
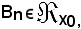
cioè Bn deve verificare KI), KII) e KIII).
KI) - E' noto che x0 E(x0), per cui si considera
E(x0), per cui si considera
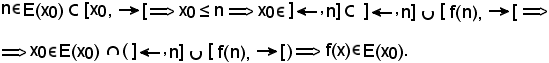
KII) - Si consideri
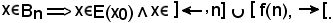
Se x E(x0), siccome E(x0) verifica KII), si ha f(x)
E(x0), siccome E(x0) verifica KII), si ha f(x) E(x0).
E(x0).
Sia allora
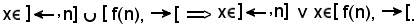
Supponendo
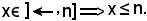
Se
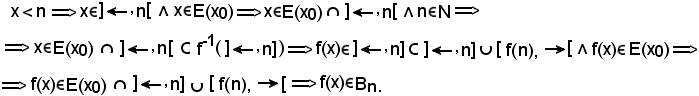
Se
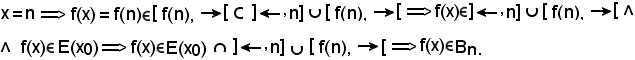
Supponendo ora
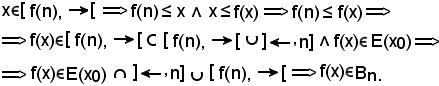
KIII) - Si considerino
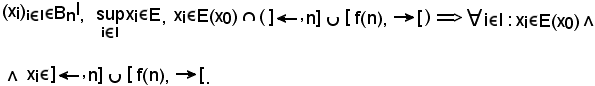
Siccome E(x0) verifica la KIII), se
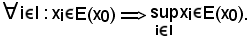
Inoltre, se
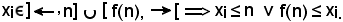
Supponendo che
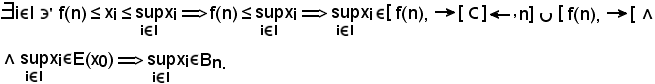
Se invece
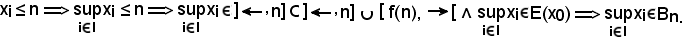
Dunque, in ogni caso,
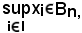
quindi Bn verifica KIII) ed è così dimostrato che
Bn = E(x0).
Dimostrazione 2).
Si deve dimostrare che:
N = E(x0).
Per come è stato definito N, risulta
N E(x0).
E(x0).
Allora, per il principio d'induzione completa, basta dimostrare che N verifica le proprietà KI), KII) e KIII).
KI) Se
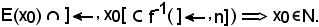
Si ricorda ora una proprietà sulla relazione d'inclusione
A B
B  A
A  C
C  B
B  C,
C,
in virtù della quale, essendo
si ha:
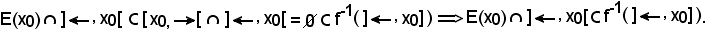
KII) Si deve dimostrare che, considerato
n N
N  f(n)
f(n) N.
N.
Per ipotesi, dunque, è noto che
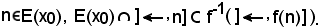
La tesi è la seguente:
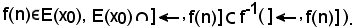
Infatti, che f(n) E(x0) è ovvio, perchè E(x0) verifica KII), allora si deve dimostrare che:
E(x0) è ovvio, perchè E(x0) verifica KII), allora si deve dimostrare che:
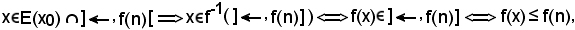
dunque
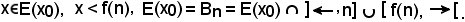
Essendo x E(x0), dal momento che
E(x0), dal momento che
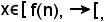
in quanto x < f(n), deve risultare
x ≤ a.
Se
x = n f(x) = f(n)
f(x) = f(n)  f(x) ≤ f(n).
f(x) ≤ f(n).
Se
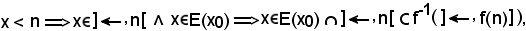
dunque
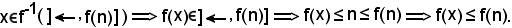
KIII) Sia
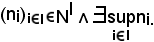
Per ipotesi, dunque, è noto che
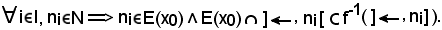
Si deve dimostrare che, considerato
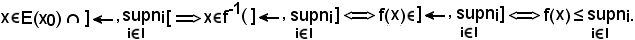
Infatti,

Inoltre, siccome
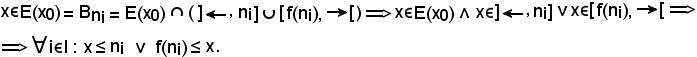
Si osserva ora che la condizione f(ni) ≤ x è da scartare perchè è contro l'ipotesi, infatti supponendo
 i
i I : f(ni) ≤ x,
I : f(ni) ≤ x,
essendo
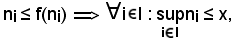
Allora,
 i
i I
I  x ≤ ni.
x ≤ ni.
Se
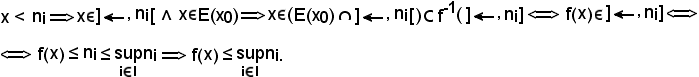
Se x = ni, è noto che:
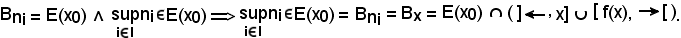
Certamente
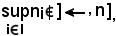
perchè
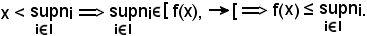
Si è così dimostrato che
N = E(x0).
Dunque, in conclusione:
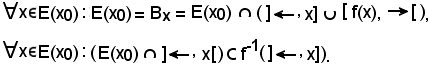
Si dimostra ora che E(x0) è un insieme bene ordinato, cioè che presa una parte non vuota di E(x0), questa è dotata del più piccolo elemento. Sia
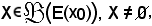
si vuole dimostrare che X ha il più piccolo elemento.
Siccome
 x
x E(x0) : Bx = E(x0),
E(x0) : Bx = E(x0),
si ricava che E(x0) è una parte di E totalmente ordinata per ≤.
Infatti, se
x E(x0), y
E(x0), y E(x0)
E(x0)  y ≤ x v f(x) ≤ y,
y ≤ x v f(x) ≤ y,
e, per l'ipotesi su f, si ha che x ≤ f(x) ed x ed y sono paragonabili per ≤.
Si suppone che X abbia più di due elementi, si presentano due casi:
1) x0 X,
X,
2) x0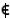 X.
X.
Dimostrazione 1).
Sia
x0 X
X  E(x0)
E(x0) 
 x
x X
X  E(x0) : x0 ≤ x;
E(x0) : x0 ≤ x;
dunque x0 è un minorante di X, derivante dal fatto che x0 è il più piccolo elemento di E(x0). Quindi x0 X, inoltre
X, inoltre
 x
x X : x0 ≤ x;
X : x0 ≤ x;
e ciò dice che E(x0) è un insieme bene ordinato, risultando X fornito del più piccolo elemento.
Dimostrazione 1).
Sia
x0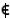 X
X  E(x0),
E(x0),
essendo x0 il più piccolo elemento di E(x0), risulta che x0 è un minorante di X, cioè
 x
x X : x0 ≤ x.
X : x0 ≤ x.
Si indica ora con A l'insieme dei minoranti di X, cioè:
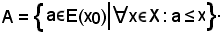
Ovviamente
A ≠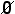 ,
,
in quanto x0 A.
A.
Si consideri ora una famiglia

e si supponga esistente il
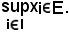
Si dimostra che
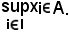
Infatti:
 i
i I : xi ≤ x,
I : xi ≤ x,
cioè x è un maggiorante degli xi, per cui si ha che

Ciò esprime che
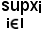
è un minorante, e come tale è elemento di A, cioè
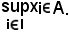
Quindi:
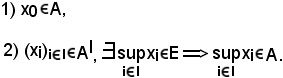
Pertanto, A verifica KI) e KIII); si può notare che A non verifica KII), cioè che:
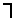 (
( a
a A : f(a)
A : f(a) A).
A).
Supponendo per assurdo che ciò sia vero, essendo
A E(x0)
E(x0)
e verificando KI), KII) e KIII), risulta
A = E(x0),
e ciò non è possibile, infatti se
 a
a E(x0), x
E(x0), x X : a ≤ x;
X : a ≤ x;
inoltre se
X E(x0),
E(x0),
cioè
x E(x0),
E(x0),
il tutto implica che x è il più grande elemento di E(x0), ma al massimo ne può esistere soltanto uno, e ciò esprime che X si dovrebbe ridurre ad un unico elemento, contro l'ipotesi che X è formato da più di due elementi. Dunque A non verifica KII), cioè deve
 a
a A
A  f(a)
f(a)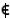 A,
A,
vale a dire che f(a) non è un minorante di X, cioè f(a) non può essere minore o uguale di ogni elemento di X, allora deve
 x
x X
X  f(a) > x.
f(a) > x.
Si dimostra che x è il più piccolo elemento di X.
Infatti:
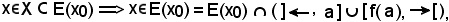
ciò è possibile, in quanto
 x
x E(x0), E(x0) = Bx,
E(x0), E(x0) = Bx,
in particolare per A.
Non potendo essere
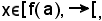
deve risultare x ≤ a; ma a è un minorante di X, risultante minore di un minorante, pertanto anch'esso è tale. Inoltre, x X e pertanto X ha il più piccolo elemento ed E(x0) risulta bene ordinato.
X e pertanto X ha il più piccolo elemento ed E(x0) risulta bene ordinato.
Sia (E, ≤) un insieme ordinato induttivo e si consideri l'applicazione
f : E E
E
così definita:
 x
x E : x ≤ f(x);
E : x ≤ f(x);
si vuole dimostrare che:
1) supE(x0) = x*0,
supE(x0) = x*0,
2) x*0 è il più grande elemento di E(x0),
3) x*0 = f(x*0).
Si ricorda che E è un insieme ordinato induttivo se
 B
B  E, B ≠
E, B ≠ 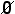 , B bene ordinato
, B bene ordinato 
 supB.
supB.
Dimostrazione 1).Siccome E è un insieme ordinato induttivo, essendo E(x0) E, con E(x0) bene ordinato e diverso dalla parte vuota, in quanto x0
E, con E(x0) bene ordinato e diverso dalla parte vuota, in quanto x0 E(x0), si ha che
E(x0), si ha che
 supE(x0) = x*0.
supE(x0) = x*0.
Dimostrazione 2).
Affinchè x*0 soddisfi la 2) basta dimostrare che x*0 E(x0), essendo già estremo superiore e di conseguenza un maggiorante.
E(x0), essendo già estremo superiore e di conseguenza un maggiorante.
Allo scopo, si consideri la famiglia
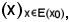
dal momento che E(x0) verifica KIII), deve verificarsi che
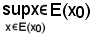
e di conseguenza
x*0 E(x0).
E(x0).
Dimostrazione 3).
Per come è stata definita f, risulta
x*0 ≤ f(x*0);
inoltre
f(x*0) E(x0),
E(x0),
in quanto E(x0) verifica KII.
Ma x*0 è il più grande elemento di E(x0), pertanto risulta
f(x*0) ≤ x*0.
Dunque
x*0 = f(x*0).
Si dimostra ora che le seguenti tre proposizioni sono equivalenti:
a) Assioma della scelta: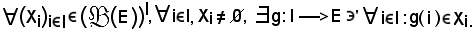
b) Teorema di Zermelo:
c) Teorema di Zorn; se (E, ≤) è un insieme ordinato induttivo, x0
x0 E,
E,  m
m E, massimale per
E, massimale per
≤ x0 ≤ m.
x0 ≤ m.
Dimostrazione
a) b)
b)
Si consideri l'insieme E ≠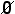 e si associ ad esso l'insieme
e si associ ad esso l'insieme
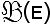
delle sue parti, e si indichi con
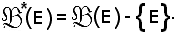
Si dimostra ora che
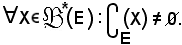
Siccome
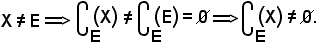
Si consideri pertanto la famiglia
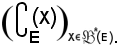
Siccome ci si trova nelle ipotesi dell'assioma della scelta, vero per l'ipotesi a),
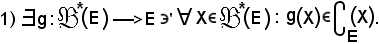
Si consideri ora l'applicazione
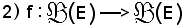
così definita:
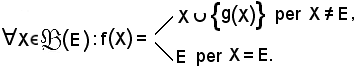
Si vuol dimostrare:
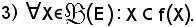
Se X ≠ E,
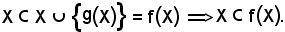
Se X = E,
f(X) = f(E) = E,
inoltre è noto che
E E = f(E),
E = f(E),
e, considerando X al posto di E, si ha:
X f(X).
f(X).
Si dimostra inoltre che:
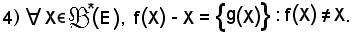
Infatti,
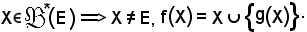
Considerando f(X) - X, per definizione si ha:
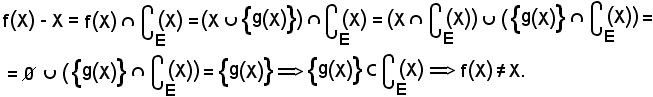
Dunque, l'unico elemento che è trasformato in se stesso da f è solo E.
Nota bene
Si ricorda quanto segue.
1)-Considerata la coppia
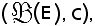
si è costruita un'applicazione
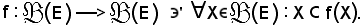
2)-Considerato l'insieme ordinato (E, ≤) si è costruita un'applicazione f : E E
E 
 x
x E : x ≤ f(x) ed inoltre si è stabilito che
E : x ≤ f(x) ed inoltre si è stabilito che  x0
x0 E si poteva considerare E(x0) che risultava ben ordinato da ≤.
E si poteva considerare E(x0) che risultava ben ordinato da ≤.
3)-Considerato
E insieme ordinato induttivo
 supE(x0) = x*.
supE(x0) = x*.
Sulla scorta di quanto ora detto, nel caso in questione si può considerare X0 =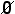 ed in corrispondenza di esso costruire
ed in corrispondenza di esso costruire
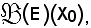
che risulterà bene ordinato dalla relazione , e quindi totalmente ordinato.
, e quindi totalmente ordinato.
Si ricorda ora che è stato dimostrato che
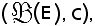
è un reticolo completo, e quindi
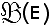
è un insieme induttivo, pertanto X*0 estremo superiore di
X*0 estremo superiore di 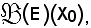 essendo X*0 la riunione di tutte le
essendo X*0 la riunione di tutte le
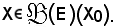
Quindi risulta:
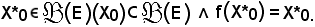
Siccome è stato detto che l'unico elemento che la f trasforma in se stessa è E, si può concludere che X*0 = E.
Pertanto:
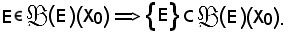
Si indica ora con
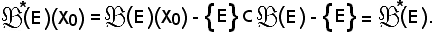
Si può in tal modo considerare la restrizione di g a
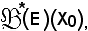
indicata con
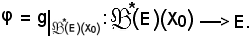
Siccome
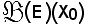
è un insieme bene ordinato, tale è pure
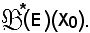
Nell'ipotesi che φ sia bigettiva, essendo
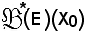
bene ordinato, esiste su E una relazione d'ordine ≤' ottenuta per trasporto, in modo tale che φ sia un isomorfismo.
Pertanto, essendo
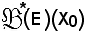
bene ordinato, tale è E.
In tal modo, resta dimostrato il teorema di Zermelo.
Si dimostra ora che φ è bigettiva, pertanto basta provare che φ è ingettiva e surgettiva.
Per la surgettività di φ, si deve dimostrare che:
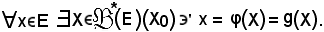
Si fissi un x E e si indichi con a gotica il seguente insieme:
E e si indichi con a gotica il seguente insieme:
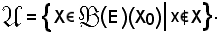
Certamente si verifica quanto segue:
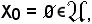
in quanto l'insieme vuoto non è formato da alcun elemento.
Quest'ultima condizione esprime che verifica KI).
verifica KI).
Si consideri ora la famiglia

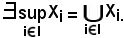
Logicamente risulta
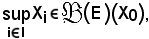
in quanto
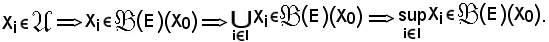
Si osserva ora che

Infatti, supponendo che
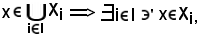
ma
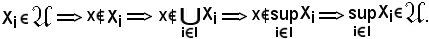
Quest'ultima condizione esprime che verifica KIII).
verifica KIII).
A tal punto verifica KI e KIII); si prova ora che non verifica KII).
verifica KI e KIII); si prova ora che non verifica KII).
Supponendo che verifichi anche KII), ci si troverebbe nelle seguenti condizioni:
verifichi anche KII), ci si troverebbe nelle seguenti condizioni: verifica KI, KII) e KIII), inoltre, per come è stato definito, risulta
verifica KI, KII) e KIII), inoltre, per come è stato definito, risulta
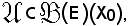
allora, per il principio d'induzione completa, si avrebbe
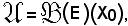
e ciò è impossibile, in virtù del fatto che
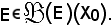
Infatti, se dovesse risultare
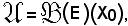
si svrebbe
E

 x
x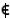 E,
E,
e ciò è contro l'ipotesi, in quanto x E.
E.
Dunque, non verifica KII) e ciò equivale a dire che
non verifica KII) e ciò equivale a dire che
 X
X
 : f(X)
: f(X) 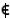

 x
x f(X).
f(X).
Essendo inoltre
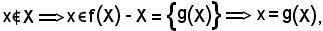
e ciò si verifica quando E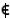
 e quando, considerato X
e quando, considerato X
 , si ha
, si ha
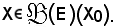
Di conseguenza risulta
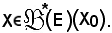
Resta dunque dimostrato che φ è surgettiva.
Si dimostra ora che φ è ingettiva, cioè:
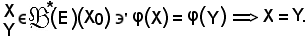
Tenendo conto che
φ(X) = g(X), φ(Y) = g(Y),
è sufficiente dimostrare che
g(X) = g(Y) X = Y.
X = Y.
Si suppone per assurdo che X ≠ Y, essendo
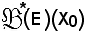
bene ordinato, sarà pure totalmente ordinato, pertanto X ed Y si troveranno nelle seguenti due possibili condizioni:
1) X Y,
Y,
2) Y X.
X.
A tal punto, si ricorda che:
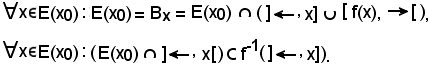
Si esamina ora il caso 1).
Allo scopo, si considera
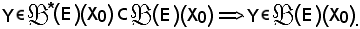
Per il richiamo suddetto si ha:
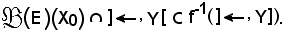
Siccome
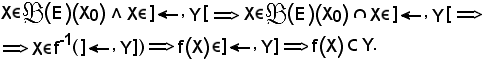
Inoltre, se
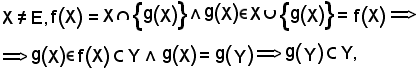
e ciò è assurdo, perchè per ipotesi
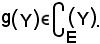
Quindi X non può essere contenuto strettamente in Y; analogamente, si dimostra che Y non può essere contenuto strettamente in X. L'unica conclusione possibile è quindi che X = Y.
b) c)
c)
Si ricorda che:
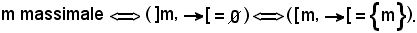
Si consideri ora x0 E, se fosse
E, se fosse
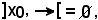
ne dedurremmo che x0 è elemento massimale, pertanto m coinciderebbe con x0. Logicamente, dire che x0 non è elemento massimale, equivale a dire che
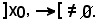
Si vuole dunque dimostrare che esiste almeno un elemento massimale dell'intervallo
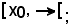
si ragiona per assurdo, cioè
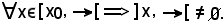
Si consideri l'insieme E; essendo vera la b), su E dovrà esistere una relazione di buon ordine, indicata con ≤'. Si costruisce ora l'applicazione
f : E E
E
così definita:

Pertanto, fissato x E,
E,
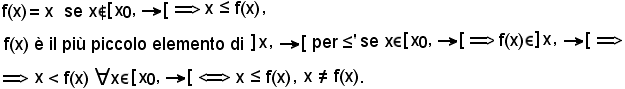
In ogni caso,
 x
x E : x ≤ f(x).
E : x ≤ f(x).
Inoltre, siccome E è un insieme ordinato induttivo,
 x*0
x*0 E
E  x0 ≤ x*0 = f(x*0),
x0 ≤ x*0 = f(x*0),
tenendo conto che quest'ultima uguaglianza è stata dimostrata in precedenza.
Essendo
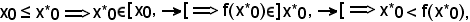
si è così pervenuti ad un assurdo, in quanto x*0 = f(x*0) e quindi esiste almeno un
x E
E  x0 ≤ x
x0 ≤ x
che risulta massimale per ≤.
Si indichi con
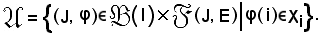
Si fissi
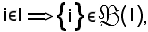
in corrispondenza di tale i si consideri Xi E ed x
E ed x Xi; in tal modo, si può considerare l'applicazione
Xi; in tal modo, si può considerare l'applicazione
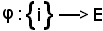
e porre
φ(i) = x Xi.
Xi.
Allora
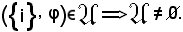
Si fissi ora su una relazione ≤' così definita:
una relazione ≤' così definita:
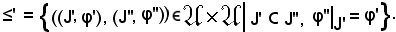
Si dimostra che ≤' è una relazione d'ordine, cioè che è riflessiva, antisimmetrica e transitiva.
E' logico che se
Dunque, ≤' è riflessiva.
Si dimostra ora che ≤' è antisimmetrica, cioè che
(J', φ') ≤' (J'', φ''), (J'', φ'') ≤' (φ'', J'') (J', φ') = (J'', φ'').
(J', φ') = (J'', φ'').
Infatti:
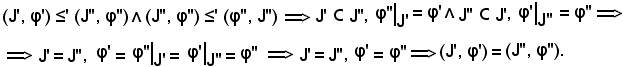
Dunque, ≤' è antisimmetrica.
Si dimostra infine che ≤' è transitiva, cioè che
(J', φ') ≤' (J'', φ''), (J'', φ'') ≤' (J''', φ'''), (J', φ') ≤' (J''', φ''').
(J', φ') ≤' (J''', φ''').
Infatti:
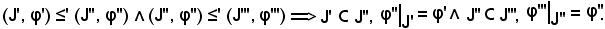
Pertanto risulta
J' J'', J''
J'', J''  J'''
J'''  J'
J'  J''',
J''',
quindi ha senso considerare e dimostrare quanto segue:
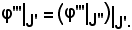
Infatti, considerato
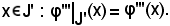
Essendo poi x J'', in quanto J'
J'', in quanto J'  J'', sarà
J'', sarà
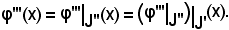
Quindi
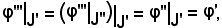
allora
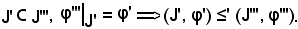
Dunque, ≤' è transitiva.
Si è così dimostrato che ≤' è una relazione d'ordine.
Prima di dimostrare la parte finale del teorema, si dimostra quanto segue:
sia E un insieme e si consideri una famiglia di parti di E, cioè
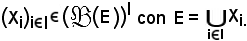
Si considera ora un nuovo insieme E' e l'applicazione
fi : Xi E',
E',  i
i I.
I.
Si dimostra che le seguenti due proposizioni sono equivalenti:
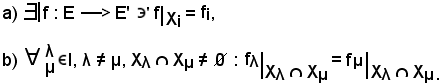
Si ricorda prima che se
f : E  E'
E'
e se
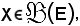
si può considerare
 b)
b)
Si considerino,
λ, μ I, λ ≠ μ,
I, λ ≠ μ,  ≠ Xλ
≠ Xλ  Xμ
Xμ
e si osserva che
Xλ Xμ
Xμ  Xλ, Xλ
Xλ, Xλ  Xμ
Xμ  Xμ,
Xμ,
ed inoltre che
fλ : Xλ E', fμ : Xμ
E', fμ : Xμ  E'.
E'.
Si consideri ora
x Xλ
Xλ  Xμ,
Xμ,
ed inoltre
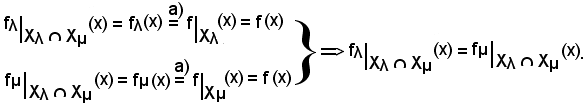
Resta quindi dimostrata la b), cioè:
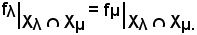
Si dimostra ora che:
b) a)
a)
Si suppone che ogni
fi = (Xi, E', Gi),
in cui
Gi Xi
Xi  E'
E'
e si indica con

Si dimostra che G è una relazione funzionale, e quindi si può considerare l'applicazione f(E, E' G).
Allo scopo, si deve dimostrare che considerato x E, la sezione G(x) e non vuota e si riduce ad un solo elemento.
E, la sezione G(x) e non vuota e si riduce ad un solo elemento.
Infatti, considerato
x E
E 
 i
i I
I  x
x Xi
Xi  Gi ≠
Gi ≠  ,
,
ed inoltre sia
y Gi(x)
Gi(x)  (x, y)
(x, y) Gi
Gi  G
G  y
y G(x)
G(x)  G(x) ≠
G(x) ≠ 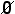 .
.
Si dimostra ora che la sezione G(x) è formata da un solo elemento.
Allo scopo, se ne considerano due:
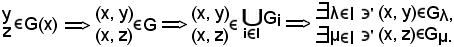
Supponendo che
λ = μ,
allora
(x, y) G, (x, z)
G, (x, z) G
G  y
y Gλ(x), z
Gλ(x), z Gλ(x).
Gλ(x).
Essendo Gλ una relazione funzionale, Gλ(x) si riduce ad un unico elemento, il che implica che
y = z.
Supponendo invece che
λ ≠ μ,
allora
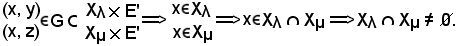
Pertanto, si consideri
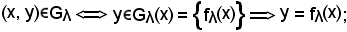
siccome
x Xλ
Xλ  Xμ,
Xμ,
ha senso considerare l'uguaglianza
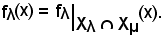
Analogamente, si consideri
(x, z) Gμ
Gμ  z = fμ(x),
z = fμ(x),
ma
x Xλ
Xλ  Xμ,
Xμ,
quindi ha senso considerare l'uguaglianza
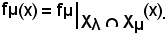
Per la validità della b), deve risultare
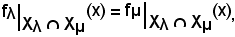
il che ha come ovvia conseguenza che
y = z.
Si è così dimostrato che Gi è una relazione funzionale, si può pertanto considerare la terna
f = (E, E', G).
Si dimostra ora che, quale che sia x in Xi,
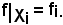
Si può allora fissare:
(x, f(x)) G,
G,
se si considera
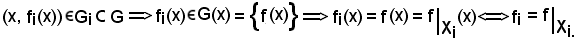
Si dimostra ora l'unicità della f.
Siano
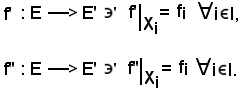 Sia
Sia
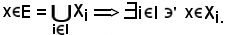
In tali condizioni, si può considerare:
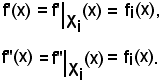
Essendo uguali i secondi membri di tali uguaglianze, si ha:
f'(x) = f''(x) x
x E
E  f' = f''.
f' = f''.
Dopo aver dimostrato l'equivalenza delle proposizioni a) e b), si continua ora con la dimostrazione finale del teorema: è
un insieme ordinato induttivo, cioè ogni parte non vuota e bene
ordinata ammette estremo superiore. Allo scopo, sia
è
un insieme ordinato induttivo, cioè ogni parte non vuota e bene
ordinata ammette estremo superiore. Allo scopo, sia
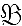

 ,
,
con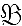 bene ordinata, e di conseguenza totalmente ordinata; si dimostra che tale parte di
bene ordinata, e di conseguenza totalmente ordinata; si dimostra che tale parte di  ammette estremo superiore.
ammette estremo superiore.
Si indichi con

Si consideri ora la famiglia di applicazioni
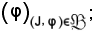
se si dimostra che per tale famiglia è vera la b) ora dimostrata, allora si può asserire che è vera la a).
Si considerino due elementi
(J', φ') e (J'', φ'')
dell'insieme degl'indici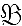 , totalmente ordinato da ≤', può verificarsi che:
, totalmente ordinato da ≤', può verificarsi che:
(J', φ') ≤' (J'', φ'') v (J'', φ'') ≤' (J', φ').
Se è
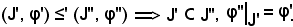
Siccome
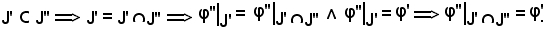
Inoltre,
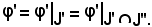
Quindi:
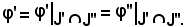
Se è
(J'', φ'') ≤' (J', φ'),
si perviene allo stesso riusultato, pertanto si può concludere che comunque si prendano due elementi dell'insieme degl'indici, si trova che le restrizioni delle due applicazioni relative sono uguali, quindi è vera la b) prima dimostrata, ed essendo quest'ultima equivalente alla a), si ha che:
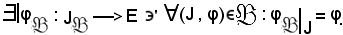
Si dimostra ora che:
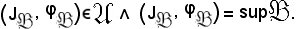
Affinchè
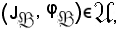
deve verificarsi che
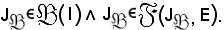
Che
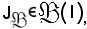
è stato già verificato.
Siccome risulta
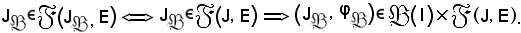
Si verifica ora che
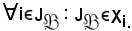
Si fissi
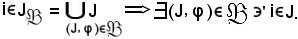
Siccome i J, si calcola ora
J, si calcola ora
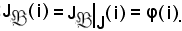
Inoltre, in quanto
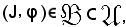
risulterà
φ(i) Xi,
Xi,
allora, sussistendo l'uguaglianza
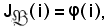
si ha:
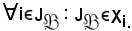
Pertanto, avendo verificato che:
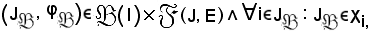
senz'altro risulta
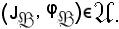
Si dimostra ora che
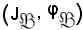
è un maggiorante e che risulta il più piccolo.
Si verifica prima che è un maggiorante, cioè che:
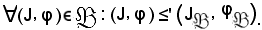
Allo scopo, si fissi
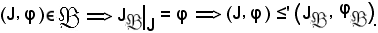
Si dimostra ora che
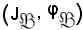
è il più piccolo dei maggioranti.
Sia
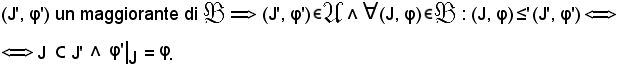
Dire che

in quanto J varia mentre J' rimane fisso, quindi
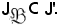
Si dimostra ora che
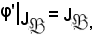
e ciò si verificherà se
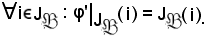
Pertanto, si consideri
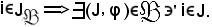
Essendo i J, si calcola quindi
J, si calcola quindi
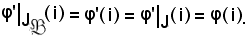
Così pure
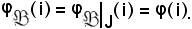
Essendo uguali gli ultimi membri, risulta:
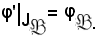
Resta così dimostrato che
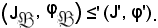
Pertanto, si può affermare che
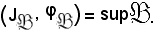
Esistendo l'estremo superiore di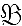 ,
,  è un insieme induttivo, si può allora applicare il teorema di Zorn, per il quale
è un insieme induttivo, si può allora applicare il teorema di Zorn, per il quale
 (L, f)
(L, f)
 massimale per
massimale per 

 i
i L : f(i)
L : f(i) Xi.
Xi.
Se si dimostra che L = I, il problema è risolto.
Si suppone per assurdo che L ≠ I e si tiene conto che L I, perchè (L, f)
I, perchè (L, f)
 .Dire che
.Dire che
L ≠ I I - L ≠
I - L ≠ 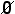 .
.
Sia
α I - L
I - L
e si indichi con
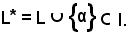
Si consideri ora l'applicazione
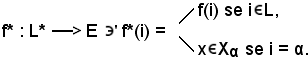
Si dimostra che
(L*, f*)
 ;
;
innanzitutto si osserva che
L* I,
I,
pertanto resta da verificare che
 i
i L* : f*(i)
L* : f*(i) Xi.
Xi.
Poichè
i L* : i
L* : i L v i = α.
L v i = α.
Se
i L : f*(i) = f(i)
L : f*(i) = f(i) Xi,
Xi,
se
i = α : f*(i) = x Xα.
Xα.
Dunque
(L*, f*)
 ,
,
si prova che
(L, f) ≤' (L*, f*).
Infatti,
L L*
L*
inoltre
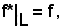
Ia qual cosa deriva dal modo in cui è stata costruita f.
D'altro canto,
(L, f) ≠ (L*, f*),
in quanto
L ≠ L*,
ne consegue pertanto che
(L, f) <' (L*, f*),
e ciò è assurdo, perchè (L, f) è massimale.
Siccome l'assurdo è derivato dall'aver supposto
L ≠ I,
si conclude che
L = I.
f(x)
In tal modo è dimostrata la (1), cioè che g о f è strettamente crescente; (2), (3) e (4) si dimostrano analogamente.
Sia (E, ≤) un insieme ordinato e si consideri la bigezione canonica
iE : E
Si vuol vedere se iE è monotòna e, allo scopo, si dimostra che è strettamente crescente.
Infatti, considerati due elementi
x
Siccome iE è bigettiva, e quindi invertibile, ed essendo iE stessa la la sua inversa, quest'ultima è anche strettamente crescente.
Tutto ciò è un prototipo di quanto è chiamato isomorfismo secondo la seguente definizione:
-isomorfismo di E in E' per ≤ e ≤' è ogni applicazione bigettiva di E in E' strettamente crescente insieme alla sua inversa.
Quando esiste un isomorfismo di E in E', (E, ≤) e (E', ≤') si dicono isomorfi per l'ordine e tale circostanza si indica con
(E, ≤) ≈ (E', ≤').
Siano (E, ≤), (E', ≤'), (E', ≤'') tre insiemi ordinati, si dimostra che:
(E, ≤) ≈ (E', ≤'), (E', ≤') ≈ (E'', ≤'')
Allo scopo, basta dimostrare che, essendo f e g bigettive e strettamente crescenti insieme alle loro inverse, anche g о f è strettamente crescente insieme alla sua inversa.
Infatti, g о f : E
(E, ≤) ≈ (E'', ≤'').
Si dimostra inoltre, in modo ovvio, che:
(E, ≤) ≈ (E', ≤')
ed anche
(E, ≤) ≈ (E, ≤),
in quanto esiste iE.
Dunque, l'isomorfismo gode delle stesse proprietà delle relazioni di equavalenza.
Sia (E, ≤) un insieme totalmente ordinato, (E', ≤') un insieme ordinato, ed
f : E
si dimostra che:
a) f è un isomorfismo di E in E' per ≤ e ≤'.
b) ≤' è una relazione di totale ordine.
Dimostrazione a).
Affinchè f sia un isomorfismo, basta dimostrare che f è bigettiva e che la sua inversa sia strettamente crescente.
Siccome per ipotesi f è surgettiva, affinchè sia bigettiva, basta dimostrare che sia anche ingettiva, cioè
Essendo E totalmente ordinato, e tenendo conto che x ≠ y, risulta
x < y v y < x.
Per la crescenza di f, risulta
x < y
se invece
y < x
Pertanto la f è ingettiva.
Essendo f bigettiva, ha senso considerare la sua inversa, chiamata
g : E'
Si dimostra che g è anch'essa strettamente crescente, cioè considerati
x'
Essendo
x'
ed E totalmente ordinato da ≤, risulta
g(x') ≤ g(y'),
oppure
g(y') ≤ g(x').
Inoltre, g è bigettiva ed x' <' y', per cui
(1) g(x') < g(y') v (2) g(y') < g(x').
La (1) dimostra quanto asserito. Si vede ora se sussiste la (2).
Per la stretta crescenza di f, risulta
f(g(y')) <' f(g(x')).
Siccome
f(g(y')) = f о g(y') = iE'(y') = y',
f(g(x')) = f о g(x') = iE'(x') = x',
cioè
y' <' x',
e ciò non può essere, perchè si è supposto che
x' <' y'.
In tal modo si è dimostrato che f è un isomorfismo di E in E' per ≤ e ≤'.
Dimostrazione b).
Si dimostra che ≤' è una relazione di totale ordine.
Infatti, siano
x'
ed essendo E totalmente ordinato, risulta
Se
x ≤ y,
per la stretta crescenza della f, si ha
f(x) ≤' f(y)
Analogamente, si dimostra che
y' ≤' x',
pertanto resta dimostrato che ≤' è una relazione di totale ordine.
Nota bene
Avendo dimostrato che una relazione di buon ordine è una relazione di totale ordine, il teorema ora dimostrato sussiste ugualmente; solo nell'ipotesi che ≤ sia una relazione di buon ordine, tale risulterà anche ≤', cioè occorre dimostrare che:
Chiaramente risulta
essendo ≤ una relazione di buon ordine su E,
Si consideri ora
f(m) = m';
essendo
m X
X  f(m)
f(m) f(X) = f(g(X')) = f о g(X') = iE'(X') = X',
f(X) = f(g(X')) = f о g(X') = iE'(X') = X',
cioè
cioè
f(m)
Si dimostra ora che m' è il più piccolo elemento di X' per ≤'.
Scelto ad arbitrio
x'
inoltre
x'
allora, essendo m il più piccolo elemento di X, risulta
m ≤ g(x').
Tenendo conto della crescenza di f,
m ≤ g(x')
cioè
f(m) ≤' x'
Quindi ≤' è una relazione di buon ordine.
Corollario
Se è assegnato un insieme totalmente ordinato o bene ordinato ed un isomorfismo di tale insieme in un altro insieme ordinato, quest'ultimo è un insieme bene ordinato.
Siano (E, ≤) un insieme ordinato, E' un altro insieme ed
f : E
un'applicazione bigettiva.
Si dimostra che esiste una ed una sola relazione d'ordine ≤' su E' in modo tale che f sia un isomorfismo di E in E', cioè:
Si indichi con
cioè
Si dimostra ora che è una relazione d'ordine.
Allo scopo, si deve verificare che:
(1) x'
(2) x'
Dimostrazione (1).
x'
Dimostrazione (2).
x'
e per la bigettività di f, si ha:
f(g(x')) = f(g(y'))
ed inoltre, tenendo conto che
f(g(x')) = f о g(x') = iE'(x') = x' e f(g(y')) = f о g(y') = iE'(y') = y'
In tal modo resta provata l'esistenza della relazione d'ordine ≤'; si prova ora l'unicità.
Allo scopo, basta riconoscere che, considerata l'ulteriore relazione d'ordine ≤'', risulta
≤' = ≤'',
cioè
≤' relazione d'ordine su E, ≤'' relazione d'ordine su E
Si dimostra prima che:
≤'
Infatti, si consideri
(x'', y')
e, siccome ≤'' è una relazione d'ordine su E, si ha:
x' = f(g(x')) ≤'' f(g(y')) = y'
Per ≤'' si dimostra, analogamente che:
≤''
Si dimostra ora che f è un isomorfismo, cioè che f è strettamente crescente insieme alla sua inversa g.
Siano ora
x
essendo f bigettiva e quindi ingettiva.
f(x) ≤' f(y),
per come è stata definita ≤', basta dimostrare che
g(f(x)) < g(f(y)),
e ciò è già vero, in quanto
g(f(x)) = x, g(f(y)) = y,
vale a dire che
x < y.
La relazione ≤' così costruita su E' si dice ottenuta per trasporto di ≤ su E' per f.
Nota bene
Se ≤ è una relazione di totale ordine, anche ≤' è tale, e lo stesso dicasi se ≤ è una relazione di buon ordine.
Tra le assunzioni fondamentali della "Teoria degl'insiemi" figurano le seguenti:
a) Assioma della scelta, b) Teorema di Zermelo, c) Teorema di Zorn.
L'assioma della scelta esprime:
Il teorema di Zermelo esprime:
Il teorema di Zorn esprime:
se (E, ≤) è un insieme ordinato induttivo,
Si riconosce che dall'assioma della scelta consegue il teorema di Zermelo, e da questi quello di Zorn, e da quest'ultimo l'assioma della scelta, cioè:
a)
Per facilitare tali dimostrazioni, si premettono alcuni lemmi.
Lemma 1
Si consideri l'insieme ordinato (E, ≤) e l'applicazione
f : E
Si fissi x0
l'insieme delle parti K di E che verifichi le condizioni KI, KII, KIII, cioè:
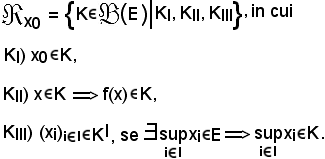
A tal punto, si dimostra quanto segue:
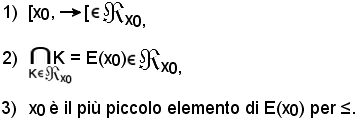
Dimostrazione 1).
Allo scopo, è necessario che essa verifichi KI), KII) e KIII), cioè:
e ciò è vero, in quanto
pertanto, si ha:
e ciò è vero, perchè:
In tal modo è dimostrata la 1).
Dimostrazione 2).
Allo scopo, è necessario che essa verifichi KI), KII) e KIII):
KI) è verificato, in quanto si ha:
KII) è verificato, in quanto si ha:
KIII) è verificato, in quanto, considerata la famiglia
Infatti:
perchè per K è valida KIII).
Si deve dimostrare che x0 è il più piccolo elemento di E(x0), cioè un minorante degli elementi di E(x0).
Infatti:
e, scegliendo come K l'intervallo
Si consideri ora
Pertanto resta dimostrato il lemma 1).
Nota bene
Si dimostra anche che:
Ciò rappresenta il principio di induzione completa.
A
ed essendo noto che
è dimostrato quanto asserito.
Lemma 2
Si considerino l'insieme ordinato (E, ≤), l'applicazione f : E
Supponendo per ipotesi che
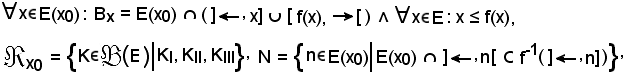
si dimostra:
1)
Dimostrazione 1).
E' ovvio che:
Per il principio d'induzione completa, affinchè risulti Bn = E(x0), bisogna dimostrare che:
cioè Bn deve verificare KI), KII) e KIII).
KI) - E' noto che x0
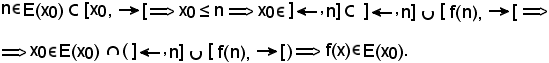
KII) - Si consideri
Se x
Sia allora
Supponendo
Se
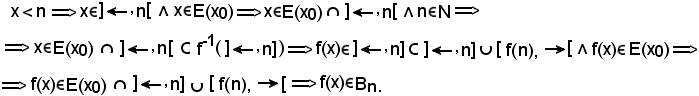
Se
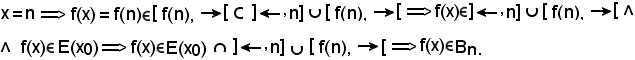
Supponendo ora
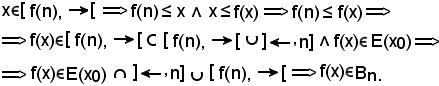
KIII) - Si considerino
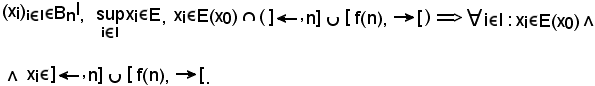
Siccome E(x0) verifica la KIII), se
Inoltre, se
Supponendo che
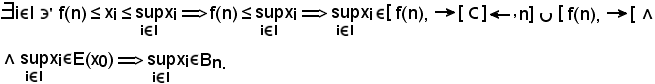
Se invece
Dunque, in ogni caso,
quindi Bn verifica KIII) ed è così dimostrato che
Bn = E(x0).
Dimostrazione 2).
Si deve dimostrare che:
N = E(x0).
Per come è stato definito N, risulta
N
Allora, per il principio d'induzione completa, basta dimostrare che N verifica le proprietà KI), KII) e KIII).
KI) Se
Si ricorda ora una proprietà sulla relazione d'inclusione
A
in virtù della quale, essendo
si ha:
KII) Si deve dimostrare che, considerato
n
Per ipotesi, dunque, è noto che
La tesi è la seguente:
Infatti, che f(n)
dunque
Essendo x
in quanto x < f(n), deve risultare
x ≤ a.
Se
x = n
Se
dunque
KIII) Sia
Per ipotesi, dunque, è noto che
Si deve dimostrare che, considerato
Infatti,
Inoltre, siccome
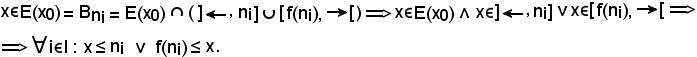
Si osserva ora che la condizione f(ni) ≤ x è da scartare perchè è contro l'ipotesi, infatti supponendo
essendo
e ciò non è possibile, perchè

Allora,
Se
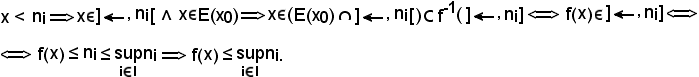
Se x = ni, è noto che:
Certamente
perchè
Si è così dimostrato che
N = E(x0).
Dunque, in conclusione:
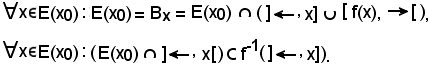
Si dimostra ora che E(x0) è un insieme bene ordinato, cioè che presa una parte non vuota di E(x0), questa è dotata del più piccolo elemento. Sia
si vuole dimostrare che X ha il più piccolo elemento.
Siccome
si ricava che E(x0) è una parte di E totalmente ordinata per ≤.
Infatti, se
x
e, per l'ipotesi su f, si ha che x ≤ f(x) ed x ed y sono paragonabili per ≤.
Si suppone che X abbia più di due elementi, si presentano due casi:
1) x0
2) x0
Dimostrazione 1).
Sia
x0
dunque x0 è un minorante di X, derivante dal fatto che x0 è il più piccolo elemento di E(x0). Quindi x0
e ciò dice che E(x0) è un insieme bene ordinato, risultando X fornito del più piccolo elemento.
Dimostrazione 1).
Sia
x0
essendo x0 il più piccolo elemento di E(x0), risulta che x0 è un minorante di X, cioè
Si indica ora con A l'insieme dei minoranti di X, cioè:
Ovviamente
A ≠
in quanto x0
Si consideri ora una famiglia
e si supponga esistente il
Si dimostra che
Infatti:
cioè x è un maggiorante degli xi, per cui si ha che
Ciò esprime che
è un minorante, e come tale è elemento di A, cioè
Quindi:
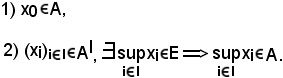
Pertanto, A verifica KI) e KIII); si può notare che A non verifica KII), cioè che:
Supponendo per assurdo che ciò sia vero, essendo
A
e verificando KI), KII) e KIII), risulta
e ciò non è possibile, infatti se
inoltre se
X
cioè
x
il tutto implica che x è il più grande elemento di E(x0), ma al massimo ne può esistere soltanto uno, e ciò esprime che X si dovrebbe ridurre ad un unico elemento, contro l'ipotesi che X è formato da più di due elementi. Dunque A non verifica KII), cioè deve
vale a dire che f(a) non è un minorante di X, cioè f(a) non può essere minore o uguale di ogni elemento di X, allora deve
Si dimostra che x è il più piccolo elemento di X.
Infatti:
ciò è possibile, in quanto
in particolare per A.
Non potendo essere
deve risultare x ≤ a; ma a è un minorante di X, risultante minore di un minorante, pertanto anch'esso è tale. Inoltre, x
Sia (E, ≤) un insieme ordinato induttivo e si consideri l'applicazione
f : E
così definita:
si vuole dimostrare che:
1)
2) x*0 è il più grande elemento di E(x0),
3) x*0 = f(x*0).
Si ricorda che E è un insieme ordinato induttivo se
Dimostrazione 1).
Dimostrazione 2).
Affinchè x*0 soddisfi la 2) basta dimostrare che x*0
Allo scopo, si consideri la famiglia
dal momento che E(x0) verifica KIII), deve verificarsi che
e di conseguenza
x*0
Dimostrazione 3).
Per come è stata definita f, risulta
x*0 ≤ f(x*0);
inoltre
f(x*0)
in quanto E(x0) verifica KII.
Ma x*0 è il più grande elemento di E(x0), pertanto risulta
f(x*0) ≤ x*0.
Dunque
x*0 = f(x*0).
Si dimostra ora che le seguenti tre proposizioni sono equivalenti:
a) Assioma della scelta:
b) Teorema di Zermelo:
c) Teorema di Zorn; se (E, ≤) è un insieme ordinato induttivo,
≤
Dimostrazione
a)
Si consideri l'insieme E ≠
delle sue parti, e si indichi con
Si dimostra ora che
Siccome
Si consideri pertanto la famiglia
Siccome ci si trova nelle ipotesi dell'assioma della scelta, vero per l'ipotesi a),
Si consideri ora l'applicazione
così definita:
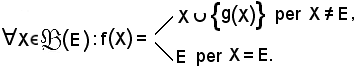
Si vuol dimostrare:
Se X ≠ E,
Se X = E,
f(X) = f(E) = E,
inoltre è noto che
E
e, considerando X al posto di E, si ha:
X
Si dimostra inoltre che:
Infatti,
Considerando f(X) - X, per definizione si ha:
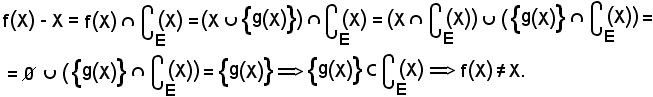
Dunque, l'unico elemento che è trasformato in se stesso da f è solo E.
Nota bene
Si ricorda quanto segue.
1)-Considerata la coppia
si è costruita un'applicazione
2)-Considerato l'insieme ordinato (E, ≤) si è costruita un'applicazione f : E
3)-Considerato
E insieme ordinato induttivo
Sulla scorta di quanto ora detto, nel caso in questione si può considerare X0 =
che risulterà bene ordinato dalla relazione
Si ricorda ora che è stato dimostrato che
è un reticolo completo, e quindi
è un insieme induttivo, pertanto
Quindi risulta:
Siccome è stato detto che l'unico elemento che la f trasforma in se stessa è E, si può concludere che X*0 = E.
Pertanto:
Si indica ora con
Si può in tal modo considerare la restrizione di g a
indicata con
Siccome
è un insieme bene ordinato, tale è pure
Nell'ipotesi che φ sia bigettiva, essendo
bene ordinato, esiste su E una relazione d'ordine ≤' ottenuta per trasporto, in modo tale che φ sia un isomorfismo.
Pertanto, essendo
bene ordinato, tale è E.
In tal modo, resta dimostrato il teorema di Zermelo.
Si dimostra ora che φ è bigettiva, pertanto basta provare che φ è ingettiva e surgettiva.
Per la surgettività di φ, si deve dimostrare che:
Si fissi un x
Certamente si verifica quanto segue:
in quanto l'insieme vuoto non è formato da alcun elemento.
Quest'ultima condizione esprime che
Si consideri ora la famiglia
Logicamente risulta
in quanto
Si osserva ora che
Infatti, supponendo che
ma
Quest'ultima condizione esprime che
A tal punto
Supponendo che
allora, per il principio d'induzione completa, si avrebbe
e ciò è impossibile, in virtù del fatto che
Infatti, se dovesse risultare
si svrebbe
E
e ciò è contro l'ipotesi, in quanto x
Dunque,
Essendo inoltre
e ciò si verifica quando E
Di conseguenza risulta
Resta dunque dimostrato che φ è surgettiva.
Si dimostra ora che φ è ingettiva, cioè:
Tenendo conto che
φ(X) = g(X), φ(Y) = g(Y),
è sufficiente dimostrare che
g(X) = g(Y)
Si suppone per assurdo che X ≠ Y, essendo
bene ordinato, sarà pure totalmente ordinato, pertanto X ed Y si troveranno nelle seguenti due possibili condizioni:
1) X
2) Y
A tal punto, si ricorda che:
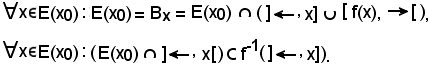
Si esamina ora il caso 1).
Allo scopo, si considera
Per il richiamo suddetto si ha:
Siccome
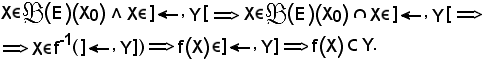
Inoltre, se
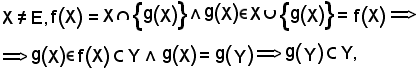
e ciò è assurdo, perchè per ipotesi
Quindi X non può essere contenuto strettamente in Y; analogamente, si dimostra che Y non può essere contenuto strettamente in X. L'unica conclusione possibile è quindi che X = Y.
b)
Si ricorda che:
Si consideri ora x0
ne dedurremmo che x0 è elemento massimale, pertanto m coinciderebbe con x0. Logicamente, dire che x0 non è elemento massimale, equivale a dire che
Si vuole dunque dimostrare che esiste almeno un elemento massimale dell'intervallo
si ragiona per assurdo, cioè
Si consideri l'insieme E; essendo vera la b), su E dovrà esistere una relazione di buon ordine, indicata con ≤'. Si costruisce ora l'applicazione
f : E
così definita:

Pertanto, fissato x
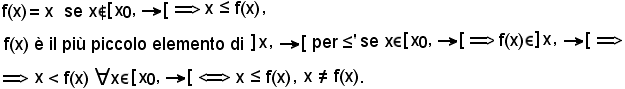
In ogni caso,
Inoltre, siccome E è un insieme ordinato induttivo,
tenendo conto che quest'ultima uguaglianza è stata dimostrata in precedenza.
Essendo
si è così pervenuti ad un assurdo, in quanto x*0 = f(x*0) e quindi esiste almeno un
x
che risulta massimale per ≤.
Si indichi con
Si fissi
in corrispondenza di tale i si consideri Xi
e porre
φ(i) = x
Allora
Si fissi ora su
Si dimostra che ≤' è una relazione d'ordine, cioè che è riflessiva, antisimmetrica e transitiva.
E' logico che se
(J, φ)

 (J, φ) ≤' (φ, J),
(J, φ) ≤' (φ, J),
in quanto risulta
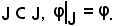
in quanto risulta
Dunque, ≤' è riflessiva.
Si dimostra ora che ≤' è antisimmetrica, cioè che
(J', φ') ≤' (J'', φ''), (J'', φ'') ≤' (φ'', J'')
Infatti:
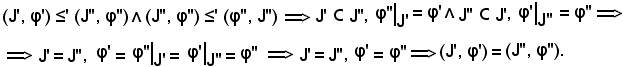
Dunque, ≤' è antisimmetrica.
Si dimostra infine che ≤' è transitiva, cioè che
(J', φ') ≤' (J'', φ''), (J'', φ'') ≤' (J''', φ'''),
Infatti:
Pertanto risulta
J'
quindi ha senso considerare e dimostrare quanto segue:
Infatti, considerato
Essendo poi x
Quindi
allora
Dunque, ≤' è transitiva.
Si è così dimostrato che ≤' è una relazione d'ordine.
Prima di dimostrare la parte finale del teorema, si dimostra quanto segue:
sia E un insieme e si consideri una famiglia di parti di E, cioè
Si considera ora un nuovo insieme E' e l'applicazione
fi : Xi
Si dimostra che le seguenti due proposizioni sono equivalenti:
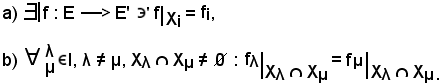
Si ricorda prima che se
e se
si può considerare
jX : X  E,
E,
e quindi l'applicazione composta
f ο jX : X E,
E,
indicata con
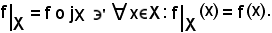
Si dimostra ora che:
a) e quindi l'applicazione composta
f ο jX : X
indicata con
Si dimostra ora che:
Si considerino,
e si osserva che
Xλ
ed inoltre che
fλ : Xλ
Si consideri ora
x
ed inoltre
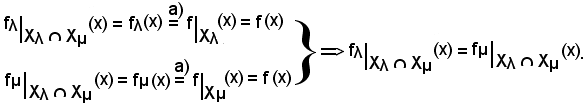
Resta quindi dimostrata la b), cioè:
Si dimostra ora che:
b)
Si suppone che ogni
fi = (Xi, E', Gi),
in cui
Gi
e si indica con
Si dimostra che G è una relazione funzionale, e quindi si può considerare l'applicazione f(E, E' G).
Allo scopo, si deve dimostrare che considerato x
Infatti, considerato
x
ed inoltre sia
y
Si dimostra ora che la sezione G(x) è formata da un solo elemento.
Allo scopo, se ne considerano due:
Supponendo che
λ = μ,
allora
(x, y)
Essendo Gλ una relazione funzionale, Gλ(x) si riduce ad un unico elemento, il che implica che
y = z.
Supponendo invece che
λ ≠ μ,
allora
Pertanto, si consideri
siccome
x
ha senso considerare l'uguaglianza
Analogamente, si consideri
(x, z)
ma
x
quindi ha senso considerare l'uguaglianza
Per la validità della b), deve risultare
il che ha come ovvia conseguenza che
y = z.
Si è così dimostrato che Gi è una relazione funzionale, si può pertanto considerare la terna
f = (E, E', G).
Si dimostra ora che, quale che sia x in Xi,
Si può allora fissare:
(x, f(x))
se si considera
Si dimostra ora l'unicità della f.
Siano
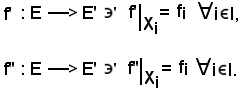
In tali condizioni, si può considerare:
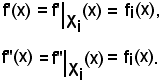
Essendo uguali i secondi membri di tali uguaglianze, si ha:
f'(x) = f''(x)
Dopo aver dimostrato l'equivalenza delle proposizioni a) e b), si continua ora con la dimostrazione finale del teorema:
con
Si indichi con
Si consideri ora la famiglia di applicazioni
se si dimostra che per tale famiglia è vera la b) ora dimostrata, allora si può asserire che è vera la a).
Si considerino due elementi
(J', φ') e (J'', φ'')
dell'insieme degl'indici
(J', φ') ≤' (J'', φ'') v (J'', φ'') ≤' (J', φ').
Se è
Siccome
Inoltre,
Quindi:
Se è
(J'', φ'') ≤' (J', φ'),
si perviene allo stesso riusultato, pertanto si può concludere che comunque si prendano due elementi dell'insieme degl'indici, si trova che le restrizioni delle due applicazioni relative sono uguali, quindi è vera la b) prima dimostrata, ed essendo quest'ultima equivalente alla a), si ha che:
Si dimostra ora che:
Affinchè
deve verificarsi che
Che
è stato già verificato.
Siccome risulta
Si verifica ora che
Si fissi
Siccome i
Inoltre, in quanto
risulterà
φ(i)
allora, sussistendo l'uguaglianza
si ha:
Pertanto, avendo verificato che:
senz'altro risulta
Si dimostra ora che
è un maggiorante e che risulta il più piccolo.
Si verifica prima che è un maggiorante, cioè che:
Allo scopo, si fissi
Si dimostra ora che
è il più piccolo dei maggioranti.
Sia
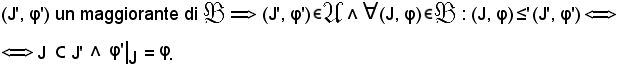
Dire che
in quanto J varia mentre J' rimane fisso, quindi
Si dimostra ora che
e ciò si verificherà se
Pertanto, si consideri
Essendo i
Così pure
Essendo uguali gli ultimi membri, risulta:
Resta così dimostrato che
Pertanto, si può affermare che
Esistendo l'estremo superiore di
Se si dimostra che L = I, il problema è risolto.
Si suppone per assurdo che L ≠ I e si tiene conto che L
L ≠ I
Sia
e si indichi con
Si consideri ora l'applicazione
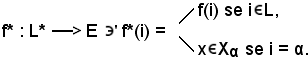
Si dimostra che
(L*, f*)
innanzitutto si osserva che
L*
pertanto resta da verificare che
Poichè
i
Se
i
se
i = α : f*(i) = x
Dunque
(L*, f*)
si prova che
(L, f) ≤' (L*, f*).
Infatti,
L
inoltre
Ia qual cosa deriva dal modo in cui è stata costruita f.
D'altro canto,
(L, f) ≠ (L*, f*),
in quanto
L ≠ L*,
ne consegue pertanto che
(L, f) <' (L*, f*),
e ciò è assurdo, perchè (L, f) è massimale.
Siccome l'assurdo è derivato dall'aver supposto
L = I.