IMMAGINI DIRETTE, RECIPROCHE E PROPRIETA' ---> INDICE
Immagini dirette
Sia f un'applicazione dell'insieme E nell'insieme F, cioè
f : E F
F
ed
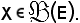
Si chiama immagine diretta di X mediante f, e s'indica con f(X), quanto segue:
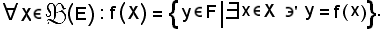
In altri termini
(y f(X))
f(X))  ((y
((y F)
F)  (
( x
x X
X  y = f(x)).
y = f(x)).
Cioè, al variare di x varia f(x) e quando x avrà percorso tutto l'insieme X, parte di E, f(x) avrà percorso una certa parte che rappresenta l'immagine diretta.
Proprietà
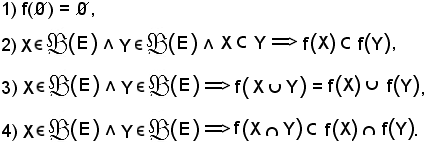
La proprietà 1) è vera per definizione.
Dimostrazione 2): si consideri y f(X), per definizione
f(X), per definizione  x
x X
X  y = f(x). Essendo x
y = f(x). Essendo x X, e per ipotesi X
X, e per ipotesi X  Y, risulta x
Y, risulta x Y per definizione di relazione d'inclusione. Però, quando
Y per definizione di relazione d'inclusione. Però, quando  x
x Y
Y  y = f(x), risulta y
y = f(x), risulta y f(Y). Quindi, essendo y comune ad f(X) ed f(Y), segue che
f(Y). Quindi, essendo y comune ad f(X) ed f(Y), segue che
come volevasi dimostrare.
Dimostrazione 3): per la proprietà 4) della riunione risulta
X X
X  Y, Y
Y, Y  X
X  Y
Y
e, per la proprietà 2), dimostrata in precedenza, si ha:
f(X) f(X
f(X  Y), f(Y)
Y), f(Y)  f(X
f(X  Y)
Y)  f(X)
f(X)  f(Y)
f(Y)  f(X
f(X  Y),
Y),
per la proprietà 5) della riunione.
E' stato quindi dimostrato che il 2° membro è contenuto nel 1°; si dimostra ora il viceversa.
Allo scopo, si consideri
z' f(X
f(X  Y)
Y) 
 z
z X
X  Y
Y  z' = f(z),
z' = f(z),
per definizione di immagine diretta.
Inoltre, siccome
z X
X  Y
Y  z
z X v z
X v z Y,
Y,
per definizione di riunione.
Se z X, per definizione di immagine diretta z'
X, per definizione di immagine diretta z' f(X)
f(X)  f(X
f(X  Y) f
Y) f f(X)
f(X)  f(X
f(X  Y),
Y),
se z Y, per definizione di immagine diretta z'
Y, per definizione di immagine diretta z' f(Y)
f(Y)  f(X
f(X  Y)
Y)  f(Y)
f(Y)  f(X
f(X  Y),
Y),
quindi
f(X  Y)
Y)  f(X)
f(X)  f(Y).
f(Y).
Avendo dimostrato che il 2° membro è contenuto nel 1° e che il 1° è contenuto nel 2°, risulta:
f(X  Y) = f(X)
Y) = f(X)  f(Y),
f(Y),
come volevasi dimostrare.
Dimostrazione 4): per la proprietà 4') dell'intersezione risulta
X Y
Y  X, X
X, X  Y
Y  Y
Y
e, per la proprietà 2), dimostrata in precedenza, si ha:
f(X Y)
Y)  f(X), f(X
f(X), f(X  Y)
Y)  f(Y).
f(Y).
Pertanto, siccome f(X Y) è contenuto sia in f(X) che in f(Y, esso è contenuto nella loro intersezione, cioè:
Y) è contenuto sia in f(X) che in f(Y, esso è contenuto nella loro intersezione, cioè:
come volevasi dimostrare.
6)-Estensione di un'applicazione alle parti di un insieme
Si è già visto, e si riporta in quanto fa parte di questa trattazione, che se
f : E F
F
è un'applicazione dell'insieme E nell'insieme F ed
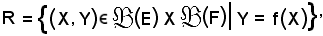
come è stato dimostrato, è una relazione funzionale, e l'applicazione
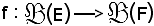
si chiama estensione di f alle parti di un insieme.
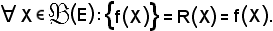
E' bene osservare che f(X) R(X) è il nuovo valore di X nella nuova applicazione e coincide proprio con f(X) dell'applicazione di partenza.
R(X) è il nuovo valore di X nella nuova applicazione e coincide proprio con f(X) dell'applicazione di partenza.
Immagini reciproche
Sia f un'applicazione dell'insieme E nell'insieme F, cioè
f : E  F
F
ed
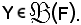
Si chiama immagine reciproca di Y mediante f, e s'indica con f-1(Y), quanto segue:
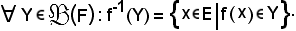
In altri termini
(x f-1(Y))
f-1(Y))  ((x
((x E)
E)  (f(x)
(f(x) Y).
Y).
Proprietà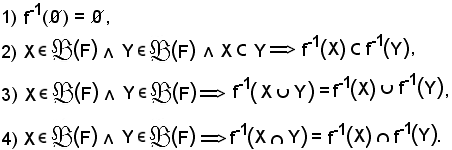
La proprietà 1) è vera per definizione, però vi sono insiemi che pur essendo non vuoti hanno immagine reciproca vuota; in particolare hanno quegli elementi
f(x)  Y
Y  f(E) =
f(E) = 
 f-1(F) =
f-1(F) =  .
.
Dimostrazione 2): si consideri x f-1(X), per definizione x
f-1(X), per definizione x E ed f(x)
E ed f(x) X.
X.
Essendo
f(x) X
X  Y
Y  f(x)
f(x) Y
Y  x
x f-1(Y).
f-1(Y).
Quindi è dimostrato che:
f-1(X) f-1(Y).
f-1(Y).
Dimostrazione 3): per la proprietà 4) della riunione risulta
X  X
X  Y, Y
Y, Y  X
X  Y
Y
e, per la proprietà 2), dimostrata in precedenza, si ha:
f-1(X) f-1(X
f-1(X  Y), f-1(Y)
Y), f-1(Y)  f-1(X
f-1(X  Y)
Y)  f-1(X)
f-1(X)  f-1(Y)
f-1(Y) f-1(X
f-1(X  Y),
Y),
per la proprietà 5) della riunione.E' stato quindi dimostrato che il 2° membro è contenuto nel 1°; si dimostra ora il viceversa.
Allo scopo, si consideri
Se f(x) X, risulta x
X, risulta x f-1(X)
f-1(X)  f-1(X)
f-1(X)  f-1(Y),
f-1(Y),
se f(x) Y, risulta x
Y, risulta x f-1(Y)
f-1(Y)  f-1(X)
f-1(X)  f-1(Y),
f-1(Y),
In entrambi i casi
x f-1(X)
f-1(X)  f-1(Y),
f-1(Y),
quindi
f-1(X Y)
Y)  f-1(X)
f-1(X)  f-1(Y),
f-1(Y),
Avendo dimostrato che il 2° membro è contenuto nel 1° e che il 1° è contenuto nel 2°, risulta:
f-1(X Y) = f-1(X)
Y) = f-1(X)  f-1(Y).
f-1(Y).
Dimostrazione 4): per la proprietà 4') dell'intersezione risulta
X Y
Y  X, X
X, X  Y
Y  Y
Y
e, per la proprietà 2), dimostrata in precedenza, si ha:
f-1(X Y)
Y)  f-1(X), f-1(X
f-1(X), f-1(X  Y)
Y)  f-1(Y).
f-1(Y).
Pertanto, siccome f-1(X Y) è contenuto sia in f-1(X) che in f-1(Y) è contenuto nella loro intersezione, cioè:
Y) è contenuto sia in f-1(X) che in f-1(Y) è contenuto nella loro intersezione, cioè:
f-1(X Y)
Y)  f-1(X)
f-1(X)  f-1(Y),
f-1(Y),
E' stato quindi dimostrato che il 1° membro è contenuto nel 2°; si dimostra ora il viceversa.
Allo scopo, si consideri un elemento arbitrario
z f-1(X)
f-1(X)  f-1(Y)
f-1(Y)  f(z)
f(z) X, f(z)
X, f(z) Y
Y  f(z)
f(z) X
X  Y
Y  z
z f-1(X
f-1(X  Y),
Y),
quindi
f-1(X) f-1(Y)
f-1(Y)  f-1(X
f-1(X  Y)
Y)
Avendo anche dimostrato che il 2° membro è contenuto nel 1°, si conclude che:
f-1(X Y) = f-1(X)
Y) = f-1(X)  f-1(Y),
f-1(Y),
come volevasi dimostrare.
Proprietà
Sia f un'applicazione dell'insieme E nell'insieme E', cioè
f : E E'.
E'.
si dimostra che:
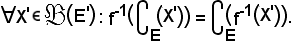
Infatti, sia
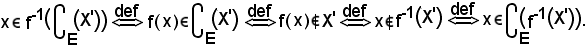
Estensione reciproca di un'applicazione alle parti di un insieme
E' bene osservare che f-1(Y) R1(Y) è il nuovo valore di Y nella nuova applicazione e coincide proprio con f-1(Y) dell'applicazione di partenza.
R1(Y) è il nuovo valore di Y nella nuova applicazione e coincide proprio con f-1(Y) dell'applicazione di partenza.
Relazioni fra immagini dirette, reciproche, applicazioni surgettive, ingettive e bigettive
Sia
f : E E'
E'
un'applicazione dell'insieme E nell'insieme E', si dimostrano le seguenti proprietà:
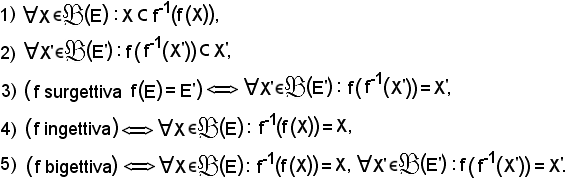
Dimostrazione 1): si consideri x X, per definizione di immagine reciproca f(x)
X, per definizione di immagine reciproca f(x) f(X) e quindi x
f(X) e quindi x f-1(f(X)). Essendo x elemento comune ad X ed f-1(f(X)), si ha:
f-1(f(X)). Essendo x elemento comune ad X ed f-1(f(X)), si ha:
Dimostrazione 2): si consideri x' f(f-1(X')), per definizione di immagine diretta
f(f-1(X')), per definizione di immagine diretta
 x
x f-1(X')
f-1(X')  f(x) = x',
f(x) = x',
inoltre, essendo
x f-1(X'),
f-1(X'),
per definizione di immagine reciproca, si ha f(x) X', e poichè f(x) = x', risulta x'
X', e poichè f(x) = x', risulta x' X'.Essendo x' elemento comune ad f(f-1(X')) ed X', si ha:
X'.Essendo x' elemento comune ad f(f-1(X')) ed X', si ha:
f(f-1(X')) X',
X',
come volevasi dimostrare.
Dimostrazione 3): per ipotesi f è surgettiva, cioè f(E) = E' e sia
x' X'
X'
 x
x E
E  f(x) = x',
f(x) = x',
inoltre, per definizione di immagine reciproca, essendo
f(x) X'
X'  x
x f-1(X')
f-1(X')  f(x) = x',
f(x) = x',
cioè
x' f(f-1(X')),
f(f-1(X')),
per definizione di immagine diretta.Essendo x' elemento comune ad X' e ad f(f-1(X')), si ha:
X' f(f-1(X')).
f(f-1(X')).
E' stato così dimostrato che il 2° membro è contenuto nel 1°; si dimostra ora il viceversa, che il 1° membro è contenuto nel 2°, cioè:
f(f-1(X')) X'.
X'.
Ciò è vero per la proprietà 2) suddetta.
Ora, nell'ipotesi che
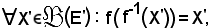
si dimostra che f è surgettiva.
Infatti, siccome
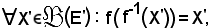
si ha anche
f(f-1(E')) = E',
ed essendo
f-1(E') = E,
si ha
f(E) = E',
cioè f è surgettiva, come volevasi dimostrare.
Dimostrazione 4): per ipotesi risulta
(f ingettiva) (
( x
x E
E  x'
x' E f(x) = f(x')
E f(x) = f(x')  x = x').
x = x').
Si considera ora un arbitrario elemento
x f-1(f(X)),
f-1(f(X)),
per definizione di immagine diretta
f(x) f(X),
f(X),
siccome per l'ingettività
 x'
x' X
X  f(x) = f(x')
f(x) = f(x')  x = x',
x = x',
si ha che
x X.
X.
E' stato così dimostrato che
f-1(f(X)) X.
X.
Si dimostra ora il viceversa, cioè che
X f-1(f(X)).
f-1(f(X)).
Ciò è vero per la proprietà 1) suddetta.
Ora, nell'ipotesi che
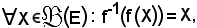
si dimostra che f è ingettiva.
Infatti, siccome
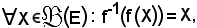
se x E ed x'
E ed x' E, si ha:
E, si ha:
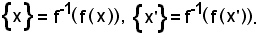
Se poi
f(x) = f(x'),
si ha:
x = x',
cioè f è ingettiva, come volevasi dimostrare.
Dimostrazione 5): è noto che risulta
(f bigettiva) (f ingettiva
(f ingettiva  f surgettiva).
f surgettiva).
La dimostrazione è banale, in quanto si ottiene dalle proprietà 3) e 4).
Sia f un'applicazione dell'insieme E nell'insieme F, cioè
f : E
ed
Si chiama immagine diretta di X mediante f, e s'indica con f(X), quanto segue:
In altri termini
(y
Cioè, al variare di x varia f(x) e quando x avrà percorso tutto l'insieme X, parte di E, f(x) avrà percorso una certa parte che rappresenta l'immagine diretta.
Proprietà
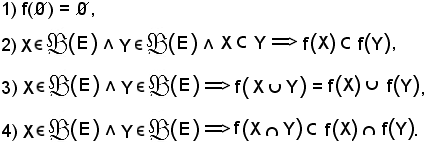
La proprietà 1) è vera per definizione.
Dimostrazione 2): si consideri y
f(X)  f(Y),
f(Y),
come volevasi dimostrare.
Dimostrazione 3): per la proprietà 4) della riunione risulta
X
e, per la proprietà 2), dimostrata in precedenza, si ha:
f(X)
per la proprietà 5) della riunione.
E' stato quindi dimostrato che il 2° membro è contenuto nel 1°; si dimostra ora il viceversa.
Allo scopo, si consideri
per definizione di immagine diretta.
Inoltre, siccome
per definizione di riunione.
Se z
se z
quindi
Avendo dimostrato che il 2° membro è contenuto nel 1° e che il 1° è contenuto nel 2°, risulta:
come volevasi dimostrare.
Dimostrazione 4): per la proprietà 4') dell'intersezione risulta
X
e, per la proprietà 2), dimostrata in precedenza, si ha:
f(X
Pertanto, siccome f(X
f(X  Y)
Y)  f(X)
f(X)  f(Y),
f(Y),
come volevasi dimostrare.
6)-Estensione di un'applicazione alle parti di un insieme
Si è già visto, e si riporta in quanto fa parte di questa trattazione, che se
f : E
è un'applicazione dell'insieme E nell'insieme F ed
come è stato dimostrato, è una relazione funzionale, e l'applicazione
si chiama estensione di f alle parti di un insieme.
Per definizione
E' bene osservare che f(X)
Immagini reciproche
Sia f un'applicazione dell'insieme E nell'insieme F, cioè
ed
Si chiama immagine reciproca di Y mediante f, e s'indica con f-1(Y), quanto segue:
In altri termini
Proprietà
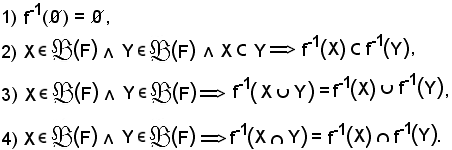
La proprietà 1) è vera per definizione, però vi sono insiemi che pur essendo non vuoti hanno immagine reciproca vuota; in particolare hanno quegli elementi
Dimostrazione 2): si consideri x
Essendo
f(x)
Quindi è dimostrato che:
f-1(X)
Dimostrazione 3): per la proprietà 4) della riunione risulta
e, per la proprietà 2), dimostrata in precedenza, si ha:
f-1(X)
per la proprietà 5) della riunione.
Allo scopo, si consideri
x f-1(X
f-1(X  Y)
Y)  f(x)
f(x) (X
(X  Y),
Y),
per definizione di immagine reciproca.
per definizione di immagine reciproca.
Se f(x)
se f(x)
In entrambi i casi
x
quindi
f-1(X
Avendo dimostrato che il 2° membro è contenuto nel 1° e che il 1° è contenuto nel 2°, risulta:
f-1(X
Dimostrazione 4): per la proprietà 4') dell'intersezione risulta
X
e, per la proprietà 2), dimostrata in precedenza, si ha:
f-1(X
Pertanto, siccome f-1(X
f-1(X
E' stato quindi dimostrato che il 1° membro è contenuto nel 2°; si dimostra ora il viceversa.
Allo scopo, si consideri un elemento arbitrario
z
quindi
f-1(X)
Avendo anche dimostrato che il 2° membro è contenuto nel 1°, si conclude che:
f-1(X
come volevasi dimostrare.
Proprietà
Sia f un'applicazione dell'insieme E nell'insieme E', cioè
f : E
si dimostra che:
Infatti, sia
Estensione reciproca di un'applicazione alle parti di un insieme
Si è già visto, e si riporta in quanto fa parte di questa trattazione, che se
f : E F
F
è un'applicazione dell'insieme E nell'insieme F ed
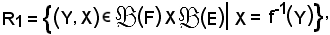
come è stato dimostrato, è una relazione funzionale, e l'applicazione
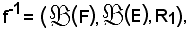
si chiama estensione reciproca di f alle parti di un insieme.
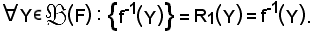
f : E
è un'applicazione dell'insieme E nell'insieme F ed
come è stato dimostrato, è una relazione funzionale, e l'applicazione
si chiama estensione reciproca di f alle parti di un insieme.
Per definizione
E' bene osservare che f-1(Y)
Relazioni fra immagini dirette, reciproche, applicazioni surgettive, ingettive e bigettive
Sia
f : E
un'applicazione dell'insieme E nell'insieme E', si dimostrano le seguenti proprietà:
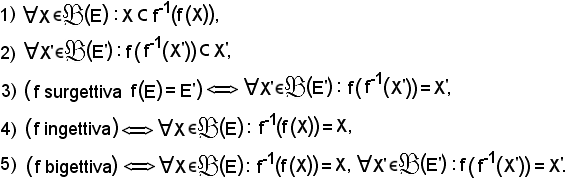
Dimostrazione 1): si consideri x
X  f-1(f(X)),
f-1(f(X)),
come volevasi dimostrare.
Dimostrazione 2): si consideri x'
inoltre, essendo
per definizione di immagine reciproca, si ha f(x)
f(f-1(X'))
come volevasi dimostrare.
Dimostrazione 3): per ipotesi f è surgettiva, cioè f(E) = E' e sia
x'
inoltre, per definizione di immagine reciproca, essendo
f(x)
cioè
per definizione di immagine diretta.
X'
E' stato così dimostrato che il 2° membro è contenuto nel 1°; si dimostra ora il viceversa, che il 1° membro è contenuto nel 2°, cioè:
f(f-1(X'))
Ciò è vero per la proprietà 2) suddetta.
Ora, nell'ipotesi che
si dimostra che f è surgettiva.
Infatti, siccome
si ha anche
f(f-1(E')) = E',
ed essendo
f-1(E') = E,
si ha
f(E) = E',
cioè f è surgettiva, come volevasi dimostrare.
Dimostrazione 4): per ipotesi risulta
(f ingettiva)
Si considera ora un arbitrario elemento
x
per definizione di immagine diretta
siccome per l'ingettività
si ha che
x
E' stato così dimostrato che
f-1(f(X))
Si dimostra ora il viceversa, cioè che
X
Ciò è vero per la proprietà 1) suddetta.
Ora, nell'ipotesi che
si dimostra che f è ingettiva.
Infatti, siccome
se x
Se poi
f(x) = f(x'),
si ha:
cioè f è ingettiva, come volevasi dimostrare.
Dimostrazione 5): è noto che risulta
(f bigettiva)
La dimostrazione è banale, in quanto si ottiene dalle proprietà 3) e 4).