INSIEMI PARTICOLARI ---> INDICE
1)-Insieme reticolato
Sia E un insieme ordinato dalla relazione d'ordine ≤; se esso gode della seguente proprieta:
 x
x E,
E,  y
y E
E  sup(x, y),
sup(x, y),  inf(x, y),
inf(x, y),
si chiama insieme reticolato.
2)-Insieme completamente reticolato
Sia E un insieme ordinato dalla relazione d'ordine ≤; se esso gode della seguente proprieta:
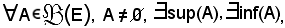
allora A si dice insieme completamente reticolato.
3)-Insieme filtrante superiormente
Sia E un insieme ordinato dalla relazione d'ordine ≤:
E filtrante superiormente
 x
x E,
E,  y
y E,
E,  z
z E
E  x ≤ z, y ≤ z.
x ≤ z, y ≤ z.
4)-Insieme filtrante inferiormente
Sia E un insieme ordinato dalla relazione d'ordine ≤:
E filtrante inferiormente
 x
x E,
E,  y
y E,
E,  z
z E
E  z ≤ x, z ≤ y.
z ≤ x, z ≤ y.
5)-Casistica degl'insiemi filtrantiEsistono i seguenti tipi d'insiemi filtranti:
-insiemi filtranti superiormente ed inferiormente;
-insiemi filtranti superiormente e non inferiormente;
-insiemi filtranti inferiormente e non superiormente;
-insiemi non filtranti superiormente ed inferiormente.
Si dimostra che:
E totalmente ordinato E filtrante superiormente ed inferiormente.
E filtrante superiormente ed inferiormente.
Infatti, dire che E è un insieme ordinato dalla relazione d'ordine ≤, significa che se
può verificarsi che
x ≤ y v y ≤ z.
Se x ≤ y, scelto z = y, si ha:
x ≤ z, y ≤ z E filtrante superiormente.
E filtrante superiormente.
Se x ≤ y, scelto z = x, si ha:
z ≤ x, z ≤ y E filtrante inferiormente.
E filtrante inferiormente.
Se y ≤ z, scelto z = x, si ha:
y ≤ z, x ≤ z E filtrante superiormente.
E filtrante superiormente.
Se y ≤ z, scelto z = y, si ha:
z ≤ x, z ≤ y E filtrante inferiormente.
E filtrante inferiormente.
Un insieme filtrante superiormente ed inferiormente non è detto che sia totalmente ordinato, in quanto non si sa se x ed y siano paragonabili.
Elementi massimali e minimali
m E, m massimale
E, m massimale 
 x
x E
E  m ≤ x : x = m.
m ≤ x : x = m.
m E, m minimale
E, m minimale 
 x
x E
E  x ≤ m : x = m.
x ≤ m : x = m.
E' chiaro che un insieme può non avere elemento massimale o minimale.
Sia E un insieme ordinato dalla relazione d'ordine ≤, si dimostra che:
E filtrante superiormente, m massimale di E m è il più grande elemento di E per ≤.
m è il più grande elemento di E per ≤.
Allo scopo, basta dimostrare che:
 x
x E : m ≤ x.
E : m ≤ x.
Infatti,
x E, m
E, m E, E filtrante inferiormente
E, E filtrante inferiormente 
 z
z E
E  z ≤ m, z ≤ x.
z ≤ m, z ≤ x.
Siccome però m è minimale,
z = m,
quindi
m ≤ x.
Sia E un insieme ordinato dalla relazione d'ordine ≤; se esso gode della seguente proprieta:
si chiama insieme reticolato.
2)-Insieme completamente reticolato
Sia E un insieme ordinato dalla relazione d'ordine ≤; se esso gode della seguente proprieta:
allora A si dice insieme completamente reticolato.
3)-Insieme filtrante superiormente
Sia E un insieme ordinato dalla relazione d'ordine ≤:
E filtrante superiormente
4)-Insieme filtrante inferiormente
Sia E un insieme ordinato dalla relazione d'ordine ≤:
E filtrante inferiormente
5)-Casistica degl'insiemi filtranti
-insiemi filtranti superiormente ed inferiormente;
-insiemi filtranti superiormente e non inferiormente;
-insiemi filtranti inferiormente e non superiormente;
-insiemi non filtranti superiormente ed inferiormente.
Si dimostra che:
E totalmente ordinato
Infatti, dire che E è un insieme ordinato dalla relazione d'ordine ≤, significa che se
x E, y
E, y E,
E,
può verificarsi che
x ≤ y v y ≤ z.
Se x ≤ y, scelto z = y, si ha:
x ≤ z, y ≤ z
Se x ≤ y, scelto z = x, si ha:
z ≤ x, z ≤ y
Se y ≤ z, scelto z = x, si ha:
y ≤ z, x ≤ z
Se y ≤ z, scelto z = y, si ha:
z ≤ x, z ≤ y
Un insieme filtrante superiormente ed inferiormente non è detto che sia totalmente ordinato, in quanto non si sa se x ed y siano paragonabili.
Elementi massimali e minimali
m
m
E' chiaro che un insieme può non avere elemento massimale o minimale.
Sia E un insieme ordinato dalla relazione d'ordine ≤, si dimostra che:
E filtrante superiormente, m massimale di E
Allo scopo, basta dimostrare che:
Infatti,
x
Siccome però m è minimale,
z = m,
quindi
m ≤ x.