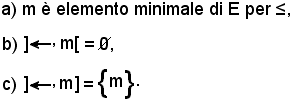INTERVALLI ---> INDICE
Sia (E, ≤) un insieme ordinato e si considerino a
E e bE; si definiscono i seguenti intervalli.1)-Intervallo chiuso di origine a e di estremo b, cioè:
Se a = b, l'intervallo si riduce ad un solo elemento, cioè:
Se a < b,
a
[a, b], b[a, b],perchè
a ≤ a < b ≤ b.
Nota bene
Condizione necessaria e sufficiente affinchè tale intervallo sia non vuoto è che a ≤ b.
2)-Intervallo semiaperto inferiormente di origine a e di estremo b
Se a = b, l'intervallo è vuoto.
Se a < b,
b
]a, b],perchè
a < b ≤ b.
Nota bene
Condizione necessaria e non sufficiente affinchè tale intervallo sia non vuoto è che a < b.
3)-Intervallo semiaperto superiormente di origine a e di estremo b
Se a = b, l'intervallo è vuoto.
Se a < b,
a
[a, b[,perchè
a ≤ a < b.
Nota bene
Condizione necessaria e non sufficiente affinchè tale intervallo sia non vuoto è che a < b.
4)-Intervallo aperto di origine a e di estremo b
Se a = b, l'intervallo è vuoto.
Nota bene
Condizione necessaria e non sufficiente affinchè tale intervallo sia non vuoto è che a < b.
5)-Intervallo chiuso superiormente da c
E ed illimitato inferiormente
6)-Intervallo aperto illimitato inferiormente di estremo c
E
Può essere vuoto, se esiste il più piccolo elemento di E.
7)-Intervallo chiuso illimitato superiormente di origine c
E
8)-Intervallo illimitato superiormente aperto inferiormente di origine c
E
Può essere vuoto, se esiste il più grande elemento di E.
Sia (E, ≤) un insieme ordinato, si dimostra che le seguenti tre proposizioni sono equivalenti:
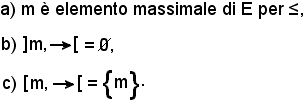
Dimostrazione
a)
b)Si suppone per assurdo che
Siccome per la a) m è elemento massimale di E per ≤, dev'essere m = x, contrariamente a quanto scaturito dall'aver supposto l'intervallo in questione diverso dall'insieme vuoto, quindi si puà concludere che esso è vuoto.
b)
c)Si premette la dimostrazione della seguente uguaglianza:
Si consideri un elemento
Se
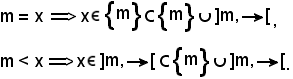
In tal modo resta dimostrato che il primo membro è contenuto nel secondo; si dimostra ora il viceversa.
Infatti, si ha:
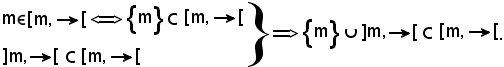
A tal punto, tenendo conto di tale uguaglianza, si dimostra la c):
c)
a)Si deve dimostrare che m è elemento massimale di E per ≤, cioè
x
E 
m ≤ x m = x.Infatti,
Analogamente si dimostra che le seguenti tre proposizioni sono equivalenti:
