OPERAZIONI SULLE FAMIGLIE DI INSIEMI ---> INDICE
Famiglia di un insieme
Si definisce famiglia di elementi di un dato insieme E, avente I come insieme degl'indici, una qualsiasi applicazione
f : I E.
E.
L'immagine diretta
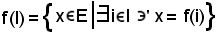
è chiamata insieme degli elementi della famiglia.
Si definisce famiglia di elementi di un dato insieme E, avente I come insieme degl'indici, una qualsiasi applicazione
f : I
L'immagine diretta
è chiamata insieme degli elementi della famiglia.
Inoltre,  i
i I, il valore che l'applicazione f assume in I, cioè f(i), si chiama elemento di indice i della famiglia.
I, il valore che l'applicazione f assume in I, cioè f(i), si chiama elemento di indice i della famiglia.
Per convenzione la famiglia si indica con
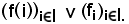
Famiglia doppia
Si consideri l'applicazione
f : I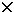 L
L  E,
E,
per convenzione la famiglia si indica con
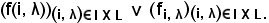
Tale famiglia è quindi formata da due indici, i e λ, e prende il nome di famiglia doppia.
Sottofamiglia di una famiglia
Si consideri l'applicazione
f : I E
E
e sia
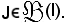
La restrizione di f a J,
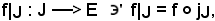
è chiamata sottofamiglia della famiglia data, cioè
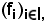
ha J come insieme degl'indici e la si indica come segue:
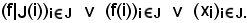
Siccome
J I,
I,
l'insieme degli elementi della sottofamiglia è contenuto nell'insieme degli elementi della famiglia di partenza, cioè
f(J) f(I),
f(I),
ossia
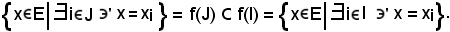
Famiglia di parti di un insieme
Si chiama famiglia di parti di un insieme E, avente I come insieme degl'indici, ogni famiglia di elementi delle parti di E avente I come insieme degl'indici.
Se si indica con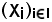 la famiglia di parti di E, tale simbolo indica l'applicazione
la famiglia di parti di E, tale simbolo indica l'applicazione
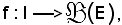
il cui valore in i I viene indicato con xi e chiamato elemento di indice i della famiglia. Logicamente risulta
I viene indicato con xi e chiamato elemento di indice i della famiglia. Logicamente risulta
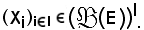
Riunione della famiglia
Sia (Xi)i I una
famiglia di parti dell'insieme E; gli elementi di E che appartengono ad
almeno un elemento di indice i della famiglia, cioè ad almeno un Xi, costituiscono una parte di E chiamata riunione della famiglia, che si indica con
I una
famiglia di parti dell'insieme E; gli elementi di E che appartengono ad
almeno un elemento di indice i della famiglia, cioè ad almeno un Xi, costituiscono una parte di E chiamata riunione della famiglia, che si indica con

Quindi:
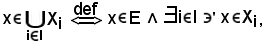
o anche
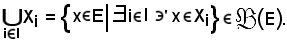
Intersezione della famiglia
Sia (Xi)i I una
famiglia di parti dell'insieme E; gli elementi di E che appartengono a
ciascun elemento di indice i della famiglia, cioè a ciascuno
degli Xi, costituiscono una parte di E chiamata intersezione della famiglia, che si indica con
I una
famiglia di parti dell'insieme E; gli elementi di E che appartengono a
ciascun elemento di indice i della famiglia, cioè a ciascuno
degli Xi, costituiscono una parte di E chiamata intersezione della famiglia, che si indica con

Quindi:
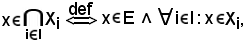
o anche
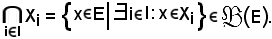
Caso particolare di riunione e di intersezione
Si considerino l'insieme E ed una parte dell'insieme delle parti di E, indicata con erre gotica, cioè
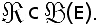
L'ingezione canonica
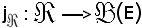
rappresenta la famiglia di parti di E che ha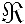 come insieme degl'indici e che per ogni X appartenente ad
come insieme degl'indici e che per ogni X appartenente ad 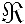 considera come elemento di indice X lo stesso X inteso come elemento di
considera come elemento di indice X lo stesso X inteso come elemento di 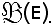
Conformemente a quanto visto, la famiglia si indica con
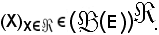
Pertanto la riunione e l'intersezione risultano rispettivamente:
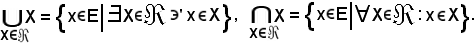
Proprietà
Se A e B sono parti dell'insieme E:
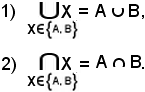
Dimostrazione 1).
Si consideri
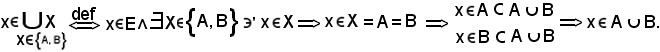
E' stato quindi dimostrato che:
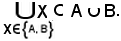
Si dimostra ora che:
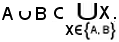
Allo scopo, si consideri
x A
A  B,
B,
per definizione di riunione
x A v x
A v x B.
B.
Se
x A,
A,
fissando
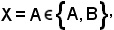
x X
X
e, per definizione:
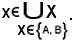
Se
x B,
B,
fissando
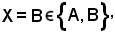
x X
X
e, per definizione:
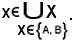
E' stato dimostrato che in ogni caso x appartiene alla riunione della famiglia, cioè
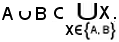
In definitiva la 1) è vera.
Dimostrazione 2).
Si consideri
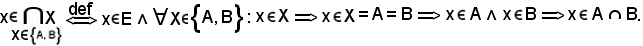
E' stato quindi dimostrato che:
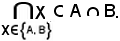
Si dimostra ora che:
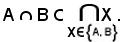
Allo scopo, si consideri
x A
A  B
B  x
x A
A  x
x B.
B.
Siccome
x A
A  x
x B,
B,
fissando
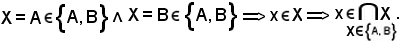
E' stato dimostrato che x appartiene all'intersezione della famiglia, cioè
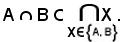
In definitiva la 2) è vera.
Proprietà
Sia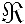 l'insieme degli elementi della famiglia
l'insieme degli elementi della famiglia
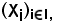
in altri termini:
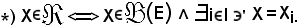
Si dimostra che:
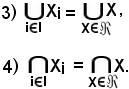
Per dimostrare tali proprietà, si tiene conto delle seguenti definizioni:
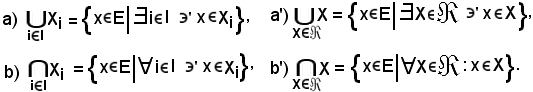
Dimostrazione 3).
Si consideri
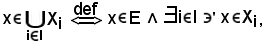
e tenendo conto che per *)
X = Xi,
e quindi
x X,
X,
per la definizione a') risulta
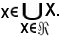
Pertanto, risulta dimostrato che:
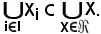
Si consideri ora
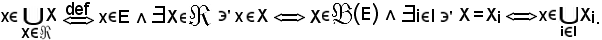
Pertanto risulta:
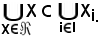
Per la validità della rispettiva inclusione dei due membri, la 3) è vera.
Dimostrazione 3).
Si consideri
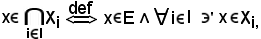
e tenendo conto che per *)
X = Xi,
e quindi
x X,
X,
per la definizione b') risulta
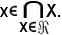
Pertanto, risulta dimostrato che:
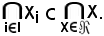
Si consideri ora
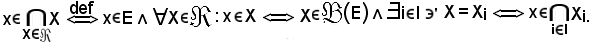
Pertanto risulta:
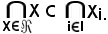
Per la validità della rispettiva inclusione dei due membri, la 4) è vera.
Proprietà della riunione e dell'intersezione di famiglie
Sia
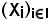
una famiglia di parti dell'insieme E, cioè
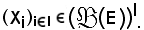
Si dimostrano le seguenti proprietà:
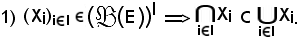
Dimostrazione
Si consideri un elemento
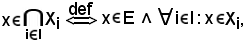
quindi
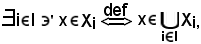
dunque

come volevasi dimostrare.
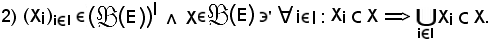
Dimostrazione
Si consideri un elemento
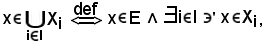
d'altronde, essendo
Xi = X,
x è anche elemento di X, pertanto la 2) è vera.
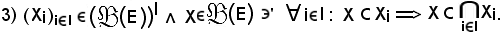
Dimostrazione
Si consideri un elemento
x X,
X,
essendo per ipotesi
 i
i I : X
I : X  Xi,
Xi,
x Xi,
Xi,
e per definizione
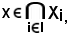
dunque

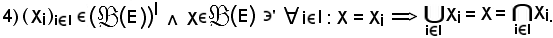
Dimostrazione
Si dimostrano separatamente le seguenti relazioni di inclusione, da cui segue:
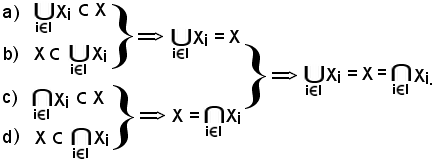
Dimostrazione a)
La a) è vera per la proprietà 2).
Dimostrazione b)
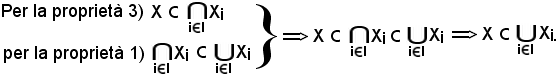
Pertanto la b) è vera.
Dimostrazione c)

Pertanto la c) è vera.
Dimostrazione d)
La d) è vera per la proprietà 3).
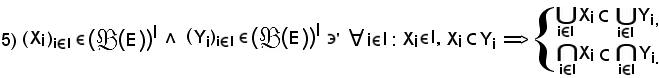
Dimostrazione
Si consideri
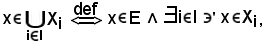
poichè
 i
i I
I  Xi
Xi  Yi,
Yi,
risulta
x Yi,
Yi,
e quindi

Pertanto, resta dimostrata la prima relazione della proprietà 5).
Si consideri ora
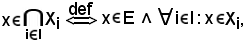
poichè
 i
i I : Xi
I : Xi  Yi,
Yi,
risulta
x Yi,
Yi,
e quindi
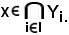
Pertanto, resta dimostrata la seconda relazione della proprietà 5).
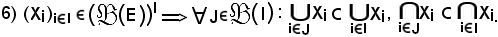
Dimostrazione
Si consideri
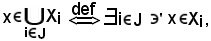
poichè
J I,
I,
 i
i I
I  x
x Xi,
Xi,
quindi risulta

Pertanto, resta dimostrata la prima relazione della proprietà 6).
Si consideri ora
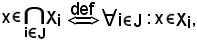
poichè
J I,
I, i
i I : x
I : x Xi,
Xi,
quindi risulta
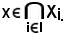
Pertanto, resta dimostrata la seconda relazione della proprietà 6).
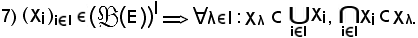
Dimostrazione
Si consideri
λ I,
I,
quindi
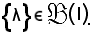
Pertanto
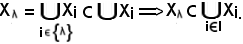
Pertanto, resta dimostrata la prima relazione della proprietà 7).
Si consideri
λ I,
I,
quindi
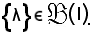
Pertanto
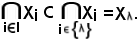
Nota bene: la proprietà 7) è ovvia conseguenza della 6), considerando in quest'ultima l'insieme ridotto all'unico elemento λ come parte di I.
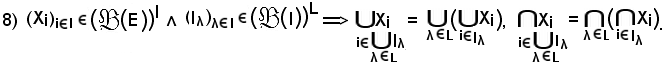
Dimostrazione
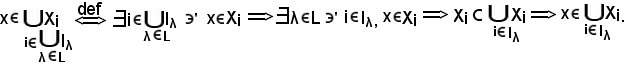
Quindi, per un particolare λ L, si ha:
L, si ha:
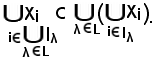
Viceversa, si consideri
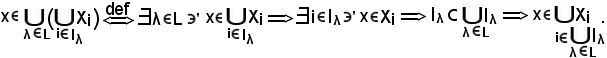
Quindi, si ha:
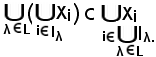
In definitiva si è trovato che:
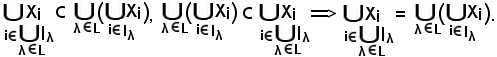
Pertanto, resta dimostrata la prima relazione della proprietà 8).
Si consideri
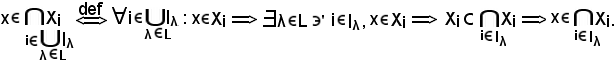
Quindi, per un particolare λ L, si ha:
L, si ha:
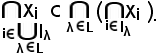
Viceversa, si consideri
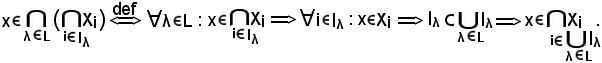
In definitiva si è trovato che:
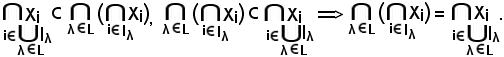
Pertanto, resta dimostrata la seconda relazione della proprietà 8).
Nota bene: in tale proprietà si è supposto che
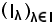
sia una famiglia di parti di I e che
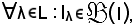
pertanto, si è considerata la famiglia
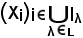
che equivalentemente è rappresentata dall'applicazione
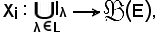
e quindi
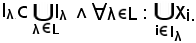
Per la 8) vale la proprietà associativa: considerare l'intersezione o la riunione totale equivale a considerare le sottofamiglie facendone poi l'intersezione oppure la riunione.
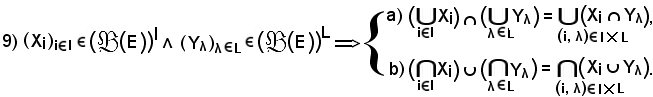
Si osserva dapprima che:
la a) esprime la proprietà distributiva dell'intersezione rispetto alla riunione; la b) esprime la proprietà distributiva della riunione rispetto all'intersezione.
Dimostrazione a).
Si consideri
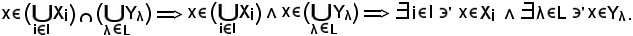
Essendo
i I, λ
I, λ L
L  (i, λ)
(i, λ) I
I 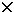 L,
L,
ed inoltre
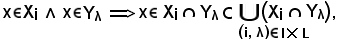
si ha che il primo membro è contenuto nel secondo, cioè:
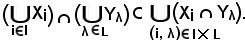
Viceversa, si consideri
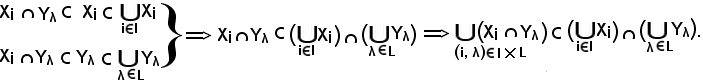
Pertanto, avendo dimostrato che
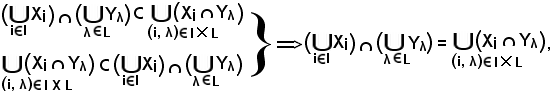
quindi la a) è vera.
Dimostrazione b).
Si consideri
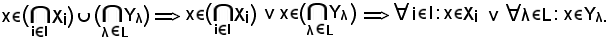
Essendo
i I v λ
I v λ L
L  (i, λ)
(i, λ) I
I 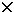 L,
L,
ed in ogni caso
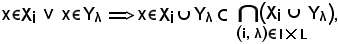
risulta che il primo membro è contenuto nel secondo, cioè:
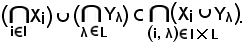 Viceversa, si consideri
Viceversa, si consideri
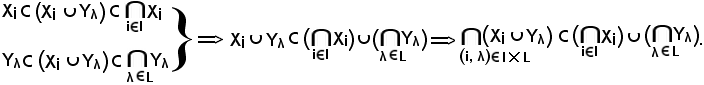
Pertanto, avendo dimostrato che
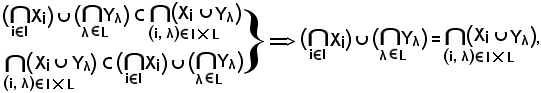
quindi la b) è vera.
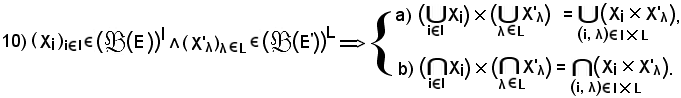
Si osserva dapprima che:
la a) esprime la proprietà distributiva del prodotto rispetto alla riunione;
la b) esprime la proprietà distributiva del prodotto rispetto all'intersezione.
Dimostrazione a).
Si consideri
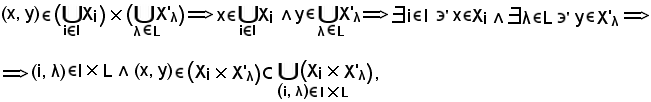
risulta che il primo membro è contenuto nel secondo, cioè:
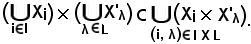
Viceversa, si consideri
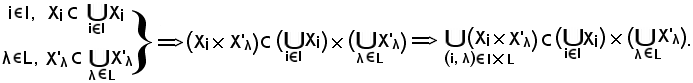
Pertanto, avendo dimostrato che
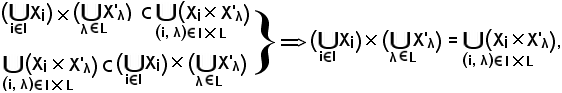
quindi la a) è vera.
Dimostrazione b).
Si consideri
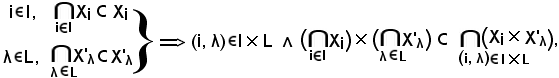
cioè che il primo membro è contenuto nel secondo.
Viceversa, si consideri
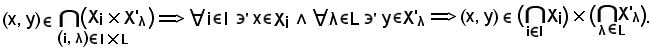
Pertanto, avendo dimostrato che
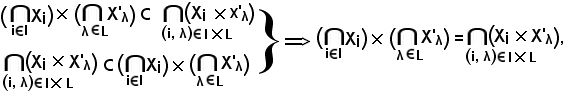
quindi la a) è vera.
11) Formule di De Morgan
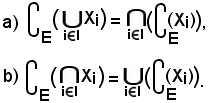
Dimostrazione a).
Si consideri
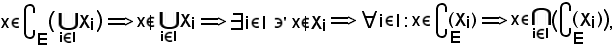
risulta che il primo membro è contenuto nel secondo, cioè:
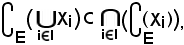
Viceversa, si consideri
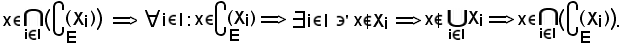
Pertanto, avendo dimostrato che
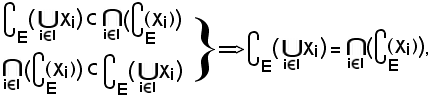
quindi la a) è vera.
Dimostrazione b).
Si consideri
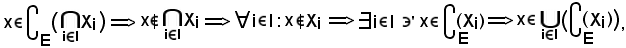
risulta che il primo membro è contenuto nel secondo, cioè:
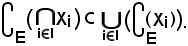
Viceversa, si consideri
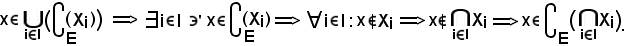
Pertanto, avendo dimostrato che
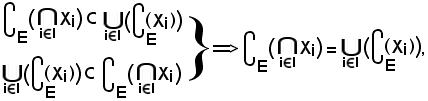
quindi la b) è vera.
Caratterizzazione della riunione e dell'intersezione delle famiglie
Si considerino le famiglie
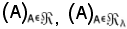
e si supponga che

Applicando la proprietà associativa della riunione e dell'intersezione, si ottengono le seguenti due uguaglianze analoghe a quelle della proprietà 8), che pertanto si dimostrano allo stesso modo:
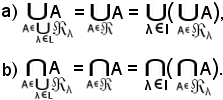
A tal punto, si vuole dimostrare che ad esempio, assegnati tre insiemi X, Y, Z, essendo la proprietà associativa dell'intersezione e della riunione espressa da:
a') (X Y)
Y)  Z = X
Z = X  (Y
(Y  Z),
Z),
b') (X Y)
Y)  Z = X
Z = X  (Y
(Y  Z),
Z),
le due relazioni a') e b') sono rispettivamente caratterizzazioni di a) e b).
Dimostrazione: la relazione a') è una caratterizzazione di a).
Allo scopo, si consideri
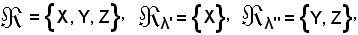
di modo che
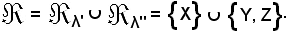
Inoltre si consideri
L = λ' λ''
λ''
e quindi, in riferimento alla relazione
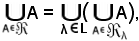
si ha: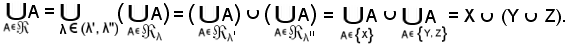
Si è quindi dimostrato che
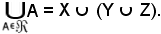
Si consideri ora
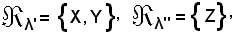
di modo che
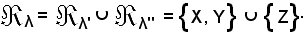
Inoltre si consideri
L = λ' λ''
λ''
e quindi, in riferimento alla relazione
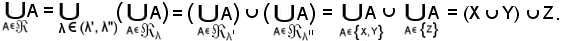
Si è quindi dimostrato che
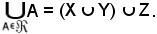
In definitiva, risulta:
(X Y)
Y)  Z = X
Z = X  (Y
(Y  Z),
Z),
come volevasi dimostrare.
Dimostrazione: la relazione b') è una caratterizzazione di b).
Allo scopo, si consideri
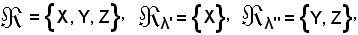
di modo che
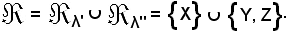
Inoltre si consideri
L = λ' λ''
λ''
e quindi, in riferimento alla relazione
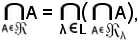
si ha:
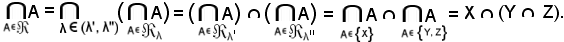
Si è quindi dimostrato che
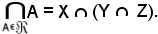
Si consideri ora
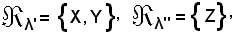
di modo che
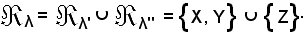
Inoltre si consideri
L = λ' λ''
λ''
e quindi, in riferimento alla relazione
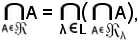
si ha:
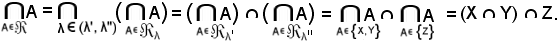
Si è quindi dimostrato che
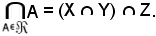
In definitiva, risulta:
(X Y)
Y)  Z = X
Z = X  (Y
(Y  Z).
Z).
Proprietà distributiva della riunione rispetto all'intersezione della famiglia
Se A, B e C sono insiemi, si ha:
A (B
(B  C) = (A
C) = (A  B)
B)  (A
(A  C).
C).
Si vuole dimostrare che tale relazione è una particolare caratterizzazione della seguente uguaglianza:
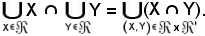
Allo scopo si consideri
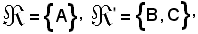
quindi si ha:
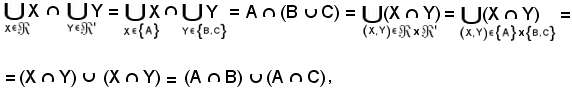
tenendo conto che
(X, Y) = (A, B) e (X, Y) = (A, C),
risulta
A (B
(B  C) = (A
C) = (A  B)
B)  (A
(A  C),
C),
come volevasi dimostrare.
Proprietà distributiva dell'intersezione rispetto alla riunione della famiglia
Se A, B, C sono insiemi, si ha:
A (B
(B  C) = (A
C) = (A  B)
B)  (A
(A  C).
C).
Si vuole dimostrare che tale relazione è una particolare caratterizzazione della seguente uguaglianza:
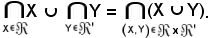
Allo scopo si consideri
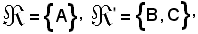
quindi si ha:
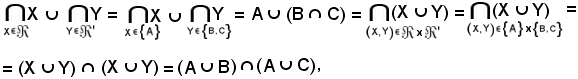
tenendo conto che
(X, Y) = (A, B) e (X, Y) = (A, C),
risulta
A (B
(B  C) = (A
C) = (A  B)
B)  (A
(A  C),
C),
come volevasi dimostrare.
Comportamento della riunione e dell'intersezione di una famiglia rispetto alle immagini dirette mediante un'applicazione
Si consideri l'applicazione
f : E E',
E',
per ogni famiglia di parti di E, cioè
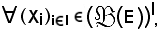
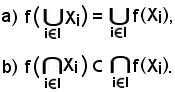
Dimostrazione a).
Si consideri
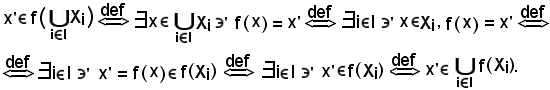
Essendo x' elemento comune sia al primo che al secondo membro, e viceversa, si conclude che la a) è vera.
Dimostrazione b).
Si consideri
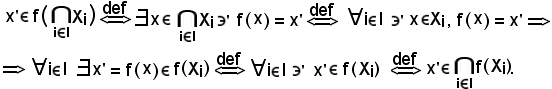
Essendo x' elemento comune sia al primo che al secondo membro, si conclude che la b) è vera.
Comportamento della riunione e dell'intersezione di una famiglia rispetto alle immagini reciproche mediante un'applicazione
Si consideri l'applicazione
f : E E',
E',
per ogni famiglia di parti di E', cioè
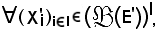
risulta quanto segue:
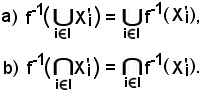
Dimostrazione a).
Si consideri
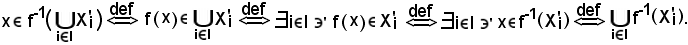
Essendo x elemento comune sia al primo che al secondo membro, e viceversa, si conclude che la a) è vera.
Dimostrazione b).
Si consideri
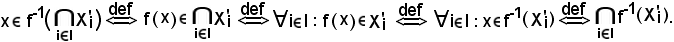
Essendo x elemento comune sia al primo che al secondo membro, e viceversa, si conclude che la b) è vera.
Prodotto di una famiglia di insiemi
Tale espressione prende il nome di Assioma Moltiplicativo, della scelta o di Zermelo, e si denota con

pertanto all'insieme delle famiglie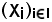 di elementi di E
di elementi di E 
 i
i I : xi
I : xi Xi si attribuisce il nome di insieme prodotto delle famiglie
Xi si attribuisce il nome di insieme prodotto delle famiglie 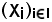 mentre ogni viene Xi chiamato i-esimo fattore del prodotto.
mentre ogni viene Xi chiamato i-esimo fattore del prodotto.
In altri termini: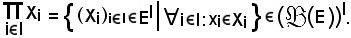
Nota bene
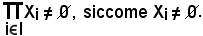
b)-Per definizione
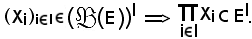
c)-Si dimostra che
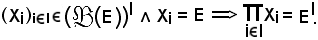
Infatti, si considera la famiglia di parti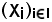

 i
i I : Xi = E, che è l'applicazione
I : Xi = E, che è l'applicazione
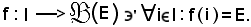
Siccome EI è l'insieme delle famiglie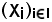

 i
i I : xi
I : xi E = Xi, quindi risulta xi
E = Xi, quindi risulta xi Xi.
Xi.
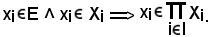
In tal modo resta dimostrato che

ed essendo inoltre valido il viceversa per la definizione b), è vero quanto asserito.
Proiezione di una famiglia di insiemi
Siano E ed F due insiemi ed E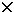 F l'insieme delle coppie ordinate aventi prima
coordinata E e seconda coordinata F. Si consideri ora una famiglia
di parti di E avente I come insieme degl'indici, cioè
F l'insieme delle coppie ordinate aventi prima
coordinata E e seconda coordinata F. Si consideri ora una famiglia
di parti di E avente I come insieme degl'indici, cioè
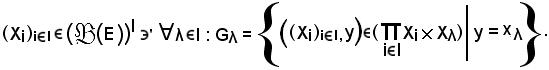
xλ si chiama lambdesima proiezione o coordinata della famiglia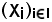 e quindi Gλ è una relazione tra elementi del primo insieme ed elementi del secondo, cioè
e quindi Gλ è una relazione tra elementi del primo insieme ed elementi del secondo, cioè
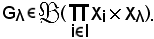
Gλ è addirittura una relazione funzionale e quindi la sezione Gλ relativa ad ogni elemento del primo fattore è non vuota ed è formata da un unico elemento, cioè:

e quindi l'applicazione
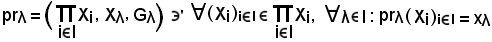
è la lambdesima proiezione del prodotto.
Per convenzione la famiglia si indica con
Famiglia doppia
Si consideri l'applicazione
f : I
per convenzione la famiglia si indica con
Tale famiglia è quindi formata da due indici, i e λ, e prende il nome di famiglia doppia.
Caso particolare di famiglia
Sia
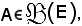
cioè una parte dell'insieme E; A si può sempre supporre come l'insieme degli elementi della famiglia e, allo scopo, è sufficiente considerare l'ingezione canonica
jA : A E.
E.
Evidentemente, essendo A E, A è l'immagine di A mediante jA, cioè
E, A è l'immagine di A mediante jA, cioè
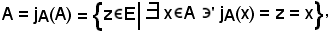
e nello stesso tempo A è l'insieme degli elementi della famiglia. La famiglia così ottenuta si indica con
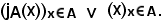
Sia
cioè una parte dell'insieme E; A si può sempre supporre come l'insieme degli elementi della famiglia e, allo scopo, è sufficiente considerare l'ingezione canonica
jA : A
Evidentemente, essendo A
e nello stesso tempo A è l'insieme degli elementi della famiglia. La famiglia così ottenuta si indica con
Sottofamiglia di una famiglia
Si consideri l'applicazione
f : I
e sia
La restrizione di f a J,
è chiamata sottofamiglia della famiglia data, cioè
ha J come insieme degl'indici e la si indica come segue:
Siccome
J
l'insieme degli elementi della sottofamiglia è contenuto nell'insieme degli elementi della famiglia di partenza, cioè
f(J)
ossia
Famiglia di parti di un insieme
Si chiama famiglia di parti di un insieme E, avente I come insieme degl'indici, ogni famiglia di elementi delle parti di E avente I come insieme degl'indici.
Se si indica con
il cui valore in i
Riunione della famiglia
Sia (Xi)i
Quindi:
o anche
Intersezione della famiglia
Sia (Xi)i
Quindi:
o anche
Caso particolare di riunione e di intersezione
Si considerino l'insieme E ed una parte dell'insieme delle parti di E, indicata con erre gotica, cioè
L'ingezione canonica
rappresenta la famiglia di parti di E che ha
Conformemente a quanto visto, la famiglia si indica con
Pertanto la riunione e l'intersezione risultano rispettivamente:
Proprietà
Se A e B sono parti dell'insieme E:
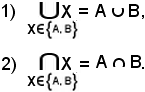
Dimostrazione 1).
Si consideri
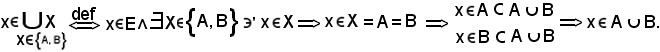
E' stato quindi dimostrato che:
Si dimostra ora che:
Allo scopo, si consideri
x
per definizione di riunione
x
Se
x
fissando
x
e, per definizione:
Se
x
fissando
x
e, per definizione:
E' stato dimostrato che in ogni caso x appartiene alla riunione della famiglia, cioè
In definitiva la 1) è vera.
Dimostrazione 2).
Si consideri
E' stato quindi dimostrato che:
Si dimostra ora che:
Allo scopo, si consideri
x
Siccome
x
fissando
E' stato dimostrato che x appartiene all'intersezione della famiglia, cioè
In definitiva la 2) è vera.
Proprietà
Sia
in altri termini:
Si dimostra che:
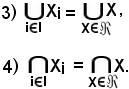
Per dimostrare tali proprietà, si tiene conto delle seguenti definizioni:
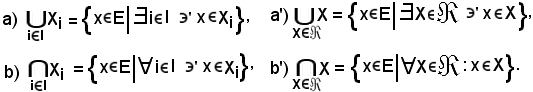
Dimostrazione 3).
Si consideri
e tenendo conto che per *)
X = Xi,
e quindi
x
per la definizione a') risulta
Pertanto, risulta dimostrato che:
Si consideri ora
Pertanto risulta:
Per la validità della rispettiva inclusione dei due membri, la 3) è vera.
Dimostrazione 3).
Si consideri
e tenendo conto che per *)
X = Xi,
e quindi
x
per la definizione b') risulta
Pertanto, risulta dimostrato che:
Si consideri ora
Pertanto risulta:
Per la validità della rispettiva inclusione dei due membri, la 4) è vera.
Proprietà della riunione e dell'intersezione di famiglie
Sia
una famiglia di parti dell'insieme E, cioè
Si dimostrano le seguenti proprietà:
Dimostrazione
Si consideri un elemento
quindi
dunque
come volevasi dimostrare.
Dimostrazione
Si consideri un elemento
d'altronde, essendo
Xi = X,
x è anche elemento di X, pertanto la 2) è vera.
Dimostrazione
Si consideri un elemento
x
essendo per ipotesi
x
e per definizione
dunque
Dimostrazione
Si dimostrano separatamente le seguenti relazioni di inclusione, da cui segue:
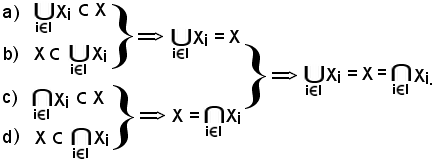
Dimostrazione a)
La a) è vera per la proprietà 2).
Dimostrazione b)
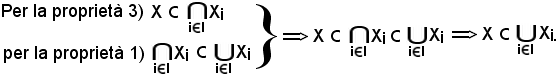
Pertanto la b) è vera.
Dimostrazione c)

Pertanto la c) è vera.
Dimostrazione d)
La d) è vera per la proprietà 3).
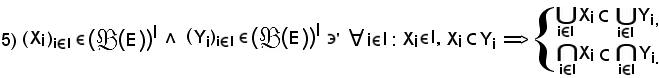
Dimostrazione
Si consideri
poichè
risulta
x
e quindi
Pertanto, resta dimostrata la prima relazione della proprietà 5).
Si consideri ora
poichè
risulta
x
e quindi
Pertanto, resta dimostrata la seconda relazione della proprietà 5).
Dimostrazione
Si consideri
poichè
J
quindi risulta
Pertanto, resta dimostrata la prima relazione della proprietà 6).
Si consideri ora
poichè
J
quindi risulta
Pertanto, resta dimostrata la seconda relazione della proprietà 6).
Dimostrazione
Si consideri
λ
quindi
Pertanto
Pertanto, resta dimostrata la prima relazione della proprietà 7).
Si consideri
λ
quindi
Pertanto
Nota bene: la proprietà 7) è ovvia conseguenza della 6), considerando in quest'ultima l'insieme ridotto all'unico elemento λ come parte di I.
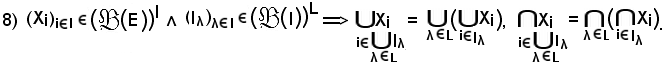
Dimostrazione
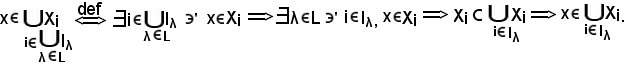
Quindi, per un particolare λ
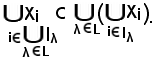
Viceversa, si consideri
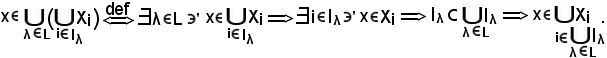
Quindi, si ha:
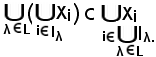
In definitiva si è trovato che:
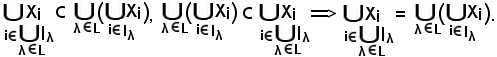
Pertanto, resta dimostrata la prima relazione della proprietà 8).
Si consideri
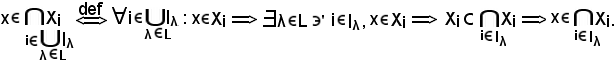
Quindi, per un particolare λ
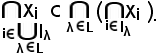
Viceversa, si consideri
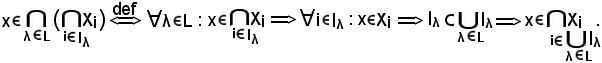
In definitiva si è trovato che:
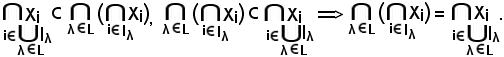
Pertanto, resta dimostrata la seconda relazione della proprietà 8).
Nota bene: in tale proprietà si è supposto che
sia una famiglia di parti di I e che
pertanto, si è considerata la famiglia
che equivalentemente è rappresentata dall'applicazione
e quindi
Per la 8) vale la proprietà associativa: considerare l'intersezione o la riunione totale equivale a considerare le sottofamiglie facendone poi l'intersezione oppure la riunione.
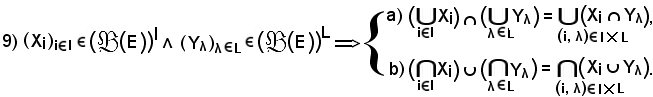
Si osserva dapprima che:
la a) esprime la proprietà distributiva dell'intersezione rispetto alla riunione; la b) esprime la proprietà distributiva della riunione rispetto all'intersezione.
Dimostrazione a).
Si consideri
Essendo
i
ed inoltre
si ha che il primo membro è contenuto nel secondo, cioè:
Viceversa, si consideri
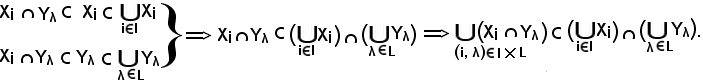
Pertanto, avendo dimostrato che
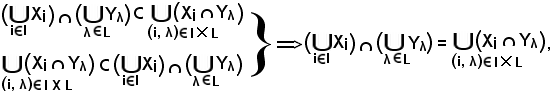
quindi la a) è vera.
Dimostrazione b).
Si consideri
Essendo
i
ed in ogni caso
risulta che il primo membro è contenuto nel secondo, cioè:
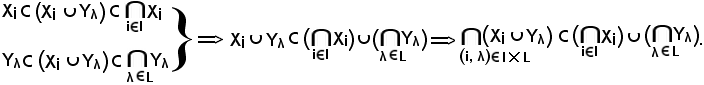
Pertanto, avendo dimostrato che
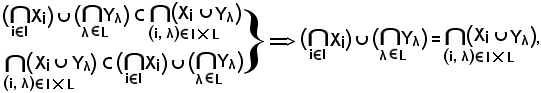
quindi la b) è vera.
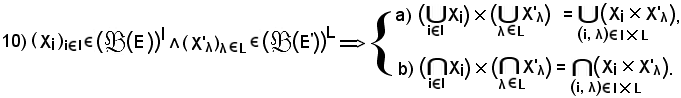
Si osserva dapprima che:
la a) esprime la proprietà distributiva del prodotto rispetto alla riunione;
la b) esprime la proprietà distributiva del prodotto rispetto all'intersezione.
Dimostrazione a).
Si consideri
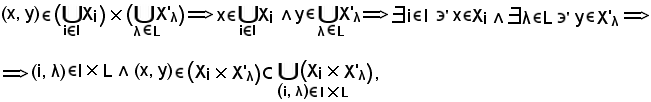
risulta che il primo membro è contenuto nel secondo, cioè:
Viceversa, si consideri
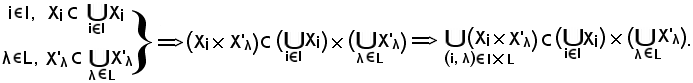
Pertanto, avendo dimostrato che
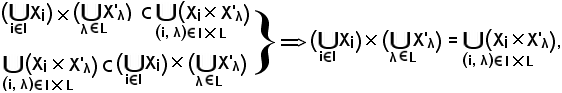
quindi la a) è vera.
Dimostrazione b).
Si consideri
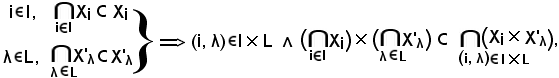
cioè che il primo membro è contenuto nel secondo.
Viceversa, si consideri
Pertanto, avendo dimostrato che
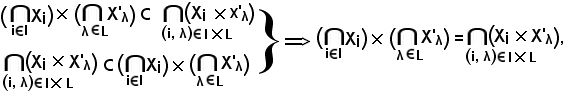
quindi la a) è vera.
11) Formule di De Morgan
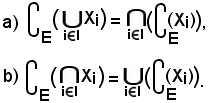
Dimostrazione a).
Si consideri
risulta che il primo membro è contenuto nel secondo, cioè:
Viceversa, si consideri
Pertanto, avendo dimostrato che
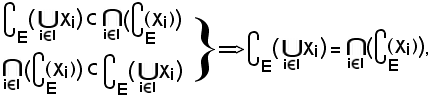
quindi la a) è vera.
Dimostrazione b).
Si consideri
risulta che il primo membro è contenuto nel secondo, cioè:
Viceversa, si consideri
Pertanto, avendo dimostrato che
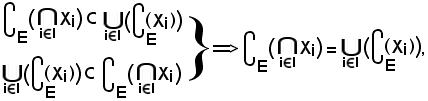
quindi la b) è vera.
Caratterizzazione della riunione e dell'intersezione delle famiglie
Si considerino le famiglie
e si supponga che
Applicando la proprietà associativa della riunione e dell'intersezione, si ottengono le seguenti due uguaglianze analoghe a quelle della proprietà 8), che pertanto si dimostrano allo stesso modo:
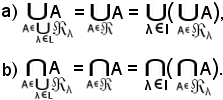
A tal punto, si vuole dimostrare che ad esempio, assegnati tre insiemi X, Y, Z, essendo la proprietà associativa dell'intersezione e della riunione espressa da:
a') (X
b') (X
le due relazioni a') e b') sono rispettivamente caratterizzazioni di a) e b).
Dimostrazione: la relazione a') è una caratterizzazione di a).
Allo scopo, si consideri
di modo che
Inoltre si consideri
L = λ'
e quindi, in riferimento alla relazione
si ha:
Si è quindi dimostrato che
Si consideri ora
di modo che
Inoltre si consideri
L = λ'
e quindi, in riferimento alla relazione
Si è quindi dimostrato che
In definitiva, risulta:
(X
come volevasi dimostrare.
Dimostrazione: la relazione b') è una caratterizzazione di b).
Allo scopo, si consideri
di modo che
Inoltre si consideri
L = λ'
e quindi, in riferimento alla relazione
si ha:
Si è quindi dimostrato che
Si consideri ora
di modo che
Inoltre si consideri
L = λ'
e quindi, in riferimento alla relazione
si ha:
Si è quindi dimostrato che
In definitiva, risulta:
(X
Proprietà distributiva della riunione rispetto all'intersezione della famiglia
Se A, B e C sono insiemi, si ha:
A
Si vuole dimostrare che tale relazione è una particolare caratterizzazione della seguente uguaglianza:
Allo scopo si consideri
quindi si ha:
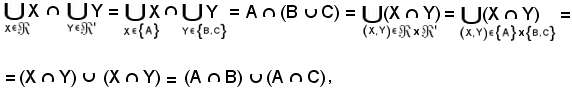
tenendo conto che
(X, Y) = (A, B) e (X, Y) = (A, C),
risulta
A
come volevasi dimostrare.
Proprietà distributiva dell'intersezione rispetto alla riunione della famiglia
Se A, B, C sono insiemi, si ha:
A
Si vuole dimostrare che tale relazione è una particolare caratterizzazione della seguente uguaglianza:
Allo scopo si consideri
quindi si ha:
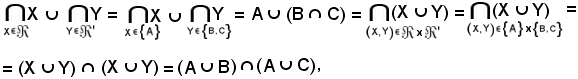
tenendo conto che
(X, Y) = (A, B) e (X, Y) = (A, C),
risulta
A
come volevasi dimostrare.
Comportamento della riunione e dell'intersezione di una famiglia rispetto alle immagini dirette mediante un'applicazione
Si consideri l'applicazione
f : E
per ogni famiglia di parti di E, cioè
risulta quanto segue:
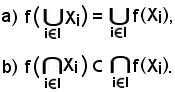
Dimostrazione a).
Si consideri
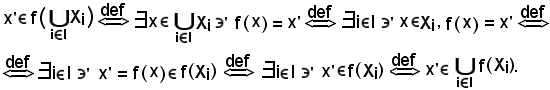
Essendo x' elemento comune sia al primo che al secondo membro, e viceversa, si conclude che la a) è vera.
Dimostrazione b).
Si consideri
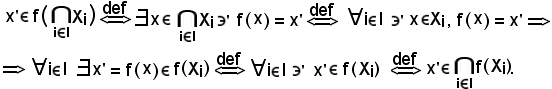
Essendo x' elemento comune sia al primo che al secondo membro, si conclude che la b) è vera.
Comportamento della riunione e dell'intersezione di una famiglia rispetto alle immagini reciproche mediante un'applicazione
Si consideri l'applicazione
f : E
per ogni famiglia di parti di E', cioè
risulta quanto segue:
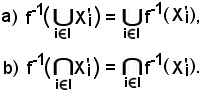
Dimostrazione a).
Si consideri
Essendo x elemento comune sia al primo che al secondo membro, e viceversa, si conclude che la a) è vera.
Dimostrazione b).
Si consideri
Essendo x elemento comune sia al primo che al secondo membro, e viceversa, si conclude che la b) è vera.
Prodotto di una famiglia di insiemi
Si consideri una famiglia di parti di E, cioè
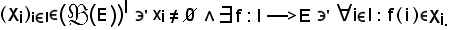
Tale espressione prende il nome di Assioma Moltiplicativo, della scelta o di Zermelo, e si denota con
pertanto all'insieme delle famiglie
In altri termini:
Nota bene
a)-Evidentemente l'assioma della scelta esprime che
b)-Per definizione
c)-Si dimostra che
Infatti, si considera la famiglia di parti
Siccome EI è l'insieme delle famiglie
Pertanto, essendo
In tal modo resta dimostrato che
ed essendo inoltre valido il viceversa per la definizione b), è vero quanto asserito.
Proiezione di una famiglia di insiemi
Siano E ed F due insiemi ed E
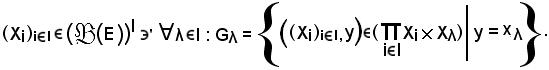
xλ si chiama lambdesima proiezione o coordinata della famiglia
Gλ è addirittura una relazione funzionale e quindi la sezione Gλ relativa ad ogni elemento del primo fattore è non vuota ed è formata da un unico elemento, cioè:
e quindi l'applicazione
è la lambdesima proiezione del prodotto.