RELAZIONI DI EQUIVALENZA ---> INDICE
Si
chiama relazione di equivalenza su un insieme E, ogni relazione R su E assoggettata ai seguenti tre assiomi:
RE-1) (x, y) R
R  (y, z)
(y, z) R
R  (x, z)
(x, z) R, proprietà transitiva;
R, proprietà transitiva;
RE-2) (x, y) R
R  (y, x)
(y, x) R, proprietà simmetrica;
R, proprietà simmetrica;
RE-3) x
x E : (x, x)
E : (x, x) R, proprietà riflessiva.
R, proprietà riflessiva.
Ricordando che la coppia (x, y) R si può scrivere xRy, equivalentemente si ha:
R si può scrivere xRy, equivalentemente si ha:
RE-1) xRy yRz
yRz  xRz, proprietà transitiva;
xRz, proprietà transitiva;
RE-2) xRy yRx, proprietà simmetrica;
yRx, proprietà simmetrica;
RE-3) x
x E : xRx, proprietà riflessiva.
E : xRx, proprietà riflessiva.
Ed ancora, scrivendo x≡y(modR) al posto di (x, y) R, si ha:
R, si ha:
RE-1) x≡y(modR) y≡z(modR)
y≡z(modR)  x≡z(modR), proprietà transitiva;
x≡z(modR), proprietà transitiva;
RE-2) x≡y(modR) y≡x(modR), proprietà simmetrica;
y≡x(modR), proprietà simmetrica;
RE-3) x
x E : x≡x(modR), proprietà riflessiva.
E : x≡x(modR), proprietà riflessiva.
La forma x≡y(modR) si legge "x equivalente o congruo y modulo R".
Esempio di relazione di equivalenza
Si consideri l'applicazione
f : E E'
E'
e, se con Rf si indica l'insieme delle coppie ordinate (x, y) E X E
E X E  f(x) = f(y), cioè
f(x) = f(y), cioè
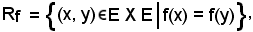
si dimostra che Rf è una relazione di equivalenza definita dall'applicazione f, pertanto Rf deve verificare gli assiomi RE-1), RE-2) ed RE-3).
Dimostrazione RE-1).
Per come è stato definito Rf, si ha:
(x, y) R
R  (y, z)
(y, z) R
R  f(x) = f(y)
f(x) = f(y)  f(y) = f(z)
f(y) = f(z)  f(x) = f(z)
f(x) = f(z)  (x, z)
(x, z) R.
R.
Dimostrazione RE-2).
Per come è stato definito Rf, si ha:
(x, y) R
R  f(x) = f(y)
f(x) = f(y)  f(y) = f(x)
f(y) = f(x)  (y, x)
(y, x) R.
R.
Dimostrazione RE-3).
Per come è stato definito Rf, si ha:
(x, x) R
R  f(x) = f(x),
f(x) = f(x),
e ciò è sempre vero.
Esempio
Assegnati un insieme E e la relazione R su E, per caso esistono un insieme E' ed un'applicazione f : E E' tale che l'ulteriore relazione d'equivalenza Rf, definita da f, sia uguale a quella di partenza? Cioè:
E' tale che l'ulteriore relazione d'equivalenza Rf, definita da f, sia uguale a quella di partenza? Cioè:
 E',
E',  f : E
f : E  E'
E'  Rf = R?
Rf = R?
Prima di verificare ciò, si dimostra che le seguenti due proposizioni sono equivalenti:
a) x≡y(modR),
b) R(x) = R(y).
a) b)
b)
x≡y(modR) (x, y)
(x, y) R,
R,
si deve dimostrare che R(x) = R(y), cioè che R(x) R(y) e R(y)
R(y) e R(y)  R(x).
R(x).
Infatti, considerato un qualsiasi elemento
z R(x)
R(x)  (x, z)
(x, z) R,
R,
ed essendo
(x, y) R
R  (y, x)
(y, x) R,
R,
si ha:
(y, z) R
R  z
z R(y),
R(y),
quindi
R(x) R(y).
R(y).
Viceversa, si consideri un qualsiasi elemento
z R(y)
R(y)  (y, z)
(y, z) R,
R,
ed essendo
(x, y) R,
R,
si ha:
(x, z) R
R  z
z R(x),
R(x),
quindi
R(y) R(x).
R(x).
b) a)
a)
Si consideri l'applicazione
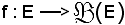
così definita:
 x
x E : f(x) = R(x),
E : f(x) = R(x),
si dimostra che
Rf = R,
cioè che
Rf R ed R
R ed R  Rf.
Rf.
Infatti, si ha:
(x, y) Rf
Rf  f(x) = f(y)
f(x) = f(y)  R(x) = R(y)
R(x) = R(y)  (x, z)
(x, z) R,
R,
per l'equivalenza delle due proposizioni suddette. Poichè è valida l'implicazione nei due sensi, si conclude che:
Rf R ed R
R ed R  Rf,
Rf,
cioè
Rf = R.
Si consideri l'applicazione surgettiva
f : E E',
E',
cioè
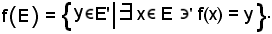
Si costruisce ora l'applicazione f* : E f(E) così definita:
f(E) così definita:
 x
x E : f*(x) = f(x)
E : f*(x) = f(x) f(E).
f(E).
Le proprietà dell'applicazione f*, detta ridotta dell'applicazione f, sono le seguenti:
1) f* è surgettiva,
2) Rf = Rf*,
3) f = jf(E) ο f*.
Dimostrazione 1).
Si deve dimostrare che
f*(E) = f(E).
Infatti,
 x
x E : f*(x) = f(x).
E : f*(x) = f(x).
Dimostrazione 2).
Si consideri
(x, y) Rf
Rf  (x, y)
(x, y) E X E
E X E  f(x) = f(y)
f(x) = f(y)  f*(x) = f*(y)
f*(x) = f*(y)  (x, y)
(x, y) Rf*.
Rf*.
Dimostrazione 3).
Si ha:
 x
x E jf(E) ο f*(x) = jf(E)(f*(x)) = jf(E)(f(x)) = f(x).
E jf(E) ο f*(x) = jf(E)(f*(x)) = jf(E)(f(x)) = f(x).
Ponendo
f(E) = E/R
ed indicando con
φ : E E/R,
E/R,
l'applicazione di E in E/R è detta surgezione canonica, e l'insieme E/R è detto insieme quoziente.
La surgezione canonica gode di due proprietà:
1) φ è surgettiva,
2) Rφ = R.
Dimostrazione 1).
Deriva dalla surgettività di f* di cui sopra.
Dimostrazione 2).
Si ha:
Rφ = Rf* = Rf = R.
Si esamina ora il significato dell'insieme quoziente:
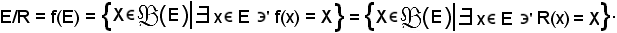
La nozione di equivalenza permette di introdurre il concetto di applicazione indotta.
Siano
f : E E', s : E
E', s : E  Q, s' : E'
Q, s' : E'  Q',
Q',
ci si chiede se esiste un'applicazione
f* : Q Q'
Q'  f* ο s = s' ο f,
f* ο s = s' ο f,
o equivalentemente che il seguente diagramma sia commutativo:
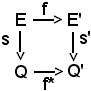
In generale non si sa se esista una tale applicazione, ed ammesso che esista, sia unica.
Nel caso in cui s ed s' siano surgettive, cioè se
s(E) = Q, s'(E') = Q',
se esiste f* essa è unica ed è definita indotta da f per s ed s'.
Si dimostra prima che se s è un'applicazione surgettiva, cioè s : E Q, e se f e g sono le applicazioni di Q nell'insieme E', cioè
Q, e se f e g sono le applicazioni di Q nell'insieme E', cioè
f : Q E', g : Q
E', g : Q  E',
E',
allora
f ο s = g ο s f = g.
f = g.
Dimostrazione
Si consideri un elemento
q Q, essendo s(E) = Q, q
Q, essendo s(E) = Q, q s(E)
s(E) 
 x
x E
E  q = s(x).
q = s(x).
Da ciò segue che
f(q) = f(s(x)) = f ο s(x) = g ο s(x) = g(s(x)) = g(q),
come volevasi dimostrare.
Si dimostra ora che se per caso s ed s' sono surgettive, ed esiste f*, essa è unica.
Se per caso esistessero due f*, cioè f*1 e f*2, risulterebbe:
f*1 ο s = s' ο f f*2 ο s = s' ο f
f*2 ο s = s' ο f  f*1 ο s = f*2 ο s
f*1 ο s = f*2 ο s  f*1 = f*2.
f*1 = f*2.
Per quanto concerne l'esistenza dell'applicazione indotta, si dimostra che le seguenti due proposizioni sono equivalenti:
a) f*: Q
f*: Q  Q'
Q'  f* ο s = s' ο f,
f* ο s = s' ο f,
b) x
x E,
E,  y
y E x≡y(modRs)
E x≡y(modRs) f(x)≡f(y)(modRs').
f(x)≡f(y)(modRs').
Si ricorda che
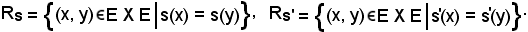
a) b)
b)
Si consideri
(x, y) Rs
Rs  s(x) = s(y)
s(x) = s(y)  f*(s(x)) = f*(s(y))
f*(s(x)) = f*(s(y))  f* ο s(x) = f* ο s(y)
f* ο s(x) = f* ο s(y)  s' ο f(x) = s' ο f(y)
s' ο f(x) = s' ο f(y) 
 s'(f(x)) = s'(f(y))
s'(f(x)) = s'(f(y))  (f(x), f(y))
(f(x), f(y)) Rs'.
Rs'.
b) a)
a)
Sia Gf* la parte del prodotto Q X Q' e quindi relazione tra elementi di Q e Q', l'insieme delle coppie
(q, q') Q X Q'
Q X Q'  q'
q' s' ο f(s-1(q)),
s' ο f(s-1(q)),
cioè 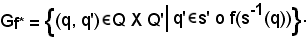
Osservato che:
 q
q Q : Gf* = s' ο f(s-1(q)),
Q : Gf* = s' ο f(s-1(q)),
si dimostra ora che Gf* è una relazione funzionale, cioè q
q Q : s' ο f(s-1(q)) ≠
Q : s' ο f(s-1(q)) ≠  , ed è formata da un solo elemento.
, ed è formata da un solo elemento.
Infatti, preso un elemento q Q, ed essendo per ipotesi s(E) = Q, si ha s-1(q) =
Q, ed essendo per ipotesi s(E) = Q, si ha s-1(q) =  e quindi s' ο f(s-1(q)) ≠
e quindi s' ο f(s-1(q)) ≠  .Inoltre, supponendo che esistano due elementi di Gf*, cioè
.Inoltre, supponendo che esistano due elementi di Gf*, cioè
q'1 f(s-1(q))
f(s-1(q))  q'2
q'2 f(s-1(q))
f(s-1(q)) 
 x1
x1 s-1(q)
s-1(q)  q'1 = s' ο f(x1)
q'1 = s' ο f(x1) 
 x2
x2 s-1(q)
s-1(q)  q'2 = s' ο f(x2),
q'2 = s' ο f(x2),
iE : E E, s : E
E, s : E  Q, s' : E
Q, s' : E  Q,
Q,
si consideri il seguente diagramma:
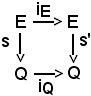
Nell'ipotesi che s sia surgettiva, si dimostra che l'applicazione indotta da iE per s ed s' esiste ed è iQ. Infatti, si verifica che:
iQ ο s = s' ο iE.
TeoremaSe
s : E Q, s : E
Q, s : E  Q, s' : E
Q, s' : E  Q, s'' : E
Q, s'' : E  Q''
Q''
sono surgezioni e se
f' : E E', f'' : E'
E', f'' : E'  E'',
E'',
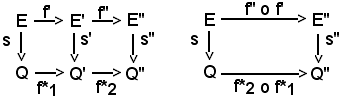
e se f' induce f*1 ed f'' induce f*2, allora f'' ο f' induce f*2 ο f*1, cioè risulta
f*2 ο f*1 = (f'' ο f')*.
Dimostrazione
Per ipotesi risulta
f*1 ο s = s' ο f', f*2 ο s' = s'' ο f''.
Per la proprietà associativa delle applicazioni, si ha:
(f*2 ο f*1) ο s = f*2 ο (f*1 ο s) = f*2 ο (s' ο f') = (f*2 ο s') ο f' = (s'' ο f'') ο f' = s'' ο (f'' ο f'),
Si considerino due insiemi E ed F, siano R ed R' le relazioni di equivalenza rispettivamente sull'insieme E e sull'insieme F, e l'applicazione
f' : E F.
F.
Si considerino inoltre gl'insiemi quoziente E/R ed F/R' e le applicazioni
φ : E E/R
E/R  φ(E) = E/R
φ(E) = E/R  Rφ = R,
Rφ = R,
ψ : F F/R'
F/R'  ψ(F) = F/R'
ψ(F) = F/R'  Rψ = R'.
Rψ = R'.
Si traccia ora il relativo diagramma:
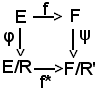
La condizione che esista f* si traduce nell'equivalenza delle seguenti due proposizioni:
a) f* : E/R
f* : E/R  F/R'
F/R'  f* ο φ = ψ ο f,
f* ο φ = ψ ο f,
b) x
x E,
E,  y
y E
E  x≡y(modRφ) : f(x)≡f(y)(modRψ).
x≡y(modRφ) : f(x)≡f(y)(modRψ).
Si osserva ora che:
 x
x E,
E,  y
y E
E  x≡y(modR) : f(x)≡f(y)(modR'),
x≡y(modR) : f(x)≡f(y)(modR'),
la f* così definita prende il nome di applicazione indotta da f per R ed R'.
f' : E' F', f'' : E''
F', f'' : E''  F''
F''
e si costruisce l'applicazione prodotto
f' X f'' : E' X E'' F' X F''
F' X F''
così definita:
 (x', x'')
(x', x'') E' X E'' : (f' X f'')(x', x'') = (f'(x'), f''(x'')).
E' X E'' : (f' X f'')(x', x'') = (f'(x'), f''(x'')).
Si considerino ulteriormente le relazioni di equivalenza Rf' ed Rf'' definite da f' ed f'' e quindi, dopo aver costruito Rf'Xf'', definita da f' X f'', si dimostra che le seguenti due proposizioni sono equivalenti:
a) (a', a'')≡(b', b'')(modRf'Xf''),
b) a' ≡ b'(modRf'), a'' ≡ b''(modRf'').
Dimostrazione
a) b)
b)
Si considerino le coppie
(a', a'') E' X E'', (b', b'')
E' X E'', (b', b'') E' X E''
E' X E''  (a', a'') ≡ (b', b'')(modRf'Xf'')
(a', a'') ≡ (b', b'')(modRf'Xf'')  (f' X f'')(a', a'') =
(f' X f'')(a', a'') =
= (f' X f'')(b', b'') (f'(a'), f''(a'')) = (f'(b'), f''(b''))
(f'(a'), f''(a'')) = (f'(b'), f''(b''))  (f'(a') = f'(b')
(f'(a') = f'(b')  f''(a'') = f''(b''))
f''(a'') = f''(b'')) 
 a' ≡ b'(modRf')
a' ≡ b'(modRf')  a'' ≡ b''(modRf'').
a'' ≡ b''(modRf'').
Si considerino le applicazioni
φ : E X, ψ : F
X, ψ : F  Y, χ : G
Y, χ : G  Z,
Z,
ed inoltre
f : E x F  G,
G,
φ x ψ : E x F X x Y
X x Y
e si tracci il relativo diagramma:
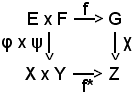
Considerando φ e ψ surgettive, cioè
φ(E) = X e ψ(F) = Y (φ x ψ)(E x F) = X x Y,
(φ x ψ)(E x F) = X x Y,
anche φ x ψ è surgettiva.
Se esiste f* indotta da f per φ x ψ e χ, essa è unica e la sua esistenza si esprime nella sua equivalenza delle seguenti due proposizioni:
a) f* : X x Y
f* : X x Y  Z
Z  f* ο (φ x ψ) = χ ο f,
f* ο (φ x ψ) = χ ο f,
b) (x', x'')
(x', x'') E x F,
E x F,  (y', y'')
(y', y'') E x F
E x F  (x', x'')≡(y', y'')(modRφ x ψ) : f(x', x'')≡(y', y'')(modRχ).
(x', x'')≡(y', y'')(modRφ x ψ) : f(x', x'')≡(y', y'')(modRχ).
Tenendo presente l'equivalenza vista in precedenza, cioè:
a) (a', a'')≡(b', b'')(modRf'Xf''),
b) a' ≡ b'(modRf'), a'' ≡ b''(modRf''),
le due proposizioni in esame si possono scrivere
a) f* : X x Y
f* : X x Y  Z
Z  f* ο (φ x ψ) = χ ο f,
f* ο (φ x ψ) = χ ο f,
b) (x', x'')
(x', x'') E x F,
E x F,  (y', y'')
(y', y'') E x F
E x F  x'≡y'(modRφ), x''≡y''(modRψ) : f(x', x'')≡f(y', y'')(modRχ).
x'≡y'(modRφ), x''≡y''(modRψ) : f(x', x'')≡f(y', y'')(modRχ).
Quindi, fissate le applicazioni φ, ψ e χ, è sufficiente e necessario che si verifichino a) e b) ora scritte, affinchè esista l'applicazione f*.
RE-1) (x, y)
RE-2) (x, y)
RE-3)
Ricordando che la coppia (x, y)
RE-1) xRy
RE-2) xRy
RE-3)
Ed ancora, scrivendo x≡y(modR) al posto di (x, y)
RE-1) x≡y(modR)
RE-2) x≡y(modR)
RE-3)
La forma x≡y(modR) si legge "x equivalente o congruo y modulo R".
Esempio di relazione di equivalenza
Si consideri l'applicazione
f : E
e, se con Rf si indica l'insieme delle coppie ordinate (x, y)
si dimostra che Rf è una relazione di equivalenza definita dall'applicazione f, pertanto Rf deve verificare gli assiomi RE-1), RE-2) ed RE-3).
Dimostrazione RE-1).
Per come è stato definito Rf, si ha:
(x, y)
Dimostrazione RE-2).
Per come è stato definito Rf, si ha:
(x, y)
Dimostrazione RE-3).
Per come è stato definito Rf, si ha:
(x, x)
e ciò è sempre vero.
Esempio
Assegnati un insieme E e la relazione R su E, per caso esistono un insieme E' ed un'applicazione f : E
Prima di verificare ciò, si dimostra che le seguenti due proposizioni sono equivalenti:
a) x≡y(modR),
b) R(x) = R(y).
a)
x≡y(modR)
si deve dimostrare che R(x) = R(y), cioè che R(x)
Infatti, considerato un qualsiasi elemento
z
ed essendo
(x, y)
si ha:
(y, z)
quindi
R(x)
Viceversa, si consideri un qualsiasi elemento
z
ed essendo
(x, y)
si ha:
(x, z)
quindi
R(y)
b)
Si consideri l'applicazione
così definita:
si dimostra che
Rf = R,
cioè che
Rf
Infatti, si ha:
(x, y)
per l'equivalenza delle due proposizioni suddette. Poichè è valida l'implicazione nei due sensi, si conclude che:
Rf
cioè
Rf = R.
Si consideri l'applicazione surgettiva
f : E
cioè
Si costruisce ora l'applicazione f* : E
Le proprietà dell'applicazione f*, detta ridotta dell'applicazione f, sono le seguenti:
1) f* è surgettiva,
2) Rf = Rf*,
3) f = jf(E) ο f*.
Dimostrazione 1).
Si deve dimostrare che
f*(E) = f(E).
Infatti,
Dimostrazione 2).
Si consideri
(x, y)
Dimostrazione 3).
Si ha:
Ponendo
f(E) = E/R
ed indicando con
φ : E
l'applicazione di E in E/R è detta surgezione canonica, e l'insieme E/R è detto insieme quoziente.
La surgezione canonica gode di due proprietà:
1) φ è surgettiva,
2) Rφ = R.
Dimostrazione 1).
Deriva dalla surgettività di f* di cui sopra.
Dimostrazione 2).
Si ha:
Rφ = Rf* = Rf = R.
Si esamina ora il significato dell'insieme quoziente:
La nozione di equivalenza permette di introdurre il concetto di applicazione indotta.
Siano
f : E
ci si chiede se esiste un'applicazione
f* : Q
o equivalentemente che il seguente diagramma sia commutativo:

In generale non si sa se esista una tale applicazione, ed ammesso che esista, sia unica.
Nel caso in cui s ed s' siano surgettive, cioè se
s(E) = Q, s'(E') = Q',
se esiste f* essa è unica ed è definita indotta da f per s ed s'.
Si dimostra prima che se s è un'applicazione surgettiva, cioè s : E
f : Q
allora
f ο s = g ο s
Dimostrazione
Si consideri un elemento
q
Da ciò segue che
f(q) = f(s(x)) = f ο s(x) = g ο s(x) = g(s(x)) = g(q),
come volevasi dimostrare.
Si dimostra ora che se per caso s ed s' sono surgettive, ed esiste f*, essa è unica.
Se per caso esistessero due f*, cioè f*1 e f*2, risulterebbe:
f*1 ο s = s' ο f
Per quanto concerne l'esistenza dell'applicazione indotta, si dimostra che le seguenti due proposizioni sono equivalenti:
a)
b)
Si ricorda che
a)
Si consideri
(x, y)
b)
Sia Gf* la parte del prodotto Q X Q' e quindi relazione tra elementi di Q e Q', l'insieme delle coppie
(q, q')
cioè
Osservato che:
si dimostra ora che Gf* è una relazione funzionale, cioè
Infatti, preso un elemento q
q'1
e tenendo conto che per le ipotesi b)
(x, y) Rs
Rs  (f(x1), f(x2))
(f(x1), f(x2)) Rs'
Rs' s'(f(x1)) = s'(f(x2)),
s'(f(x1)) = s'(f(x2)),
si ha:
q'1 = s' ο f(x1) = s'(f(x1)) = s'(f(x2)) = s' ο f(x2) = q'2.
Avendo dimostrato che Gf* è una relazione funzionale fra elementi di Q ed elementi di Q', esiste quindi un'applicazione
f*: Q Q'
Q'
di cui Gf* è il grafico, cioè
f* = (Q, Q', Gf*).
Si dimostra ora che
f* ο s = s' ο f.
Infatti, dopo aver osservato che q
q Q f*(q) è l'unico elemento di Q del quale è formata la sezione Gf*(q) = s' ο f(s-1(q)), sia x
Q f*(q) è l'unico elemento di Q del quale è formata la sezione Gf*(q) = s' ο f(s-1(q)), sia x E.
E.
Quindi, da un lato si ha che f*(s(x)) è l'unico elemento di Q del quale è s' ο f(s-1(q)), e dall'altro, essendo x s-1(s(x)), si ha s' ο f(x)
s-1(s(x)), si ha s' ο f(x) s' ο f(s-1(s(x))), e quindi anche s' ο f(x) è l'unico elemento di Q del quale è formato s' ο f(s-1(s(x)).
s' ο f(s-1(s(x))), e quindi anche s' ο f(x) è l'unico elemento di Q del quale è formato s' ο f(s-1(s(x)).
In conclusione risulta
f* ο s(x) = s' ο f(x),
cioè
f* ο s = s' ο f.
Esempio di applicazione indotta
Date le applicazioni
(x, y)
si ha:
Avendo dimostrato che Gf* è una relazione funzionale fra elementi di Q ed elementi di Q', esiste quindi un'applicazione
f*: Q
di cui Gf* è il grafico, cioè
f* = (Q, Q', Gf*).
Si dimostra ora che
f* ο s = s' ο f.
Infatti, dopo aver osservato che
Quindi, da un lato si ha che f*(s(x)) è l'unico elemento di Q del quale è s' ο f(s-1(q)), e dall'altro, essendo x
In conclusione risulta
f* ο s(x) = s' ο f(x),
cioè
f* ο s = s' ο f.
Esempio di applicazione indotta
Date le applicazioni
iE : E
si consideri il seguente diagramma:

Nell'ipotesi che s sia surgettiva, si dimostra che l'applicazione indotta da iE per s ed s' esiste ed è iQ. Infatti, si verifica che:
iQ ο s = s' ο iE.
Teorema
s : E
sono surgezioni e se
f' : E
e se f' induce f*1 ed f'' induce f*2, allora f'' ο f' induce f*2 ο f*1, cioè risulta
f*2 ο f*1 = (f'' ο f')*.
Dimostrazione
Per ipotesi risulta
f*1 ο s = s' ο f', f*2 ο s' = s'' ο f''.
Per la proprietà associativa delle applicazioni, si ha:
(f*2 ο f*1) ο s = f*2 ο (f*1 ο s) = f*2 ο (s' ο f') = (f*2 ο s') ο f' = (s'' ο f'') ο f' = s'' ο (f'' ο f'),
da ciò segue che f'' ο f' induce f*2 ο f*1, quindi
f*2 ο f*1 = (f'' ο f')*.
Si tracciano ora i relativi diagrammi:
f*2 ο f*1 = (f'' ο f')*.
Si tracciano ora i relativi diagrammi:

Si considerino due insiemi E ed F, siano R ed R' le relazioni di equivalenza rispettivamente sull'insieme E e sull'insieme F, e l'applicazione
f' : E
Si considerino inoltre gl'insiemi quoziente E/R ed F/R' e le applicazioni
φ : E
ψ : F
Si traccia ora il relativo diagramma:
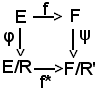
La condizione che esista f* si traduce nell'equivalenza delle seguenti due proposizioni:
a)
b)
Si osserva ora che:
la f* così definita prende il nome di applicazione indotta da f per R ed R'.
Si considerino le applicazioni
f' : E'
e si costruisce l'applicazione prodotto
f' X f'' : E' X E''
così definita:
Si considerino ulteriormente le relazioni di equivalenza Rf' ed Rf'' definite da f' ed f'' e quindi, dopo aver costruito Rf'Xf'', definita da f' X f'', si dimostra che le seguenti due proposizioni sono equivalenti:
a) (a', a'')≡(b', b'')(modRf'Xf''),
b) a' ≡ b'(modRf'), a'' ≡ b''(modRf'').
Dimostrazione
a)
Si considerino le coppie
(a', a'')
= (f' X f'')(b', b'')
Si considerino le applicazioni
φ : E
ed inoltre
φ x ψ : E x F
e si tracci il relativo diagramma:
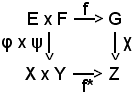
Considerando φ e ψ surgettive, cioè
φ(E) = X e ψ(F) = Y
anche φ x ψ è surgettiva.
Se esiste f* indotta da f per φ x ψ e χ, essa è unica e la sua esistenza si esprime nella sua equivalenza delle seguenti due proposizioni:
a)
b)
Tenendo presente l'equivalenza vista in precedenza, cioè:
a) (a', a'')≡(b', b'')(modRf'Xf''),
b) a' ≡ b'(modRf'), a'' ≡ b''(modRf''),
le due proposizioni in esame si possono scrivere
a)
b)
Quindi, fissate le applicazioni φ, ψ e χ, è sufficiente e necessario che si verifichino a) e b) ora scritte, affinchè esista l'applicazione f*.