RELAZIONI FRA GLI ELEMENTI DEGLI INSIEMI ---> INDICE
S'inizia con alcune premesse.
1)-Coppia non ordinata
sono due insiemi ridotti, rispettivamente, al solo elemento x ed al solo elemento y, posto
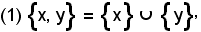
l'insieme definito dalla (1), cioè dalla riunione degl'insiemi ridotti ai soli elementi x ed y, si chiama coppia non ordinata.
Proprietà
1)-Per la proprietà commutativa della riunione, risulta:
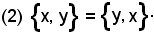
Si deve inoltre tener presente che non si esclude il caso in cui sia x = y.
2)-Se z è un elemento della coppia non ordinata (1), si ha:

3)-Se l'insieme ridotto al solo elemento z è uguale alla coppia non ordinata (1), si ha:
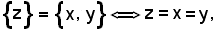
cioè gli elementi x, y e z sono uguali.
Infatti, essendo per ipotesi
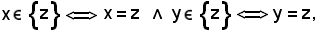
si ha
x = y = z.
4)-Due coppie non ordinate sono uguali se e solo se si verifica quanto segue:
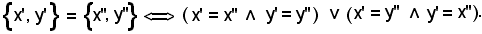
Infatti, si presentano due casi:
a) x' = y',
b) x' ≠ y'.
Nel caso a), in cui x' = x'', sia z l'elemento comune, cioè sia x' = y' = z; per la proprietà 3), si ha:
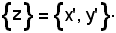
Inoltre, per ipotesi risulta
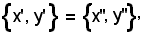
pertanto
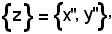
cioè
z = x'' = y'',
sempre per la proprietà 3).
Nel caso b), siccome x' appartiene alla prima coppia non ordinata, per ipotesi uguale alla seconda coppia non ordinata, esso appartiene anche alla seconda coppia non ordinata, cioè:
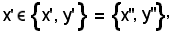
pertanto, per la proprietà 2), si ha
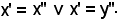
Nel caso in cui x' = x'', poichè
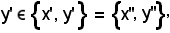
si hanno ancora due alternative
1^) y' = x'' e 2^) y' = y''.
La prima alternativa non è vera, perchè se lo fosse, poichè x' = x'', si avrebbe y' = x'' = x', e ciò è assurdo, perchè per ipotesi x' ≠ y'. Quindi y' = y''.
Osservazione
In generale, dati gl'insiemi X, Y e Z, per la proprietà associativa della riunione e dell'intersezione, si può scrivere:
X (Y
(Y  Z) = (X
Z) = (X  Y)
Y)  Z = X
Z = X  Y
Y  Z,
Z,
X  (Y
(Y  Z) = (X
Z) = (X  Y)
Y)  Z = X
Z = X  Y
Y  Z.
Z.
2)-Terna non ordinata
Dati gli oggetti x, y e z, la riunione degl'insiemi ridotti ai soli elementi x, y e z si chiama terna non ordinata e, per l'osservazione precedente, si indica:
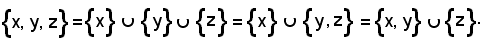
3)-Coppia ordinata
Alla formulazione del concetto fondamentale di coppia ordinata si perviene più agevolmente dopo aver stabilito i seguenti lemmi, cioè proposizioni che fungono da prima premessa di un ragionamento.
Lemma 1 - Se A', B', A'', B'' sono insiemi, e se
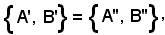
si ha:
(1) A' B' = A''
B' = A''  B''
B''  A'
A'  B' = A''
B' = A''  B''.
B''.
Dimostrazione
Siccome per ipotesi
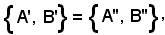
applicando la proprietà 4) si hanno due alternative:
1^) A'= A'' B'= B''
B'= B''
2^) A' = B'' A'' = B'
A'' = B'
Nel primo caso le (1) sono ovvie.
Nel secondo caso si ha:
A'  B' = B''
B' = B''  A'' = A''
A'' = A''  B''
B''  A'
A'  B' = B''
B' = B''  A'' = A''
A'' = A''  B''.
B''.
Lemma 2 - Se x', y', x'', y'' sono oggetti, si ha
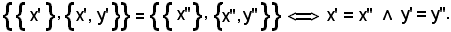
DimostrazioneIn prima analisi, per le proprietà dell'intersezione e dell'unione, risulta:
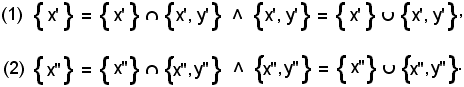
Inoltre, dall' ipotesi
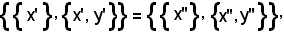
e dal lemma 1, in cui si assume
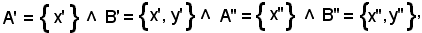
richiamate 1) e 2), si ha:
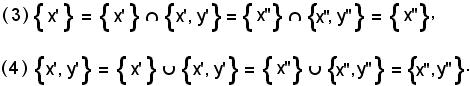
La (3) esprime che:
(5) x' = x''.
Analogamente si dimostra che
y' = y''.
Allo scopo si distinguono due casi:
Nel 1° caso, essendo per la (5) x' = x'', si ha x' = y'; inoltre, essendo vera la proprietà 4), risulta:
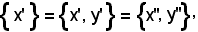
da ciò segue
y' = y''.
Nel 2° caso, per la proprietà 4), si ha:
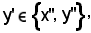
quindi
y' = y''.
Si è quindi dimostrato che
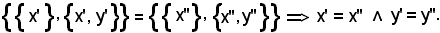
Il viceversa è ovvio.
Definizione di coppia ordinata
Se x ed y sono oggetti, si chiama coppia ordinata di prima coordinata x e di seconda coordinata y, e si denota con (x, y), la coppia non ordinata
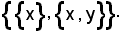
Quindi risulta:
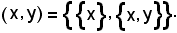
Teorema fondamentale - Condizione necessaria e sufficiente affinchè due coppie ordinate siano uguali, è che la prima coordinata della prima coppia sia uguale alla prima coordinata della seconda coppia e che la seconda coordinata della prima coppia sia uguale alla seconda coordinata della seconda coppia.
Cioè, se x', x'', y', y'' sono oggetti, risulta:
(x', y') = (x'', y'') x' = x''
x' = x''  y' = y''.
y' = y''.
Dimostrazione
Siccome per ipotesi le due coppie ordinate sono uguali, applicando il lemma 2) si ha:
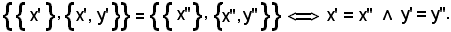
4)-Definizione di terna ordinata
Se x, y e z sono oggetti, si chiama terna ordinata di prima coordinata x, di seconda coordinata y, di terza coordinata z, e si indica con (x, y, z), la coppia ordinata ((x, y), z).
Teorema fondamentale - Condizione necessaria e sufficiente affinchè due terne ordinate siano uguali, è che la prima coordinata della prima terna sia uguale alla prima coordinata della seconda terna, che la seconda coordinata della prima terna sia uguale alla seconda coordinata della seconda terna e che la terza coordinata della prima terna sia uguale alla terza coordinata della seconda terna.
Cioè, se x', x'', y', y'' sono oggetti, risulta:
(x', y', z') = (x'', y'', z'')  x' = x''
x' = x''  y' = y''
y' = y''  z' = z''.
z' = z''.
La dimostrazione è banale.
Sulla base di queste nozioni, s'introduce il concetto di relazione.
Definizione di relazione - Si chiama relazione ogni insieme i cui elementi sono coppie ordinate.
Quindi, se si denota con R una relazione, i suoi elementi sono del tipo (x, y). Spesso, invece di scrivere (x, y) R, si scrive xRy, cioè x legato ad y dalla relazione R.
R, si scrive xRy, cioè x legato ad y dalla relazione R.
In altri termini, R è una relazione se e solo se R è un insieme tale che
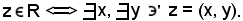
Siano E ed F due insiemi.
Definizione - Si chiama relazione fra gli elementi di E e gli elementi di F ogni relazione R tale che se
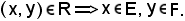
Sia E = F.
Definizione - Si chiama relazione sull'insieme E ogni relazione R tra gli elementi dello stesso insieme, secondo la definizione precedente.
Siano E ed F insiemi.
Definizione di relazione inversa
Si chiama relazione inversa della relazione R, e si denota con R-1, l'insieme delle coppie ordinate (y, x) F X E
F X E  (x, y)
(x, y) R.
R.
In altri termini:
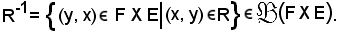
Siano E ed F insiemi.
Definizione di relazione inversa dell'inversa
Si chiama relazione inversa dell'inversa R-1, e si denota con
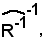
l'insieme delle coppie ordinate (x, y) E X F
E X F  (y, x)
(y, x) R-1.
R-1.
In altri termini:
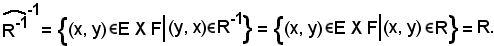
Relazione composta di due relazioni
Sia R una relazione fra elementi di E ed elementi di F ed S una relazione fra elementi di F ed elementi di G, cioè
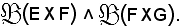
Si consideri la relazione composta delle due relazioni, definita e indicata come segue:

e si legge S cerchietto R.
Relazione inversa di una relazione composta di due relazioni
E' definita come segue:
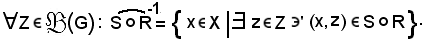
Relazione fondamentale - Prodotto di due insiemi
Si chiama prodotto dell'insieme E per l'insieme F, e si indica con E X F, l'insieme delle coppie ordinate (x, y), tali che x E e y
E e y F; E si chiama 1° fattore ed F secondo fattore del prodotto.
F; E si chiama 1° fattore ed F secondo fattore del prodotto.
Osservazioni
1)-Il prodotto E X F è diverso dal prodotto F X E; i due prodotti sono uguali solo nel caso in cui sia E = F.
Infatti, considerata la coppia ordinata (x, y), per definizione essa è diversa dalla coppia (y, x), pertanto E X F è diverso da F X E.
Se (x, y) = (y, x), allora E = F. Infatti, se x E, y
E, y F, la coppia ordinata (x, y)
F, la coppia ordinata (x, y) E X F = F X E per ipotesi, e per definizione di coppia ordinata x
E X F = F X E per ipotesi, e per definizione di coppia ordinata x F, y
F, y E. Quindi E
E. Quindi E  F, F
F, F  E, cioè E = F.
E, cioè E = F.
2)-Il prodotto E X F non è vuoto se i due insiemi non sono vuoti, cioè:
E X F ≠ 
 E ≠
E ≠ 
 F ≠
F ≠  .
.
3)-Il prodotto E X F è vuoto se uno dei due insiemi è vuoto, cioè:
E X F = 
 E =
E =  v F =
v F =  .
.
4)-Il prodotto E X F è una relazione tra elementi di E ed elementi di F e, se R è una qualsiasi altra relazione tra elementi di E ed elementi di F, risulta:
R E X F,
E X F,
ossia
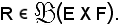
Infatti, considerata la coppia ordinata (x, y) R, con x
R, con x E ed y
E ed y F, ovviamente (x, y)
F, ovviamente (x, y) E
X F, le relazioni fra gli elementi di E e gli elementi di F sono
tutte le parti contenute nell'insieme prodotto E X F, che è la
più vasta relazione tra E ed F, poichè contiene tutte le
altre.
E
X F, le relazioni fra gli elementi di E e gli elementi di F sono
tutte le parti contenute nell'insieme prodotto E X F, che è la
più vasta relazione tra E ed F, poichè contiene tutte le
altre.
5)-Siano A', B', A'', B'' quattro insiemi, si dimostra che:
(A' X B')  (A'' X B'') = (A'
(A'' X B'') = (A'  A'') X (B'
A'') X (B'  B''),
B''),
(A' X B') (A'' X B'')
(A'' X B'')  (A'
(A'  A'')
A'')  (B'
(B'  B'').
B'').
La dimostrazione segue facilmente dalle definizioni.
6)-Siano A, B, C tre insiemi, si dimostra che:
(A B) X C = (A X C)
B) X C = (A X C)  (B X C).
(B X C).
La dimostrazione segue facilmente dalle definizioni.
Diagonale del prodotto
Sia E un insieme.
Si chiama diagonale del prodotto E X E, dell'insieme E per se stesso o più brevemente diagonale di E, e si indica con ΔE, l'insieme delle coppie (x, y) E X E tali che x = y.
E X E tali che x = y.
In altri termini:
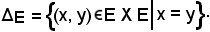
Sezione di una relazione
Se R è una parte del prodotto E X F, o equivalentemente una relazione tra elementi dell'insieme E ed elementi dell'insieme F, per ogni altra parte X di E si chiama sezione di R relativa ad X e si indica con R(X), l'insieme degli elementi y F tali che (x, y)
F tali che (x, y) R per almeno un x
R per almeno un x E.
E.
In altri termini, se
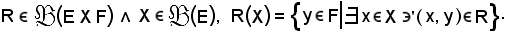
Con le stesse notazioni della definizione suddetta, per ogni x E si chiama sezione di R relativa ad x e si
indica con R(x), la sezione relativa a
E si chiama sezione di R relativa ad x e si
indica con R(x), la sezione relativa a
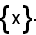
In altri termini, se
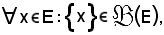
si considera per convenzione
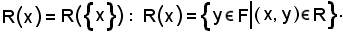
Proprietà delle sezioni
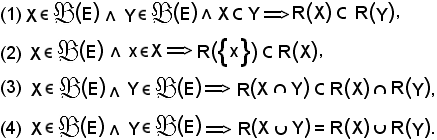
Dimostrazione (1): si consideri z R(X)
R(X)  z
z F
F 
 x
x X
X  (x, z)
(x, z) R; inoltre, se z
R; inoltre, se z F
F  x
x Y
Y  (x, z)
(x, z) R, siccome per ipotesi X
R, siccome per ipotesi X  Y
Y  x
x X
X  x
x Y. Cioè, per definizione z
Y. Cioè, per definizione z R(Y), quindi R(X)
R(Y), quindi R(X)  R(Y).
R(Y).
Dimostrazione (2): si consideri
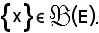
Siccome per ipotesi
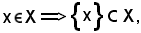
applicando la proprietà (1) si ha
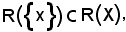
o equivalentemente
R(x) R(X).
R(X).
Dimostrazione (3): è noto che X Y
Y  X
X  X
X  Y
Y  Y
Y  R(X
R(X  Y)
Y)  R(X)
R(X)  R(X
R(X  Y)
Y)  R(Y), per la proprietà (1), quindi R(X
R(Y), per la proprietà (1), quindi R(X  Y)
Y)  R(X)
R(X)  R(Y).
R(Y).
Dimostrazione (4): è noto che X X
X  Y
Y  Y
Y  X
X  Y
Y R(X)
R(X)  R(X
R(X  Y)
Y)  R(Y)
R(Y)  R(X
R(X  Y), per la proprietà (1), quindi R(X)
Y), per la proprietà (1), quindi R(X)  R(Y)
R(Y)  R(X
R(X  Y).
Y).
Viceversa, si deve dimostrare che R(X Y)
Y)  R(X)
R(X)  R(Y). Allo scopo, si assume un elemento arbitrario
R(Y). Allo scopo, si assume un elemento arbitrario
k R(X
R(X  Y)
Y)  k
k F
F 
 z
z X
X  Y
Y  (z, k)
(z, k) R.
R.
Se z X
X 
 z
z X
X  (z, k)
(z, k) R
R  k
k R(X).
R(X).
Se z Y
Y 
 z
z Y
Y  (z, k)
(z, k) R
R  k
k R(Y).
R(Y).
In definitiva
k R(X)
R(X)  R(Y).
R(Y).
Avendo dimostrato che
R(X) R(Y)
R(Y)  R(X
R(X  Y)
Y)  R(X
R(X  Y)
Y)  R(X)
R(X)  R(Y),
R(Y),
segue che
R(X Y) = R(X)
Y) = R(X)  R(Y).
R(Y).
Proposizione
Se R ed S sono parti del prodotto E X F dell'insieme E per l'insieme F, o equivalentemente se R d S sono relazioni fra elementi di E ed elementi di F, condizione necessaria e sufficiente affinchè R = S è che:
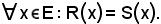
In altri termini, se
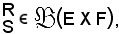
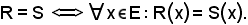
Dimostrazione
Considerato un elemento x E, per definizione si ha
E, per definizione si ha
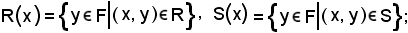
inoltre, essendo per ipotesi R = S, si conclude che gl'insiemi R(x) ed S(x) sono uguali.
Viceversa, considerata la coppia (x, y) R, per definizione y
R, per definizione y R(x)= S(x), per cui y
R(x)= S(x), per cui y S(x) e per definizione (x, y)
S(x) e per definizione (x, y) S, cioè R
S, cioè R  S.
S.
Inoltre, se (x, y) S, si ha anche che (x, y)
S, si ha anche che (x, y) R, per cui S
R, per cui S  R, e quindi R = S.
R, e quindi R = S.
Sezione della relazione inversa
Siano E, F insiemi e
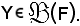
La sezione della relazione inversa è espressa da:
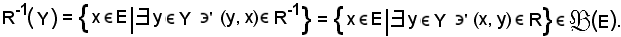
Sezione inversa della sezione
Sia X parte dell'insieme E ed R(X) parte dell'insieme F, cioè
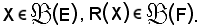
Si dimostra che:

Al posto della (1) si dimostra che le seguenti due proposizioni sono equivalenti:
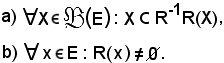
Dimostrazione a) b)
b)
Si fissi un arbitrario x E, cioè
E, cioè
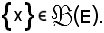
Essendo vera la a) per ipotesi, risulta
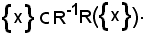
Ciò significa che:
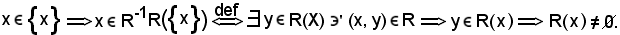
Dimostrazione b) a)
a)
Si fissi un arbitrario x X
X E.
E.
Essendo vera la b) per ipotesi, risulta

Avendo trovato che x X e x
X e x R-1R(X), si conclude che:
R-1R(X), si conclude che:
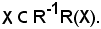
Sia Y parte dell'insieme F ed R-1(Y) parte dell'insieme E, cioè
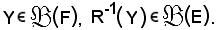
Si dimostra che:
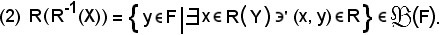
Al posto della (2) si dimostra che le seguenti due proposizioni sono equivalenti:

Allo scopo, si dimostra prima la seguente proposizione:
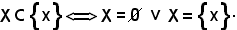
Ragionando per assurdo, si suppone che X ≠ , pertanto:
, pertanto:
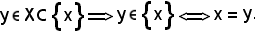
Quindi:
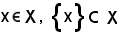
e, essendo per ipotesi
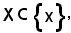
si ha:
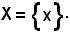
Quindi:
X = .
.
Il viceversa è immediato:
se
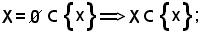
se
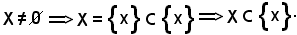
Ciò premesso, si dimostra che:
a') b'), cioè supponendo per ipotesi R-1(R(x))
b'), cioè supponendo per ipotesi R-1(R(x)) Y, risulta R(x) =
Y, risulta R(x) =  v R(x) formato da un solo elemento.
v R(x) formato da un solo elemento.
quindi
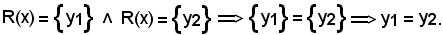
Si dimostra ora che:
b') a')Allo scopo, si fissi un elemento
a')Allo scopo, si fissi un elemento
y R(R-1(Y))
R(R-1(Y)) 
 x
x R-1(Y)
R-1(Y)  (x, y)
(x, y) R
R  y
y R(x)
R(x)  R(x) ≠
R(x) ≠ ed R(x) è formato dal solo elemento y, cioè
ed R(x) è formato dal solo elemento y, cioè
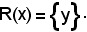
Sia ora
y R-1(Y)
R-1(Y) 
 z
z Y
Y  (z, x)
(z, x) R-1
R-1 
 z
z Y (x, z)
Y (x, z) R
R  z
z R(x)
R(x)  R(x) ≠
R(x) ≠ ed R(x) è formato
ed R(x) è formato
dal solo elemento z, cioè
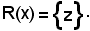
Quindi:
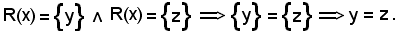
Si è quindi dimostrato che, fissato un elemento
y R(R-1(Y)), y = z
R(R-1(Y)), y = z Y
Y  R(R-1(Y))
R(R-1(Y)) Y.
Y.
Sezione della relazione compostaSia X parte dell'insieme E, la sezione della relazione composta si definisce e si indica come segue:
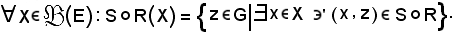
Proprietà
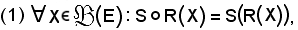
assunta per definizione.
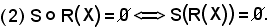
Applicando la (1) la dimostrazione è banale.

Si assume un elemento
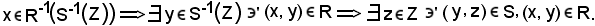
Essendo R una relazione fra elementi dell'insieme E e dell'insieme F, ed S una relazione fra elementi dell'insieme F e dell'insieme G, siccome
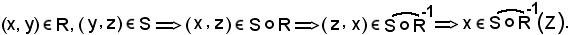
Si è dimostrato che:
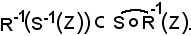
Si assume ora un elemento
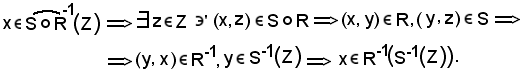
Dunque, avendo anche dimostrato che

si ha:
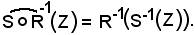
1)-Coppia non ordinata
Se
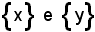
sono due insiemi ridotti, rispettivamente, al solo elemento x ed al solo elemento y, posto
l'insieme definito dalla (1), cioè dalla riunione degl'insiemi ridotti ai soli elementi x ed y, si chiama coppia non ordinata.
Proprietà
1)-Per la proprietà commutativa della riunione, risulta:
Si deve inoltre tener presente che non si esclude il caso in cui sia x = y.
2)-Se z è un elemento della coppia non ordinata (1), si ha:
3)-Se l'insieme ridotto al solo elemento z è uguale alla coppia non ordinata (1), si ha:
cioè gli elementi x, y e z sono uguali.
Infatti, essendo per ipotesi
si ha
x = y = z.
4)-Due coppie non ordinate sono uguali se e solo se si verifica quanto segue:
Infatti, si presentano due casi:
a) x' = y',
b) x' ≠ y'.
Nel caso a), in cui x' = x'', sia z l'elemento comune, cioè sia x' = y' = z; per la proprietà 3), si ha:
Inoltre, per ipotesi risulta
pertanto
cioè
z = x'' = y'',
sempre per la proprietà 3).
Nel caso b), siccome x' appartiene alla prima coppia non ordinata, per ipotesi uguale alla seconda coppia non ordinata, esso appartiene anche alla seconda coppia non ordinata, cioè:
pertanto, per la proprietà 2), si ha
Nel caso in cui x' = x'', poichè
si hanno ancora due alternative
1^) y' = x'' e 2^) y' = y''.
La prima alternativa non è vera, perchè se lo fosse, poichè x' = x'', si avrebbe y' = x'' = x', e ciò è assurdo, perchè per ipotesi x' ≠ y'. Quindi y' = y''.
Nel
caso in cui x' = y'', si esclude che sia y' = y'', perchè se lo
fosse, si avrebbe x' = y'' = y', e ciò è contro l'ipotesi,
quindi si ha y' = x''.
Osservazione
In generale, dati gl'insiemi X, Y e Z, per la proprietà associativa della riunione e dell'intersezione, si può scrivere:
X
2)-Terna non ordinata
Dati gli oggetti x, y e z, la riunione degl'insiemi ridotti ai soli elementi x, y e z si chiama terna non ordinata e, per l'osservazione precedente, si indica:
3)-Coppia ordinata
Alla formulazione del concetto fondamentale di coppia ordinata si perviene più agevolmente dopo aver stabilito i seguenti lemmi, cioè proposizioni che fungono da prima premessa di un ragionamento.
Lemma 1 - Se A', B', A'', B'' sono insiemi, e se
si ha:
(1) A'
Dimostrazione
Siccome per ipotesi
applicando la proprietà 4) si hanno due alternative:
1^) A'= A''
2^) A' = B''
Nel primo caso le (1) sono ovvie.
Nel secondo caso si ha:
Lemma 2 - Se x', y', x'', y'' sono oggetti, si ha
Dimostrazione
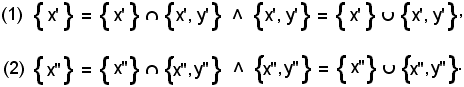
Inoltre, dall' ipotesi
e dal lemma 1, in cui si assume
richiamate 1) e 2), si ha:
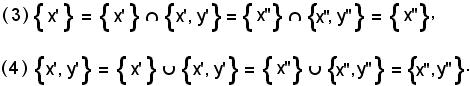
La (3) esprime che:
(5) x' = x''.
Analogamente si dimostra che
y' = y''.
Allo scopo si distinguono due casi:
1° y' = x'',
2° y' ≠ x''.
Nel 1° caso, essendo per la (5) x' = x'', si ha x' = y'; inoltre, essendo vera la proprietà 4), risulta:
da ciò segue
y' = y''.
Nel 2° caso, per la proprietà 4), si ha:
quindi
Si è quindi dimostrato che
Il viceversa è ovvio.
Definizione di coppia ordinata
Se x ed y sono oggetti, si chiama coppia ordinata di prima coordinata x e di seconda coordinata y, e si denota con (x, y), la coppia non ordinata
Quindi risulta:
Teorema fondamentale - Condizione necessaria e sufficiente affinchè due coppie ordinate siano uguali, è che la prima coordinata della prima coppia sia uguale alla prima coordinata della seconda coppia e che la seconda coordinata della prima coppia sia uguale alla seconda coordinata della seconda coppia.
Cioè, se x', x'', y', y'' sono oggetti, risulta:
(x', y') = (x'', y'')
Dimostrazione
Siccome per ipotesi le due coppie ordinate sono uguali, applicando il lemma 2) si ha:
4)-Definizione di terna ordinata
Se x, y e z sono oggetti, si chiama terna ordinata di prima coordinata x, di seconda coordinata y, di terza coordinata z, e si indica con (x, y, z), la coppia ordinata ((x, y), z).
Teorema fondamentale - Condizione necessaria e sufficiente affinchè due terne ordinate siano uguali, è che la prima coordinata della prima terna sia uguale alla prima coordinata della seconda terna, che la seconda coordinata della prima terna sia uguale alla seconda coordinata della seconda terna e che la terza coordinata della prima terna sia uguale alla terza coordinata della seconda terna.
Cioè, se x', x'', y', y'' sono oggetti, risulta:
La dimostrazione è banale.
Sulla base di queste nozioni, s'introduce il concetto di relazione.
Definizione di relazione - Si chiama relazione ogni insieme i cui elementi sono coppie ordinate.
Quindi, se si denota con R una relazione, i suoi elementi sono del tipo (x, y). Spesso, invece di scrivere (x, y)
In altri termini, R è una relazione se e solo se R è un insieme tale che
Siano E ed F due insiemi.
Definizione - Si chiama relazione fra gli elementi di E e gli elementi di F ogni relazione R tale che se
Sia E = F.
Definizione - Si chiama relazione sull'insieme E ogni relazione R tra gli elementi dello stesso insieme, secondo la definizione precedente.
Siano E ed F insiemi.
Definizione di relazione inversa
Si chiama relazione inversa della relazione R, e si denota con R-1, l'insieme delle coppie ordinate (y, x)
In altri termini:
Siano E ed F insiemi.
Definizione di relazione inversa dell'inversa
Si chiama relazione inversa dell'inversa R-1, e si denota con
l'insieme delle coppie ordinate (x, y)
In altri termini:
Relazione composta di due relazioni
Sia R una relazione fra elementi di E ed elementi di F ed S una relazione fra elementi di F ed elementi di G, cioè
Si consideri la relazione composta delle due relazioni, definita e indicata come segue:
e si legge S cerchietto R.
Relazione inversa di una relazione composta di due relazioni
E' definita come segue:
Relazione fondamentale - Prodotto di due insiemi
Si chiama prodotto dell'insieme E per l'insieme F, e si indica con E X F, l'insieme delle coppie ordinate (x, y), tali che x
Osservazioni
1)-Il prodotto E X F è diverso dal prodotto F X E; i due prodotti sono uguali solo nel caso in cui sia E = F.
Infatti, considerata la coppia ordinata (x, y), per definizione essa è diversa dalla coppia (y, x), pertanto E X F è diverso da F X E.
Se (x, y) = (y, x), allora E = F. Infatti, se x
2)-Il prodotto E X F non è vuoto se i due insiemi non sono vuoti, cioè:
3)-Il prodotto E X F è vuoto se uno dei due insiemi è vuoto, cioè:
4)-Il prodotto E X F è una relazione tra elementi di E ed elementi di F e, se R è una qualsiasi altra relazione tra elementi di E ed elementi di F, risulta:
R
ossia
Infatti, considerata la coppia ordinata (x, y)
5)-Siano A', B', A'', B'' quattro insiemi, si dimostra che:
(A' X B')
La dimostrazione segue facilmente dalle definizioni.
6)-Siano A, B, C tre insiemi, si dimostra che:
(A
La dimostrazione segue facilmente dalle definizioni.
Diagonale del prodotto
Sia E un insieme.
Si chiama diagonale del prodotto E X E, dell'insieme E per se stesso o più brevemente diagonale di E, e si indica con ΔE, l'insieme delle coppie (x, y)
In altri termini:
Sezione di una relazione
Se R è una parte del prodotto E X F, o equivalentemente una relazione tra elementi dell'insieme E ed elementi dell'insieme F, per ogni altra parte X di E si chiama sezione di R relativa ad X e si indica con R(X), l'insieme degli elementi y
In altri termini, se
Con le stesse notazioni della definizione suddetta, per ogni x
In altri termini, se
si considera per convenzione
Proprietà delle sezioni
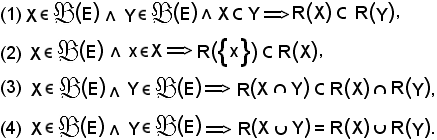
Dimostrazione (1): si consideri z
Dimostrazione (2): si consideri
Siccome per ipotesi
applicando la proprietà (1) si ha
o equivalentemente
R(x)
Dimostrazione (3): è noto che X
Dimostrazione (4): è noto che X
Viceversa, si deve dimostrare che R(X
k
Se z
Se z
In definitiva
k
Avendo dimostrato che
R(X)
segue che
R(X
Proposizione
Se R ed S sono parti del prodotto E X F dell'insieme E per l'insieme F, o equivalentemente se R d S sono relazioni fra elementi di E ed elementi di F, condizione necessaria e sufficiente affinchè R = S è che:
In altri termini, se
Dimostrazione
Considerato un elemento x
inoltre, essendo per ipotesi R = S, si conclude che gl'insiemi R(x) ed S(x) sono uguali.
Viceversa, considerata la coppia (x, y)
Inoltre, se (x, y)
Sezione della relazione inversa
Siano E, F insiemi e
La sezione della relazione inversa è espressa da:
Sezione inversa della sezione
Sia X parte dell'insieme E ed R(X) parte dell'insieme F, cioè
Si dimostra che:
Al posto della (1) si dimostra che le seguenti due proposizioni sono equivalenti:
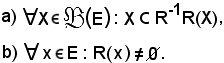
Dimostrazione a)
Si fissi un arbitrario x
Essendo vera la a) per ipotesi, risulta
Ciò significa che:
Dimostrazione b)
Si fissi un arbitrario x
Essendo vera la b) per ipotesi, risulta
Avendo trovato che x
Sia Y parte dell'insieme F ed R-1(Y) parte dell'insieme E, cioè
Si dimostra che:
Al posto della (2) si dimostra che le seguenti due proposizioni sono equivalenti:

Allo scopo, si dimostra prima la seguente proposizione:
Ragionando per assurdo, si suppone che X ≠
Quindi:
e, essendo per ipotesi
si ha:
Quindi:
X =
Il viceversa è immediato:
se
Ciò premesso, si dimostra che:
a')
Allo scopo, si fissi un elemento x E e si consideri R(x) ≠
E e si consideri R(x) ≠  ; si deve dimostrare che R(x) è formato da un solo elemento.
; si deve dimostrare che R(x) è formato da un solo elemento.
Supponiamo che ce ne siano due:
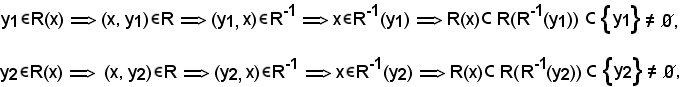
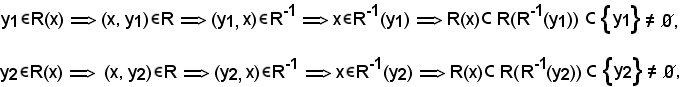
quindi
Si dimostra ora che:
b')
y
Sia ora
y
dal solo elemento z, cioè
Quindi:
Si è quindi dimostrato che, fissato un elemento
y
Sezione della relazione composta
Proprietà
assunta per definizione.
Applicando la (1) la dimostrazione è banale.
Si assume un elemento
Si è dimostrato che:
Si assume ora un elemento
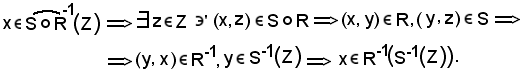
Dunque, avendo anche dimostrato che
si ha: