RELAZIONI FUNZIONALI ---> INDICE
Siano E ed F due insiemi e G una relazione fra elementi di E ed elementi di F, cioè
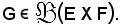
Definizione di relazione funzionale
Si chiama relazione funzionale tra elementi di E ed elementi di F ogni relazione G che verifica le seguenti condizioni:
1)- x
x E la sezione G(x), di G relativa ad x, è non vuota, cioè:
E la sezione G(x), di G relativa ad x, è non vuota, cioè:
 x
x E : G(x) ≠
E : G(x) ≠  .
.
2)- x
x E la sezione G(x), di G relativa ad x, è formata da un solo elemento, cioè:
E la sezione G(x), di G relativa ad x, è formata da un solo elemento, cioè:
 x
x E
E  x'
x' G(x)
G(x) 
 y'
y' G(x) : x' = y'.
G(x) : x' = y'.
(G grafico)  (
( x
x E
E  y
y F
F  (x, y)
(x, y) G)
G) 
 x
x E : G(x) ≠
E : G(x) ≠ 
 G(x) è formato da un solo
G(x) è formato da un solo
Definizione di funzione, o applicazione o trasformazione
Sia f un'applicazione fra elementi di E ed elementi di F a cui corrisponda una terna ordinata f = (E, F, G) nella quale la 1^ e la 2^ coordinata sono insiemi e la 3^ una relazione funzionale tra elementi di E ed elementi di F.
A queste coordinate si assegnano i seguenti nomi:
-ad E insieme di definizione o di partenza,
-ad F insieme di variabilità o di arrivo,
-a G di grafico dell'applicazione f.Si
chiama funzione, o applicazione o trasformazione dell'insieme E
nell'insieme F ogni applicazione f che abbia E come insieme di
definizione ed F come insieme di variabilità.
In tal caso si può anche dire che f è una funzione definita in E che assume valori in F.
Spesso, un'applicazione di E in F si indica soltanto con una lettera minuscola, ad esempio f, e si scrive:
f : E F.
F.
Valore dell'applicazioneSe f è un'applicazione dell'insieme E nell'insieme F, cioè
f : E F,
F,
 x
x E si
chiama valore di f in x, e s'indica con f(x), l'unico elemento di F a
cui si riduce la sezione G(x) del grafico G dell'applicazione f.
E si
chiama valore di f in x, e s'indica con f(x), l'unico elemento di F a
cui si riduce la sezione G(x) del grafico G dell'applicazione f.
Essendo
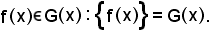
Se G è un grafico, si dimostra che:
(x, y) G
G  y = f(x).
y = f(x).
Infatti, siccome y G(x), si ha:
G(x), si ha:
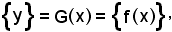
cioè
y = f(x).
Viceversa, se
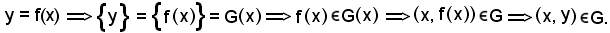
Teorema - Se f' ed f'' sono due applicazioni dell'insieme E nell'insieme E', risulta f' = f'', se e solo se per ogni x E risulta f'(x) = f''(x), cioè se
E risulta f'(x) = f''(x), cioè se
f' : E E'
E'  f'' : E
f'' : E  E'
E'
f' = f'''
 x
x E : f'(x) = f''(x).
E : f'(x) = f''(x).
Infatti, considerati i grafici G' e G'' delle funzioni f' ed f'', essendo f' = (E, E', G'), f'' = (E, E', G'') e per ipotesi f' = f'', dev'essere G' = G''; ciò equivale a dire che
 x
x E : f'(x) = f''(x).
E : f'(x) = f''(x).
Nota bene
In tema di notazioni, se A e B sono insiemi, esiste un insieme che si indica con B elevato ad A oppure con effe gotica di A, B, cioè
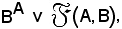
i cui elementi sono tutte e sole le applicazioni di A in B:
f : A B.
B.
Caratterizzazioni di relazioni funzionali
1)-Applicazione costante
Siano E ed F insiemi e y0 F.
F.
Si consideri la relazione tra elementi di E ed elementi di F, in corrispondenza dell'elemento y0 F, cioè:
F, cioè:
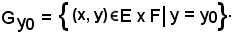
Si dimostra che

è una relazione funzionale, quindi la sezione
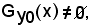
ed è formata da un solo elemento.
Infatti, si prenda una coppia arbitraria
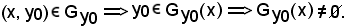
Quindi, si è dimostrato che la sezione è non vuota; si dimostra ora che essa è formata da un solo elemento. Allo scopo, si considerano due elementi e si dimostra che essi coincidono.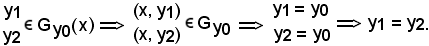
Avendo dimostrato che

è una relazione funzionale, ha senso considerare l'applicazione
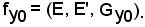
Essa si chiama applicazione costante di costante valore y0.
Per definizione
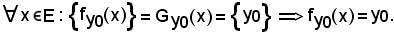
2)-Applicazione identica o bigezione canonica
Sia E un insieme.
Si consideri la diagonale del prodotto E X E, dell'insieme E per se stesso o più brevemente diagonale di E, indicata con ΔE, cioè l'insieme delle coppie (x, y) E X, tali che x = y.
E X, tali che x = y.
In altri termini:
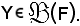
Si dimostra che
ΔE
è una relazione funzionale, quindi la sezione
ΔE(x) ≠ ,
,
ed è formata da un solo elemento.
Infatti, si prenda una coppia arbitraria
(x, x) ΔE(x)
ΔE(x)  x
x ΔE(x)
ΔE(x)  ΔE(x) ≠
ΔE(x) ≠  .
.
Quindi, si è dimostrato che la sezione è non vuota; si dimostra ora che essa è formata da un solo elemento. Allo scopo, si considerano due elementi e si dimostra che essi coincidono.
Siano essi
Avendo dimostrato che
ΔE
è una relazione funzionale, ha senso considerare l'applicazione
iE = (E, E, ΔE).
Essa si chiama applicazione identica, o bigezione canonica o identità dell'insieme E.
Per definizione
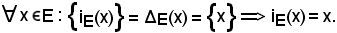
3)-Ingezione canonica
Sia E un insieme, A una parte dell'insieme E e ΔA la diagonale del prodotto A X E, definita come segue:

Si dimostra che
ΔA
è una relazione funzionale, quindi la sezione
ΔA(x) ≠ ,
,
ed è formata da un solo elemento.
Infatti, si prenda una coppia arbitraria
(x, x) A X A
A X A  A X E
A X E  (x, x)
(x, x) ΔA
ΔA  x
x ΔA(x)
ΔA(x)  ΔA(x) ≠
ΔA(x) ≠  .
.
Quindi, si è dimostrato che la sezione è non vuota; si dimostra ora che essa è formata da un solo elemento. Allo scopo, si considerano due elementi e si dimostra che essi coincidono.
Siano essi
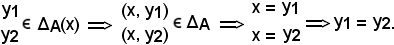
Avendo dimostrato che
ΔA
è una relazione funzionale, ha senso considerare l'applicazione
jA = (A, E, ΔA).
Essa si chiama ingezione canonica o applicazione inclusione di A in E.
Per definizione
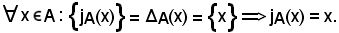
Convenzione
Siano E, F, G insiemi; se
f : E X F  G,
G,
è un'applicazione dell'insieme E X F, prodotto dell'insieme E per l'insieme F, nell'insieme G, x
x E X F il valore che f assume in (x, y) è indicato con f(x, y).
E X F il valore che f assume in (x, y) è indicato con f(x, y).
La circostanza che il valore f(x, y) dipenda da x E e da y
E e da y F spiega il motivo per cui f si chiama funzione di due variabili.
F spiega il motivo per cui f si chiama funzione di due variabili.
E' bene tener presente che tale valore si sarebbe dovuto indicare con f((x, y)), ma è preferibile indicarlo con f(x, y) per snellire la terminologia.
4)-Prima e seconda proiezione del prodotto di due insiemi
Siano E ed F insiemi ed R1 la relazione fra elementi dell'insieme (E X F) e l'insieme E, definita
come segue:
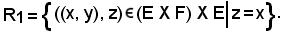
Si dimostra che
R1
è una relazione funzionale, quindi la sezione
R1(x) ≠ ,
,
ed è formata da un solo elemento.
Infatti, si prenda una coppia arbitraria
((x, y), x) R1
R1  (x, y)
(x, y) R1(x, y)
R1(x, y)  R1(x, y)≠
R1(x, y)≠ .
.
Quindi, si è dimostrato che la sezione è non vuota; si dimostra ora che essa è formata da un solo elemento. Allo scopo, si considerano due elementi e si dimostra che essi coincidono.
Siano essi
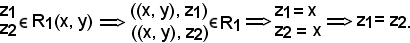
Avendo dimostrato che
R1
è una relazione funzionale, ha senso considerare l'applicazione
pr1 = (E X F, E, R1).
Essa si chiama prima proiezione del prodotto E X F.
Per definizione
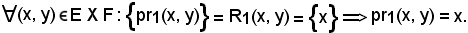
Analogamente, sia R2 la relazione fra elementi dell'insieme (E X F) e l'insieme F, definita come segue:
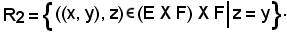
Si dimostra, come è stato fatto in precedenza, che
R2
è una relazione funzionale, quindi la sezione
R2(x) ≠ ,
,
ed è formata da un solo elemento.
Quindi, ha senso considerare l'applicazione
pr2 = (E X F, F, R2).
Essa si chiama seconda proiezione del prodotto E X F.
Per definizione
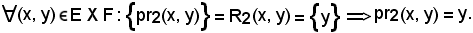
5)-Applicazione fondamentali
Siano E ed F insiemi ed R1v la relazione fra elementi dell'insieme E e dell'insieme (E X F), con v F, definita come segue:
F, definita come segue:
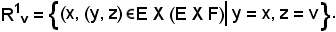
Si dimostra che
R1v
è una relazione funzionale, quindi la sezione
R1v (x)≠ ,
,
ed è formata da un solo elemento.
Infatti, si prenda una coppia arbitraria
(x, (x, v)) R1v
R1v  (x, v)
(x, v) R1v(x)
R1v(x)  R1v(x, y)≠
R1v(x, y)≠ .
.
Quindi, si è dimostrato che la sezione è non vuota; si dimostra ora che essa è formata da un solo elemento. Allo scopo, si considerano due elementi e si dimostra che essi coincidono.
Siano essi
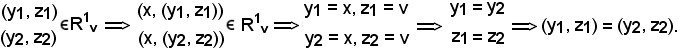
Avendo dimostrato che
R1v
è una relazione funzionale, ha senso considerare l'applicazione
φ1v = (E, E X F, R1v).
Per definizione
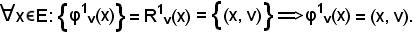
Analogamente, sia R2u la relazione fra elementi di F ed (E X F), così definita:
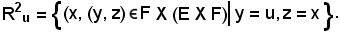
Si dimostra che
R2u
è una relazione funzionale, quindi la sezione
R2u(x) ≠ ,
,
ed è formata da un solo elemento.Quindi, ha senso considerare l'applicazione
φ2u = (F, E X F, R2u).
Per definizione
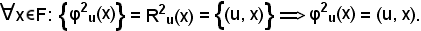
6)-Estensione di un'applicazione alle parti di un insieme
Si consideri l'applicazione f = (E, F, G), cioè f : E F e
F e
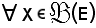
si consideri l'insieme
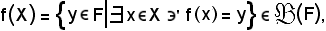
che rappresenta, come si vedrà in seguito, l'immagine diretta di X mediante f.
Si considerino ora
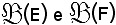
insiemi di partenza e di arrivo e si indichi con R la relazione tra i loro elementi, cioè:
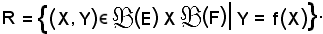
Si dimostra che
R
è una relazione funzionale, quindi la sezione
R(X) ≠ ,
,
ed è formata da un solo elemento.
Infatti,
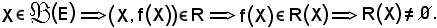
Quindi, si è dimostrato che la sezione è non vuota; si dimostra ora che essa è formata da un solo elemento. Allo scopo, si considerano due elementi e si dimostra che essi coincidono.
Siano essi
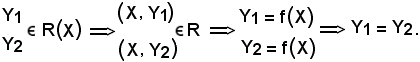
Avendo dimostrato che
R
è una relazione funzionale, ha senso considerare l'applicazione
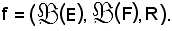
Essa si chiama estensione di f alle parti di un insieme.
Per definizione
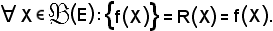
E' bene osservare che f(X) R(X) è il nuovo valore di X nella nuova applicazione e coincide proprio con f(X) dell'applicazione di partenza.
R(X) è il nuovo valore di X nella nuova applicazione e coincide proprio con f(X) dell'applicazione di partenza.
Proposizione
Sia f = (E, F, G), cioè f : E F e
F e
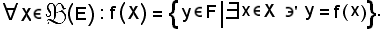
Si consideri ora la sezione G(X), di G relativa ad X, si dimostra che:
f(X) = G(X).
Allo scopo, si suppone che:
X ≠ ,
,
e quindi
f(X) ≠ .
.
Sia
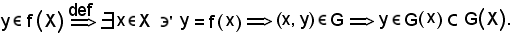
Resta dimostrato che
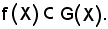
Viceversa, sia
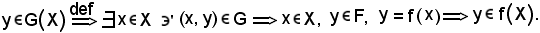
Resta anche dimostrato che
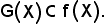
Quindi:
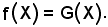
7)-Estensione reciproca
Si consideri l'applicazione f = (E, F, G), cioè f : E F e
F e
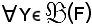
si consideri l'insieme
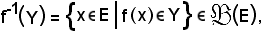
che rappresenta, come si vedrà in seguito, l'immagine reciproca di Y mediante f.
Si considerino ora
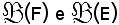
insiemi di partenza e di arrivo e si indichi con R1 la relazione tra i loro elementi, cioè:
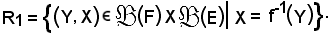
Si dimostra che
R1
è una relazione funzionale, quindi la sezione
R1(Y) ≠ ,
,
ed è formata da un solo elemento.
Infatti,
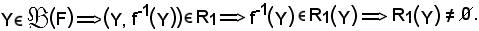
Quindi, si è dimostrato che la sezione è non vuota; si dimostra ora che essa è formata da un solo elemento. Allo scopo, si considerano due elementi e si dimostra che essi coincidono.
Siano essi
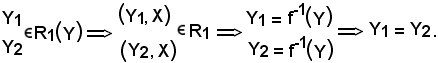
Avendo dimostrato che
R1
è una relazione funzionale, ha senso considerare l'applicazione
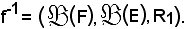
Essa si chiama estensione reciproca di f alle parti di un insieme.
Per definizione
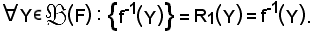
Proposizione
Sia f = (E, F, G), cioè f : E F e
F e
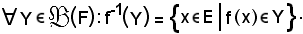
Si consideri ora la sezione inversa G-1(Y), di G relativa ad Y, si dimostra che:
f-1(Y) = G-1(Y),
per ogni parte Y di F.
Allo scopo, si suppone che:
Y ≠ ,
,
e quindi
f-1(Y) ≠ .
.
Sia
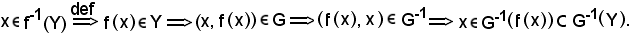
Resta dimostrato che
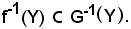
Viceversa, sia
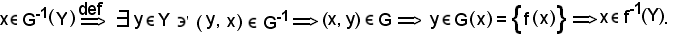
Resta anche dimostrato che
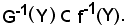
Quindi:
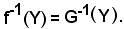
8)-Applicazione prodotto di due applicazioni
Siano f = (E, F, R) e g = (E', F', R') due applicazioni; la relazione associata all'applicazione prodotto delle due è:
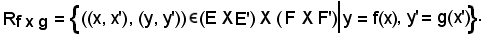
Essa è una relazione funzionale così definita:
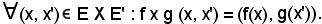
9)-Applicazione parziale
e, fissato x E, si può considerare
E, si può considerare
f(x, .) : F E' X F'
E' X F' 
 y
y F f(x, .)(x) = f(x, y).
F f(x, .)(x) = f(x, y).
Definizione di relazione funzionale
Si chiama relazione funzionale tra elementi di E ed elementi di F ogni relazione G che verifica le seguenti condizioni:
1)-
2)-
in cui il simbolo  esprime "uno ed un solo".
esprime "uno ed un solo".
In altri termini, si dice che G è una relazione funzionale o grafico, se si verifica quanto segue:
elemento.
Definizione di funzione, o applicazione o trasformazione
Sia f un'applicazione fra elementi di E ed elementi di F a cui corrisponda una terna ordinata f = (E, F, G) nella quale la 1^ e la 2^ coordinata sono insiemi e la 3^ una relazione funzionale tra elementi di E ed elementi di F.
A queste coordinate si assegnano i seguenti nomi:
-ad E insieme di definizione o di partenza,
-ad F insieme di variabilità o di arrivo,
-a G di grafico dell'applicazione f.
In tal caso si può anche dire che f è una funzione definita in E che assume valori in F.
Spesso, un'applicazione di E in F si indica soltanto con una lettera minuscola, ad esempio f, e si scrive:
f : E
Valore dell'applicazione
f : E
Essendo
Se G è un grafico, si dimostra che:
(x, y)
Infatti, siccome y
cioè
y = f(x).
Viceversa, se
Teorema - Se f' ed f'' sono due applicazioni dell'insieme E nell'insieme E', risulta f' = f'', se e solo se per ogni x
f' : E
f' = f'''
Infatti, considerati i grafici G' e G'' delle funzioni f' ed f'', essendo f' = (E, E', G'), f'' = (E, E', G'') e per ipotesi f' = f'', dev'essere G' = G''; ciò equivale a dire che
Nota bene
In tema di notazioni, se A e B sono insiemi, esiste un insieme che si indica con B elevato ad A oppure con effe gotica di A, B, cioè
i cui elementi sono tutte e sole le applicazioni di A in B:
f : A
Caratterizzazioni di relazioni funzionali
1)-Applicazione costante
Siano E ed F insiemi e y0
Si consideri la relazione tra elementi di E ed elementi di F, in corrispondenza dell'elemento y0
Si dimostra che
è una relazione funzionale, quindi la sezione
ed è formata da un solo elemento.
Infatti, si prenda una coppia arbitraria
Quindi, si è dimostrato che la sezione è non vuota; si dimostra ora che essa è formata da un solo elemento. Allo scopo, si considerano due elementi e si dimostra che essi coincidono.
- Siano essi
Avendo dimostrato che
è una relazione funzionale, ha senso considerare l'applicazione
Essa si chiama applicazione costante di costante valore y0.
Per definizione
2)-Applicazione identica o bigezione canonica
Sia E un insieme.
Si consideri la diagonale del prodotto E X E, dell'insieme E per se stesso o più brevemente diagonale di E, indicata con ΔE, cioè l'insieme delle coppie (x, y)
In altri termini:
Si dimostra che
ΔE
è una relazione funzionale, quindi la sezione
ΔE(x) ≠
ed è formata da un solo elemento.
Infatti, si prenda una coppia arbitraria
(x, x)
Quindi, si è dimostrato che la sezione è non vuota; si dimostra ora che essa è formata da un solo elemento. Allo scopo, si considerano due elementi e si dimostra che essi coincidono.
Siano essi
Avendo dimostrato che
ΔE
è una relazione funzionale, ha senso considerare l'applicazione
iE = (E, E, ΔE).
Essa si chiama applicazione identica, o bigezione canonica o identità dell'insieme E.
Per definizione
3)-Ingezione canonica
Sia E un insieme, A una parte dell'insieme E e ΔA la diagonale del prodotto A X E, definita come segue:
Si dimostra che
ΔA
è una relazione funzionale, quindi la sezione
ΔA(x) ≠
ed è formata da un solo elemento.
Infatti, si prenda una coppia arbitraria
(x, x)
Quindi, si è dimostrato che la sezione è non vuota; si dimostra ora che essa è formata da un solo elemento. Allo scopo, si considerano due elementi e si dimostra che essi coincidono.
Siano essi
Avendo dimostrato che
ΔA
è una relazione funzionale, ha senso considerare l'applicazione
jA = (A, E, ΔA).
Essa si chiama ingezione canonica o applicazione inclusione di A in E.
Per definizione
Convenzione
Siano E, F, G insiemi; se
è un'applicazione dell'insieme E X F, prodotto dell'insieme E per l'insieme F, nell'insieme G,
La circostanza che il valore f(x, y) dipenda da x
E' bene tener presente che tale valore si sarebbe dovuto indicare con f((x, y)), ma è preferibile indicarlo con f(x, y) per snellire la terminologia.
4)-Prima e seconda proiezione del prodotto di due insiemi
Siano E ed F insiemi ed R1 la relazione fra elementi dell'insieme (E X F) e l'insieme E, definita
come segue:
Si dimostra che
R1
è una relazione funzionale, quindi la sezione
R1(x) ≠
ed è formata da un solo elemento.
Infatti, si prenda una coppia arbitraria
((x, y), x)
Quindi, si è dimostrato che la sezione è non vuota; si dimostra ora che essa è formata da un solo elemento. Allo scopo, si considerano due elementi e si dimostra che essi coincidono.
Siano essi
Avendo dimostrato che
R1
è una relazione funzionale, ha senso considerare l'applicazione
pr1 = (E X F, E, R1).
Essa si chiama prima proiezione del prodotto E X F.
Per definizione
Analogamente, sia R2 la relazione fra elementi dell'insieme (E X F) e l'insieme F, definita come segue:
Si dimostra, come è stato fatto in precedenza, che
R2
è una relazione funzionale, quindi la sezione
R2(x) ≠
ed è formata da un solo elemento.
Quindi, ha senso considerare l'applicazione
pr2 = (E X F, F, R2).
Essa si chiama seconda proiezione del prodotto E X F.
Per definizione
5)-Applicazione fondamentali
Siano E ed F insiemi ed R1v la relazione fra elementi dell'insieme E e dell'insieme (E X F), con v
Si dimostra che
R1v
è una relazione funzionale, quindi la sezione
R1v (x)≠
ed è formata da un solo elemento.
Infatti, si prenda una coppia arbitraria
(x, (x, v))
Quindi, si è dimostrato che la sezione è non vuota; si dimostra ora che essa è formata da un solo elemento. Allo scopo, si considerano due elementi e si dimostra che essi coincidono.
Siano essi
Avendo dimostrato che
R1v
è una relazione funzionale, ha senso considerare l'applicazione
φ1v = (E, E X F, R1v).
Per definizione
Analogamente, sia R2u la relazione fra elementi di F ed (E X F), così definita:
Si dimostra che
R2u
è una relazione funzionale, quindi la sezione
R2u(x) ≠
ed è formata da un solo elemento.
φ2u = (F, E X F, R2u).
Per definizione
6)-Estensione di un'applicazione alle parti di un insieme
Si consideri l'applicazione f = (E, F, G), cioè f : E
si consideri l'insieme
che rappresenta, come si vedrà in seguito, l'immagine diretta di X mediante f.
Si considerino ora
insiemi di partenza e di arrivo e si indichi con R la relazione tra i loro elementi, cioè:
Si dimostra che
R
è una relazione funzionale, quindi la sezione
R(X) ≠
ed è formata da un solo elemento.
Infatti,
Quindi, si è dimostrato che la sezione è non vuota; si dimostra ora che essa è formata da un solo elemento. Allo scopo, si considerano due elementi e si dimostra che essi coincidono.
Siano essi
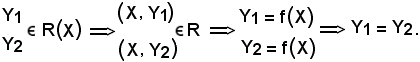
Avendo dimostrato che
R
è una relazione funzionale, ha senso considerare l'applicazione
Essa si chiama estensione di f alle parti di un insieme.
Per definizione
E' bene osservare che f(X)
Proposizione
Sia f = (E, F, G), cioè f : E
Si consideri ora la sezione G(X), di G relativa ad X, si dimostra che:
f(X) = G(X).
Allo scopo, si suppone che:
X ≠
e quindi
f(X) ≠
Sia
Resta dimostrato che
Viceversa, sia
Resta anche dimostrato che
Quindi:
7)-Estensione reciproca
Si consideri l'applicazione f = (E, F, G), cioè f : E
si consideri l'insieme
che rappresenta, come si vedrà in seguito, l'immagine reciproca di Y mediante f.
Si considerino ora
insiemi di partenza e di arrivo e si indichi con R1 la relazione tra i loro elementi, cioè:
Si dimostra che
R1
è una relazione funzionale, quindi la sezione
R1(Y) ≠
ed è formata da un solo elemento.
Infatti,
Quindi, si è dimostrato che la sezione è non vuota; si dimostra ora che essa è formata da un solo elemento. Allo scopo, si considerano due elementi e si dimostra che essi coincidono.
Siano essi
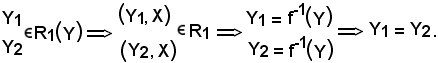
Avendo dimostrato che
R1
è una relazione funzionale, ha senso considerare l'applicazione
Essa si chiama estensione reciproca di f alle parti di un insieme.
Per definizione
Proposizione
Sia f = (E, F, G), cioè f : E
Si consideri ora la sezione inversa G-1(Y), di G relativa ad Y, si dimostra che:
f-1(Y) = G-1(Y),
per ogni parte Y di F.
Allo scopo, si suppone che:
Y ≠
e quindi
f-1(Y) ≠
Sia
Resta dimostrato che
Viceversa, sia
Resta anche dimostrato che
Quindi:
8)-Applicazione prodotto di due applicazioni
Siano f = (E, F, R) e g = (E', F', R') due applicazioni; la relazione associata all'applicazione prodotto delle due è:
Essa è una relazione funzionale così definita:
9)-Applicazione parziale
Sia assegnata un'applicazione di due variabili
f : E X F E' X F'.
E' X F'.
Si possono considerare due applicazioni, chiamate applicazioni parziali di f:
fissato y F, si può considerare l'applicazione
F, si può considerare l'applicazione
f(., y) : E E' X F'
E' X F' 
 x
x E f(., y)(x) = f(x, y)
E f(., y)(x) = f(x, y)
f : E X F
Si possono considerare due applicazioni, chiamate applicazioni parziali di f:
fissato y
f(., y) : E
e, fissato x
f(x, .) : F
10)-Applicazione composta
Siano assegnate due applicazioni:
f : E F e g : F
F e g : F  G.
G.
A partire da esse si può considerare una nuova applicazione chiamata applicazione composta di f e g.
Si dimostra che l'insieme
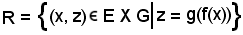
Essendo R una relazione funzionale, ha senso considerare l'applicazione
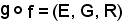
jA : A E.
E.
cioè

12)-Estensione o prolungamento di un'applicazione
Sia f : A Y, X un insieme in cui è contenuto A, si chiama estensione di f da A ad X ogni eventuale applicazione
Y, X un insieme in cui è contenuto A, si chiama estensione di f da A ad X ogni eventuale applicazione
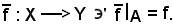
13)-Applicazione ridotta
Sia f = (E, E', G) un'applicazione dell'insieme E nell'insieme E' di grafico G.
Come si vedrà in seguito, considerata l'immagine f(E), di E mediante f, essa risulta parte di E', cioè:
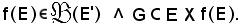
f : E
A partire da esse si può considerare una nuova applicazione chiamata applicazione composta di f e g.
Si dimostra che l'insieme
è
una relazione funzionale tra elementi di E ed elementi di G,
cioè la sezione relativa ad esso è non vuota ed è
formata da un unico elemento, cioè:
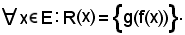
Essendo R una relazione funzionale, ha senso considerare l'applicazione
tra elementi di E ed elementi di G, che si legge g cerchietto f.
Ciò giustifica la seguente definizione:
-se f : E F e g : F
F e g : F  G sono due applicazioni, indicato con R l'insieme delle coppie ordinate (x, z)
G sono due applicazioni, indicato con R l'insieme delle coppie ordinate (x, z) E X G
E X G  z = g(f(x)), l'applicazione (E, G, R), si chiama applicazione composta di f e g.
z = g(f(x)), l'applicazione (E, G, R), si chiama applicazione composta di f e g.
Il valore che l'applicazione assume in x è il seguente:
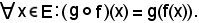
11)-Restrizione di un'applicazione ad una parte di un insieme
Sia assegnata l'applicazione f : E E',
E',
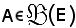
e l'ingezione canonica o applicazione inclusione di A in E
Ciò giustifica la seguente definizione:
-se f : E
Il valore che l'applicazione assume in x è il seguente:
11)-Restrizione di un'applicazione ad una parte di un insieme
Sia assegnata l'applicazione f : E
e l'ingezione canonica o applicazione inclusione di A in E
jA : A
Si chiama restrizione di f ad A, e si indica con

l'applicazione composta di f e jA, cioè:
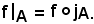
Il valore che l'applicazione assume in x è il seguente:
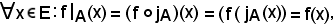
l'applicazione composta di f e jA, cioè:
Il valore che l'applicazione assume in x è il seguente:
cioè
12)-Estensione o prolungamento di un'applicazione
Sia f : A
Si distinguono due casi:
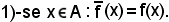
Infatti, poichè dev'essere
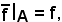
Infatti, poichè dev'essere
si ha che

13)-Applicazione ridotta
Sia f = (E, E', G) un'applicazione dell'insieme E nell'insieme E' di grafico G.
Come si vedrà in seguito, considerata l'immagine f(E), di E mediante f, essa risulta parte di E', cioè:
Si
dimostra che G è una relazione funzionale fra elementi di E ed
elementi di F(E), oltre ad esserlo fra elementi di E e di E'.
Pertanto, la terna ordinata
Pertanto, la terna ordinata
g = (E, f(E), G)
è un'applicazione di E in f(E) avente lo stesso grafico G di f e quindi si ha:
 x
x E : g(x) = f(x).
E : g(x) = f(x).
Quindi, se f = (E, E', G) è un'applicazione dell'insieme E nell'insieme E' di grafico G, l'applicazione g = (E, f(E), G) di E in f(E) si chiama applicazione ridotta di f.
E' bene osservare che se si considera l'ingezione canonica di f(E) in E, cioè
E' bene osservare che se si considera l'ingezione canonica di f(E) in E, cioè
jf(E) : f(E)  E
E
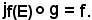
l'applicazione composta dell'insieme E nell'insieme E.
E' noto che un'applicazione di E in E è la bigezione canonica. Se si verifica la circostanza che
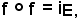
si dice che f è un'applicazione involutoria di E. Si osserva inoltre che f è anche bigettiva.
Per dimostrare ciò, basta riconoscere che f è anche invertibile, ossia è una permutazione di E cioè, essendo per ipotesi f involutoria, basta provare che

Se per caso si può dire che che g esiste, automaticamente f è invertibile, e ciò accade se si assume f = g.
Pertanto, si può anche stabilire che l'insieme delle applicazioni involutorie di E è contenuto nell'insieme delle permutazioni di E.
Si consideri l'applicazione
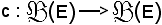
definita come segue:
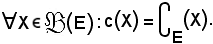
Si dimostra che è un'applicazione involutoria, cioè
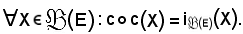
Infatti:
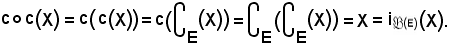
15)-Applicazione surgettiva
risulta:
Infatti, il valore che l'applicazione assume in x è dato da:
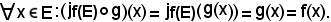
14)-Applicazione involutoria
Sia f : E E un'applicazione dell'insieme E nell'insieme E ed
E un'applicazione dell'insieme E nell'insieme E ed
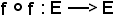
Sia f : E
l'applicazione composta dell'insieme E nell'insieme E.
E' noto che un'applicazione di E in E è la bigezione canonica. Se si verifica la circostanza che
si dice che f è un'applicazione involutoria di E. Si osserva inoltre che f è anche bigettiva.
Per dimostrare ciò, basta riconoscere che f è anche invertibile, ossia è una permutazione di E cioè, essendo per ipotesi f involutoria, basta provare che
Se per caso si può dire che che g esiste, automaticamente f è invertibile, e ciò accade se si assume f = g.
Pertanto, si può anche stabilire che l'insieme delle applicazioni involutorie di E è contenuto nell'insieme delle permutazioni di E.
Si consideri l'applicazione
definita come segue:
Si dimostra che è un'applicazione involutoria, cioè
Infatti:
Tale applicazione, essendo involutoria è anche bigettiva.
15)-Applicazione surgettiva
L'applicazione f : E  F, dell'insieme E nell'insieme F si dice surgettiva se f(E) = F, cioè:
F, dell'insieme E nell'insieme F si dice surgettiva se f(E) = F, cioè:
(f surgettiva)  (
( y
y F
F  x
x E
E  f(x) = y).
f(x) = y).
16)-Applicazione ingettiva
L'applicazione f : E  F, dell'insieme E nell'insieme F si dice ingettiva se
F, dell'insieme E nell'insieme F si dice ingettiva se
 x
x E
E  y
y F f(x) = f(y)
F f(x) = f(y)  x = y,
x = y,
cioè:
(f ingettiva) (
( x
x E
E  y
y F f(x) = f(y)
F f(x) = f(y)  x = y').
x = y').
cioè:
(f ingettiva)
17)-Applicazione bigettiva
L'applicazione f : E  E', dell'insieme E nell'insieme E' si dice bigettiva se è surgettiva e ingettiva, cioè:
E', dell'insieme E nell'insieme E' si dice bigettiva se è surgettiva e ingettiva, cioè:
(f bigettiva)  (f surgettiva
(f surgettiva  f ingettiva).
f ingettiva).