MIKY & GENNY
NUMERI DECIMALI ---> INDICE
UNITA' FRAZIONARIE DECIMALILe unità frazionarie aventi per denominatore le potenza di 10 si dicono unità frazionarie decimali. Pertanto le unità frazionarie decimali sono:
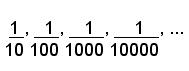
e si chiamano rispettivamente unità decimali del 1° ordine o decimi, del 2° ordine o centesimi, del 3° ordine o millesimi, del 4° ordine o decimillesimi e così via. Le seguenti scritture hanno lo stesso significato:
L'insieme di più unità decimali dello stesso ordine costitiusce una frazione decimale. Pertanto sono frazioni decimali:
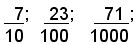
Quindi: si dice frazione decimale una frazione avente per denominatore una potenza di 10.
TRASFORMAZIONE DI UNA FRAZIONE DECIMALE IN NUMERO DECIMALE
Si consideri la frazione decimale
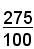
e si osservi che essa si può scrivere come segue:
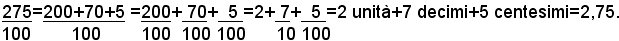
Quindi una frazione decimale è uguale ad un mumero decimale e pertanto si può enunciare la seguente regola:
Ogni frazione decimale si può scrivere sotto forma di numero decimale scrivendo il numeratore e separando con una virgola, a partire da destra, tante cifre decimali per quanti sono gli zeri del denominatore.
Esempi:
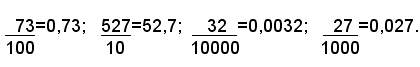
TRASFORMAZIONE DI UN NUMERO DECIMALE IN UNA FRAZIONE DECIMALE
Si è visto che 275/100=2,75, quindi in modo inverso si ha 2,75=275/100; inoltre: 0,043=43/1000; 0,13=13/100.
Un numero decimale è uguale ad una frazione avente per numeratore tutto il numero dato senza la virgola e per denominatore l'unità seguita da tanti zeri quante sono le cifre decimali del numero dato.
Quindi: si dice frazione decimale una frazione avente per denominatore una potenza di 10.
Si consideri la frazione decimale
e si osservi che essa si può scrivere come segue:
Quindi una frazione decimale è uguale ad un mumero decimale e pertanto si può enunciare la seguente regola:
Ogni frazione decimale si può scrivere sotto forma di numero decimale scrivendo il numeratore e separando con una virgola, a partire da destra, tante cifre decimali per quanti sono gli zeri del denominatore.
Esempi:
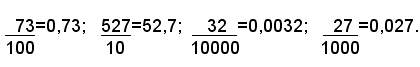
TRASFORMAZIONE DI UN NUMERO DECIMALE IN UNA FRAZIONE DECIMALE
Si è visto che 275/100=2,75, quindi in modo inverso si ha 2,75=275/100; inoltre: 0,043=43/1000; 0,13=13/100.
Un numero decimale è uguale ad una frazione avente per numeratore tutto il numero dato senza la virgola e per denominatore l'unità seguita da tanti zeri quante sono le cifre decimali del numero dato.
OPERAZIONI CON NUMERI DECIMALI
ADDIZIONE

SOTTRAZIONE
MOLTIPLICAZIONE
DIVISIONE
POTENZA
Eseguire l'addizione 2,23+4,7+5,04 scrivendo gli addendi sotto forma di frazioni decimali:

SOTTRAZIONE
Eseguire la sottrazione 27,4-11,73 scrivendo minuendo e sottraendo sotto forma di frazioni decimali:


MOLTIPLICAZIONE
Calcolare il prodotto 25,3x6,42 scrivendo i fattori sotto forma di frazioni decimali:


DIVISIONE
Eseguire la divisione 5,88:0,49 scrivendo dividendo e divisore sotto forma di frazioni decimali:

Determinare il quoziente dei numeri 66 e 7:

Si può quindi dire che 9; 9,4; 9,42; 9,428; ... sono i quozienti dei numeri dati, approssimati per difetto a meno di un decimo, un centesimo, un millesimo, ... e così via. I valori 10; 9,5; 9,43; 9,429; ... ottenuti dai quozienti segnati in grassetto, aumentati di un di un decimo, un centesimo, un millesimo, ... si dicono valori del quoziente di 66 e 7, approssimati per eccesso a meno dell'unità di un di un decimo, un centesimo, un millesimo, ... Poichè una frazione rappresenta il quoto fra numeratore e denominatore, si può dire che:
Il valore di una frazione, approssimato a meno di 1; 0,1; 0,001; ecc., per difetto o per eccesso è il quoziente del numeratore per il denominatore approssimato per difetto o per eccesso, a meno di 1; 0,1; 0,001; ecc.

Determinare il quoziente dei numeri 66 e 7:

Si può quindi dire che 9; 9,4; 9,42; 9,428; ... sono i quozienti dei numeri dati, approssimati per difetto a meno di un decimo, un centesimo, un millesimo, ... e così via. I valori 10; 9,5; 9,43; 9,429; ... ottenuti dai quozienti segnati in grassetto, aumentati di un di un decimo, un centesimo, un millesimo, ... si dicono valori del quoziente di 66 e 7, approssimati per eccesso a meno dell'unità di un di un decimo, un centesimo, un millesimo, ... Poichè una frazione rappresenta il quoto fra numeratore e denominatore, si può dire che:
Il valore di una frazione, approssimato a meno di 1; 0,1; 0,001; ecc., per difetto o per eccesso è il quoziente del numeratore per il denominatore approssimato per difetto o per eccesso, a meno di 1; 0,1; 0,001; ecc.
Calcolare la potenza: (0,7)3.

NUMERI DECIMALI FINITI
E'
noto che una frazione rappresenta il quoziente esatto fra
numeratore e denominatore, perciò per calcolare il valore
di una frazione è sufficiente eseguire la divisione fra quei due
numeri. Se si vuole trasformare la frazione 17/8 in un numero
decimale, si ha: 17/8=17:8=2,125; analogamente 7/5=7:5=1,4;
27/40=27:40=0,675. Nelle divisioni effettuate, i quozienti ottenuti
risultano esatti, allora si può dire che 2,125; 1,4; 0,675
hanno un limitato numero di cifre decimali, pertanto sono numeri
decimali finiti. Si vuole ora stabilire un criterio per riconoscere,
senza eseguire la divisione, quando una frazione ordinaria, ridotta ai
minimi termini, si può trasformare in un numero decimale finito
e quindi in una frazione decimale. Si enuncia la seguente regola:
Una frazione ordinaria, ridotta ai minimi termini, si può trasformare in un numero decimale finito, se il suo denominatore contiene i fattori primi 2 e 5, o solo il 2, o solo il 5. Esempi di frazioni ridotte ai minimi termini che si possono trasformare in numeri decimali finiti:
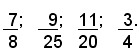
Una frazione ordinaria, ridotta ai minimi termini, si può trasformare in un numero decimale finito, se il suo denominatore contiene i fattori primi 2 e 5, o solo il 2, o solo il 5. Esempi di frazioni ridotte ai minimi termini che si possono trasformare in numeri decimali finiti:
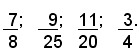
NUMERI DECIMALI PERIODICI SEMPLICI
Si suppone ora di avere tre frazioni che non si possono trasformare in frazioni decimali:
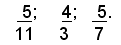
Se si divide rispettivamente il numeratore per il denominatore, si ha:

Si può quindi osservare che il resto non è mai zero, quindi i quozienti ottenuti hanno un numero illimitato di cifre decimali. Quindi, si dice che il numero 0,4545 è un numero decimale illimitato, perchè dopo la virgola vi sono le cifre 4 e 5 che si ripetono indefinitamente nello stesso ordine; il gruppo formato da queste due cifre, 45, si chiama periodo ed il numero decimale illimitato, in tal caso, si chiama periodico semplice. Analogamente i numeri 1,333...; e 0,714285714285...; hanno rispettivamente periodo 3 e 714285. Quindi:
Un numero decimale illimitato si dice periodico semplice, se una o più altre cifre decimali, a partire dalla virgola, si ripetono indefinitamente nello stesso ordine.
I numeri periodici semplici 0,4545...; con periodo 45, 1,333...; con periodo 3 e 0,714285714285...; con periodo 714285 si indicano come segue:

Per riconoscere, senza eseguire la divisione, quando una frazione ridotta ai minimi termini dà luogo ad un numero decimale periodico semplice, si applica la regola seguente:
Una frazione ordinaria, ridotta ai minimi termini, dà luogo ad un numero periodico semplice, se il suo denominatore non contiene nè il fattore 2, nè il fattore 5.
In base a tale regola le frazioni
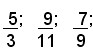
danno luogo ai numeri periodici semplici seguenti:
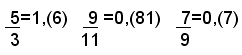
Pertanto le frazioni irriducibili come:
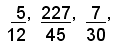
danno luogo a numeri misti.
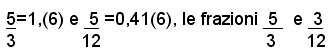
si dicono frazioni generatrici dei numeri periodici 1,(6) e 0,41(6).Si può quindi enunciare la seguente regola:
Si dice frazione generatrice, una frazione che dà luogo ad un numero periodico assegnato.
Le seguenti regole permettono di determinare la frazione generatrice di un numero periodico:
1)-La frazione generatrice di un numero periodico semplice ha per numeratore il numero dato senza la virgola, diminuito della parte intera, e per denominatore tanti 9 quante sono le cifre del periodo.
Esempi:
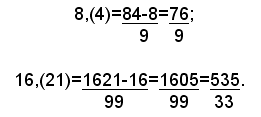
2)-La frazione generatrice di un numero periodico misto ha per numeratore il numero dato senza la virgola, diminuito del numero formato dalla parte intera dell'antiperiodo, e per denominatore tanti 9 quante sono le cifre del periodo e tanti zeri quante sono le cifre dell'antiperiodo.
Esempi:
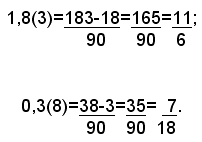
Per eseguire le operazioni con i numeri decimali periodici, basta sostituire ad essi le frazioni generatrici ed effettuare poi i calcoli secondo le regole già note.
Se si divide rispettivamente il numeratore per il denominatore, si ha:

Si può quindi osservare che il resto non è mai zero, quindi i quozienti ottenuti hanno un numero illimitato di cifre decimali. Quindi, si dice che il numero 0,4545 è un numero decimale illimitato, perchè dopo la virgola vi sono le cifre 4 e 5 che si ripetono indefinitamente nello stesso ordine; il gruppo formato da queste due cifre, 45, si chiama periodo ed il numero decimale illimitato, in tal caso, si chiama periodico semplice. Analogamente i numeri 1,333...; e 0,714285714285...; hanno rispettivamente periodo 3 e 714285. Quindi:
Un numero decimale illimitato si dice periodico semplice, se una o più altre cifre decimali, a partire dalla virgola, si ripetono indefinitamente nello stesso ordine.
I numeri periodici semplici 0,4545...; con periodo 45, 1,333...; con periodo 3 e 0,714285714285...; con periodo 714285 si indicano come segue:

Per riconoscere, senza eseguire la divisione, quando una frazione ridotta ai minimi termini dà luogo ad un numero decimale periodico semplice, si applica la regola seguente:
Una frazione ordinaria, ridotta ai minimi termini, dà luogo ad un numero periodico semplice, se il suo denominatore non contiene nè il fattore 2, nè il fattore 5.
In base a tale regola le frazioni
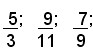
danno luogo ai numeri periodici semplici seguenti:
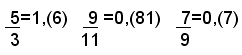
NUMERI DECIMALI PERIODICI MISTI
Una frazione ordinaria, ridotta
ai minimi termini, dà luogo ad un numero periodico misto, se
il suo denominatore scomposto in fattori primi contiene i fattori 2 e 5, o solo uno di essi, insieme ad altri fattori.Si
consideri la frazione 35/12, non trasformabile in frazione decimale; se
si esegue la divisione fra numeratore e denominatore, si ha:
25/12=2,91666... Si ottiene quindi un numero decimale illimitato,
diverso da quelli considerati in precedenza, perchè anche se la
cifra 6 si ripete indefinitamente, essa è preceduta dal numero
91, situato fra la virgola e la prima cifra del periodo 6. Tale numero
prende il nome di antiperiodo. I numeri aventi un antiperiodo ed un
periodo, si chiamano periodici misti. Quindi:
Un numero decimale illimitato si dice periodico misto, quando fra la virgola ed il periodo c'è una cifra, o più cifre che non si ripetono.
Ad esempio, il numero 3,54343... è un numero periodico misto con periodo 43 e antiperiodo 5; esso si indica con uno dei seguenti simboli:
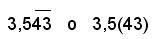
Perciò si può scrivere:
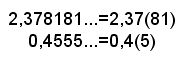
Un numero decimale illimitato si dice periodico misto, quando fra la virgola ed il periodo c'è una cifra, o più cifre che non si ripetono.
Ad esempio, il numero 3,54343... è un numero periodico misto con periodo 43 e antiperiodo 5; esso si indica con uno dei seguenti simboli:
Perciò si può scrivere:
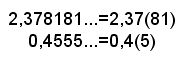
Per
riconoscere, senza eseguire la divisione, quando una frazione ordinaria dà luogo ad un numero decimale
periodico misto, si applica la regola seguente:
Pertanto le frazioni irriducibili come:
danno luogo a numeri misti.
Infatti, se si scompongono in fattori primi i loro denominatori, si ha: 12=22x3, 45=32x5, 30=2x3x5, cioè essi contengono i fattori 2 e 5, o uno solo di essi, insieme ad altri fattori primi.
Eseguendo le divisioni, si ha:
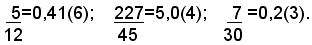
Eseguendo le divisioni, si ha:
FRAZIONI GENERATRICI DEI NUMERI DECIMALI PERIODICI
Siccome:
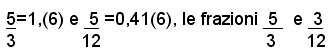
si dicono frazioni generatrici dei numeri periodici 1,(6) e 0,41(6).
Si dice frazione generatrice, una frazione che dà luogo ad un numero periodico assegnato.
Le seguenti regole permettono di determinare la frazione generatrice di un numero periodico:
1)-La frazione generatrice di un numero periodico semplice ha per numeratore il numero dato senza la virgola, diminuito della parte intera, e per denominatore tanti 9 quante sono le cifre del periodo.
Esempi:
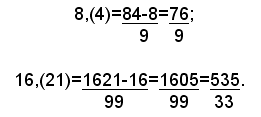
2)-La frazione generatrice di un numero periodico misto ha per numeratore il numero dato senza la virgola, diminuito del numero formato dalla parte intera dell'antiperiodo, e per denominatore tanti 9 quante sono le cifre del periodo e tanti zeri quante sono le cifre dell'antiperiodo.
Esempi:
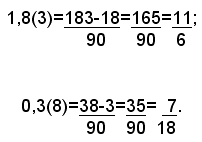
OPERAZIONI CON NUMERI DECIMALI PERIODICI
Per eseguire le operazioni con i numeri decimali periodici, basta sostituire ad essi le frazioni generatrici ed effettuare poi i calcoli secondo le regole già note.
ADDIZIONE
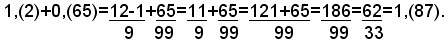
SOTTRAZIONE
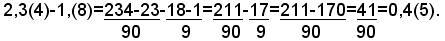
PRODOTTO
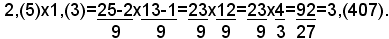
POTENZA
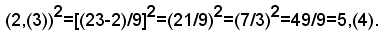
QUOZIENTE

