MIKY & GENNY
RIPARTIZIONE PROPORZIONALE ---> INDICE
GENERALITA'Gruppi di numeri direttamente proporzionali
Considerati i due gruppi di numeri:

si può osservare che ad ogni numero del primo gruppo corrisponde uno del secondo, e che il rapporto fra un qualsiasi numero del primo gruppo ed il corrispondente del secondo ha sempre lo stesso valore:
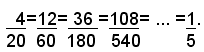
In tal caso i due gruppi di numeri si dicono direttamente proporzionali, perciò:
Due gruppi di numeri si dicono direttamente proporzionali, se è costante il rapporto di due qualsiasi numeri corrispondenti dei due gruppi.
RIPARTIZIONE SEMPLICE DIRETTA
Dividere un numero N in parti direttamente proporzionali a più altri n numeri, significa determinare n numeri la cui somma sia N, e che siano direttamente proporzionali ai numeri dati.
Esempio: Per un lavoro eseguito tre operai hanno ricevuto un compenso di € 620. Se hanno lavorato rispettivamente 2 ore, 3 ore, 5 ore, quanto spetta a ciascuno?
Basta dividere il numero 620 in parti direttamente proporzionali ai numeri 2, 3 e 5, cioè determinare 3 numeri X, Y e Z la cui somma sia 620 e che siano direttamente proporzionali ai numeri 2, 3 e 5. Tenendo presente che: X + Y + Z=620 (1) e che X:2=Y:3=Z:5 (2), e poichè in una serie di rapporti uguali la somma degli antecedenti sta a quella dei conseguenti come un antecedente sta al proprio conseguente, dalla (2) si ricava:
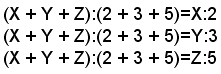
sostituendo ad X + Y + Z il valore 620, si ha: 620:10=X:2, 620:10=Y:3, 620:10=Z:5, da cui si ricava:
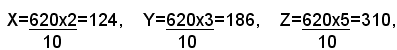
quindi ai tre operai spettano rispettivamente €124, € 186, € 310.
Si ha perciò la seguente regola:
Per dividere un numero N in parti direttamente proporzionali a più altri numeri a, b, c, ..., basta dividerlo per la somma di questi numeri, e moltiplicare il quoziente ottenuto separatamente per ciascuno di essi.
Ripartizione di un numero N in parti direttamente proporzionali a più numeri frazionari
Si vuole dividere il numero 1365 in parti direttamente proporzionali a
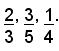
Si riducono le frazioni date allo stesso denominatore e si hanno le nuove frazioni:

e poichè se si vuole dividere un numero in parti direttamente proporzionali a più numeri dati, si ottiene lo stesso risultato dividendoli per i prodotti di tali numeri per un qualsiasi altro numero, basta in tal caso dividere il numero 1365 in parti direttamente proporzionali ai soli numeri 40, 36 e 15; pertanto si ha:
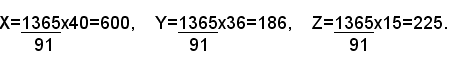
Si ha perciò la seguente regola:
per dividere un numero N in parti direttamente proporzionali ad altri numeri che siano tutti o in parte frazionari, basta dividerlo in parti direttamente proporzionali ai numeratori delle frazioni che si ottengono da quelle date riducendole allo stesso denominatore.
Serie di numeri inversamente proporzionali
Considerate le due serie di numeri (1):

e, dopo aver osservato che il rapporto di due qualsiasi numero della prima serie è uguale al rapporto inverso dei corrispondenti numeri della seconda, che cioè si ha:
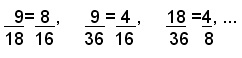
si può dire che le due serie di numeri sono inversamente proporzionali. Cioè:
Due serie di numeri si dicono inversamente proporzionali quando il rapporto di due qualsiasi numeri della prima serie è uguale al rapporto inverso dei corrispondenti numeri della seconda serie.
Considerate le serie di numeri:
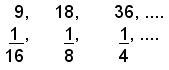
delle quali la prima è la stessa della prima delle (1), e l'altra è formata con gli inversi dei numeri della seconda della serie (1), si può facilmente verificare che esse sono direttamente proporzionali. Quindi si può asserire che:
Se due serie di numeri sono inversamente proporzionali, una di esse è direttamente proporzionale alla serie formata dagli inversi dei numeri corrispondenti dell'altra.
RIPARTIZIONE SEMPLICE INVERSA
Dividere un numero N in parti inversamente proporzionali a più altri n numeri, significa determinare n numeri la cui somma sia N, e che siano inversamente proporzionali ai numeri dati.
Esempio: il proprietario di un negozio concede ai suoi tre dipendenti una gratifica di € 297 da ripartirsi in ragione inversa alle loro giornate di assenza. Quanto spetta a ciasuno, se le rispettive assenze furono di giorni 6, 8 e 12?
Per la proprietà già vista in precedenza, basta dividere il numero 297 in parti direttamente proporzionali agli inversi dei numeri 6, 8 e 12, cioè a:
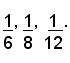
Si riducono ora le frazioni allo stesso denominatore:
e si divide il numero assegnato in parti direttamente proporzionali ai soli denominatori, cioè a 4, 3 e 2. Indicando con X, Y e Z le somme che spettano a ciascun dipendente, si ha:
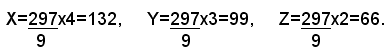
Si può quindi enunciare la seguente regola:
per dividere un numero in parti inversamente proporzionali a più numeri dati, basta dividerlo in parti direttamente proporzionali agli inversi di essi.
RIPARTIZIONE COMPOSTA
Ripartizione composta diretta
Se si deve dividere un numero in parti direttamente proporzionali a due o più serie di numeri, si dice che si ha un problema di ripartizione composta. Per risolvere tali problemi si applica la seguente regola:
per dividere un numero in parti direttamente proporzionali a due o più serie di numeri, basta dividerlo in parti direttamente proporzionali ai prodotti dei numeri corrispondenti delle date serie.
Esempio: dividere il numero 400 in tre parti direttamente proporzionali alle due serie 4, 5, 3 e 3, 4, 6.
Per quanto detto, basta dividere il numero 400 in parti direttamente proporzionali ai prodotto
4 x 3=12, 3 x 6=18, dei corrispondenti numeri delle serie date. Perciò si ha:
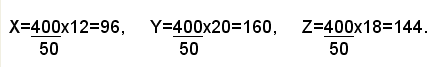
Ripartizione composta diretta e inversa
Si suppone ora di voler dividere il numero N in parti direttamente proporzionali alle serie di numeri a, b, c ed a', b', c', ed in parti inversamente proporzionali alla serie di numeri p, q, r e p', q', r'. Si può dimostrare che le parti richieste sono direttamente proporzionali ai numeri:
Si ha cioè la seguente regola:
per dividere un numero N in parti direttamente proporzionali ad una o più serie di numeri, ed in parti inversamente proporzionali ad una o più serie di numeri, basta dividerlo in parti direttamente proporzionali alle frazioni che hanno per numeratori i prodotti dei corrispondenti numeri della prima serie e per denominatori i prodotti dei corrispondenti numeri delle seconde serie.
Esempio: dividere il numero 2165 in parti direttamente proporzionali alle serie 2, 4, 8 e 2, 5, 6 ed inversamente proporzionali ai numeri della serie 4, 6, 5.
Per la regola suddetta, basta dividere il numero 2165 in parti direttamente proporzionali alle frazioni:
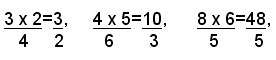
e riducendole allo stesso denominatore, si hanno le nuove frazioni:
in definitiva, basta dividere il numero dato in parti direttamente proporzionali ai numeri 45, 100, 88, ottenendo:
La regola di ripartizione prende il nome di regola di società quando si applica per dividere l'utile o la perdita, fra due o più persone che hanno costituito una società, in parti direttamente proporzionali ai capitali impiegati da ciascuno.
MISCUGLIO
Problemi di miscuglio
Si dice miscuglio l'unione di diverse qualità di una stessa merce.
I problemi del miscuglio sono dei seguenti tipi:
1)-Conoscendo i prezzi unitari e le quantità che formano un miscuglio, determinare il prezzo unitario del miscuglio ottenuto.
Esempio:
è stata effettuata una miscela con kg 3 di caffè che costa € 6 al kg e con kg 2 che costa € 8 al kg. Quale è il prezzo di un chilogrammo del miscuglio?
Poichè le due quantità di caffè, costano rispettivamente: € 6 x 3 = € 18 e € 8 x 2 = € 16, il prezzo complessivo del miscuglio è € 18 + 16 = € 34; quindi il prezzo unitario del miscuglio è 34 : 5 = € 6, 8. Si ha perciò la seguente regola:
il prezzo unitario di un miscuglio si ottiene determinando l'importo delle varie sostanze che lo compongono, sommando i diversi importi, e dividendo il risultato ottenuto per la somma delle quantità mescolate.
2)-Determinare in quale rapporto si devono mescolare due qualità di una stessa merce, di prezzi unitari noti, affinchè il miscuglio abbia un prezzo unitario assegnato.
Esempio: un oste vuole mescolare del vino che costa € 1,20 al litro con vino che costa € 0,95 al litro, in modo da ottenere un miscuglio che valga € 1,10 il litro. In quale rapporto occorrerà mescolare le due qualità di vino?
Inizialmente occorre osservare che se vende un litro di vino che costa € 1,20 al prezzo del miscuglio che è di € 1,10, ha una perdita di € (1,20 - 1,10) = € 0,10.
Vendendo poi un litro di vino che costa € 0,95 al prezzo di € 1,10, ha un guadagno di € (1,20 - 0,95) = € 0,15. Perciò, se si indica con X il numero dei litri di vino da € 1,20 e con Y quello dei litri di vino dell'altra qualità, si avrebbe dalla vendita degli X litri una perdita di € 10 x X, e dalla vendita degli Y litri dell'altra qualità, un guadagno di € 15 x Y. Poichè il guadagno deve compensare la perdita, si ha: 10 x X = 15 x Y, e dividendo per 10 x Y:
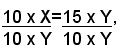
da cui si ricava:
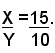
Perciò le due qualità di vino devono essere mescolate nel rapporto di 15 a 10 o ciò che è lo stesso, dividendo i due termini del rapporto per 5, nel rapporto di 3 a 2. Praticamente nei problemi di questo tipo, si usa il seguente schema:

Occorre perciò, per ottenere il dato miscuglio, che per ogni 3 litri di vino da € 1,20 se ne prendano 2 da € 0,95.
3)-Determinare le quantità di due sostanze, di dato prezzo unitario, che formano un miscuglio, sapendo la quantità ed il prezzo unitario di esso.
Esempio: quanto olio da € 1,96 il litro e quanto da € 1,78 il litro si deve mescolare per ottenere 27 litri di olio da € 1,86 il litro?
Come nell'esempio precedente, si determina in quale rapporto si devono mescolare le due qualità di olio; si ha:

Le due quantità di olio devono essere mescolate nel rapporto di 4 a 5; basta allora ripartire la quantità del miscuglio, cioè i 27 litri, in parti direttamente proporzionali ai termini del rapporto ottenuto. Indicando con X e Y le due parti, si ha:
Perciò, occorre mescolare l 12 di olio da € 1,96 e l 15 da € 1,78 per ottenere 27 litri del miscuglio.
ALLIGAZIONE
Se si fondono insieme del rame e dello stagno, si ottiene un altro metallo che si chiama bronzo. Si dice in tal caso che il bronzo è una lega.
L'oro ed il platino raramente si usano allo stato puro, ma si adoperano in genere misti a metalli di qualità inferiore, quali argento e rame, per renderli più adatti alla lavirazione e più resistenti al logorio. La quantità di metallo prezioso contenuto in una lega prende il nome di fino.
Si dice titolo di una lega il rapporto fra il peso del metallo fino e quello della lega.
Perciò, se una lega di oro e rame ha titolo
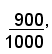
o 0,900, significa che su 1000 grammi, essa contiene 900 grammi di oro puro e 100 di rame.
Il titolo dell'oro si esprime in 24mi, detti carati; perciò se si dice che un anello d'oro è a 18 carati, si intende che il titolo di quell'anello è 18, cioè che su 24 parti della lega solo18/24 sono di oro fino.
Calcolo del titolo di una lega
Per determinare il titolo di una lega si applica la seguente regola:
Il titolo di una lega si ottiene dividendo il peso del metallo fino in essa contenuto, per il peso della lega.
Esempi:
1)-Quale è il titolo di un lingotto d'oro che pesa g 260 e contiene g 214,5 di metallo fino?
Si ha: 214,5:260=0.825. Il titolo del lingotto è quindi
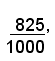
perciò, chiamando P il peso della lega, F il peso del metallo fino e T il titolo, si ha:
da cui si ricava:
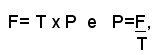
che permettono di risolvere i problemi inversi.
2)-Quale è la quantità di fino contenuto in un lingotto che pesa g 424, avente il titolo 0,925?
Si ha: F=g 424 x 0,925 =g 392,2.
3)-Quale è il peso di un lingotto d'oro del titolo 0,800 che contiene g 520 di fino?
Si ha: P= g 520:0,800= g 520x1000:800 = g 650.
Problemi di alligazione
I problemi di alligazione sono analoghi a quelli del miscuglio, e sono dei seguenti tipi.
1)-Dato il peso ed il titolo di due o più leghe contenenti lo stesso metallo prezioso, determinare il titolo della lega che si ottiene fondendoli insieme.
Esempio: quale è il titolo di una verga d'oro ottenuta dalla fusione di tre oggetti d'oro aventi rispettivamente i pesi di g 200, g 360 e g 240 e i titoli rispettivi di 0, 750; 0,850 e 0,900?
I pesi del fino contenuti in ciascun oggetto sono:
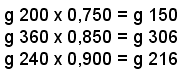
perciò il peso di oro fino contenuto nella verga ricavata dalla fusione dei tre oggetti, è:
g (150 + 306 + 216) = g 672 e poichè il peso della verga è di g (200 + 360 + 240) = g 800, Si ha che il titolo richiesto è: T = 672: 800 = 0,840.
2)-Dato il titolo di due metalli greggi, determinare in quale rapporto devono essere fusi per ottenere una lega di titolo assegnato.
Esempio: in quale rapporto devono essere i pesi di due leghe di oro aventi i titoli 0,830 e 0, 720 affinchè dalla loro fusione si ottenga una lega del titolo 0,770?
Il problema proposto è dello stesso tipo (2), risolto in precedenza per il miscuglio, pertanto si considera il seguente schema:
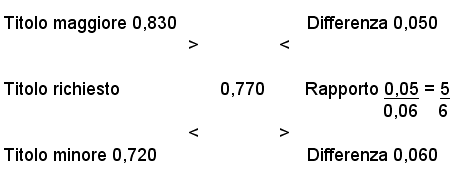
Quindi per ottenere una lega di titolo 0,770, occorrono per ogni 5 grammi della lega avente titolo 0,830, 6 grammi di quella del titolo 0,720.