MIKY & GENNY

ADERENZE ---> INDICE

Punto aderente ad una parte dei reali
Assegnati

si dà la seguente definizione:

L'insieme degli elementi aderenti ad X è indicato e definito come segue:

In definitiva, assegnati

si ha:

Si osserva ora che se

le seguenti due proposizioni sono equivalenti:



Dimostrazione
a) b)

Infatti, considerati

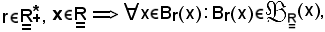
cioè la sfera aperta è intorno di x, ed essendo x aderente ad X per l'ipotesi della a), si ha:

B_r(x)  X ≠ .

Dimostrazione

b) a)

Si deve dimostrare che;

Pertanto, si consideri

Nota bene
Considerato

si possono considerare l'aderenza di X, il complementare di X rispetto all'insieme dei reali, il complementare dell'aderenza di X rispetto all'insieme dei reali e l'interno del complementare di X rispetto all'insieme dei reali, cioè:

Si dimostra che:
1)-il complementare dell'aderenza di X rispetto all'insieme dei reali è uguale all'interno del complementare di X rispetto all'insieme dei reali, cioè:

Infatti, sia

Pertanto, risulta che:

Si dimostra ora il viceversa, infatti, sia

Pertanto, risulta che:

Quindi, per la validità della doppia inclusione, la 1) è vera.

2)-se X ed Y sono parti dell'insieme dei reali, X Y, segue che l'aderenza di X è contenuta nell'aderenza di Y, cioè:

Infatti, sia

Proprietà dell'aderenza



Dimostrazione
Infatti, si considera

Analogamente, si considera

Dimostrazione
Infatti, si considera

Dimostrazione
Infatti, si considera

Dimostrazione
Infatti, si considera

Si dimostra infine che le seguenti due proposizioni sono equivalenti:



Dimostrazione
a) b)

Dire che X è un insieme chiuso equivale a dire che il suo complementare è aperto. Ma un insieme è aperto se il suo interno coincide con sé stesso, quindi:

Dimostrazione
b) a)

Per dimostrare che X è un insieme chiuso, basta dimostrare che il suo complementare è un insieme aperto, cioè:

o equivalentemente che

Ciò è vero, perchè un insieme è aperto se il suo interno coincide con sé stesso.