ELEMENTI NOTEVOLI DEI REALI ---> INDICE
Maggioranti e minoranti
Sia
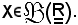
Si chiama maggiorante di X, quando esiste ogni eventuale
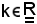
che gode della seguente proprietà:
 x
x X : x ≤ k.
X : x ≤ k.
Quando un insieme è tale che esista un maggiorante, ne esistono infiniti; di conseguenza l'insieme dei maggioranti è vuoto, oppure è formato da infiniti elementi.
Si chiama minorante di X, quando esiste ogni eventuale
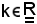
che gode della seguente proprietà:
 x
x X : k ≤ x.
X : k ≤ x.
Quando un insieme è tale che esista un minorante, ne esistono infiniti; di conseguenza l'insieme dei minoranti è vuoto, oppure è formato da infiniti elementi.
Parte dei reali maggiorata o minorata
Una parte X dell'insieme dei reali si dice maggiorata, se esiste almeno un maggiorante di X.
Una parte X dell'insieme dei reali si dice minorata, se esiste almeno un minorante di X.
Più grande e più piccolo elemento di una parte dei reali
Sia
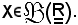
Si dice che un elemento m di X, quando esiste, è il più grande elemento di X, se e solo se
 x
x X : x ≤ m.
X : x ≤ m.
Il più grande elemento è unico.
Infatti, se ne esistessero due, m ed m', si avrebbe
 x
x X : x ≤ m',
X : x ≤ m',
 x
x X : x ≤ m'';
X : x ≤ m'';
e quindi:
m' ≤ m'', m'' ≤ m' m' = m''.
m' = m''.
Si dice che un elemento n di X, quando esiste, è il più piccolo elemento di X, se e solo se
 x
x X : n ≤ x.
X : n ≤ x.
Nota bene
Se esiste il più grande elemento di X, esso è un maggiorante; se invece esiste il più piccolo elemento di X, esso è un minorante.
Estremo superiore - Teorema fondamentale
Si consideri il sottoinsieme X, non vuoto, dei reali:
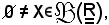
e sia M l'insieme dei maggioranti di X.
Si dimostra che esiste sempre il più piccolo elemento di M, ed è unico, e si indica con sup(X) o supX, a cui si dà il nome di estremo superiore dell'insieme X, cioè
 |supX.
|supX.
Quando esiste almeno un maggiorante di X, ne esisteranno infiniti, e l'insieme X si dice limitato superiormente.
Si osserva ora che le seguenti tre proposizioni sono equivalenti:

Dimostrazione
a) b)
b)
La 1) della b) è senz'altro vera perchè, essendo l'estremo superiore dell'insieme X, e'' è il più piccolo elemento dell'insieme dei maggioranti e, come tale, è un maggiorante. Ma per definizione di maggiorante, si ha:
 x
x X : x ≤ e'',
X : x ≤ e'',
e quindi la 1) della b) è dimostrata.
Si consideri ora
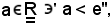
si vuole dimostrare la 2) della b), cioè che
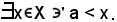
Ragionando per assurdo si suppone che
 x
x X : x ≤ a.
X : x ≤ a.
Ma ciò non può accadere, dal momento che, se a ≥ x X, a diventerebbe un maggiorante di X e ciò non può essere, perchè si è supposto a ≤
e'', dove e'' è il più piccolo elemento dell'insieme dei
maggioranti. Siccome l'assurdo è derivato dall'aver supposto
a ≥ x, si può concludere che a < x.
X, a diventerebbe un maggiorante di X e ciò non può essere, perchè si è supposto a ≤
e'', dove e'' è il più piccolo elemento dell'insieme dei
maggioranti. Siccome l'assurdo è derivato dall'aver supposto
a ≥ x, si può concludere che a < x.
In tal modo resta dimostrata la 2) della b).
Dimostrazione
b) c)
c)
La 1) della c) è vera, in quanto è espressa dall'ipotesi 1) della b).
Si consideri ora
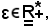
si vuole dimostrare che
 x
x X
X  e'' - ε < x.
e'' - ε < x.
Infatti, preso
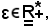
risulta:
e'' - ε < e''.
Inoltre, se nella 2) della b), vera per ipotesi, si considera a = e'' - ε, si ha:
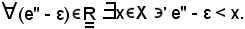
In tal modo resta dimostrata la 2) della c).
Dimostrazione
c) a)
a)
Supposta vera la c), si deve dimostrare che e'' è l'estremo superiore dell'insieme X, cioè che e'' è un maggiorante di X ed è il più piccolo.
Infatti, che e'' sia un maggiorante di X, segue immediatamente dalla 1) della c); affinchè sia il più piccolo, basta dimostrare che preso un maggiorante m di X, risulta m ≥ e''.
e per la 2) della c),
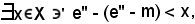
cioè risulta
m < x.
Ma ciò è assurdo, perchè essendo m maggiorante di X, dev'essere maggiore di qualsiasi elemento x X. Siccome l'assurdo è derivato dall'aver supposto m < e'', si può concludere che m ≥ e''.
X. Siccome l'assurdo è derivato dall'aver supposto m < e'', si può concludere che m ≥ e''.
Estremo inferiore - Teorema fondamentale
Si consideri il sottoinsieme X, non vuoto, dei reali:
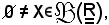
e sia P l'insieme dei minoranti di X.
Si dimostra che esiste sempre il più grande elemento di P, ed è unico, e si indica con inf(X) o infX, a cui si dà il nome di estremo inferiore dell'insieme X, cioè
 |infX.
|infX.
Quando esiste almeno un minorante di X, ne esisteranno infiniti, e l'insieme X si dice limitato inferiormente.
Si osserva ora che le seguenti tre proposizioni sono equivalenti:

Anche in tal caso si dimostra, in modo analogo al precedente teorema, che
a) b)
b)  c)
c)  a),
a),
pertanto, si tralascia la dimostrazione.
Massimo
Se X è un insieme numerico che ha il più grande elemento, tale elemento è l'estremo superiore che, se fa parte dell'insieme, viene detto massimo.
Minimo
Se X è un insieme numerico che ha il più piccolo elemento, tale elemento è l'estremo inferiore che, se fa parte dell'insieme, viene detto minimo.
Sia
Si chiama maggiorante di X, quando esiste ogni eventuale
che gode della seguente proprietà:
Quando un insieme è tale che esista un maggiorante, ne esistono infiniti; di conseguenza l'insieme dei maggioranti è vuoto, oppure è formato da infiniti elementi.
Si chiama minorante di X, quando esiste ogni eventuale
che gode della seguente proprietà:
Quando un insieme è tale che esista un minorante, ne esistono infiniti; di conseguenza l'insieme dei minoranti è vuoto, oppure è formato da infiniti elementi.
Parte dei reali maggiorata o minorata
Una parte X dell'insieme dei reali si dice maggiorata, se esiste almeno un maggiorante di X.
Una parte X dell'insieme dei reali si dice minorata, se esiste almeno un minorante di X.
Più grande e più piccolo elemento di una parte dei reali
Sia
Si dice che un elemento m di X, quando esiste, è il più grande elemento di X, se e solo se
Il più grande elemento è unico.
Infatti, se ne esistessero due, m ed m', si avrebbe
e quindi:
m' ≤ m'', m'' ≤ m'
Si dice che un elemento n di X, quando esiste, è il più piccolo elemento di X, se e solo se
Nota bene
Se esiste il più grande elemento di X, esso è un maggiorante; se invece esiste il più piccolo elemento di X, esso è un minorante.
Estremo superiore - Teorema fondamentale
Si consideri il sottoinsieme X, non vuoto, dei reali:
e sia M l'insieme dei maggioranti di X.
Si dimostra che esiste sempre il più piccolo elemento di M, ed è unico, e si indica con sup(X) o supX, a cui si dà il nome di estremo superiore dell'insieme X, cioè
Quando esiste almeno un maggiorante di X, ne esisteranno infiniti, e l'insieme X si dice limitato superiormente.
Si osserva ora che le seguenti tre proposizioni sono equivalenti:

Dimostrazione
a)
La 1) della b) è senz'altro vera perchè, essendo l'estremo superiore dell'insieme X, e'' è il più piccolo elemento dell'insieme dei maggioranti e, come tale, è un maggiorante. Ma per definizione di maggiorante, si ha:
e quindi la 1) della b) è dimostrata.
Si consideri ora
si vuole dimostrare la 2) della b), cioè che
Ragionando per assurdo si suppone che
Ma ciò non può accadere, dal momento che, se a ≥ x
In tal modo resta dimostrata la 2) della b).
Dimostrazione
b)
La 1) della c) è vera, in quanto è espressa dall'ipotesi 1) della b).
Si consideri ora
si vuole dimostrare che
Infatti, preso
risulta:
e'' - ε < e''.
Inoltre, se nella 2) della b), vera per ipotesi, si considera a = e'' - ε, si ha:
In tal modo resta dimostrata la 2) della c).
Dimostrazione
c)
Supposta vera la c), si deve dimostrare che e'' è l'estremo superiore dell'insieme X, cioè che e'' è un maggiorante di X ed è il più piccolo.
Infatti, che e'' sia un maggiorante di X, segue immediatamente dalla 1) della c); affinchè sia il più piccolo, basta dimostrare che preso un maggiorante m di X, risulta m ≥ e''.
Ragionando per assurdo si suppone m < e'' e, se ciò accade, risulterà
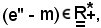
e per la 2) della c),
cioè risulta
m < x.
Ma ciò è assurdo, perchè essendo m maggiorante di X, dev'essere maggiore di qualsiasi elemento x
Estremo inferiore - Teorema fondamentale
Si consideri il sottoinsieme X, non vuoto, dei reali:
e sia P l'insieme dei minoranti di X.
Si dimostra che esiste sempre il più grande elemento di P, ed è unico, e si indica con inf(X) o infX, a cui si dà il nome di estremo inferiore dell'insieme X, cioè
Quando esiste almeno un minorante di X, ne esisteranno infiniti, e l'insieme X si dice limitato inferiormente.
Si osserva ora che le seguenti tre proposizioni sono equivalenti:

Anche in tal caso si dimostra, in modo analogo al precedente teorema, che
a)
pertanto, si tralascia la dimostrazione.
Massimo
Se X è un insieme numerico che ha il più grande elemento, tale elemento è l'estremo superiore che, se fa parte dell'insieme, viene detto massimo.
Minimo
Se X è un insieme numerico che ha il più piccolo elemento, tale elemento è l'estremo inferiore che, se fa parte dell'insieme, viene detto minimo.