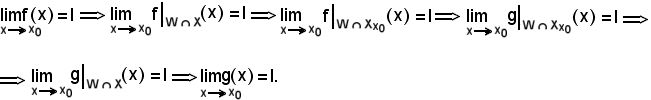FUNZIONI CONVERGENTI ---> INDICE
Si
considerino una parte X non vuota dell'insieme dei reali, un'applicazione f di tale parte X nell'insieme dei reali, x0 punto di accumulazione di X ed l appartenente all'insieme dei reali, cioè
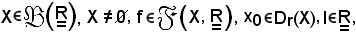
e si dà la seguente definizione:
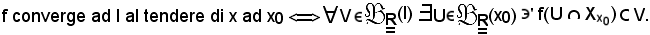
Dopo aver osservato che
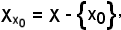
e che per definizione
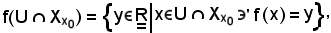
la definizione suddetta di convergenza si traduce in
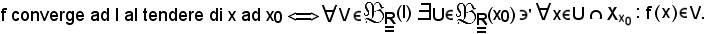
Si osserva infine che
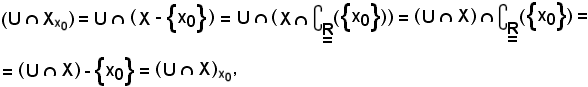
di conseguenza, la definizione suddetta di convergenza si trasforma ancora in
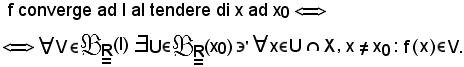
La circostanza che esista il limite di una funzione è un fatto eccezionale, inoltre si dimostra che se esso esiste è unico.
Supponendo che f converga verso due limiti, l' ed l'', al tendere di x ad x0, si dimostra che:
l = l'.
Si suppone che
l' ≠ l''.
E' noto che:
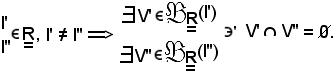
Siccome f converge verso l' ed l'', al tendere di x ad x0, in corrispondenza di
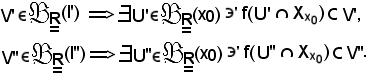
Si indica ora
U = U'
U'',
poichè U' ed U'' sono intorni di x0, anche U è intorno di x0, cioè
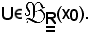
Si osserva che
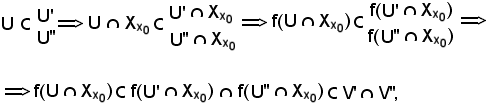
e ciò significa che
V' V'' ≠ 
,
e ciò è assurdo, derivato dall'aver supposto che l' ≠ l'', quindi necessariamente l' = l'', come volevasi dimostrare.La circostanza che f converga ad l al tendere di x ad x0, si esprime come segue:
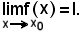
Nota bene
Non accade quasi mai che f(x0) = l, poichè non sempre ha senso parlare di f(x0), dal momento che x0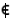
X quasi sempre.
Se x0
X e
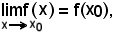
la funzione è particolarissima e si chiama funzione continua.
Si dimostra che le seguenti due proposizioni sono equivalenti:
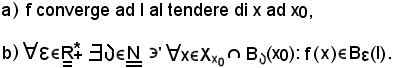
Dimostrazione
a)
b)
Si fissa
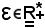
e si considera la sfera aperta di centro l e raggio ε, che è intorno di l, cioè
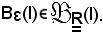
Siccome per ipotesi f converge ad l al tendere di x ad x0, in corrispondenza di questo particolare intorno:
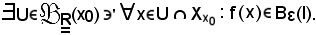
Inoltre, dire che U è intorno di x0, equivale a dire che
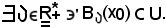
Si consideri ora
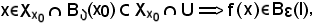
come volevasi dimostrare.
Dimostrazione
b) a)
Supposta vera la b), si deve dimostrare che f converge ad l al tendere di x ad x0, cioè:
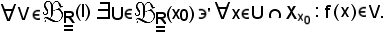
Si fissa
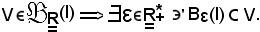
In corrispondenza di ε, per la b),
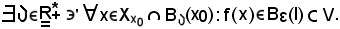
Indicando
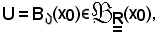
è dimostrata la b).
Nota bene
La proposizione b) si può scrivere equivalentemente come segue:
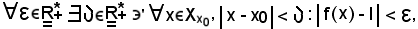
o anche
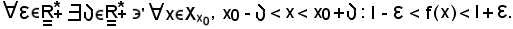
Si dimostra che le seguenti due proposizioni sono equivalenti:
Dimostrazione
a) b)
Osservato che
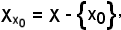
e che
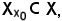
ha senso considerare la restrizione dell'applicazione f rispetto ad
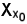
così definita:
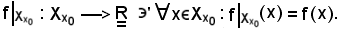
Si osserva inoltre che:
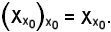
Infatti:
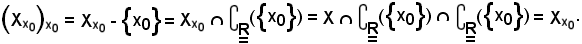
A tal punto si dimostra che:
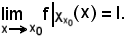
Infatti, considerato arbitrariamente un intorno V di l, per la proposizione a), vera per ipotesi,
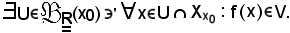
Inoltre,
e quindi
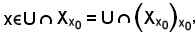
e ciò esprime, per come è stata definita f, che
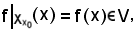
come volevasi dimostrare.
Dimostrazione
b) a)
Si deve dimostrare che f converge ad l al tendere di x ad x0, cioè
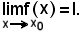
Si prende ad arbitrio
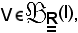
in sua corrispondenza per la b)
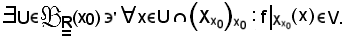
Ora, preso
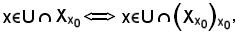
ed essendo per ipotesi
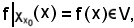
è dimostrato che
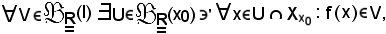
cioè
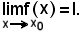
Nota bene
Ciò ha senso, in quanto
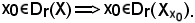
Si osserva inoltre che l'equivalenza delle due proposizioni ora viste esprime che il limite di una funzione f, al tendere di x ad x0, non dipende dal valore che f assume nel punto di accumulazione x0.
Se
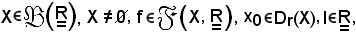
si dimostra che le seguenti tre proposizioni sono equivalenti:
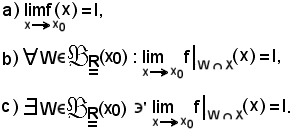
Si osserva prima che se
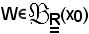
risulta
W X 
X,
quindi ha senso considerare l'applicazione
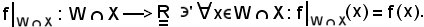
Per poter parlare di eventuale
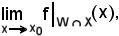
occorre dimostrare che
x0Dr(W X),
cioè bisogna riconoscere che
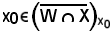
e cioè che, preso un intorno di x0, in esso va a finire almeno un elemento di W X che non sia lo stesso x0.
Fissato
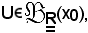
poichè
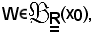
risulta
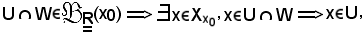
quindi si può parlare del limite suddetto.
Dimostrazione
a) b)
Fissato
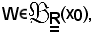
poichè per ipotesi f converge ad l al tendere di x ad x0, per definizione si ha che
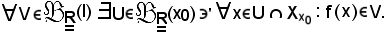
Si osserva ora che
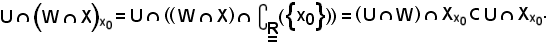
Ora, preso
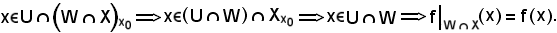
D'altronde, dall'essere
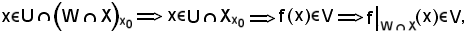
per l'ipotesi a).
Dimostrazione
b) c)
E' ovvia.
Dimostrazione
c) a)
Preso ad arbitrio
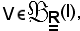
per la c) si ha che
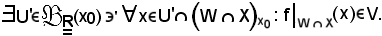
Si indica ora
e si osserva che
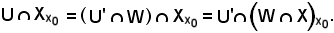
Preso
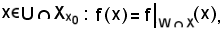
e poichè
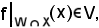
si ha
f(x)V,
e questa è la condizione per cui
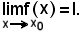
Anche tali equivalenze dimostrano che il limite di una funzione f, al tendere di x ad x0, non dipende dal valore che f assume nel punto di accumulazione x0.
Corollario
Siano
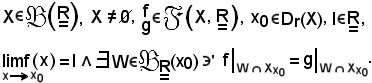
In tali ipotesi si dimostra che:
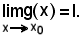
Infatti, per ipotesi:
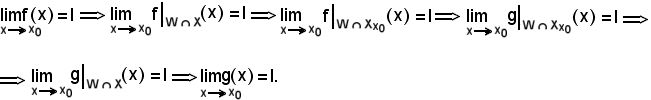
e si dà la seguente definizione:
Dopo aver osservato che
e che per definizione
la definizione suddetta di convergenza si traduce in
Si osserva infine che
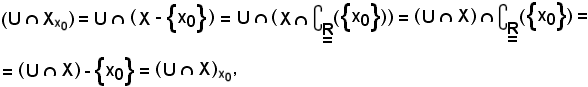
di conseguenza, la definizione suddetta di convergenza si trasforma ancora in
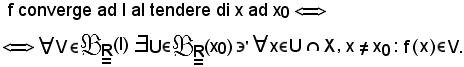
La circostanza che esista il limite di una funzione è un fatto eccezionale, inoltre si dimostra che se esso esiste è unico.
Supponendo che f converga verso due limiti, l' ed l'', al tendere di x ad x0, si dimostra che:
l = l'.
Si suppone che
l' ≠ l''.
E' noto che:
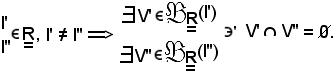
Siccome f converge verso l' ed l'', al tendere di x ad x0, in corrispondenza di
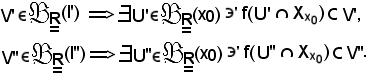
Si indica ora
U = U'
U'',poichè U' ed U'' sono intorni di x0, anche U è intorno di x0, cioè
Si osserva che
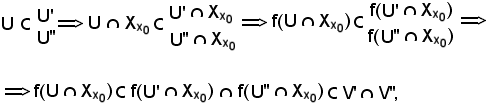
e ciò significa che
V'
V'' ≠ ,e ciò è assurdo, derivato dall'aver supposto che l' ≠ l'', quindi necessariamente l' = l'', come volevasi dimostrare.
Nota bene
Non accade quasi mai che f(x0) = l, poichè non sempre ha senso parlare di f(x0), dal momento che x0
X quasi sempre.Se x0
X ela funzione è particolarissima e si chiama funzione continua.
Si dimostra che le seguenti due proposizioni sono equivalenti:
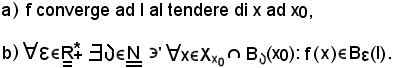
Dimostrazione
a)
b)Si fissa
e si considera la sfera aperta di centro l e raggio ε, che è intorno di l, cioè
Siccome per ipotesi f converge ad l al tendere di x ad x0, in corrispondenza di questo particolare intorno:
Inoltre, dire che U è intorno di x0, equivale a dire che
Si consideri ora
come volevasi dimostrare.
Dimostrazione
b)
a)Supposta vera la b), si deve dimostrare che f converge ad l al tendere di x ad x0, cioè:
Si fissa
In corrispondenza di ε, per la b),
Indicando
è dimostrata la b).
Nota bene
La proposizione b) si può scrivere equivalentemente come segue:
o anche
Si dimostra che le seguenti due proposizioni sono equivalenti:
Dimostrazione
a)
b)Osservato che
e che
ha senso considerare la restrizione dell'applicazione f rispetto ad
così definita:
Si osserva inoltre che:
Infatti:
A tal punto si dimostra che:
Infatti, considerato arbitrariamente un intorno V di l, per la proposizione a), vera per ipotesi,
Inoltre,
e quindi
e ciò esprime, per come è stata definita f, che
come volevasi dimostrare.
Dimostrazione
b)
a)Si deve dimostrare che f converge ad l al tendere di x ad x0, cioè
Si prende ad arbitrio
in sua corrispondenza per la b)
Ora, preso
ed essendo per ipotesi
è dimostrato che
cioè
Nota bene
Ciò ha senso, in quanto
Si osserva inoltre che l'equivalenza delle due proposizioni ora viste esprime che il limite di una funzione f, al tendere di x ad x0, non dipende dal valore che f assume nel punto di accumulazione x0.
Se
si dimostra che le seguenti tre proposizioni sono equivalenti:
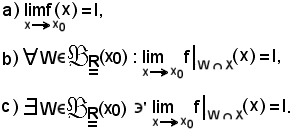
Si osserva prima che se
risulta
W
X X,quindi ha senso considerare l'applicazione
Per poter parlare di eventuale
occorre dimostrare che
x0
Dr(W X),cioè bisogna riconoscere che
e cioè che, preso un intorno di x0, in esso va a finire almeno un elemento di W
X che non sia lo stesso x0.Fissato
poichè
risulta
quindi si può parlare del limite suddetto.
Dimostrazione
a)
b)Fissato
poichè per ipotesi f converge ad l al tendere di x ad x0, per definizione si ha che
Si osserva ora che
Ora, preso
D'altronde, dall'essere
per l'ipotesi a).
Dimostrazione
b)
c)E' ovvia.
Dimostrazione
c)
a)Preso ad arbitrio
per la c) si ha che
Si indica ora
e si osserva che
Preso
e poichè
si ha
f(x)
V,e questa è la condizione per cui
Anche tali equivalenze dimostrano che il limite di una funzione f, al tendere di x ad x0, non dipende dal valore che f assume nel punto di accumulazione x0.
Corollario
Siano
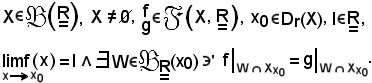
In tali ipotesi si dimostra che:
Infatti, per ipotesi: