FUNZIONI DIVERGENTI ---> INDICE
Funzioni divergenti positivamente
Sia
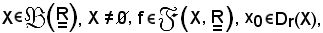
si dà la seguente definizione:
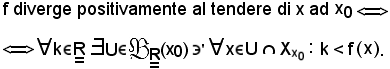
La circostanza che f diverga positivamente al tendere di x ad x0, si esprime con il seguente simbolo:
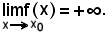
Inoltre, per definizione:
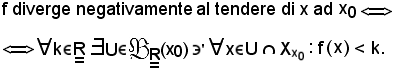
La circostanza che f diverga negativamente al tendere di x ad x0, si esprime con il seguente simbolo:
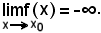
Si dimostra che le seguenti due proposizioni sono equivalenti:
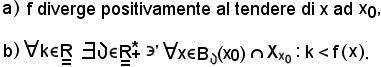
Dimostrazione
a) b)
b)
Fissato
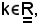
per la a), vera per ipotesi, in sua corrispondenza:
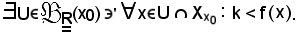
Dire che U è intorno di x0 equivale a dire che esiste una sfera aperta di raggio x0 contenuta in esso, cioè:
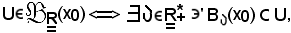
e da quest'ultima inclusione, segue che
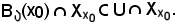
Se si considera
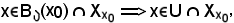
e per ipotesi, si ha
k < f(x),
come volevasi dimostrare.
Dimostrazione
b) a)
a)
La b) esprime l'esistenza di una sfera di centro x0 e quindi l'esistenza di un intorno di x0 tale che
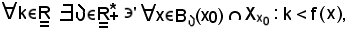
e questa è la condizione per cui f diverge positivamente al tendere di x ad x0.
Nota bene
La proposizione b) precedente si può scrivere equivalentemente come segue:
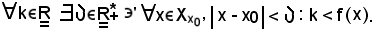
Si osserva inoltre che le condizioni f(x) > k ed f(x) < k si possono considerare come segue:
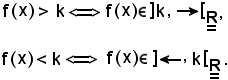
In modo analogo al precedente, si dimostra che le seguenti due proposizioni sono equivalenti:
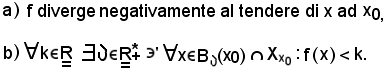
Nota bene
Anche in tale caso la proposizione b) si può scrivere equivalentemente come segue:
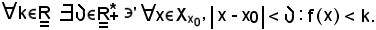
La funzione f si chiama regolare se è convergente, oppure divergente positivamente o negativamente.
Si dimostra che se una funzione f converge, non può divergere e viceversa.
Si riconosce, nel caso specifico, che se f converge ad l al tendere di x ad x0, essa non può divergere positivamente al tendere di x ad x0, cioè:
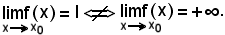
IInfatti, per ipotesi f converge ad l al tendere di x ad x0, cioè fissato
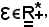
in sua corrispondenza
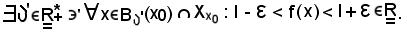
Si suppone ora che f diverge positivamente al tendere di x ad x0, cioè che fissato
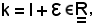
in sua corrispondenza
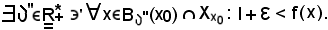
Si indica ora
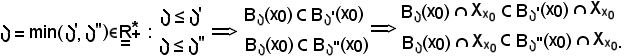
Quindi, considerato
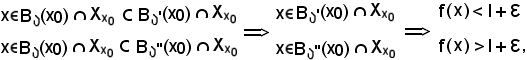
e ciò è assurdo, derivato dall'aver supposto f divergente positivamente al tendere di x ad x0, dunque si può concludere che essa non è tale, come volevasi dimostrare.
Si dimostra allo stesso modo delle funzioni convergenti che le seguenti due coppie di proposizioni sono equivalenti:
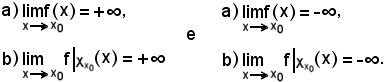
Si dimostra allo stesso modo delle funzioni convergenti che le seguenti tre coppie di proposizioni sono equivalenti:
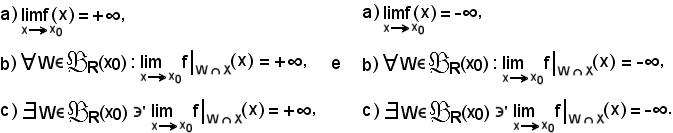
Siano

In tali ipotesi si dimostra che
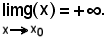
La dimostrazione si effettua allo stesso modo delle funzioni convergenti.
Siano
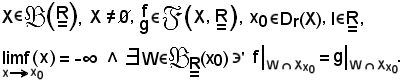
In tali ipotesi si dimostra che
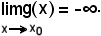
si dà la seguente definizione:
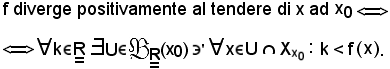
La circostanza che f diverga positivamente al tendere di x ad x0, si esprime con il seguente simbolo:
Inoltre, per definizione:
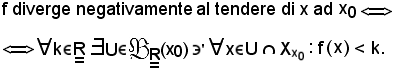
La circostanza che f diverga negativamente al tendere di x ad x0, si esprime con il seguente simbolo:
Si dimostra che le seguenti due proposizioni sono equivalenti:
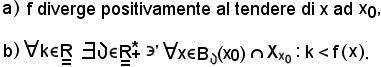
Dimostrazione
a)
Fissato
per la a), vera per ipotesi, in sua corrispondenza:
Dire che U è intorno di x0 equivale a dire che esiste una sfera aperta di raggio x0 contenuta in esso, cioè:
e da quest'ultima inclusione, segue che
Se si considera
e per ipotesi, si ha
k < f(x),
come volevasi dimostrare.
Dimostrazione
b)
La b) esprime l'esistenza di una sfera di centro x0 e quindi l'esistenza di un intorno di x0 tale che
e questa è la condizione per cui f diverge positivamente al tendere di x ad x0.
Nota bene
La proposizione b) precedente si può scrivere equivalentemente come segue:
Si osserva inoltre che le condizioni f(x) > k ed f(x) < k si possono considerare come segue:
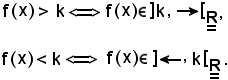
In modo analogo al precedente, si dimostra che le seguenti due proposizioni sono equivalenti:
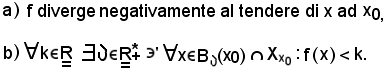
Nota bene
Anche in tale caso la proposizione b) si può scrivere equivalentemente come segue:
La funzione f si chiama regolare se è convergente, oppure divergente positivamente o negativamente.
Si dimostra che se una funzione f converge, non può divergere e viceversa.
Si riconosce, nel caso specifico, che se f converge ad l al tendere di x ad x0, essa non può divergere positivamente al tendere di x ad x0, cioè:
IInfatti, per ipotesi f converge ad l al tendere di x ad x0, cioè fissato
in sua corrispondenza
Si suppone ora che f diverge positivamente al tendere di x ad x0, cioè che fissato
in sua corrispondenza
Si indica ora
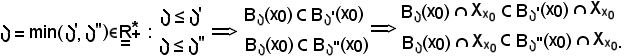
Quindi, considerato
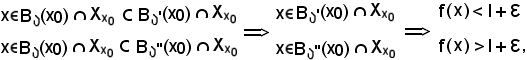
e ciò è assurdo, derivato dall'aver supposto f divergente positivamente al tendere di x ad x0, dunque si può concludere che essa non è tale, come volevasi dimostrare.
Si dimostra allo stesso modo delle funzioni convergenti che le seguenti due coppie di proposizioni sono equivalenti:
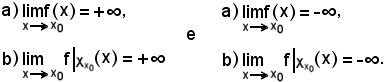
Si dimostra allo stesso modo delle funzioni convergenti che le seguenti tre coppie di proposizioni sono equivalenti:
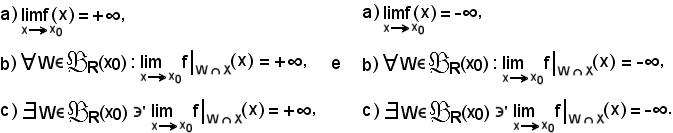
Siano

In tali ipotesi si dimostra che
La dimostrazione si effettua allo stesso modo delle funzioni convergenti.
Siano
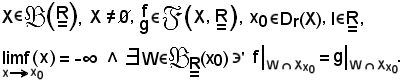
In tali ipotesi si dimostra che