INSIEMI ---> INDICE
Insieme aperto
Un sottoinsieme U dei reali si dice aperto se si trova in una delle seguenti condizioni:
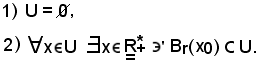
Si indichi ora con
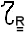
l'insieme degl'insiemi aperti; esso è non vuoto perchè almeno l'insieme vuoto è una delle sue parti.
Tale insieme si chiama Topologia sull'insieme dei reali.
Si dimostra che:
1)-ogni intervallo aperto è un insieme aperto, cioè
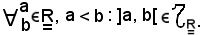
Pertanto, quale che sia
x ]a, b[,
]a, b[,
basta dimostrare che esiste una sfera aperta di centro x e raggio r contenuta nell'intervallo.
Allo scopo, si consideri
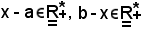
e si indichi con r il minimo di tali numeri, cioè:
r = min(x - a, b - x);
si deve dimostrare che
Br(x) ]a, b[.
]a, b[.
Infatti, sia
y Br(x)
Br(x)
e, per definizione di sfera aperta, si ha
|y - x| < r,
cioè
a = x - x + a ≤ x - r < y < x + r ≤ x + b - x = b,
tenendo conto che, per come è stata definita r, risulta
x - a ≤ r ≤ b - x.
Si è quindi trovato che:
a < y < b,
e quindi
y ]a, b[.
]a, b[.
Siccome l'elemento y Br(x) va a finire nell'intervallo ]a, b[, si può concludere che
Br(x) va a finire nell'intervallo ]a, b[, si può concludere che
Br(x) ]a, b[,
]a, b[,
come volevasi dimostrare.
Richiamo
Quando sono state trattate le sfere, è stato dimostrato che:
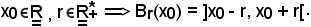
Quindi, in virtù del fatto che ogni sfera aperta è un intervallo aperto, ovviamente si ha:
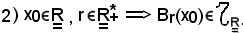
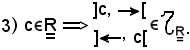
Se
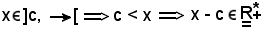
e, assumendo
r = x - c,
si può considerare la sfera aperta di centro x e raggio r, Br(x).
Sia ora
y Br(x)
Br(x)  x - r < y < x + r,
x - r < y < x + r,
ma
x - r = x - x + c = c,
dunque
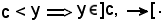
Avendo trovato che
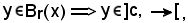
risulta
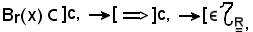
come volevasi dimostrare.
Analogamente, si dimostra che l'altro intervallo appartiene all'insieme degl'insiemi aperti.
Proprietà degl'insiemi aperti
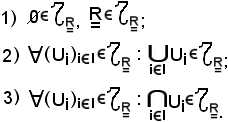
Dimostrazione 1)
L'insieme vuoto ovviamente appartiene all'insieme degl'insiemi aperti perchè esso figura fra le sue parti; l'insieme dei reali appartiene all'insieme degl'insiemi aperti perchè, considerato un suo elemento x, esiste la sfera aperta di centro x e raggio r contenuta in esso.
Dimostrazione 2)
Posto

e tenendo conto della definizione di riunione, cioè
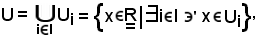
si deve dimostrare che

Allo scopo, si consideri
x U,
U,
poichè gli Ui sono insiemi aperti per ipotesi,

Ma

quindi si è trovato che
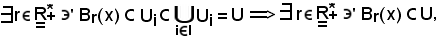
Dimostrazione 3)
Posto
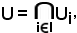
e tenendo conto della definizione di intersezione, cioè
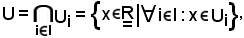
si deve dimostrare che

Si consideri
x U,
U,
poichè gli Ui sono insiemi aperti per ipotesi,
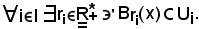
Siccome di ri ne esistono infiniti, essendo I finito, anche gli ri saranno finiti e, di essi si considera il più piccolo, indicato con

Dunque, r si trova nelle seguenti due situazioni:
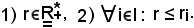
Dalla 2) segue:
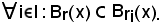
Pertanto,

Essendo noto che
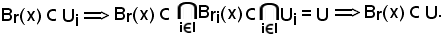
Resta così dimostrata la 3).
Retta numerica
Quando si considerano l'insieme dei reali e la totalità degl'insiemi aperti, si dice che è stata assegnata la retta numerica.
Insiemi chiusi
Considerato l'insieme dei reali ed una sua parte F, cioè
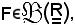
si dice che F è un insieme chiuso se e solo se
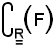
è un insieme aperto.
L'insieme degl'insiemi chiusi si indica con
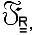
ed è così definito:
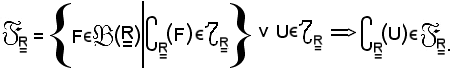
Vale anche la seguente proprietà:
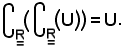
Si dimostra che:
1)-ogni intervallo chiuso è un insieme chiuso, cioè:
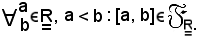
Allo scopo, basta dimostrare che
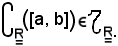
Infatti, per definizione si ha
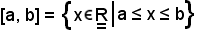
e, pertanto, risulta
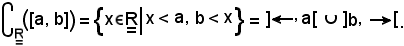
Dunque, il complementare dell'intervallo chiuso [a, b] rispetto all'insieme dei reali, essendo uguale all'unione di due intervalli aperti, è anch'esso un intervallo aperto, come volevasi dimostrare.
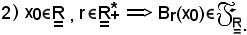
Dimostrazione 2)
E' ovvia, perchè: ogni sfera chiusa è un intervallo chiuso, ogni intervallo chiuso è un insieme chiuso ogni sfera chiusa è un insieme chiuso.
ogni sfera chiusa è un insieme chiuso.
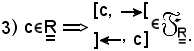
Dimostrazione 3)
Si deve dimostrare che:

Infatti,
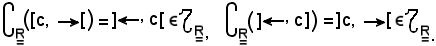
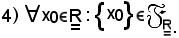
Dimostrazione 4)
Si deve dimostrare che:
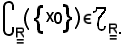
Infatti,
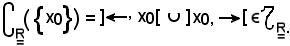
Proprietà degl'insiemi chiusi
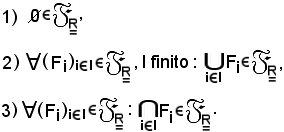
Le dimostrazioni sono ovvie, tenendo presente che:

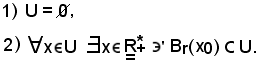
Si indichi ora con
l'insieme degl'insiemi aperti; esso è non vuoto perchè almeno l'insieme vuoto è una delle sue parti.
Tale insieme si chiama Topologia sull'insieme dei reali.
Si dimostra che:
1)-ogni intervallo aperto è un insieme aperto, cioè
Pertanto, quale che sia
x
basta dimostrare che esiste una sfera aperta di centro x e raggio r contenuta nell'intervallo.
Allo scopo, si consideri
e si indichi con r il minimo di tali numeri, cioè:
r = min(x - a, b - x);
si deve dimostrare che
Br(x)
Infatti, sia
y
e, per definizione di sfera aperta, si ha
|y - x| < r,
cioè
a = x - x + a ≤ x - r < y < x + r ≤ x + b - x = b,
tenendo conto che, per come è stata definita r, risulta
x - a ≤ r ≤ b - x.
Si è quindi trovato che:
a < y < b,
e quindi
y
Siccome l'elemento y
Br(x)
come volevasi dimostrare.
Richiamo
Quando sono state trattate le sfere, è stato dimostrato che:
Quindi, in virtù del fatto che ogni sfera aperta è un intervallo aperto, ovviamente si ha:
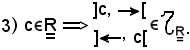
Se
e, assumendo
r = x - c,
si può considerare la sfera aperta di centro x e raggio r, Br(x).
Sia ora
y
ma
x - r = x - x + c = c,
dunque
Avendo trovato che
risulta
come volevasi dimostrare.
Analogamente, si dimostra che l'altro intervallo appartiene all'insieme degl'insiemi aperti.
Proprietà degl'insiemi aperti
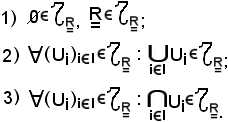
Dimostrazione 1)
L'insieme vuoto ovviamente appartiene all'insieme degl'insiemi aperti perchè esso figura fra le sue parti; l'insieme dei reali appartiene all'insieme degl'insiemi aperti perchè, considerato un suo elemento x, esiste la sfera aperta di centro x e raggio r contenuta in esso.
Dimostrazione 2)
Posto
e tenendo conto della definizione di riunione, cioè
si deve dimostrare che
Allo scopo, si consideri
x
poichè gli Ui sono insiemi aperti per ipotesi,
Ma
quindi si è trovato che
come volevasi dimostrare.
Dimostrazione 3)
Posto
e tenendo conto della definizione di intersezione, cioè
si deve dimostrare che
Si consideri
x
poichè gli Ui sono insiemi aperti per ipotesi,
Siccome di ri ne esistono infiniti, essendo I finito, anche gli ri saranno finiti e, di essi si considera il più piccolo, indicato con
Dunque, r si trova nelle seguenti due situazioni:
Dalla 2) segue:
Pertanto,
Essendo noto che
Resta così dimostrata la 3).
Retta numerica
Quando si considerano l'insieme dei reali e la totalità degl'insiemi aperti, si dice che è stata assegnata la retta numerica.
Insiemi chiusi
Considerato l'insieme dei reali ed una sua parte F, cioè
si dice che F è un insieme chiuso se e solo se
è un insieme aperto.
L'insieme degl'insiemi chiusi si indica con
ed è così definito:
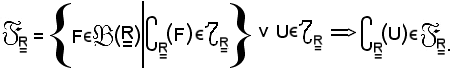
Vale anche la seguente proprietà:
Si dimostra che:
1)-ogni intervallo chiuso è un insieme chiuso, cioè:
Allo scopo, basta dimostrare che
Infatti, per definizione si ha
e, pertanto, risulta
Dunque, il complementare dell'intervallo chiuso [a, b] rispetto all'insieme dei reali, essendo uguale all'unione di due intervalli aperti, è anch'esso un intervallo aperto, come volevasi dimostrare.
Dimostrazione 2)
E' ovvia, perchè: ogni sfera chiusa è un intervallo chiuso, ogni intervallo chiuso è un insieme chiuso
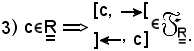
Dimostrazione 3)
Si deve dimostrare che:
Infatti,
Dimostrazione 4)
Si deve dimostrare che:
Infatti,
Proprietà degl'insiemi chiusi
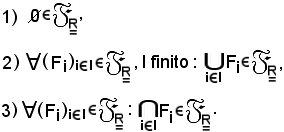
Le dimostrazioni sono ovvie, tenendo presente che:
