INTORNI ---> INDICE
Intorno di un punto
Assegnati
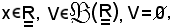
si dà la seguente definizione:
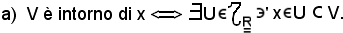
E' evidente che se
V è intorno di x x
x V.
V.
Si osserva ora che l'insieme degl'intorni del punto x è indicato con bi gotica di x e definito come segue:
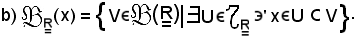
Proprietà degl'intorni
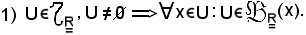
Dimostrazione 1)
E' ovvia, in quanto nella definizione a) basta sostituire U a V, ed essendo U U, risulta:
U, risulta:
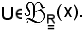
Da tale proprietà si deduce che, considerate la sfera aperta e la sfera chiusa aventi stesso centro x0 e stesso raggio r, essendo
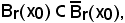
la sfera chiusa è intorno di ciascun punto della sfera aperta, cioè si deve dimostrare che
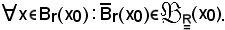
Infatti, si considera
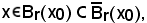
per la definizione a), sostituendo ad U e V rispettivamente la sfera aperta e la sfera chiusa, si ha:
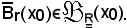
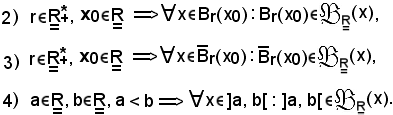
Le proprietà 2), 3) e 4) si dimostrano facilmente.
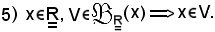
Dimostrazione 5)
Siano
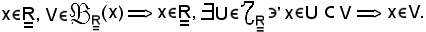
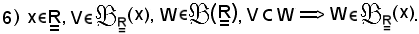
Dimostrazione 6)
Siano
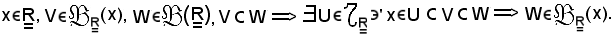
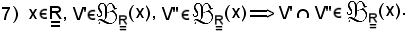
Dimostrazione 7)
Siano
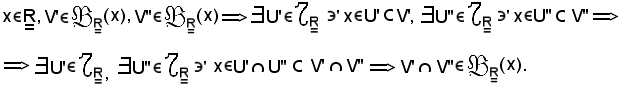
Assioma di separazione
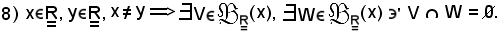
Dimostrazione 8)
Per ipotesi sia
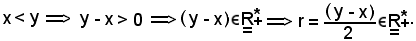
Si pongono ora, rispettivamente, uguali a V e W le sfere aperte di raggio r e centri x ed y, cioè:
Br(x) = V e Br(y) = W,
che sono intorni di x e di y, cioè:
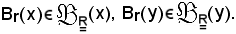
Si deve dimostrare che:
V W =
W =  ,
,
o equivalentemente che:
Br(x) Br(y) =
Br(y) =  .
.
Si ragiona per assurdo, cioè si considera non vuota tale intersezione, quindi si suppone che esista l'elemento
z Br(x)
Br(x)  Br(y)
Br(y)  z
z Br(x), z
Br(x), z Br(y)
Br(y)  |z - x| < r, |z - y| < r
|z - x| < r, |z - y| < r 
 x - r < z < x + r, y - r < z < y + r
x - r < z < x + r, y - r < z < y + r  y - r < x + r, y - x < 2r.
y - r < x + r, y - x < 2r.
Essendo
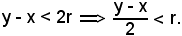
Ma per ipotesi
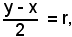
quindi si ha:
r < r,
è ciò è assurdo.
Siccome l'assurdo è derivato dall'aver supposto
Br(x) Br(y) ≠
Br(y) ≠ ,
,
si può concludere che
Br(x) Br(y) =
Br(y) =  ,
,
come volevasi dimostrare.
Assegnati
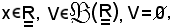
si dimostra che le seguenti due proposizioni sono equivalenti:
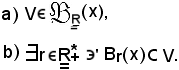
Dimostrazione
a) b)
b)
Per ipotesi è vera la a), quindi
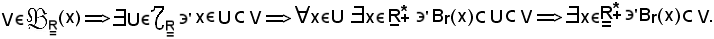
Dimostrazione
b) a)
a)
E' ovvia, se si tiene conto che Br(x) è un insieme aperto contenuto in V e, di conseguenza, V è intorno di x.
Assegnati
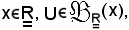
si dimostra che le seguenti due proposizioni sono equivalenti:
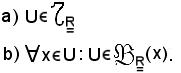
Dimostrazione
a) b)
b)
La b) è vera per la proprietà
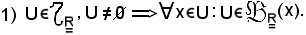 Dimostrazione
Dimostrazione
b) a)
a)
Considerato
x U,
U,
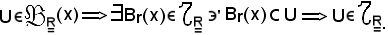
Assegnati
si dà la seguente definizione:
E' evidente che se
V è intorno di x
Si osserva ora che l'insieme degl'intorni del punto x è indicato con bi gotica di x e definito come segue:
Proprietà degl'intorni
Dimostrazione 1)
E' ovvia, in quanto nella definizione a) basta sostituire U a V, ed essendo U
Da tale proprietà si deduce che, considerate la sfera aperta e la sfera chiusa aventi stesso centro x0 e stesso raggio r, essendo
la sfera chiusa è intorno di ciascun punto della sfera aperta, cioè si deve dimostrare che
Infatti, si considera
per la definizione a), sostituendo ad U e V rispettivamente la sfera aperta e la sfera chiusa, si ha:
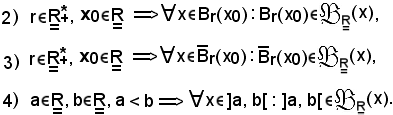
Le proprietà 2), 3) e 4) si dimostrano facilmente.
Dimostrazione 5)
Siano
Dimostrazione 6)
Siano
Dimostrazione 7)
Siano
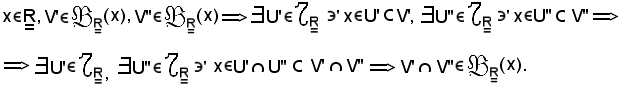
Assioma di separazione
Dimostrazione 8)
Per ipotesi sia
Si pongono ora, rispettivamente, uguali a V e W le sfere aperte di raggio r e centri x ed y, cioè:
Br(x) = V e Br(y) = W,
che sono intorni di x e di y, cioè:
Si deve dimostrare che:
V
o equivalentemente che:
Br(x)
Si ragiona per assurdo, cioè si considera non vuota tale intersezione, quindi si suppone che esista l'elemento
z
Essendo
Ma per ipotesi
quindi si ha:
r < r,
è ciò è assurdo.
Siccome l'assurdo è derivato dall'aver supposto
Br(x)
si può concludere che
Br(x)
come volevasi dimostrare.
Assegnati
si dimostra che le seguenti due proposizioni sono equivalenti:
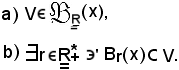
Dimostrazione
a)
Per ipotesi è vera la a), quindi
Dimostrazione
b)
E' ovvia, se si tiene conto che Br(x) è un insieme aperto contenuto in V e, di conseguenza, V è intorno di x.
Assegnati
si dimostra che le seguenti due proposizioni sono equivalenti:
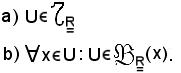
Dimostrazione
a)
La b) è vera per la proprietà
b)
Considerato
x