LEGGI DI COMPOSIZIONE SULL'INSIEME DELLE FUNZIONI ---> INDICE
Si
considerino la parte X dell'insieme dei reali, cioè
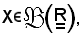
e l'insieme delle applicazioni di X in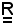 , indicato con
, indicato con
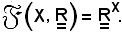
In altri termini:

Sull'insieme
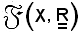
si può definire una "legge di composizione interna ovunque definita" indicata con .
.
Quindi
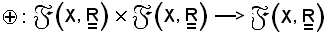
è un'applicazione così definita:
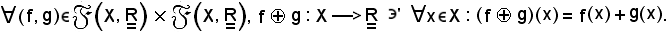
Nota bene

Definizione - Si chiama funzione reale ogni funzione avente per insieme d'arrivo l'insieme dei reali.
Siccome per definizione
+(f, g) = f + g,
ha senso considerare il gruppoide
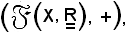
ricordando che per definizione esso è una coppia ordinata la cui prima coordinata è un insieme e la seconda è una legge di composizione interna ovunque definita sullo stesso insieme, che gode delle seguenti proprietà:
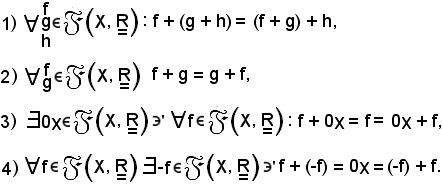
Queste quattro proprietà esprimono che
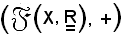
è un gruppo abeliano.
Dimostrazione 1).
Infatti,
(f + (g + h))(x) = f(x) + (g + h)(x) = f(x) + g(x) + h(x) = (f(x) + g(x)) + h(x) = (f + g)(x) + h(x) =
= ((f + g) + h)(x).
Dimostrazione 2).
E' ovvia.
Dimostrazione 3).
Si consideri l'applicazione costante di costante valore zero, così definita:
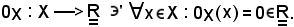
Per dimostrare tale proprietà, basta riconoscere che le funzioni dei due membri assumono lo stesso valore in ogni
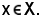
Infatti,
(f + 0X)(x) = f(x) + 0X(x) = f(x) + 0 = f(x).
Dimostrazione 4).
Si consideri l'applicazione -f così definita:
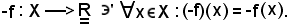
Per dimostrare tale proprietà, basta riconoscere che le funzioni dei due membri assumono lo stesso valore in ogni
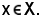
Infatti,
(f + (-f))(x) = f(x) + (-f)(x) = f(x) - (f)(x) = 0 = 0X.
Sull'insieme
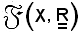
si può definire una "legge di composizione interna ovunque definita" indicata con .
.
Quindi
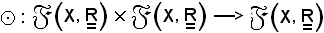
è un'applicazione così definita:
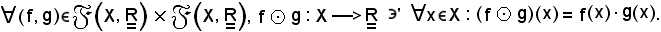
Nota bene

Siccome per definizione
·(f, g) = f · g,
ha senso considerare la terna
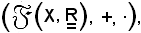
che gode delle seguenti proprietà:
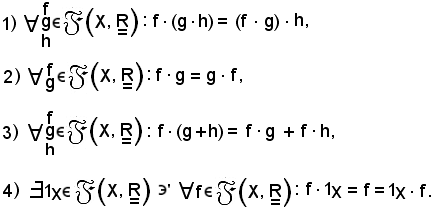
Dimostrazione 1).
Infatti,
(f · (g · h))(x) = f(x) · (g · h)(x) = f(x) · g(x) · h(x) = (f(x) · g(x)) · h(x) = (f · g)(x) · h(x) =
= ((f · g) · h)(x).
Dimostrazione 2).
Dimostrazione 3).
(f · (g + h))(x) = f(x) · (g + h)(x) = f(x) · (g(x) + h(x)) = f(x) · g(x) + f(x) · h(x) = (f · g)(x) + (f · h)(x).
Dimostrazione 4).
Si consideri l'applicazione costante di costante valore uno, così definita:
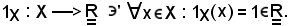
Per dimostrare tale proprietà, basta riconoscere che le funzioni dei due membri assumono lo stesso valore in ogni
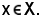
Infatti,
(f · 1X)(x) = f(x) · 1X(x) = f(x) · 1 = f(x).
Dopo aver dimostrato queste proprietà, si ricava la seguente:
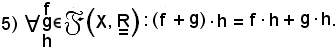
Nota bene
Si ricordano alcune definizioni di Algebra:
1)-si chiama gruppoide ogni coppia ordinata la cui prima coordinata è un insieme e la seconda è una legge di composizione interna ovunque definita sullo stesso insieme.
Esempio: (A, T) è un gruppoide in cui la prima coordinata è l'insieme A e T una legge di composizione interna ovunque definita su A.
2)-il gruppoide (A, T) si chiama monoide quando la legge T è associativa ed è dotata di elemento neutro.
3)-considerati l'insieme A e le due leggi di composizione interna · e +, alla terna (A, +, ·) si dà il nome di anello quando si verificano le seguenti condizioni:

4)-si chiama corpo ogni anello (A, +, .) unitario dotato di elemento neutro per la moltiplicazione, assoggettato alla seguente altra condizione
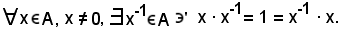
Questa condizione esprime che x è simmetrizzabile e che il suo simmetrico è x-1.
Osservato ciò, e tenendo conto, come si è visto, che
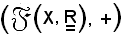
è un gruppo abeliano, che
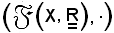
è un monoide perchè la legge · è associativa e dotata di elemento neutro 1X, e che la legge · è doppiamente distributiva rispetto a +, si ha che la terna
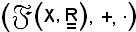
è un anello unitario.
Si osserva ora che l'insieme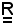 dei
reali è un corpo, in quanto esso verifica tutte le proprietà per
renderlo tale e siccome, in quanto si è visto, si nota un certo
parallelismo nel comportamento dell'insieme
dei
reali è un corpo, in quanto esso verifica tutte le proprietà per
renderlo tale e siccome, in quanto si è visto, si nota un certo
parallelismo nel comportamento dell'insieme
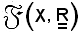
con l'insieme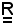 , sorge la domanda: "per caso
, sorge la domanda: "per caso
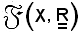
è un corpo?", cioè tutti gli elementi diversi da zero sono simmetrizzabili per la moltiplicazione?
Ciò non è vero, anzi gli elementi dell'anello che sono simmetrizzabili per sono tutte e solo le applicazioni f che verificano la proprietà che, in
un generico elemento dell'insieme X, assumono valore non nullo, cioè
sono tutte e solo le applicazioni f che verificano la proprietà che, in
un generico elemento dell'insieme X, assumono valore non nullo, cioè

Si osservi:
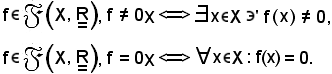
Si indica ora con f-1 l'applicazione così definita:
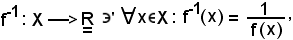
e si dimostra che f-1 è il simmetrico di f per , cioè che
, cioè che
f · f-1 = 1X.
Infatti, considerato:
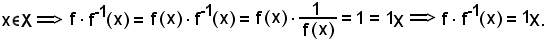
Pertanto, si ha:
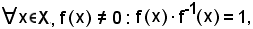
e quindi, l'applicazione f-1 simmetrica di f per , si indica con 1/f.
, si indica con 1/f.
Quindi:
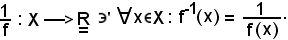
Nota bene
e l'insieme delle applicazioni di X in
In altri termini:
Sull'insieme
si può definire una "legge di composizione interna ovunque definita" indicata con
Quindi
è un'applicazione così definita:
Nota bene

Definizione - Si chiama funzione reale ogni funzione avente per insieme d'arrivo l'insieme dei reali.
Siccome per definizione
+(f, g) = f + g,
ha senso considerare il gruppoide
ricordando che per definizione esso è una coppia ordinata la cui prima coordinata è un insieme e la seconda è una legge di composizione interna ovunque definita sullo stesso insieme, che gode delle seguenti proprietà:
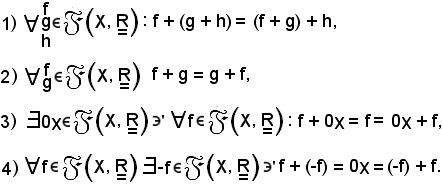
Queste quattro proprietà esprimono che
è un gruppo abeliano.
Dimostrazione 1).
Per dimostrare tale proprietà, basta riconoscere che le funzioni dei due membri assumono lo stesso valore in ogni
Infatti,
(f + (g + h))(x) = f(x) + (g + h)(x) = f(x) + g(x) + h(x) = (f(x) + g(x)) + h(x) = (f + g)(x) + h(x) =
= ((f + g) + h)(x).
Dimostrazione 2).
E' ovvia.
Dimostrazione 3).
Si consideri l'applicazione costante di costante valore zero, così definita:
Per dimostrare tale proprietà, basta riconoscere che le funzioni dei due membri assumono lo stesso valore in ogni
Infatti,
(f + 0X)(x) = f(x) + 0X(x) = f(x) + 0 = f(x).
Dimostrazione 4).
Si consideri l'applicazione -f così definita:
Per dimostrare tale proprietà, basta riconoscere che le funzioni dei due membri assumono lo stesso valore in ogni
Infatti,
(f + (-f))(x) = f(x) + (-f)(x) = f(x) - (f)(x) = 0 = 0X.
Sull'insieme
si può definire una "legge di composizione interna ovunque definita" indicata con
Quindi
è un'applicazione così definita:
Nota bene

Siccome per definizione
·(f, g) = f · g,
ha senso considerare la terna
che gode delle seguenti proprietà:
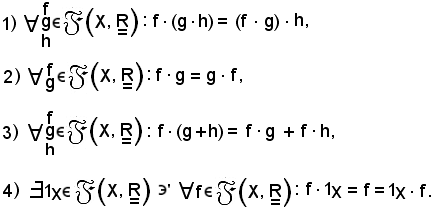
Dimostrazione 1).
Per dimostrare tale proprietà, basta riconoscere che le funzioni dei due membri assumono lo stesso valore in ogni
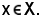
Infatti,
(f · (g · h))(x) = f(x) · (g · h)(x) = f(x) · g(x) · h(x) = (f(x) · g(x)) · h(x) = (f · g)(x) · h(x) =
= ((f · g) · h)(x).
Dimostrazione 2).
E' ovvia.
Dimostrazione 3).
Per dimostrare tale proprietà, basta riconoscere che le funzioni dei due membri assumono lo stesso valore in ogni
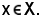
Infatti,
Infatti,
(f · (g + h))(x) = f(x) · (g + h)(x) = f(x) · (g(x) + h(x)) = f(x) · g(x) + f(x) · h(x) = (f · g)(x) + (f · h)(x).
Dimostrazione 4).
Si consideri l'applicazione costante di costante valore uno, così definita:
Per dimostrare tale proprietà, basta riconoscere che le funzioni dei due membri assumono lo stesso valore in ogni
Infatti,
(f · 1X)(x) = f(x) · 1X(x) = f(x) · 1 = f(x).
Dopo aver dimostrato queste proprietà, si ricava la seguente:
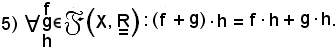
Nota bene
Si ricordano alcune definizioni di Algebra:
1)-si chiama gruppoide ogni coppia ordinata la cui prima coordinata è un insieme e la seconda è una legge di composizione interna ovunque definita sullo stesso insieme.
Esempio: (A, T) è un gruppoide in cui la prima coordinata è l'insieme A e T una legge di composizione interna ovunque definita su A.
2)-il gruppoide (A, T) si chiama monoide quando la legge T è associativa ed è dotata di elemento neutro.
3)-considerati l'insieme A e le due leggi di composizione interna · e +, alla terna (A, +, ·) si dà il nome di anello quando si verificano le seguenti condizioni:

4)-si chiama corpo ogni anello (A, +, .) unitario dotato di elemento neutro per la moltiplicazione, assoggettato alla seguente altra condizione
Questa condizione esprime che x è simmetrizzabile e che il suo simmetrico è x-1.
Osservato ciò, e tenendo conto, come si è visto, che
è un gruppo abeliano, che
è un monoide perchè la legge · è associativa e dotata di elemento neutro 1X, e che la legge · è doppiamente distributiva rispetto a +, si ha che la terna
è un anello unitario.
Si osserva ora che l'insieme
con l'insieme
è un corpo?", cioè tutti gli elementi diversi da zero sono simmetrizzabili per la moltiplicazione?
Ciò non è vero, anzi gli elementi dell'anello che sono simmetrizzabili per
Si osservi:
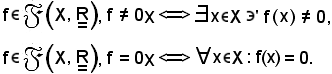
Si indica ora con f-1 l'applicazione così definita:
e si dimostra che f-1 è il simmetrico di f per
f · f-1 = 1X.
Infatti, considerato:
Pertanto, si ha:
e quindi, l'applicazione f-1 simmetrica di f per
Quindi:
Nota bene
In tema di notazioni e terminologie, se
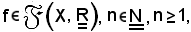
si indica
fn = f · f · f · ... f.
Sull'insieme
si può definire una "legge di composizione esterna ovunque definita", indicata con .
.
Quindi
è un'applicazione così definita:
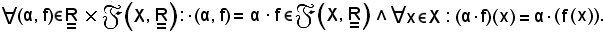
Essa gode delle seguenti proprietà:
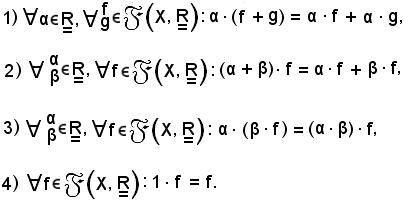
Dimostrazione 1).
Infatti,
(α · (f + g))(x) = α · ((f + g)(x)) = α · (f(x) + g(x)) = α · f(x) + α · g(x) = (α · f)(x) + (α · g)(x) =
= (α · f + α · g)(x).
Dimostrazione 2).
E' ovvia.
Dimostrazione 3).
Infatti,
(α · (β · f))(x) = α · ((β · f)(x)) = α · (β · f(x)) = (α · β) · f(x) = ((α · β) · f(x).
Dimostrazione 4).
Infatti,
(1 · f)(x) = 1 · f(x) = f(x).
L'insieme
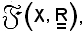
poichè verifica le quattro proprietà di gruppo abeliano e le quattro proprietà ora scritte, si chiama spazio vettoriale su .
.
Si dimostra ovviamente che:
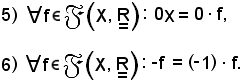
Sull'insieme
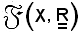
s'introduce la relazione d'ordine
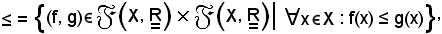
e quindi per definizione
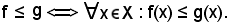
Affinchè ≤ così costruito sia una relazione d'ordine, occorre verificare i due seguenti assiomi:
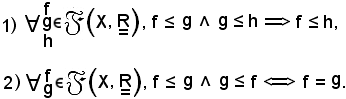
Dimostrazione 1).
Per ipotesi, risulta
f(x) ≤ g(x), g(x) ≤ h(x) f(x) ≤ h(x),
f(x) ≤ h(x),
quindi
f ≤ h,
come volevasi dimostrare.
Dimostrazione 2).
Per ipotesi, risulta
f(x) ≤ g(x), g(x) ≤ f(x) f(x) = g(x),
f(x) = g(x),
quindi
f = g,
come volevasi dimostrare.
Si è quindi dimostrato che
è un insieme ordinato dalla relazione d'ordine ≤; si dimostra ora che ≤ è compatibile con la legge additiva del gruppo abeliano, cioè che le seguenti due proposizioni sono equivalenti:
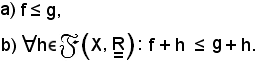
Dimostrazione
a) b)
b)
Per dimostrare tale proprietà, basta riconoscere che le funzioni dei due membri assumono lo stesso valore in ogni
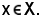
Per ipotesi, risulta
f(x) ≤ g(x),
si consideri ora
(f + h)(x) = f(x) + h(x) ≤ g(x) + h(x) = (g+ h)(x) (f + h)(x) ≤ (g+ h)(x),
(f + h)(x) ≤ (g+ h)(x),
quindi
f + h ≤ g+ h,
come volevasi dimostrare.
b) a)
a)
Per ipotesi, risulta
f + h ≤ g+ h,
si deve dimostrare che
f ≤ g.
Infatti,
f = f + 0X ≤ g + 0X = g f ≤ g,
f ≤ g,
come volevasi dimostrare.
Se la legge del gruppo diventa ·, si riconoscono facilmente le seguenti equivalenze:
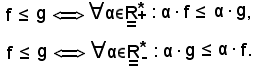
Assegnato
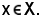
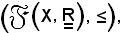
insieme ordinato dalla relazione d'ordine ≤, si dimostra che ogni sua parte non vuota maggiorata (rispettivamente minorata) per ≤ è dotata di estremo superiore (rispettivamente inferiore) per ≤, cioè se
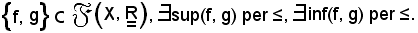
Infatti, si consideri l'applicazione φ così definita:
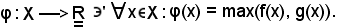
Tale applicazione esiste certamente, perchè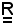 è dotato di una relazione di totale ordine, inoltre f(x) e g(x) sono paragonabili, quindi esiste max(f(x), g(x)).
è dotato di una relazione di totale ordine, inoltre f(x) e g(x) sono paragonabili, quindi esiste max(f(x), g(x)).
Si dimostra che:
sup(f, g) = φ,
cioè che φ è un maggiorante di
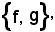
ed è il più piccolo di essi. Pertanto, occorre dimostrare:
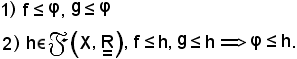
Dimostrazione 1).
Fissato
x X,
X,
per ipotesi si sa che:
f(x) ≤ φ(x), g(x) ≤ φ(x) f ≤ φ, g ≤ φ,
f ≤ φ, g ≤ φ,
come volevasi dimostrare.
Dimostrazione 2).
Sia h un maggiorante dell'insieme
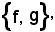
cioè
f ≤ h,
inoltre per ipotesi è noto che:
 x
x X : f(x) ≤ h(x), g(x) ≤ h(x)
X : f(x) ≤ h(x), g(x) ≤ h(x)  max(f(x), g(x)) ≤ h(x)
max(f(x), g(x)) ≤ h(x)  φ(x) ≤ h(x)
φ(x) ≤ h(x)  φ ≤ h,
φ ≤ h,
come volevasi dimostrare.
Analogamente, se si considera
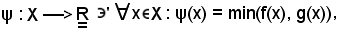
si dimostra che
inf(f, g) = ψ.
Data l'applicazione
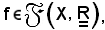
con il simbolo |f|, si indica l'applicazione
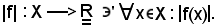
Si dimostra che, considerando le applicazioni f e -f e l'insieme ad esse ridotto
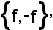
si ha:
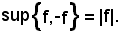
si indica
fn = f · f · f · ... f.
Sull'insieme
si può definire una "legge di composizione esterna ovunque definita", indicata con
Quindi
è un'applicazione così definita:
Essa gode delle seguenti proprietà:
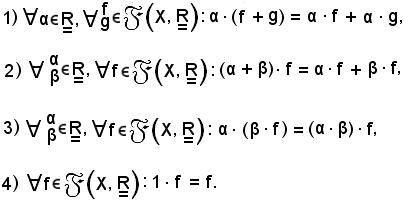
Dimostrazione 1).
Per dimostrare tale proprietà, basta riconoscere che le funzioni dei due membri assumono lo stesso valore in ogni
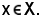
Infatti,
(α · (f + g))(x) = α · ((f + g)(x)) = α · (f(x) + g(x)) = α · f(x) + α · g(x) = (α · f)(x) + (α · g)(x) =
= (α · f + α · g)(x).
Dimostrazione 2).
E' ovvia.
Dimostrazione 3).
Per dimostrare tale proprietà, basta riconoscere che le funzioni dei due membri assumono lo stesso valore in ogni
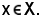
Infatti,
(α · (β · f))(x) = α · ((β · f)(x)) = α · (β · f(x)) = (α · β) · f(x) = ((α · β) · f(x).
Dimostrazione 4).
Per dimostrare tale proprietà, basta riconoscere che le funzioni dei due membri assumono lo stesso valore in ogni
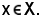
Infatti,
(1 · f)(x) = 1 · f(x) = f(x).
L'insieme
poichè verifica le quattro proprietà di gruppo abeliano e le quattro proprietà ora scritte, si chiama spazio vettoriale su
Si dimostra ovviamente che:
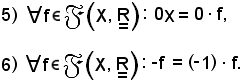
Sull'insieme
s'introduce la relazione d'ordine
e quindi per definizione
Affinchè ≤ così costruito sia una relazione d'ordine, occorre verificare i due seguenti assiomi:
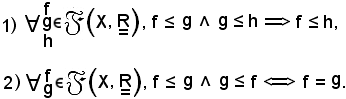
Dimostrazione 1).
Per dimostrare tale proprietà, basta riconoscere che le funzioni dei due membri assumono lo stesso valore in ogni
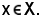
Per ipotesi, risulta
f(x) ≤ g(x), g(x) ≤ h(x)
quindi
f ≤ h,
come volevasi dimostrare.
Dimostrazione 2).
Per dimostrare tale proprietà, basta riconoscere che le funzioni dei due membri assumono lo stesso valore in ogni
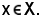
Per ipotesi, risulta
f(x) ≤ g(x), g(x) ≤ f(x)
quindi
f = g,
come volevasi dimostrare.
Si è quindi dimostrato che
è un insieme ordinato dalla relazione d'ordine ≤; si dimostra ora che ≤ è compatibile con la legge additiva del gruppo abeliano, cioè che le seguenti due proposizioni sono equivalenti:
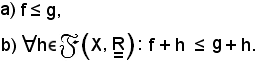
Dimostrazione
a)
Per dimostrare tale proprietà, basta riconoscere che le funzioni dei due membri assumono lo stesso valore in ogni
Per ipotesi, risulta
f(x) ≤ g(x),
si consideri ora
(f + h)(x) = f(x) + h(x) ≤ g(x) + h(x) = (g+ h)(x)
quindi
f + h ≤ g+ h,
come volevasi dimostrare.
b)
Per ipotesi, risulta
f + h ≤ g+ h,
si deve dimostrare che
f ≤ g.
Infatti,
f = f + 0X ≤ g + 0X = g
come volevasi dimostrare.
Se la legge del gruppo diventa ·, si riconoscono facilmente le seguenti equivalenze:
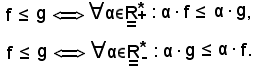
Assegnato
insieme ordinato dalla relazione d'ordine ≤, si dimostra che ogni sua parte non vuota maggiorata (rispettivamente minorata) per ≤ è dotata di estremo superiore (rispettivamente inferiore) per ≤, cioè se
Infatti, si consideri l'applicazione φ così definita:
Tale applicazione esiste certamente, perchè
Si dimostra che:
sup(f, g) = φ,
cioè che φ è un maggiorante di
ed è il più piccolo di essi. Pertanto, occorre dimostrare:
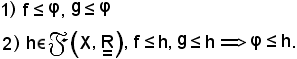
Dimostrazione 1).
Fissato
x
per ipotesi si sa che:
f(x) ≤ φ(x), g(x) ≤ φ(x)
come volevasi dimostrare.
Dimostrazione 2).
Sia h un maggiorante dell'insieme
cioè
f ≤ h,
inoltre per ipotesi è noto che:
come volevasi dimostrare.
Analogamente, se si considera
si dimostra che
inf(f, g) = ψ.
Data l'applicazione
con il simbolo |f|, si indica l'applicazione
Si dimostra che, considerando le applicazioni f e -f e l'insieme ad esse ridotto
si ha: