RELAZIONI NELLE SUCCESSIONI ---> INDICE
1)-Se una successione di numeri reali è convergente, essa è limitata limitata (superiormente ed inferiormente), cioè se
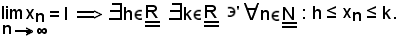
Dimostrazione
Siccome per ipotesi la successione converge al limite l, si ha:
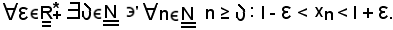
Si considerino ora gli elementi della successione che hanno indice minore di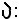
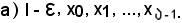
Si ha così un insieme finito di numeri reali che, come è noto, è dotato del più piccolo elemento, indicato con
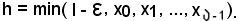
Oltre all'insieme finito a) si considera l'insieme finito
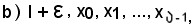
che è dotato del più grande elemento, indicato con
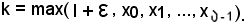
Si fissa ora arbitrariamente
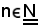
e si considera l'elemento xn, si presentano due casi:
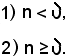
Nel caso 1), xn è uno degli elementi della successione a) che sono maggiori o uguali ad h, cioè
h ≤ xn.
Ma xn è anche uno degli elementi della successione b) che sono minori o uguali a k, cioè
xn ≤ k.
Quindi, nel caso 1), si ha:
h ≤ xn ≤ k.
Nel caso 2), si ha
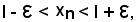
ed essendo
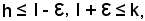
risulta:
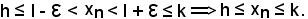
Quindi, in ogni caso, è vero che ogni successione convergente è limitata.
2)-In generale, ogni successione di numeri reali limitata non è convergente.
Ad esempio, la successione
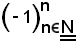
è limitata ma non convergente.
3)-Se una successione di numeri reali diverge positivamente non è limitata.
Ciò è vero, in quanto non è limitata superiormente.
Infatti:
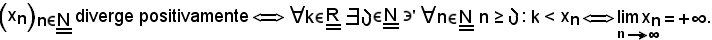
Si tiene ora conto delle seguenti due proposizioni equivalenti dimostrate in precedenza:
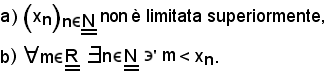
Quindi, fissato un
4)-Se una successione di numeri reali diverge negativamente non è limitata.Ciò è vero, in quanto non è limitata inferiormente.
La dimostrazione è analoga alla precedente.
5)-In generale, ogni successione di numeri reali non limitata non diverge positivamente.
Ad esempio,
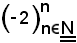
è una successione non limitata e non divergente positivamente.
Nota bene
Si è visto che ad ogni successione
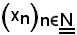
si attribuiscono i requisiti dell'insieme dei suoi elementi
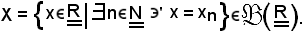
Se esistono supX ed infX, essi si chiamano estremo superiore ed estremo inferiore della successione e si indicano con
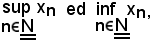
in cui sup ed inf sono rispettivamente gli estremi superiore ed inferiore dell'insieme numerico degli elementi della successione.
Si dimostra che:
-se una successione è limitata superiormente, esiste l'estremo superiore.
Infatti, se la successione è limitata superiormente, X è maggiorato ed esiste l'estremo superiore.
-se una successione è limitata superiormente, esiste l'estremo superiore.
Infatti, se la successione è limitata inferiormente, X è minorato ed esiste l'estremo inferiore.
Gli eventuali estremi superiore ed inferiore di una successione godono delle stesse proprietà di cui godevano gli estremi superiore ed inferiore di un insieme.
Si consideri il sottoinsieme X di E, non vuoto e maggiorato, si dimostra che le seguenti tre proposizioni equivalenti:
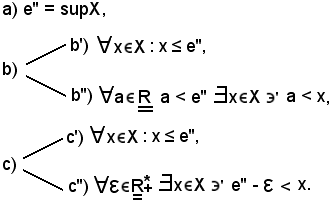
La dimostrazione segue dalle definizioni.
Tenendo conto che

ovviamente anche le seguenti tre proposizioni sono equivalenti:
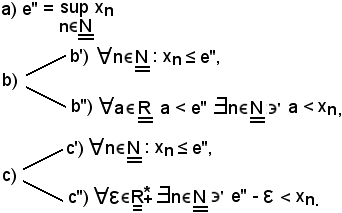
Si consideri il sottoinsieme X di E, non vuoto e maggiorato, si dimostra che le seguenti tre proposizioni sono equivalenti:
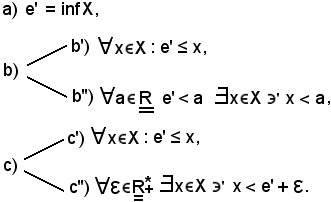
La dimostrazione segue dalle definizioni.
Tenendo conto che

ovviamente anche le seguenti tre proposizioni sono equivalenti:
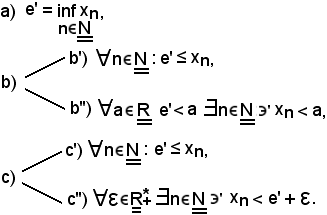
Si considerino le seguenti due successioni
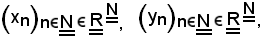
si dimostra:
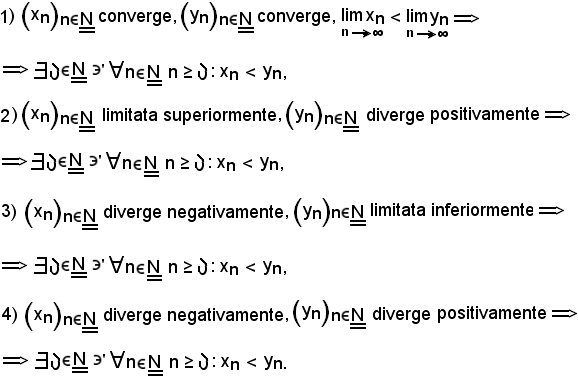
Dimostrazione 1).
Sia
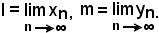
Pertanto, per ipotesi, risulta:
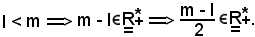
Assumendo
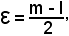
data la convergenza delle due successioni suddette, si ha:
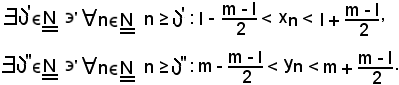
Se si indica con
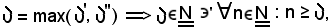
si ha:
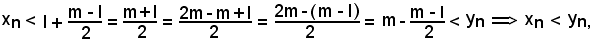
come volevasi dimostrare.
Dimostrazione 2).
Per ipotesi è noto che:

ed inoltre che
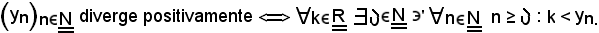
Dalla validità delle due, segue che
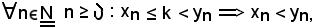
come volevasi dimostrare.
Dimostrazione 3).
Per ipotesi è noto che:
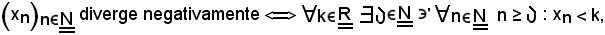
ed inoltre che

Dalla validità delle due, segue che
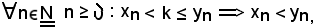
come volevasi dimostrare.
Dimostrazione 4).
Per ipotesi è noto che:

ed inoltre che
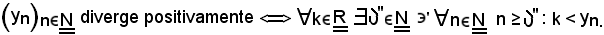
Se si indica con
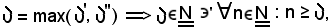
valgono contemporaneamente le due proposizioni suddette, pertanto si ha:
xn < k < yn,
cioè
xn < yn,
come volevasi dimostrare.
Nota bene
Tenendo presente che ogni successione convergente è limitata, 2) e 3) valgono ancora se al posto delle condizioni di successione limitata superiormente e di successione limitata inferiormente, si sostituisce la condizione che le due successioni siano convergenti. Si osservi ora che in riferimento alla 1), il secondo membro non implica il primo, comunque si può dimostrare il seguente teorema.
Teorema del confronto
Si dimostra che:
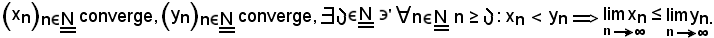
Dimostrazione.
Ragionando per assurdo, si smentisce la tesi, ed essendo ≤ una relazione di totale ordine sull'insieme dei reali, si ha:
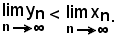
Pertanto, per la 1),
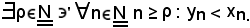
Se si indica con
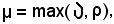
quando
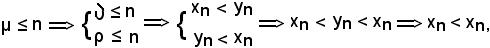
e ciò è assurdo, derivato dall'aver supposto
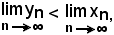
quindi si può concludere che
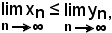
come volevasi dimostrare.
Teorema della permanenza del segno
Si dimostra che:
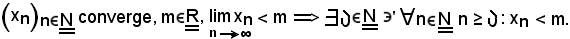
Dimostrazione.
Si pone
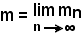
e si ricorda che la successione
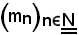
è così definita:
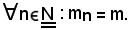
Se m = 0, per la 1) si ha:
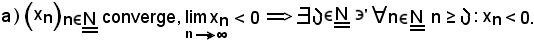
Tale relazione esprime la circostanza che se il limite di una successione è negativo, gli elementi della successione, a partire da un certo indice n, sono anch'essi negativi.
Ora, si esamina il seguente teorema:
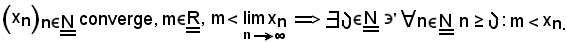
Ponendo in esso m = 0, si ha:
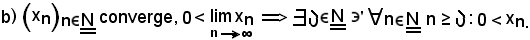
Tale relazione esprime la circostanza che, se il limite di una successione è positivo, gli elementi della successione, a partire da un certo indice n, sono anch'essi positivi. La a) e la b) esprimono il teorema della permanenza del segno.
Teorema del criterio di regolarità per successioni convergenti
Siano assegnate le seguenti successioni:
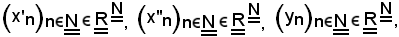
si dimostra che:
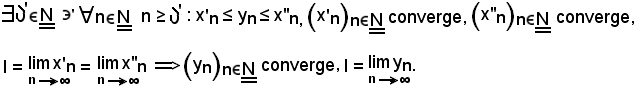
Dimostrazione.
Per ipotesi è noto che
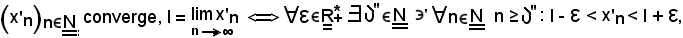
e
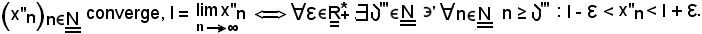
Pertanto, considerato
ed indicato con
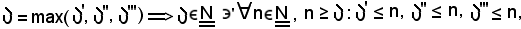
valgono contemporaneamente le seguenti condizioni:
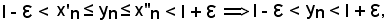
come volevasi dimostrare.
Un teorema analogo si ha per le successioni non convergenti, quindi si considerino le successioni
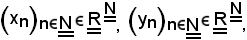
si dimostra che:

Dimostrazione.
Per ipotesi è noto che
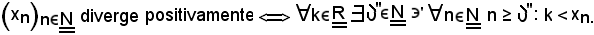
Pertanto, considerato
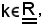
ed indicato con
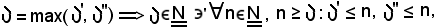
valgono contemporaneamente le seguenti condizioni:
k < xn ≤ yn,
cioè
k < yn,
come volevasi dimostrare.
Si dimostra infine che:

Dimostrazione.
Per ipotesi è noto che
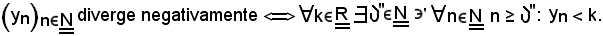
Pertanto, considerato
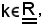
ed indicato con
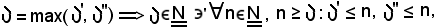
valgono contemporaneamente le seguenti condizioni:
xn ≤ yn < k,
cioè
xn < k,
come volevasi dimostrare.
Dimostrazione
Siccome per ipotesi la successione converge al limite l, si ha:
Si considerino ora gli elementi della successione che hanno indice minore di
Si ha così un insieme finito di numeri reali che, come è noto, è dotato del più piccolo elemento, indicato con
Oltre all'insieme finito a) si considera l'insieme finito
che è dotato del più grande elemento, indicato con
Si fissa ora arbitrariamente
e si considera l'elemento xn, si presentano due casi:
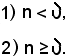
Nel caso 1), xn è uno degli elementi della successione a) che sono maggiori o uguali ad h, cioè
h ≤ xn.
Ma xn è anche uno degli elementi della successione b) che sono minori o uguali a k, cioè
xn ≤ k.
Quindi, nel caso 1), si ha:
h ≤ xn ≤ k.
Nel caso 2), si ha
ed essendo
risulta:
Quindi, in ogni caso, è vero che ogni successione convergente è limitata.
2)-In generale, ogni successione di numeri reali limitata non è convergente.
Ad esempio, la successione
è limitata ma non convergente.
3)-Se una successione di numeri reali diverge positivamente non è limitata.
Ciò è vero, in quanto non è limitata superiormente.
Infatti:
Si tiene ora conto delle seguenti due proposizioni equivalenti dimostrate in precedenza:
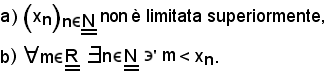
Quindi, fissato un
4)-Se una successione di numeri reali diverge negativamente non è limitata.Ciò è vero, in quanto non è limitata inferiormente.
La dimostrazione è analoga alla precedente.
5)-In generale, ogni successione di numeri reali non limitata non diverge positivamente.
Ad esempio,
è una successione non limitata e non divergente positivamente.
Nota bene
Si è visto che ad ogni successione
si attribuiscono i requisiti dell'insieme dei suoi elementi
Se esistono supX ed infX, essi si chiamano estremo superiore ed estremo inferiore della successione e si indicano con
in cui sup ed inf sono rispettivamente gli estremi superiore ed inferiore dell'insieme numerico degli elementi della successione.
Si dimostra che:
-se una successione è limitata superiormente, esiste l'estremo superiore.
Infatti, se la successione è limitata superiormente, X è maggiorato ed esiste l'estremo superiore.
-se una successione è limitata superiormente, esiste l'estremo superiore.
Infatti, se la successione è limitata inferiormente, X è minorato ed esiste l'estremo inferiore.
Gli eventuali estremi superiore ed inferiore di una successione godono delle stesse proprietà di cui godevano gli estremi superiore ed inferiore di un insieme.
Si consideri il sottoinsieme X di E, non vuoto e maggiorato, si dimostra che le seguenti tre proposizioni equivalenti:
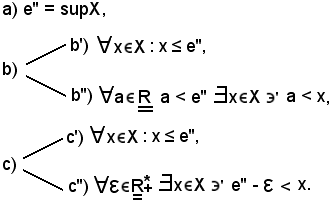
La dimostrazione segue dalle definizioni.
Tenendo conto che
ovviamente anche le seguenti tre proposizioni sono equivalenti:
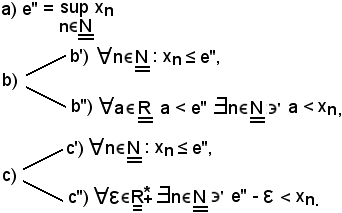
Si consideri il sottoinsieme X di E, non vuoto e maggiorato, si dimostra che le seguenti tre proposizioni sono equivalenti:
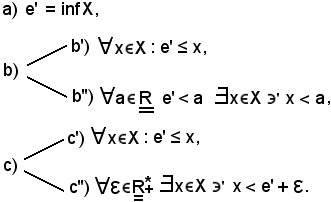
La dimostrazione segue dalle definizioni.
Tenendo conto che
ovviamente anche le seguenti tre proposizioni sono equivalenti:
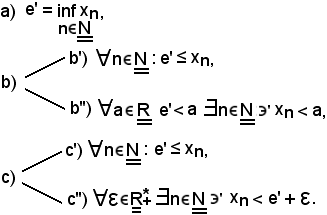
Si considerino le seguenti due successioni
si dimostra:
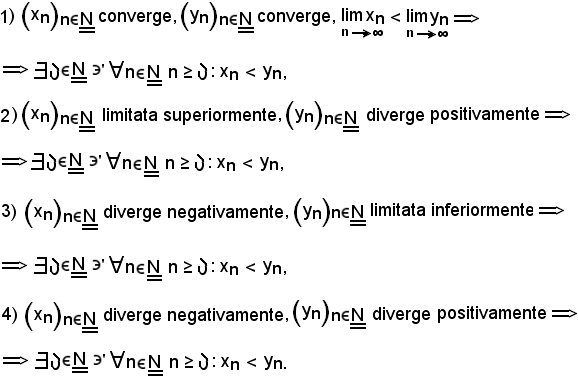
Dimostrazione 1).
Sia
Pertanto, per ipotesi, risulta:
Assumendo
data la convergenza delle due successioni suddette, si ha:
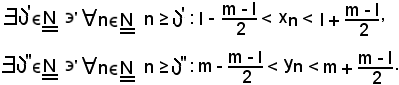
Se si indica con
si ha:
come volevasi dimostrare.
Dimostrazione 2).
Per ipotesi è noto che:
ed inoltre che
Dalla validità delle due, segue che
come volevasi dimostrare.
Dimostrazione 3).
Per ipotesi è noto che:
ed inoltre che
Dalla validità delle due, segue che
come volevasi dimostrare.
Dimostrazione 4).
Per ipotesi è noto che:
ed inoltre che
Se si indica con
valgono contemporaneamente le due proposizioni suddette, pertanto si ha:
xn < k < yn,
cioè
xn < yn,
come volevasi dimostrare.
Nota bene
Tenendo presente che ogni successione convergente è limitata, 2) e 3) valgono ancora se al posto delle condizioni di successione limitata superiormente e di successione limitata inferiormente, si sostituisce la condizione che le due successioni siano convergenti. Si osservi ora che in riferimento alla 1), il secondo membro non implica il primo, comunque si può dimostrare il seguente teorema.
Teorema del confronto
Si dimostra che:
Dimostrazione.
Ragionando per assurdo, si smentisce la tesi, ed essendo ≤ una relazione di totale ordine sull'insieme dei reali, si ha:
Pertanto, per la 1),
Se si indica con
quando
e ciò è assurdo, derivato dall'aver supposto
quindi si può concludere che
come volevasi dimostrare.
Teorema della permanenza del segno
Si dimostra che:
Dimostrazione.
Si pone
e si ricorda che la successione
è così definita:
Se m = 0, per la 1) si ha:
Tale relazione esprime la circostanza che se il limite di una successione è negativo, gli elementi della successione, a partire da un certo indice n, sono anch'essi negativi.
Ora, si esamina il seguente teorema:
Ponendo in esso m = 0, si ha:
Tale relazione esprime la circostanza che, se il limite di una successione è positivo, gli elementi della successione, a partire da un certo indice n, sono anch'essi positivi. La a) e la b) esprimono il teorema della permanenza del segno.
Teorema del criterio di regolarità per successioni convergenti
Siano assegnate le seguenti successioni:
si dimostra che:
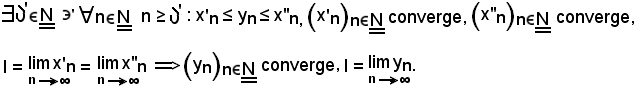
Dimostrazione.
Per ipotesi è noto che
e
Pertanto, considerato
ed indicato con
valgono contemporaneamente le seguenti condizioni:
come volevasi dimostrare.
Un teorema analogo si ha per le successioni non convergenti, quindi si considerino le successioni
si dimostra che:

Dimostrazione.
Per ipotesi è noto che
Pertanto, considerato
ed indicato con
valgono contemporaneamente le seguenti condizioni:
k < xn ≤ yn,
cioè
k < yn,
come volevasi dimostrare.
Si dimostra infine che:

Dimostrazione.
Per ipotesi è noto che
Pertanto, considerato
ed indicato con
valgono contemporaneamente le seguenti condizioni:
xn ≤ yn < k,
cioè
xn < k,
come volevasi dimostrare.