SUCCESSIONI COMPOSTE ED ESTRATTE ---> INDICE
Si
considerino la successione di numeri reali

e la successione di numeri interi naturali

Per come sono state definite le applicazioni n ed x, si può considerare l'applicazione composta
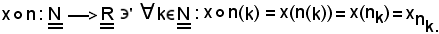
Si è dunque ottenuta la successione
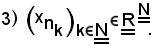
Definizione - Se la successione 2) è strettamente crescente, cioè
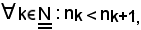
si dice che la successione 3) è una successione estratta dalla 1) mediante la 2), oppure è una sottosuccessione della 1).
Teorema - Ogni successione estratta da una successione convergente è anch'essa convergente ed ha per limite lo stesso limite della successione di partenza.
Prima di dimostrare tale teorema, si deve osservare quanto segue:
-se una successione di numeri interi naturali è strettamente crescente, cioè se
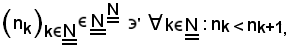
si dimostra che:
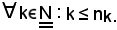
Se k = 0, è senz'altro verificata la condizione k ≤ nk, poichè

Ragionando per induzione completa su k, se la proprietà è vera per k, sarà anche vera per k + 1.
Infatti,
k ≤ nk k +1 ≤ nk +1
k +1 ≤ nk +1  nk < nk+1
nk < nk+1  k +1 ≤ nk +1 ≤ nk+1
k +1 ≤ nk +1 ≤ nk+1  k +1 ≤ nk+1.
k +1 ≤ nk+1.
Si dimostra ora il teorema, che si può esprimere mediante l'equivalenza delle seguenti due proposizioni:
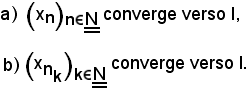
Dimostrazione
a) b)
b)
Per ipotesi risulta
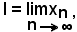
si deve dimostrare che:
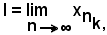
cioè che
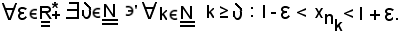
Siccome per ipotesi la successione
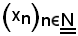
converge verso l, considerato ad arbirio
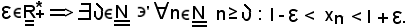
Ora, se si considera

per quanto è stato dimostrato in precedenza, si ha
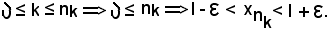
Dimostrazione
b) a)
a)
Si deve dimostrare che ogni sottosuccessione convergente è tale che la successione da cui è estratta sia convergente. Ciò si verifica se si tiene conto conto che ogni sottosuccessione si può considerare sottosuccessione di se stessa.
Teorema - Ogni successione estratta da una successione divergente positivamente (negativamente) è anch'essa divergente positivamente (negativamente).
Sia
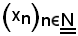
una successione divergente positivamente, cioè:
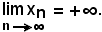
Si deve dimostrare che ogni sottosuccessione estratta da essa è divergente positivamente, cioè:
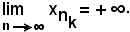
Allo scopo, deve risultare che
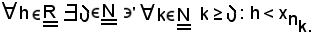
Si considera arbitrariamente
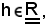
per la divergenza della successione di partenza, si ha che
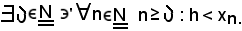
Per quanto è stato dimostrato in precedenza,
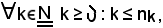
quindi da
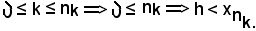
Nota bene
Per tale teorema vale anche il viceversa, perchè ogni sottosuccessione è una sottosuccessione estratta da se stessa mediante la successione
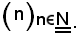
Teorema - Da una successione non limitata superiormente (inferiormente) se ne puòestrarre almeno una divergente positivamente (negativamente).
Si consideri la successione
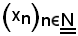
non limitata superiormente, e ciò vuol dire che l'insieme numerico della successione non ha maggioranti, ossia
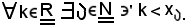
A tal punto, si costruisce prima una successione estratta dalla data e poi si dimostra che essa diverge positivamente. Per costruire una successione di numeri interi naturali si procede come segue.
Si considera 0 e si indica con A0 l'insieme non vuoto delle parti dell'insieme dei numeri interi naturali così definito, cioè
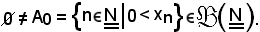
L'insieme A0 è dunque non vuoto, inoltre esso ammette il più piccolo elemento perchè l'insieme dei numeri interi naturali è bene ordinato.
Si indichi il più piccolo elemento con
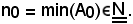
Si considera 1 e si indica con A1 l'insieme delle parti dell'insieme dei numeri interi naturali così definito, cioè
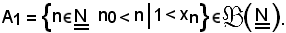
Si dimostra che l'insieme A1 è non vuoto.
Infatti, se fosse vuoto, si avrebbe
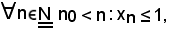
e ciò non può accadere per come è stato definito A1.
Si indichi ora con
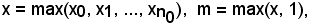
si nota che
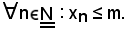
Infatti, se n0 < n, è noto che xn ≤ 1 ≤ m, quindi xn ≤ m.
Se n ≤ n0, xn è uno degli elementi della successione
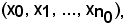
quindi risulta
xn ≤ x.
Ciò è assurdo, perchè la successione non è limitata per ipotesi, e quindi A1 è diverso dall'insieme vuoto.
Per tale motivo, esiste il più piccolo elemento di A1, indicato con
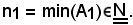
Si considera 2 e si indica con A2 l'insieme delle parti dell'insieme dei numeri interi naturali così definito, cioè
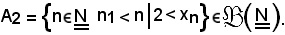
Anche l'insieme A2 è non vuoto.
Per tale motivo, esiste il più piccolo elemento di A2, indicato con

Seguendo lo stesso procedimento, si consideri ora Ak, insieme delle parti dell'insieme dei numeri interi naturali così definito, cioè
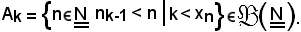
Anche l'insieme Ak è non vuoto.
Per tale motivo, esiste il più piccolo elemento di Ak, indicato con
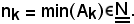
In tal modo è stata costruita la successione
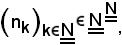
che ad ogni numero intero naturale fa corrispondere
n1, n2,..., nk,
ossia
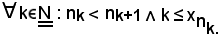
Pertanto, essa è una successione monotòna strettamente crescente.
Resta da dimostrare che la successione
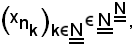
estratta da
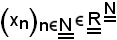
mediante la successione
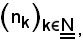
è divergente positivamente, cioè
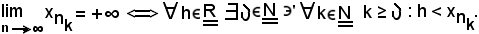
Infatti, si consideri arbitrariamente
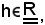
e si prenda un numero naturale più grande di esso, cioè
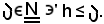
Si considera ora un qualunque
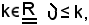
e poiche è noto che
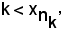
si ha
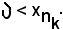
Essendo inoltre
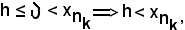
come volevasi dimostrare.
e la successione di numeri interi naturali
Per come sono state definite le applicazioni n ed x, si può considerare l'applicazione composta
Si è dunque ottenuta la successione
Definizione - Se la successione 2) è strettamente crescente, cioè
si dice che la successione 3) è una successione estratta dalla 1) mediante la 2), oppure è una sottosuccessione della 1).
Teorema - Ogni successione estratta da una successione convergente è anch'essa convergente ed ha per limite lo stesso limite della successione di partenza.
Prima di dimostrare tale teorema, si deve osservare quanto segue:
-se una successione di numeri interi naturali è strettamente crescente, cioè se
si dimostra che:
Se k = 0, è senz'altro verificata la condizione k ≤ nk, poichè
Ragionando per induzione completa su k, se la proprietà è vera per k, sarà anche vera per k + 1.
Infatti,
k ≤ nk
Si dimostra ora il teorema, che si può esprimere mediante l'equivalenza delle seguenti due proposizioni:
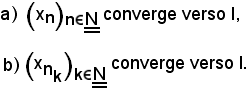
Dimostrazione
a)
Per ipotesi risulta
si deve dimostrare che:
cioè che
Siccome per ipotesi la successione
converge verso l, considerato ad arbirio
Ora, se si considera
per quanto è stato dimostrato in precedenza, si ha
Dimostrazione
b)
Si deve dimostrare che ogni sottosuccessione convergente è tale che la successione da cui è estratta sia convergente. Ciò si verifica se si tiene conto conto che ogni sottosuccessione si può considerare sottosuccessione di se stessa.
Teorema - Ogni successione estratta da una successione divergente positivamente (negativamente) è anch'essa divergente positivamente (negativamente).
Sia
una successione divergente positivamente, cioè:
Si deve dimostrare che ogni sottosuccessione estratta da essa è divergente positivamente, cioè:
Allo scopo, deve risultare che
Si considera arbitrariamente
per la divergenza della successione di partenza, si ha che
Per quanto è stato dimostrato in precedenza,
quindi da
Nota bene
Per tale teorema vale anche il viceversa, perchè ogni sottosuccessione è una sottosuccessione estratta da se stessa mediante la successione
Teorema - Da una successione non limitata superiormente (inferiormente) se ne può
Si consideri la successione
non limitata superiormente, e ciò vuol dire che l'insieme numerico della successione non ha maggioranti, ossia
A tal punto, si costruisce prima una successione estratta dalla data e poi si dimostra che essa diverge positivamente. Per costruire una successione di numeri interi naturali si procede come segue.
Si considera 0 e si indica con A0 l'insieme non vuoto delle parti dell'insieme dei numeri interi naturali così definito, cioè
L'insieme A0 è dunque non vuoto, inoltre esso ammette il più piccolo elemento perchè l'insieme dei numeri interi naturali è bene ordinato.
Si indichi il più piccolo elemento con
Si considera 1 e si indica con A1 l'insieme delle parti dell'insieme dei numeri interi naturali così definito, cioè
Si dimostra che l'insieme A1 è non vuoto.
Infatti, se fosse vuoto, si avrebbe
e ciò non può accadere per come è stato definito A1.
Si indichi ora con
si nota che
Infatti, se n0 < n, è noto che xn ≤ 1 ≤ m, quindi xn ≤ m.
Se n ≤ n0, xn è uno degli elementi della successione
quindi risulta
xn ≤ x.
Ciò è assurdo, perchè la successione non è limitata per ipotesi, e quindi A1 è diverso dall'insieme vuoto.
Per tale motivo, esiste il più piccolo elemento di A1, indicato con
Si considera 2 e si indica con A2 l'insieme delle parti dell'insieme dei numeri interi naturali così definito, cioè
Anche l'insieme A2 è non vuoto.
Per tale motivo, esiste il più piccolo elemento di A2, indicato con
Seguendo lo stesso procedimento, si consideri ora Ak, insieme delle parti dell'insieme dei numeri interi naturali così definito, cioè
Anche l'insieme Ak è non vuoto.
Per tale motivo, esiste il più piccolo elemento di Ak, indicato con
In tal modo è stata costruita la successione
che ad ogni numero intero naturale fa corrispondere
n1, n2,..., nk,
ossia
Pertanto, essa è una successione monotòna strettamente crescente.
Resta da dimostrare che la successione
estratta da
mediante la successione
è divergente positivamente, cioè
Infatti, si consideri arbitrariamente
e si prenda un numero naturale più grande di esso, cioè
Si considera ora un qualunque
e poiche è noto che
si ha
Essendo inoltre
come volevasi dimostrare.