SUCCESSIONI CON ELEMENTI IN VALORE ASSOLUTO ---> INDICE
Si premettono alcune proprietÓ dei numeri reali:

Si dimostra inoltre che:

Dimostrazione 2).
Considerati
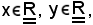
Ŕ noto che
x ≤ |x|, -x ≤ |x|,
x + y ≤ |x| + |y|,
-(x + y) ≤ |x| + |y|,
per la proprietÓ 1), si ha:
|x + y| ≤ |x| + |y|,
come volevasi dimostrare.
Dimostrazione 3).
Considerati
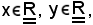
si nota che
|x| = |(x - y) + y| ≤ |x - y| + |y|,
per la proprietÓ 1).
Portando |y| al primo membro, si ha:
|x| - |y| ≤ |x - y|.
Cambiando di posto |x| e |y| e cambiando anche il segno, risulta:
-(|x| - |y|) = |y| - |x| ≤ |y - x| = |-(y - x)| = |x - y|
e, per la 1), si ha:
||x| - |y|| ≤ |x - y|,
come volevasi dimostrare.
Sia

si dimostra: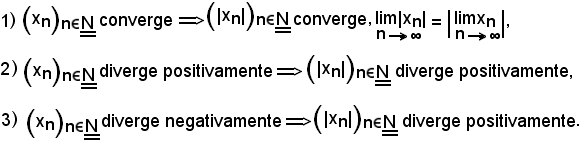
Dimostrazione 1).
Sia
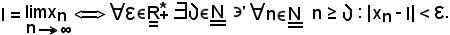
Si osserva ora che, per la proprietÓ 3) si ha:

e quindi, considerato

come volevasi dimostrare.
Dimostrazione 2).
Per ipotesi,
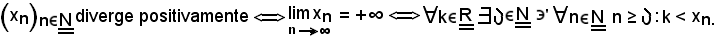
Inoltre, tenendo conto che
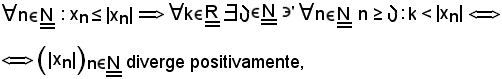
come volevasi dimostrare.
Dimostrazione 3).

Inoltre, tenendo conto che

come volevasi dimostrare.
Si dimostra inoltre che:

Dimostrazione 2).
Considerati
Ŕ noto che
x ≤ |x|, -x ≤ |x|,
y ≤ |y|, -y ≤ |y|.
Si considerano ora le seguenti somme:
Si considerano ora le seguenti somme:
x + y ≤ |x| + |y|,
-(x + y) ≤ |x| + |y|,
per la proprietÓ 1), si ha:
|x + y| ≤ |x| + |y|,
come volevasi dimostrare.
Dimostrazione 3).
Considerati
si nota che
|x| = |(x - y) + y| ≤ |x - y| + |y|,
per la proprietÓ 1).
Portando |y| al primo membro, si ha:
|x| - |y| ≤ |x - y|.
Cambiando di posto |x| e |y| e cambiando anche il segno, risulta:
-(|x| - |y|) = |y| - |x| ≤ |y - x| = |-(y - x)| = |x - y|
e, per la 1), si ha:
||x| - |y|| ≤ |x - y|,
come volevasi dimostrare.
Sia
si dimostra:
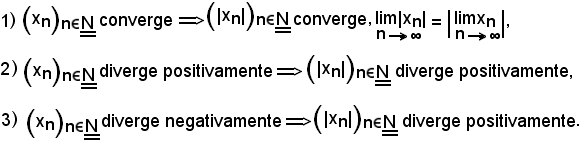
Dimostrazione 1).
Sia
Si osserva ora che, per la proprietÓ 3) si ha:
e quindi, considerato
come volevasi dimostrare.
Dimostrazione 2).
Per ipotesi,
Inoltre, tenendo conto che
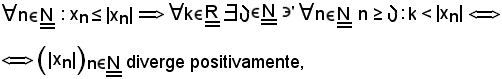
come volevasi dimostrare.
Dimostrazione 3).
Per ipotesi,

Inoltre, tenendo conto che

come volevasi dimostrare.