SUCCESSIONI DIVERGENTI ---> INDICE
Successioni divergenti positivamente e negativamente
Si
consideri la successione
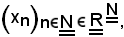
si danno le seguenti definizioni:
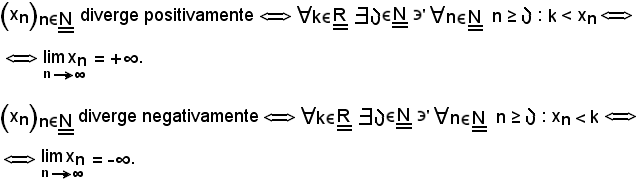
Nota bene
Per ogni successione di numeri reali si può verificare una sola delle seguenti circostanze:
1)-converge,
2)-diverge positivamente,
3)-diverge negativamente,
4)-nè converge, nè diverge positivamente, nè diverge negativamente.
Esempio di successione divergente positivamente
Siano assegnati
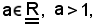
e la successione
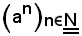
che ad ogni n associa an.
Si dimostra che:
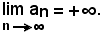
Infatti, per definizione, si deve dimostrare che:
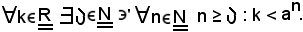
Se
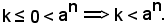
Se
k > 0,
invece di dimostrare che
k < an,
si può dimostrare che
logak < logaan = n.
Allo scopo, si considera
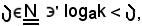
ed essendo
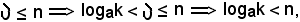
come volevasi dimostrare.
Esempio di successione divergente negativamente
Siano assegnati
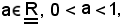
e la successione
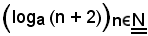
che ad ogni n associa loga(n + 2).
Si dimostra che:
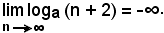
Successione oscillante
Una successione si dice oscillante se non è convergente, nè divergente positivamente e nè divergente negativamente.
Esempio di successione oscillante
Si consideri la successione
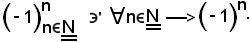
Si dimostra che tale successione è oscillante, cioè:
1)-non diverge positivamente.
infatti, se divergesse positivamente, si avrebbe:
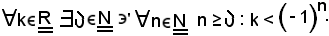
Essendo
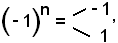
se si prende K = 2, la relazione suddetta non è soddisfatta, quindi la successione non diverge positivamente.
2)-non diverge negativamente.
La dimostrazione è analoga alla precedente.
2)-non converge.
Infatti, se convergesse, si avrebbe:
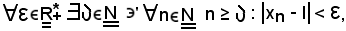
in cui
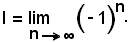
Si presentano due casi:
1) l = 0, pertanto, si ha:
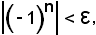
e ciò non è vero, quindi in tal caso la successione non converge al limite zero.
2) l ≠ 0, pertanto, si ha: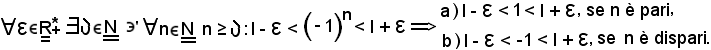
Si moltiplica ciascuno dei membri della a) per -1, ottenendo:
c) - l - ε < -1 < - l + ε.
Dalla b) e dalla c) si ottengono:
d) -2l < 2ε -l < ε,
-l < ε,
e) -2ε < -2l l < ε.
l < ε.
La d) e la e) esprimono che
max(l, -l) < ε.
Ma, essendo l ≠ 0, anche il
max(l, -l) ≠ 0.
Si è quindi pervenuti ad un assurdo, nato dall'aver supposto che la successione fosse convergente, dunque, non lo è, come volevasi dimostrare.
Successione regolare
Una successione si dice regolare se è convergente, o divergente positivamente, oppure divergente negativamente.
Teorema 1 - Se una successione converge ad un limite finito l, essa non può divergere ad un limite infinito positivamente.
Cioè, si deve dimostrare che, considerata la successione
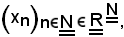
se
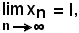
non può essere
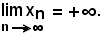
Infatti, siccome per ipotesi la successione converge ad l, per definizione si ha:
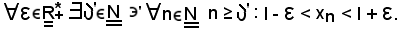
Ragionando per assurdo, si suppone che la successione diverga positivamente, cioè
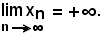
Pertanto, considerando
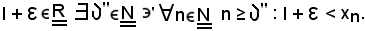
Si indichi ora
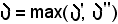
e si fissi
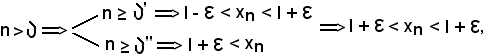
e ciò è assurdo, quindi la successione non diverge positivamente, come volevasi dimostrare.
Teorema 2 - Se una successione converge ad un limite finito l, essa non può divergere ad un limite infinito negativamente.
Cioè, si deve dimostrare che, considerata la successione
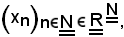
se
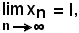
non può essere
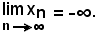
La dimostrazione di questo teorema è analoga a quella del teorema 1.
Teorema 3 - Se una successione diverge positivamente, essa non può convergere ad un limite finito l.
Cioè, si deve dimostrare che, considerata la successione
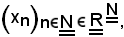
se
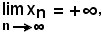
non può essere
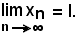
La dimostrazione di questo teorema è analoga a quella del teorema 1.
Teorema 4 - Se una successione diverge positivamente, essa non può divergere negativamente.
Cioè, si deve dimostrare che, considerata la successione
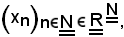
se
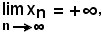
non può essere
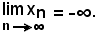
Supponendo per assurdo che la successione diverga negativamente, per definizione si ha:
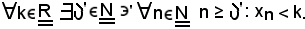
Siccome per ipotesi la successione diverge positivamente, per definizione si ha:
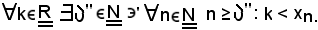
Si indichi ora
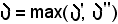
e si fissi
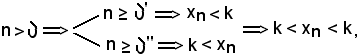
e ciò è assurdo, quindi la successione non diverge negativamente, come volevasi dimostrare.
si danno le seguenti definizioni:
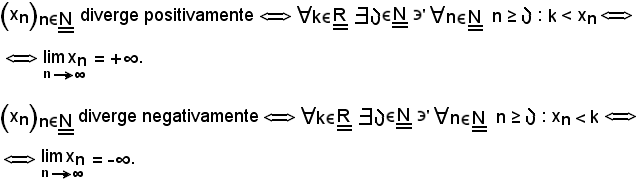
Nota bene
Per ogni successione di numeri reali si può verificare una sola delle seguenti circostanze:
1)-converge,
2)-diverge positivamente,
3)-diverge negativamente,
4)-nè converge, nè diverge positivamente, nè diverge negativamente.
Esempio di successione divergente positivamente
Siano assegnati
e la successione
che ad ogni n associa an.
Si dimostra che:
Infatti, per definizione, si deve dimostrare che:
Se
Se
k > 0,
invece di dimostrare che
k < an,
si può dimostrare che
logak < logaan = n.
Allo scopo, si considera
ed essendo
come volevasi dimostrare.
Esempio di successione divergente negativamente
Siano assegnati
e la successione
che ad ogni n associa loga(n + 2).
Si dimostra che:
Successione oscillante
Una successione si dice oscillante se non è convergente, nè divergente positivamente e nè divergente negativamente.
Esempio di successione oscillante
Si consideri la successione
Si dimostra che tale successione è oscillante, cioè:
1)-non diverge positivamente.
infatti, se divergesse positivamente, si avrebbe:
Essendo
se si prende K = 2, la relazione suddetta non è soddisfatta, quindi la successione non diverge positivamente.
2)-non diverge negativamente.
La dimostrazione è analoga alla precedente.
2)-non converge.
Infatti, se convergesse, si avrebbe:
in cui
Si presentano due casi:
1) l = 0, pertanto, si ha:
e ciò non è vero, quindi in tal caso la successione non converge al limite zero.
2) l ≠ 0, pertanto, si ha:
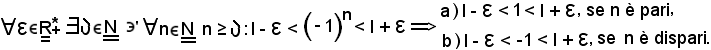
Si moltiplica ciascuno dei membri della a) per -1, ottenendo:
c) - l - ε < -1 < - l + ε.
Dalla b) e dalla c) si ottengono:
d) -2l < 2ε
e) -2ε < -2l
La d) e la e) esprimono che
max(l, -l) < ε.
Ma, essendo l ≠ 0, anche il
max(l, -l) ≠ 0.
Si è quindi pervenuti ad un assurdo, nato dall'aver supposto che la successione fosse convergente, dunque, non lo è, come volevasi dimostrare.
Successione regolare
Una successione si dice regolare se è convergente, o divergente positivamente, oppure divergente negativamente.
Teorema 1 - Se una successione converge ad un limite finito l, essa non può divergere ad un limite infinito positivamente.
Cioè, si deve dimostrare che, considerata la successione
se
non può essere
Infatti, siccome per ipotesi la successione converge ad l, per definizione si ha:
Ragionando per assurdo, si suppone che la successione diverga positivamente, cioè
Pertanto, considerando
Si indichi ora
e si fissi
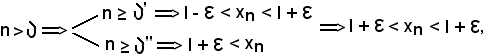
e ciò è assurdo, quindi la successione non diverge positivamente, come volevasi dimostrare.
Teorema 2 - Se una successione converge ad un limite finito l, essa non può divergere ad un limite infinito negativamente.
Cioè, si deve dimostrare che, considerata la successione
se
non può essere
La dimostrazione di questo teorema è analoga a quella del teorema 1.
Teorema 3 - Se una successione diverge positivamente, essa non può convergere ad un limite finito l.
Cioè, si deve dimostrare che, considerata la successione
se
non può essere
La dimostrazione di questo teorema è analoga a quella del teorema 1.
Teorema 4 - Se una successione diverge positivamente, essa non può divergere negativamente.
Cioè, si deve dimostrare che, considerata la successione
se
non può essere
Supponendo per assurdo che la successione diverga negativamente, per definizione si ha:
Siccome per ipotesi la successione diverge positivamente, per definizione si ha:
Si indichi ora
e si fissi
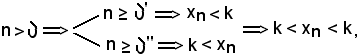
e ciò è assurdo, quindi la successione non diverge negativamente, come volevasi dimostrare.