SUCCESSIONI MONOTONE ---> INDICE
Si
consideri la successione di numeri reali
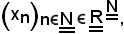
cioè l'applicazione
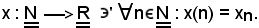
Poichè gl'insiemi dei numeri interi naturali e dei reali sono insiemi ordinati, una successione è un'applicazione fra due insiemi ordinati, pertanto si danno le seguenti definizioni:
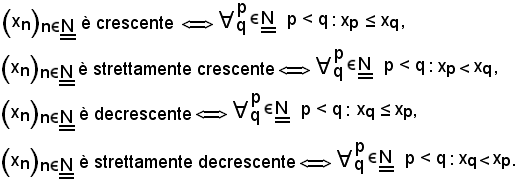
Se la successione rispecchia uno dei quattro casi suddetti, si chiama monotòna.
Si consideri ora la successione di numeri reali
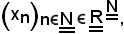
si dimostra che le seguenti due proposizioni sono equivalenti:

Dimostrazione
a) b)
b)
Si consideri
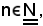
poichè
n < n + 1,
è anche
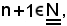
quindi, per definizione di successione strettamente crescente, si ha:
xn < xn+1.
Dimostrazione
b) a)
a)
Si consideri
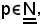
si dimostra prima che
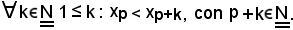
Si riconosce che tale proposizione è vera per il principio di induzione completa su k, cioè se è vera per p + k, è anche vera per p + k + 1.
Supponendo k = 1, si dimostra che
xp < xp+1,
e cio è vero per la b).
Siccome
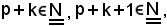
per la b) segue:
xp+k < xp+k+1.
Essendo inoltre
xp < xp+k,
risulta
xp < xp+k+1.
Si considera ora

In tali condizioni, essendo
xp < xp+k,
risulta anche
xp < xp+k = xq,
quindi
xp < xq.
Resta pertanto dimostrato che la successione è strettamente crescente.
Analogamente, si dimostra che le seguenti due proposizioni sono equivalenti:

Teorema - Ogni successione di numeri reali che sia monotòna, è regolare ed è convergente se è limitata.
Si consideri la successione di numeri reali
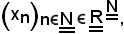
e sia essa monòtona, cioè crescente, pertanto si ha:
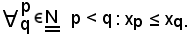
Si dimostra che:
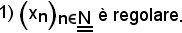
Allo scopo, basta dimostrare che
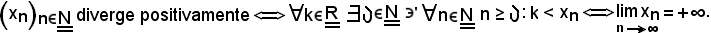
Siccome tale successione è limitata inferiormente, è noto che
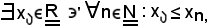
ed essendo non limitata superiormente, è anche noto che
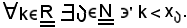
Quindi, fissato
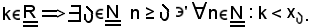
Si osserva ora che
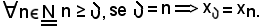
Inoltre, tenendo conto che la successione è crescente,
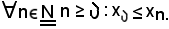
Quindi, in ogni caso, si ha:
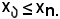
Dunque, essendo
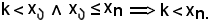
Quest'ultima condizione esprime che la successione diverge positivamente, quindi essa è regolare.
2) Si dimostra infine che, considerando la successione limitata, essa converge.
Allo scopo, supponendo che essa sia limitata superiormente, si può considerare l'estremo superiore, indicato con

e dimostrare che essa converge e che il suo limite è s, cioè:
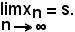
Infatti, dire che s è l'estremo superiore della successione, significa:
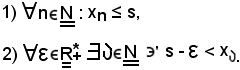
Si fissi ad arbitrio
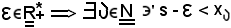
ed
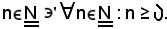
Per definizione di successione crescente, essendo
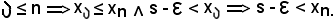
Inoltre, dalla 1), essendo ogni
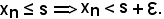
Pertanto, risulta
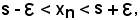
e questa è la condizione per cui
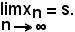
Quindi, se una successione crescente è limitata superiormente, essa converge ed il suo limite è l'estremo superiore.
Si dimostra anche che, se una successione decrescente è limitata inferiormente, essa converge ed il suo limite è l'estremo inferiore.
Nota bene
In generale, ogni successione limitata non è convergente, ma se le successioni sono monòtone esse convergono.
cioè l'applicazione
Poichè gl'insiemi dei numeri interi naturali e dei reali sono insiemi ordinati, una successione è un'applicazione fra due insiemi ordinati, pertanto si danno le seguenti definizioni:
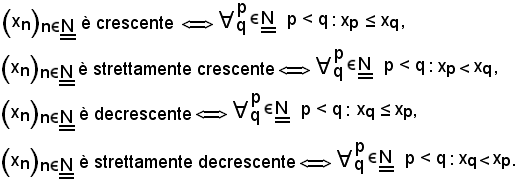
Se la successione rispecchia uno dei quattro casi suddetti, si chiama monotòna.
Si consideri ora la successione di numeri reali
si dimostra che le seguenti due proposizioni sono equivalenti:

Dimostrazione
a)
Si consideri
poichè
n < n + 1,
è anche
quindi, per definizione di successione strettamente crescente, si ha:
xn < xn+1.
Dimostrazione
b)
Si consideri
si dimostra prima che
Si riconosce che tale proposizione è vera per il principio di induzione completa su k, cioè se è vera per p + k, è anche vera per p + k + 1.
Supponendo k = 1, si dimostra che
xp < xp+1,
e cio è vero per la b).
Siccome
per la b) segue:
xp+k < xp+k+1.
Essendo inoltre
xp < xp+k,
risulta
xp < xp+k+1.
Si considera ora
In tali condizioni, essendo
xp < xp+k,
risulta anche
xp < xp+k = xq,
quindi
xp < xq.
Resta pertanto dimostrato che la successione è strettamente crescente.
Analogamente, si dimostra che le seguenti due proposizioni sono equivalenti:

Teorema - Ogni successione di numeri reali che sia monotòna, è regolare ed è convergente se è limitata.
Si consideri la successione di numeri reali
e sia essa monòtona, cioè crescente, pertanto si ha:
Si dimostra che:
Allo scopo, basta dimostrare che
Siccome tale successione è limitata inferiormente, è noto che
ed essendo non limitata superiormente, è anche noto che
Quindi, fissato
Si osserva ora che
Inoltre, tenendo conto che la successione è crescente,
Quindi, in ogni caso, si ha:
Dunque, essendo
Quest'ultima condizione esprime che la successione diverge positivamente, quindi essa è regolare.
2) Si dimostra infine che, considerando la successione limitata, essa converge.
Allo scopo, supponendo che essa sia limitata superiormente, si può considerare l'estremo superiore, indicato con
e dimostrare che essa converge e che il suo limite è s, cioè:
Infatti, dire che s è l'estremo superiore della successione, significa:
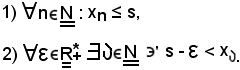
Si fissi ad arbitrio
ed
Per definizione di successione crescente, essendo
Inoltre, dalla 1), essendo ogni
Pertanto, risulta
e questa è la condizione per cui
Quindi, se una successione crescente è limitata superiormente, essa converge ed il suo limite è l'estremo superiore.
Si dimostra anche che, se una successione decrescente è limitata inferiormente, essa converge ed il suo limite è l'estremo inferiore.
Nota bene
In generale, ogni successione limitata non è convergente, ma se le successioni sono monòtone esse convergono.