SUCCESSIONI PRODOTTO ---> INDICE
Si considerino le seguenti due successioni
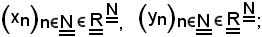
ad esse se ne associa una terza così definita:
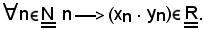
In tal modo è stata costruita la successione
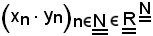
chiamata successione prodotto delle due assegnate.
Si dimostrano i seguenti teoremi:
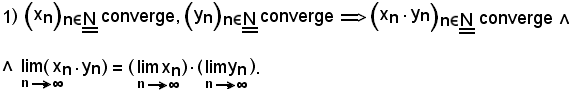
Dimostrazione 1).
Sia
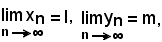
per il teorema visto sulle successioni i cui elementi sono stati considerati in valore assoluto e, tenendo conto delle ipotesi, si ha:
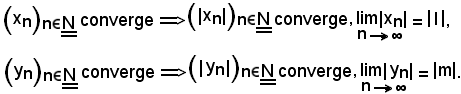
Inoltre, siccome è noto che ogni successione convergente è limitata, essendo
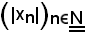
limitata superiormente,
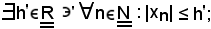
analogamente, essendo
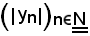
limitata superiormente,
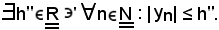
Si considera
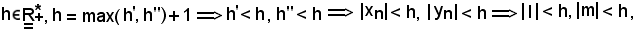
quest'ultime relazioni si hanno per il teorema del confronto.
Si osserva ora che:
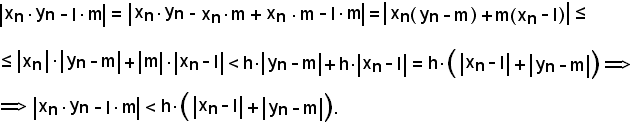
Siccome per ipotesi le due successioni sono convergenti, considerato
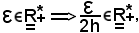
in sua corrispondenza, rispettivamente, si ha:
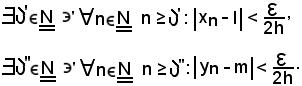
Indicato con
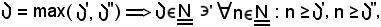
quindi, si verificano le due condizioni trovate, pertanto risulta
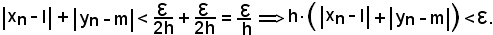
Dunque, avendo trovato che
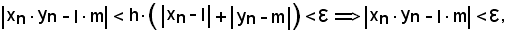
e questa è la condizione per cui
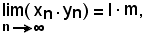
come volevasi dimostrare.

Dimostrazione 2).
Per ipotesi,
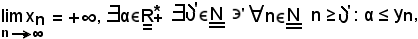
si deve dimostrare che
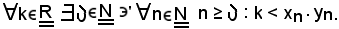
Infatti, si considera ad arbitrio
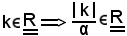
e, siccome la successione
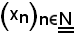
diverge positivamente, in corrispondenza di
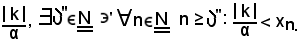
Indicato con
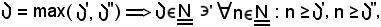
quindi, si verificano le seguenti condizioni:
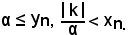
Moltiplicando membro a membro le due disequazioni, si ha:
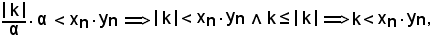
come volevasi dimostrare.
Dimostrazione 2').
Per ipotesi,
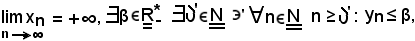
si deve dimostrare che
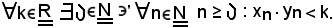
Infatti, si considera ad arbitrio
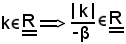
e, siccome la successione
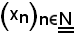
diverge positivamente, in corrispondenza di
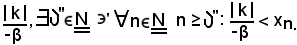
Indicato con
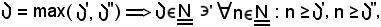
quindi, si verificano le seguenti condizioni:
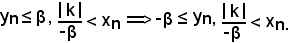
Moltiplicando membro a membro le due disequazioni, si ha:
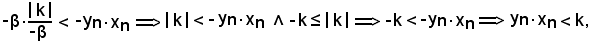
come volevasi dimostrare.

Dimostrazione 3).
E' analoga alla 2).
Dimostrazione 3').
E' analoga alla 2').

Dimostrazione 4).
Tenendo conto delle ipotesi e della 2), la dimostrazione è banale:

Dimostrazione 4').
Tenendo conto delle ipotesi e della 3'), la dimostrazione è banale:


Dimostrazione 5).
Tenendo conto delle ipotesi e della 2'), la dimostrazione è banale:

Si dimostrano i seguenti teoremi.

Dimostrazione 1).
Per la dimostrazione, ci si mette nelle ipotesi del teorema 2) trattato in precedenza, che si riporta di seguito:

Per ipotesi, la successione
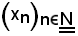
diverge positivamente, se si dimostra che
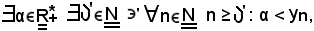
per il teorema suddetto,
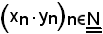
diverge positivamente.
Infatti, si considera
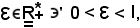
ed essendo per ipotesi
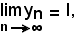
ad esse se ne associa una terza così definita:
In tal modo è stata costruita la successione
chiamata successione prodotto delle due assegnate.
Si dimostrano i seguenti teoremi:
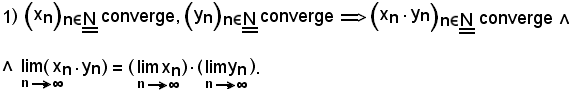
Dimostrazione 1).
Sia
per il teorema visto sulle successioni i cui elementi sono stati considerati in valore assoluto e, tenendo conto delle ipotesi, si ha:
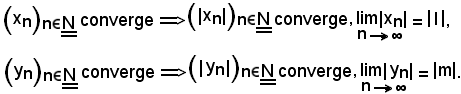
Inoltre, siccome è noto che ogni successione convergente è limitata, essendo
limitata superiormente,
analogamente, essendo
limitata superiormente,
Si considera
quest'ultime relazioni si hanno per il teorema del confronto.
Si osserva ora che:
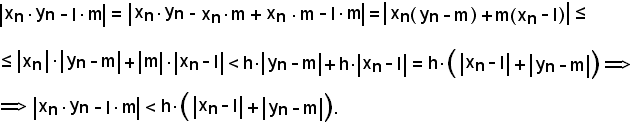
Siccome per ipotesi le due successioni sono convergenti, considerato
in sua corrispondenza, rispettivamente, si ha:
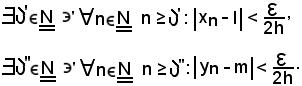
Indicato con
quindi, si verificano le due condizioni trovate, pertanto risulta
Dunque, avendo trovato che
e questa è la condizione per cui
come volevasi dimostrare.

Dimostrazione 2).
Per ipotesi,
si deve dimostrare che
Infatti, si considera ad arbitrio
e, siccome la successione
diverge positivamente, in corrispondenza di
Indicato con
quindi, si verificano le seguenti condizioni:
Moltiplicando membro a membro le due disequazioni, si ha:
come volevasi dimostrare.
Dimostrazione 2').
Per ipotesi,
si deve dimostrare che
Infatti, si considera ad arbitrio
e, siccome la successione
diverge positivamente, in corrispondenza di
Indicato con
quindi, si verificano le seguenti condizioni:
Moltiplicando membro a membro le due disequazioni, si ha:
come volevasi dimostrare.

Dimostrazione 3).
E' analoga alla 2).
Dimostrazione 3').
E' analoga alla 2').

Dimostrazione 4).
Tenendo conto delle ipotesi e della 2), la dimostrazione è banale:

Dimostrazione 4').
Tenendo conto delle ipotesi e della 3'), la dimostrazione è banale:


Dimostrazione 5).
Tenendo conto delle ipotesi e della 2'), la dimostrazione è banale:

Si dimostrano i seguenti teoremi.

Dimostrazione 1).
Per la dimostrazione, ci si mette nelle ipotesi del teorema 2) trattato in precedenza, che si riporta di seguito:

Per ipotesi, la successione
diverge positivamente, se si dimostra che
per il teorema suddetto,
diverge positivamente.
Infatti, si considera
ed essendo per ipotesi
in sua corrispondenza
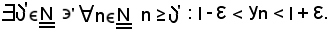
Si assume ora
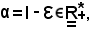
quindi
α < yn,
come volevasi dimostrare.

Dimostrazione 2).
Per la dimostrazione, ci si mette nelle ipotesi del teorema 2') trattato in precedenza, che si riporta di seguito:

Per ipotesi, la successione
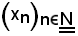
diverge positivamente, se si dimostra che
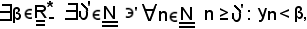
per il teorema suddetto,
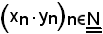 diverge negativamente.
diverge negativamente.
Infatti, si considera
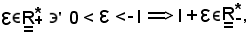
ed essendo per ipotesi
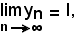
in sua corrispondenza
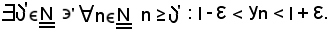
Si assume ora
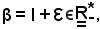
quindi
yn< β,
come volevasi dimostrare.

Dimostrazione 3).
Si ottiene dalla 3) precedentemente dimostrata.

Dimostrazione 4).Si ottiene dalla 3') precedentemente dimostrata.
Nota bene
Considerate due successioni, se una delle due diverge, e l'altra converge al limite zero, nulla si può dire sulla successione prodotto.
Siano
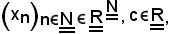
si dimostra:
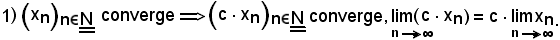
Dimostrazione 1).
Considerando c come la successione di valore costante c, cioè
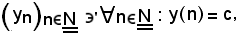
logicamente
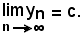
Applicando il seguente teorema
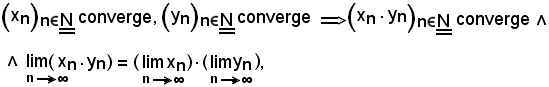
dimostrato in precedenza, è vero quanto asserito.
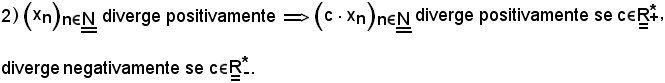
Dimostrazione 2).
Dimostrazione 3).
Si assume ora
quindi
α < yn,
come volevasi dimostrare.

Dimostrazione 2).
Per la dimostrazione, ci si mette nelle ipotesi del teorema 2') trattato in precedenza, che si riporta di seguito:

Per ipotesi, la successione
diverge positivamente, se si dimostra che
per il teorema suddetto,
Infatti, si considera
ed essendo per ipotesi
in sua corrispondenza
Si assume ora
quindi
yn< β,
come volevasi dimostrare.

Dimostrazione 3).
Si ottiene dalla 3) precedentemente dimostrata.

Dimostrazione 4).
Nota bene
Considerate due successioni, se una delle due diverge, e l'altra converge al limite zero, nulla si può dire sulla successione prodotto.
Siano
si dimostra:
Dimostrazione 1).
Considerando c come la successione di valore costante c, cioè
logicamente
Applicando il seguente teorema
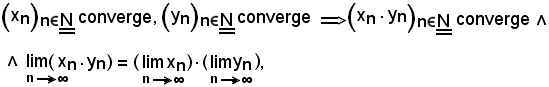
dimostrato in precedenza, è vero quanto asserito.
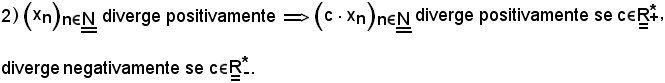
Dimostrazione 2).
Per la dimostrazione, si fa riferimento a due teoremi trattati in precedenza, che si riportano di seguito, ponendo rispettivamente in essi c = l:

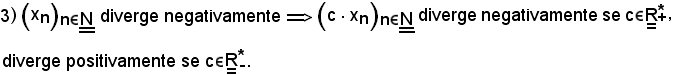

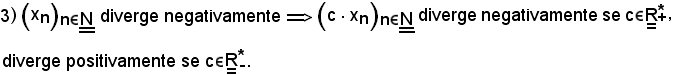
Dimostrazione 3).
Per la dimostrazione, si fa riferimento a due teoremi trattati in precedenza, che si riportano di seguito, ponendo rispettivamente in essi c = l:

Siano assegnati
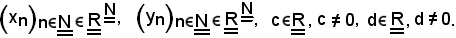
A partire da queste due successioni, si costruisce la successione seguente:
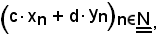
chiamata combinazione lineare mediante c e d delle successioni date.
Nota bene
Quando si hanno informazioni sulle successioni date, si è in grado di stabilire la natura della successione somma.

Siano assegnati
A partire da queste due successioni, si costruisce la successione seguente:
chiamata combinazione lineare mediante c e d delle successioni date.
Nota bene
Quando si hanno informazioni sulle successioni date, si è in grado di stabilire la natura della successione somma.