TEOREMA DI CAUCHY ---> INDICE
Sia assegnata la successione
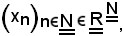
si dimostra che le seguenti due proposizioni sono equivalenti:
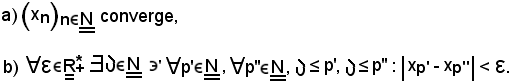
Dimostrazione
a)
b)
Per ipotesi, la successione converge, e sia
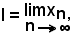
pertanto, considerato
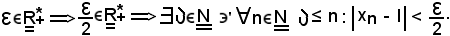
Si considerino ora arbitrariamente
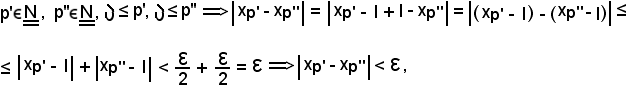
come volevasi dimostrare.
Si chiama successione di Cauchy, ogni successione che verifica la condizione della proposizione b).
Dimostrazione
b) a)
Supposta vera la condizione di Cauchy, si deve dimostrare che la successione in questione è convergente.
Allo scopo, si dimostra che essa è limitata, cioè che l'insieme
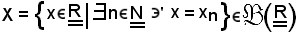
dei suoi elementi è limitato.
Per dimostrare ciò, occorre far vedere che esistono almeno un minorante ed un maggiorante dell'insieme X; si procede come segue: si considera
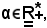
per l'ipotesi della b),
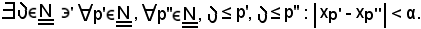
Considerato
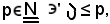
e, tenendo conto che fra i numeri interi naturali maggiori o uguali a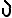
c'è lo stesso 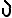, quindi
≤ ,
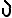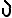si ha:
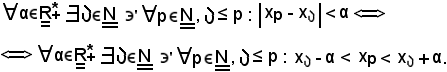
Ora si indica con
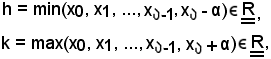
e si dimostra che
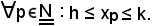
Infatti, considerato
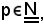
si presentano due casi:
1°) p ≤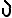 - 1, 2°) 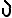≤ p.
Nel 1°) caso xp è uno degli elementi dell'insieme
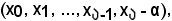
e quindi risulta
h ≤ xp.
Nel 2°) caso si ha:
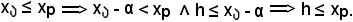
Ragionando allo stesso modo per k, si ha:
xp ≤ k,
quindi
h ≤ xp ≤ k,
e ciò esprime che X è limitato, come volevasi dimostrare, cioè che la successione
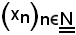
è limitata; si dimostra ora che essa converge.
Allo scopo, si ponga:
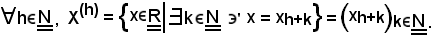
Si riconosce quanto segue:
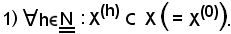
Dimostrazione 1).
Si consideri
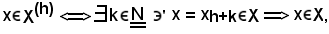
per definizione di relazione d'inclusione, la 1) è vera.
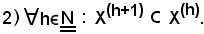
Dimostrazione 2).
Si consideri
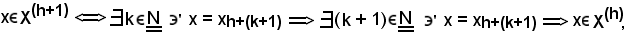
per definizione di relazione d'inclusione, la 2) è vera.
Si osserva che la 1) esprime che l'insieme X(h) è limitato inferiormente e superiormente, quindi si possono considerare:
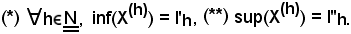
E' noto che:
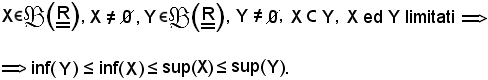
Dalla 1) e da tale osservazione, indicando
inf(X(0)) = l'0, sup(X(0)) = l''0,
si ricava:
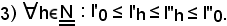
Dalla 2) si ricava:
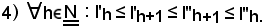
Si considera ora la successione
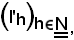
che per la 4) risulta monotòna crescente e limitata superiormente.
Poichè ogni successione monotòna è convergente se è limitata, e poichè il suo limite è l'estremo superiore della successione, si ha:
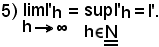
Lo stesso dicasi per la successione
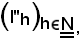
per la quale risulta:
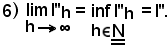
Essendo la successione monotòna decrescente e limitata inferiormente, il suo limite è l'estremo inferiore. Si noti immediatamente che
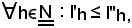
e per il teorema del confronto, si ha:
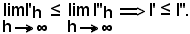
Resta da dimostrare che l' = l'', e che la successione
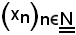
converge verso questo limite.
Si consideri
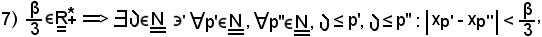
e ciò per l'ipotesi della proposizione b).
A tal punto, si esamina l'elemento
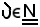
l'insieme così definito:
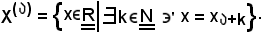
Ora, considerato l'elemento
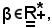
si dimostra che le seguenti due proposizioni sono equivalenti:
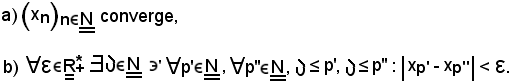
Dimostrazione
a)
b)Per ipotesi, la successione converge, e sia
pertanto, considerato
Si considerino ora arbitrariamente
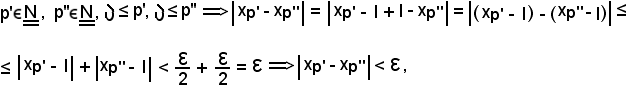
come volevasi dimostrare.
Si chiama successione di Cauchy, ogni successione che verifica la condizione della proposizione b).
Dimostrazione
b)
a)Supposta vera la condizione di Cauchy, si deve dimostrare che la successione in questione è convergente.
Allo scopo, si dimostra che essa è limitata, cioè che l'insieme
dei suoi elementi è limitato.
Per dimostrare ciò, occorre far vedere che esistono almeno un minorante ed un maggiorante dell'insieme X; si procede come segue: si considera
per l'ipotesi della b),
Considerato
e, tenendo conto che fra i numeri interi naturali maggiori o uguali a
c'è lo stesso , quindi ≤ ,si ha:
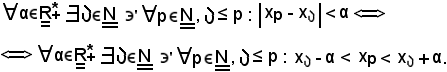
Ora si indica con
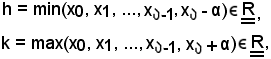
e si dimostra che
Infatti, considerato
si presentano due casi:
1°) p ≤
- 1, 2°) ≤ p.Nel 1°) caso xp è uno degli elementi dell'insieme
e quindi risulta
h ≤ xp.
Nel 2°) caso si ha:
Ragionando allo stesso modo per k, si ha:
xp ≤ k,
quindi
h ≤ xp ≤ k,
e ciò esprime che X è limitato, come volevasi dimostrare, cioè che la successione
è limitata; si dimostra ora che essa converge.
Allo scopo, si ponga:
Si riconosce quanto segue:
Dimostrazione 1).
Si consideri
per definizione di relazione d'inclusione, la 1) è vera.
Dimostrazione 2).
Si consideri
per definizione di relazione d'inclusione, la 2) è vera.
Si osserva che la 1) esprime che l'insieme X(h) è limitato inferiormente e superiormente, quindi si possono considerare:
E' noto che:
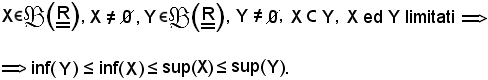
Dalla 1) e da tale osservazione, indicando
inf(X(0)) = l'0, sup(X(0)) = l''0,
si ricava:
Dalla 2) si ricava:
Si considera ora la successione
che per la 4) risulta monotòna crescente e limitata superiormente.
Poichè ogni successione monotòna è convergente se è limitata, e poichè il suo limite è l'estremo superiore della successione, si ha:
Lo stesso dicasi per la successione
per la quale risulta:
Essendo la successione monotòna decrescente e limitata inferiormente, il suo limite è l'estremo inferiore. Si noti immediatamente che
e per il teorema del confronto, si ha:
Resta da dimostrare che l' = l'', e che la successione
converge verso questo limite.
Si consideri
e ciò per l'ipotesi della proposizione b).
A tal punto, si esamina l'elemento
l'insieme così definito:
Ora, considerato l'elemento
in sua corrispondenza, per la condizione (*) e per la seconda caratterizzazione dell'estremo inferiore di una successione,
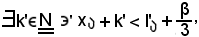
inoltre, per la condizione (**) e per la seconda caratterizzazione dell'estremo superiore di una successione,
'
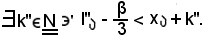Da quest'ultime due relazioni e per la 5) e la 6), si ha:
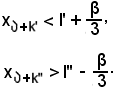
Si molltiplicano ora per -1 entrambi i membri della prima disequazione, lasciando la seconda invariata, e si ottiene:
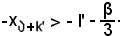
Ricordando che in precedenza si è trovato
l' ≤ l'' l'' - l' ≥ 0,
sommando membro a membro le due disequazioni, si ha:
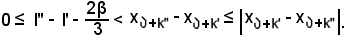
Inoltre,
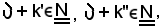
e quindi per la 7), essendo
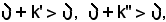
poichè
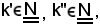si ha:
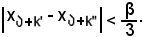
A tal punto, la situazione è la seguente:
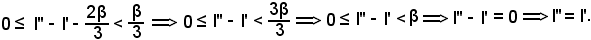
Infine, indicato con l tale limite, si dimostra che la successione
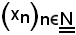
converge verso questo limite.
Essendo ovviamente
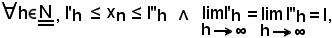
per il criterio di regolarità delle successioni convergenti, anche
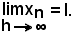
Nota bene
Le successioni di Cauchy sono tutte, e soltanto, le successioni convergenti.
Sia assegnata la successione convergente
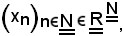si dimostra che:
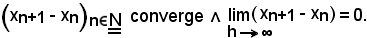
Infatti, se
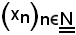
è convergente, essa soddisfa la condizione di Cauchy e quindi, fissato un elemento
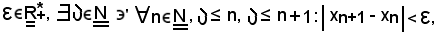
e questa non è altro che la condizione di convergenza a zero della successione
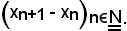
inoltre, per la condizione (**) e per la seconda caratterizzazione dell'estremo superiore di una successione,
Da quest'ultime due relazioni e per la 5) e la 6), si ha:
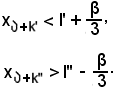
Si molltiplicano ora per -1 entrambi i membri della prima disequazione, lasciando la seconda invariata, e si ottiene:
Ricordando che in precedenza si è trovato
l' ≤ l''
l'' - l' ≥ 0,sommando membro a membro le due disequazioni, si ha:
Inoltre,
e quindi per la 7), essendo
poichè
A tal punto, la situazione è la seguente:
Infine, indicato con l tale limite, si dimostra che la successione
converge verso questo limite.
Essendo ovviamente
per il criterio di regolarità delle successioni convergenti, anche
Nota bene
Le successioni di Cauchy sono tutte, e soltanto, le successioni convergenti.
Sia assegnata la successione convergente
Infatti, se
è convergente, essa soddisfa la condizione di Cauchy e quindi, fissato un elemento
e questa non è altro che la condizione di convergenza a zero della successione