TEOREMI DELLE FUNZIONI ---> INDICE
Siano
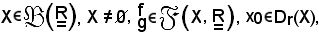
si dimostra il seguente teorema suddiviso in quattro parti.
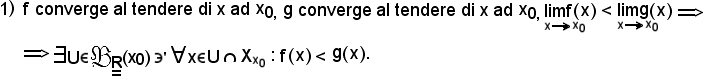
Dimostrazione 1).
Supposto
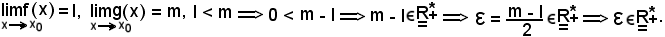
Quindi, fissato
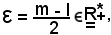
data la convergenza di f e g, rispettivamente ad l ed m al tendere di x ad x0, in sua corrispondenza si ha:
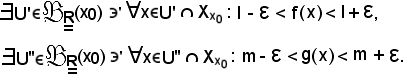
Si indica ora
U = U' U'',
U'',
poichè U' ed U'' sono intorni di x0, anche U è intorno di x0, cioè
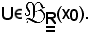
Si osserva inoltre che:
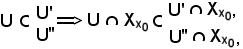
quindi per questo particolare
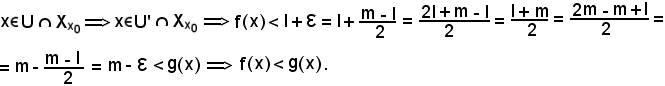
Pertanto,
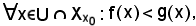
come volevasi dimostrare.
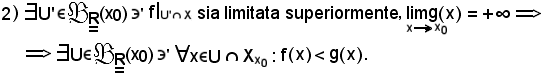
Dimostrazione 2).
Dire che la restrizione di f ad U' X è limitata in U'
X è limitata in U' X, significa che è limitato l'insieme dei valori dell'applicazione, cioè l'insieme f(U'
X, significa che è limitato l'insieme dei valori dell'applicazione, cioè l'insieme f(U' X) è
limitato superiormente, quindi esiste almeno un maggiorante, di tale
insieme, indicato con k. Siccome gli elementi di tale insieme sono
tutti i reali, che sono valori di f in qualche elemento di U'
X) è
limitato superiormente, quindi esiste almeno un maggiorante, di tale
insieme, indicato con k. Siccome gli elementi di tale insieme sono
tutti i reali, che sono valori di f in qualche elemento di U' X, si ha:
X, si ha:
 x
x U'
U'  X : f(x) ≤ k.
X : f(x) ≤ k.
Poichè la funzione g diverge positivamente, in corrispondenza di tale k
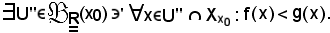
Si indica ora
U = U' U'',
U'',
poichè U' ed U'' sono intorni di x0, anche U è intorno di x0, cioè
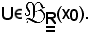
Si osserva inoltre che:
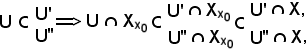
quindi per questo particolare
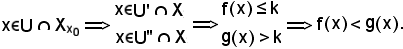
Pertanto,
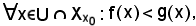
come volevasi dimostrare.
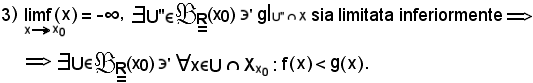
Dimostrazione 3).
E' analoga alla dimostrazione 2).

Dimostrazione 4).
E' ovvia.
Corollario
Nelle stesse ipotesi precedenti, si dimostra che:
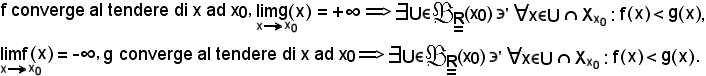
Le dimostrazioni derivano da 2) e da 3).
Teorema della permanenza del segno
Siano
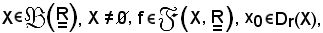
si dimostra che:

Dimostrazione 1).
Si considerino
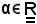
e l'applicazione gα di costante valore α così definita:
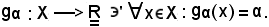
Si dimostra che:
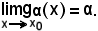
Infatti, fissato
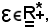
in sua corrispondenza
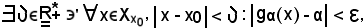
e ciò è sempre verificato, poichè
gα(x) - α = 0.
Ora, se al posto di α si mette la funzione gα, applicando il teorema 1) precedente, si dimostra quanto asserito, cioè:
α < f(x).
Dimostrazione 2).
E' analoga alla 1).
Tale teorema si chiama della permanenza del segno, perchè sussiste anche nel caso in cui
α = 0,
ed in tal caso si esprime come segue:

Ciò esprime che se il limite è positivo, la funzione assume sempre valori positivi, mentre se il limite è negativo, la funzione assume sempre valori negativi.
Nota bene
Si dimostra:
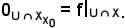
Corollario
Siano
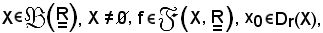
si dimostra che:
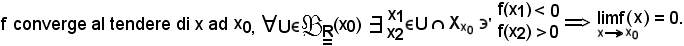
Dimostrazione.
Si supponga per assurdo che f non converga a zero, cioè che
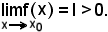
Per la 1),
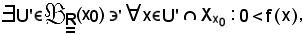
e ciò contraddice l'ipotesi, perchè deve esistere almeno un
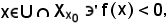
quindi f converge a zero, come volevasi dimostrare.
Nota bene
Si è visto che se
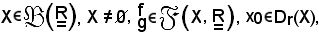
risulta:
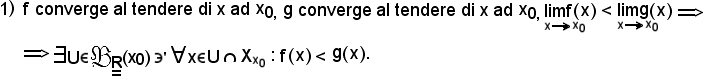
In generale il viceversa non si verifica, non solo, ma anche se si suppone che f e g convergano, non si verifica che
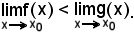
Comunque, aggiungendo ulteriori ipotesi, si dimostra il seguente teorema.
Teorema del confronto
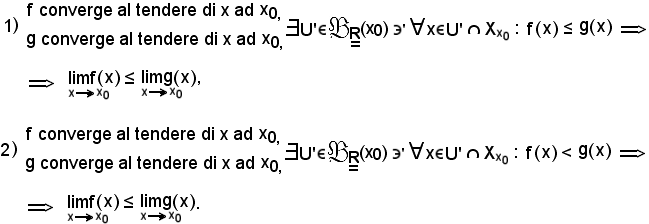
Dimostrazione 1).
Si ragiona per assurdo, quindi se non è
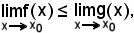
essendo ≤ una relazione di total ordine sui reali, necessariamente dev'essere
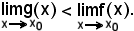
Ora, per il teorema 1) precedente, si può asserire che, date due funzioni f e g convergenti entrambe al tendere di x ad x0, ed il limite della prima è minore del limite della seconda,

Si indica ora
U = U' U'',
U'',
poichè U' ed U'' sono intorni di x0, anche U è intorno di x0, cioè
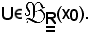
Si osserva inoltre che:
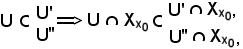
quindi, preso
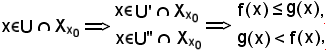
e ciò è assurdo, quindi deve risultare
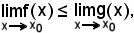
come volevasi dimostrare.
Nota bene
Nei ragionamenti fatti finora, si arriva sempre al punto in cui si considera un elemento
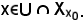
Ciò è possibile, in quanto certamente
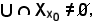
perchè essendo U intorno di x0, in esso va a finire almeno un elemento di X che non sia x0.
Dimostrazione 2).
E' conseguenza immediata della 1).
A tal punto, si fornisce un esempio in cui, pur essendo
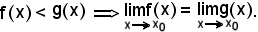
Si procede come segue: si considerino le applicazioni
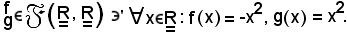
Si prende come punto di accumulazione lo
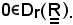
Innanzitutto esiste un intorno dello zero in tutti i punti in cui f(x) < g(x), ad esempio
U' = ]-1, 1[.
Ora si ha che
 x
x U'0 : -1 < x < 0, 0 < x < 1, f(x) < g(x).
U'0 : -1 < x < 0, 0 < x < 1, f(x) < g(x).
In tali condizioni, si riconosce che
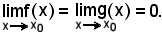
Criterio di regolarità delle funzioni convergenti
Siano
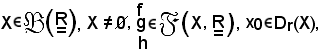
si dimostra che:
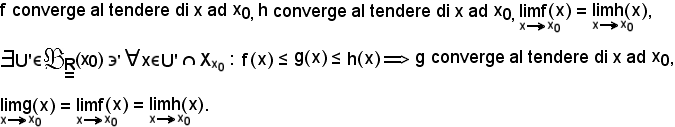
Dimostrazione.
Poichè f ed h convergono allo stesso limite, si pone
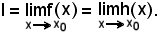
Fissato
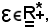
in sua corrispondenza, data la convergenza rispettivamente di f e di h,
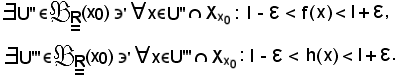
Inoltre, per ipotesi è noto che
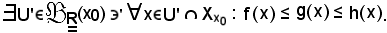
Si indica ora
U = U' U''
U''  U''',
U''',
poichè U', U'' ed U''' sono intorni di x0, anche U è intorno di x0, cioè
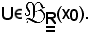
Si osserva inoltre che:
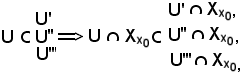
quindi, preso
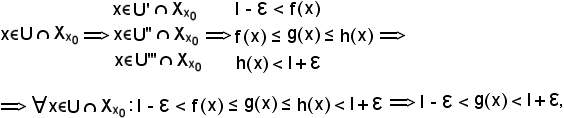
e questa è la condizione per cui
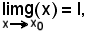
come volevasi dimostrare.
Corollario
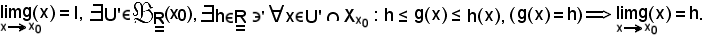
Dimostrazione.
Il teorema si riporta al precedente, considerando h il limite delle due funzioni f e g, costanti di costante valore h.
Nota bene
Si osserva che il limite di una funzione costante è già noto, ma in quel caso la funzione era costante in tutto l'insieme X, mentre nel caso specifico la funzione è costante solo per gli elementi dell'insieme
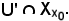
Criterio di regolarità delle funzioni divergenti
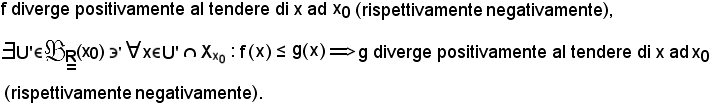
Dimostrazione.
Siccome per ipotesi f diverge positivamente al tendere di x ad x0, fissato
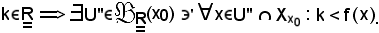
Inoltre, per ipotesi, è noto che
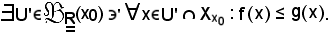
Si indica ora
U = U' U'',
U'',
poichè U' ed U'' sono intorni di x0, anche U è intorno di x0, cioè
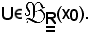
Si osserva inoltre che:
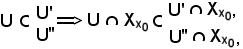
quindi, preso
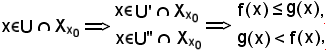
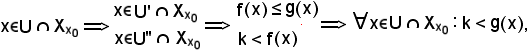
e questa è la condizione per cui
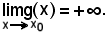
Analogamente, si dimostra che
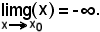
si dimostra il seguente teorema suddiviso in quattro parti.
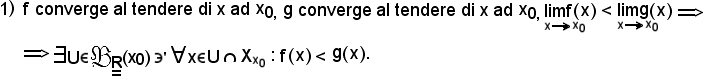
Dimostrazione 1).
Supposto
Quindi, fissato
data la convergenza di f e g, rispettivamente ad l ed m al tendere di x ad x0, in sua corrispondenza si ha:
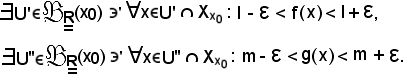
Si indica ora
U = U'
poichè U' ed U'' sono intorni di x0, anche U è intorno di x0, cioè
Si osserva inoltre che:
quindi per questo particolare
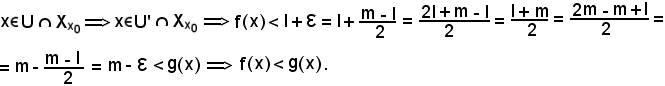
Pertanto,
come volevasi dimostrare.
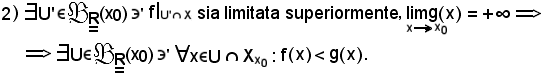
Dimostrazione 2).
Dire che la restrizione di f ad U'
Poichè la funzione g diverge positivamente, in corrispondenza di tale k
Si indica ora
U = U'
poichè U' ed U'' sono intorni di x0, anche U è intorno di x0, cioè
Si osserva inoltre che:
quindi per questo particolare
Pertanto,
come volevasi dimostrare.
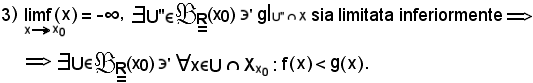
Dimostrazione 3).
E' analoga alla dimostrazione 2).
Dimostrazione 4).
E' ovvia.
Corollario
Nelle stesse ipotesi precedenti, si dimostra che:
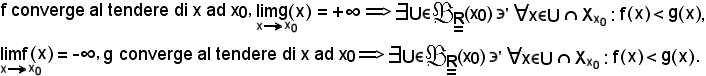
Le dimostrazioni derivano da 2) e da 3).
Teorema della permanenza del segno
Siano
si dimostra che:

Dimostrazione 1).
Si considerino
e l'applicazione gα di costante valore α così definita:
Si dimostra che:
Infatti, fissato
in sua corrispondenza
e ciò è sempre verificato, poichè
gα(x) - α = 0.
Ora, se al posto di α si mette la funzione gα, applicando il teorema 1) precedente, si dimostra quanto asserito, cioè:
α < f(x).
Dimostrazione 2).
E' analoga alla 1).
Tale teorema si chiama della permanenza del segno, perchè sussiste anche nel caso in cui
α = 0,
ed in tal caso si esprime come segue:

Ciò esprime che se il limite è positivo, la funzione assume sempre valori positivi, mentre se il limite è negativo, la funzione assume sempre valori negativi.
Nota bene
Si dimostra:
Corollario
Siano
si dimostra che:
Dimostrazione.
Si supponga per assurdo che f non converga a zero, cioè che
Per la 1),
e ciò contraddice l'ipotesi, perchè deve esistere almeno un
quindi f converge a zero, come volevasi dimostrare.
Nota bene
Si è visto che se
risulta:
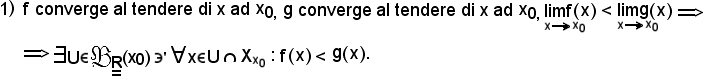
In generale il viceversa non si verifica, non solo, ma anche se si suppone che f e g convergano, non si verifica che
Comunque, aggiungendo ulteriori ipotesi, si dimostra il seguente teorema.
Teorema del confronto
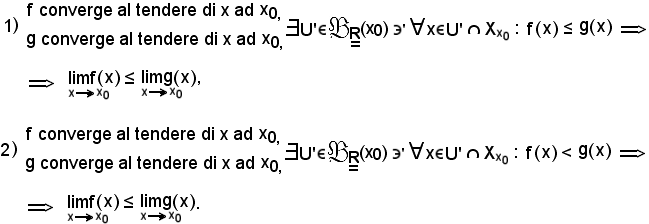
Dimostrazione 1).
Si ragiona per assurdo, quindi se non è
essendo ≤ una relazione di total ordine sui reali, necessariamente dev'essere
Ora, per il teorema 1) precedente, si può asserire che, date due funzioni f e g convergenti entrambe al tendere di x ad x0, ed il limite della prima è minore del limite della seconda,
Si indica ora
U = U'
poichè U' ed U'' sono intorni di x0, anche U è intorno di x0, cioè
Si osserva inoltre che:
quindi, preso
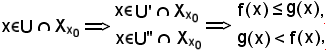
e ciò è assurdo, quindi deve risultare
come volevasi dimostrare.
Nota bene
Nei ragionamenti fatti finora, si arriva sempre al punto in cui si considera un elemento
Ciò è possibile, in quanto certamente
perchè essendo U intorno di x0, in esso va a finire almeno un elemento di X che non sia x0.
Dimostrazione 2).
E' conseguenza immediata della 1).
A tal punto, si fornisce un esempio in cui, pur essendo
Si procede come segue: si considerino le applicazioni
Si prende come punto di accumulazione lo
Innanzitutto esiste un intorno dello zero in tutti i punti in cui f(x) < g(x), ad esempio
U' = ]-1, 1[.
Ora si ha che
In tali condizioni, si riconosce che
Criterio di regolarità delle funzioni convergenti
Siano
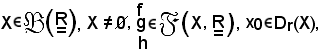
si dimostra che:
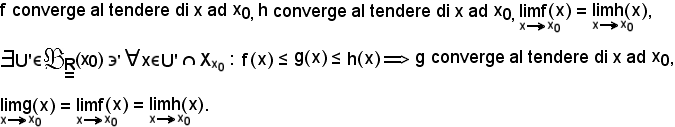
Dimostrazione.
Poichè f ed h convergono allo stesso limite, si pone
Fissato
in sua corrispondenza, data la convergenza rispettivamente di f e di h,
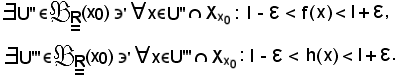
Inoltre, per ipotesi è noto che
Si indica ora
U = U'
poichè U', U'' ed U''' sono intorni di x0, anche U è intorno di x0, cioè
Si osserva inoltre che:
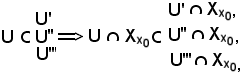
quindi, preso
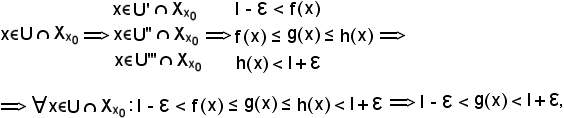
e questa è la condizione per cui
come volevasi dimostrare.
Corollario
Dimostrazione.
Il teorema si riporta al precedente, considerando h il limite delle due funzioni f e g, costanti di costante valore h.
Nota bene
Si osserva che il limite di una funzione costante è già noto, ma in quel caso la funzione era costante in tutto l'insieme X, mentre nel caso specifico la funzione è costante solo per gli elementi dell'insieme
Criterio di regolarità delle funzioni divergenti
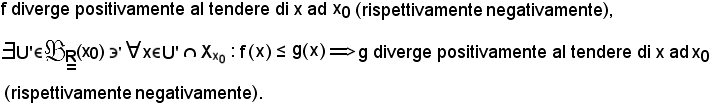
Dimostrazione.
Siccome per ipotesi f diverge positivamente al tendere di x ad x0, fissato
Inoltre, per ipotesi, è noto che
Si indica ora
U = U'
poichè U' ed U'' sono intorni di x0, anche U è intorno di x0, cioè
Si osserva inoltre che:
quindi, preso
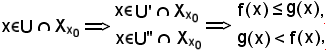
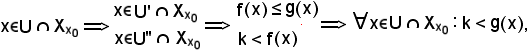
e questa è la condizione per cui
Analogamente, si dimostra che