AFFINITA' E TRASLAZIONI SULLA RETTA ---> INDICE
Sia
r la retta euclidea,  (O, U) un riferimento ed
(O, U) un riferimento ed

il sistema coordinato relativo al riferimento (O, U); si chiama affinità sulla retta euclidea r l'applicazione A di r in se stessa, cioè
(O, U); si chiama affinità sulla retta euclidea r l'applicazione A di r in se stessa, cioè
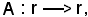
tale che esista una trasformazione lineare intera soddisfacente alla condizione
A = f-1Tf.
Si osserva che, se f associa ad ogni punto una determinata ascissa, f-1 è la bigezione dell'insieme R dei reali sulla retta r che associa ad ogni reale quei punti, inoltre A si può pensare composta dal prodotto suddetto, in cui T è una trasformazione lineare intera.
Se X è un punto generico della retta r, mediante f si può passare alla relativa ascissa x mediante la trasformazione lineare intera T, che opera nell'insieme dei reali, si può passare ad x', cioè da x ad x', e mediante f-1 si può passare ad un nuovo punto X'.
La trasformazione lineare intera è un'affinità ed il seguente diagramma è verificato:
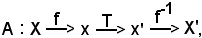
oppure, dire che A è data dal prodotto f-1Tf, equivale a dire che il seguente diagramma è commutativo.
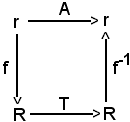
Un'affinità è una bigezione della retta in se stessa. E' una bigezione perchè è uguale al prodotto di tre bigezioni.
Valore dell'affinità al variare del sistema coordinato
Sia assegnato il riferimento (O, U) ed il suo sistema coordinato f, pertanto risulta:
(O, U) ed il suo sistema coordinato f, pertanto risulta:
A affinità 
 T
T  A = f-1Tf.
A = f-1Tf.
A tal punto si vuol vedere a cosa è uguale l'affinità A quando, al posto del sistema coordinato f, si considera un altro sistema coordinato f'.
Si indichi con la
trasformazione lineare intera che associa all'ascissa di ogni punto
della retta nel primo riferimento l'ascissa dello stesso punto nel
secondo riferimento. Pertanto, esiste
la
trasformazione lineare intera che associa all'ascissa di ogni punto
della retta nel primo riferimento l'ascissa dello stesso punto nel
secondo riferimento. Pertanto, esiste
f' = f.
f.
Moltiplicando ambo i membri per l'inverso di , si ha:
, si ha:
 -1f' =
-1f' =  -1(
-1( f) = (
f) = (
 -1)f = iRf = f,
-1)f = iRf = f,
essendo

 -1 = iR,
-1 = iR,
cioè l'applicazione identica di R.
Dalle uguaglianze suddette risulta quindi
f = -1f'.
-1f'.
Si consideri ora l'inversa
f-1 = ( -1f)-1 = f-1
-1f)-1 = f-1
e si sostituisca tale valore in
A = f-1Tf = (f-1 )T(
)T( -1f') = (f-1
-1f') = (f-1 T
T -1)f'
-1)f'
e, posto
 T
T -1 = T',
-1 = T',
si ha:
A = f-1T'f'.
Però, la trasformazione T associa ad ogni reale x il reale x' = αx + β, pertanto:
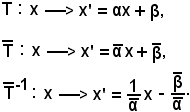
Ora, conoscendo T e , si vuol vedere il corrispondente di x in T'; esso risulta:
, si vuol vedere il corrispondente di x in T'; esso risulta:
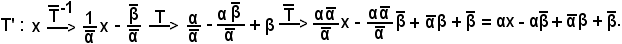
In definitiva, si è ottenuto
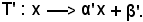
Si deve notare che:
1) il numero da moltiplicare ad x per ottenere il corrispondente nella f' è lo stesso α iniziale, cioè α = α',
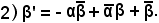
Costanza del rapporto semplice
Si considerino due punti qualsiasi distinti della retta r e le rispettive affinità:
 X1
X1 r,
r,  X2
X2 r, X1 ≠ X2 : A(X1) ≠ A(X2).
r, X1 ≠ X2 : A(X1) ≠ A(X2).
Si indichi ora con
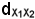
la distanza di X1 ed X2 rispetto al riferimento (O, U), e con
(O, U), e con
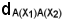
la distanza di A(X1) ed A(X2) rispetto al riferimento (O, U).
(O, U).
Si dimostra che il seguente rapporto è costante ed è uguale ad α:
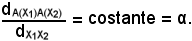
Si indichino con x1 ed x2 le ascisse di X1 ed X2, cioè
x1 = f(X1), x2 = f(X2), x1 ≠ x2,
e con x'1 ed x'2 le ascisse di A(X1) ed A(X2), cioè
x'1 = f(A(X1)), x'2 = f(A(X2)).
Si consideri ora l'uguaglianza
A = f-1Tf,
moltiplicando a sinistra ambo i membri, si ha:
fA = ff-1Tf = Tf,
e quindi
x'1 = f(A(X1)) = Tf(X1) = T(x1).
Si è trovato che
x'1 = T(x1)
è il corrispondente di x1 nella trasformazione lineare intera.
Analogamente, risulta:
x'2 = f(A(X2)) = Tf(X2) = T(x2),
e quindi
x'2 = T(x2).
Pertanto:
x'1 = T(x1) x'1 = αx1 + β,
x'1 = αx1 + β,
x'2 = T(x2) x'2 = αx2 + β,
x'2 = αx2 + β,
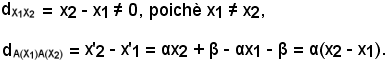
In conclusione:
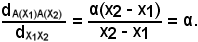
Si è dimostrato quindi che tale rapporto è costante al variare di x1 ed x2.
D'altronde, nel riferimento (O', U') si giunge allo stesso risultato, essendo α = α':
(O', U') si giunge allo stesso risultato, essendo α = α':
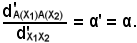
Si consideri una terna ordinata di punti di r, purchè gli ultimi due siano distinti, il rapporto semplice della terna ordinata di punti considerati è uguale al rapporto semplice dei punti trasformati dei precedenti mediante un'affinità.
Allo scopo, si consideri una terna ordinata di punti (X1 X2 X3), con la condizione che gli ultimi due siano distinti, cioè X2 ≠ X3. Mediante un'affinità, si suppone che i punti (X1 X2 X3) vengano trasformati in (X'1 X'2 X'3), cioè
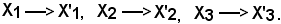
A questo punto, si deve calcolare in un certo riferimento il rapporto semplice, per vedere se i rapporti semplici sono uguali.
Essendo
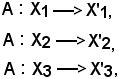
si considerino il rapporto semplice (X1 X2 X3), le ascisse nel riferimento (O, U) ed i valori di f che assumono in X1, X2, X3, cioè:
(O, U) ed i valori di f che assumono in X1, X2, X3, cioè:
f(X1) = x1, f(X2) = x2, f(X3) = x3.
Il rapporto semplice, come è noto, è dato da:
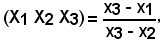
e, nei punti corrispondenti, è dato da
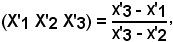
essendo
f(X'1) = x'1, f(X'2) = x'2, f(X'3) = x'3.
Si considerino i punti X ed il corrispondente X', e si indichino con x = f(X) ed x' = f(X') = f(A(X)),
f(A(X)) = f(f-1(T(f(X)))) = T(x) = x'.
Siccome
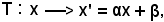
tenendo conto che
x'1 = αx1 + β, x'2 = αx2 + β, x'3 = αx3 + β,
si ha:
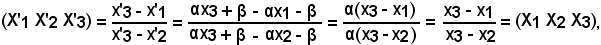
come volevasi dimostrare.
Tra le proprietà caratteristiche delle affinità si è visto che:
 X1
X1 r,
r,  X2
X2 r,
r,  X3
X3 r, X2 ≠ X3 : (X1 X2 X3) = (A(X1) A(X2) A(X3)).
r, X2 ≠ X3 : (X1 X2 X3) = (A(X1) A(X2) A(X3)).
Ogni affinità conserva i rapporti semplici, perchè il rapporto semplice dei tre punti è uguale a quello dei trasformati.
Si dimostra che se A è una bigezione di r in r, e se A conserva i rapporti semplici essa è un'affinità, cioè:

Si deve dimostrare che, fissati un riferimento (O, U) ed il sistema coordinato ad esso relativo
(O, U) ed il sistema coordinato ad esso relativo
 ,
,
esiste una trasformazione lineare intera tale che
A = f-1Tf.
Infatti, si fissino due punti distinti della retta r, cioè
X1 r, X2
r, X2 r, X1 ≠ X2,
r, X1 ≠ X2,
siccome per ipotesi A è una bigezione, si ha:
A(X1) ≠ A(X2),
Inoltre, A conserva i rapporti semplici, quindi
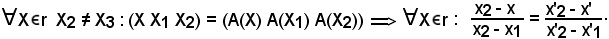
Quanto ora espresso è valido, in quanto
x = f(X) è l'ascissa del punto X,
x1 = f(X1) è l'ascissa del punto X1,
x2 = f(X2) è l'ascissa del punto X2,
inoltre, si indicano con
x' = f(A(X)) il punto trasformato di x,
x'1 = f(A(X1)) il punto trasformato di x1,
x'2 = f(A(X2)) il punto trasformato di x2.
Riducendo a forma intera l'uguaglianza suddetta, si ha:
(x2 - x)(x'2 - x'1) = (x'2 - x')(x2 - x1),
x2x'2 - x'1x2 - xx'2 + x'1x = x'2x2 - x1x'2 - x'x2 + x'x1,
x'x2 - x'x1 = x'2x - x'1x - x2x'2 + x2x'1 + x'2x2 - x'2x1,
x'(x2 - x1) = x(x'2 - x'1) - x2x'2 + x2x'1 + x'2x2 - x'2x1,
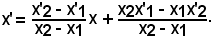
Questa è una trasformazione lineare intera, quindi
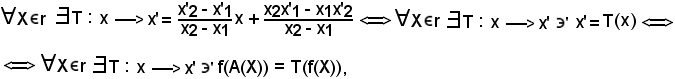
essendo
x = f(X).
Quindi, segue che esiste T trasformazione lineare intera, tale che
f(A) = Tf.
Moltiplicando ambo i membri per l'inverso di f, si ha:
f(A) = Tf
 T
T  (f-1f)A = f-1Tf
(f-1f)A = f-1Tf 
 T
T  A = f-1Tf.
A = f-1Tf.
In conclusione, è dimostrato che A è un'affinità.
Teorema di esistenza e di unicità delle affinità
Se X1 r, X2
r, X2 r, X1 ≠ X2, e se X'1
r, X1 ≠ X2, e se X'1 r, X'2
r, X'2 r, X'1 ≠ X'2, si dimostra che esiste una ed una sola affinità, tale che
r, X'1 ≠ X'2, si dimostra che esiste una ed una sola affinità, tale che
A(X1) = X'1, A(X2) = X'2,
cioè
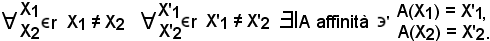
Prima di dimostrare tale teorema, si prova il seguente lemma:

Dimostrazione lemma.
Si supponga che esista una trasformazione lineare intera T che trasforma x1 ed x2 in x'1 ed x'2, definita da
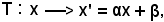
con
α R, β
R, β R, α ≠ 0.
R, α ≠ 0.
D'altronde, se T è una trasformazione lineare intera, essa soddisfa le seguenti condizioni:
T(x1) = x'1, T(x2) = x'2,
pertanto anche α e β devono soddisfare
x'1 = αx1 + β, x'2 = αx2 + β.
Risolvendo le due equazioni con il metodo di Cramer, si ha:
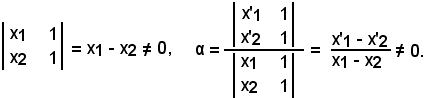
Si nota che il sistema ammette un'unica soluzione di α, e quest'ultima risulta anche diversa da zero.
D'altronde
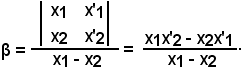
Quindi, sono definiti i valori di α e β, che soddisfano la trasformazione lineare intera, cioè:
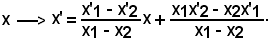
Questo sistema ammette quindi una ed una sola soluzione, pertanto il lemma è dimostrato.
Dimostrazione del teorema.
Si consideri un riferimento (O, U) sulla retta euclidea r, e sia
(O, U) sulla retta euclidea r, e sia

il sistema coordinato relativo.
D'altronde,
f(X1) = x1, f(X2) = x2,
f(X'1) = x'1, f(X'2) = x'2.
Si consideri a tal punto la trasformazione lineare intera T, tale che siano
T(x1) = x'1 e T(x2) = x'2,
cioè, per il lemma precedentemente dimostrato,
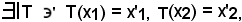
e quindi risultano
X1 ≠ X2 ed X'1 ≠ X'2.
Si consideri l'affinità costruita in tale modo:
A = f-1Tf,
si vede che A è un'affinità di r in sé, e con ciò si prova la sua esistenza e la sua unicità.
A = f-1Tf affinità A(X1) = X'1, A(X2) = X'2,
A(X1) = X'1, A(X2) = X'2,
cioè
A(X1) = f-1T(f(X1)),
essendo
f(X1) = x1,
A(X1) = f-1T(x1),
ed essendo
T(x1) = x'1,
A(X1) = f-1(x'1),
ma l'inverso di
f-1(x'1) = x'1,
A(X1) = x'1.
Parimenti,
A(X2) = f-1T(f(X2)),
essendo
f(X2) = x2,
A(X2) = f-1T(x2),
ed essendo
A(X2) = f-1(x'2),
ma l'inverso di
f-1(x'2) = x'2,
A(X2) = x'2.
Restano così dimostrate l'esistenza e l'unicità di A.
Nota bene
L'insieme delle affinità è l'insieme delle trasformazioni in sé ed il gruppo relativo è isomorfo al gruppo delle trasformazioni lineari intere.
Prodotto di due affinità
Siano A ed A' due affinità, (O, U) un riferimento fissato sulla retta r ed
(O, U) un riferimento fissato sulla retta r ed

il sistema coordinato ad esso relativo, allora esistono due trasformazioni lineari intere T e T', tali che
A = f-1Tf ed A' = f-1T'f,
cioè

Si consideri il prodotto di tali affinità:
A'A = (f-1T'f)(f-1Tf).
Applicando la proprietà associativa, si ha:
A'A = (f-1T')(ff-1)(Tf),
ma (ff-1) = iR, cioè è la trasformazione identica in (O, U), quindi
(O, U), quindi
A'A = (f-1T')iR(Tf).
Applicando nuovamente la proprietà associativa, si ha:
A'A = f-1(T'T)f.
Essendo T'T una trasformazione lineare intera, si conclude che AA' è un'affinità, come volevasi dimostrare.
Quindi, il prodotto di due affinità è un'affinità.
Inversa di un'affinità
φ(TT') = φ(T)φ(T').
Infatti,
φ(T) = f-1Tf,φ(T') = f-1T'f.
Componendo, si ha:
φ(T)φ(T') = (f-1Tf)(f-1T'f) = f-1(TT')f,
ma questa è l'affinità trasformata mediante f, cioè
f-1(TT')f = φ(TT'),
quindi
φ(T)φ(T') = φ(TT').
Per tale motivo, essendo φ una bigezione che conserva il prodotto operativo, si chiama isomorfismo del gruppo delle trasformazioni intere sul gruppo delle affinità. Esso dipende dal riferimento, perchè variando il riferimento varia anche la bigezione.
Si consideri ora un riferimento (O, U) della retta euclidea r e l'applicazione
(O, U) della retta euclidea r e l'applicazione
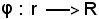
così definita:
 X1
X1 r,
r,  X2
X2 r, X1 ≠ X2,
r, X1 ≠ X2,  X
X r : φ(X) = φ(XX1X2).
r : φ(X) = φ(XX1X2).
Si vuole dimostrare che φ è una bigezione, cioè che viene associato un solo numero dato dal rapporto semplice.
Infatti, sia h R, per trovare che esiste X
R, per trovare che esiste X r tale che (XX1X2) = h, basta considerare un qualsiasi riferimento e le ascisse ad esso associate.
r tale che (XX1X2) = h, basta considerare un qualsiasi riferimento e le ascisse ad esso associate.
Si fissi quindi un riferimento, si consideri il suo sistema coordinato e si supponga che
f(X) = x,
f(X1) = x1,
f(X2) = x2,
cioè che x, x1, x2, siano rispettivamentele ascisse dei punti X. X1, X2.
Per provare che esiste un numero reale h, l'ascissa di x deve soddisfare la relazione
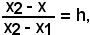
da cui
x2 - x = h(x2 - x1),
-x = h(x2 - x1) - x2,
x = h(x1 - x2) + x2.
Da ciò si deduce che esiste un solo punto X, e che φ è una bigezione.
Come ovvia osservazione si ha che, se X1 ed X2 sono due punti distinti, e se X ed X1 sono due punti di r, tali che
(X X1 X2) = (X' X'1 X'2),
si ha
X = X'.
Punto unito di un'affinità
Si consideri un riferimento (O, U) della retta euclidea r ed il sistema coordinato f; si dice che un punto X di r è unito nell'affinità A, se e solo se
(O, U) della retta euclidea r ed il sistema coordinato f; si dice che un punto X di r è unito nell'affinità A, se e solo se
A(X) = X.
Siccome è noto che
fA = Tf,
si ha che
X unito in A A(X) = X
A(X) = X  f(A(X)) = f(X)
f(A(X)) = f(X)  T(f(X)) = f(X).
T(f(X)) = f(X).
Indicando con x l'ascissa di X, cioè
x = f(X),
si ha:
T(x) = x x = αx + β
x = αx + β  -x + αx + β = 0
-x + αx + β = 0  (α - 1)x + β = 0,
(α - 1)x + β = 0,
con α ≠ 0.
Si distinguono due casi:
1°) α = 1 e β = 0.
Tutti i punti della retta sono uniti, cioè A è una bigezione identica sulla retta euclidea r, o meglio un'affinità identica.
2°) α = 1 e β ≠ 1.
In tal caso, non esiste nessun x tale che soddisfi la relazione, e non ci sono punti uniti.

In tal caso, si ha solo un punto unito, perciò si hanno particolari affinità.
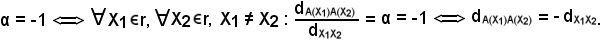
Tale uguaglianza vale anche se X1 ≠ X2.
D'altronde,
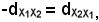
quindi
 X1
X1 r,
r,  X2
X2 r : A(X1)A(X2) = X2X1,
r : A(X1)A(X2) = X2X1,
ed il punto unito avrà ascissa
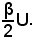
Allora,
 X
X r : A(X)A(U) = UX
r : A(X)A(U) = UX 
 X
X r : A(XU) = UX
r : A(XU) = UX 
 X
X r : U punto medio tra X ed A(X).
r : U punto medio tra X ed A(X).
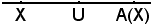
Le affinità che godono di questa proprietà si chiamano simmetriche rispetto al punto unito U.
In generale, un'affinità è diversa dall'inversa, però non nel caso delle simmetrie. Si ha quindi:
A = A-1.
Traslazione sulla retta euclidea
Si dice che A è una traslazione sulla retta euclidea se e solo se l'affinità A è tale che, per ogni punto X1 ed X2, X1 ≠ X2, il rapporto semplice delle distanze è uguale ad uno.
Quindi, per quanto è stato visto in precedenza, dev'essere α = 1, cioè
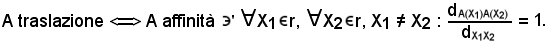
A tal punto, si deducono altre definizioni equivalenti:
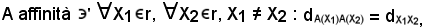
quest' ultima uguaglianza sussiste anche se X1 = X2.
A affinità
 X1
X1 r,
r,  X2
X2 r : A(X1)A(X2) = X1X2.
r : A(X1)A(X2) = X1X2.
Si può dire anche che una traslazione è un'affinità in cui i segmenti orientati corrispondenti sono uguali.
Ed ancora
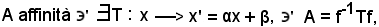
oppure
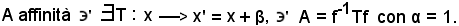
Una traslazione è un'affinità tale che esista T che trasformi x' in x + β e che risulti A = f-1Tf.
L'insieme delle traslazioni della retta euclidea è un gruppo.
Prodotto di due traslazioni
Il prodotto di due traslazioni è una traslazione, cioè
A, A' traslazioni AA' traslazione.
AA' traslazione.
Siano
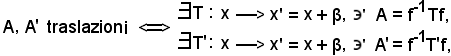
quindi
A'A = (f-1T'f)f-1Tf) = f-1(T'T)f = f-1 f,
f,
avendo indicato
 = T'T.
= T'T.
Siccome tale prodotto rappresenta una trasformazione lineare intera, si deve dimostrare che è dello stesso tipo di T e T'.
Infatti,
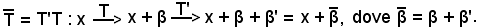
Inversa di una traslazione
Considerando α = 1, si ha:
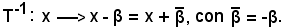
Quindi, si può asserire che l'inversa di una traslazione è una traslazione, e che l'insieme di esse è un gruppo.
Inoltre, l'insieme delle traslazioni è un sottoinsieme dell'insieme delle affinità, allora si dice che le traslazioni sono un sottogruppo del gruppo delle affinità.
Proprietà
1)-Date due affinità A ed A'
AA' ≠ A'A.
2)-Date due traslazioni A ed A'
AA' = A'A.
3)-Il prodotto di due traslazioni A ed A' è commutabile.
Infatti,
AA' = (f-1Tf)(f-1T'f) = f-1(TT')f = f-1 f,
f,
avendo indicato
 = TT'.
= TT'.
Siccome tale prodotto rappresenta una trasformazione lineare intera, si deve dimostrare che è dello stesso tipo di T e T'.
Infatti,
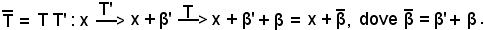
il sistema coordinato relativo al riferimento
tale che esista una trasformazione lineare intera soddisfacente alla condizione
A = f-1Tf.
Si osserva che, se f associa ad ogni punto una determinata ascissa, f-1 è la bigezione dell'insieme R dei reali sulla retta r che associa ad ogni reale quei punti, inoltre A si può pensare composta dal prodotto suddetto, in cui T è una trasformazione lineare intera.
Se X è un punto generico della retta r, mediante f si può passare alla relativa ascissa x mediante la trasformazione lineare intera T, che opera nell'insieme dei reali, si può passare ad x', cioè da x ad x', e mediante f-1 si può passare ad un nuovo punto X'.
La trasformazione lineare intera è un'affinità ed il seguente diagramma è verificato:
oppure, dire che A è data dal prodotto f-1Tf, equivale a dire che il seguente diagramma è commutativo.

Un'affinità è una bigezione della retta in se stessa. E' una bigezione perchè è uguale al prodotto di tre bigezioni.
Valore dell'affinità al variare del sistema coordinato
Sia assegnato il riferimento
A tal punto si vuol vedere a cosa è uguale l'affinità A quando, al posto del sistema coordinato f, si considera un altro sistema coordinato f'.
Si indichi con
f' =
Moltiplicando ambo i membri per l'inverso di
essendo
cioè l'applicazione identica di R.
Dalle uguaglianze suddette risulta quindi
f =
Si consideri ora l'inversa
f-1 = (
e si sostituisca tale valore in
A = f-1Tf = (f-1
e, posto
si ha:
A = f-1T'f'.
Però, la trasformazione T associa ad ogni reale x il reale x' = αx + β, pertanto:
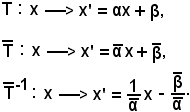
Ora, conoscendo T e
In definitiva, si è ottenuto
Si deve notare che:
1) il numero da moltiplicare ad x per ottenere il corrispondente nella f' è lo stesso α iniziale, cioè α = α',
Costanza del rapporto semplice
Si considerino due punti qualsiasi distinti della retta r e le rispettive affinità:
Si indichi ora con
la distanza di X1 ed X2 rispetto al riferimento
la distanza di A(X1) ed A(X2) rispetto al riferimento
Si dimostra che il seguente rapporto è costante ed è uguale ad α:
Si indichino con x1 ed x2 le ascisse di X1 ed X2, cioè
x1 = f(X1), x2 = f(X2), x1 ≠ x2,
e con x'1 ed x'2 le ascisse di A(X1) ed A(X2), cioè
x'1 = f(A(X1)), x'2 = f(A(X2)).
Si consideri ora l'uguaglianza
A = f-1Tf,
moltiplicando a sinistra ambo i membri, si ha:
fA = ff-1Tf = Tf,
e quindi
x'1 = f(A(X1)) = Tf(X1) = T(x1).
Si è trovato che
x'1 = T(x1)
è il corrispondente di x1 nella trasformazione lineare intera.
Analogamente, risulta:
x'2 = f(A(X2)) = Tf(X2) = T(x2),
e quindi
x'2 = T(x2).
Pertanto:
x'1 = T(x1)
x'2 = T(x2)
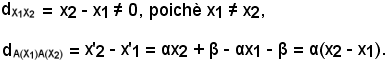
In conclusione:
Si è dimostrato quindi che tale rapporto è costante al variare di x1 ed x2.
D'altronde, nel riferimento
Si consideri una terna ordinata di punti di r, purchè gli ultimi due siano distinti, il rapporto semplice della terna ordinata di punti considerati è uguale al rapporto semplice dei punti trasformati dei precedenti mediante un'affinità.
Allo scopo, si consideri una terna ordinata di punti (X1 X2 X3), con la condizione che gli ultimi due siano distinti, cioè X2 ≠ X3. Mediante un'affinità, si suppone che i punti (X1 X2 X3) vengano trasformati in (X'1 X'2 X'3), cioè
A questo punto, si deve calcolare in un certo riferimento il rapporto semplice, per vedere se i rapporti semplici sono uguali.
Essendo
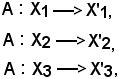
si considerino il rapporto semplice (X1 X2 X3), le ascisse nel riferimento
f(X1) = x1, f(X2) = x2, f(X3) = x3.
Il rapporto semplice, come è noto, è dato da:
e, nei punti corrispondenti, è dato da
essendo
f(X'1) = x'1, f(X'2) = x'2, f(X'3) = x'3.
Si considerino i punti X ed il corrispondente X', e si indichino con x = f(X) ed x' = f(X') = f(A(X)),
rispettivamente, le ascisse dei punti X ed X'; essendo
A = f-1Tf,
si ha:
A = f-1Tf,
si ha:
f(A(X)) = f(f-1(T(f(X)))) = T(x) = x'.
Siccome
tenendo conto che
x'1 = αx1 + β, x'2 = αx2 + β, x'3 = αx3 + β,
si ha:
come volevasi dimostrare.
Tra le proprietà caratteristiche delle affinità si è visto che:
Ogni affinità conserva i rapporti semplici, perchè il rapporto semplice dei tre punti è uguale a quello dei trasformati.
Si dimostra che se A è una bigezione di r in r, e se A conserva i rapporti semplici essa è un'affinità, cioè:
Si deve dimostrare che, fissati un riferimento
esiste una trasformazione lineare intera tale che
A = f-1Tf.
Infatti, si fissino due punti distinti della retta r, cioè
X1
siccome per ipotesi A è una bigezione, si ha:
A(X1) ≠ A(X2),
Inoltre, A conserva i rapporti semplici, quindi
Quanto ora espresso è valido, in quanto
x = f(X) è l'ascissa del punto X,
x1 = f(X1) è l'ascissa del punto X1,
x2 = f(X2) è l'ascissa del punto X2,
inoltre, si indicano con
x' = f(A(X)) il punto trasformato di x,
x'1 = f(A(X1)) il punto trasformato di x1,
x'2 = f(A(X2)) il punto trasformato di x2.
Riducendo a forma intera l'uguaglianza suddetta, si ha:
(x2 - x)(x'2 - x'1) = (x'2 - x')(x2 - x1),
x2x'2 - x'1x2 - xx'2 + x'1x = x'2x2 - x1x'2 - x'x2 + x'x1,
x'x2 - x'x1 = x'2x - x'1x - x2x'2 + x2x'1 + x'2x2 - x'2x1,
x'(x2 - x1) = x(x'2 - x'1) - x2x'2 + x2x'1 + x'2x2 - x'2x1,
Questa è una trasformazione lineare intera, quindi
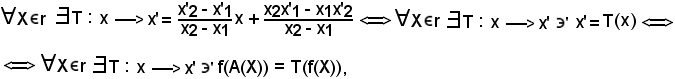
essendo
x = f(X).
Quindi, segue che esiste T trasformazione lineare intera, tale che
f(A) = Tf.
Moltiplicando ambo i membri per l'inverso di f, si ha:
f(A) = Tf
In conclusione, è dimostrato che A è un'affinità.
Teorema di esistenza e di unicità delle affinità
Se X1
A(X1) = X'1, A(X2) = X'2,
cioè
Prima di dimostrare tale teorema, si prova il seguente lemma:
Dimostrazione lemma.
Si supponga che esista una trasformazione lineare intera T che trasforma x1 ed x2 in x'1 ed x'2, definita da
con
α
D'altronde, se T è una trasformazione lineare intera, essa soddisfa le seguenti condizioni:
T(x1) = x'1, T(x2) = x'2,
pertanto anche α e β devono soddisfare
x'1 = αx1 + β, x'2 = αx2 + β.
Risolvendo le due equazioni con il metodo di Cramer, si ha:
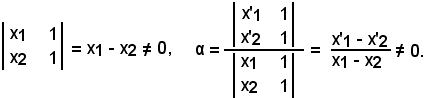
Si nota che il sistema ammette un'unica soluzione di α, e quest'ultima risulta anche diversa da zero.
D'altronde
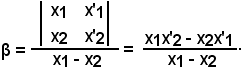
Quindi, sono definiti i valori di α e β, che soddisfano la trasformazione lineare intera, cioè:
Questo sistema ammette quindi una ed una sola soluzione, pertanto il lemma è dimostrato.
Dimostrazione del teorema.
Si consideri un riferimento
il sistema coordinato relativo.
D'altronde,
f(X1) = x1, f(X2) = x2,
f(X'1) = x'1, f(X'2) = x'2.
Si consideri a tal punto la trasformazione lineare intera T, tale che siano
T(x1) = x'1 e T(x2) = x'2,
cioè, per il lemma precedentemente dimostrato,
e quindi risultano
X1 ≠ X2 ed X'1 ≠ X'2.
Si consideri l'affinità costruita in tale modo:
A = f-1Tf,
si vede che A è un'affinità di r in sé, e con ciò si prova la sua esistenza e la sua unicità.
A = f-1Tf affinità
cioè
A(X1) = f-1T(f(X1)),
essendo
f(X1) = x1,
A(X1) = f-1T(x1),
ed essendo
T(x1) = x'1,
A(X1) = f-1(x'1),
ma l'inverso di
f-1(x'1) = x'1,
A(X1) = x'1.
Parimenti,
A(X2) = f-1T(f(X2)),
essendo
f(X2) = x2,
A(X2) = f-1T(x2),
ed essendo
T(x2) = x'2,
A(X2) = f-1(x'2),
ma l'inverso di
f-1(x'2) = x'2,
A(X2) = x'2.
Restano così dimostrate l'esistenza e l'unicità di A.
Nota bene
L'insieme delle affinità è l'insieme delle trasformazioni in sé ed il gruppo relativo è isomorfo al gruppo delle trasformazioni lineari intere.
Prodotto di due affinità
Siano A ed A' due affinità,
il sistema coordinato ad esso relativo, allora esistono due trasformazioni lineari intere T e T', tali che
A = f-1Tf ed A' = f-1T'f,
cioè

Si consideri il prodotto di tali affinità:
A'A = (f-1T'f)(f-1Tf).
Applicando la proprietà associativa, si ha:
A'A = (f-1T')(ff-1)(Tf),
ma (ff-1) = iR, cioè è la trasformazione identica in
A'A = (f-1T')iR(Tf).
Applicando nuovamente la proprietà associativa, si ha:
A'A = f-1(T'T)f.
Essendo T'T una trasformazione lineare intera, si conclude che AA' è un'affinità, come volevasi dimostrare.
Quindi, il prodotto di due affinità è un'affinità.
Inversa di un'affinità
Si consideri l'inverso di un prodotto di più trasformazioni:
A-1 = (f-1Tf)-1,
si ha
A = f-1T-1(f-1)-1,
ed essendo T-1 una trasformazione lineare intera, risulta che A è un'affinita.
Si consideri ora un riferimento (O, U) della retta euclidea r e l'applicazione φ del gruppo delle trasformazioni lineari intere sul gruppo delle affinità definite dalla seguente relazione:
(O, U) della retta euclidea r e l'applicazione φ del gruppo delle trasformazioni lineari intere sul gruppo delle affinità definite dalla seguente relazione:
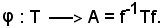
inoltre conserva il prodotto operativo.
Si prova che φ è ingettiva, cioè che
φ(T) = φ(T') T = T'.
T = T'.
Infatti,
f-1Tf = f-1T'f T = T'.
T = T'.
Con ciò resta provato che φ è ingettiva, ed essendo surgettiva, essa è bigettiva.
Si prova ora che tale bigezione φ conserva il prodotto operativo, cioè che
A-1 = (f-1Tf)-1,
si ha
A = f-1T-1(f-1)-1,
ed essendo T-1 una trasformazione lineare intera, risulta che A è un'affinita.
Quindi, l'inversa di un'affinità è un'affinità.
Si consideri ora un riferimento
Tale applicazione è una bigezione ed è tale che
 T,
T,  T' trasformazioni lineari intere : φ(TT') = φ(T)φ(T'),
T' trasformazioni lineari intere : φ(TT') = φ(T)φ(T'),
inoltre conserva il prodotto operativo.
Si prova che φ è ingettiva, cioè che
φ(T) = φ(T')
Infatti,
f-1Tf = f-1T'f
Con ciò resta provato che φ è ingettiva, ed essendo surgettiva, essa è bigettiva.
Si prova ora che tale bigezione φ conserva il prodotto operativo, cioè che
φ(TT') = φ(T)φ(T').
Infatti,
φ(T) = f-1Tf,φ(T') = f-1T'f.
Componendo, si ha:
φ(T)φ(T') = (f-1Tf)(f-1T'f) = f-1(TT')f,
ma questa è l'affinità trasformata mediante f, cioè
f-1(TT')f = φ(TT'),
quindi
φ(T)φ(T') = φ(TT').
Per tale motivo, essendo φ una bigezione che conserva il prodotto operativo, si chiama isomorfismo del gruppo delle trasformazioni intere sul gruppo delle affinità. Esso dipende dal riferimento, perchè variando il riferimento varia anche la bigezione.
Si consideri ora un riferimento
così definita:
Si vuole dimostrare che φ è una bigezione, cioè che viene associato un solo numero dato dal rapporto semplice.
Infatti, sia h
Si fissi quindi un riferimento, si consideri il suo sistema coordinato e si supponga che
f(X) = x,
f(X1) = x1,
f(X2) = x2,
cioè che x, x1, x2, siano rispettivamentele ascisse dei punti X. X1, X2.
Per provare che esiste un numero reale h, l'ascissa di x deve soddisfare la relazione
da cui
x2 - x = h(x2 - x1),
-x = h(x2 - x1) - x2,
x = h(x1 - x2) + x2.
Da ciò si deduce che esiste un solo punto X, e che φ è una bigezione.
Come ovvia osservazione si ha che, se X1 ed X2 sono due punti distinti, e se X ed X1 sono due punti di r, tali che
(X X1 X2) = (X' X'1 X'2),
si ha
X = X'.
Punto unito di un'affinità
Si consideri un riferimento
A(X) = X.
Siccome è noto che
fA = Tf,
si ha che
X unito in A
Indicando con x l'ascissa di X, cioè
x = f(X),
si ha:
T(x) = x
con α ≠ 0.
Si distinguono due casi:
1°) α = 1 e β = 0.
Tutti i punti della retta sono uniti, cioè A è una bigezione identica sulla retta euclidea r, o meglio un'affinità identica.
2°) α = 1 e β ≠ 1.
In tal caso, non esiste nessun x tale che soddisfi la relazione, e non ci sono punti uniti.
In tal caso, si ha solo un punto unito, perciò si hanno particolari affinità.
Tale uguaglianza vale anche se X1 ≠ X2.
D'altronde,
quindi
ed il punto unito avrà ascissa
Allora,
Quindi, il punto U è medio tra una coppia di punti corrispondenti.
Le affinità che godono di questa proprietà si chiamano simmetriche rispetto al punto unito U.
In generale, un'affinità è diversa dall'inversa, però non nel caso delle simmetrie. Si ha quindi:
A = A-1.
Traslazione sulla retta euclidea
Si dice che A è una traslazione sulla retta euclidea se e solo se l'affinità A è tale che, per ogni punto X1 ed X2, X1 ≠ X2, il rapporto semplice delle distanze è uguale ad uno.
Quindi, per quanto è stato visto in precedenza, dev'essere α = 1, cioè
A tal punto, si deducono altre definizioni equivalenti:
quest' ultima uguaglianza sussiste anche se X1 = X2.
A affinità
Si può dire anche che una traslazione è un'affinità in cui i segmenti orientati corrispondenti sono uguali.
Ed ancora
oppure
Una traslazione è un'affinità tale che esista T che trasformi x' in x + β e che risulti A = f-1Tf.
L'insieme delle traslazioni della retta euclidea è un gruppo.
Prodotto di due traslazioni
Il prodotto di due traslazioni è una traslazione, cioè
A, A' traslazioni
Siano
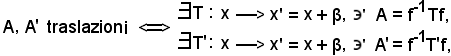
quindi
A'A = (f-1T'f)f-1Tf) = f-1(T'T)f = f-1
avendo indicato
Siccome tale prodotto rappresenta una trasformazione lineare intera, si deve dimostrare che è dello stesso tipo di T e T'.
Infatti,
Inversa di una traslazione
L'inversa di una traslazione è una traslazione, cioè
A traslazione A-1 traslazione.
A-1 traslazione.
Sia
A-1 = (f-1Tf)-1 = f-1T-1f;
per dimostrare che A-1 è una traslazione, si deve provare che T' è della stessa natura di T.
Si osserva ora che
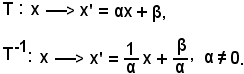
A traslazione
Sia
A-1 = (f-1Tf)-1 = f-1T-1f;
per dimostrare che A-1 è una traslazione, si deve provare che T' è della stessa natura di T.
Si osserva ora che
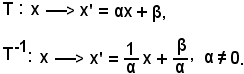
Considerando α = 1, si ha:
Quindi, si può asserire che l'inversa di una traslazione è una traslazione, e che l'insieme di esse è un gruppo.
Inoltre, l'insieme delle traslazioni è un sottoinsieme dell'insieme delle affinità, allora si dice che le traslazioni sono un sottogruppo del gruppo delle affinità.
Proprietà
1)-Date due affinità A ed A'
AA' ≠ A'A.
2)-Date due traslazioni A ed A'
AA' = A'A.
3)-Il prodotto di due traslazioni A ed A' è commutabile.
Infatti,
AA' = (f-1Tf)(f-1T'f) = f-1(TT')f = f-1
avendo indicato
Siccome tale prodotto rappresenta una trasformazione lineare intera, si deve dimostrare che è dello stesso tipo di T e T'.
Infatti,